WPROWADZENIE DO GEOMATYKI

Prof. dr hab. Jerzy B. Rogowski

B

L

B

L

B

n

e

sin

sin

cos

cos

cos

sin

sin

cos

cos

cos

g

g

n

g

g

e

n

n

cos

iloczyn skalarny!

g

e

n

n

arccos

Odchylenie pionu

– ważna wielkość

W geodezji wiąże pomiary geodezyjne wykonane instrumentami zorientowanymi zgodnie
z kierunkiem pionu z elementami które zostaną zredukowane na elipsoidę.

Dlaczego w geodezji używamy elipsoidy jako powierzchni aproksymującej
powierzchnię Ziemi?

Jest to wynikiem:

1. Tradycji

2. Łatwości odwzorowania elementów przedstawionych na jej powierzchni na
płaszczyznę (mapę)

3. Niewielkie zniekształcenie przy redukcji pomierzonych elementów z fizycznej
powierzchni Ziemi na elipsoidę.

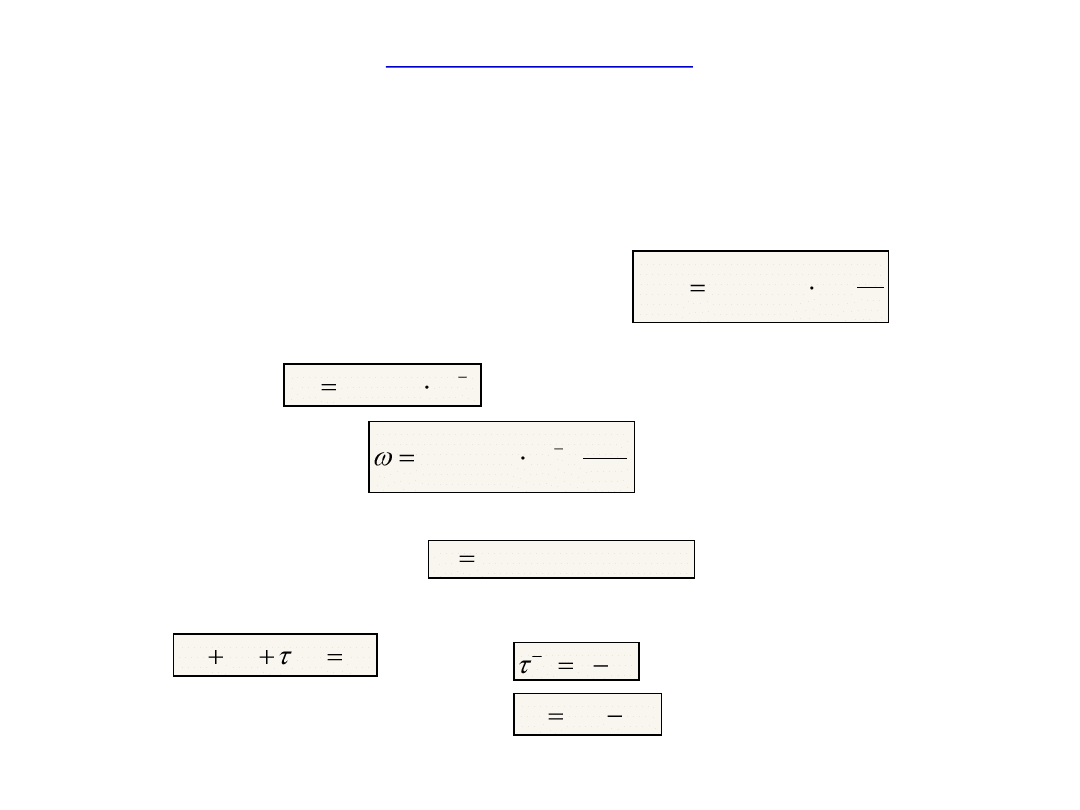
ELIPSOIDA ZIEMSKA

Obecnie obowiązuje Geodezyjny System Odniesienia 1980 (GRS’80 – Geodetic Reference
System 1980) przyjęty na XVII Zgromadzeni Generalnym Międzynarodowej Unii Geodezji i
Geofizyki (IUGG) w Canberze w grudniu 1997 roku.

Stosowana rezolucja zaleca aby:

2

8

10

3986005

s

m

GM

8

2

10

108263

J

• równikowy promień Ziemi: a = 6378137 m
• geocentryczna stała grawitacji Ziemi (z atmosferą)

• dynamiczny współczynnik kształtu Ziemi, wyłączając stałą deformacje pływową (o tym

będzie później):

• kątowa prędkość Ziemi:

Wynikają z niej pochodne stałe zarówno geometryczne jak i fizyczne. Jedną z tych
stałych jest spłaszczenie elipsoidy

8118

0033528106

,

0

f

Równanie geocentrycznej elipsoidy obrotowej w układzie współrzędnych prostokątnych
ma postać:

2

2

2

2

a

z

y

x

Gdzie:

2

1

1 e

2

2

2

f

f

e

- kwadrat mimośrodu

a – duża półoś

f – spłaszczenie elipsoidy

sek

rad

11

10

7297115

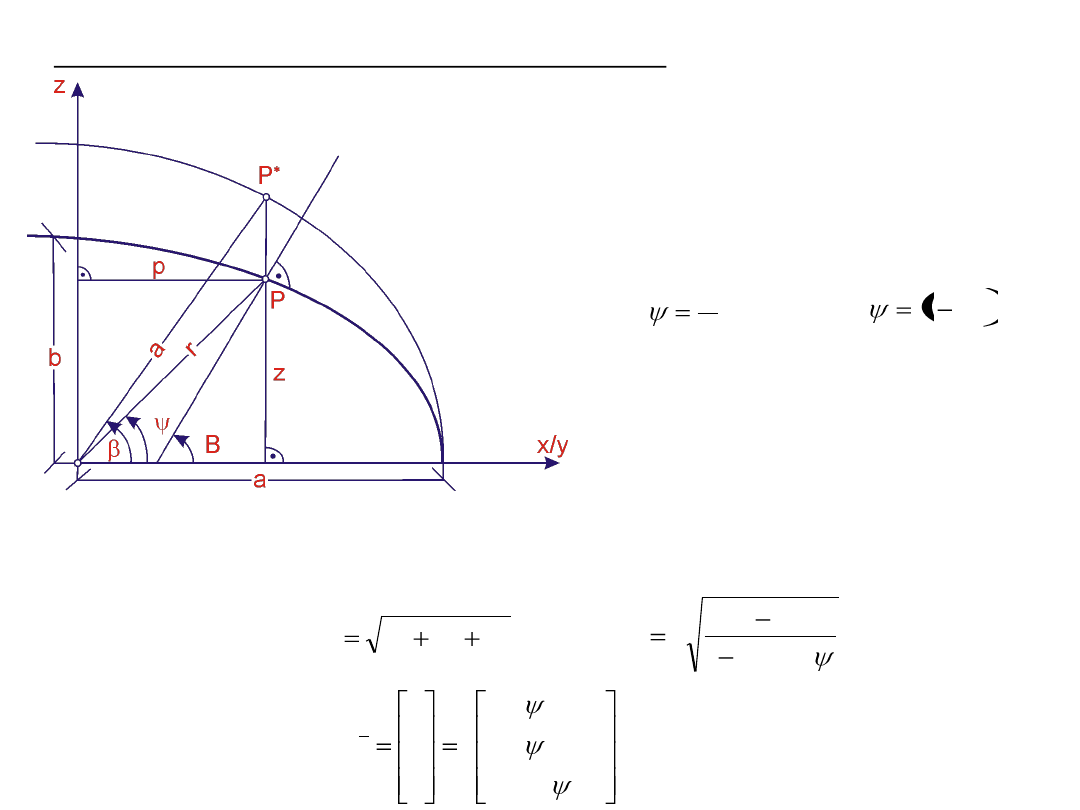
Szerokość geocentryczna i zredukowana

Szerokość geodezyjna, geocentryczna i zredukowana

p

z

tan

lub

B

e tan

1

tan

2

Szerokość geocentryczna pozwala na określenie współrzędnych prostokątnych
punktów leżących na powierzchni elipsoidy

sin

sin

sin

cos

cos

L

L

r

z

y

x

r

gdzie

2

2

2

z

y

x

r

lub

2

2

2

cos

1

1

e

e

a

r

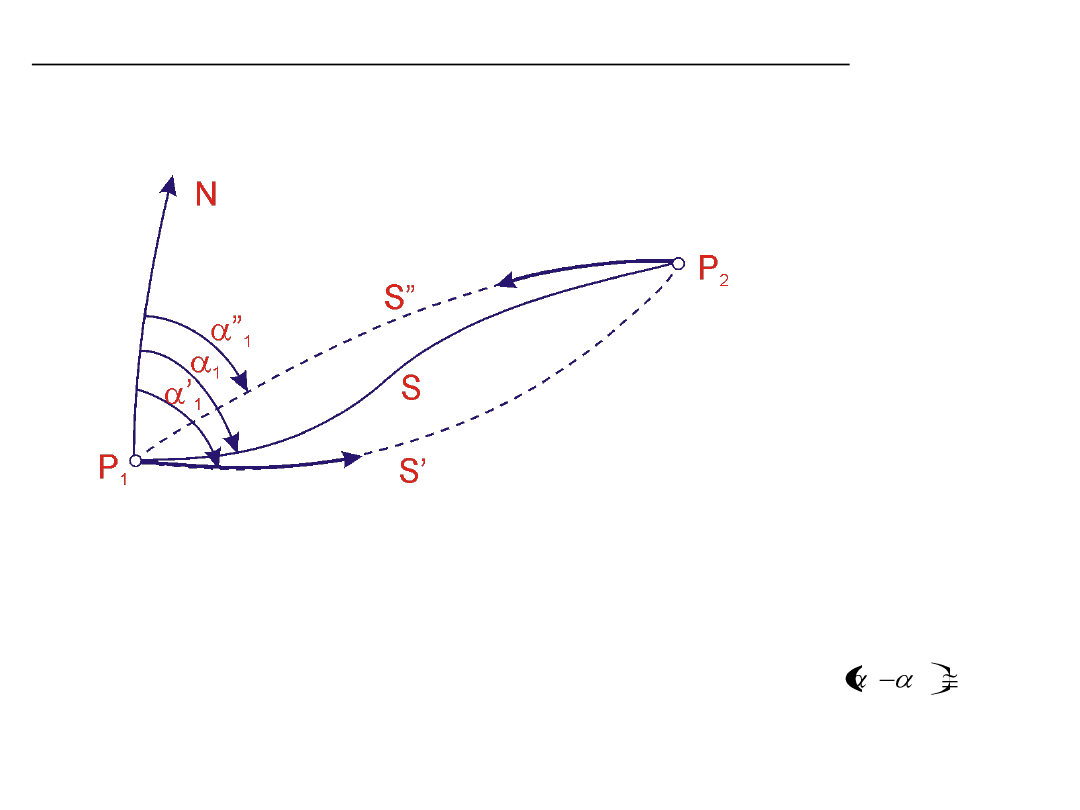
Linia geodezyjna na powierzchni elipsoidy obrotowej

Linia geodezyjna (geodetyka) – najkrótsza odległość pomiędzy dwoma
punktami na elipsoidzie

Wzajemne położenie linii geodezyjnej i przekrojów normalnych

Dla odległości S = 50km rozbieżność przekrojów normalnych

"

2

,

0

"

'

1

1

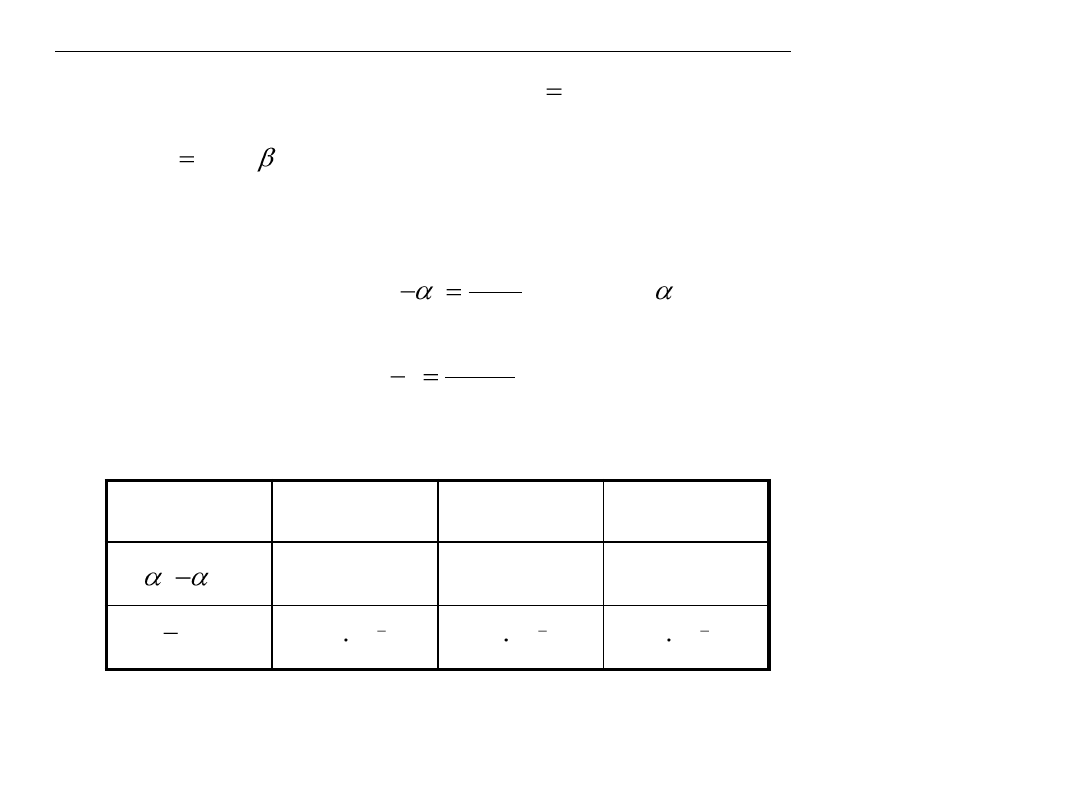
Równanie linii geodezyjnej (równanie Clairauta)

c

A

B

N

sin

cos

gdzie

A

a

c

sin

cos

Linię geodezyjną i przekroje normalne charakteryzują następujące wzory

1

1

2

2

2

2

1

1

2

sin

cos

12

'

B

a

s

e

a

B

a

s

e

s

s

4

4

5

4

cos

360

'

Na których podstawie można wyliczyć:

S=

100 km

200 km

0,028”

1

1

'

s

s

s

/

)

'

(

50 km

0,007”

0,112”

11

10

2

10

10

9

8

10

2

Pomiary grawimetryczne.

(przyśpieszenia siły ciężkości)

Jednostki: 1 cm· sek

-2

= 1 gal (gal)

10

-3

cm· sek

-2

= 1 mgal (miligal)

10

-6

cm· sek

-2

= 1 gal (mikrogal)

Średnia wartość przyspieszenia ziemskiego

g 981 gal

Rodzaje pomiarów grawimetrycznych

1. Bezwzględne

- wahadło fizyczne

- balistyczne

2. Względne

- wahadłowe

- grawimetr strunowy

- grawimetr statyczny