Autor :

Barbara Chorąży

Opiekun:

mgr Mirosław Trociuk

Bibliografia:

1. Mitchell Begelman, Martin Rees – „Ta siła fatalna. Czarne dziury we Wszechświecie”,

Prószyński i S-ka, W-wa 1999.

2. Quang Ho-Kim, Naddera Kumar, Chi-Sing Lam – „Zaproszenie do fizyki współczesnej”,

Stowarzyszenie Symetria i Własności Strukturalne, Poznań 1995.

3. John D. Barrow – „Teorie Wszystkiego”, Wydawnictwo ZNAK, Kraków 1995.
4. Marek Demiński, Marian Kozielski – „Fizyka dla szkół średnich. T. 4”, BZ Kozielski,

Warszawa 1998.

5. Itty Ferguson, - „Czarne dziury, czyli uwięzione światło”, Prószyński i S-ka, W-wa 1999.
6. Brian Green – „Piękno Wszechświata. Superstruny, ukryte wymiary i poszukiwania teorii

ostatecznej”, Prószyński i S-ka, W-wa 2001.

7. Honorata Korpikiewicz – „Koncepcja wzrostu entropii a rozwój świata”, Wydawnictwo

Naukowe UAM, Poznań 1998.

8. Igor Nowikow – „Czarne Dziury i Wszechświat”, Prószyński i S-ka, W-wa 1995.
9. Multimedialna Encyklopedia Powszechna – edycja 2001, Onet.pl S.A.
10. John Taylor – „Czarne dziury: koniec wszechświata?”, PIW, W-wa 1987.

WŁODAWA 2003

Czarne dziury i cząstki elementarne

Przed powstaniem teorii strun, wbrew intuicyjnemu przeświadczeniu, że

prawa natury powinny tworzyć jednolitą całość, istniała sprzeczność między

ogólną teoria względności a mechaniką kwantową. Pozornie trudno znaleźć

dwie rzeczy różniące się od siebie tak jak czarne dziury i cząstki elementarne.

Czarne dziury w naszej wyobraźni to największe ciała niebieskie, zaś cząstki

elementarne to najdrobniejsze struktury materii. Badania prowadzone na

przełomie lat sześćdziesiątych i siedemdziesiątych przez wielu wybitnych

fizyków wykazały, że istniejąca odmienność nie jest tak drastyczna.

Fakt, że z wyjątkiem niewielkiej liczby charakterystycznych właściwości

wszystkie czarne dziury są do siebie podobne, powinien przywoływać pewne

skojarzenia. Te właściwości to masa, ładunek elektryczny i inne ładunki sił oraz

moment pędu. John Wheeler ujął ten fakt w stwierdzeniu: „czarne dziury nie

mają włosów”, czyli brakuje im indywidualnych cech, dzięki którym dwie

czarne dziury posiadające te same w ymienione właściwości miałyby różną

postać. Dokładnie takie właściwości – masa, ładunki sił i spin – odróżniają

poszczególne cząstki elementarne.

Istnieje jednak pewien haczyk. Astrofizyczne czarne dziury o masach

wielokrotnie większych od masy Słońca są tak duże i masywne, że mechanika

kwantowa właściwie nie ma znaczenia do ich opisu. Aby zrozumieć ich cechy,

wystarczy posłużyć się ogólną teoria względności

1

. Stosując eksperyment

myślowy tworząc coraz mniejsze czarne dziury, dochodzimy do momentu, gdy

staje się one tak lekkie i małe, ze mechanika kwantowa może służyć do ich

opisu. Momentem tym jest osiągnięcie przez czarną dziurę masy Plancka lub

mniejszej. (Z punktu widzenia fizyki cząstek elementarnych masa Plancka jest

olbrzymia – ok. dziesięć miliardów miliardów razy większa od masy protonu.

1

Chodzi o ogólną strukturę czarnej dziury, a nie o osobliwy środkowy punkt, do którego zapada się materia i

którego mała średnica wymaga opisu kwantowomechanicznego.

Czarne dziury z punktu widzenia teorii strun Barbara Chorąży

W odniesieniu do kosmicznych czarnych dziur jest nieporównywalnie mała,

równa się bowiem masie typowej drobiny kurzu.) Przypuszczenie, że małe

czarne dziury łączy z cząstkami elementarnymi ścisły związek napotyka tu na

sprzeczność ogólnej teorii względności – teoretycznej podstawy czarnych dziur

– z mechaniką kwantową. Po raz pierwszy logiczny związek został ukazany

dzięki ujęciu kwestii czarnych dziur według teorii strun.

Postęp, który umożliwia teoria strun

Do zrozumienia związku między czarnymi dziurami i cząstkami

elementarnymi w ujęciu teorii strun warto zapoznać się wcześniej z kilkoma

faktami.

Podczas, gdy sześć wymiarów przestrzennych zwija się w kształt

Calabiego-Yau, mogą występować dwa typy sfer. Jeden rodzaj to sfery

dwuwymiarowe, takie jak powierzchnia piłki plażowej, które odgrywają istotną

role w

przejściach z rozrywaniem przestrzeni. Drugi rodzaj to sfery

trójwymiarowe, trudniejsze do wyobrażenia. Zwykła piłka plażowa w naszym

świecie jest obiektem trójwymiarowym, ale jej powierzchnia posiada dwa

wymiary – do określenia punktu wystarczy podać dwie współrzędne. Do

wyobrażenia drugiego typu sfer należy dodać jeden wymiar więcej. Badania

równań teorii strun uświadomiły fizykom, że jest prawdopodobne, iż z biegiem

czasu trójwymiarowe sfery skurczą się - zapadną się – do niezwykle małej

objętości. Pojawiło się pytanie: „Co by się stało gdyby proces ten objął strukturę

przestrzeni?” Jednowymiarowe struny umożliwiają uniknięcie katastrofalnych

skutków w odniesieniu do zapadania się sfer dwuwymiarowych. Jednobrana nie

da jednak rady owinąć się wokół sfery trójwymiarowej. Katastroficzne

przypuszczenia sprzed połowy lat dziewięćdziesiątych rozwiał w 1995 Andrew

Strominger. Poszedł on śladami Wittena i Seiberga i wykorzystał drugą

rewolucję superstrunową. Okazało się, ze teoria ta obejmuje nie tylko

1

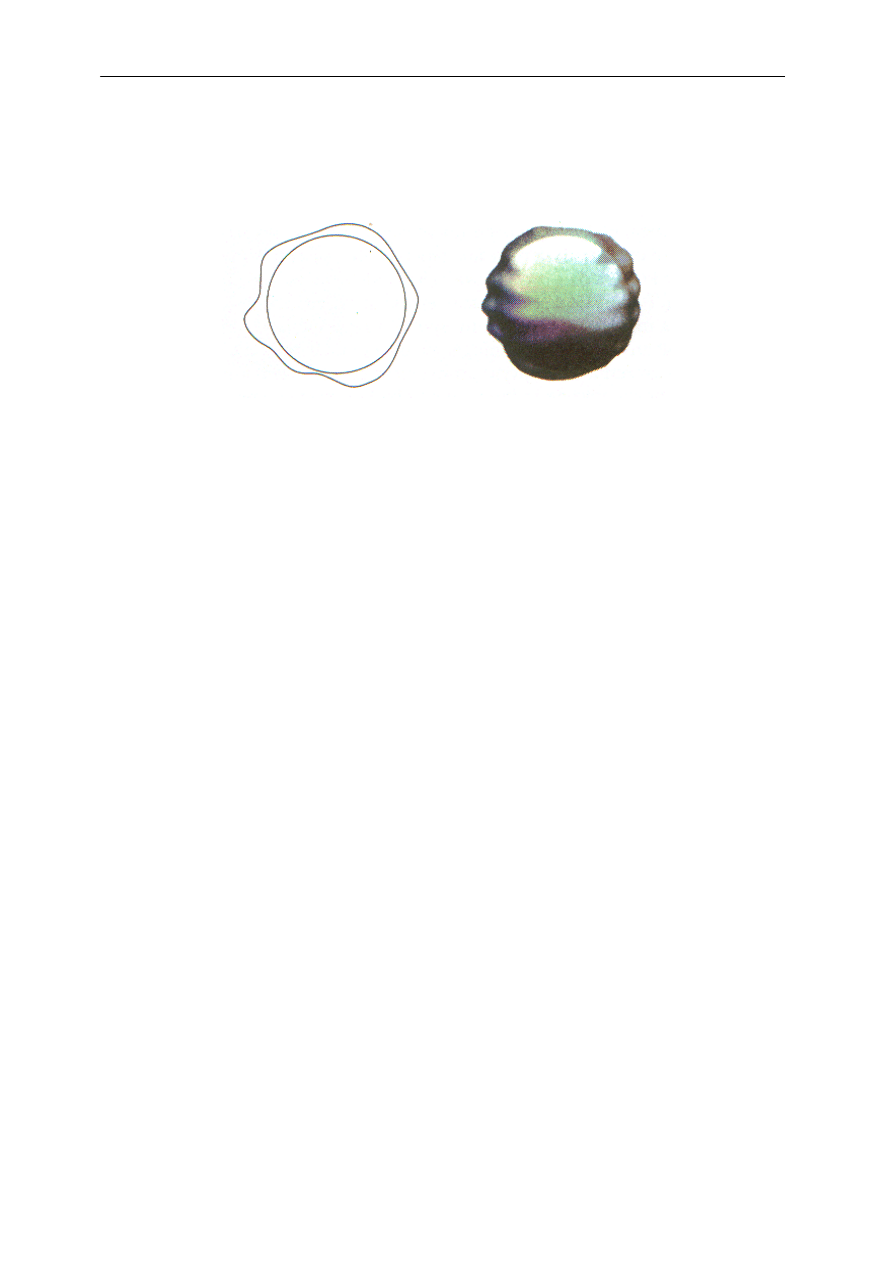
Czarne dziury z punktu widzenia teorii strun Barbara Chorąży

jednowymiarowe struny. Jednobrana może całkowicie otoczyć jednowymiarowy

fragment przestrzeni, taki jak okrąg, co pokazuje rycina 1. (Rycinę należy

traktować jako ujecie w danej chwili.).

Ryc. 1. Struna otacza jednowymiarowy, zakrzywiony kawałek struktury przestrzennej;
dwuwymiarowa membrana otacza fragment dwuwymiarowy.

Podobnie dwuwymiarowa membrana – dwubrana – potrafi otoczyć

i całkowicie zakryć dwuwymiarową strefę. Doprowadziło to Stromingera

do wniosków, że trójwymiarowe składniki teorii strun – trójbrany – dadzą radę

otoczyć i zakryć w całości sferę trójwymiarową. Obliczenia potwierdzają, że

owinięta trójbrana stanowi świetnie dopasowaną osłonę. Znosi ona wszelkie

potencjalnie groźne efekty, które powstawałyby w wyniku zapadania się

trójwymiarowej sfery.

Osiągnięcia Stromingera prowadziły fizyków do dalszych rozważań.

Uświadomili sobie, że gdy zapada się trójwymiarowa sfera jest prawdopodobne,

że przestrzeń Calabiego-Yau ulegnie rozerwaniu, a następnie zreperuje się

dzięki ponownemu powstaniu sfery, jak ma to miejsce w przypadku sfery

o dwóch wymiarach. Do zobrazowania podobnego zjawiska posłużymy się

analogią do mniejszej liczby wymiarów.

Dwuwymiarową sferę tworzy zbiór punktów w trójwymiarowej przestrzeni

jednakowo odległych od środka (rycina 2.a). Na tej samej zasadzie

jednowymiarowa sfera jest zbiorem punktów jednakowo odległych

od wspólnego środka w dwuwymiarowej przestrzeni. Jest to po prostu okrąg

(rycina 2. b).

2

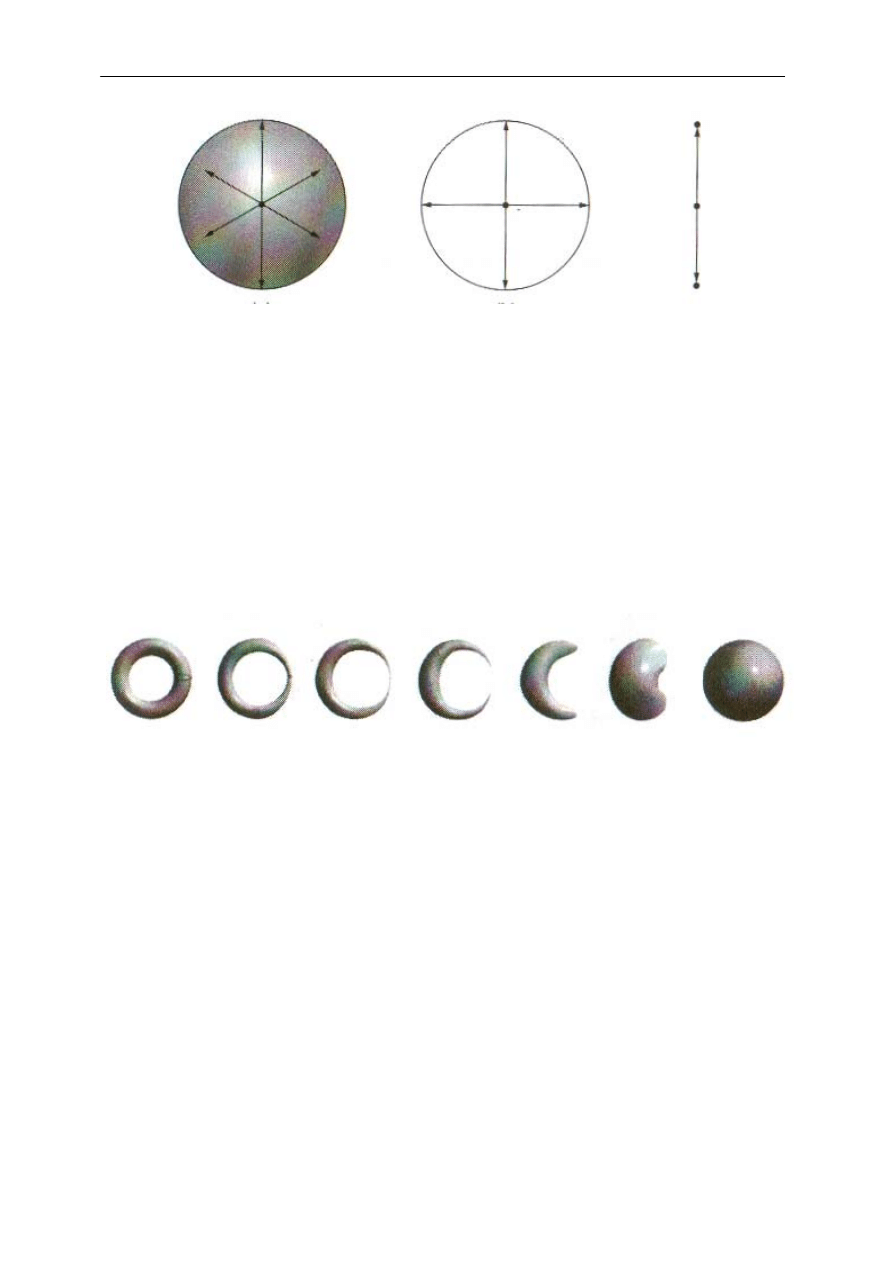
Czarne dziury z punktu widzenia teorii strun Barbara Chorąży

Ryc. 2. Sfery: (a) dwuwymiarowa , (b) jednowymiarowa, (c) o zerowej liczbie wymiarów

Sfera o zerowej liczbie wymiarów jest po prostu ograniczona do dwóch

punktów na jednej prostej o takiej samej odległości od punktu środkowego

(rycina 2.c). W sytuacji analogicznej do opisanej w poprzednim akapicie po

skurczeniu się okręgu (jednowymiarowej sfery) i rozerwaniu przestrzeni okrąg

zostaje zastąpiony sferą bezwymiarową (dwoma punktami).

Powierzchnią wyjściową będzie powierzchnia obwarzanka z zanurzoną

w niej jednowymiarową sferą – okręgiem. Sytuację tą przedstawia rycina 3.

Ryc. 3. Przekrój obwarzanka (torusa) kurczy się do wielkości punktu. Przestrzeń rozrywa się
i powstają dwie dziury. W miejsca te „wklejamy” bezwymiarową sferę, która zastępuje
początkową jednowymiarową i w ten sposób reperujemy rozerwaną przestrzeń. Pozwala to
na przekształcenie początkowego kształtu przestrzeni Calabiego-Yau w inny.

Gdy hipotetyczny okrąg zapada się, powoduje zwężenie przestrzeni. Gdy

przestrzeń na chwilę się rozerwie, zreperujemy ją zastępując jednowymiarową

sferę bezwymiarową – a więc dwoma punktami. Likwidujemy w ten sposób

dziury, które powstały w górnej i dolnej części rozerwanego obwarzanka.

Powstał kształt przypominający banana, który po małych deformacjach (bez

rozrywania) da się przekształcić w powierzchnię piłki plażowej. Topologia

początkowego obwarzanka uległa więc zdecydowanej zmianie. Analogia do

mniejszej liczby wymiarów pozwoliła stwierdzić, że po zapadnięciu się

3

Czarne dziury z punktu widzenia teorii strun Barbara Chorąży

trójwymiarowej sfery w przestrzeni Calabiego-Yau, przestrzeń powinna się

rozerwać i połączyć za pomocą dwuwymiarowej sfery. Jeden kształt Calabiego-

Yau przeistoczyłby się w zupełnie inny kształt– podobnie jak obwarzanek

w piłkę plażową – podczas gdy wszystkie prawa teorii strun zachowały by

poprawność.

Teoria strun wobec czarnych dziur

Przejścia stożkowate – tak w specjalistycznym żargonie nazywa się rodzaj

transformacji z gwałtownym rozerwaniem przestrzeni – nie powodują fizycznej

katastrofy, ale da się zauważyć ich konsekwencje. Trójbrana owinięta wokół

trójwymiarowej sfery wytwarza pole grawitacyjne przypominające pole

grawitacyjne czarnej dziury. Staje się to jasne dzięki szczegółowej analizie

równań rządzących branami. W swoim przełomowym artykule z 1995 roku

Strominger dowodził, że masa trójbrany – czyli masa czarnej dziury – jest

proporcjonalna do objętości trójwymiarowej sfery, którą otacza. Im większa

objętość tym większa musi być trójbrana, aby się wokół niej owinąć, a więc tym

większą ma masę. Podobnie, im mniejsza objętość sfery, tym mniejsza

otaczającej trójbrany. Gdy sfera się zapada, owinięta wokół niej trójbrana,

widoczna jako czarno dziura, staje się coraz lżejsza. Kiedy trójwymiarowa sfera

przybiera wielkość punktu, odpowiadająca jej czarna dziura zostaje pozbawiona

masy.

Należy także napomnieć, że liczba dziur w kształcie Calabiego-Yau określa

liczbę niskoenergetycznych, a więc mających niewielką masę, drgań struny,

które prawdopodobnie odpowiadają cząstkom materialnym. Ponieważ przejścia

stożkowate z rozrywaniem przestrzeni zmieniają liczbę dziur, powinniśmy się

spodziewać zmiany w liczbie wzorów drgań o małej masie. I rzeczywiście

zastąpieniu nowej dwuwymiarowej sfery skurczoną trójwymiarową sferą

4

Czarne dziury z punktu widzenia teorii strun Barbara Chorąży

w zwiniętych wymiarach przestrzeni Calabiego-Yau towarzyszy wzrost liczby

bezmasowych drgań struny dokładnie o jeden.

Spostrzeżenia z dwóch ostatnich akapitów posłużą nam do wyobrażenia

sobie przestrzeni Calabiego-Yau, w której rozmiary trójwymiarowej sfery coraz

bardziej się zmniejszają. Z pierwszego spostrzeżenia wynika, że trójbrana

otaczająca tę trójwymiarową sferę – czarna dziura – będzie miała coraz mniejszą

masę, aż w końcowym punkcie kurczenia się sfery przybierze formą

bezmasową. Odwołując się do drugiego spostrzeżenia : nowy bezmasowy wzór

drgań, powstały na skutek stożkowatego przejścia z rozdarciem przestrzeni,

stanowi mikroskopowy opis bezmasowej cząstki, w którą przekształciła się

czarna dziura. Doszliśmy do wniosku, że w czasie transformacji kształtu

Calabiego-Yau początkowo masywna czarna dziura staje się coraz lżejsza, aż

zupełnie traci masę, stając się bezmasową cząstką – taką jak pozbawiony masy

foton. W teorii strun jest ona struną wykonującą drgania według pewnego

wzoru. W ten sposób teoria strun ustaliła ścisły, ilościowo niepodważalny

związek miedzy czarnymi dziurami a cząstkami elementarnymi.

Przejścia fazowe czarnych dziur

David Morrison, Strominger i Brian Green pokazali, że istnieje dokładna

matematyczna i fizyczna analogia miedzy przejściami fazowymi a przejściami

stożkowatymi z rozrywaniem przestrzeni z jednego kształtu Calabiego-Yau

w inny. Czarne dziury i cząstki elementarne to w rzeczywistości dwa stany tej

samej materii strunowej. O tym, czy jakaś fizyczna konfiguracja w teorii strun

wygląda jak czarna dziura czy cząstka elementarna, decyduje topologiczna

forma dodatkowych wymiarów tworzących przestrzeń Calabiego-Yau. Gdy

czarne dziury podlegają przejściu fazowemu, powstają fundamentalne drgania

struny. Dzięki przejściom stożkowatym z rozerwaniem przestrzeni da się

w sposób ciągły przekształcić każdą przestrzeń Calabiego-Yau w inną. Kiedy

5

Czarne dziury z punktu widzenia teorii strun Barbara Chorąży

zmieniamy stałe sprzężenia i geometrię zwiniętych wymiarów tworzących

przestrzeń Calabiego-Yau, stwierdzamy, że wszystkie strunowe konfiguracje są

różnymi fazami tej samej teorii – M-teorii.

Entropia czarnych dziur

Entropia jest miarą nieuporządkowania układu fizycznego – liczbą

przestawień składników układu, które nie zmieniają jego wyglądu. Ścisła

definicja entropii wymaga określenia liczby możliwych przestawień

mikroskopowych właściwości kwantowomechanicznych elementarnych

składników układu fizycznego, przestawień, które można wykonać, nie

zmieniając jego całościowych, makroskopowych właściwości (takich jak

energia czy ciśnienie). W 1970 roku Jacob Bekenstein postawił hipotezę,

według której czarne dziury mają entropię i to wysoką. Motywacja była druga

zasada termodynamiki, zgodnie z którą entropia układu zawsze rośnie. Jedynym

sposobem uczynienia zadość drugiej zasadzie termodynamiki, jak dowodził

Bekenstein, byłoby posiadanie przez czarną dziurę entropii oraz jej wzrost przy

przenoszeniu materii do czarnej dziury tak, aby ów wzrost przekroczył

obserwowany spadek entropii na zewnątrz czarnej dziury.

Aby wzmocnić swoje wnioski Bekenstein odwołał się do wyniku Stephana

Hawkinga. Udowodnił on, że powierzchnia horyzontu czarnej dziury w trakcie

każdego oddziaływania fizycznego zwiększa się. Hawking wykazał, że gdy

do czarnej dziury wpada planetoida lub z powierzchni pobliskiej gwiazdy spada

na czarną dziurę gaz albo gdy dwie czarne dziury łączą się, a także w innych

procesach, całkowita powierzchnia horyzontu zdarzeń rośnie. Ewolucja

w kierunku coraz większej całkowitej powierzchni horyzontu zwróciła uwagę

Bekensteina na zjawisko nieuniknionej ewolucji ku coraz większej całkowitej

entropii, którą wyraża druga zasada termodynamiki. Badacz postawił hipotezę,

6

Czarne dziury z punktu widzenia teorii strun Barbara Chorąży

że powierzchnia horyzontu zdarzeń czarnej dziury stanowi dokładną miarę jej

entropii.

Podobne rozważania przeprowadzał Hawking. Doszedł on do wniosku, że

gdyby poważnie potraktować analogię między prawami dotyczącymi czarnych

dziur a prawami termodynamiki, trzeba by nie tyko utożsamić powierzchnie

horyzontu zdarzeń z entropią, lecz także przypisać czarnej dziurze temperaturę

(o wartości określonej przez siłę pola grawitacyjnego czarnej dziury

na horyzoncie zdarzeń). Jeśli czarna dziura ma niezerową temperaturę, to

zgodnie z prawami fizyki musiałaby wysyłać promieniowanie. W 1974 roku

Hawking dokonał niezwykłego odkrycia. Wykorzystując mechanikę kwantową

ogłosił, że czarne dziury nie są całkowicie czarne.

Rezultat badań Hawkinga otrzymano w wyniku długich i żmudnych

obliczeń, ale główna myśl wydaje się prosta. Z zasady nieoznaczoności wynika,

że nawet w pustej przestrzeni próżni pełno jest wirtualnych cząstek, które

powstają na krótką chwilę, aby następnie ze sobą zanihilować. Ten kwantowy

proces zachodzi również w obszarze tuż nad horyzontem czarnej dziury.

Hawking uświadomił sobie, że prawdopodobnie silne pole grawitacyjne czarnej

dziury przekazuje na przykład parze wirtualnej cząstki i antycząstki energię,

która odrzuca je od siebie na tyle daleko, ze tylko jeden z nich zostaje

pochłonięty przez czarna dziurę.

Ryc. 4.

7

Czarne dziury z punktu widzenia teorii strun Barbara Chorąży

Niepochłonięta cząstka traci partnera do anihilacji. Pozostała cząstka

w rzeczywistości otrzymuje energię od pola grawitacyjnego czarnej dziury i gdy

jej partner do niej wpada, ona zostaje od niej odrzucona na pewna odległość.

Dla obserwatora z daleka, ostateczny rezultat rozerwania pary cząstka –

antycząstka, które następuje wielokrotnie wokół całego horyzontu zdarzeń

czarnej dziury, wygląda jak jednostajny strumień promieniowania. Czarne

dziury świecą.

Hawking potrafił też obliczyć temperaturę, jaką odległy obserwator

przypisałby temu promieniowaniu. Stwierdziłby on, że temperaturę określa

wielkość pola grawitacyjnego na horyzoncie czarnej dziury, tak jak to wynikało

z analogii między prawami fizyki czarnych dziur a prawami termodynamiki.

Odkrycia Hawkinga dowiodły, że nie jest to tylko analogia, ale wręcz

tożsamość.

Obliczenia Hawkinga dowiodły, że z większą masą czarnej dziury wiąże

się jej niższa temperatura i mniejsze promieniowanie. Dla zobrazowania skali:

czarna dziura o masie trzech Słońc ma temperaturę około jednej stumilionowej

stopnia powyżej zera bezwzględnego. Powoduje to, że wysyłają one słabe

światło, którego nie da się wykryć. W przeciwieństwie do bardzo niskich

temperatur, kiedy obliczamy entropię otrzymujemy wynik w postaci olbrzymiej

liczby: ta samo przykładowa czarno dziura miałaby entropię równą 10

78

.

Im większą masą odznacza się czarna dziura, tym większą ma entropię.

Pozostało jeszcze pytanie: miarą nieuporządkowania czego jest entropia

czarnych dziur? Są one przecież prostymi obiektami. Stworzone przez

Hawkinga częściowe połączenie ogólnej teorii względności z mechaniką

kwantową dawało się wykorzystać do wyznaczenia liczbowej wartości entropii

czarnej dziury, ale nie wyjaśniało jej mikroskopowego sensu.

8

Czarne dziury z punktu widzenia teorii strun Barbara Chorąży

Teoria strun wobec entropii czarnych dziur

W styczniu 1996 roku Andrew Strominger i Cumrun Vafa wysłali

do elektronicznego archiwum fizyki artykuł zatytułowany „Mikroskopowe

pochodzenie entropii Bekensteina-Hawkinga”. W pracy określili mikroskopowe

składniki pewnej klasy czarnych dziur i dokładnie obliczyli związaną z nimi

entropię. Otrzymany wynik dokładnie zgadzał się z tym co przewidzieli

Bekenstein i Hawking. Odkrycie to było możliwe dzięki wykorzystaniu drugiej

rewolucji superstrunowej (umożliwiającej wykroczenie poza przybliżenia

perturbacyjne).

Strominger i Vafa skupili uwagę na klasie tak zwanych ekstremalnych

czarnych dziur. Mają one ładunek i minimalną masę, zgodną z wielkością tego

ładunku. Wynika z tego, że owe czarne dziury pozostają w ścisłym związku ze

stanami BPS

2

. Fizycy pokazali, że potrafią teoretycznie skonstruować pewne

ekstremalne czarne dziury, poczynając od szczególnego zbioru bran BPS

(o określonej liczbie wymiarów) i łącząc je zgodnie z precyzyjnym

matematycznym schematem.

Strominger i Vafa udowodnili, że w systematyczny sposób – w wyobraźni

teoretyka – można skonstruować czarne dziury tworząc precyzyjną kombinację

bran odkrytych w trakcie drugiej rewolucji superstrunowej. Mając pełną

teoretyczną kontrolę nad mikroskopową konstrukcją czarnych dziur wyznaczyli

liczbę możliwych przestawień mikroskopowych składników czarnej dziury,

które nie zmieniałyby jej całkowitych, dających się obserwować właściwości,

takich jak masa i ładunki sił. Następnie porównali te liczbę z powierzchnią

horyzontu czarnej dziury – a więc z entropią przewidzianą przez Bekensteina

i Hawkinga. Otrzymali całkowitą zgodność. Teoria strun pozwoliła wziąć pod

2

Stany BPS – konfiguracje w teorii supersymetrycznej; składniki o minimalnej masie dla danej wartości

ładunku; ich właściwości da się jednoznacznie wyznaczyć dzięki teorii symetrii, a więc z pominięciem obliczeń
perturbacyjnych

9

Czarne dziury z punktu widzenia teorii strun Barbara Chorąży

uwagę mikroskopowe składniki czarnych dziur i dokładnie przewidzieć

związaną z nimi entropię.

Nierozwiązane tajemnice czarnych dziur

Pomimo wspaniałych dokonań dwie wielkie zagadki łączące się z czarnymi

dziurami nie zostały jeszcze rozwiązane. Pierwsza z nich dotyczy determinizmu

kwantowego. Mówi on o tym, że znajomość funkcji falowych wszystkich

podstawowych składników Wszechświata w jakiejś chwili pozwala

„wystarczająco silnej inteligencji” wyznaczyć funkcje falowe w dowolnym

momencie. Determinizm kwantowy głosi więc, że prawdopodobieństwo zajścia

danego zdarzenia w danej chwili jest całkowicie określone przez znajomość

funkcji falowej w dowolnej wcześniejszej chwili.

W 1976 roku Hawking stwierdził, że obecność czarnych dziur narusza

determinizm. Gdy dowolny obiekt wpada do czarnej dziury, trafia tam również

jego funkcja falowa. Wobec tego powstaje problem, w jaki sposób wyznaczyć

funkcje falowe, które pojawiają się we wszystkich przyszłych chwilach. Należy

postawić pytanie, czy stracone informacje niesione przez funkcje falowe

pochłonięte przez czarne dziury, zostają odzyskane.

Jak wiemy czarne dziury promieniują. Promieniowanie niesie energię, a

więc gdy czarna dziura promieniuje – jej masa wolno maleje. Na skutek tego

zmniejsza się odległość między środkiem czarnej dziury a jej horyzontem

zdarzeń i obszary, które wcześniej były odcięte od świata znowu wkraczają

na kosmiczną scenę. Narzuca się więc pytanie, czy informacje zawarte

w pochłoniętej przez czarna dziurę materii wydostają się na zewnątrz w miarę

kurczenia się czarnej dziury. Wobec tej kwestii fizycy podzielili się na dwa

obozy. Niektórzy twierdzą, że czarne dziury niszczą informacje, które wobec

tego nie wydostają się ponownie z ich wnętrza. Obóz przeciwny jest zdania, że

dane ponownie się pojawiają gdy czarna dziura emituje energię i się kurczy.

10

Czarne dziury z punktu widzenia teorii strun Barbara Chorąży

Choć kwestia nie jest do tej pory rozstrzygnięta, Hawking przypuszcza, że

podejście do czarnych dziur w ramach teorii strun daje możliwość ponownego

pojawienia się utraconej informacji. Pomysł polega na tym, że informację

można przechowywać w branach tworzących czarne dziury i z nich odzyskiwać.

Druga nierozwiązana zagadka wynikająca z istnienia czarnych dziur

dotyczy natury czasoprzestrzeni w środkowym punkcie tych obiektów. Otóż

cała materia, która przekroczyła horyzont czarnej dziury, w nieunikniony sposób

zmierz ku jej środkowi. Bardzo duże masy i małe rozmiary prowadzące

do niewyobrażalnych gęstości powodują, że nie można używać tylko klasycznej

teorii Einsteina – trzeba również odwołać się do mechaniki kwantowej.

Powstaje pytanie, co o osobliwości czasoprzestrzennej w centrum czarnej dziury

mówi teoria strun. Choć radzi on sobie świetnie z różnymi zagadnieniami –

rozdarciami, szczelinami w przestrzeni, to na razie nie potrafi wniknąć w naturę

zjawiska, jakim jest osobliwość związana z wnętrzem czarnej dziury.

Nadzieję na rychłe rozwiązanie zagadki daje niesamowite tempo, z jakim

dokonał się ostatnio wielki postęp w dziedzinie metod nieperturbacyjnych i ich

zastosowania do innych zagadnień związanych z czarnymi dziurami.

11