dr Dušan Bogdanov

1

Ekonometria 1

Wykład 7

Weryfikacja jednorównaniowego modelu liniowego

1

Weryfikacja jednorównaniowego modelu liniowego szacowanego klasyczn

ą

metod

ą

najmniejszych

kwadratów polega na zbadaniu:

•

merytorycznej oceny sensowno

ś

ci ocen parametrów strukturalnych modelu,

•

dopasowania modelu do danych empirycznych,

•

istotno

ś

ci parametrów strukturalnych modelu,

•

rozkładu składnika losowego.

Uzyskane w wyniku estymacji szacunki parametrów modelu wskazywa

ć

powinny kierunek

zale

ż

no

ś

ci mi

ę

dzy zmienn

ą

obja

ś

nian

ą

i odpowiedni

ą

zmienn

ą

obja

ś

niaj

ą

c

ą

, zgodny z zale

ż

no

ś

ci

ą

wynikaj

ą

c

ą

z danych empirycznych, to znaczy,

ż

e współczynnik korelacji pomi

ę

dzy tymi zmiennymi

i znak oceny parametru powinny by

ć

jednakowe. W przypadku zbyt du

ż

ej korelacji pomi

ę

dzy

zmiennymi obja

ś

niaj

ą

cymi wprowadzonymi do modelu ta prawidłowo

ść

mo

ż

e zosta

ć

zakłócona. Jest

to tak zwane zjawisko koincydencji. W takiej sytuacji nale

ż

y zmodyfikowa

ć

zestaw zmiennych

obja

ś

niaj

ą

cych.

Dopasowanie modelu do danych empirycznych ocenia si

ę

na podstawie współczynnika zgodno

ś

ci,

który jest unormowan

ą

wielko

ś

ci

ą

mierz

ą

c

ą

rozproszenie punktów empirycznych wokół oszacowanej

funkcji. Wyra

ż

a si

ę

on wzorem:

(

)

2

2

1

2

1

2

1

2

y

n

t

t

n

t

k

j

tk

k

t

S

S

y

y

x

a

y

=

−















−

=

∑

∑

∑

=

=

=

ϕ

(7.1)

gdzie:

2

S

- wariancja wektora reszt,

2

y

S

- wariancja zmiennej obja

ś

nianej,

U

ż

ywa si

ę

równie

ż

współczynnika determinacji (korelacji wielorakiej):

2

2

1

ϕ

−

=

R

(7.2)

oraz, zbli

ż

onego do powy

ż

szych, w interpretacji, współczynnika zmienno

ś

ci przypadkowej (losowej):

y

S

W

=

(7.3)

1

Wykład został przygotowany na podstawie K. Hanusik, U. Łangowska, Modelowanie ekonometryczne procesów

społeczno-gospodarczych, UO Opole 1994

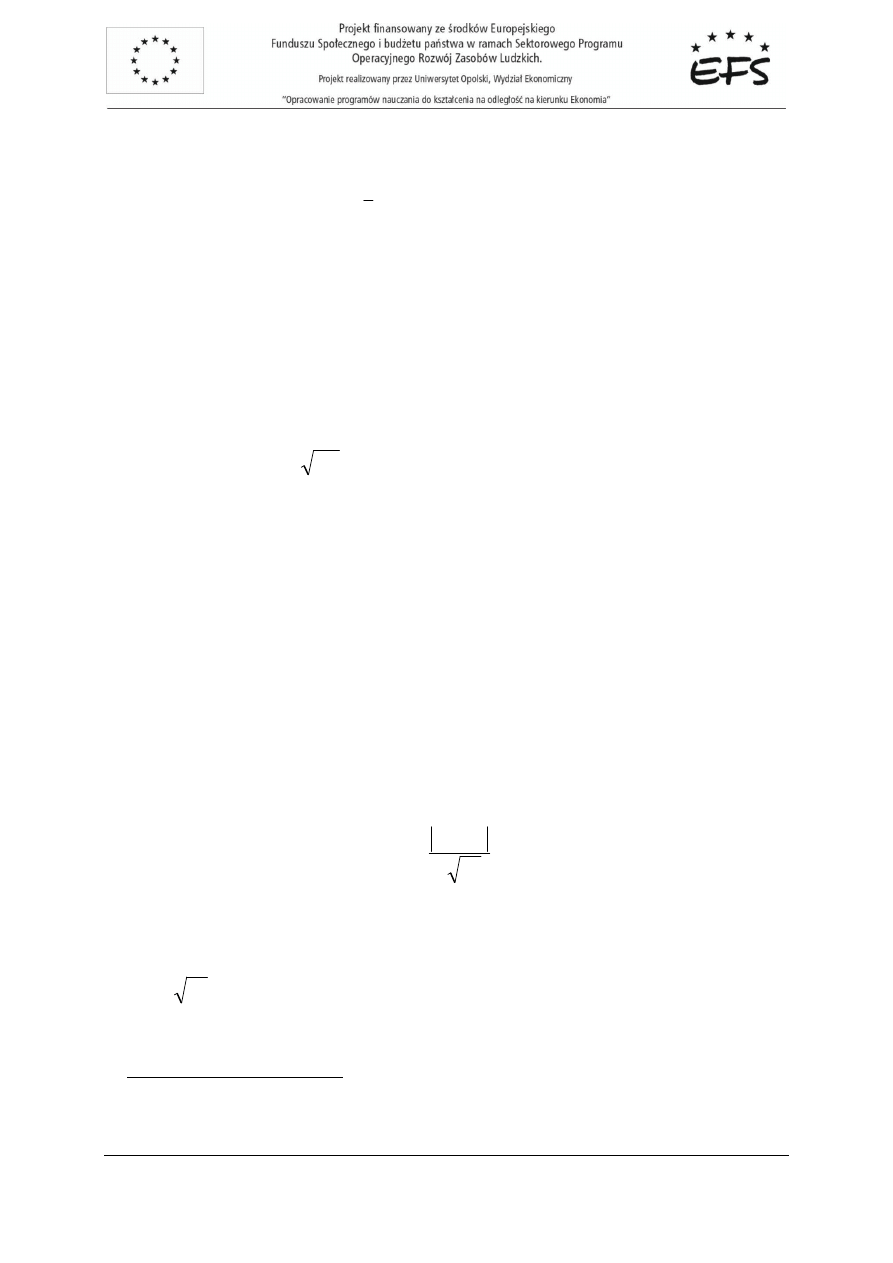
dr Dušan Bogdanov

2

Ekonometria 1

Współczynnik zmienno

ś

ci

2

ϕ

przybiera warto

ś

ci z przedziału [0,l]. Przypadek

2

ϕ

= 1

otrzymujemy, gdy:

∑

=

=

k

j

ij

j

x

a

y

1

(7.4)

co oznacza,

ż

e nie ma

ż

adnej zale

ż

no

ś

ci zmiennej obja

ś

nianej od zmiennych obja

ś

niaj

ą

cych.

Przypadek

2

ϕ

= 0 otrzymujemy, gdy wszystkie warto

ś

ci empiryczne zmiennej obja

ś

nianej s

ą

to

ż

same

z jej warto

ś

ciami teoretycznymi, to znaczy wyznaczonymi z modelu.

Współczynnik zgodno

ś

ci w przybli

ż

eniu pokazuje, jaka cz

ęść

zmienno

ś

ci zmiennej obja

ś

nianej nie

została przez model obja

ś

niona.

Interpretacja współczynnika determinacji jest odwrotna. W literaturze przedmiotu u

ż

ywa si

ę

czasem współczynnika

2

R

R

=

, nosz

ą

cego nazw

ę

współczynnika korelacji wielorakiej.

Współczynnik zmienno

ś

ci losowej informuje, jak

ą

cz

ęść

ś

redniej warto

ś

ci zmiennej obja

ś

nianej

stanowi odchylenie standardowe modelu. Lepsze dopasowanie modelu do danych empirycznych

odpowiada bli

ż

szej zeru warto

ś

ci miernika.

W procesie weryfikacji porównujemy warto

ś

ci współczynników wyznaczone dla analizowanego

modelu z warto

ś

ciami granicznymi. Warto

ś

ci krytyczne przyjmowane s

ą

obligatoryjnie przez

prowadz

ą

cego badanie, na poziomie gwarantuj

ą

cym po

żą

dane dopasowanie modelu do danych

empirycznych.

W dalszej cz

ęś

ci weryfikacji modelu ekonometrycznego wykorzystywana jest teoria testowania

hipotez statystycznych. Podstawy teorii weryfikacji hipotez przedstawione s

ą

mi

ę

dzy innymi

w podr

ę

cznikach do statystyki

2

.

Do badania istotno

ś

ci parametrów strukturalnych modelu mo

ż

na wykorzysta

ć

nast

ę

puj

ą

c

ą

funkcj

ę

testow

ą

(por. wykład 6, twierdzenie 6):

( )

ii

i

i

i

c

s

a

f

α

α

−

=

(7.5)

gdzie:

i

a

- szacunek i-tego parametru,

i

α

- jego warto

ść

rzeczywista (i=1,2,...m),

ii

c

s

- bł

ę

dy standardowe ocen parametrów.

2

Z. Hellwig, Elementy rachunku prawdopodobie

ń

stwa i statystyki matematycznej, PWN Warszawa 1987,

s.253 i nast. A. Luszniewicz, T. Słaby, Statystyka stosowana, PWE Warszawa 1996, s.138 i nast. S. Ostasiewicz,
Z. Rusnak, U. Siedlecka Wyd. AE we Wrocławiu, Wrocław 1998, s. 235 i nast.

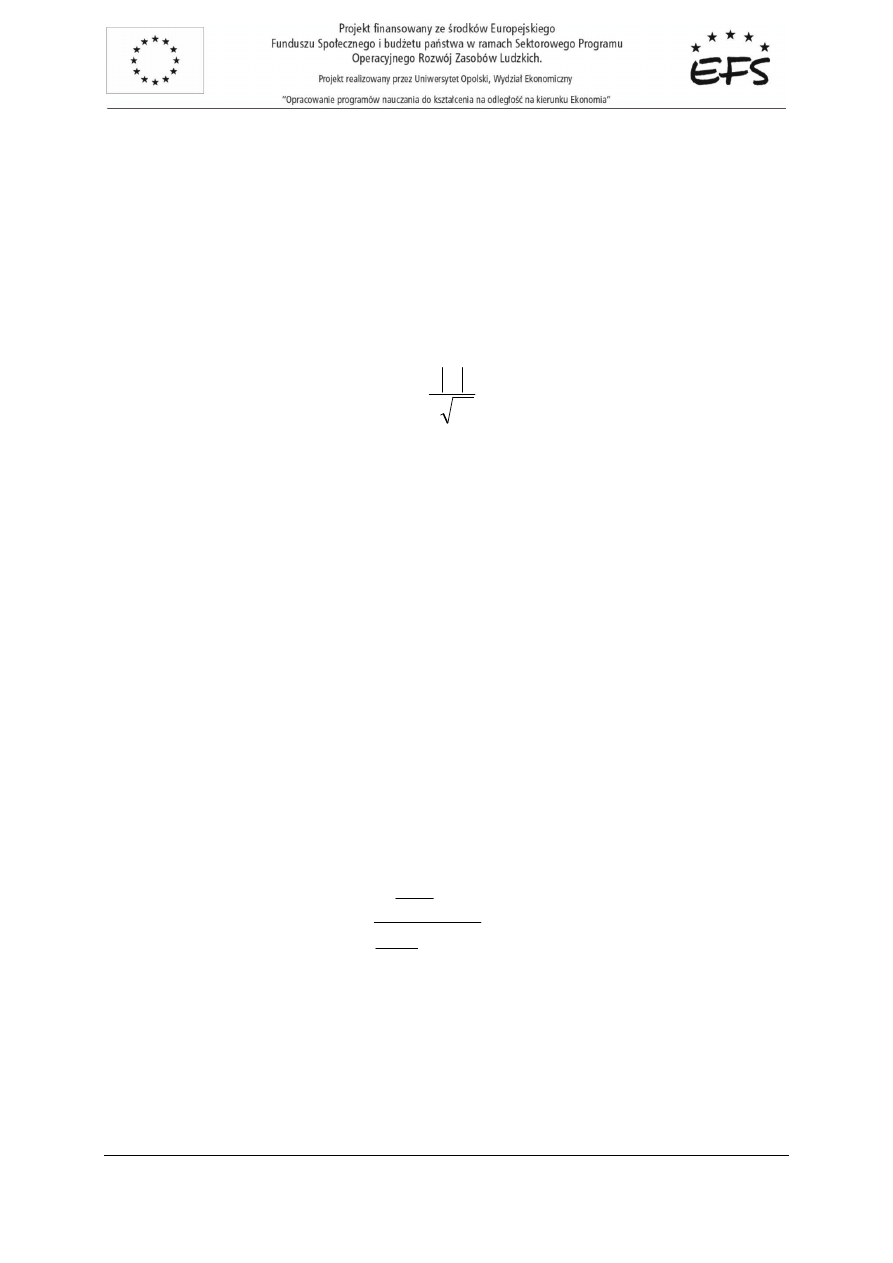
dr Dušan Bogdanov

3

Ekonometria 1

Zmienna losowa

( )

i

t

α

ma rozkład Studenta o n-k stopniach swobody, gdzie k oznacza ilo

ść

szacowanych parametrów, n - liczebno

ść

próby.

Badanie istotno

ś

ci parametrów polega na sprawdzeniu, czy ró

ż

ni

ą

si

ę

one istotnie od zera.

Stawiamy hipotez

ę

zerow

ą

,

ż

e rzeczywista warto

ść

parametru jest równa zero:

0

:

0

=

i

H

α

wobec hipotezy alternatywnej,

ż

e rzeczywista warto

ść

parametru ró

ż

ni si

ę

od zera:

0

:

1

≠

i

H

α

Hipoteza

0

H

prowadzi do zale

ż

no

ś

ci:

( )

ii

i

c

s

a

f

=

0

(7.6)

Ustalamy z rozkładu Studenta o n-k stopniach swobody warto

ść

krytyczn

ą

*

f

dla przyj

ę

tego

poziomu istotno

ś

ci

µ

. Jest to taka warto

ść

,

ż

e prawdopodobie

ń

stwo, i

ż

zmienna losowa

f

przyjmie

warto

ść

wi

ę

ksz

ą

ni

ż

*

f

, jest mniejsze ni

ż

µ

.

Je

ż

eli

( )

*

0

f

f

>

, to oznacza,

ż

e zaszło zdarzenie mało prawdopodobne, czyli inaczej mówi

ą

c,

zdarzenie,

ż

e rzeczywista warto

ść

parametru wynosi zero, jest mało prawdopodobne. W tej sytuacji

hipotez

ę

zerow

ą

odrzucamy na rzecz hipotezy alternatywnej i przyjmujemy,

ż

e warto

ść

parametru

istotnie ró

ż

ni si

ę

od zera.

W przeciwnym przypadku, to jest gdy

( )

*

0

f

f

≤

, nie ma podstaw do odrzucenia hipotezy

zerowej. Oznacza to konieczno

ść

modyfikacji zestawu zmiennych obja

ś

niaj

ą

cych modelu.

Przedstawione badanie dotyczy istotno

ś

ci pojedynczych parametrów modelu. Natomiast przy

badaniu istotno

ś

ci całego wektora parametrów weryfikowana jest hipoteza zakładaj

ą

ca,

ż

e wszystkie

parametry strukturalne modelu oprócz wyrazu wolnego s

ą

równe zeru. Na podstawie twierdzenia 7

przedstawionego na wykładzie 6 zmienna losowa:

(

)

2

2

1

1

1

1

R

k

n

R

k

f

−

−

−

=

(7.7)

ma rozkład Fishera-Snedecora o k-1 i n-k stopniach swobody.

dr Dušan Bogdanov

4

Ekonometria 1

Stawiamy hipotez

ę

:

0

H

nie zachodzi zale

ż

no

ść

korelacyjna pomi

ę

dzy zmienn

ą

obja

ś

nian

ą

i zmiennymi

obja

ś

niaj

ą

cymi wobec hipotezy alternatywnej,

:

1

H

zachodzi zale

ż

no

ść

korelacyjna pomi

ę

dzy zmienn

ą

obja

ś

nian

ą

i zmiennymi obja

ś

niaj

ą

cymi.

Dla danego poziomu istotno

ś

ci odczytujemy z tablic warto

ść

krytyczn

ą

*

f

. Je

ż

eli wyliczone

f

jest wi

ę

ksze od warto

ś

ci krytycznej, to znaczy,

ż

e hipoteza zerowa prowadzi do zdarzenia mało

prawdopodobnego i nale

ż

y j

ą

odrzuci

ć

na rzecz hipotezy alternatywnej. W przeciwnym przypadku nie

ma podstaw do odrzucenia hipotezy zerowej i przyjmujemy wtedy,

ż

e zmienne obja

ś

niaj

ą

ce

w analizowanym modelu nie wpływaj

ą

istotnie na kształtowanie si

ę

zmiennej obja

ś

nianej.

Kolejnym elementem weryfikacji jest badanie rozkładu składnika losowego modelu. Polega ono

na sprawdzeniu prawdziwo

ś

ci zało

ż

e

ń

, które pozwoliły na zastosowanie do szacowania modelu

klasycznej metody najmniejszych kwadratów. Na podstawie wcze

ś

niejszych rozwa

ż

a

ń

teoretycznych

wiemy,

ż

e wektor reszt modelu, który jest empiryczn

ą

realizacj

ą

składnika losowego, powinien by

ć

realizacj

ą

zmiennej losowej o rozkładzie normalnym

( )

σ

,

0

N

. W celu sprawdzenia, czy składniki

losowe

t

ε

; spełniaj

ą

przyj

ę

te a priori zało

ż

enia, przedstawimy zaproponowan

ą

przez S. Bartosiewicz

procedur

ę

badania składnika losowego na podstawie wektora reszt modelu

3

. Istotn

ą

cech

ą

opisywanej

metody jest to,

ż

e sprawdzane s

ą

kolejno według stopnia zło

ż

ono

ś

ci własno

ś

ci, które powinien

spełnia

ć

wektor reszt, je

ż

eli składniki losowe spełniaj

ą

warunki stosowalno

ś

ci metody najmniejszych

kwadratów.

Badanie wektora reszt rozpoczyna analiza symetrii jego rozkładu. Rozkład normalny jest

symetryczny, a wi

ę

c w wektorze reszt prawdopodobie

ń

stwo wyst

ę

powania reszt dodatnich i ujemnych

jest jednakowe. Stawiana jest hipoteza zerowa

)

0

(

)

0

(

:

0

<

=

>

t

t

e

P

e

P

H

wobec hipotezy alternatywnej

)

0

(

)

0

(

:

1

<

≠

>

t

t

e

P

e

P

H

Do sprawdzenia hipotezy zerowej, stosowana jest statystyka:

1

1

2

1

−













−

−

=

n

n

m

n

m

n

m

f

(7.8)

gdzie n jest liczb

ą

obserwacji, m liczb

ą

reszt dodatnich. Dla dostatecznie du

ż

ej próby statystyka

f

3

S. Bartosiewicz, Ekonometria, PWE Warszawa 1978 r. s. 133 i nast.

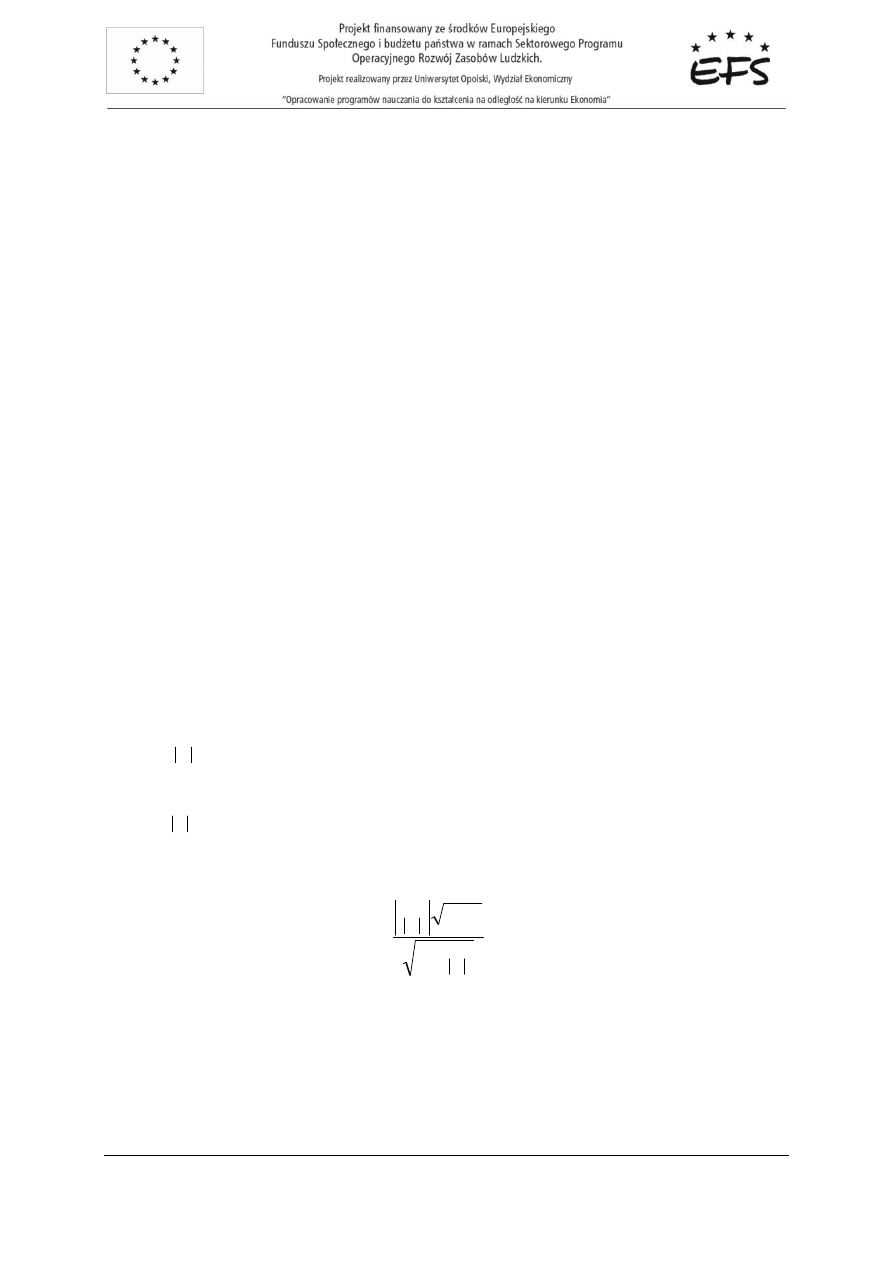
dr Dušan Bogdanov

5

Ekonometria 1

ma rozkład zbli

ż

ony do normalnego. Je

ż

eli dla przyj

ę

tego poziomu istotno

ś

ci warto

ść

krytyczna

*

f

odczytana z tablic jest wi

ę

ksza od obliczonej to hipotez

ę

zerow

ą

nale

ż

y przyj

ąć

.

Dla małych prób statystyka

f

ma rozkład Studenta o n-1 stopniach swobody. Ponadto

w przypadku małych prób stosuje si

ę

test symetrii oparty na zało

ż

eniu,

ż

e liczba reszt dodatnich jest

zmienn

ą

losow

ą

o rozkładzie dwumianowym z parametrami p = q = 1/2 . Opracowane s

ą

tablice

do tego testu podaj

ą

ce dla ustalonego poziomu istotno

ś

ci przedział, w którym powinna si

ę

znale

źć

liczba reszt dodatnich, aby wektor reszt mo

ż

na było uzna

ć

za symetryczny.

W przypadku modeli dynamicznych bada si

ę

losowo

ść

składnika losowego gwarantuj

ą

c

ą

równomierne rozproszenie danych empirycznych wokół oszacowanej linii. Przy czym symetria

rozkładu wektora reszt nie gwarantuje losowo

ś

ci składnika losowego. W przypadku, gdy w wektorze

reszt wyst

ą

pi taka sama ilo

ść

reszt dodatnich i ujemnych, ale ich uło

ż

enie (np. dla dziesi

ę

ciu

obserwacji i, pi

ęć

pierwszych pod oszacowan

ą

krzyw

ą

i pi

ęć

nast

ę

pnych nad krzyw

ą

) trudno uzna

ć

za przypadkowe, przyjmuje si

ę

,

ż

e jest ono ukształtowane na skutek działania czynników

systematycznych. Do sprawdzenia losowo

ś

ci rozkładu reszt mo

ż

na stosowa

ć

test serii. Przez seri

ę

rozumiemy ci

ą

g kolejnych reszt o tym samym znaku. Testy serii podaj

ą

dla ustalonego poziomu

istotno

ś

ci i liczebno

ś

ci wektora reszt minimaln

ą

liczb

ę

serii lub maksymaln

ą

długo

ść

najdłu

ż

szej serii.

Jedno z zało

ż

e

ń

stosowalno

ś

ci klasycznej metody najmniejszych kwadratów dotyczy stało

ś

ci

wariancji składnika losowego modelu. Ta jego wła

ś

ciwo

ść

sprawdzana jest poprzez badanie

stacjonarno

ś

ci wektora reszt, a wi

ę

c jego niezale

ż

no

ś

ci od czasu. Zatem badanie stacjonarno

ś

ci

wektora reszt odnosi si

ę

do modeli dynamicznych. Procedura tego kroku weryfikacji polega

na sprawdzeniu stopnia skorelowania modułów reszt i zmiennej czasowej. Je

ż

eli współczynnik

korelacji modułów reszt z czasem nieistotnie ró

ż

ni si

ę

od zera, przyjmuje si

ę

,

ż

e wektor reszt modelu

jest stacjonarny. W tym celu sprawdzana jest hipoteza zerowa:

0

:

0

=

t

e

t

r

H

wobec hipotezy alternatywnej:

0

:

1

≠

t

e

t

r

H

.

Statystyk

ę

słu

żą

c

ą

do sprawdzenia hipotezy zerowej przedstawia wzór:

2

1

1

t

e

t

e

t

t

r

n

r

f

−

−

=

(7.9)

Statystyka

f

ma rozkład Studenta o n-2 stopniach swobody. Z tablic rozkładu Studenta

odczytujemy dla ustalonego poziomu istotno

ś

ci i stopni swobody warto

ść

krytyczn

ą

*

f

i je

ż

eli jest

ona wi

ę

ksza lub równa warto

ś

ci empirycznej

f

, wektor reszt mo

ż

na uzna

ć

za stacjonarny.

Je

ż

eli parametry modelu liniowego były szacowane klasyczn

ą

metod

ą

najmniejszych kwadratów,

dr Dušan Bogdanov

6

Ekonometria 1

to zapewniona jest nieobci

ąż

ono

ść

składnika losowego, w tym sensie,

ż

e warto

ść

oczekiwana

składnika losowego jest równa zero. Zatem dla tej klasy modeli nie ma potrzeby bada

ć

warto

ś

ci

oczekiwanej składnika losowego. Natomiast w przypadku, gdy weryfikowany jest model segmentowy,

model adaptacyjny czy te

ż

model liniowy bez wyrazu wolnego procedura powinna obejmowa

ć

sprawdzenie warto

ś

ci oczekiwanej składnika losowego. W tym celu przyjmuje si

ę

hipotez

ę

:

( )

0

0

=

=

t

E

H

ε

wobec hipotezy alternatywnej:

( )

0

1

≠

=

t

E

H

ε

Sprawdzianem

0

H

jest statystyka:

s

n

e

f

1

−

=

(7.10)

gdzie:

e

oznacza

ś

redni

ą

warto

ść

wektora reszt modelu, natomiast

2

s

- ocen

ę

wariancji składnika losowego,

n - liczb

ę

obserwacji wektora reszt.

Analizowana statystyka ma rozkład Studenta o n-1 stopniach swobody.

0

H

mo

ż

e by

ć

zatem

uznana za prawdziw

ą

, gdy empiryczna warto

ść

f

jest nie wi

ę

ksza od warto

ś

ci krytycznej

*

f

odczytanej z tablic dla ustalonego poziomu istotno

ś

ci i stopni swobody.

W modelach dynamicznych mo

ż

e wyst

ą

pi

ć

zale

ż

no

ść

składników losowych z ró

ż

nych momentów

czasu. T

ę

niepo

żą

dan

ą

wła

ś

ciwo

ść

składnika losowego nazywa si

ę

autokorelacj

ą

. Przejawia si

ę

ona

istnieniem istotnego skorelowania pomi

ę

dzy ci

ą

giem reszt

(

)

τ

−

=

n

t

e

t

,...

2

,

1

,

oraz ci

ą

giem reszt

oddalonych o pewien okres

τ

to jest

τ

+

t

e

. Ograniczeniem dla warto

ś

ci

τ

jest wymóg formalny,

ż

e do obliczenia współczynnika korelacji potrzebne s

ą

wektory obserwacji dwóch zmiennych

o conajmniej 3 elementach. Do sprawdzenia czy warto

ść

współczynnika korelacji badanej pary ci

ą

gów

reszt jest dostatecznie bliska zeru, stosuje si

ę

procedur

ę

analogiczn

ą

jak w przypadku badania

stacjonarno

ś

ci składnika losowego.

Ponadto do badania autokorelacji składnika losowego został opracowany test Durbina-Watsona.

Dla zaobserwowanego wektora reszt uporz

ą

dkowanego w czasie statystyka słu

żą

ca do weryfikacji

hipotezy o niezale

ż

no

ś

ci składników losowych wyra

ż

a si

ę

wzorem:

(

)

∑

∑

=

=

−

−

=

n

t

t

n

t

t

t

e

e

e

f

1

2

2

2

1

(7.11)

dr Dušan Bogdanov

7

Ekonometria 1

Rozkład statystyki

f

jest uzale

ż

niony od liczby obserwacji oraz od liczby zmiennych

obja

ś

niaj

ą

cych w modelu. Dla rozkładu statystyki Durbina-Watsona wyznaczane s

ą

warto

ś

ci

krytyczne. Je

ś

li warto

ść

zaobserwowana mie

ś

ci si

ę

w wyznaczonym przedziale, to test nie rozstrzyga

wyst

ę

powania autokorelacji wektora reszt. Je

ż

eli za

ś

warto

ść

empiryczna jest mniejsza lub równa

dolnej granicy przedziału, to zjawisko autokorelacji wyst

ę

puje, natomiast, gdy jest wi

ę

ksza od górnej

granicy przedziału krytycznego autokorelacja składnika losowego nie wyst

ę

puje.

Sprawdzenie czy reszty modelu podlegaj

ą

prawu rozkładu normalnego jest szczególnie wa

ż

ne

w przypadku modeli przeznaczonych do prognozowania. Wykorzystywane s

ą

tutaj testy zgodno

ś

ci,

dla du

ż

ych prób test

λ

-Kołmogorowa, dla małych prób test Hellwiga. Testy te polegaj

ą

na porównaniu dystrybuanty empirycznej reszt

( )

t

e

G

z dystrybuant

ą

teoretyczn

ą

rozkładu

normalnego. Formułuje si

ę

nast

ę

puj

ą

c

ą

hipotez

ę

zerow

ą

:

( ) ( )

t

t

e

F

e

G

H

=

:

0

wobec alternatywy:

( )

( )

t

t

e

F

e

G

H

≠

:

1

gdzie:

( )

t

e

G

- warto

ść

dystrybuanty empirycznej w punkcie

t

e

;

( )

t

e

F

- warto

ść

dystrybuanty rozkładu normalnego o warto

ś

ci

ś

redniej 0 i odchyleniu standardowym

wektora reszt w punkcie

t

e

.

W te

ś

cie

λ

-Kołmogorowa, ze wzgl

ę

du na du

żą

liczb

ę

obserwacji ci

ą

g reszt zast

ę

puje si

ę

szeregiem rozdzielczym.

Sprawdzenie hipotezy o normalno

ś

ci rozkładu reszt testem

λ

-Kołmogorowa przebiega według

nast

ę

puj

ą

cego algorytmu:

1. uporz

ą

dkowa

ć

reszty rosn

ą

co, utworzy

ć

szereg rozdzielczy kumulacyjny reszt dla przyj

ę

tej

arbitralnie liczby m równych klas

m

i

w

u

i

i

...

2

,

1

,

,

=

, w ka

ż

dej klasie, na ko

ń

cu przedziału

,

i

w

obliczy

ć

cz

ę

sto

ść

skumulowan

ą

( )

i

w

G

,

2. wyznaczy

ć

odchylenie standardowe wektora reszt

e

s

:

3. wyznaczy

ć

warto

ś

ci dystrybuanty rozkładu normalnego

( )

e

s

N

,

0

na ko

ń

cach przedziałów

( )

i

w

F

4. wyznaczy

ć

ci

ą

g ró

ż

nic pomi

ę

dzy dystrybuant

ą

empiryczn

ą

( )

i

w

G

i dystrybuant

ą

rozkładu

normalnego

( )

i

w

F

:

5. wyznaczy

ć

warto

ść

statystyki:

dr Dušan Bogdanov

8

Ekonometria 1

( ) ( )

m

w

F

w

G

i

i

i

⋅

−

=

max

λ

(7.12)

Otrzymana warto

ść

empiryczna. powinna by

ć

nie wi

ę

ksza od odczytanej z tablic rozkładu

−

λ

Kołmogorowa warto

ś

ci teoretycznej przy zało

ż

onym poziomie istotno

ś

ci.

Sprawdzenie hipotezy

0

H

testem Hellwiga

4

przebiega natomiast według nast

ę

puj

ą

cego

algorytmu:

1. uporz

ą

dkowa

ć

reszty

t

e

; w ci

ą

g rosn

ą

cy i wyznaczy

ć

odchylenie standardowe wektora reszt

e

s

:

2. wyznaczy

ć

warto

ś

ci

( )

t

e

F

dystrybuanty rozkładu normalnego,

3. przedział zmienno

ś

ci dystrybuanty (0,1) podzieli

ć

na n równych cz

ęś

ci, zwanych celami,

4. wyznaczy

ć

ilo

ść

K cel pustych, to znaczy takich, do których nie trafiła

ż

adna warto

ść

dystrybuanty

( )

t

e

F

. Rozkład reszt nale

ż

y uzna

ć

za normalny, je

ż

eli liczba K cel pustych

znajduje si

ę

wewn

ą

trz przedziału podanego w tablicach testu Hellwiga.

Z powy

ż

szego wynika,

ż

e procedura weryfikacji modelu ekonometrycznego składa si

ę

z szeregu

kroków, przy czym ka

ż

dy z nich ko

ń

czy si

ę

ocen

ą

pewnej własno

ś

ci modelu decyduj

ą

cej o jego

jako

ś

ci. Brak pozytywnej oceny na danym etapie dyskwalifikuje model i przerywa procedur

ę

weryfikacji. Model wymaga modyfikacji, co z reguły oznacza konieczno

ść

powrotu do wcze

ś

niejszych

etapów modelowania. Rozwa

ż

my najcz

ęś

ciej spotykane wady modeli, wykrywane w trakcie weryfikacji

i ich przyczyn.

Wyst

ą

pienie zbyt wysokiej warto

ś

ci współczynnika zgodno

ś

ci

2

ϕ

jest dowodem braku zale

ż

no

ś

ci

liniowej pomi

ę

dzy zmienn

ą

obja

ś

nian

ą

a zmiennymi obja

ś

niaj

ą

cymi. W takiej sytuacji nale

ż

y albo

znale

źć

zestaw zmiennych obja

ś

niaj

ą

cych liniowo zwi

ą

zanych ze zmienn

ą

obja

ś

nian

ą

, albo dobra

ć

wła

ś

ciw

ą

posta

ć

analityczn

ą

funkcji, co oznacza powrót do etapu doboru zmiennych do modelu

lub do etapu doboru postaci analitycznej modelu. Analogicznie post

ę

pujemy w przypadku braku

dostatecznej wyrazisto

ś

ci modelu.

Analiza istotno

ś

ci parametrów strukturalnych modelu rozstrzyga o poprawno

ś

ci doboru zmiennych

do modelu. W sytuacji, gdy wszystkie parametry s

ą

istotnie ró

ż

ne od zera mo

ż

na przyj

ąć

,

ż

e zmienne

obja

ś

niaj

ą

ce dostatecznie silnie wpływaj

ą

na zmienn

ą

obja

ś

nian

ą

. Zatem ze wzgl

ę

du na zestaw

zmiennych obja

ś

niaj

ą

cych model jest poprawny. W przeciwnym przypadku nale

ż

y modyfikowa

ć

zestaw zmiennych. Najcz

ęś

ciej eliminuje si

ę

ze zbioru zmiennych obja

ś

niaj

ą

cych te, które nie

wpływaj

ą

istotnie na zmienn

ą

obja

ś

nian

ą

. Jednak przyczyn

ą

zbyt małych warto

ś

ci odpowiednich

statystyk testuj

ą

cych istotno

ść

parametrów strukturalnych modelu mo

ż

e by

ć

współliniowo

ść

4

Por. Z. Hellwig, Elementy rachunku prawdopodobie

ń

stwa i statystyki matematycznej, PWN Warszawa 1987,

s.270 i nast.

dr Dušan Bogdanov

9

Ekonometria 1

zmiennych obja

ś

niaj

ą

cych, a nie ich zbyt niskie skorelowanie ze zmienn

ą

obja

ś

nian

ą

. W takiej sytuacji

zastosowanie innej kombinacji zmiennych obja

ś

niaj

ą

cych mo

ż

e da

ć

po

żą

dane efekty.

Niepo

żą

dane własno

ś

ci składnika losowego modelu mog

ą

powsta

ć

na skutek nieprawidłowej

postaci analitycznej szacowanej linii. Wtedy wektor reszt b

ę

dzie niesymetryczny lub nielosowy.

Równie

ż

zmiana postaci analitycznej modelu mo

ż

e by

ć

konieczna w przypadku, gdy warto

ść

oczekiwana wektora reszt modelu oka

ż

e si

ę

istotnie ró

ż

na od zera. Badanie tego parametru struktury

stochastycznej modelu jest bowiem wymagane w odniesieniu do modeli nieliniowych, których liniowe

transformanty szacowane s

ą

klasyczn

ą

metod

ą

najmniejszych kwadratów, modeli segmentowych

oraz modeli adaptacyjnych. W pierwszym przypadku pozytywny efekt mo

ż

e przynie

ść

zmiana typu

zastosowanej funkcji lub sposobu estymacji funkcji. W przypadku modeli segmentowych mo

ż

e by

ć

konieczna zmiana długo

ś

ci segmentów lub zmiana modulatorów w poszczególnych segmentach

modelu. Modele adaptacyjne mog

ą

by

ć

poprawione poprzez zmian

ę

długo

ś

ci segmentów.

W sytuacji braku stacjonarno

ś

ci wektora reszt modelu, a wi

ę

c niejednorodno

ś

ci wariancji składnika

losowego, popraw

ę

własno

ś

ci estymatorów parametrów modelu daje zastosowanie uogólnionej

metody najmniejszych kwadratów.

Autokorelacja składnika losowego modelu bywa skutkiem: złego dopasowania postaci analitycznej

modelu, nieprawidłowego doboru zmiennych lub specyfiki modelowanego zjawiska ekonomicznego.

Dwie pierwsze przyczyny wykryte zostan

ą

w trakcie badania symetrii i losowo

ś

ci wektora reszt.

W sytuacji, gdy wyst

ą

pi autokorelacja składnika losowego nale

ż

y zmieni

ć

metod

ę

estymacji modelu.

Badanie normalno

ś

ci rozkładu składnika losowego jest po

żą

dane, gdy model ma by

ć

zastosowany

do prognozowania. Wyst

ą

pienie tego typu rozkładu daje, bowiem wi

ę

ksz

ą

gwarancj

ę

otrzymania

prognoz dopuszczalnych. Natomiast brak normalno

ś

ci rozkładu nie dyskwalifikuje modelu.

dr Dušan Bogdanov

10

Ekonometria 1

Pytania kontrolne:

1. O czym nas informuje współczynnik zgodno

ś

ci?

2. Jaka jest zale

ż

no

ść

pomi

ę

dzy współczynnikiem zgodno

ś

ci a współczynnikiem

determinacji?

3. W jakiej klasie modeli nie ma potrzeby bada

ć

warto

ś

ci oczekiwanej składnika losowego?

4. Do czego słu

ż

y i na czym polega test Durbina-Watsona?

5. Jakie mog

ą

by

ć

przyczyny wyst

ę

powania zjawiska autokorelacji składnika losowego?