J.Ch. 2001

WM2_EgzZAD_01.doc

14.02.2001

Egzamin Nr 2 z Wytrzymałości Materiałów, WIL II, sem. 3

Czas: 150 min.

Nazwisko Imię Podpis Grupa Sala

Uwagi: Wyłożyć indeks do kontroli. Każde zadanie rozwiązywać na osobnej kartce.

Góra każdej kartki musi być opisana wg wzoru zawartego w pierwszym wierszu tabelki.
Można mieć przy sobie tylko czysty papier, kalkulator i przybory do pisania / rysowania.
Po zakończeniu egzaminu składować każde zadanie na osobny stos.

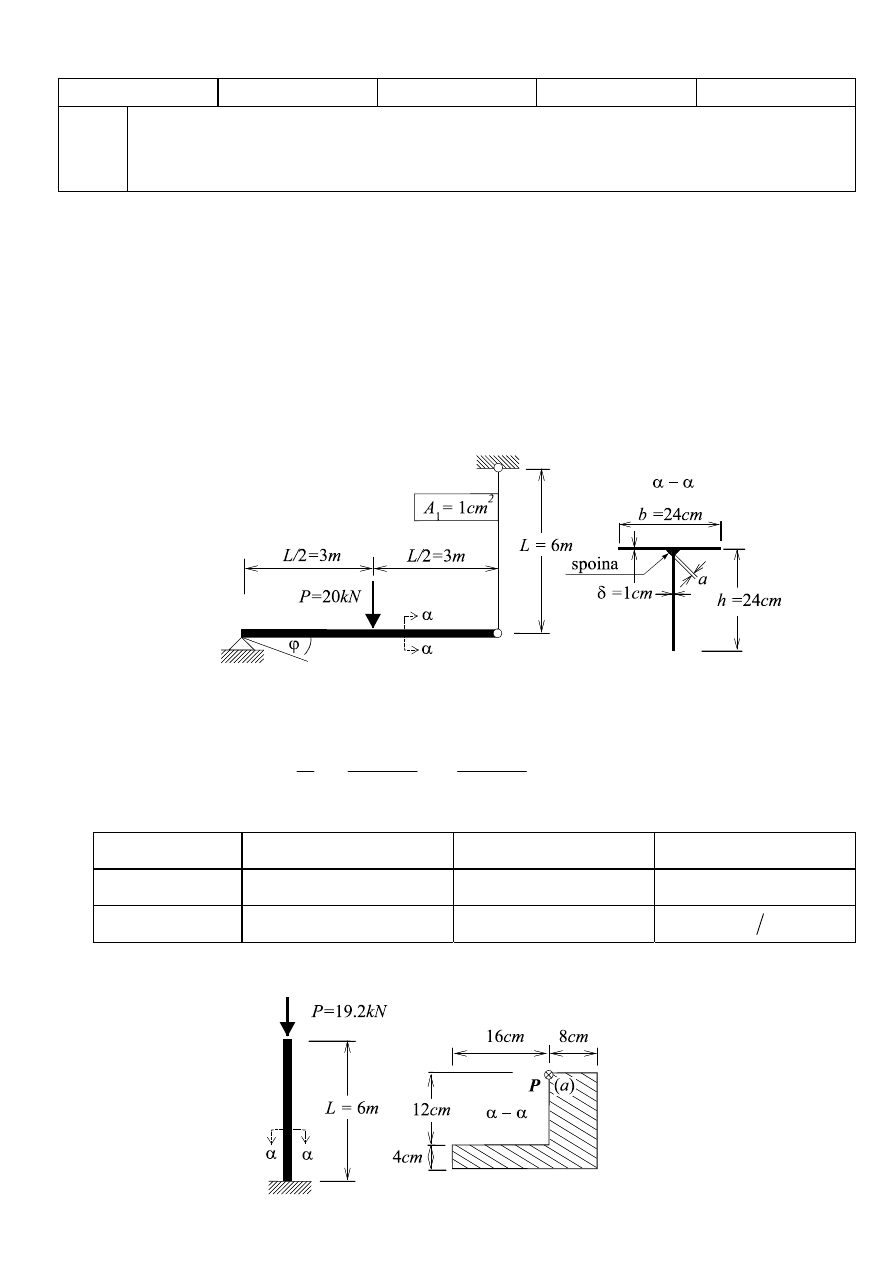
Zadanie 1 (25 pkt.). Stalowa belka o rozpiętości

6

L

m

=

wykonana z teownika o

i stałej

grubości

24

b

h

cm

= =

1cm

δ

=

podwieszona jest na pręcie o polu przekroju

2

1

1

A

cm

=

i długości

6

L

m

=

.

Przyjmując wartość siły

działającej w środku rozpiętości wyznaczyć:

20

P

k

=

N

a) wykresy ekstremalnych naprężeń normalnych

σ

i stycznych

τ

,

b) konieczną grubość

spoin łączących półkę ze środnikiem jeśli naprężenie

dopuszczalne na ścinanie dla spoin wynosi

a

100

ts

k

MPa

=

,

c) obrót

ϕ belki na podporze nieprzesuwnej, jeżeli moduł Younga wynosi

200

E

GPa

=

,

d) wartość graniczną obciążenia

gr

P oraz odpowiadający jej wykres naprężeń normalnych

jeżeli

200

pl

MPa

σ

=

.

Rys. 1.

Zadanie 2

(25 pkt.) Dla podanego przekroju poprzecznego wyznaczyć:

a) wykresy naprężeń normalnych od siły ściskającej

( )19.2

P

kN

= −

w punkcie

,

( )

a

2

2

( , )

1

x

xy

y

xy

x

y

xy

x

y

xy

uJ

vJ

vJ

uJ

N

x y

Ax

A

J J

J

J J

J

σ

⎡

⎤

−

−

=

+

+

⎢

⎥

−

−

⎣

⎦

Ay

,

b) rdzeń przekroju,

wierzchołek \ bok

i

i

y

a x

b

=

+

,

i

0

i

a

≠

0

i

b

≠

0

i

y

b

= ≠

,

(

,

x

)

∈ −∞ +∞

0

i

x

c

= ≠

,

(

,

y

)

∈ −∞ +∞

i

u

(

) /

i

y

xy

i

a J

J

b A

−

/ A

xy

i

J

b

−

/

y

i

J

c A

−

i

v

(

) /

i

xy

x

i

a J

J

b A

−

/

x

i

J

b A

−

xy

i

J

c A

−

c)

płaszczyznę wyboczenia oraz siłę krytyczną w zakresie liniowym, jeżeli

40

E

GPa

=

6

L

m

=

.

Rys. 2.

J.Ch. 2002

WM2_EgzZAD_02.doc

13.02.2002

Egzamin Nr 2 z Wytrzymałości Materiałów, WIL II, sem. 3

Czas: 150 min.

Nazwisko Imię Podpis Grupa Sala

Uwagi: Wyłożyć indeks do kontroli. Każde zadanie rozwiązywać na osobnej kartce.

Góra każdej kartki musi być opisana wg wzoru zawartego w pierwszym wierszu tabelki.
Można mieć przy sobie tylko czysty papier, kalkulator i przybory do pisania / rysowania.
Po zakończeniu egzaminu odłożyć każde zadanie na osobny stos.

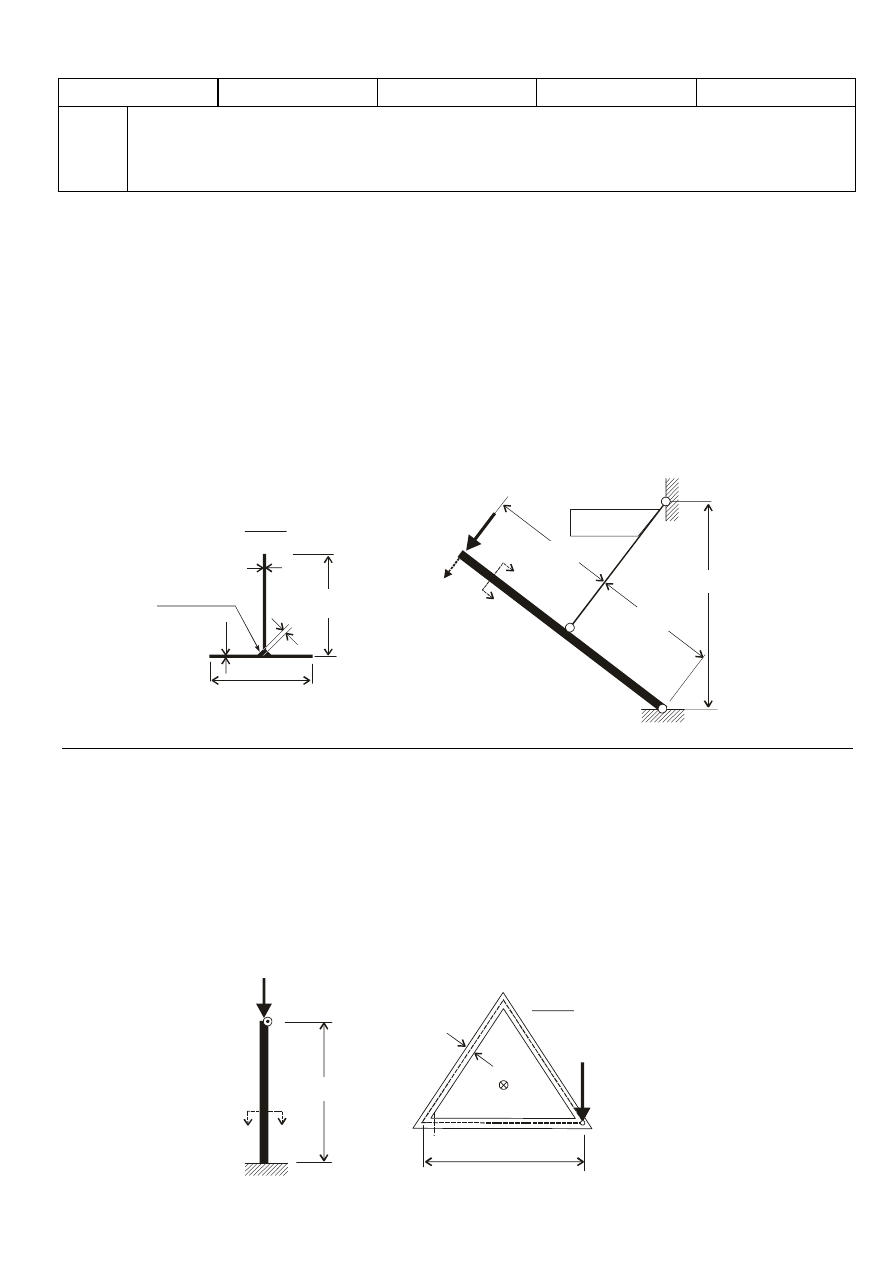
Zadanie 1 (25 pkt.). Nachylona belka teowa (rys. 1)

24

b h

cm

= =

, stała grubość

, długość

1

t

cm

=

6

L

m

=

,

podwieszona jest w środku na pręcie o polu przekroju

2

1

2

A

cm

=

zaczepionym na wysokości

5

H

m

=

.

Przyjmując siłę

działającą prostopadle do belki na jej końcu wyznaczyć:

10

P

k

=

N

a) (12 pkt.) wykresy ekstremalnych naprężeń normalnych

σ i stycznych τ ,

b) (5 pkt.) konieczną grubość spoin łączących półkę ze środnikiem jeśli naprężenie dopuszczalne na

ścinanie dla spoin wynosi

,

a

100

ts

k

M

=

Pa

c) (4 pkt.) przemieszczenie

δ

⊥

prostopadłe do osi belki na jej końcu, jeżeli moduł Younga

,

200

E

G

=

Pa

d) (4 pkt.) wartość graniczną obciążenia

gr

P

oraz odpowiadający jej wykres naprężeń normalnych jeżeli

200

pl

MPa

σ

=

.

δ

P

kN

=10

A = cm

1

2

2

H = m

5

t = cm

1

t = cm

1

b = cm

24

h = cm

24

a

spoina

A A

-

L/ = m

2 3

L/ = m

2 3

A

A

Rys. 1.

Zadanie 2 (25 pkt.) Dla słupa stalowego utwierdzonego w przekroju dolnym (rys. 2) wyznaczyć:

a) (11 pkt.) wykresy ekstremalnych naprężeń normalnych,
b) (2 pkt.) rdzeń przekroju,
c) (4 pkt.) siłę krytyczną wyboczenia, jeżeli moduł sprężystości

200

E

GPa

=

,

a granica proporcjonalności

200

prop

H

R

MPa

σ

=

=

,

d) (4 pkt.) maksymalny kąt skręcenia i maksymalne przemieszczenie poziome,

jeżeli liczba Poissona

1/ 3

ν

=

,

e) (4 pkt.) maksymalne naprężenia zredukowane według hipotezy HMH w przekroju

α α

−

.

α

α

δ =1cm

P = kN

90

H= kN

2.7

L = m

5

A

A A

-

A

a cm

= 30

P

H

( )

a

ŚC

Rys. 2.

J.Ch. & W.G. 2003

WM2_EgzZAD_03.doc

07.02.2003

Egzamin Nr 1 z Wytrzymałości Materiałów, WIL II, sem. 3

Czas: 150 min.

Nazwisko Imię Podpis Grupa Sala

Uwagi: Wyłożyć indeks do kontroli. Każde zadanie rozwiązywać na osobnej kartce.

Góra każdej kartki musi być opisana wg wzoru zawartego w pierwszym wierszu tabelki.
Można mieć przy sobie tylko czysty papier, kalkulator i przybory do pisania / rysowania.
Po zakończeniu egzaminu składować każde zadanie na osobny stos.

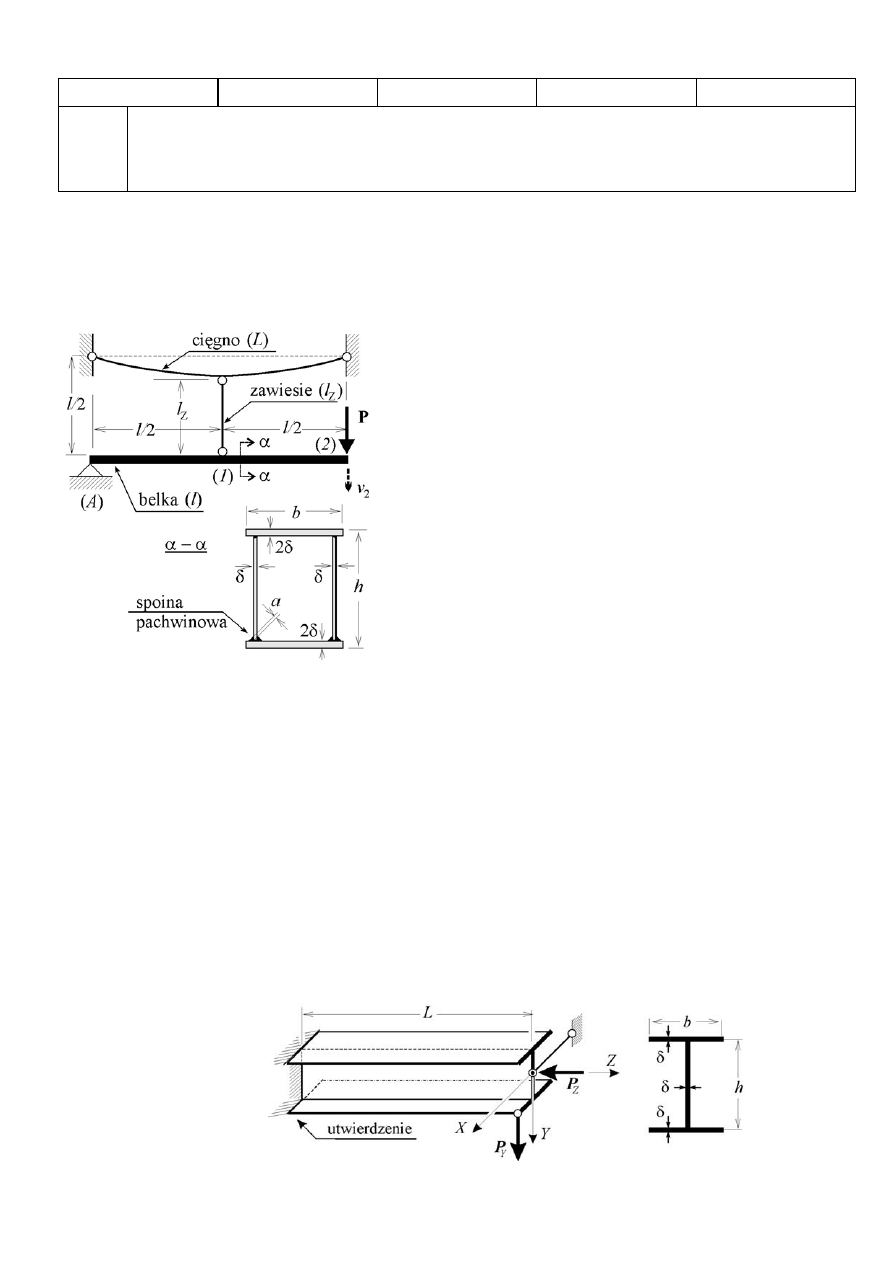
Zadanie 1 (25 pkt.). Stalowa belka skrzynkowa (

200

E

GPa

=

,

36

h

cm

=

,

24

b

cm

=

,

, zob. rys. 1)

o rozpiętości

, podparta przegubowo na lewym końcu (A) jest podwieszona w środku (1)

za pośrednictwem zawiesia (dł.

1

δ

cm

=

m

12

l

=

Z

l

) do cięgna (dł.

12,1

L

m

=

). Założyć, że cała konstrukcja jest

nieważka a zawiesie i cięgno niepodatne. Na swobodnym końcu belki (2) działa pionowa siła .

P

Rys. 1.

a) Dla obciążenia użytkowego

wyznaczyć

wykres naprężeń normalnych

60

P

k

=

N

σ i stycznych τ w

najbardziej wytężonym przekroju belki.

b) Dla

60

P

kN

=

dobrać konieczną grubość

spoin

pachwinowych łączących półkę dolną ze blachami
ścianek pionowych, jeżeli naprężenie dopuszczalne na
ścinanie dla spoin wynosi

.

a

160

ts

k

M

=

Pa

N

c) Dla

60

P

k

=

określić długość zawiesia

Z

l

z warunku

(

2

0

v

=

) zerowego przem. pionowego końca belki (2).

d) Wyznaczyć, tylko ze względu na nośność belki, wartość

dopuszczalną siły

, jeżeli

dop

P

200

dop

MPa

σ

=

.

e) Tak jak w punkcie d) wyznaczyć wartość graniczną siły

gr

P oraz odpowiadający jej wykres naprężeń

normalnych, jeżeli 250

pl

MPa

σ

=

.

Zadanie 2

(25 pkt.) Dla cienkościennej dwuteowej belki stalowej (

24

h

cm

=

,

,

12

b

cm

=

1

δ

cm

=

stałe,

) podpartej i obciążonej (

6

L

= m

96

Z

P

kN

=

,

6,4

Y

P

kN

=

) przestrzenie jak na rys.

2,

wyznaczyć:
a) wykresy ekstremalnych naprężeń normalnych,
b) rdzeń przekroju,
c) siłę krytyczną wyboczenia, jeżeli moduł sprężystości

200

E

GPa

=

, a granica

proporcjonalności

200

prop

H

R

MPa

σ

=

=

,

d) maksymalny kąt skręcenia i maksymalne przemieszczenie pionowe, jeżeli liczba Poissona

,

1/ 4

ν

=

e) maksymalne naprężenia zredukowane według hipotezy HMH w półce w obszarze jej styku ze

środnikiem.

Rys. 2.

J.Ch. & W.G. 2003

WM2_Egz2ZAD_03.doc

17.02.2003

Egzamin Nr 2 z Wytrzymałości Materiałów, WIL II, sem. 3

Czas: 150 min.

Nazwisko Imię Podpis Grupa Sala

Uwagi: Wyłożyć indeks do kontroli. Każde zadanie rozwiązywać na osobnej kartce.

Góra każdej kartki musi być opisana wg wzoru zawartego w pierwszym wierszu tabelki.
Można mieć przy sobie tylko czysty papier, kalkulator i przybory do pisania / rysowania.
Po zakończeniu egzaminu składować każde zadanie na osobny stos.

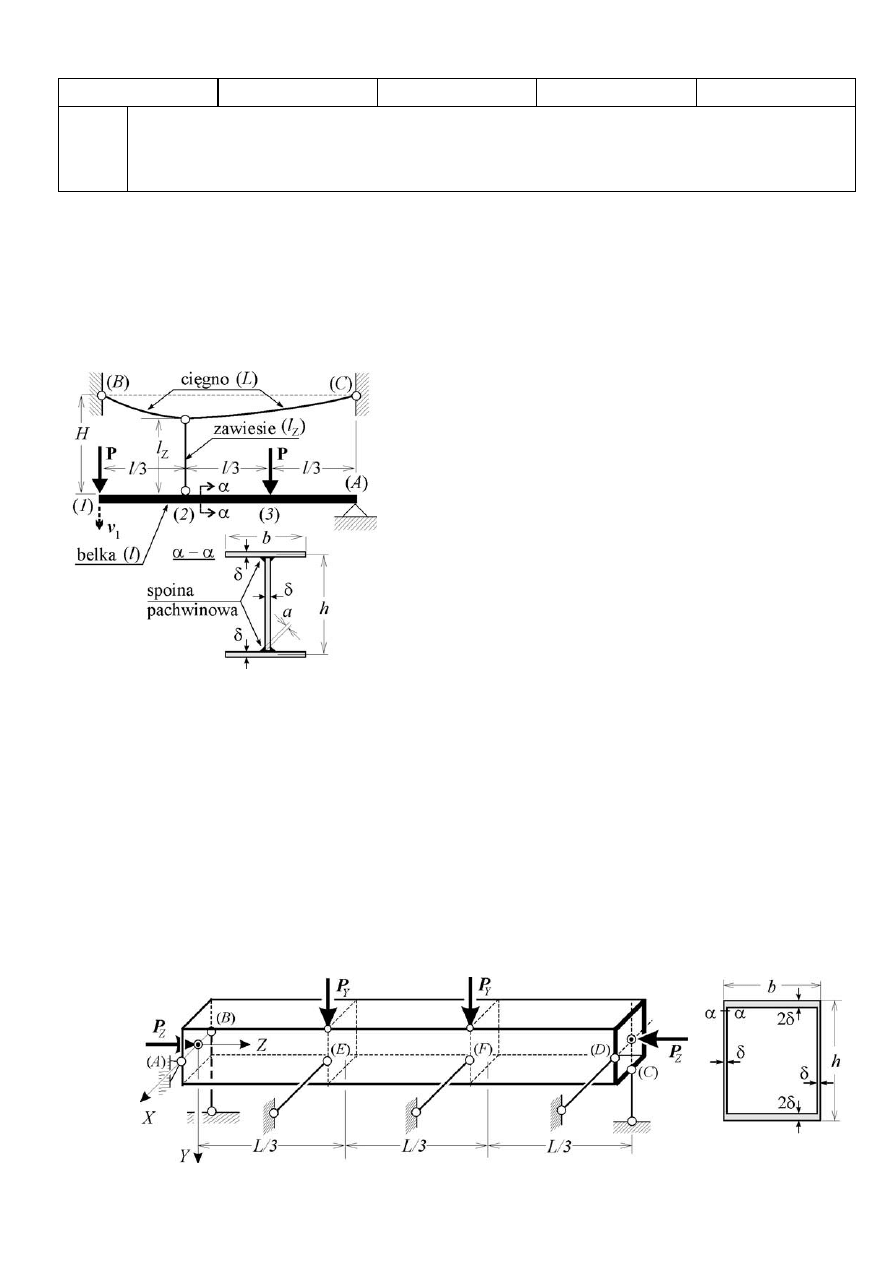
Zadanie 1 (25 pkt.). Stalowa dwuteowa belka cienkościenna (

200

E

GPa

=

,

,

,

36

h

c

=

18

b

c

=

1

δ

cm

m

m

=

,

rys. 1) o rozpiętości

, podparta przegubowo na prawym końcu (A) jest

podwieszona w

1/

rozpiętości (2) za pośrednictwem zawiesia (dł.

3 6 18

l

= × = m

3

Z

l

) do cięgna

(dł.

). Założyć, że cała konstrukcja jest nieważka a zawiesie i cięgno niepodatne. Na

swobodnym końcu belki pkt. 1 i w

rozpiętości pkt. 3 działają dwie równe pionowe siły .

18,05

L

=

m

2 / 3

P

Rys. 1.

a) Dla obciążenia użytkowego

wyznaczyć

wykres naprężeń normalnych

24

P

k

=

N

σ i stycznych τ w

najbardziej wytężonym przekroju belki.

b) Dla

24

P

kN

=

dobrać konieczną grubość

spoin

pachwinowych

łączących półki ze środnikiem.

Naprężenie dop. na ścinanie dla spoin

.

a

160

ts

k

M

=

Pa

N

c) Dla

24

P

k

=

i różnicy poziomów

(zawieszenia

cięgna i wierzchu belki) określić długość zawiesia

4

H

m

=

Z

l

, tak

aby po obciążeniu pkt. (1) na początku belki znalazł się
na tym samym poziomie co podpora (A).

d) Wyznaczyć, tylko ze względu na nośność belki, wartość

dopuszczalną siły

, jeżeli

dop

P

200

dop

MPa

σ

=

.

e) Tak jak w punkcie d), wyznaczyć wartość graniczną sił

gr

P

i odpowiadający im wykres naprężeń normalnych,

jeżeli

260

pl

MPa

σ

=

.

Zadanie 2

(25 pkt.) Dla skrzynkowej belki stalowej ze czterema sztywnymi przeponami (rys. 2,

1

δ

cm

=

,

wymiary całkowite:

,

50

h

cm

=

25

b

cm

=

,

3 7 21

L

m

= × =

), podpartej (w pkt. od A do F)

i obciążonej (

192

Z

P

kN

=

,

84

Y

P

kN

=

) przestrzenie jak na rys. 2, wyznaczyć:

a) wykresy ekstremalnych naprężeń normalnych, b) rdzeń przekroju,
c) siłę krytyczną wyboczenia od ściskania osiowego (

), jeżeli moduł sprężystości

KR

Z

P

200

E

GPa

=

, a granica proporcjonalności

210

prop

H

R

MPa

σ

=

=

,

d) maksymalny kąt skręcenia i maksymalne przemieszczenie pionowe (wsp. Poissona

1/4

ν

=

),

e) ekstremalne naprężenia zredukowane według hipotezy HMH w lewej ściance pionowej

pod półką (

.

α α)

−

Rys. 2.

07.03.2003

Egzamin Nr 3 z Wytrzymałości Materiałów, WIL II, sem. 3

Czas: 150 min.

____________________________________________________________________________________________________________________________________
J.Ch. & W.G. 2003

Zadanie nr 1, str. 1/6

WM2_Egz3ZAD1_03.doc

Nazwisko Imię Podpis

Nr

albumu

Grupa

Sala

Uwaga.

Wypełnić górę każdej z kartek. Wyłożyć indeks do kontroli. Można mieć przy sobie tylko kalkulator i przybory
do pisania/rysowania. Rozwiązania (także brudnopis) zmieścić tylko w otrzymanym zeszycie egzaminacyjnym.

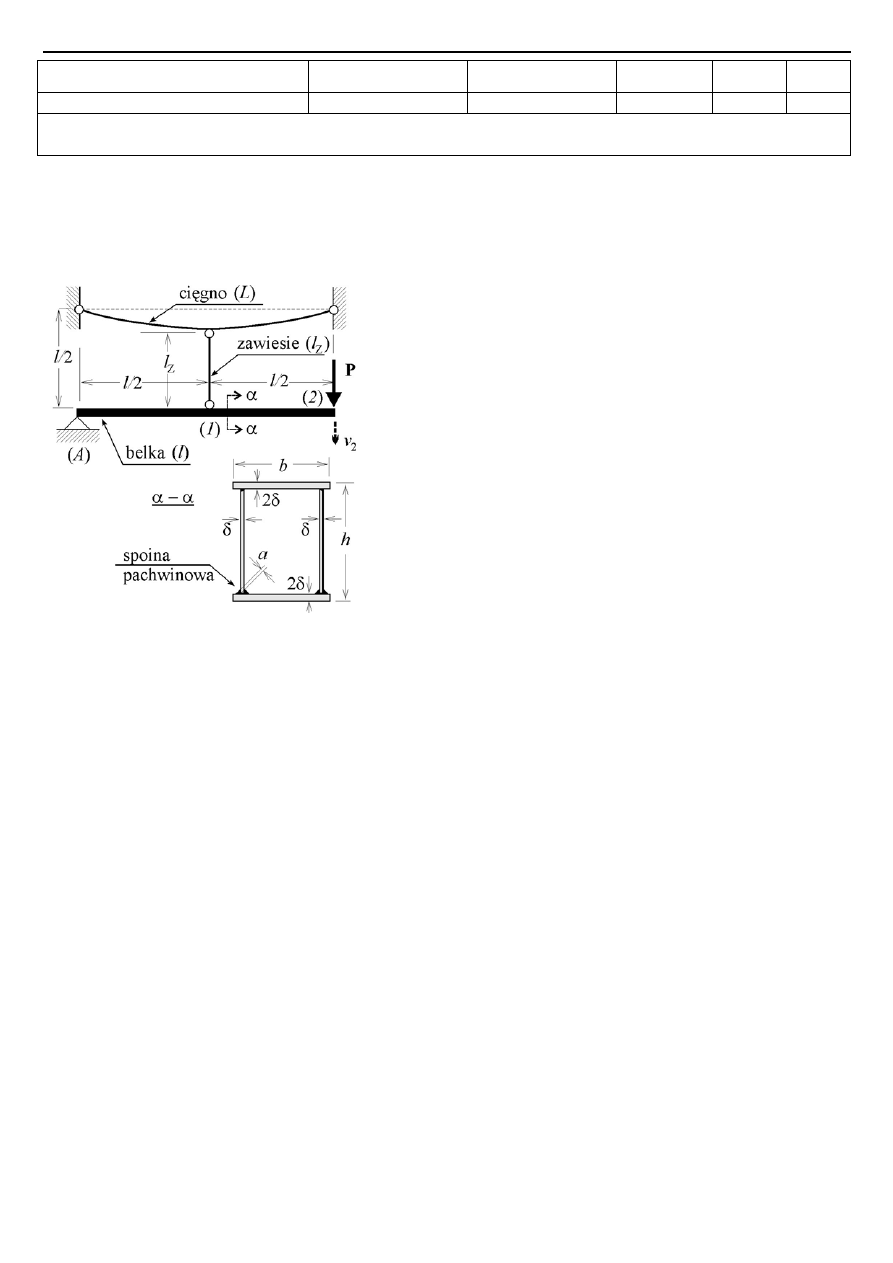
Zadanie 1 (25 pkt.). Stalowa belka skrzynkowa (

200

E

GPa

=

, 36

h

cm

=

, 24

b

cm

=

,

, zob. rys. 1)

o rozpiętości

, podparta przegubowo na lewym końcu (A) jest podwieszona w środku (1) za

pośrednictwem zawiesia (dł.

1

δ

cm

=

m

12

l

=

Z

l

) do cięgna (dł. 12,1

L

m

=

). Założyć, że cała konstrukcja jest

nieważka a zawiesie i cięgno niepodatne. Na swobodnym końcu belki (2) działa pionowa siła .

P

Rys. 1.

a) Dla obciążenia użytkowego

wyznaczyć wykres

naprężeń normalnych

60

P

k

=

N

σ i stycznych τ w najbardziej

wytężonym przekroju belki.

b) Dla 60

P

kN

=

dobrać konieczną grubość

spoin

pachwinowych łączących półkę dolną ze blachami
ścianek pionowych, jeżeli naprężenie dopuszczalne na
ścinanie dla spoin wynosi

.

a

160

ts

k

M

=

Pa

N

c) Dla 60

P

k

=

określić długość zawiesia

Z

l

, tak aby po

obciążeniu pkt. (2) na końcu belki znalazł się na tym
samym poziomie co podpora (A).

d) Wyznaczyć, tylko ze względu na nośność belki, wartość

dopuszczalną siły

, jeżeli

dop

P

200

dop

MPa

σ

=

.

e) Tak jak w punkcie d) wyznaczyć wartość graniczną siły

gr

P oraz odpowiadający jej wykres naprężeń normalnych,

jeżeli 250

pl

MPa

σ

=

.

07.03.2003

Egzamin Nr 3 z Wytrzymałości Materiałów, WIL II, sem. 3

Czas: 150 min.

____________________________________________________________________________________________________________________________________
J.Ch. & W.G. 2003

Zadanie nr 2, str. 1/6

WM2_Egz3ZAD2_03.doc

Nazwisko Imię Podpis

Nr

albumu

Grupa

Sala

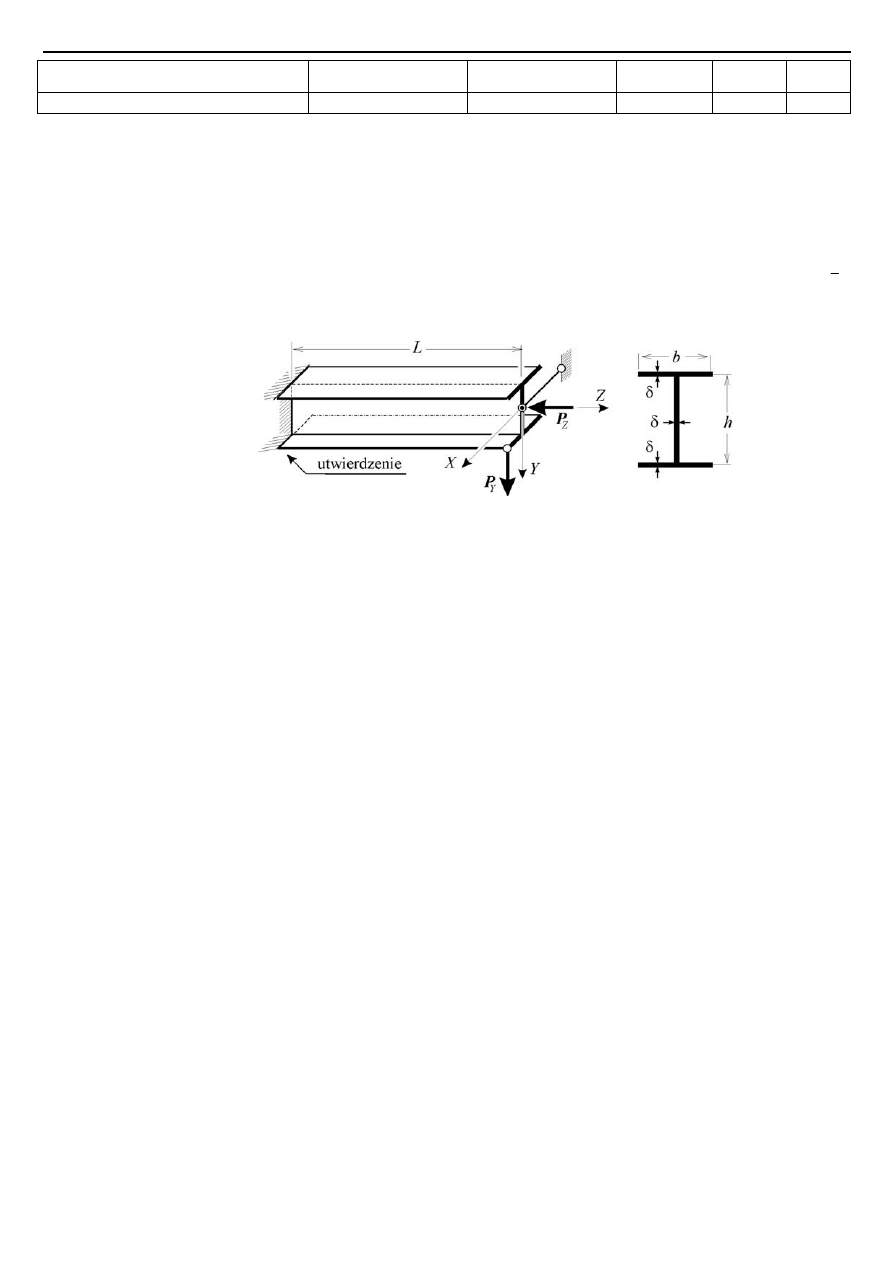
Zadanie 2 (25 pkt.) Dla cienkościennej dwuteowej belki stalowej (

24

h

cm

=

,

,

12

b

c

=

m

1

δ

cm

=

stałe,

6

L

m

=

) podpartej i obciążonej (

96

Z

P

kN

=

,

6,4

Y

P

kN

=

) przestrzenie jak na rys. 2, wyznaczyć:

a) wykresy ekstremalnych naprężeń normalnych, b) rdzeń przekroju,
c) siłę krytyczną wyboczenia, jeżeli moduł sprężystości

200

E

GPa

=

, a granica proporcjonalności

200

prop

H

R

MPa

σ

=

=

,

d) maksymalny kąt skręcenia i maksymalne przemieszczenie pionowe, jeżeli liczba Poissona

1

4

ν

= ,

e) maksymalne naprężenia zredukowane według hipotezy HMH w półce w obszarze jej styku ze

środnikiem.

Rys. 2.

02.02.2004

Egzamin Nr 1 z Wytrzymałości Materiałów, WIL II, sem. 3

Czas: 150 min.

____________________________________________________________________________________________________________________________________
J.Ch. & W.G. 2004

Zadanie nr 1, str. 1/6

WM2_Egz1ZAD1_04.doc

Nazwisko Imię Podpis

Nr

albumu

Grupa

Sala

Uwaga.

Wypełnić górę każdej z kartek. Wyłożyć indeks do kontroli. Można mieć przy sobie tylko kalkulator i przybory
do pisania/rysowania. Rozwiązania (także brudnopis) zmieścić tylko w otrzymanym zeszycie egzaminacyjnym.

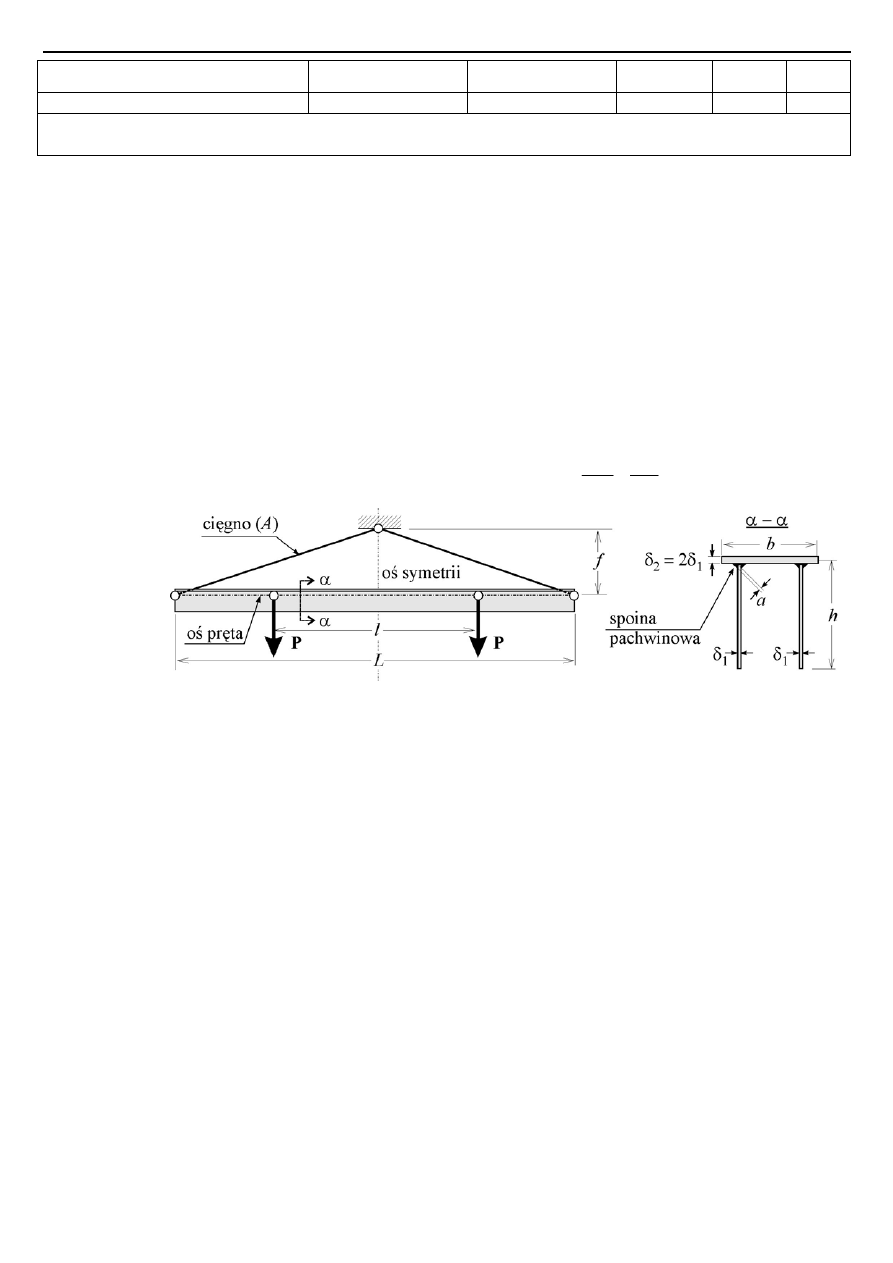
Zadanie 1 (25 pkt.). Stalową (

E

G

,

200 P

=

a

240

dop

σ

MPa

=

, 350

pl

σ

MPa

=

) cienkościenną belkę korytkową

( h

c ,

,

,

60

=

m

48

=

b

cm

1

śr

δ δ

odników

2cm

≡

=

δ

δ

2

półki

4cm

≡

=

, zob. rys. 1) o rozpiętości 16

L

m

=

,

zawieszono na cięgnie o strzałce 4

f

m

=

. Stalowe cięgno (o tych samych stałych materiałowych co

belka) zaczepiono na końcach belki w środku ciężkości przekroju. Symetrycznie w rozstawie

działają dwie siły skupione . Wyznaczyć co następuje, w obliczeniach założyć, że cała

konstrukcja jest nieważka a cięgno niepodatne.

8

l

m

=

P

1) Dla obciążenia użytkowego 150

P

kN

=

określić niezbędny przekrój cięgna.

A

2) Dla

wyznaczyć wykres ekstremalnych naprężeń normalnych

150

P

k

=

N

σ .

3) Dla

wyznaczyć maksymalne wygięcie belki względem punktów zawieszenia.

150

P

k

=

N

4) Wyznaczyć, tylko ze względu na nośność belki, wartość dopuszczalną siły

.

dop

P

5) Wyznaczyć, tylko ze względu na nośność belki, wartość graniczną siły

gr

P wykorzystując,

obowiązujący dla przekrojów cienkościennych warunek

1

gr

gr

M

N

M

N

+

=

.

Rys. 1

2.02.2004

Egzamin Nr 1 z Wytrzymałości Materiałów, WIL II, sem. 3

Czas: 150 min.

____________________________________________________________________________________________________________________________________
J.Ch. & W.G. 2004

Zadanie nr 2, str. 1/6

WM2_Egz1ZAD2_04.doc

Nazwisko Imię Podpis

Nr

albumu

Grupa

Sala

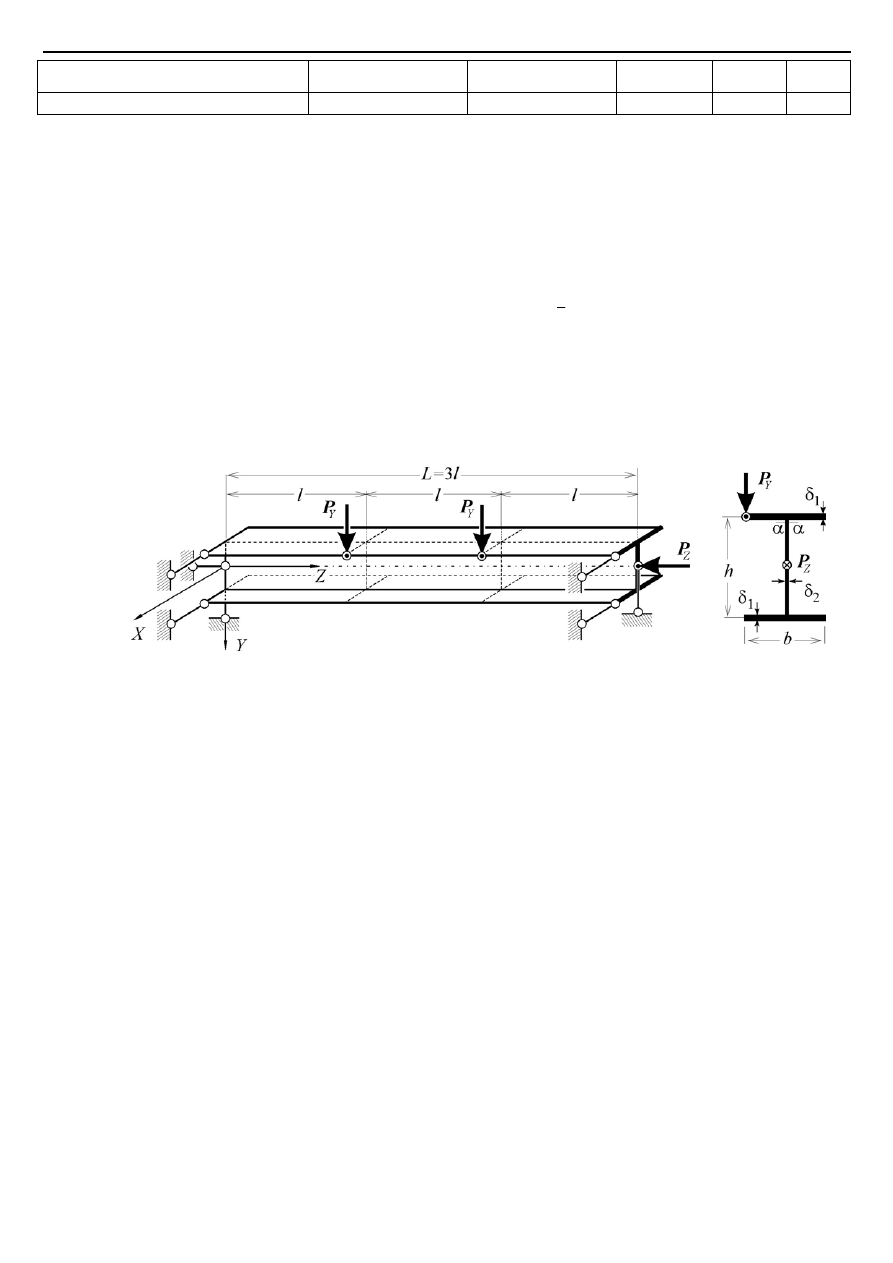
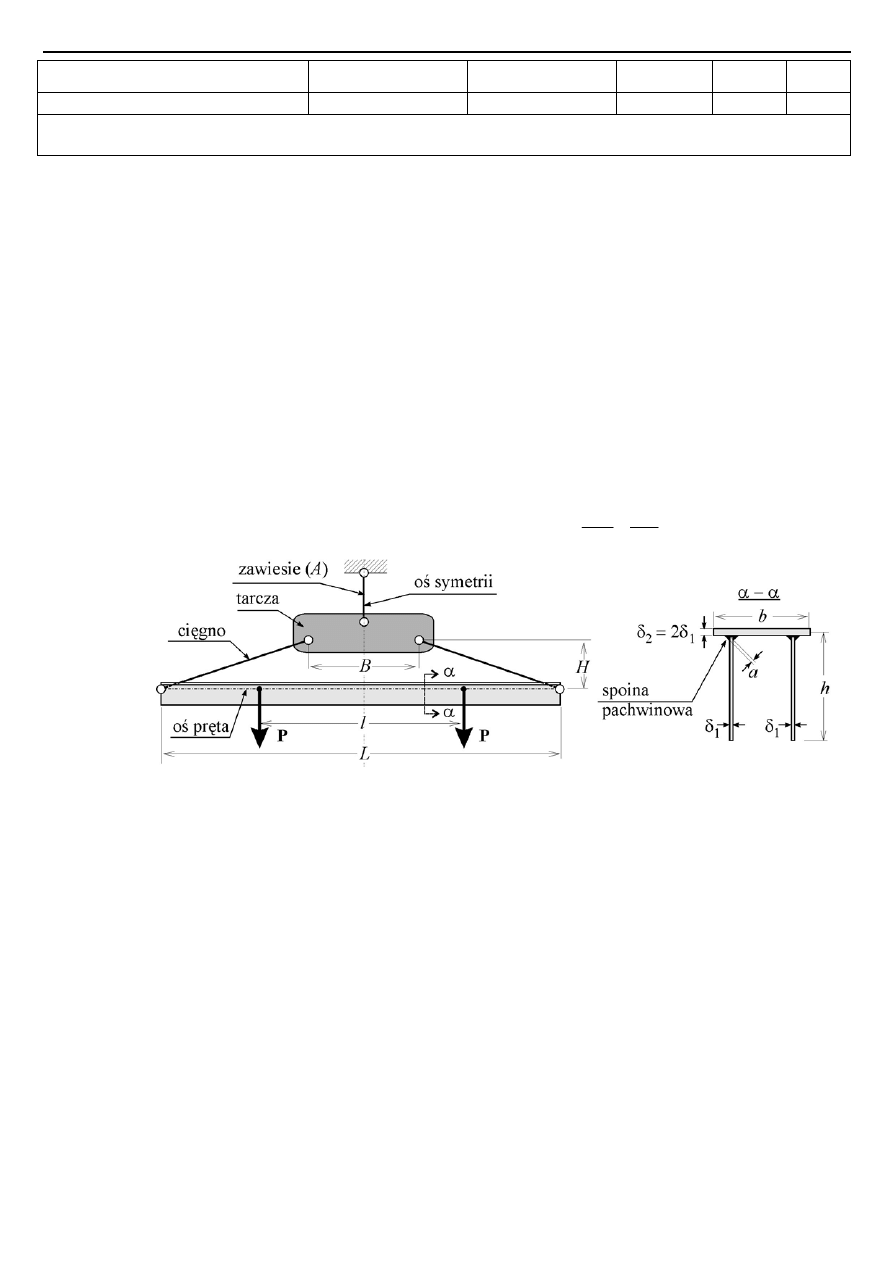
Zadanie 2 (25 pkt.) Dla cienkościennej dwuteowej belki stalowej (

36

h

cm

=

,

,

24

b

c

=

m

1

półek

2

δ δ

cm

≡

=

100

Y

P

k

,

,

) swobodnie podpartej na zginanie i obustronnie

utwierdzonej na skręcanie oraz obciążonej przestrzenie dwoma siłami pionowymi

2

środnika

1

δ

δ

cm

≡

=

3

3 4

12

L

l

m

= × = ×

=

m

N

=

i

poziomą siłą ściskającą

jak na rys. 2, wyznaczyć:

400

Z

P

kN

=

1) siłę krytyczną wyboczenia sprężystego, jeżeli moduł sprężystości

,

200

E

G

=

Pa

2) wykres ekstremalnych naprężeń normalnych (

),

( )

σ y

3) maksymalny kąt skręcenia, jeżeli liczba Poissona

1

4

ν

= ,

4) naprężenia styczne w:

τ

4.1) skręcaniu swobodnym – wartości maksymalne w półce (

) i środniku

,

max

półka

τ

max

środnik

τ

4.2) ścinaniu przy zginaniu – wykres naprężeń ekstremalnych

,

( )

τ s

6) naprężenia zredukowane według hipotezy HMH w przekroju

α α

−

górnej części środnika.

Rys. 2

19.02.2004

Egzamin Nr 2 z Wytrzymałości Materiałów, WIL II, sem. 3

Czas: 150 min.

____________________________________________________________________________________________________________________________________
J.Ch. & W.G. 2004

Zadanie nr 1, str. 1/6

WM2_Egz2ZAD1_04.doc

Nazwisko Imię Podpis

Nr

albumu

Grupa

Sala

Uwaga.

Wypełnić górę każdej z kartek. Wyłożyć indeks do kontroli. Można mieć przy sobie tylko kalkulator i przybory
do pisania/rysowania. Rozwiązania (także brudnopis) zmieścić tylko w otrzymanym zeszycie egzaminacyjnym.

Zadanie 1 (25 pkt.). Stalową (

E

G

,

200 P

=

a

240

dop

σ

MPa

=

, 350

pl

σ

MPa

=

) cienkościenną belkę korytkową

( h

c ,

,

,

60

=

m

48

=

b

cm

1

śr

δ δ

odników

2cm

≡

=

δ

δ

2

półki

4cm

≡

=

, zob. rys. 1) o rozpiętości 16

L

m

=

,

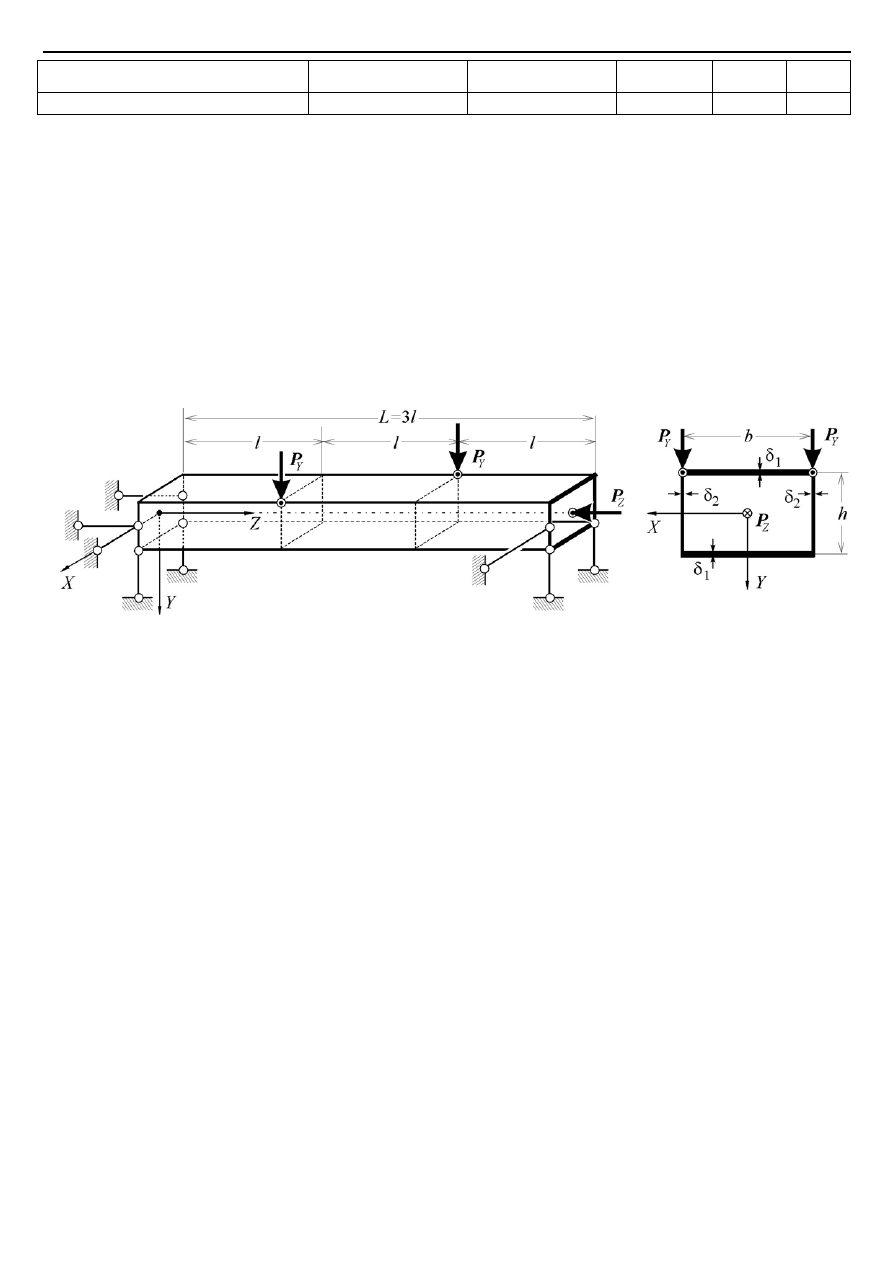
zawieszono na symetrycznym układzie podtrzymującym złożonym ze sztywnej tarczy

4

B

m

=

,

cięgien

i zawiesia. Cięgna łączące tarczę z belką zaczepiono na końcach belki w środku

ciężkości przekroju. Na belkę symetrycznie w rozstawie l

3m

H

=

8m

=

działają dwie siły skupione .

W obliczeniach założyć, że cała konstrukcja jest nieważka a układ podtrzymujący niepodatny.
Wyznaczyć:

P

1) minimalny przekrój zawiesia dla obciążenia użytkowego

A

150

P

kN

=

i

,

300

dop

σ

MPa

=

2) wykres ekstremalnych naprężeń normalnych

σ w belce przy

,

150

P

k

=

N

N

3) niezbędną grubość spoin pachwinowych łączących półkę ze środnikami (dla

a

150

P

k

=

i

naprężeń dopuszczalnych na ścinanie dla spoin

k

M

160

ts

Pa

=

),

4) maksymalne wygięcie belki względem punktów zawieszenia dla

,

150

P

k

=

N

5) wartość graniczną obciążenia

gr

P , tylko ze względu na nośność belki, wykorzystując

obowiązujący dla przekrojów cienkościennych warunek

1

gr

gr

M

N

M

N

+

=

.

Rys. 1

19.02.2004

Egzamin Nr 2 z Wytrzymałości Materiałów, WIL II, sem. 3

Czas: 150 min.

____________________________________________________________________________________________________________________________________
J.Ch. & W.G. 2004

Zadanie nr 2, str. 1/6

WM2_Egz2ZAD2_04.doc

Nazwisko Imię Podpis

Nr

albumu

Grupa

Sala

Zadanie 2 (25 pkt.) Belka (

3

3 4

12

L

l

m

m

= × = ×

=

) stalowa (

200

E

GPa

=

,

) o cienkościennym

przekroju skrzynkowym (

,

0.25

ν

=

24

h

cm

=

48

b

cm

=

,

1

półek

2cm

δ δ

≡

=

2

,

ścianki

1

δ

δ

cm

≡

=

kN

) jest podparta w

sposób zróżnicowany w płaszczyznach zginania i obustronnie utwierdzona na skręcanie (rys. 2).
Belka obciążona jest przestrzennie dwoma siłami pionowymi

140

Y

P

=

i poziomą siłą ściskającą

jak na rys. 2. Wyznaczyć:

420

Z

P

=

kN

1) siły krytyczne wyboczenia sprężystego w obu płaszczyznach wyboczenia

X Z

− i Y Z

− ,

2) wykres ekstremalnych naprężeń normalnych (

),

( )

σ Y

3) rdzeń przekroju,
4) wykres kąta skręcenia belki,
5) maksymalne naprężenia styczne w półce

i środniku

w skręcaniu swobodnym.

max

półka

τ

max

środnik

τ

Rys. 2

31.01.2005

Egzamin Nr 1 z Wytrzymałości Materiałów, WILiŚ II, sem. 3

Czas: 150 min.

____________________________________________________________________________________________________________________________________
J.Ch. & W.G / M.S.. 2005

Zadanie nr 1, str. 1/1

WM2_Egz1ZAD1_05.doc

Nazwisko Imię Podpis

Nr

albumu

Grupa

Sala

Uwaga.

Wypełnić górę w obu formularzach. Wyłożyć indeks do kontroli. Można mieć przy sobie tylko kalkulator i przybory
do pisania/rysowania. Rozwiązania (także brudnopis) zmieścić tylko na otrzymanym formularzu egzaminacyjnym.

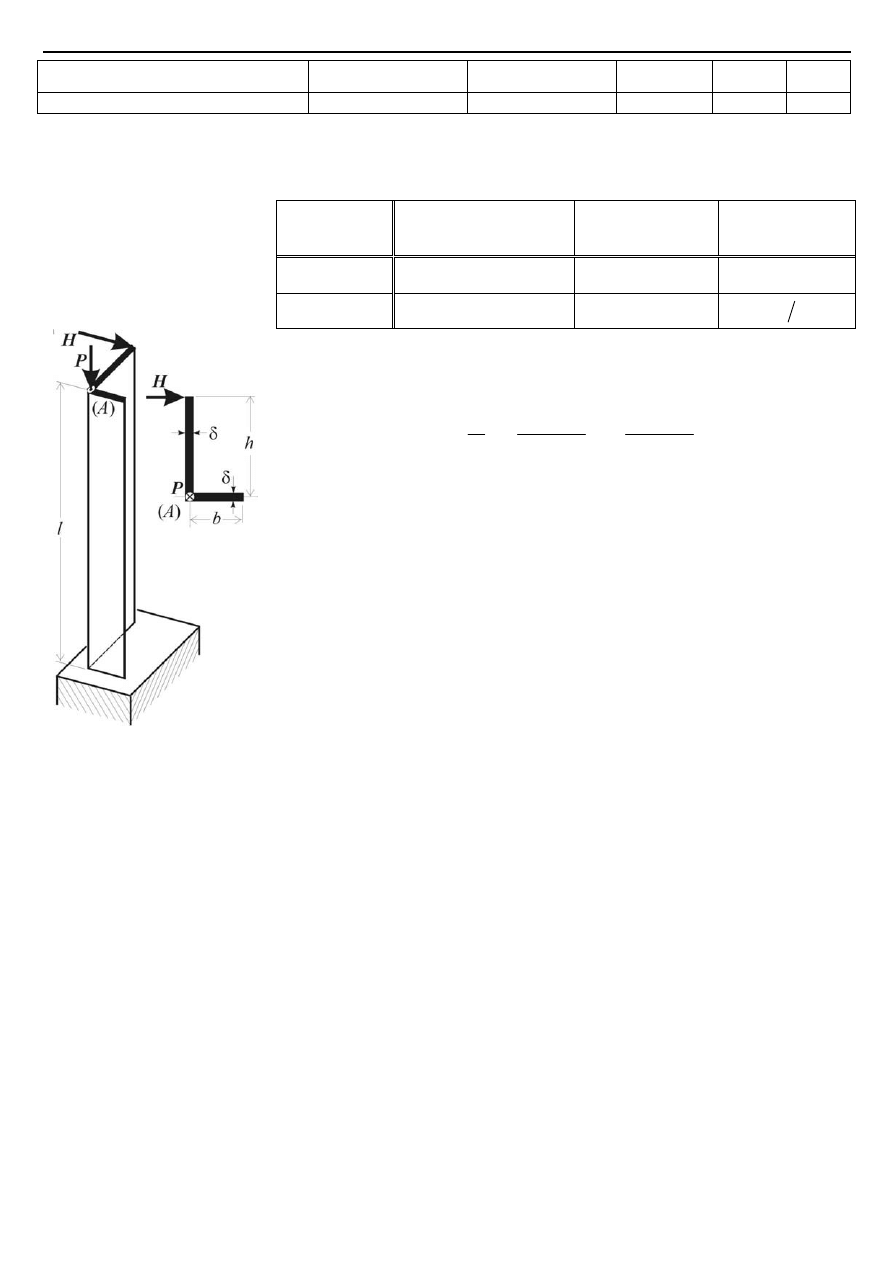
Zadanie 1 (30 pkt.). Stalową (

200

E

GPa

=

,

280

pl

σ

MPa

=

) grubościenną belkę dwuteową (

24

h

cm

=

,

,

,

), o rozpiętości

12

b

cm

=

1

2

δ

cm

=

2

4

δ

cm

=

3

3 2

6

L

a

m

m

= × = ×

=

, podwieszono na wysokości

1.5

H

m

=

na ukośnym cięgnie (rys.

1). Stalowe cięgno (

200

E

GPa

=

,

,

240

dop c

σ

MPa

=

,

) o przekroju zaczepiono na końcach belki w środku ciężkości przekroju.

Symetrycznie w rozstawie

działają dwie siły skupione . W obliczeniach założyć, że cała

konstrukcja jest nieważka, a skrócenie belki pomijalnie małe. Dla obciążenia użytkowego

obliczyć:

,

380

pl c

σ

MPa

=

A

2

a

= m

N

Pa

P

60

P

k

=

1) niezbędny przekrój cięgna,

A

2) wyznaczyć wykres ekstremalnych naprężeń normalnych ,

σ

3) wyznaczyć wykres ekstremalnych naprężeń stycznych ,

τ

4) zaprojektować niezbędną wysokość spoiny pachwinowej, przyjmując

,

a

60

spoiny

t

dop

k

M

≡

=

τ

5) naprężenia zredukowane wg hipotezy HMH w przecięciu

β β

−

dolnej części środnika

i przekroju wzdłuż belki położonym, tuż na zewnątrz za miejscem działania sił obciążających;

przyjmując do dalszych obliczeń przekrój cięgna równy

2

5

A

cm

=

6) wyznaczyć przemieszczenie pionowe układu w środku belki (punkt C),
7) wyznaczyć wartość graniczną siły

gr

P

całego układu, dla uproszczenia obliczeń w belce

przyjąć warunek

|

| |

|

1

gr

gr

M

N

M

N

+

=

.

Rys. 1

31.01.2005

Egzamin Nr 1 z Wytrzymałości Materiałów, WILiŚ II, sem. 3

Czas: 150 min.

____________________________________________________________________________________________________________________________________
J.Ch. & W.G. / M.S. 2005

Zadanie nr 2, str. 1/1

WM2_Egz1ZAD2_04.doc

Nazwisko Imię Podpis

Nr

albumu

Grupa

Sala

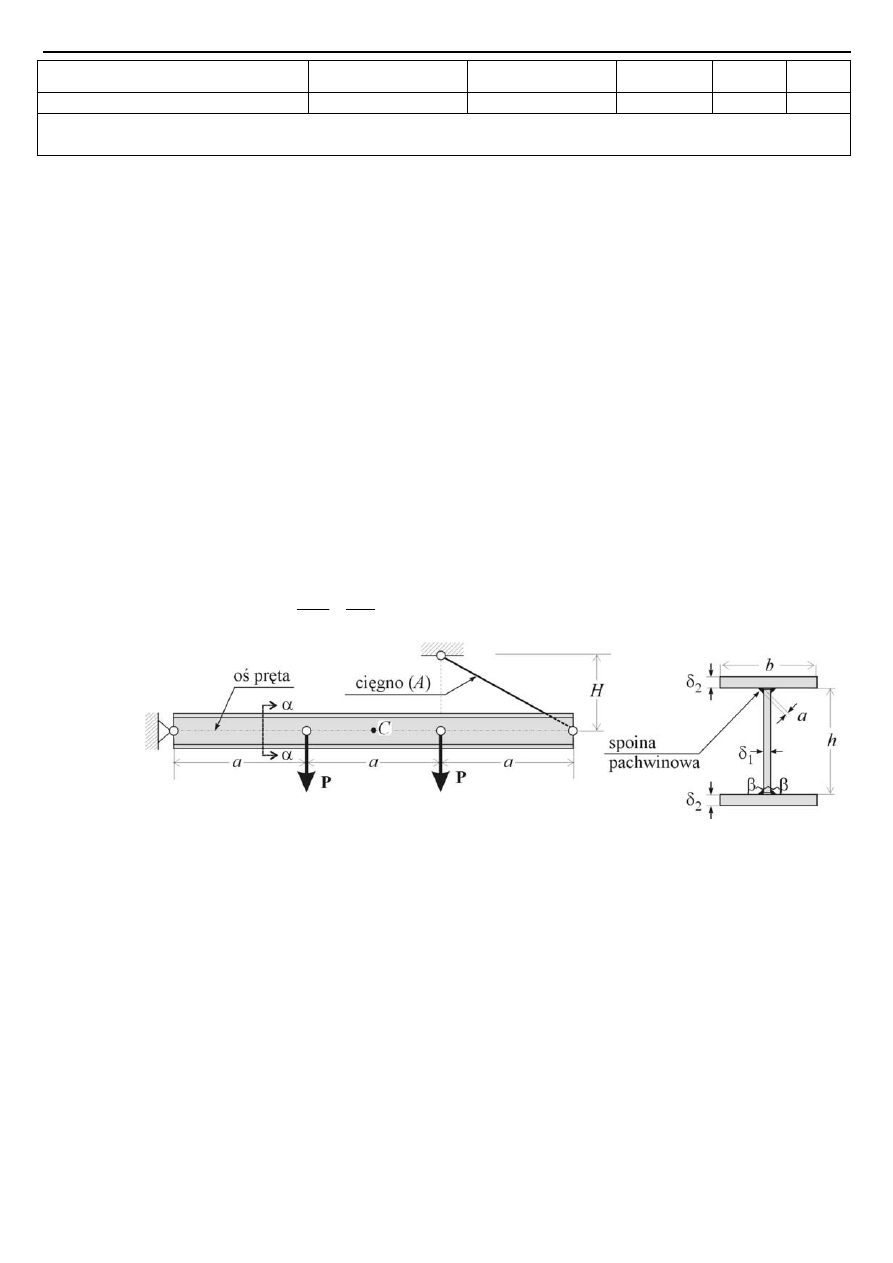
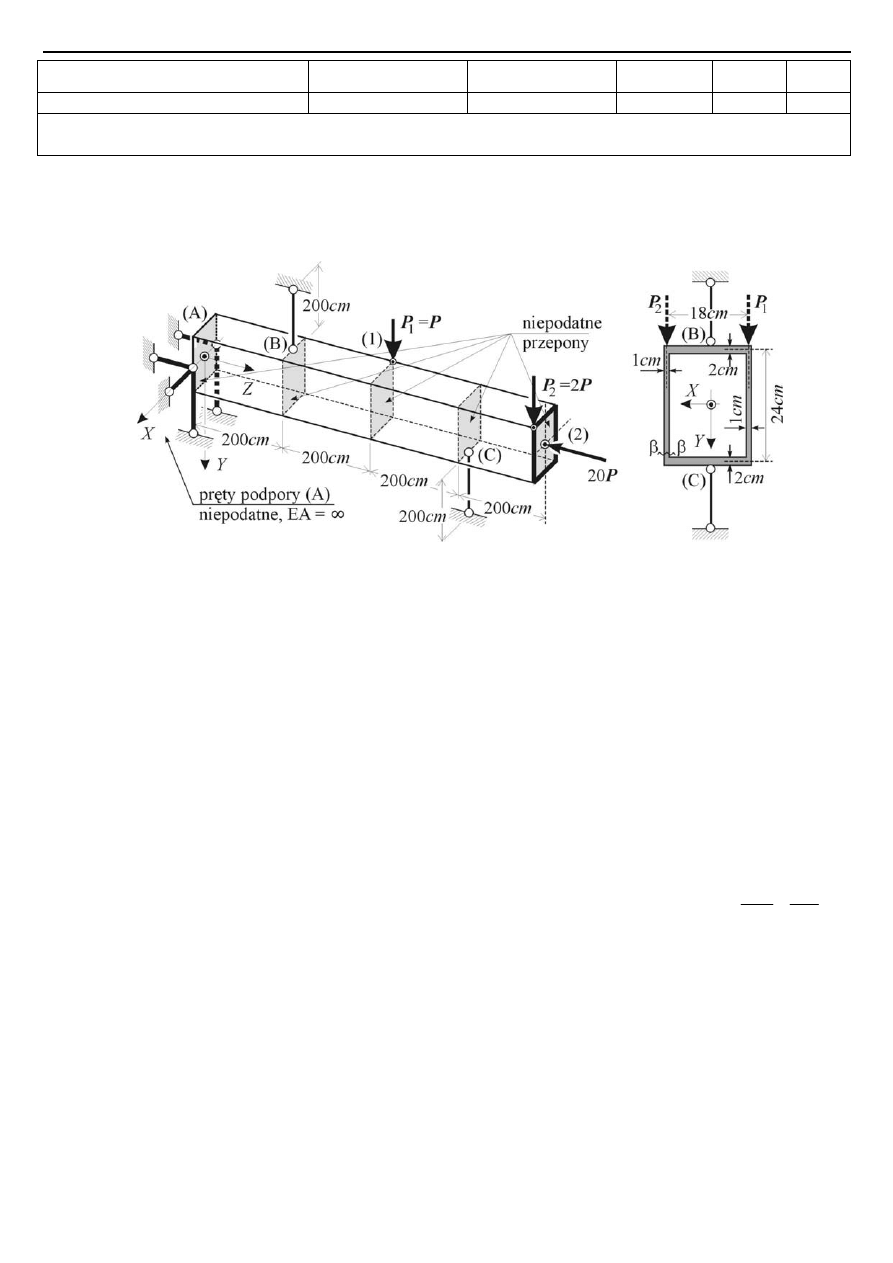
Zadanie 2 (25 pkt.) Dla cienkościennego stalowego wspornika o przekroju typu L (

200

E

GPa

=

,

24

h

cm

=

,

,

,

) obciążonego przestrzenie siłą pionową

i poziomą siłą

skręcającą

12

b

c

=

m

N

1

δ

cm

=

3

l

m

=

90

P

k

=

2,5

H

kN

=

jak na rys. 2, wyznaczyć:

bok

wierzchołek

i

i

y a x b

=

+ ,

0

i

a

≠ ,

0

i

b

≠

0

i

y b

= ≠ ,

(

,

x

)

∈ −∞ +∞

0

i

x c

= ≠ ,

(

,

y

)

∈ −∞ +∞

i

u

(

) /

i

y

xy

i

a J

J

b A

−

/

xy

i

J

b A

−

/

y

i

J c A

−

i

v

(

) /

i

xy

x

i

a J

J

b A

−

/

x

i

J b A

−

xy

i

J

c A

−

1) rdzeń przekroju,
2) wykresy naprężeń normalnych

σ

od siły ściskającej w punkcie

P

( )

A

leżącego na przecięciu osi ścianek profilu L

2

2

( , )

1

x

xy

y

xy

x

y

xy

x

y

xy

uJ vJ

vJ uJ

N

x y

Ax

A

J J J

J J J

σ

Ay

⎡

⎤

−

−

=

+

+

⎢

⎥

−

−

⎢

⎥

⎣

⎦

,

3) wskazać położenie środka skręcania (zginania),
4) maksymalny kąt skręcenia, jeżeli liczba Poissona

,

0.25

ν

=

5) naprężenia styczne od skręcania (traktowanego jak swobodne)

– wartości maksymalną (

),

τ

max

τ

6) główne centralne momenty bezwładności przekroju poprzecznego oraz

odpowiadające im kierunki główne,
sprawdzić przy pomocy koła Mohra,

7) zakładając, że siła pionowa poprzez głowicę, działa w osi pręta, wskazać

płaszczyznę wyboczenia oraz obliczyć siłę krytyczną w zakresie
liniowym.

Rys. 2.

14.02.2005

Egzamin Nr 2 z Wytrzymałości Materiałów, WILiŚ II, sem. 3

Czas: 150 min.

____________________________________________________________________________________________________________________________________
J.Ch. & W.G / M.S.. 2005

Zadanie nr 1, str. 1/1

WM2_Egz2ZAD1_05.doc

Nazwisko Imię Podpis

Nr

albumu

Grupa

Sala

Uwaga.

Wypełnić górę w obu formularzach. Wyłożyć indeks do kontroli. Można mieć przy sobie tylko kalkulator i przybory
do pisania/rysowania. Rozwiązania (także brudnopis) zmieścić tylko na otrzymanym formularzu egzaminacyjnym.

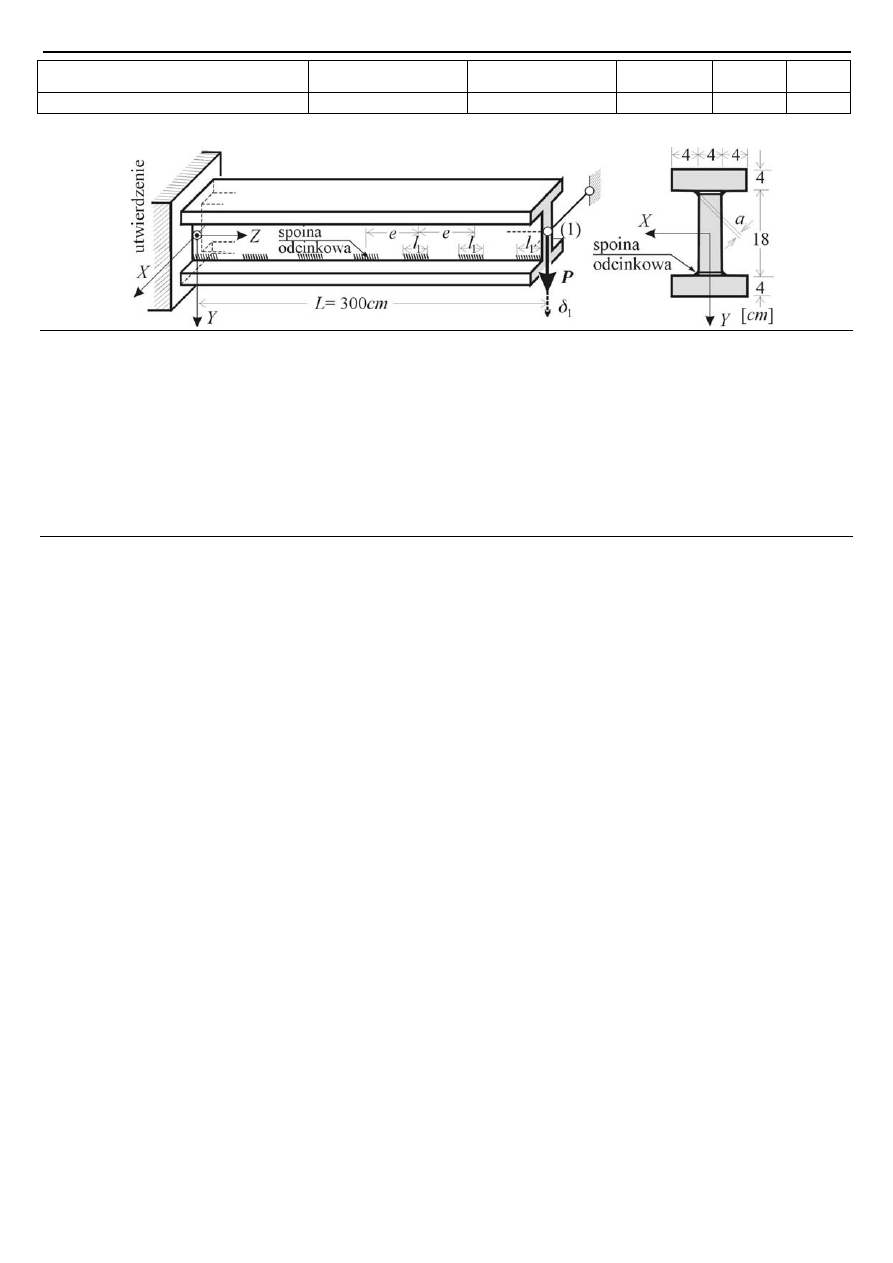
Zadanie 1 (25 pkt.). Stalową cienkościenną belkę skrzynkową z rys. 1, zaczepiono w punktach (B) i (C) na

prętach (wahaczach) o module sprężystości

160

E

GPa

=

i przekroju

2

10

A

cm

=

. Skrzynkę w

przekrojach (A), (B), (1), (C) i (1) wzmocniono niepodatnymi przeponami. Wahacze (pręty)
wizualizujące podporę (A) są niepodatne (

EA

= ∞

).

Rys. 1

W fazie pierwszej obliczając reakcje dla uproszczenia założyć, że w stosunku do sztywności wahaczy belka
jest niepodatna (nieskończenie sztywna), na tej podstawie:

1) obliczyć reakcje, wykonać wykresy momentów zginających M , sił tnących T i sił normalnych

,

N

2) określić dopuszczalne obciążenie reprezentowane wartością siły

uwzględniając różną wytrzymałość

wahaczy (prętów) na rozciąganie

i na ściskanie

oraz

ugięcie dopuszczalne belki

P

60

rozciąganie

r

dop

K

σ

MPa

≡

=

160

sciskanie

c

dop

K

σ

MPa

≡

=

0, 4

dop

f

cm

=

.

W fazie drugiej przyjąć

wykorzystując wyniki pkt. 1, po odrzuceniu założenia o niepodatności

belki (skrzynki), wykonać następujące polecenia:

30

P

k

=

N

3) sporządzić wykres ekstremalnych naprężeń normalnych

σ

w belce,

4) wykonać wykres momentów skręcających

( )

S

M Z i obliczyć maksymalne naprężenia styczne

od skręcania,

max

S

τ

5) obliczyć naprężenia zredukowane wg hipotezy HMH w przecięciu

β β

−

dolnej części lewej ścianki

skrzynki w przekroju po prawej stronie przepony (C) uwzględniając naprężenia od zginania ,
od ścinania i skręcania ,

σ

T

τ

S

τ

6) wyznaczyć wartość graniczną siły

gr

P

całego układu, w belce wykorzystać warunek

|

| |

|

1

gr

gr

M

N

M

N

+

=

,

dla uproszczenia obliczeń uwzględnić tylko stany od M i

wywołujące naprężenia normalne , do

obliczeń przyjąć

.

N

σ

350

pl

σ

MPa

=

14.02.2005

Egzamin Nr 2 z Wytrzymałości Materiałów, WILiŚ II, sem. 3

Czas: 150 min.

____________________________________________________________________________________________________________________________________
J.Ch. & W.G. / M.S. 2005

Zadanie nr 2, str. 1/1

WM2_Egz2ZAD2_05.doc

Nazwisko Imię Podpis

Nr

albumu

Grupa

Sala

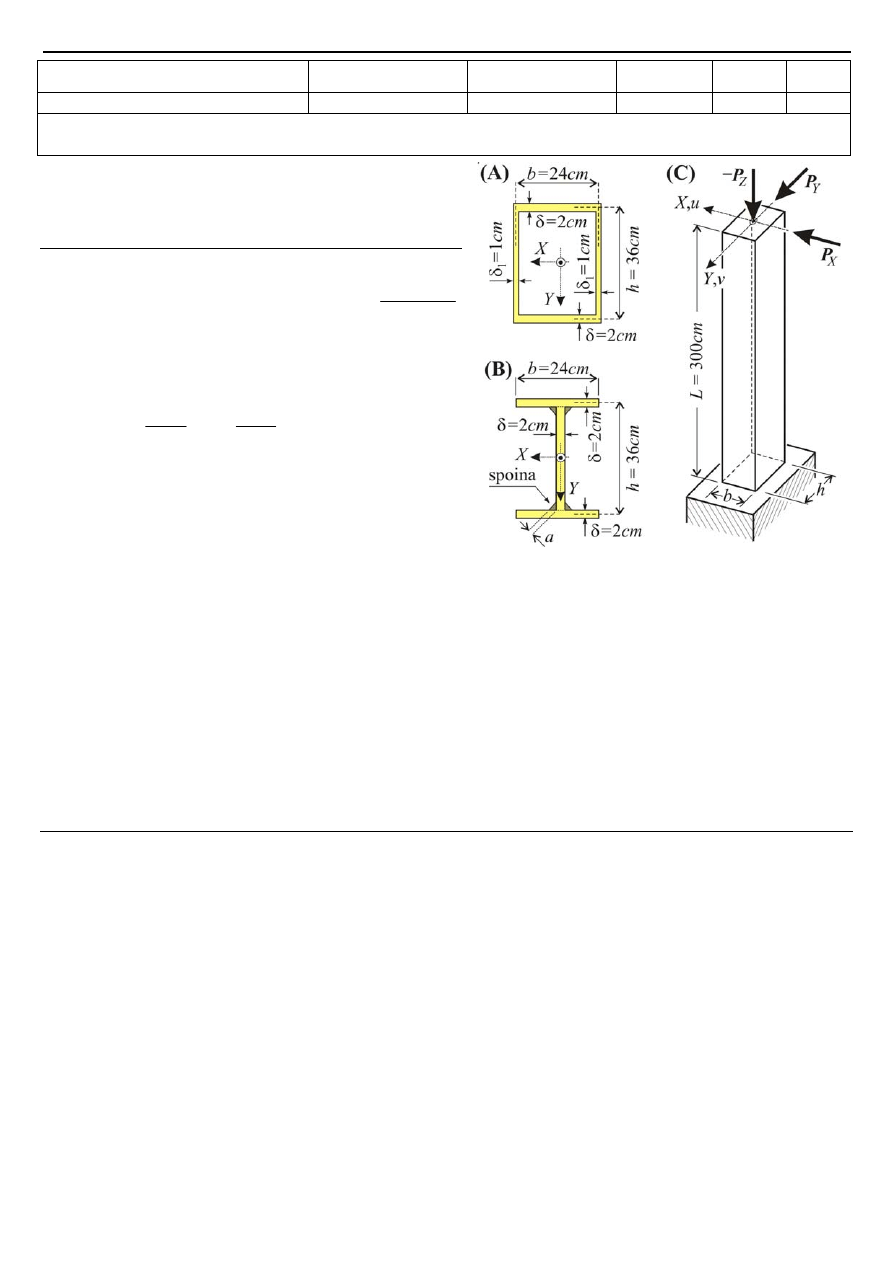
Zadanie 2 (25 pkt.) Rozpatrzyć dwa warianty dwuteowej belki grubościennej o wymiarach jak na rys. 2.

Rys. 2.

Wariant A. Przekrój jednorodny o stałym module sprężystości

140

E

GPa

=

:

1) przyjąć

, sporządzić wykresy ekstremalnych naprężeń normalnych

σ

i stycznych ;

50

P

k

=

N
N

=

1

15

l

c

=

90

spoiny

t

dop

k

MPa

≡

=

τ

τ

2) przyjąć

, dobrać rozstaw odcinkowych spoin pachwinowych, gdy dana są

,

,

;

50

P

k

=

e

0, 4

a

cm

m

3) określić dopuszczalną wartość siły

,

dop

P P

≡

A

, gdy

180

dop

σ

MPa

=

;

4) zakładając, że jedynym dociążeniem jest siła ściskająca działająca w osi pręta (

Z

− ), obliczyć

siłę krytyczną

KR

P w zakresie liniowym oraz określić płaszczyznę wyboczenia pręta.

Wariant B. Przekrój zespolony (hybrydowy) z dwóch materiałów o różnych modułach sprężystości, środnik

140

S

E

G

=

Pa

Pa

, półki

i jednakowych naprężeniach dopuszczalnych

:

210

P

E

G

=

180

dop

σ

MPa

=

5) zbadać jak zmienia się dopuszczalna wartość siły

,

dop

P P

≡

B

, obliczyć

;

, /

,

dop

dop

n P

P

≡

B

A

6) zbadać jak zmienia się ugięcie końca wspornika

1

1

, / ,

m δ

δ

≡

B

A

.

06.02.2006

Egzamin Nr 1 z Wytrzymałości Materiałów, WILiŚ II, sem. 3

Czas: 150 min.

____________________________________________________________________________________________________________________________________
J.Ch. & W.G / M.S.. 2006

Zadanie nr 1, str. 1/1

WM2_Egz1ZAD1_06.doc

Nazwisko Imię Podpis

Nr

albumu

Grupa

Sala

Uwaga.

Wypełnić górę w obu formularzach. Wyłożyć indeks do kontroli. Można mieć przy sobie tylko kalkulator i przybory
do pisania/rysowania. Rozwiązania (także brudnopis) zmieścić tylko na otrzymanym formularzu egzaminacyjnym.

Zadanie 1 (25 pkt.). Rozważyć cienkościenną belkę, słup

(rys. 1) w dwóch wariantach, jako skrzynkę
(A) o zmiennej grubości ścianek i jako
dwuteownik (B) o stałej grubości.

1) Rozpatrując tylko skręcanie swobodne obu wariantów

przekroju (A) i (B), obliczyć stosunek

( )

( )

max |

|

max |

|

τ

τ

n

τ

=

B

A

maksymalnych naprężeń stycznych z obu przekrojów
obciążonych jednakowym momentem skręcającym.

2) Przy obciążeniu siłami

X

P ,

Y

P (C) obliczyć stosunki

ugięć

( )

( )

|

|

|

|

u

u

n

u

=

B

A

,

( )

( )

|

|

|

|

v

v

n

v

=

B

A

końca wspornika w obu

wariantach przekroju (A) i (B).

3) Dla obu wariantów słupa o przekroju (A) i (B)

obliczyć siłę krytyczną wyboczenia giętnego

200

E

GPa

=

.

4) Wyznaczyć rdzeń przekroju wariantów (A) i (B).

Rys. 1

5) Dla obu wariantów przekroju (A) i (B) uwzględniając wynik pt. 5 podać (opisać, naszkicować, bez obliczeń)

charakterystyczną cechę wykresu naprężeń od ściskania mimośrodowego siłą ( )

Z

− P działającą w punkcie

(

; ) (5;0)

p

p

X Y

=

[

]

cm .

6) W przypadku obciążenia siłą 60

Y

kN

=

P

dla wariantu przekroju (B) obliczyć potrzebną grubość spoin

pachwinowych

a

łączących środnik z pasami belki jeśli

30

spoiny

τ

dop

K

MPa

≡

=

τ

.

7) Stosując metodę obciążeń dopuszczalnych dla wariantu przekroju (B), belki o schemacie (C) tylko zginanej

ukośnie obciążeniem 5

X

kN

=

P

, 40

Y

kN

=

P

zaprojektować stałą grubość

δ

blach dwuteownika ze względu

na naprężenia normalne

σ

, jeśli

200

dop

σ

MPa

=

.

8) Dla zaprojektowanej w pkt. 8 grubości

δ

i obciążenia obliczyć maksymalne naprężenia zredukowane wg

hipotezy HMH w środniku w miejscu jego połączenia z półką, traktując je jako cienkościenne (w osiach).

06.02.2006

Egzamin Nr 1 z Wytrzymałości Materiałów, WILiŚ II, sem. 3

Czas: 150 min.

____________________________________________________________________________________________________________________________________
J.Ch. & W.G. / M.S. 2006

Zadanie nr 2, str. 1/1

WM2_Egz1ZAD2_06.doc

Nazwisko Imię Podpis

Nr

albumu

Grupa

Sala

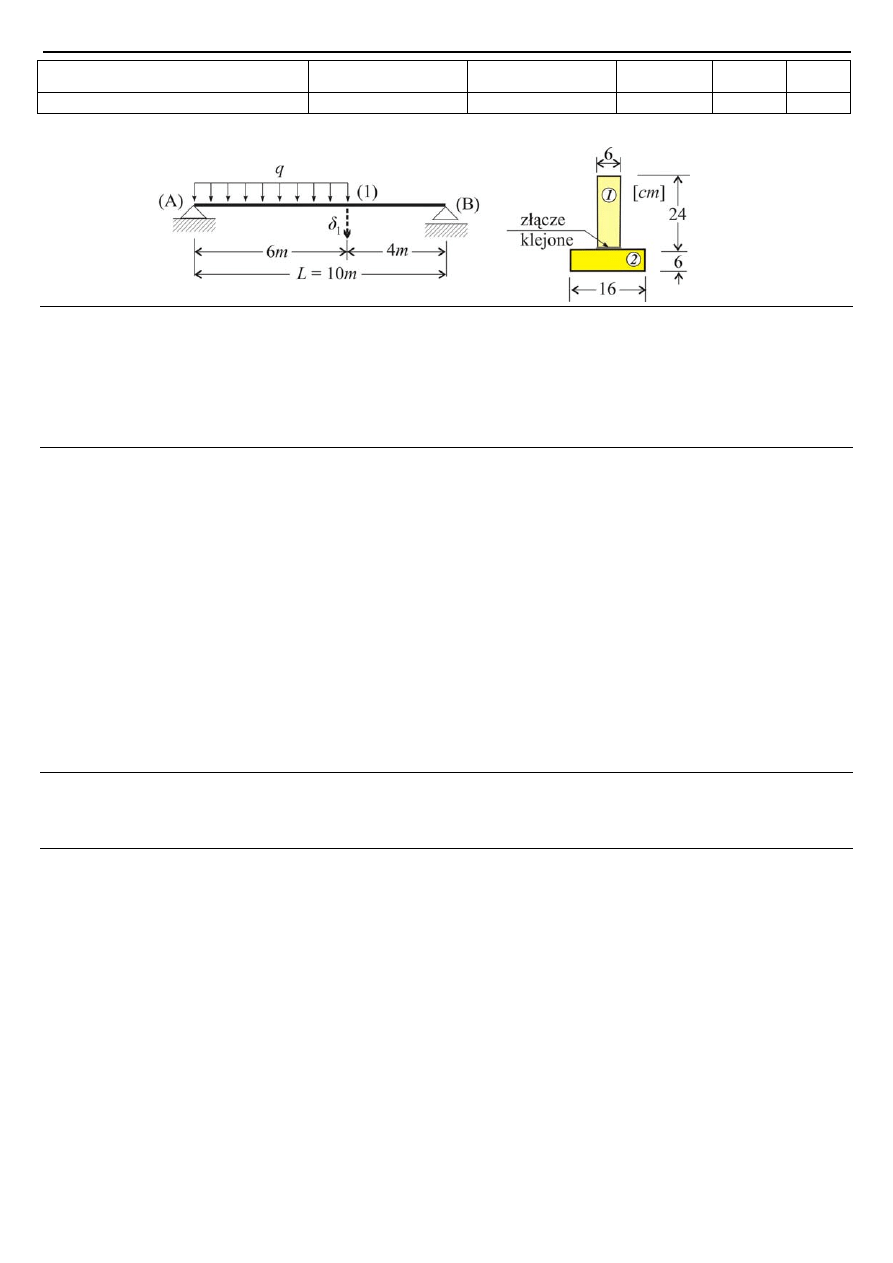
Zadanie 2 (27 pkt.) Rozpatrzyć dwa warianty teowej belki grubościennej o wymiarach jak na rys. 2.

Rys. 2.

Etap wyjściowy. Przekrój jednorodny, środnik (1) i półka (2),

(1)

(2)

10

E

E

E

GPa

=

≡ =

, przyjmując

1

/

q

kN mb

=

:

a) obliczyć i sporządzić wykres momentów zginających;
b) narysować wykres ekstremalnych naprężeń normalnych;
c) obliczyć i sporządzić wykres sił tnących;
d) narysować wykres ekstremalnych naprężeń stycznych;
e) obliczyć ugięcie

1

δ

w punkcie (1) i naszkicować linię ugięcia.

Wariant A.

Przekrój jednorodny, środnik (1) i półka (2) jednakowe

(1)

(2)

10

E

E

E

GPa

=

≡ =

. Stosując metodę

obciążeń dopuszczalnych obliczyć dopuszczalną wartość obciążenia

[

/

]

dop

q

kN mb ze względu na:

1) dopuszczalne naprężenia ściskające 15

Ściskanie

c

dop

K

σ

MPa

≡

=

;

2) dopuszczalne naprężenia rozciągające

9

Rozciąganie

r

dop

K

σ

MPa

≡

=

;

3) dopuszczalne naprężenia styczne

0,5

Ścinanie

t

dop

K

τ

MPa

≡

=

;

4) dopuszczalne naprężenia styczne w połączeniu klejowym

0, 4

spoiny

kleju

t

dop

K

MPa

≡

=

τ

, gdzie

powierzchnia klejenia obejmuje całą szerokość środnika

(1)

6

b

cm

=

na całej długości belki.

5) dopuszczalne ugięcie w punkcie (1) belki

1

/150

dop

δ

f

L

≤

≡

;

Stosując metodę obciążeń granicznych obliczyć wartość graniczną

[

/

]

gr

q

kN mb ze względu na:

6) jednakową na rozciąganie i ściskanie granicę plastyczności

0

20

plast

σ

σ

MPa

≡

=

;

7) sporządzić wykres naprężeń

gr

σ w stanie granicznym.

Wariant B.

Przekrój zespolony (hybrydowy) z dwóch materiałów o różnych modułach sprężystości, środnik

(1)

10

E

GPa

=

, półka

(2)

60

E

GPa

=

:

8) przyjąć

1

/

q

kN mb

=

sporządzić wykres ekstremalnych naprężeń

σ

.

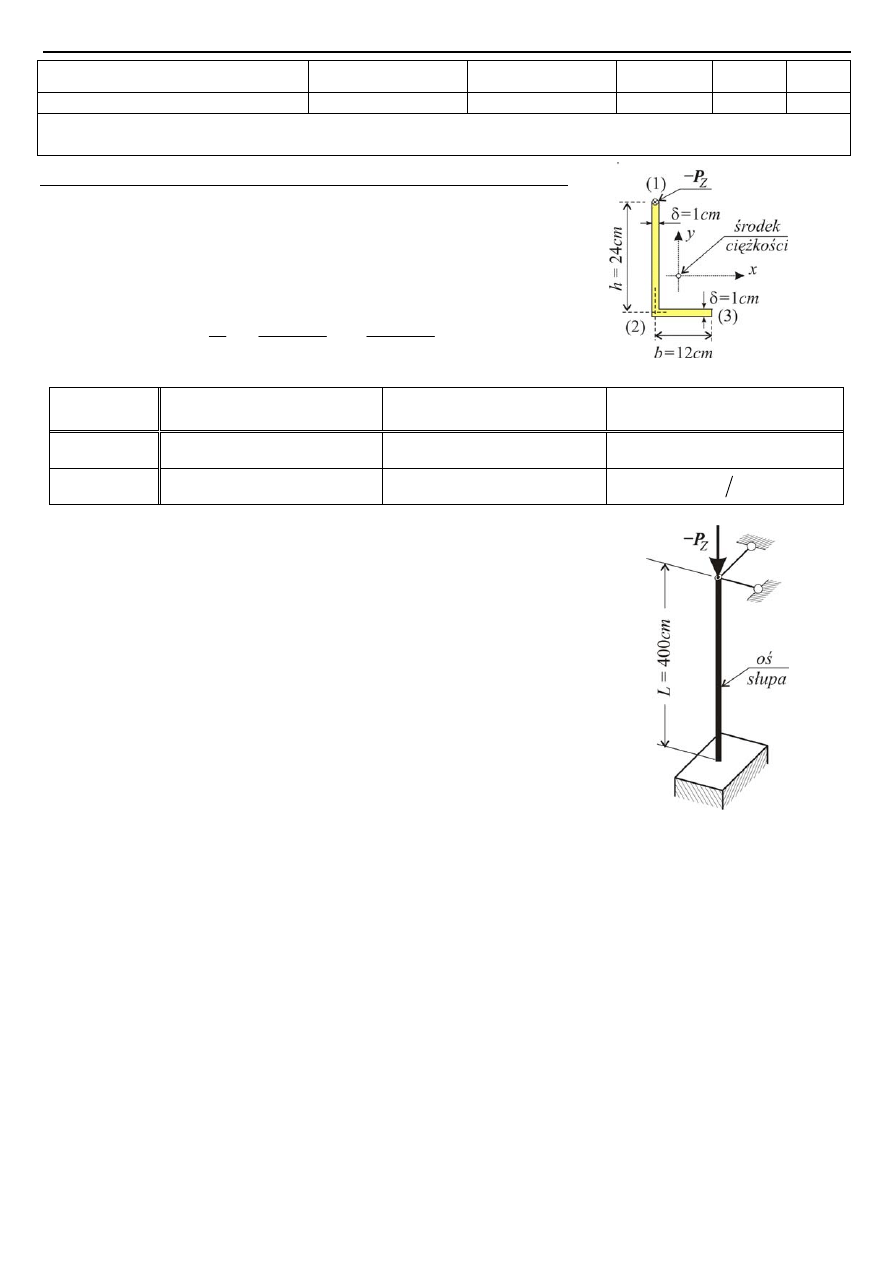
13.02.2006

Egzamin Nr 2 z Wytrzymałości Materiałów, WILiŚ II, sem. 3

Czas: 150 min.

____________________________________________________________________________________________________________________________________
J.Ch. & W.G / M.S.. 2006

Zadanie nr 1, str. 1/1

WM2_Egz2ZAD1_06.doc

Nazwisko Imię Podpis

Nr

albumu

Grupa

Sala

Uwaga.

Wypełnić górę w obu formularzach. Wyłożyć indeks do kontroli. Można mieć przy sobie tylko kalkulator i przybory
do pisania/rysowania. Rozwiązania (także brudnopis) zmieścić tylko na otrzymanym formularzu egzaminacyjnym.

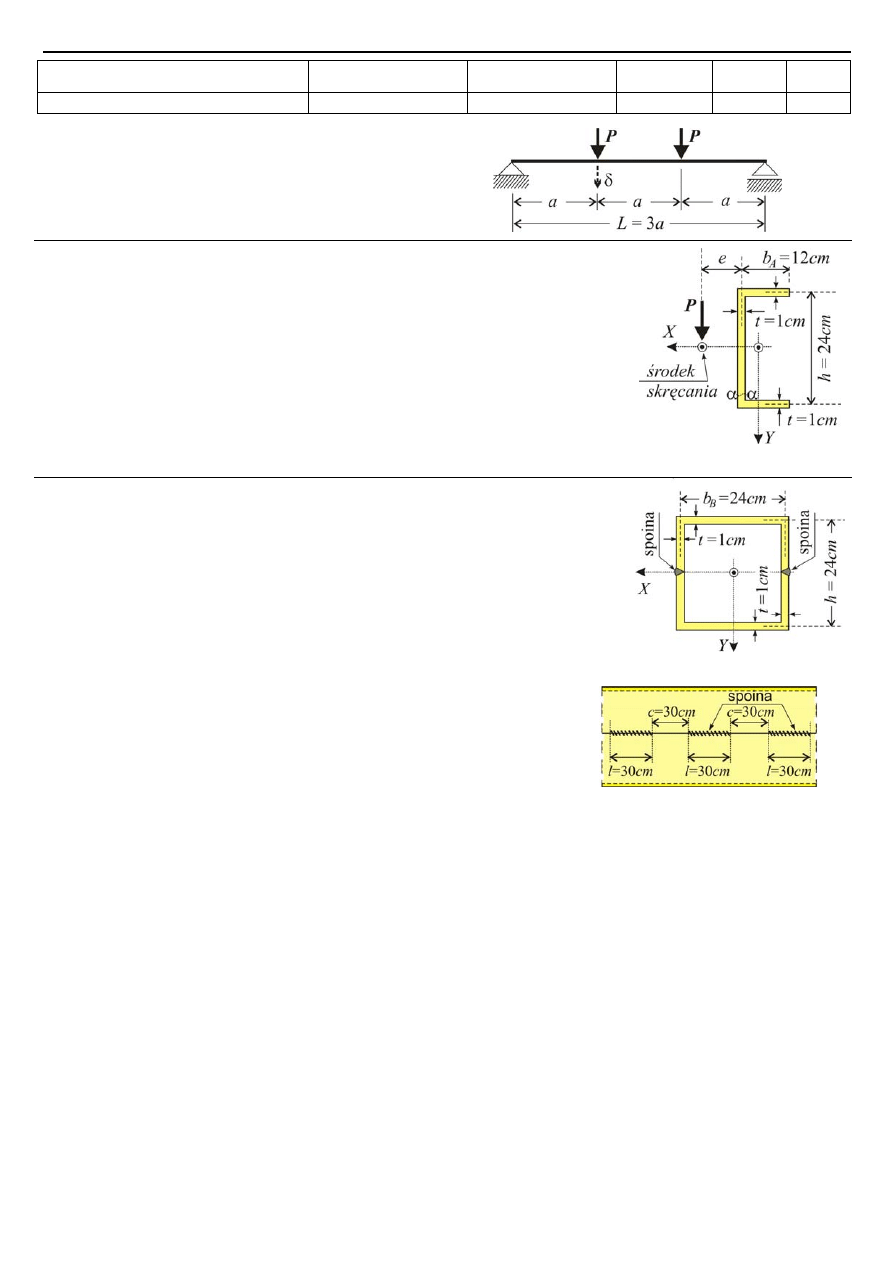
Zadanie 1 (25 pkt.)
1) Dla przekroju cienkościennego kątownika z rys. 1 A obliczyć główne

centralne momenty bezwładności, sprawdzić stosując koło Mohra.

2) wskazać położenie środka skręcania (zginania).
3) Przyjmując, że w punkcie (1) działa siła ściskająca 72

Z

kN

=

P

,

wyznaczyć oś zerową i sporządzić wykres naprężeń.

2

2

( , )

1

x

xy

y

xy

x

y

xy

x

y

xy

uJ vJ

vJ uJ

N

σ x y

Ax

Ay

A

J J J

J J J

⎡

⎤

−

−

=

+

+

⎢

⎥

−

−

⎢

⎥

⎣

⎦

Rys. 1 A

4) Wyznaczyć i narysować rdzeń przekroju.

bok

wierzchołek

i

i

y a x b

=

+ , 0

i

a

≠ , 0

i

b

≠

0

i

y b

= ≠ ,

(

,

)

x

∈ −∞ +∞

0

i

x c

= ≠ ,

(

,

)

y

∈ −∞ +∞

i

u

(

) /

i

y

xy

i

a J

J

b A

−

/

xy

i

J

b A

−

/

y

i

J c A

−

i

v

(

) /

i

xy

x

i

a J

J

b A

−

/

x

i

J b A

−

xy

i

J

c A

−

5) Stosując metodę obciążeń dopuszczalnych obliczyć dopuszczalną

wartość siły ściskającej

dop

Z

P

działającej w punkcie (1) z rys. 1 A, jeśli

założono, że

200

dop

prop

σ

σ

MPa

=

=

.

6) Dla słupa z rys. 1 B o przekroju z rys. 1 A zakładając, że siła pionowa

poprzez głowicę, działa w osi pręta, wskazać na rysunku przekroju
(1 A) ślad płaszczyzny wyboczenia oraz obliczyć siłę krytyczną
wyboczenia giętnego

200

E

GPa

=

.

7) Sprawdzić warunek zakresu wyboczenia sprężystego jeśli

200

E

GPa

=

i 200

prop

σ

MPa

=

.

Rys. 1 B

13.02.2006

Egzamin Nr 2 z Wytrzymałości Materiałów, WILiŚ II, sem. 3

Czas: 150 min.

____________________________________________________________________________________________________________________________________
J.Ch. & W.G. / M.S. 2006

Zadanie nr 2, str. 1/1

WM2_Egz2ZAD2_06.doc

Nazwisko Imię Podpis

Nr

albumu

Grupa

Sala

Zadanie 2 (25 pkt.) Etap wyjściowy (rys. 2 A):
a) sporządzić wykres momentów zginających,
b) sporządzić wykres sił tnących,
c) obliczyć ugięcie

δ

i naszkicować linię ugięcia.

Rys. 2 A

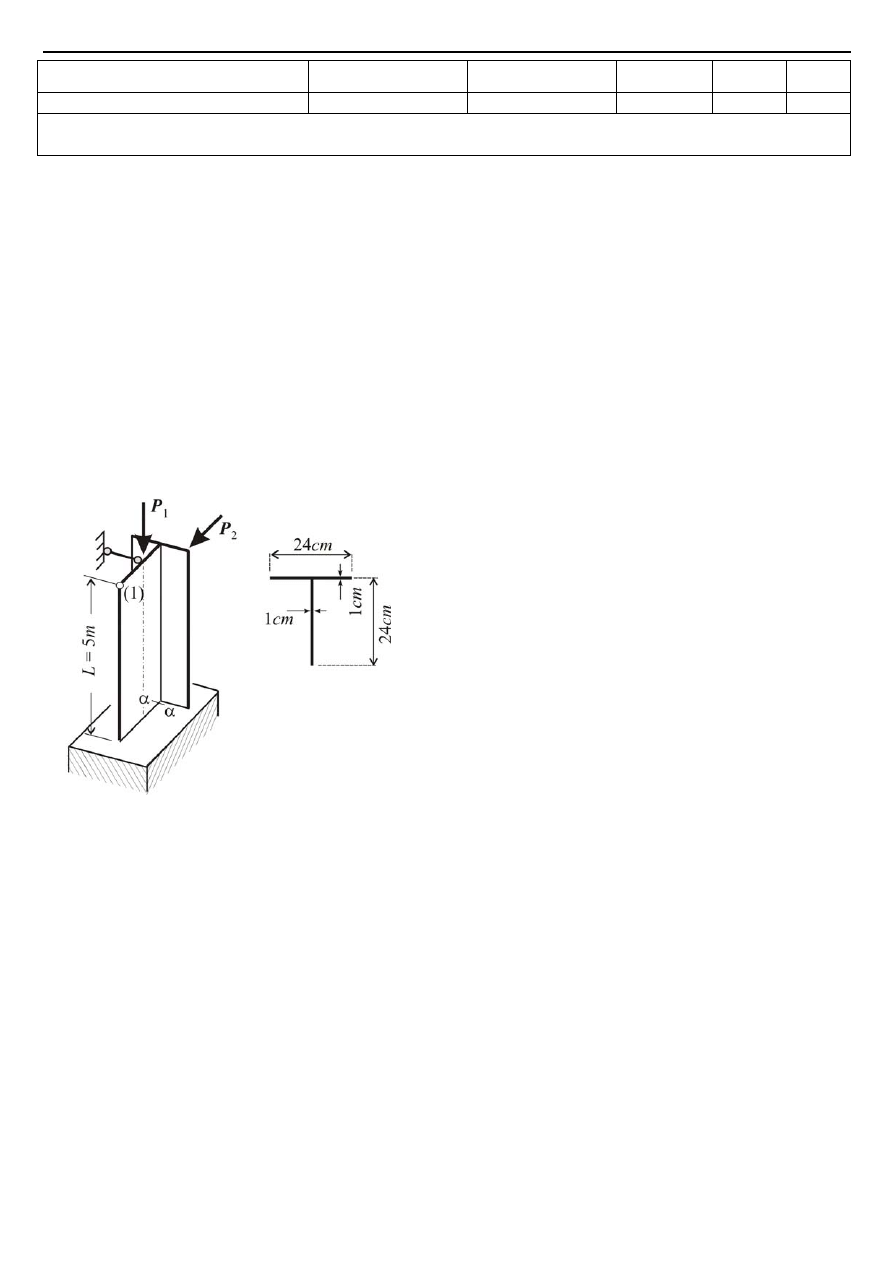
Wariant A. Dla belki o cienkościennym przekroju ceowym ze stałą grubością

ścianek t z rys. 2 B oraz o schemacie z rys. 2 A i danych

6

L

m

=

,

(

2

a

m

=

),

10

P

kN

=

wyznaczyć:

1) współrzędną

e

położenia środka skręcania (zginania) ceownika;

zakładając dalej, że linia działania obciążenia przechodzi przez środek
skręcania

(zginania):

2) obliczyć i sporządzić wykresy ekstremalnych naprężeń normalnych,
3) obliczyć i sporządzić wykresy ekstremalnych naprężeń stycznych,
4) obliczyć ekstremalne naprężenia zredukowane wg hipotezy HMH w

cięciu

α α

−

środnika w miejscu jego połączenia z półką, traktując je jako

cienkościenne (w osiach).

Rys. 2 B

Wariant B.

Przekrój belki przeprojektowano spawając dwa cewowniki z

wariantu A w przekrój kwadratowy skrzynkowy pokazany na
rys.2 C:

5) analizując rysunki 2B i 2C, podać i uzasadnić bez obliczeń, ilokrotnie

spadną naprężenia i ugięcia w wariancie B w stosunku do wariantu A;

Stosując metodę obciążeń dopuszczalnych obliczyć dopuszczalną wartość
obciążenia

[

]

dop

P

kN ze względu na:

6) dopuszczalne ugięcie

δ

(pod siłą) belki

/150

dop

δ

f

L

≤

≡

, 200

E

GPa

=

,

Rys. 2 C

7) dopuszczalne naprężenia normalne

340

r

dop

K

σ

MPa

≡

=

,

8) dopuszczalne naprężenia styczne

35

Ścinanie

t

dop

K

τ

MPa

≡

=

,

9) pełną nośność spoiny odcinkowej (wg rys. 2 D) o grubości

równej grubości łączonych elementów, jeśli dopuszczalne
naprężenia styczne w spoinie wynoszą

20

spoiny

spoiny

t

dop

K

MPa

≡

=

τ

,

Rys. 2 D

Stosując metodę obciążeń granicznych obliczyć wartość graniczną

[

]

gr

P

kN ze względu na:

10) jednakową na rozciąganie i ściskanie granicę plastyczności

0

340

plast

σ

σ

MPa

≡

=

,

11) sporządzić wykres naprężeń normalnych

gr

σ w stanie granicznym.

02.02.2007

Egzamin Nr 1 z Wytrzymałości Materiałów, WILiŚ II, sem. 3

Czas: 150 min.

____________________________________________________________________________________________________________________________________
J.Ch. & W.G / M.S.. 2007

Zadanie nr 1, str. 1/1

WM2_Egz1ZAD1_07.doc

Nazwisko Imię Podpis

Nr

albumu

Grupa

Sala

Uwaga.

Wypełnić górę w obu formularzach. Wyłożyć indeks do kontroli. Można mieć przy sobie tylko kalkulator i przybory
do pisania/rysowania. Rozwiązania (także brudnopis) zmieścić tylko na otrzymanym formularzu egzaminacyjnym.

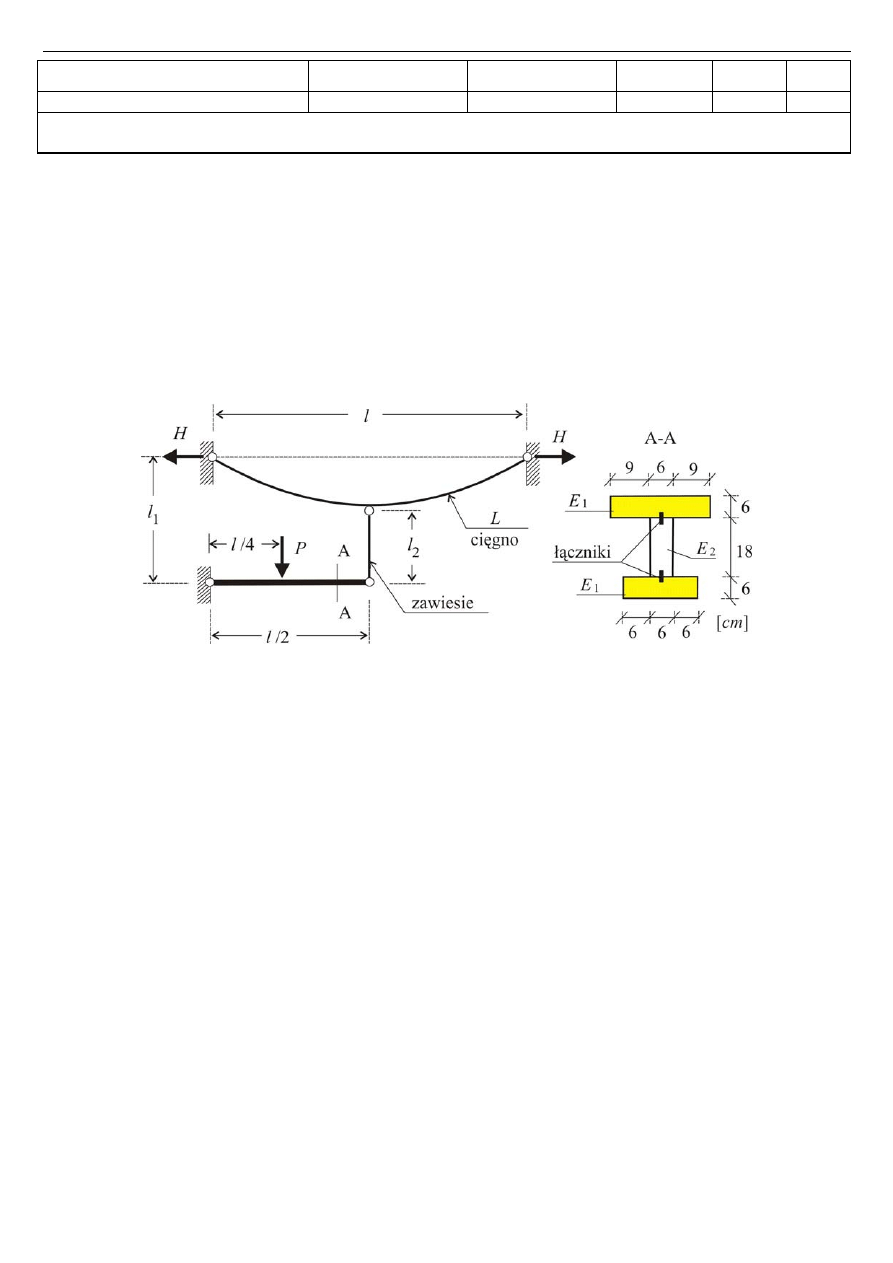
Zadanie 1 (25 punktów)
Cienkościenny pręt przestrzenny, wykonany z materiału o module sprężystości

obciążony jest

siłami P

200GPa

E

=

1

oraz P

2

, jak na Rys.1.

1) Przyjmując

,

1

100kN

P

=

2

5kN

P

=

wyznaczyć:

a) ekstremalne naprężenia normalne w pręcie,
b) maksymalny kąt skręcenia przekroju (tu i dalej skręcanie rozpatrywać jako swobodne),
c) maksymalne przemieszczenie poziome w punkcie 1,
d) maksymalne naprężenia zredukowane wg H-M-H w środniku pod półką w miejscu utwierdzenia

pręta (przekrój

α α

−

).

2) Dla cienkościennego przestrzennego słupa z Rys.1 wyznaczyć:

a) siłę krytyczną wyboczenia giętnego
b) sprawdzić warunek wyboczenia sprężystego dla

200MPa

pr

σ

=

3) Założyć

oraz przyjąć, że siła działa w osi symetrii przekroju.

1

0

P

=

2

P

Wyznaczyć graniczną wartość siły

2 gr

P

, gdy

260MPa

pl

σ

=

.

02.02.2007

Egzamin Nr 1 z Wytrzymałości Materiałów, WILiŚ II, sem. 3

Czas: 150 min.

____________________________________________________________________________________________________________________________________
J.Ch. & W.G / M.S.. 2007

Zadanie nr 2, str. 1/1

WM2_Egz1ZAD2_07.doc

Nazwisko Imię Podpis

Nr

albumu

Grupa

Sala

Uwaga.

Wypełnić górę w obu formularzach. Wyłożyć indeks do kontroli. Można mieć przy sobie tylko kalkulator i przybory
do pisania/rysowania. Rozwiązania (także brudnopis) zmieścić tylko na otrzymanym formularzu egzaminacyjnym.

Zadanie 2 (25 punktów)
Dwuteowa belka zespolona o modułach

1

50

E

GPa

=

i

2

150

E

GPa

=

podwieszona jest na niepodatnym układzie

cięgno-zawiesie. Rozstaw podpór

, a długość cięgna

10

l

= m

m

10.4

L

=

, Odstęp w pionie miedzy podporami

cięgna i belki wynosi

. Na belkę działa siła

1

4

l

= m

20

P

kN

=

.

a) Wyznaczyć reakcję poziomą

w zakotwieniu cięgna.

H

b) Wyznaczyć długość zawiesia tak, aby podpory belki były na jednym poziomie.

2

l

c) Wyznaczyć wykres maksymalnych naprężeń normalnych w przekroju zespolonym belki.
d) Zaprojektować rozstaw łączników w belce zespolonej, wiedząc, że nośność pojedynczego łącznika

wynosi

; przyjąć, że rozstaw

e

jest jednakowy dla półki górnej i dolnej.

e

1

10kN

N

=