Z. Kąkol-Notatki do Wykładu z Fizyki

38-1

Wykład 38

38. Fizyka jądrowa

38.1 Wstęp

Każde jądro atomowe składa się z protonów i neutronów wiązanych

siłami jądro-

wymi

, niezależnymi od ładunku.

Ponieważ neutron i proton mają prawie taką samą masę i bardzo zbliżone inne własno-
ści, więc obydwa określa się wspólną nazwą

nukleon

.

Nazwa

nuklid

jest używana zamiennie z terminem jądro.

Nuklidy o tej samej liczbie protonów, różniące się liczbą neutronów nazywamy

izoto-

pami

.

Łączną liczbę protonów i neutronów w jądrze nazywamy

liczbą masową

jądra i ozna-

czamy literą A. Liczba neutronów jest dana równaniem A - Z, gdzie Z jest liczbą proto-
nów zwaną

liczbą atomową

.

Wartość liczby A dla jądra atomowego jest bardzo bliska masie odpowiadającego mu
atomu.

38.2 Rozmiary jąder

Wiązka wysokoenergetycznych protonów lub neutronów może zostać rozproszona

wskutek dyfrakcji na jądrze o promieniu R. Analizując powstały obraz dyfrakcyjny (po-
łożenie maksimów) można wyznaczyć ten promień.
Wyniki pomiarów (również innymi technikami) pokazują, że średni promień dla wszyst-
kich jąder oprócz najmniejszych jest dany wzorem:

R

≈

(1.2·10

-15

m) A

1/3

W fizyce jądrowej i cząstek elementarnych wielkość 10

-15

pojawia się często i dlatego

wprowadzono dla niej osobną nazwę fermi. 1 fermi = 1 fm = 10

-15

m.

Przykład 1

Jaka jest gęstość masy i gęstość cząsteczek w materii jądrowej ?
Dla jądra o promieniu R i liczbie masowej A liczba cząstek na jednostkę objętości wy-
nosi

3

3

1

15

3

]

)

10

2

.

1

[(

3

4

3

4

A

m

A

R

A

N

−

⋅

=

=

π

π

skąd

N = 1.38·10

44

nukleonów/m

3

Gęstość masy to iloczyn tej liczby N i masy nukleonu

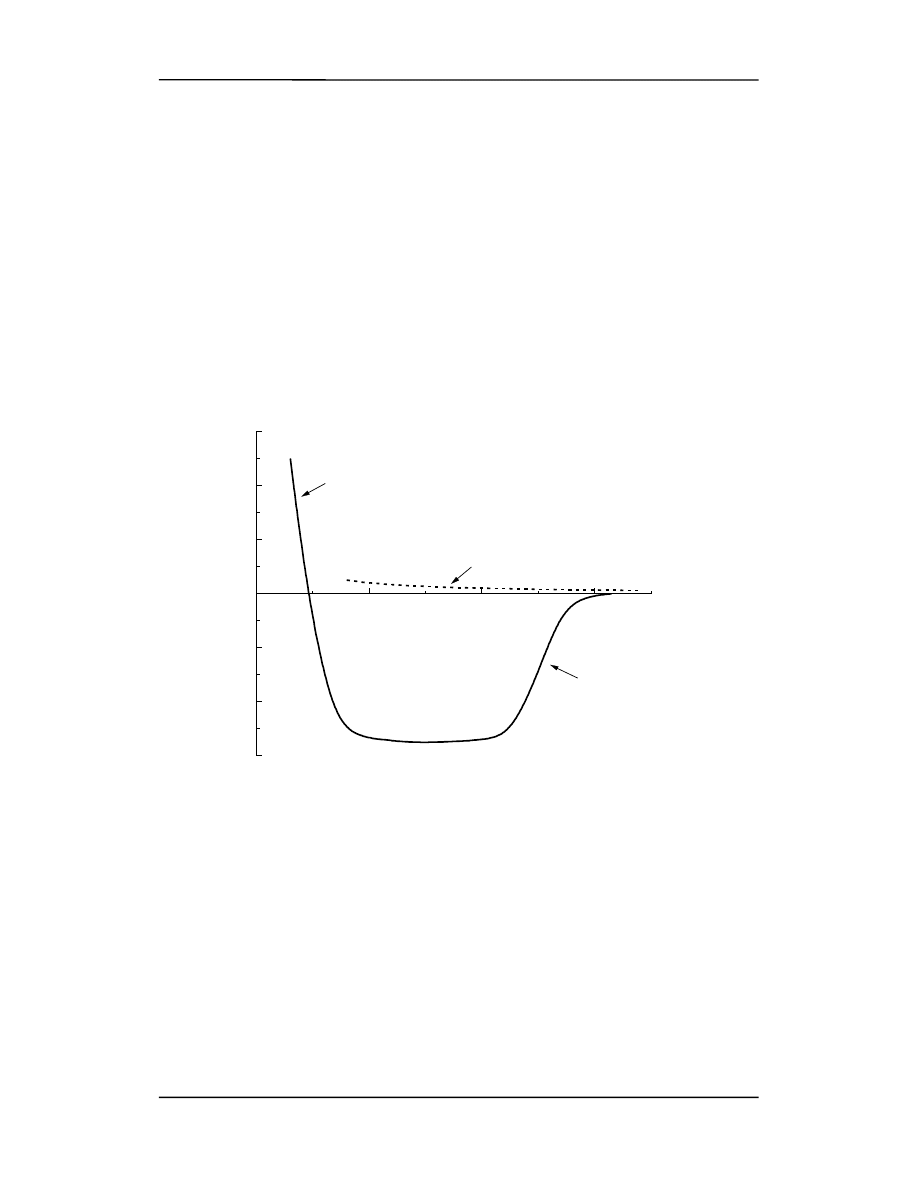
Z. Kąkol-Notatki do Wykładu z Fizyki

38-2

ρ = N M

p

= (1.38·10

44

) (1.67·10

-27

) kg/m

3

= 2.3·10

17

kg/m

3

Odpowiada to masie około 230 milionów ton dla 1 cm

3

.

Gęstość materii jądrowej nie zależy od rozmiarów jądra, ponieważ jego objętość jest
proporcjonalna do liczby masowej A.

38.3 Oddziaływanie nukleon-nukleon

Dotychczas poznane oddziaływania (grawitacyjne, elektromagnetyczne) nie po-

zwalają na wyjaśnienie struktury jądra atomowego. Aby wyjaśnić co tak silnie wiąże
nukleony w jądrach atomowych trzeba wprowadzić nowe oddziaływanie. Ta siła wiążą-
ca musi być większa niż siła odpychania elektrostatycznego występująca pomiędzy pro-
tonami. Określamy ją mianem

siły jądrowej

lub

oddziaływania silnego

.

Potencjał opisujący to oddziaływanie jest o rząd wielkości większy niż energia poten-
cjalna elektrostatycznego odpychania proton - proton. Sytuacja ta jest pokazana na ry-

sunku poniżej.
Oddziaływanie proton - proton, proton - neutron i neutron - neutron jest identyczne (je-
żeli zaniedbamy relatywnie małe efekty odpychania elektrostatycznego) i nazywamy go
oddziaływaniem nukleon - nukleon.
Masy atomowe i energie wiązań można wyznaczyć doświadczalnie w oparciu o spektro-
skopię masową lub bilans energii w reakcjach jądrowych.
W tabeli na następnej stronie zestawione są masy atomowe i energie wiązań jąder

∆

E

dla atomów wybranych pierwiastków.
Masa jest podana w

jednostkach masy atomowej

(u). Za wzorzec przyjmuje się 1/12 ma-

sy atomowej węgla

6

12

C .

1

2

3

-30

-20

-10

0

10

20

30

ke

2

/r

przyci

ąganie

odpychanie

U

(

M

e

V

)

r (fm)

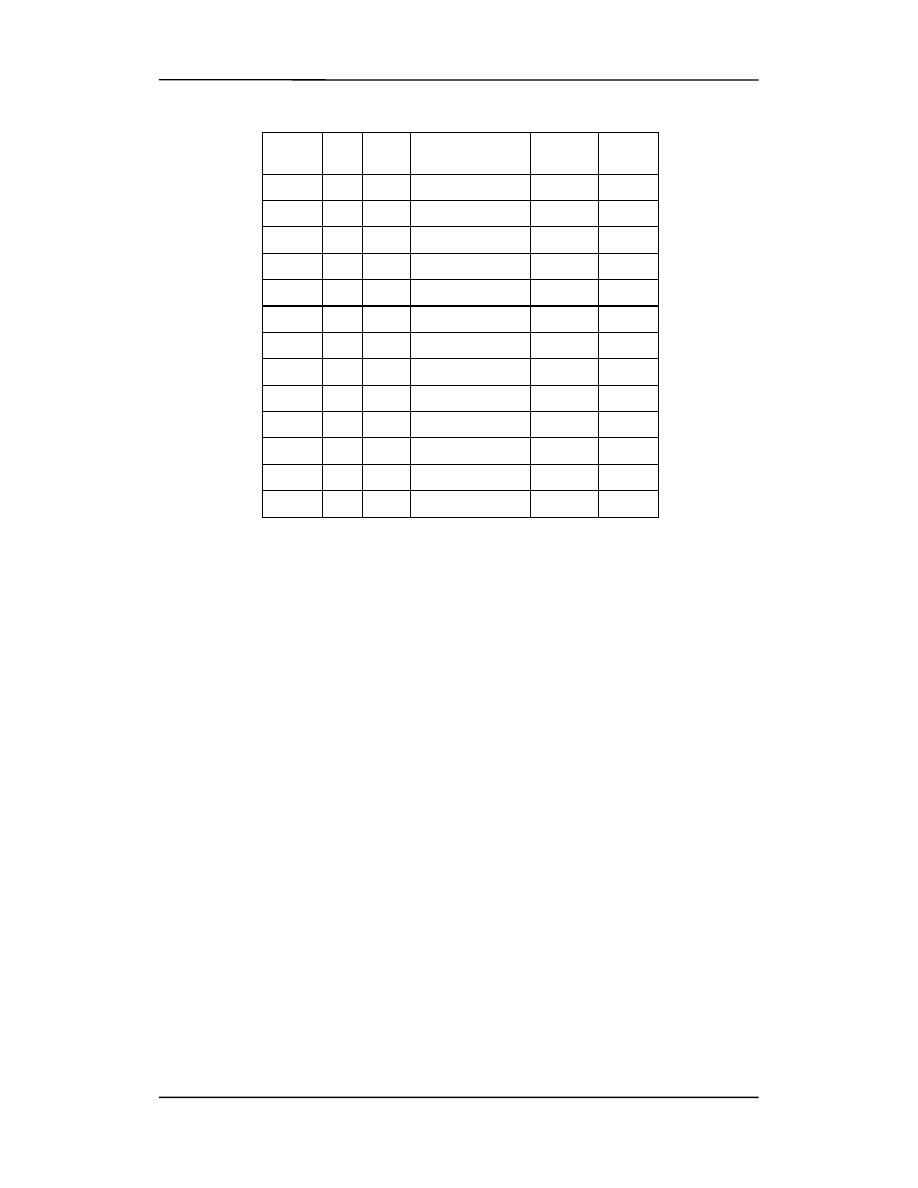
Z. Kąkol-Notatki do Wykładu z Fizyki

38-3

Z

A

Masa (u)

∆

E

(MeV)

∆

E/A

0

1

n

0

1

1.0086654

---

---

1

1

H

1

1

1.0078252

---

---

1

2

H

1

2

2.0141022

2.22

1.11

1

3

H

1

3

3.0160500

8.47

2.83

2

3

He

2

3

3.0160299

7.72

2.57

2

4

He

2

4

4.0026033

28.3

7.07

4

9

Be

4

9

9.0121858

58.0

6.45

6

12

C

6

12

12.0000000

92.2

7.68

8

16

O

8

16

15.994915

127.5

7.97

29

63

Cu

29

63

62.929594

552

8.50

50

120

Sn

50

120

119.9021

1020

8.02

74

184

W

74

184

183.9510

1476

8.02

92

238

U

92

238

238.05076

1803

7.58

W oparciu o dane zestawione w tabeli można uzyskać dalsze informacje o jądrach ato-
mowych.
Dla przykładu porównajmy masę atomu

2

4

He z sumą mas jego składników.

M(

2

4

He ) = 4.0026033 u

Całkowita masa jego składników równa jest sumie mas dwu atomów

1

1

H i dwu neutro-

nów tzn.

2M(

1

1

H ) + 2M(

0

1

n ) = 2·1.0078252 u + 2·1.0086654 u = 4.0329812 u

Uwaga: zarówno w skład masy helu jak i dwu mas wodoru wchodzą masy dwu elektro-
nów.
Wynik: masa helu jest mniejsza od masy składników o wartość 0.0303779 u.

Dla każdego atomu analogiczny rachunek pokazałby, że masa atomu jest mniejsza od
masy jego składników o wielkość

∆

M zwaną

niedoborem masy

.

Wynik ten jest świadectwem energii wiązania jąder jak i równoważności masy i energii.
Jeżeli rozważymy dowolny składnik jądra helu to skoro jest on związany z jądrem to ma
ujemną energię E < 0 (rysunek na stronie 3). Innymi słowy, żeby taki nukleon przybył
z odległości r

à

∞

(E = 0) i mógł z innym nukleonami utworzyć jądro, jego energia

musi ulec zmniejszeniu. To samo dotyczy każdego z pozostałych nukleonów w jądrze.
Oznacza to, że gdy układ oddzielnych swobodnych nukleonów łączy się w jądro energia
układu musi zmniejszyć o wartość

∆

E

energii wiązania jądra

.

Z. Kąkol-Notatki do Wykładu z Fizyki

38-4

Zmniejszeniu o

∆

E całkowitej energii układu musi towarzyszyć, zgodnie z teorią

względności, zmniejszenie masy układu o

∆

M, gdzie

∆

M c

2

=

∆

E.

Dla

2

4

He niedobór masy wynosi

∆

M = 0.0303779 u, więc energia wiązania jest równa

∆

E =

∆

M c

2

= 28.3 MeV.

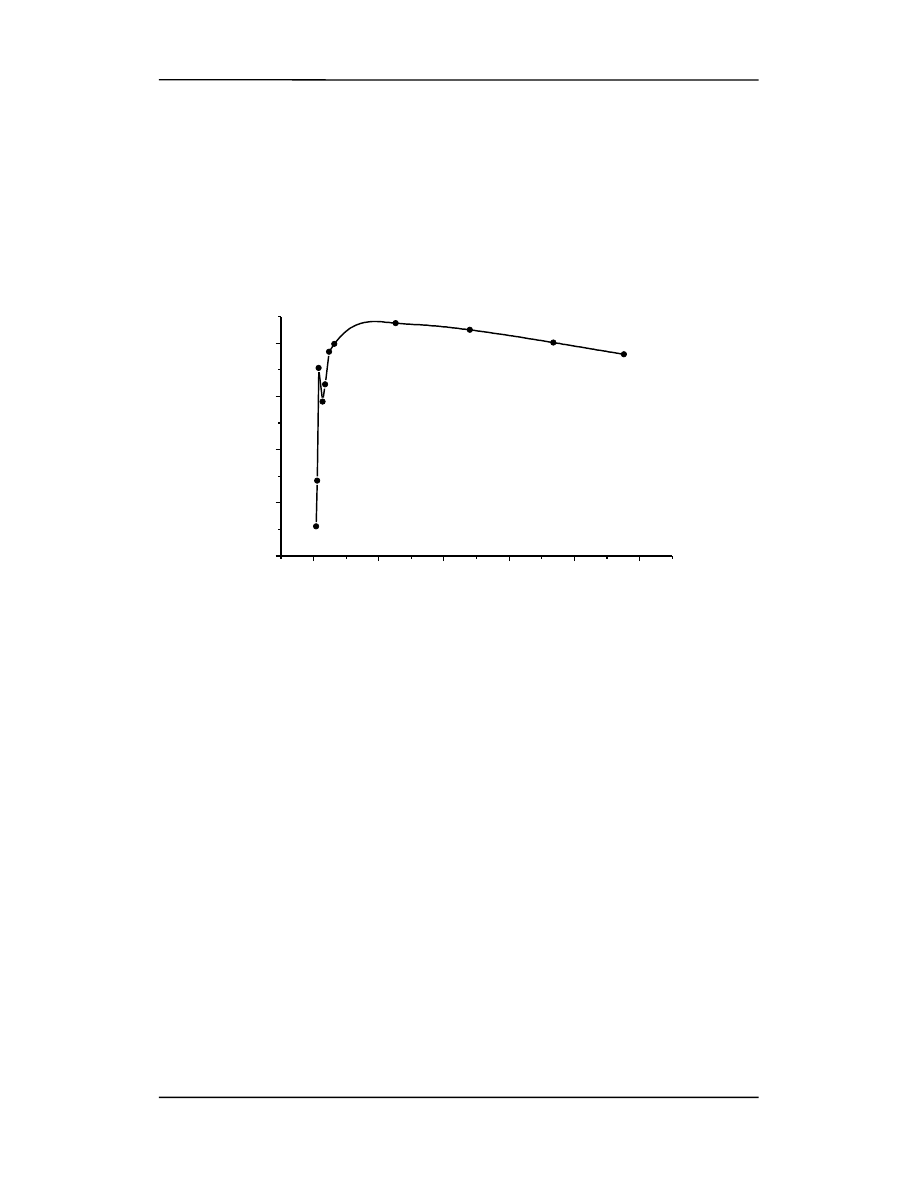
W ostatniej kolumnie tabeli podana jest wielkość energii wiązania na nukleon w jądrze.
Jest to jedna z najważniejszych cech charakteryzujących jądro.
Zauważmy, że początkowo

∆

E/A wzrasta ze wzrostem A, ale potem przybiera w przy-

bliżeniu stałą wartość około 8 MeV. Wyniki średniej energii wiązania na nukleon w
funkcji liczby masowej jądra A są pokazane na rysunku poniżej.
Gdyby każdy nukleon w jądrze przyciągał jednakowo każdy z pozostałych nukleonów to
energia wiązania na nukleon byłaby proporcjonalna do A.
Fakt, że

∆

E/A nie jest proporcjonalne do A wynika głownie z krótkiego zasięgu sił ją-

drowych.
Widać, że najsilniej są wiązane nukleony w jądrach pierwiastków ze środkowej części
układu okresowego.

38.4 Rozpady jądrowe i reakcje jądrowe

38.4.1 Rozpad alfa

Rozpady jądrowe zachodzą zawsze (prędzej czy później) jeśli jądro o pewnej liczbie

nukleonów znajdzie się w stanie energetycznym, nie będącym najniższym możliwym
dla układu o tej liczbie nukleonów.
Takie nietrwałe (w stanach niestabilnych) jądra powstają w wyniku reakcji jądrowych.
Niektóre reakcje są wynikiem działań laboratoryjnych, inne dokonały się za sprawą
przyrody podczas powstawania naszej części Wszechświata. Jądra nietrwałe pochodze-
nia naturalnego są nazywane

promieniotwórczymi

, a ich rozpady noszą nazwę

rozpadów

promieniotwórczych

(promieniotwórczości).

0

50

100

150

200

250

0

2

4

6

8

238

U

184

W

120

Sn

63

Cu

16

O

7

Li

12

C

9

Be

4

He

3

H

2

H

∆

E

/A

Liczba masowa A

Z. Kąkol-Notatki do Wykładu z Fizyki

38-5

Rozpady promieniotwórcze dostarczają wielu informacji o samych jądrach atomowych
(budowie, stanach energetycznych, oddziaływaniach) ale również wielu zasadniczych
informacji o pochodzeniu Wszechświata.
Szczególnie ważnym rozpadem promieniotwórczym jest rozpad alfa (

α) występujący

zazwyczaj w jądrach o Z

≥

82. Z przyczyn historycznych jądro

4

He jest nazywane cząst-

ką

α.

Rozpad

α polega na przemianie niestabilnego jądra w nowe jądro przy emisji jądra

4

He

tzn. cząstki

α.

Proces zachodzi samorzutnie bo jest korzystny energetycznie. Energia wyzwolona
w czasie rozpadu (energetyczny równoważnik niedoboru masy) jest unoszona przez
cząstkę

α

w postaci energii kinetycznej.

Przykładowa reakcja dla jądra uranu wygląda następująco

238

U

à

234

Th +

4

He + 4.2 MeV

Rozpatrzmy teraz układ zawierający w chwili początkowej wiele jąder tego samego ro-
dzaju. Jądra te podlegają rozpadowi

α (równie dobrze rozpadowi β) z częstością rozpa-

dów

λ. Chcemy znaleźć liczbę jąder, która nie uległa rozpadowi po czasie t od chwili

początkowej.
Oznaczamy przez N liczbę jąder. Wtedy dN (<0) oznacza liczbę jąder, które rozpadają
się w czasie dt.
Spodziewana liczba rozpadów (liczba jąder, które się rozpadną) w czasie dt tzn. (t,
t + dt) jest dana wyrażeniem

dN = – N

λdt

gdzie znak minus wskazuje, że dN jest liczbą ujemną czyli, że N maleje z czasem.
Możemy rozdzielić zmienne i scałkować równanie obustronnie

t

N

N

d

d

λ

−

=

∫

∫

−

=

t

t

N

N

t

N

N

0

)

(

)

0

(

d

d

λ

t

N

t

N

N

t

N

λ

−

=

=

−

)

0

(

)

(

ln

)

0

(

ln

)

(

ln

czyli

t

e

N

t

N

λ

−

=

)

0

(

)

(

skąd

t

e

N

t

N

λ

−

=

)

0

(

)

(

(38.1)

N(0) jest liczbą jąder w chwili t = 0, a N(t) liczbą jąder po czasie t.
Powyższy wzór nazywamy

wykładniczym prawem rozpadu

.

Z. Kąkol-Notatki do Wykładu z Fizyki

38-6

Często wyraża się N(t) poprzez średni czas życia jąder, który z definicji jest równy od-
wrotności częstości rozpadów;

τ = 1/λ.

Prawo rozpadu przyjmuje wtedy postać

N = N

0

e

-t/

τ

(38.2)

Do scharakteryzowania szybkości rozpadu używa się

czasu połowicznego rozpadu

(za-

niku) T

1/2

. Jest to taki czas, po którym liczba jąder danego rodzaju maleje do polowy

tzn. N = (1/2) N

0

. Wstawiając to do równania (38.2), otrzymujemy

τ

2

1

0

0

2

1

T

e

N

N

=

czyli

τ

2

1

2

T

e

=

skąd

T

1/2

= 0.693

τ

(38.3)

Przykładowo dla

238

U czas połowicznego zaniku wynosi 4.5·10

9

lat, a dla

212

Po jest rzę-

du 10

-6

s.

38.4.2 Promieniowanie

γ

Jeśli jądro jest wzbudzone do wyższego stanu energetycznego, to może nastąpić sa-

moczynna emisja fotonu i przejście do niższego stanu energetycznego. Ponieważ odle-
głości między poziomami energetycznymi w jądrach są rzędu MeV więc fotony emito-
wane przez jądra mają energię tysiące razy większą od energii fotonów wysyłanych
przez atomy. Takie wysokoenergetyczne fotony emitowane przez jądra nazywamy

pro-

mieniowaniem

γ

.

Jądra w stanie wzbudzonym można łatwo otrzymać używając neutronów o małej ener-
gii. Jeżeli taki powolny neutron przechodzi np. przez bryłkę uranu

238

U to zawsze gdy

znajdzie się blisko jądra działa na niego siła przyciągająca wywołana przez oddziaływa-
nie jądrowe. Dlatego jest bardzo prawdopodobne, że taki neutron zostanie wychwycony
i powstanie jądro

239

U

*

w stanie wzbudzonym (oznaczone *). Takie jądro przechodzi do

stanu podstawowego emitując jeden lub kilka kwantów

γ

. Proces ten opisują następują-

ce reakcje jądrowe:

n +

238

U

à

239

U

*

239

U

*

à

239

U +

γ

38.4.3 Rozpad

β

Badając własności promieniotwórczości stwierdzono, że istnieją trzy rodzaje pro-

mieniowania

α, β, γ. Po dalszych badaniach stwierdzono, że α to jądra helu, promienie γ

to fotony, a promienie

β to elektrony lub pozytony (cząstka elementarna dodatnia o ma-

sie równej masie elektronu).

Z. Kąkol-Notatki do Wykładu z Fizyki

38-7

Jądra, których ilość protonów Z różni się od wartości odpowiadającej stabilnym jądrom
o tej samej liczbie masowej A, mogą zmieniać Z w kierunku jąder stabilnych poprzez
rozpad

β. Współczesna teoria rozpadów β została rozwinięta przez Fermiego w 1931 r.

Najprostszym przykładem rozpadu

β jest rozpad swobodnego neutronu zachodzący z

czasem połowicznego zaniku 12 minut

v

e

p

n

+

+

→

Neutron rozpada się na proton, elektron i antyneutrino (cząstka elementarna o zerowym
ładunku i zerowej masie spoczynkowej).
Inny przykład to omawiany już uran

239

U; rozpad zachodzi z czasem połowicznego za-

niku 24 minuty

v

e

Np

U

+

+

→

239

239

Powstały izotop też nie jest trwały i podlega rozpadowi

β

v

e

Pu

Np

+

+

→

239

239

z czasem połowicznego zaniku 2.35 dnia.
W takim procesie liczba Z wzrasta o jeden a liczba A pozostaje bez zmiany.

Innym rozpadem

β, jest proces, w którym jądra emitują pozytony, a towarzyszy temu

zawsze emisja neutrina. W tym procesie liczba Z maleje o jeden, a liczba A pozostaje
bez zmiany.

38.4.4 Rozszczepienie jąder atomowych

Jak widzieliśmy w punkcie 38.3 energia wiązania na jeden nukleon wzrasta z liczbą

masową aż do A

≈

50. Jednak powyżej tej wartości ta energia maleje. Dzieje się tak dla-

tego, że siły jądrowe mają krótki zasięg i dla dwóch protonów oddalonych o więcej niż
2.5·10

-15

m ich oddziaływanie jest raczej odpychające niż przyciągające (rysunek na

stronie 38-2).
Konsekwencją tego jest występowanie zjawisk rozszczepienia i syntezy jądrowej. Jeżeli
ciężkie jądro rozdzielimy na dwa mniejsze, te dwie części mogą mieć masę mniejszą niż
masa jądra wyjściowego nawet o dziesiąte części procenta. Dlatego ciężkie jądra mają
tendencję do rozpadania się na dwa mniejsze z wydzieleniem energii.
Energia w bombie atomowej i reaktorach jądrowych jest wydzielana w procesach rozsz-
czepienia jądrowego.
Spontaniczne rozszczepienie jądra jest dozwolone przez zasadę zachowania energii.
Jednak w naturalnych jądrach prawdopodobieństwo rozszczepienia jądra jest mniejsze
niż prawdopodobieństwo rozpadu

α

. Prawdopodobieństwo rozszczepienia można wy-

datnie zwiększyć bombardując jądra neutronami. Tak dzieje się np. gdy jądro

235

U lub

239

Pu wychwyci powolny neutron.

Różnica pomiędzy masą jądra uranu a sumą mas produktów rozszczepienia jest taka, że
w przeciętnej reakcji wydziela się 200 MeV energii co stanowi równoważnik 0.1% ma-
sy uranu. Oznacza to, że z 1g uranu otrzymujemy energię równą: E = 0.001·mc

2

= 9·10

10

Z. Kąkol-Notatki do Wykładu z Fizyki

38-8

J. Jest to około 3 miliony razy więcej niż energia wydzielana przy spalaniu 1g węgla.
Z drugiej strony należy uwzględnić fakt, że uran jest dużo droższy od węgla i że instala-
cje w elektrownii jądrowej są też dużo droższe niż w konwencjonalnej. Ciągle jednak
energia jądrowa jest znacznie tańsza niż z paliw tradycyjnych.
Rozszczepienie jądrowe może w reakcji łańcuchowej stać się procesem samopodtrzy-
mującym się. W każdej reakcji rozszczepienia powstają dwa lub trzy neutrony. Jeżeli
przynajmniej jeden z nich wywoła kolejne rozszczepienie to proces będzie sam się pod-
trzymywał. Ilość materiału powyżej, której jest spełniony powyższy warunek nazywamy
masą krytyczną. Po raz pierwszy reakcję rozszczepienia przeprowadzono (Enrico Fermi)
na Uniwersytecie Chicago w 1942 r.
Masa

235

U i

239

Pu może być też nadkrytyczna. Wtedy neutrony z jednego rozszczepienia

wywołują więcej niż jedną reakcję wtórną (reakcja lawinowa). Cała masa nadkrytyczna
może być zużyta (eksplodować) w czasie t < 0.001 s ze względu na dużą szybkość neu-
tronów (3·10

8

cm/s). Tak eksploduje bomba atomowa. Najczęściej kulę o masie nadkry-

tycznej ale rozrzedzonej otacza się klasycznymi ładunkami wybuchowymi. Ich detona-
cja wywołuje wzrost ciśnienia zewnętrznego i gwałtownie zmniejsza objętość kuli.
Oczywiście w elektrowniach jądrowych spalanie paliwa odbywa się bardzo powoli.
Wymaga to spowalniania neutronów i doboru warunków stacjonarnej pracy reaktora.

38.4.5 Reakcja syntezy jądrowej

W tabeli na stronie 38-3 widzimy, że masa dwóch lekkich jąder jest większa niż ma-

sa jądra powstającego po ich połączeniu. Jeżeli takie jądra zbliżymy do siebie na dosta-
tecznie małą odległość, to przy powstawaniu nowego jądra wydzieli się energia związa-
na z różnicą mas.
Np. dwa deuterony mogą się połączyć tworząc jądro helu przy czym 0.6% masy zostanie
zamienione na energię. Widać, że ta metoda byłaby sześć razy wydajniejsza od omó-
wionego rozszczepiania jąder uranu (0.1%). Poza tym mamy nieograniczone źródło deu-
teru w wodzie mórz i oceanów. Przeszkodą w otrzymywaniu energii tą metodą jest od-
pychanie kulombowskie, które nie pozwala zbliżyć się deuteronom na odległość porów-
nywalną z zasięgiem przyciągających sił jądrowych. Reakcja ta byłaby możliwa gdyby
deuter mógł być ogrzany do temperatury około 5·10

7

K. Reakcje, które wymagają takich

temperatur nazywamy reakcjami termojądrowymi. Temperatury osiągane podczas wy-
buchu bomby atomowej są wystarczające do zapoczątkowania takiej reakcji. Raz zapo-
czątkowana reakcja termojądrowa wytwarza dostateczną ilość energii do utrzymania
wysokiej temperatury dopóki materiał (większość) nie zostanie spalony. Jest to mecha-
nizm działania bomby wodorowej.
Warunkiem uzyskania użytecznej energii z reakcji syntezy jądrowej jest prowadzenie
reakcji w sposób kontrolowany.
Prowadzone są próby skonstruowania reaktora termojądrowego. Podstawowym proble-
mem jest utrzymanie gazu o tak wysokiej temperaturze w ograniczonym obszarze przez
dostatecznie długi czas aby wytworzona energia była większa od energii zużytej na uru-
chomienie reaktora. Stwarza to wiele problemów technicznych. Np. trzeba zapobiec sto-
pieniu ścian pojemnika z gazem (plazmą). Używa się bardzo silnych pól magnetycznych
próbując nie dopuścić do zetknięcia gazu (plazmy) ze ściankami.
Jak dotąd nie udało się przeprowadzić zakończonej sukcesem kontrolowanej reakcji ter-
mojądrowej. Eksperci uważają jednak, że jest to kwestia najbliższych lat.

Z. Kąkol-Notatki do Wykładu z Fizyki

38-9

W przyrodzie obserwuje się ciągłe wytwarzanie energii termojądrowej: procesy termo-
jądrowe są źródłem energii gwiazd a więc i „naszego” słońca.

38.5 Cykl życia słońca

Na rysunku poniżej są przedstawione podstawowe fazy cyklu życia Słońca.

Uwaga na rysunku nie jest zachowana skala. Jeżeli przyjąć średnicę „naszego” Słońca
za 1 to np. średnica białego karła wynosi ~0.009, a średnica protogwiazdy jest równa

około 10

6

.

38.5.1 Chmura

Większość teorii kosmologicznych za przodka gwiazd i planet uważa gaz, którego

składnikiem był wodór.

•

średnica chmury - kilkadziesiąt lat świetlnych;

•

gęstość < 1000 atomów/cm

3

czyli doskonała próżnia (powietrze w warunkach nor-

malnych ~ 2.7·10

19

atomów/cm

3

);

•

temperatura około -230° C (nie promieniuje).

•

Chmura znajduje się w stanie bardzo nietrwałej równowagi i najmniejsze zaburzenie
powoduje, że zaczyna się kurczyć pod wpływem przyciągania grawitacyjnego.

•

W miarę zbliżania się atomów wodoru ich energia potencjalna (grawitacyjna) male-
je, a rośnie energia kinetyczna czyli temperatura gazu.

•

Tworzą się lokalne zagęszczenia materii zwane globulami.

38.5.2 Globule

•

zawierają one masę równą wielokrotności masy Słońca;

•

dalej są bardzo rzadkie ze względu na rozmiar

≈

100·średnica układu słonecznego;

•

temperatura wyższa

≈

-200° C (dalej brak promieniowania).

Dalej trwa zagęszczanie materii pod wpływem grawitacji, czemu towarzyszy wzrost
temperatury aż osiągnięte zostaje stadium protogwiazdy.

chmura

zapadanie

zapadanie

zapadanie

zapadanie

globula

protogwiazda

S

łońce

S

łońce

stabilne ~ 10

bilionów lat

czerwony

olbrzym

bia

ły

karze

ł

czarny karze

ł

gwiazda neutronowa

czarna dziura

ekspansja

Z. Kąkol-Notatki do Wykładu z Fizyki

38-10

38.5.3 Protogwiazda

•

dobrze wykształcony stabilny rdzeń;

•

początkowo rozmiar dwukrotnie większy od układu słonecznego (1 milionowa
początkowego rozmiaru chmury);

•

w wyniku dalszego zapadania się średnica

≈

średnicy orbity Marsa;

•

temperatura wnętrza około 56000° C, a powierzchni 1650° C;

•

nagrzana masa gazu osiąga ciśnienie, które hamuje dalsze zapadanie grawitacyjne;

•

przy tej temperaturze świeci (wypromieniowuje energię); źródłem tej energii jest
zapadanie się grawitacyjne a nie reakcja syntezy jądrowej, więc to jeszcze nie jest
gwiazda (Słońce);

Jednak gdy energia gazu zmniejszy się przez promieniowanie elektromagnetyczne trwa
dalsze zapadanie się protogwiazdy aż do pojawienia się nowego źródła energii, które
może temu przeciwdziałać. Tym nowym źródłem są reakcje termojądrowe - powstaje
Słońce.

38.5.4 Słońce

Nasze rozważania o Słońcu rozpocznijmy od obliczenia promienia Słońca w funkcji

jego masy.
Zakładamy stałą gęstość wewnątrz Słońca (w rzeczywistości rdzeń ma większą gęstość
niż warstwy przy powierzchni). Masa Słońca M

S

= 2·10

30

kg.

Zapadanie się tej masy gazu wodorowego zostanie zatrzymane gdy ciśnienie termiczne
wywołane ogrzewaniem gazu przez energię z reakcji termojądrowych wyrówna ciśnie-
nie grawitacyjne.
Ciśnienie grawitacyjne wewnątrz jednorodnej kuli o promieniu R, możemy wyznaczyć
z równania: p =

ρg

śr

h, gdzie g

śr

jest wartością średnią przyspieszenia równą g/2; g jest

przyspieszeniem na powierzchni kuli (w środku przyspieszenie jest równe zeru). Stąd

gR

P

g

ρ

2

1

=

gdzie

2

R

GM

g

S

=

.

Ostatecznie

R

M

G

P

S

g

ρ

2

1

=

Ciśnienie termiczne gazu (na podstawie równania stanu gazu doskonałego) wynosi

p

t

M

kT

P

ρ

=

gdzie M

p

jest masą protonu (masa cząsteczki gazu = masa atomu wodoru).

Porównanie tych dwóch ciśnień daje

Z. Kąkol-Notatki do Wykładu z Fizyki

38-11

R

GM

M

kT

S

p

2

1

=

lub

kT

M

GM

R

p

S

2

=

Teraz oceńmy jaka jest najniższa temperatura potrzebna do zbliżenia dwóch protonów
na odległość 5·10

-15

m. Każdy proton ma energię (3/2)kT, więc energia kinetyczna pary

jest równa 3kT. Musi to równoważyć energię odpychania elektrostatycznego

R

e

2

0

4

1

πε

,

stąd T = 1.1·10

9

K.

We wnętrzu gwiazdy wystarczy temperatura o jeden lub nawet dwa rzędy wielkości niż-
sza, bo zawsze znajdzie się wystarczająca ilość protonów o prędkościach większych od
średniej (rozkład prędkości) aby podtrzymać reakcję.
Tak więc temperatura, dla której zaczynają zachodzić reakcje termojądrowe jest rzędu
10

7

K. Dla tych danych otrzymujemy wartość promienia Słońca R = 7·10

8

m, co jest

wartością dobrze zgodną z obserwowaną.
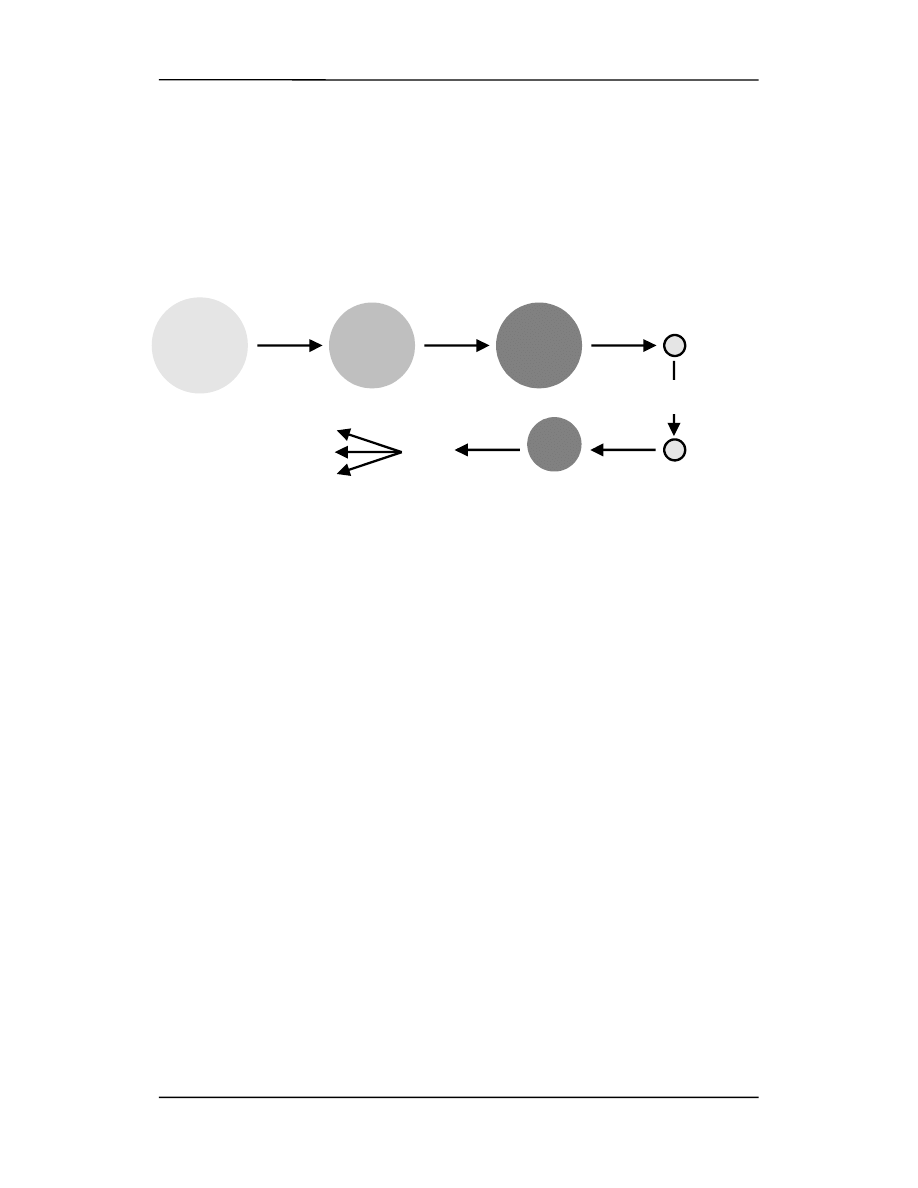
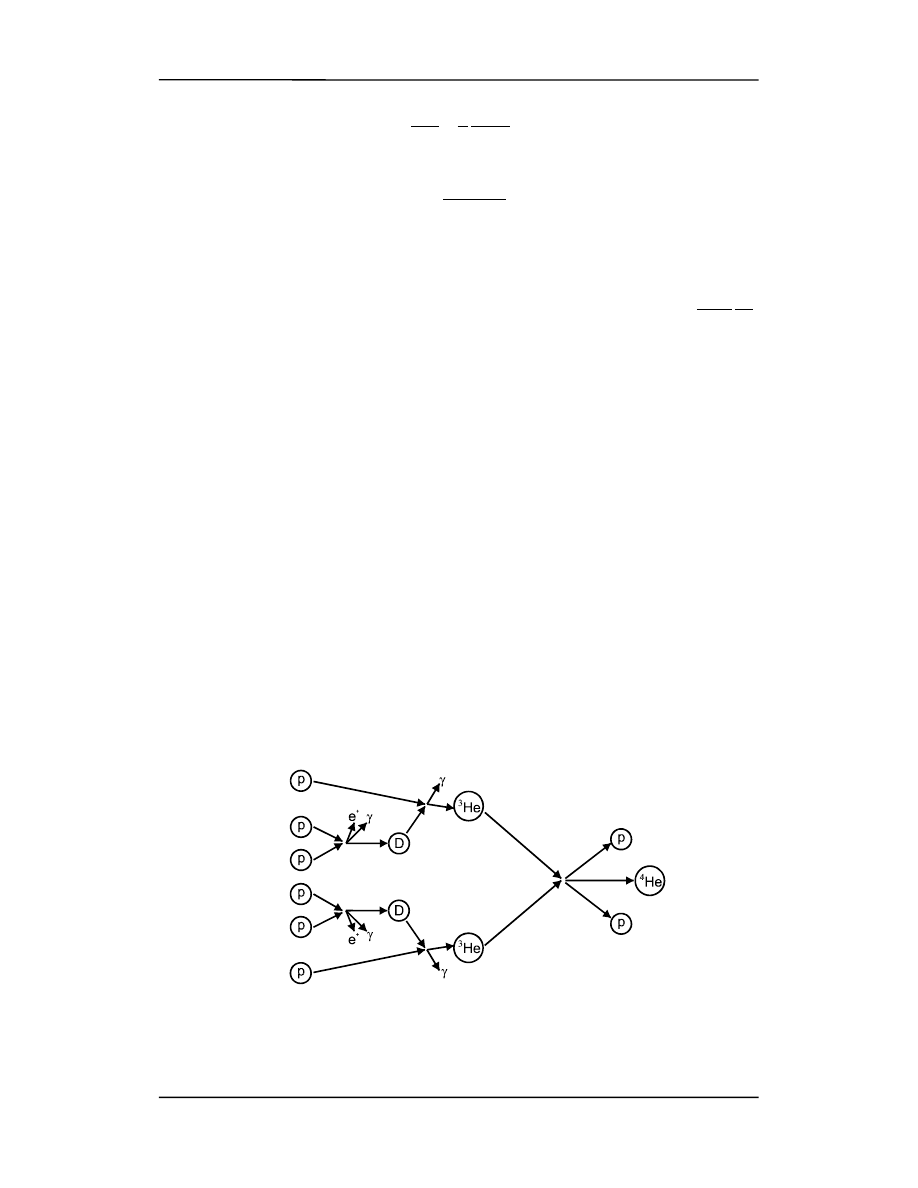
Można pokazać, że jeżeli masa początkowa jest większa niż 0.08 masy Słońca, to osią-
gnięta temperatura będzie dostatecznie wysoka, aby wywołać następujące reakcje termo-
jądrowe

p + p

à D + e

+

+ v

p + D

à

3

He +

γ

3

He +

3

He

à

4

He + p + p

Ten ciąg reakcji termojądrowych pokazany na rysunku poniżej jest znany jako cykl wo-
dorowy.

W wyniku cyklu wodorowego 4 protony są zużyte do wytworzenia cząstki

α, 2 pozyto-

nów, 2 neutrin i 2 fotonów

γ. Masa jądra helu stanowi 99.3% masy czterech protonów.

Wydziela się energia związana z różnicą mas.

Z. Kąkol-Notatki do Wykładu z Fizyki

38-12

Cykl wodorowy jest głównym mechanizmem produkcji energii przez Słońce i inne
gwiazdy bogate w wodór.
Energia wytwarzana przez Słońce jest ogromna. W ciągu sekundy 592 miliony ton wo-
doru jest zamieniane na 587.9 milionów ton helu. Różnica tj. 4.1 miliony ton jest za-
mieniana na energię (w ciągu sekundy). Odpowiada to mocy około 4·10

26

W.

Przykład 1

Obliczmy po jakim czasie wypaliłoby się Słońce tj. gdyby cały wodór zamienił się w
hel.
Energia wytwarzana w cyklu wodorowym 2·10

30

kg otrzymujemy

E = 0.007·Mc

2

= 1.3·10

45

J

Stąd

t = E/P = (1.3·10

45

J) / (4·10

26

W) = 10

11

lat

Jest to około 20 razy więcej niż dotychczasowy wiek Słońca.

Kiedy całe paliwo wodorowe w rdzeniu wypali się to rdzeń gwiazdy zacznie zapadać się
pod wpływem grawitacji (w zewnętrznej warstwie nadal spalanie wodoru). Jednak ilość
ciepła wytworzona z energii grawitacyjnej, przewyższa nawet ilość energii pochodzącej
z reakcji termojądrowej. To ciepło powoduje, że zewnętrzne warstwy zaczynają się roz-
szerzać. Zaczyna się ekspansja, Słońce staje się czerwonym olbrzymem.

38.5.5 Czerwony olbrzym

Gdy masa rdzenia osiągnie wartość około 0.5 masy Słońca, temperatura we wnętrzu

podnosi się do około 100 mln °K, co umożliwia przemianę helu w węgiel i tlen. Zapale-
nie helu przebiega bardzo gwałtownie.
Gwiazdy o małych masach nie zapalają helu w rdzeniu lecz ewoluują w stronę mgławic
planetarnych.
Jeżeli gwiazda wypali hel w rdzeniu to przy braku promieniowania podtrzymującego
warstwę zewnętrzną gwiazda zaczyna się szybko zapadać przechodząc do fazy białego
karła.

38.5.6 Białe karły

Białe karły są gwiazdami o małych rozmiarach (zbliżonych do rozmiarów Ziemi) i

olbrzymich gęstościach; np. masa 1 cm

3

materii tej gwiazdy dochodzi do kilkudziesięciu

ton (masa 1 cm

3

materii ziemskiej wynosi średnio kilka g).

Gwiazdy te dalej świecą dzięki emisji energii grawitacyjnej uwalnianej przy kurczeniu
się. Proces ten może być bardzo długotrwały.
Dalsza ewolucja zależy od masy gwiazdy.
Produktem stygnięcia białych karłów o małej masie są czarne karły.

Z. Kąkol-Notatki do Wykładu z Fizyki

38-13

38.5.7 Czarne karły

Czarne karły powstają w wyniku przejścia w procesie krystalizacji materii białych

karłów do stanu stałego. Towarzyszy temu szybkie ostygnięcie całego obiektu do bardzo
niskich temperatur (obiekt nie świeci).
Jeżeli w wyniku spalania helu masa rdzenia węglowo-tlenowego wzrośnie powyżej war-
tości około 1.4 masy Słońca to w centrum nastąpi zapalenie węgla. Proces ten jest bar-
dzo gwałtowny i nazywany wybuchem supernowej.
Otoczka gwiazdy rozprasza się w przestrzeni, a centrum zapada tworząc gwiazdę neu-
tronową.

38.5.8 Gwiazda neutronowa

W wyniku zapadania się centrum gwiazdy energie elektronów stają się tak duże, że

w procesie zwanym odwrotnym rozpadem

β protony zaczynają przechodzić w neutrony

według następującej reakcji:

e

-

+ p

à n + v

Dokładne procesy przemiany materii zwykłej w materię bogatą w neutrony są skompli-
kowane, ale obliczenia pokazują, że przy gęstościach 10

11

g/cm

3

neutrony są znacznie

liczniejsze niż protony. Stąd nazwa „gwiazda neutronowa”. Takie gęstości są osiągane
gdy gwiazda kurczy się do rozmiarów rzędu dziesiątek km.
Gwiazda neutronowa może wirować wykonując dziesiątki obrotów na sekundę. Np.
gwiazda w centrum Mgławicy Kraba jest taką gwiazdą wirującą 30 razy na sekundę.
Gwiazdy neutronowe mogą wysyłać regularne promieniowanie (sygnały radiowe wyso-
kiej częstości). Taka gwiazda nazywa się pulsarem. Pierwszy pulsar odkryto w 1967 r.
Jeżeli gwiazda ma masę początkową większą niż 8 mas Słońca to spalanie węgla prze-
biega w ich centrum spokojnie.
Następne fazy przebiegają bardzo szybko. Po wyczerpaniu węgla zapalają się kolejno:
tlen, neon, magnez, krzem, nikiel. Końcowym produktem jest jądro żelazne, które wo-
bec braku dalszych źródeł energii gwałtownie zapada się.
Implozji centrum towarzyszy eksplozja otoczki prowadząca do wybuchu bardzo jasnej
supernowej. Pozostałością po wybuchu jest prawdopodobnie czarna dziura.

38.5.9 Czarna dziura

Czarna dziura jest obiektem astronomicznym, który nie może być bezpośrednio ob-

serwowany, gdyż bardzo silne pole grawitacyjne, którego jest źródłem, uniemożliwia
wysyłanie w przestrzeń jakichkolwiek informacji tzn. nie jest możliwe komunikowanie
się z resztą świata. Pole grawitacyjne „przytrzymuje” nawet światło tzn. fotony nie mo-
gą uciec z gwiazdy i zawsze „spadają” na jej powierzchnię. Choć obserwacja czarnych
dziur nie jest możliwa to można obserwować procesy zachodzące w polu grawitacyjnym
w otoczeniu czarnej dziury. Wciąż jest to kontrowersyjny mechanizm opisujący „kata-
strofalne” zapadanie się gwiazd. Można jednak wyznaczyć warunki na masę i promień.
Graniczny promień poniżej, którego nie możemy już zobaczyć gwiazdy (tzw. promień
Schwartzschilda) jest dany wyrażeniem

Z. Kąkol-Notatki do Wykładu z Fizyki

38-14

2

0

2

c

GM

R

=

Dla masy jądra (żelaznego) równej masie Słońca otrzymujemy R

0

= 3 km.