P

K

M

elementy podatne

podstawowe zadania elementów podatnych – duża
odkształcalność (mały moduł E lub odpowiedni kształt)

1.

ustalanie położenia elementów z luzami –

kasowanie luzów

2.

wywieranie stałego nacisku

3.

amortyzacja sił zewnętrznych i rozpraszanie
energii

– łagodzenie uderzeń

4.

akumulacja energii w celu późniejszego jej

wykorzystania (napęd mechanizmów)

5.

kształtowanie charakterystyki dynamicznej - np.
przy drganiach

– częstość drgań własnych,

tłumienie drgań …

6.

pomiar wielkości (mechanicznych)

Materiał

• Duża wytrzymałość – stal sprężynowa
• Mała sztywność – guma

Sztywność sprężyny – wykres P(f) lub M(fi)
k – współczynnik sztywności (wykresy)
Charakterystyka liniowa, twarda, miękka …

Sprężyny ściskane i rozciągane

Sprężyny skręcane

Sprężyny talerzowe

Resory

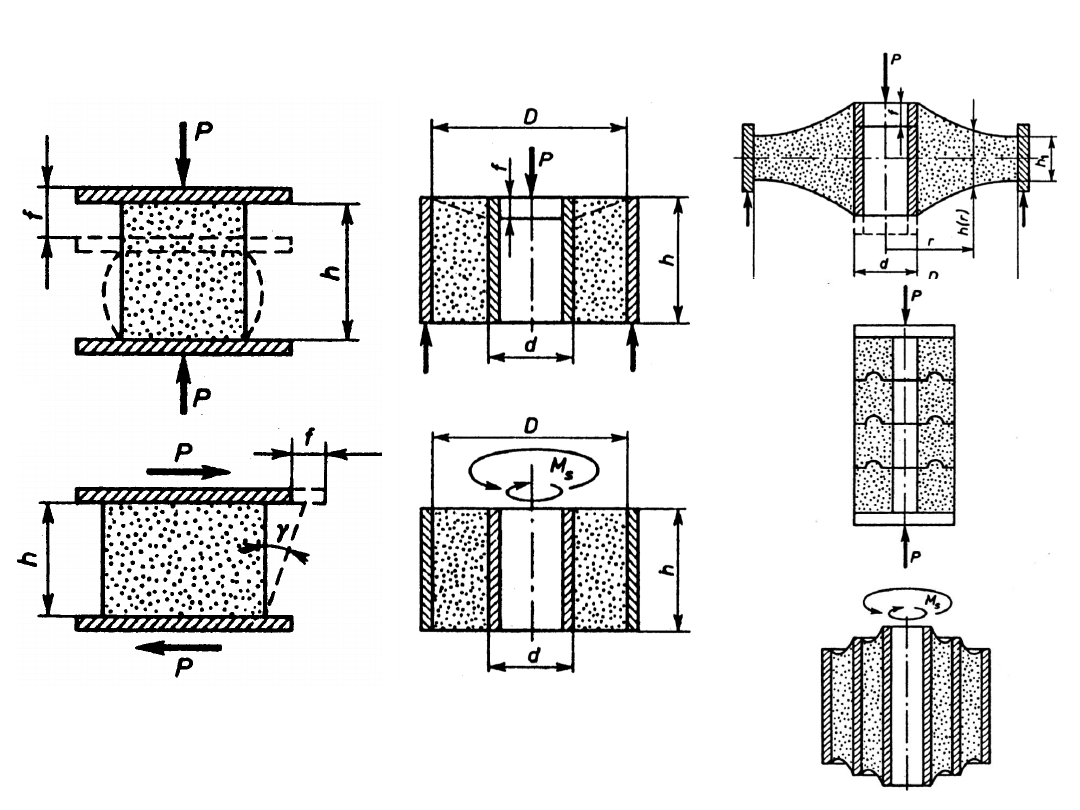
elementy elastomerowe

– wsp. Poissona = 0.5

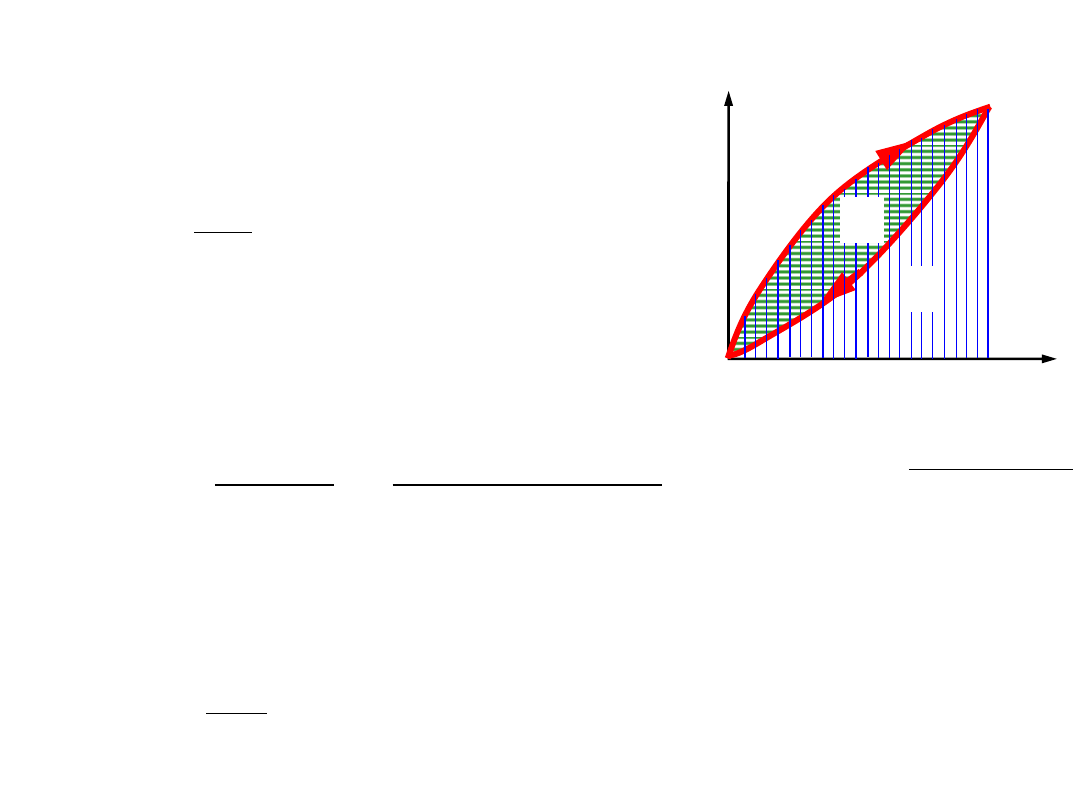
główne wielkości charakteryzujące elementy podatne

1.

sztywność

2.

zdolność do akumulacji energii

- praca

1.

zdolność do rozpraszania energii

df

dP

k



V

df

f

P

V

L

q

f

f

S







max

min

)

(

max

S

R

L

L





L

R

L

S

f

P

2

max

max

max

f

P

L

S





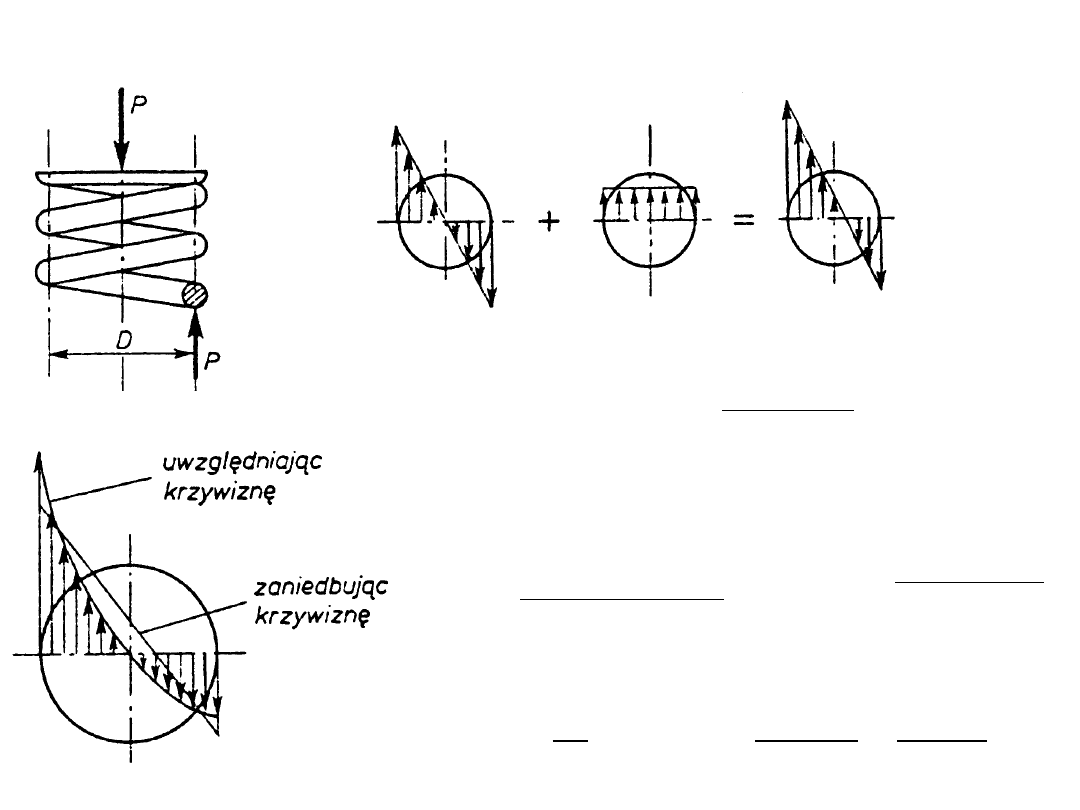
sprężyna śrubowa – skręcanie i ścinania drutu

s

q

d

P

2

max

8























615

,

0

4

4

1

4











s

q

d

D

d

G

n

P

f











3

8



n

d

G

k









3

8



Wykres qs

ZADANIE 2:

Sprężyna ma wywierać nacisk P

max

=2 kN a

towarzyszące jej wydłużenie ma

wynosić f

max

=100 mm.

Sprężyna wykonana ma być ze stali o module Kirchoffa

G=8

·10

4

MPa i dopuszczalnych

naprężeniach k

s

=460 Mpa (D/d=8)

Wyznaczyć:

średnicę drutu z którego wykonana ma być sprężyna – d;

średnicę nawinięcia sprężyny – D;

liczbę zwojów czynnych sprężyny – n.

ZADANIE 1:

Wyznaczyć wymiary kostki gumowej. Maksymalna siła ściskająca
(patrz rys.) P=1000 N, ugięcie f=10 mm, E=10 MPa, kc=4 MPa.

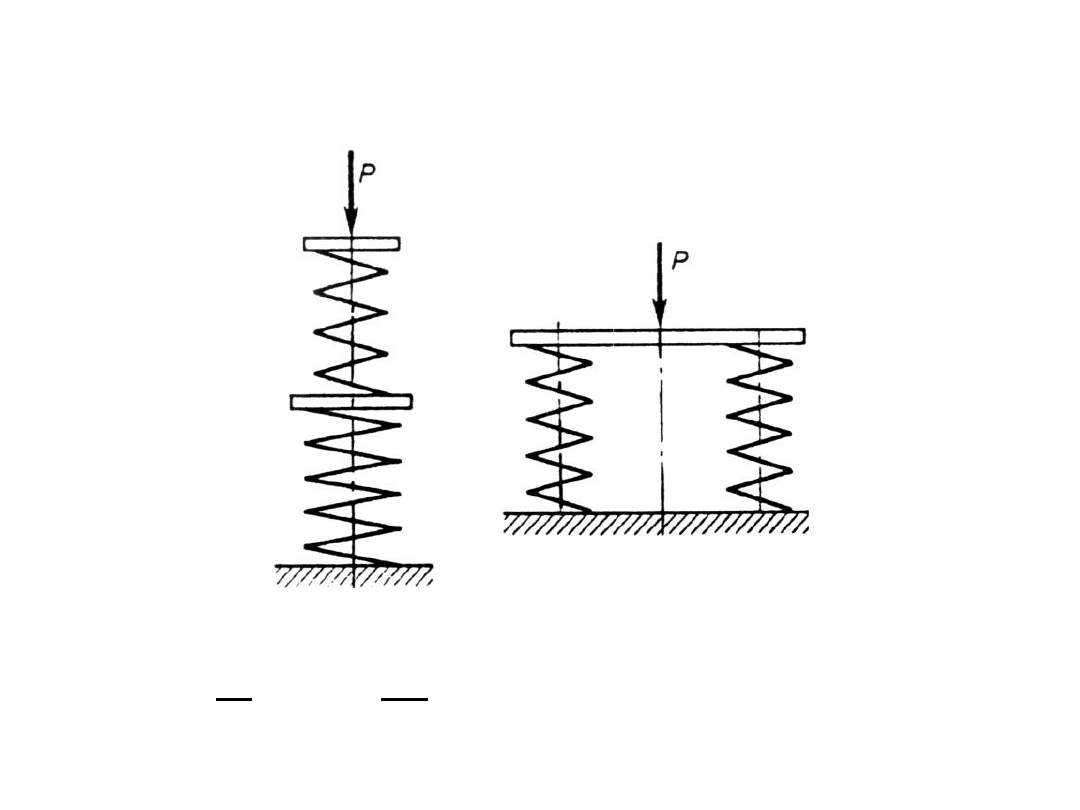
układy sprężyn

i

P

P









n

i

i

f

f

1







n

i

i

k

k

1

1

1







n

i

i

P

P

1

i

f

f









n

i

i

k

k

1

• Zad 2. Masa M=15 kg poruszająca się poziomo z prędkością liniową v=5

m/s uderza w zderzak, którego schemat pokazuje rysunek. Zderzak ma
sprężynę śrubową wykonaną z drutu o średnicy d i średnicy nawinięcia D.
Gdy zderzak jest nieobciążony z zewnątrz, w sprężynie istnieje siła naciągu
wstępnego Po a sprężyna jest ugięta wstępnie o fo=50 mm. W wyniku
uderzenia cała energia rozpędzonej masy jest pochłaniana przez sprężynę.
Występujące wówczas maksymalne odkształcenie sprężyny wynosi fmax =
fo +Δf = 150 mm, a siła w sprężynie wynosi Pmax. Dopuszczalne
naprężenia dla drutu sprężyny ks=800 MPa. Moduł sprężystości postaciowej
dla stali G=80000 MPa.

• 1. Narysować wykres akumulacji energii w trakcie hamowania.
• 2. Wyznaczyć maksymalną, obciążającą sprężynę siłę hamowania Pmax

(pominąć masę sprężyny i masę elementu pośredniczącego w zderzaku).

• 3. Wyznaczyć przyspieszenie hamowania a = x g (g – przyspieszenie

ziemskie).

• 4. Wyznaczyć średnicę drutu sprężyny d i średnicę nawinięcia D, zakładając

że współczynnik ξ=D/d = 12.

• Wyznaczyć liczbę zwojów czynnych sprężyny n, aby pod wpływem

maksymalnej siły hamowania Pmax wystąpiło ugięcie sprężyny fmax.