Prezentacja Markowitz

Analiza Portfelowa

Model Markowitza

Piotr Miszczyoski

SKN OPTEAM

Uniwersytet Łódzki

Plan prezentacji:

- Wstęp – Jak to się wszystko zaczęło…

- Podstawowe pojęcia. Stopa zwrotu, wariancja, kowariancja.

- Podstawowe założenia, idea modelu Markowitza.

- Model Markowitza dla portfela złożonego z dwóch aktywów.

- Model Markowitza dla portfela złożonego z wielu aktywów.

- Prosty przykład empiryczny. Rozwiązanie zadania Genio Szczęściarz.

- Wady i zalety modelu Markowitza.

- Podsumowanie – Jak się zabrad do budowy własnego modelu w MS Excel…

Wstęp

Analiza portfelowa powstała w latach 50’tych XX wieku. Jej fundamenty zostały
stworzone przez Harrego Markowitza, ekonomisty z University of Chicago.

Markowitz w swoich badaniach naukowych
dotyczących rynku akcji zauważył , że
współczesne mu wtedy modele oparte na
teorii

Present

Value

nie

uwzględniają

czynnika ryzyka.
Oparte na tym spostrzeżeniu późniejsze
badania doprowadziły go do stworzenia
podwalin

nowej

teorii

zwanej

alokacją

portfelową w warunkach niepewności.
Dziś popularnie zwaną analizą portfelową –
portfolio analisis.

•Markowitz, Harry M. (1952). "Portfolio Selection". Journal of Finance 7 (1): 77-91.

•Markowitz, Harry M. (1956). "The optimization of a quadratic function subject to
linear constraints". Naval Research Logistics Quarterly 3: 111-133.

•Markowitz, Harry M. (1959). Portfolio Selection: Efficient Diversification of
Investments. John Wiley & Sons, New Jersey. (reprinted in 1970 by Yale University
Press,

ISBN 978-0300013726

; second edition in 1991, Blackwell Publishing,

ISBN 978-

1557861085

)

Wstęp

Markowitz przedstawił swoją teorię w poniższych publikacjach:

Wstęp

Na marginesie warto wspomnied, że Markowitz, na spółkę z Mertonem Millerem i
Williamem Sharpem, otrzymali w 1990 roku nagrodę Nobla z dziedziny nauk
ekonomicznych „za ich pionierski wkład w teorię ekonomii finansowej”.

Harry M. Markowitz

Merton H. Miller

William F. Sharpe

Podstawowe pojęcia

Stopa zwrotu

– jest to stosunek zysku, który przynosi dane aktywo, do

nakładów poniesionych na jego zakup. Jest to miara dochodu z aktywa.

– stopa zwrotu z aktywa w okresie t

– cena akcji w okresie t

– dywidenda wypłacona w okresie t

Wariancja -

jest miarą ryzyka. Im jest większa tym większe ryzyko inwestycji

w dane aktywo.

– długość szeregu stóp zwrotu

– średnia stopa zwrotu

Odchylenie standardowe

– także miara ryzyka,

łatwiejsza w interpretacji od wariancji.

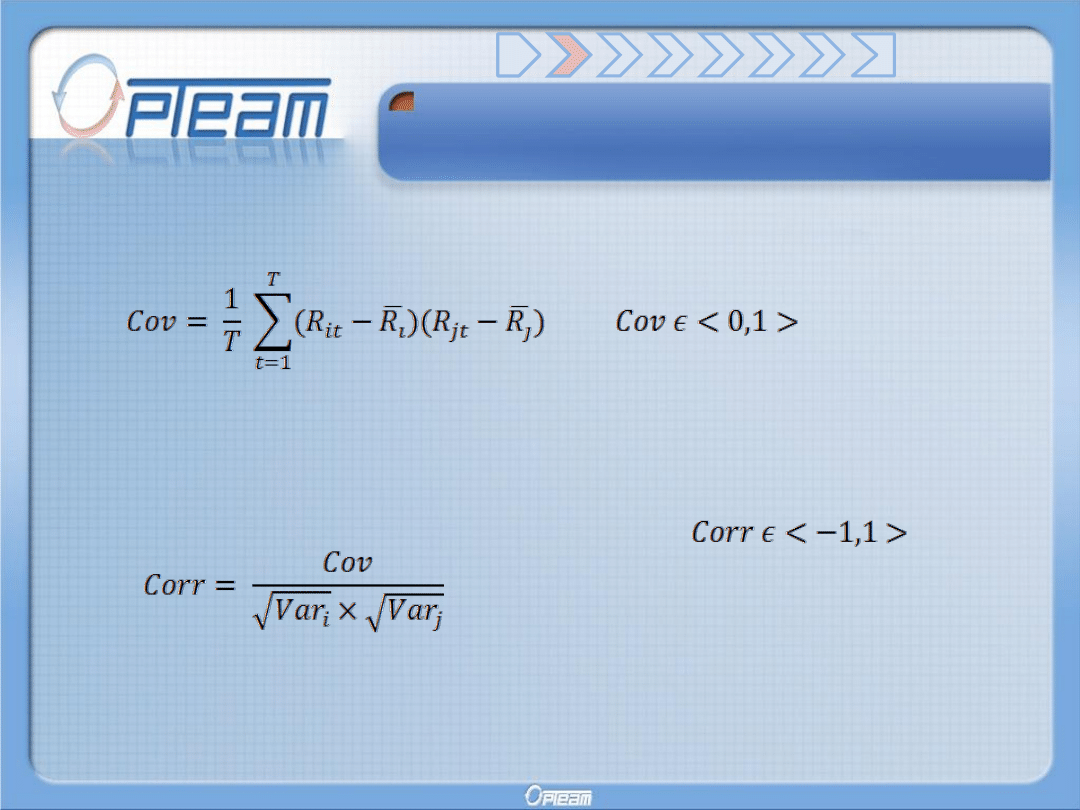
Podstawowe pojęcia

Kowariancja

– jest miarą zależności kursu jednego aktywa z kursem

innego aktywa.

– stopa zwrotu z aktywa i w okresie t

– stopa zwrotu z aktywa j w okresie t

Współczynnik korelacji – jest także miarą zależności jednego kursu
od drugiego, tyle że łatwiejszym w interpretacji.

Var

– wariancja stóp zwrotu z aktywa i

Var

– wariancja stóp zwrotu z aktywa j

Ujemna korelacja oznacza, że
gdy kurs jednego aktywa
rośnie to drugiego spada.

Dodatnia korelacja oznacza,
że gdy kurs jednego aktywa
rośnie to drugiego też rośnie.

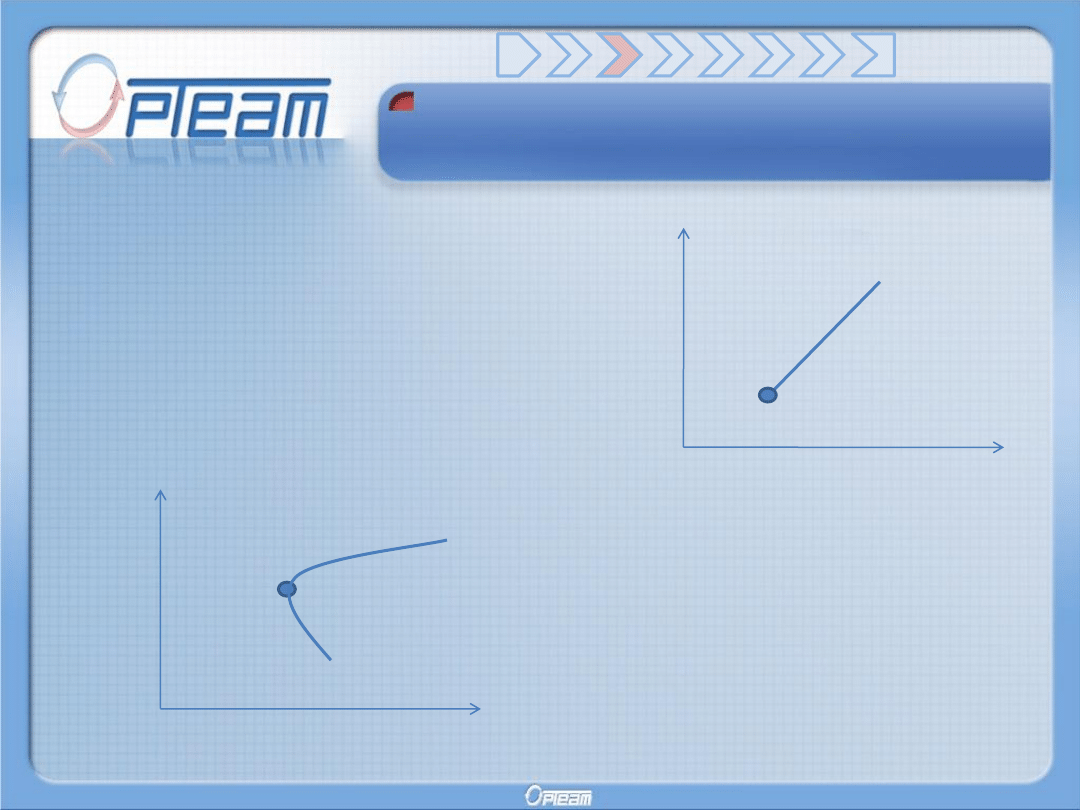
Idea modelu Markowitza

Przyjmując, iż inwestorzy

charakteryzują się awersją do ryzyka,

należy przyjąć, że każdy wzrost

ryzyka z inwestycji w jedno aktywo

jest rekompensowany wzrostem

oczekiwanego zysku.

ryzyko

zysk

ryzyko

zysk

Markowitz zauważył, że gdy
jednocześnie inwestujemy w dwa
rodzaje akcji o różnym ryzyku to
jesteśmy w stanie zmniejszyć ryzyko
inwestycji. Krzywa przedstawia różne
proporcje aktywów w portfelu.

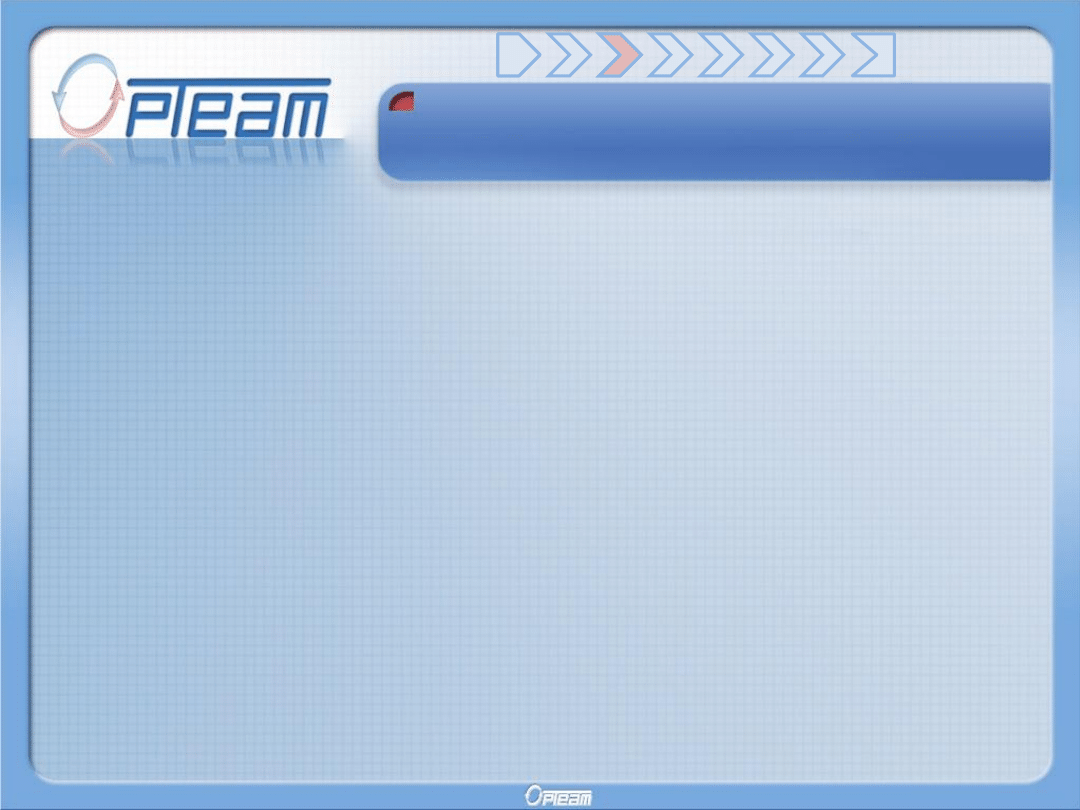
Idea modelu Markowitza

Dlaczego kombinacja dwóch rodzajów aktywów pozwala osiągnąć ten sam
zysk przy mniejszym ryzyku?

Wynika to ze

związków korelacyjnych pomiędzy aktywami. Jeżeli dwa

aktywa

są ze sobą ujemnie skorelowane to ich kombinacja w portfelu może

spowodować spadek ryzyka bez konieczności utraty zysku.

Gdy tracimy na spadku

wartości jednego aktywa to jednocześnie wzrasta

wartość aktywa ujemnie z nim skorelowanego co w zależności od stopnia
skorelowania powoduje

częściowe bądź całkowite pokrycie strat.

(Niestety w praktyce ten ostatni przypadek nie

występuje)

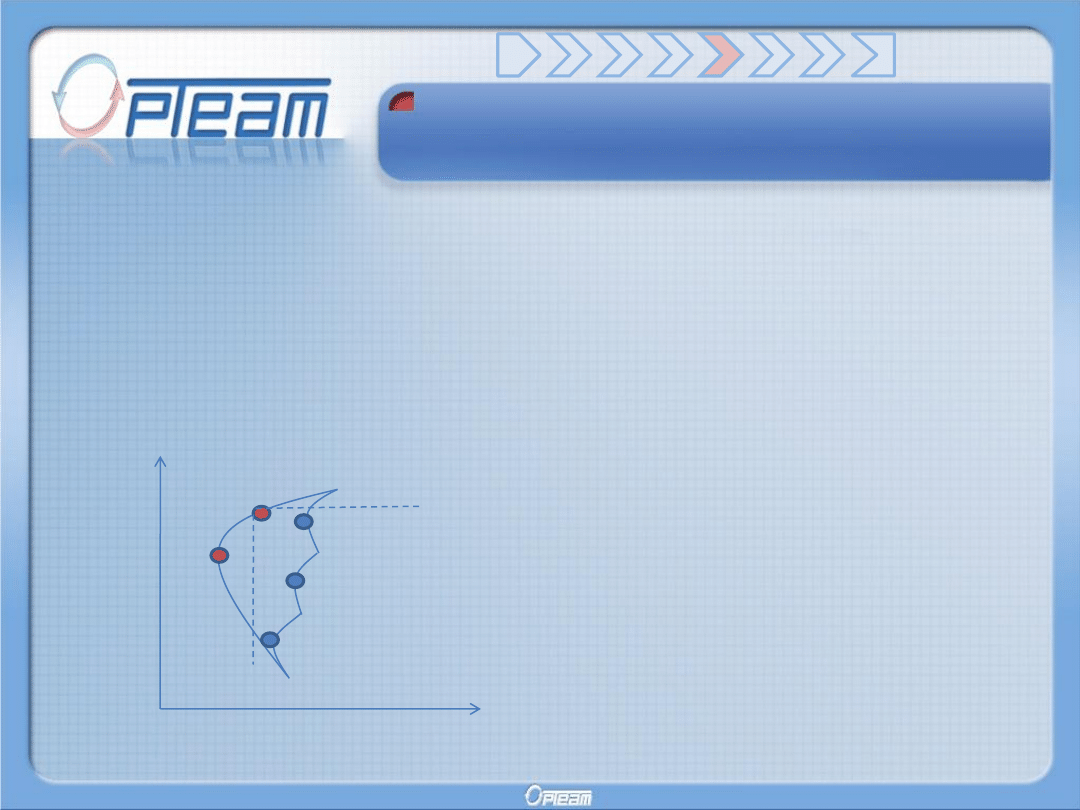
Idea modelu Markowitza

Z teorii Markowitza wynika, iż
istnieje duża ilość portfeli
efektywnych, ale tylko jeden z nich
daje minimalne ryzyko.

ryzyko

zysk

Portfel efektywny, to taki, dla

którego nie istnieje inny portfel o tej samej

oczekiwanej stopie zysku i mniejszym ryzyku oraz taki, dla

którego nie

istnieje inny portfel o tym samym ryzyku i

większej oczekiwanej stopie zysku.

(Jest to

tożsame z efektywnością w sensie Pareto)

Według Markowitza preferencją racjonalnego inwestora jest wybór portfela
efektywnego.

Model dla dwóch aktywów

– udział aktywów i w portfelu

– udział aktywów j w portfelu

W nawiasie znajduje się
ograniczenie zakładające
z góry ustaloną
minimalną stopę zwrotu
założoną przez
inwestora, oznaczoną
symbolem R

Model dla dwóch aktywów

Miniprzykład

Dane:
X

=0,5 (50%)

Var

=0,05

=0,2236 (tj. 22,36%)

Var

=0,045

=0,2121 (tj. 21,21%)

Corr

x1 x2

=-0,8

Celem jest wykazanie, że gdy dane są skorelowane to wariancja portfela jest
mniejsza od wariancji poszczególnych aktywów z osobna.

Var

portfolio

= x

*Var

+2*x

*corr

x1 x2

Var

portfolio

= 0,25*0,05+0,25*0,045+2*0,5*0,5*0,223607 *

0,212132 *-0,8=

=0,0125 +0,01125 -0,01897 =
= 0,004776

Ryzyko portfela mierzone odchyleniem standardowym

portfolio

= 0,069111 (tj. zaledwie 6,9%)

Model dla wielu aktywów

Można także skonstruować model dla wielu aktywów.
Daje to

możliwość dodatkowego zmniejszenia ryzyka przy niezmienionej

stopie zysku.

Poniższy rysunek pokazuje jak portfele względem aktywów dobranych
parami w modelach

dwuskładnikowych mają się do jednego portfela

złożonego ze wszystkich aktywów jednocześnie.

ryzyko

zysk

Model dla wielu aktywów

W ogólnym przypadku model Markowitza dla wielu
aktywów można zapisać następująco:

Model dla wielu aktywów

Lub w bardziej użytecznej formie macierzowej:

gdzie:
x

– kolumnowy wektor udziałów

kolejnych aktywów w portfelu
V

– macierz wariancji kowariancji

stóp zwrotu aktywów w portfelu
1

– kolumnowy wektor jedynkowy

– kolumnowy wektor zerowy

– wierszowy wektor

oczekiwanych stóp zwrotu dla
poszczególnych aktywów (średnie
stopy zwrotu w badanym okresie)

Przykład empiryczny

Pan Genio

Szczęściarz w swoje urodziny 10 kwietnia wygrał w loterii

znaczną sumę pieniędzy. Aby nie wydać wygranej kwoty postanowił
zainwestować. Pan Genio nie wiedział, że dane archiwalne o
notowaniach

spółek są dostępne w Internecie i stwierdził, że zacznie

spisywać z gazety notowania spółek. Ponieważ tata Pana Genia był
hutnikiem

więc chciał on zainwestować swoje pieniądze w spółki

przemysłu metalowego. 25 maja Pan Genio stwierdził, że ma
wystarczającą ilość danych by stwierdzić, że warto zainwestować w
spółki przemysłu metalowego. Ponieważ bał się zainwestować
wszystkich

pieniędzy w jedną spółkę by nie stracić pieniędzy, postanowił

zakupić akcje kilku spółek. Nie wiedział tylko w jakiej proporcji ma
zainwestować w dane spółki by zminimalizować ryzyko i jednocześnie
zarobić jak najwięcej.
Pomóż Panu Geniowi zbudować portfel inwestycyjny wykorzystując
model Markowitza i zebrane przez Pana Genia dane.

Przykład empiryczny

Dane zebrane przez Pana Genia

Za spółki przemysłu metalowego Pan Genio uznał poniższe 11 spółek.
1. Ferrum SA
2. Grupa Kęty SA
3. Hutmen SA
4. KGHM Polska Miedź SA
5. Koelner SA
6. Odlewnie Polskie SA
7. Stalexport SA
8. Stalprodukt SA
9. Śrubex SA
10. Toora Poland SA
11. Zetkama SA

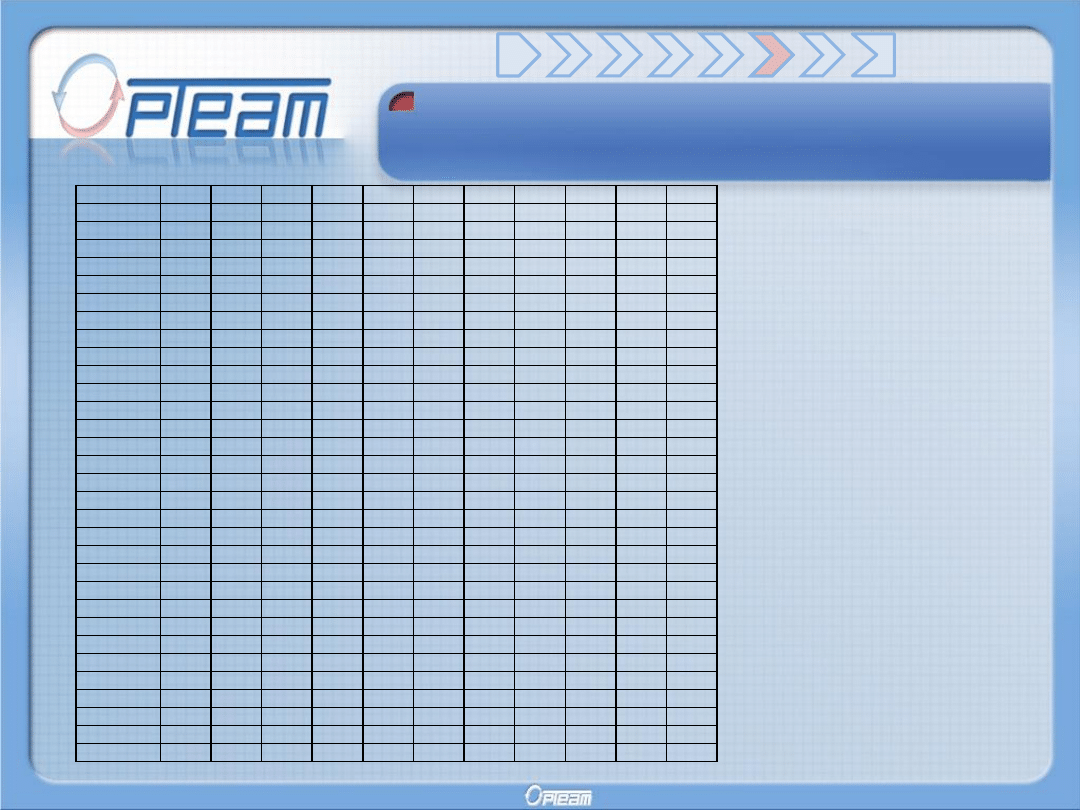
Przykład empiryczny

Data

2007-04-11

34,4 191,5

33,8 112,9

62,5 10,05

5,69

1060 45,88 27,99 18,78

2007-04-12 32,95

186 30,78 113,6 62,65

9,71

5,43

1060 45,39 27,74

17,8

2007-04-13 33,49

187

30,5 111,8

63,5

9,85

5,56

1100

46,6

27,3

18,7

2007-04-16

187 26,97 117,9

64,4

9,8

5,58

1070 46,66

27,1

18,7

2007-04-17

32,3 190,5 26,98 118,1

62,4

9,8

5,65

1100 46,45 26,54

19,2

2007-04-18

191 25,65 116,8

9,91

1110

47,9 27,34

2007-04-19

193 24,62 114,7

62,9

9,77

6,85

1100 48,29 27,35 19,35

2007-04-20 31,98

195 25,63 116,7

64,4 10,29

7,21

1097 49,08

19,1

2007-04-23 31,48 197,8 23,88 117,5

64,4 10,38

8,28

1113

48,8

26,5 18,62

2007-04-24 31,45

196 24,14 112,8 65,85

10,3

8,05

1090

46,5

18,4

2007-04-25 31,46

197 24,24 109,8

70 10,35

7,71

1090 47,48

26,5

18,2

2007-04-26 32,69 199,1

24,6

108

70 10,53

7,62

1090

46,9

27 19,04

2007-04-27

32,4

203 25,75 105,5

10,8

7,13

1120

48,9

26,7 18,22

2007-04-30

32,2 195,1 25,37

107

68 10,69

7,06

1160 48,49

27 18,72

2007-05-02 32,45

201

109 71,85 10,75

7,4

1230 48,94 27,89 18,65

2007-05-04

36,5

205 26,05 112,1

72,5

11,2

7,95

1244 49,18 28,39 21,04

2007-05-07 37,05

205

113

72,5

10,8

8,02

1270 48,26 26,11 22,02

2007-05-08 34,25

210

27,9 109,1

72,5 10,06

7,39

1256 48,25

25,5 21,99

2007-05-09

36 213,5 27,42

112

70,4

9,9

7,31

1233

47,3

24,5

2007-05-10

32,6

210

26,5 107,5

67,5

9,8

6,92

1250

46,6

23,7

21,9

2007-05-11 34,47

213

25,8

106

68,3

9,75

7,24

1230 46,87

24,5

2007-05-14

34,5

214

105

70 10,16

7,22

1280

48,5

24,5 22,19

2007-05-15 33,55

209

26 103,9

68,9

9,9

1278 48,28

24,4 22,14

2007-05-16

206

27 102,1

9,89

6,75

1293 47,69 24,43

2007-05-17 32,45 207,8

100

69,5

9,63

6,45

1284 47,39

22,1

2007-05-18 31,87 212,9 26,21

99,1 69,05

9,66

6,31

1275

46,5 24,92 22,09

2007-05-21 32,49 213,5

25,7 103,5

71 10,45

6,53

1307

47,5

25,1

2007-05-22

213 26,01 106,2

72,8 10,21

6,6

1318

48 24,95

23,5

2007-05-23

34,2

210

26,2 105,3

74,5 10,06

6,8

1318 47,78

25 24,17

2007-05-24

210 26,05 104,7

75 10,09

7,39

1315

49 25,15

23,9

2007-05-25

32,5

210 26,34

105 74,75

9,9

7,19

1318

51,1

25,3

24,6

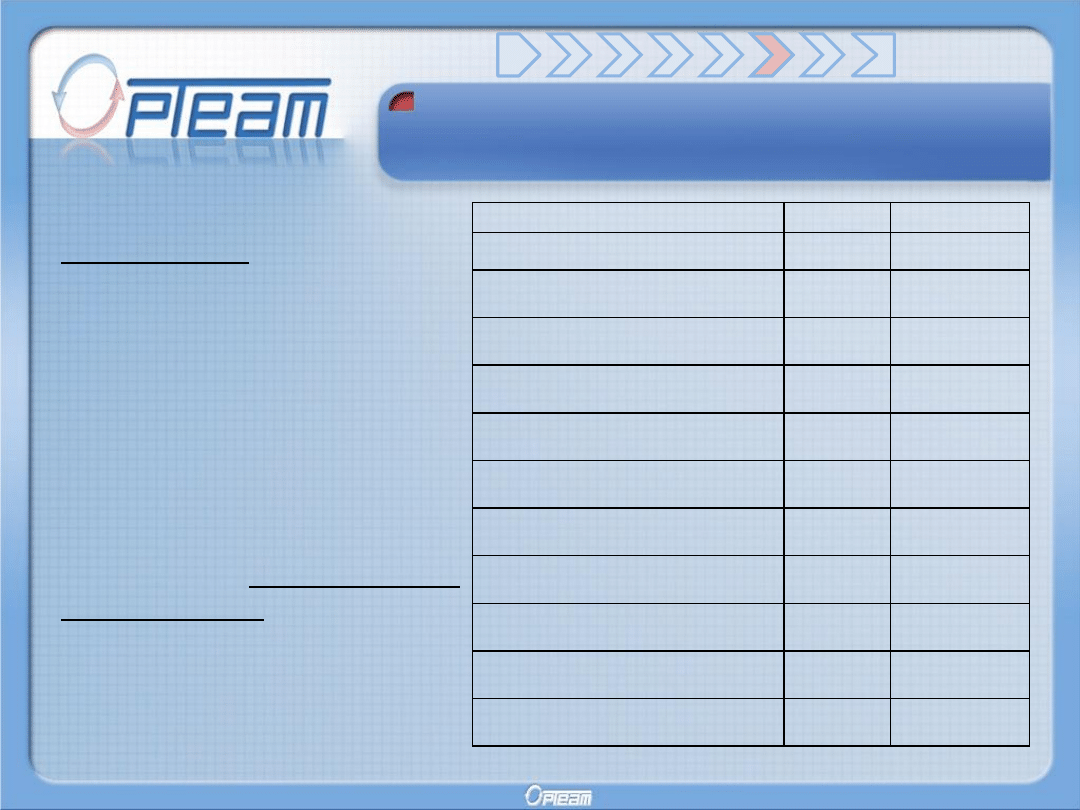
Przykład empiryczny

ROZWIĄZANIE

Wszelkie obliczenia były
prowadzone w arkuszu
kalkulacyjnym MS Excel.
Rozwiązanie otrzymano przy
pomocy dodatku Solver.

Z pomocą Solvera można
otrzymać strukturę portfela
odpowiadającą zminimalizowanej
wariancji portfela.
R

portfolio

= 0,001173 (tj.0,117%)

Var

portfolio

= 0,000109

portfolio

=0,0104 (tj. 1,04%)

Nazwa spółki

Ferrum SA

0,00%

-0,105%

Grupa Kęty SA

34,46%

0,321%

Hutmen SA

6,33%

-0,752%

KGHM Polska Miedź SA

19,85%

-0,215%

Koelner SA

1,53%

0,624%

Odlewnie Polskie SA

0,00%

-0,009%

Stalexport SA

0,00%

0,974%

Stalprodukt SA

17,77%

0,748%

Śrubex SA

2,39%

0,380%

Toora Poland SA

17,66%

-0,309%

Zetkama SA

0,00%

0,956%

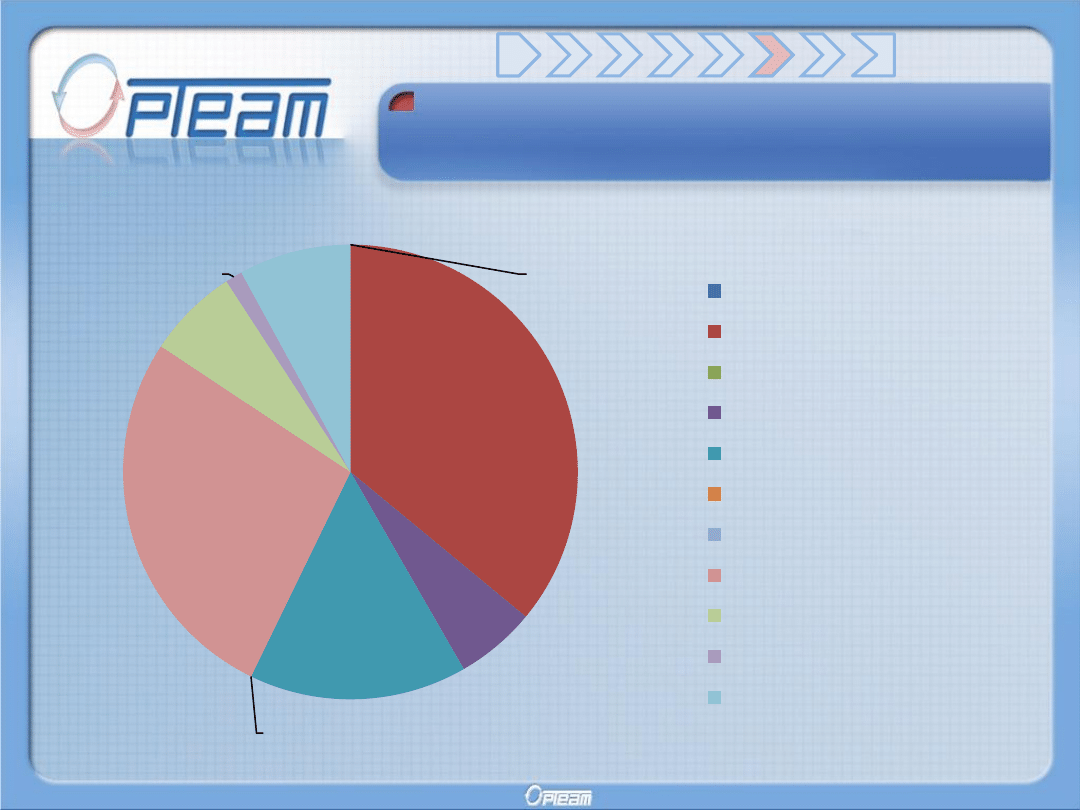
Przykład empiryczny

Struktura portfela Pana Genia:

0,00%

35,99%

0,00%

5,71%

15,51%

0,00%

27,12%

6,50%

1,21%

7,97%

Ferrum SA

Grupa Kęty SA

Hutmen SA

KGHM Polska Miedź SA

Koelner SA

Odlewnie Polskie SA

Stalexport SA

Stalprodukt SA

Śrubex SA

Toora Poland SA

Zetkama SA

Wady i zalety

Zalety:
-

model jest bardzo łatwy do zastosowania

(np. poprzez implementację w programie MS Excel)

jest punktem wyjścia dla innych modeli

(np. dla modelu Sharpe’a, zwanego także modelem CAPM)

Wady:
-

model zakłada, że inwestuje się w aktywa ryzykowne.

Można zastosować modyfikację polegającą na wymieszaniu
portfela akcji z inwestycją w obligacje.

opiera się na danych historycznych.

Pomocne mogą tu być metody symulacyjne i ekonometryczne
mogące służyć przy prognozowaniu danych, na podstawie
których rozwiązujemy model Markowitza.

Podsumowanie

•Należy zebrać dane z GPW.

Są one dostępne w internecie:

www.parkiet.com
www.money.pl

Najlepiej brać kursy zamknięcia (CLOSE)
Dla wygody obliczeń należy uporządkować dane od najstarszych do najmłodszych w kolumnach

umieszczając kolejne spółki.
(Uwaga, należy sprawdzić czy dane są poprawnie ułożone względem dat)

•Należy obliczyć dzienne stopy zwrotu dla wszystkich spółek.
•Następnie należy wyliczyć średnie z dziennych stóp zwrotu dla całego okresu próby.

•Należy stworzyć Macierz wariancji-kowariancji stóp zwrotu za pomocą funkcji =KOWARIANCJA

•Następnie tworzymy wektor udziałów. Na początek wpisujemy ręcznie równe udziały (np. dla 10 spółek
będzie to dziesięć komórek z wartością 10%)

•W jednej z komórek należy obliczyć wariancje portfela działaniem na macierzach.

•Obliczeń dokonujemy przy pomocy dodatku Solver.

Minimalizowaną komórką celu jest wariancja portfela. Komórki zmieniane to udziały poszczególnych akcji.

Należy dodać ograniczenie, że suma udziałów jest równa 100%.

Jak się zabrać do budowy własnego modelu w MS Excel…

Podsumowanie

Źródła książkowe:

Trzaskalik T. (red), „Metody wielokryterialne na polskim rynku

finansowym”, PWE Warszawa, 2006

Jajuga K, Jajuga T. „Inwestycje”, PWN, 2005

Luenberger D.G., „Teoria inwestycji finansowych”, PWN, 2003

Źródła internetowe:

-Wikipedia the free encyklopedia - http://en.wikipedia.org
-Oficjalna strona fundacji Nobla -

http://nobelprize.org

- money.pl
- www.parkiet.com

Dziękuję za uwagę

Piotr Miszczyoski

SKN OPTEAM

Uniwersytet Łódzki

www.opteam.uni.lodz.pl

Studenckie Koło Naukowe Wspomagania Decyzji Gospodarczych

Wyszukiwarka

Podobne podstrony:
prezentacja finanse ludnosci
prezentacja mikro Kubska 2
Religia Mezopotamii prezentacja
Prezentacja konsument ostateczna
Strategie marketingowe prezentacje wykład
motumbo www prezentacje org
lab5 prezentacja
Prezentacja 18
Materialy pomocnicze prezentacja maturalna
Prezentacja na seminarium
Lato prezentacja 3
Prezentacja1
Prezentacja 2 analiza akcji zadania dla studentow

więcej podobnych podstron