Architektura Systemów Komputerowych
Laboratorium
Nr ćwiczenia: 2
Temat ćwiczenia: Układy kombinacyjne.
Imię i nazwisko prowadzącego kurs: Maciej Huk
Wykonawca:
Jakub Bartusiak
Imię i Nazwisko
nr Indeksu, wydział
Jakub Bartusiak
197914, SKP
Termin zajęć: dzień tygodnia, godzina
Wtorek, 15
15
Data oddania sprawozdania:
Ocena końcowa
Ewentualne adnotacje dotyczące wymaganych poprawek oraz daty otrzymania
poprawionego sprawozdania:
1 |
S t r o n a
S
PIS TREŚCI
PRZEDSTAWIENIE FUNKCJI ZA POMOCĄ BRAMEK NAND ............................................. 6
PRZEDSTAWIENIE FUNKCJI ZA POMOCĄ MUX ............................................................. 7
4. ODRĘCZNE RYSUNKI ................................................................................................. 10
2 |
S t r o n a
1.
C
EL ĆWICZENIA
Dwie funkcje przedstawione poniżej:
a) ( ) (
̅̅̅̅̅̅̅ ̅
̅̅̅̅̅̅̅̅̅̅̅̅)
̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅,
b) ( ) ̅ ̅ ̅
̅̅̅̅̅̅̅̅̅̅̅̅̅,
należy zrealizować w minimalnym (dwupoziomowym) układzie wykorzystującym bramki
NAND, oraz w układzie wykorzystującym Multiplekser 74151 (MUX). Należy też wykazać, że
układy zrealizowane za pomocą bramek NAND i MUX realizują te same funkcje.
2.
M
ULTIPLEKSER
74151
(MUX)
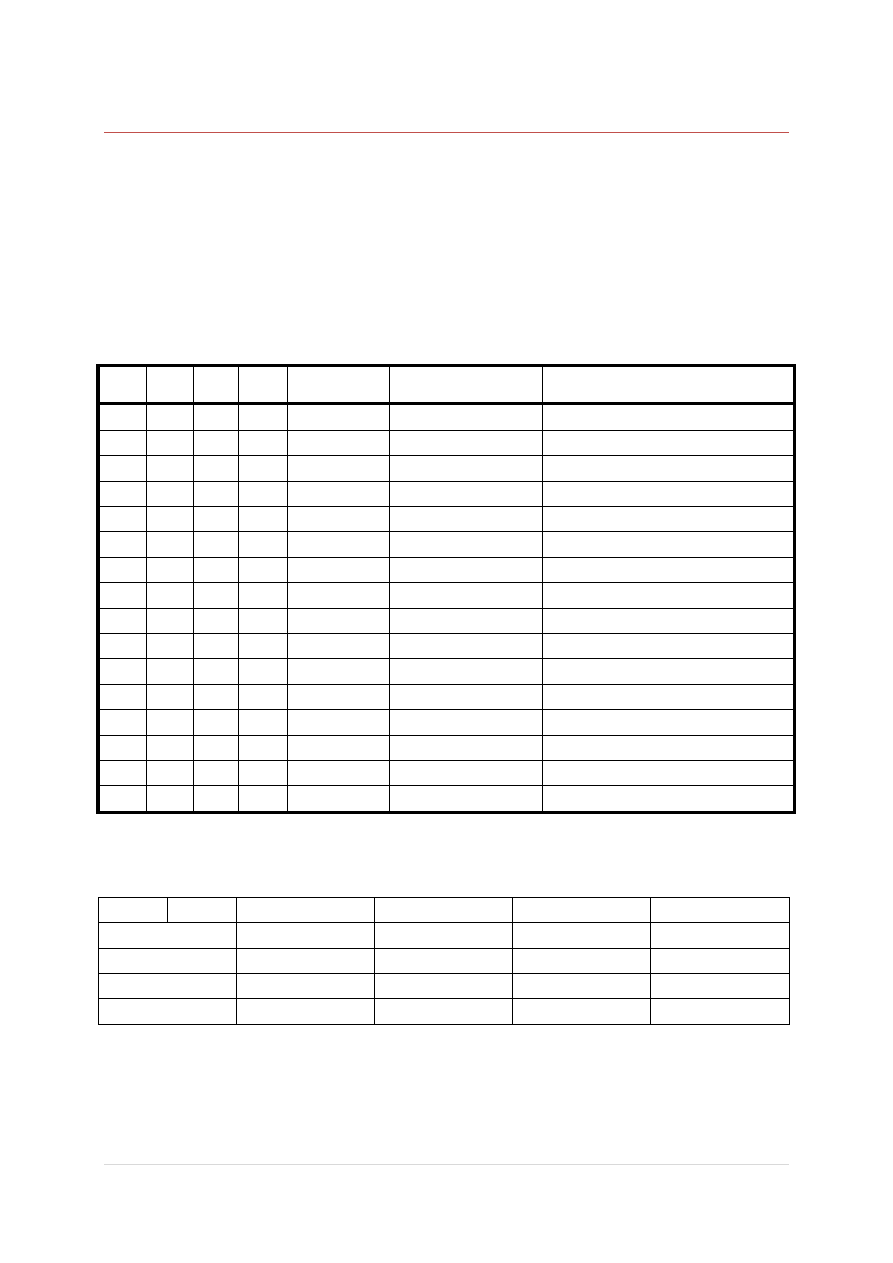
Multiplekser
jest
układem
kombinacyjnym
służącym do wyboru jednego z kilku sygnałów
wejściowych i przekazania go na wyjście.
Multiplekser
z
serii
danych
wejściowych
przekazuje na wyjście odpowiednią wartość, w
zależności
od
danych
sterujących.
Legenda rysunku:
V
CC
- Zasilanie,
A, B, C- wejścia przełączające,
D0-D7- wejścia danych,
Y- wyjście jednej z przekazanych danych,
W-
zaprzeczenia
wyjścia
jednej
z
przekazanych danych,
STROBE- gdy wejście ma wysoki stan logiczny, na wyjściu Y jest niski stan logiczny, a
na wyjściu W- wysoki stan logiczny,
GDN- uziemienie.
3 |
S t r o n a
1. S
YNTEZA FUNKCJI
1.1 Funkcja a.
( ) (
̅̅̅̅̅̅̅ ̅
̅̅̅̅̅̅̅̅̅̅̅̅)
̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅,
Aby zminimalizować funkcję, korzystam z tablicy prawdy, aby sprawdzić jakie dane mam
wpisać do tablicy Karnougha:
̅̅̅̅̅̅̅
̅̅̅̅̅̅̅ ̅
̅̅̅̅̅̅̅̅̅̅̅̅̅
(
̅̅̅̅̅̅̅ ̅
̅̅̅̅̅̅̅̅̅̅̅̅̅)
̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅
0
0
0
0
1
0
1
0
0
0
1
1
0
0
0
0
1
0
1
0
1
0
0
1
1
1
0
0
0
1
0
0
0
0
1
0
1
0
1
0
0
0
0
1
1
0
0
1
0
0
1
1
1
0
1
0
1
0
0
0
0
0
1
1
0
0
1
0
0
0
1
0
1
0
0
1
0
1
0
1
1
0
1
0
1
1
0
0
0
0
1
1
1
0
1
0
0
0
1
1
1
0
0
1
0
1
1
1
1
0
1
0
Odpowiednie wartości wpisuję do tablicy Karnougha:
cd↓
ab→
00
01
11
10
00
1
1
1
1
01
0
0
0
0
11
0
0
0
0
10
1
0
0
0
4 |
S t r o n a
Jak widać, w pary można połączyć cały pierwszy wiersz, oraz pierwszy i ostatni wiersz
pierwszej kolumny. Tak zminimalizowana funkcja będzie wyglądała w taki sposób:
( ) ̅ ̅ ̅ ̅ ̅( ̅) ̅ ̅ ̅ ̅ ̅
Aby przedstawić funkcję za pomocą bramek NAND, korzystam z praw de Morgana, które
mówią:
̅̅̅ ̅ ̅
̅̅̅̅̅̅̅ ̅ ̅
A więc:
( ) ̅ ̅ ̅ ̅ ̅
̿̿̿̿̿̿̿
̅
̅
̅̅̅̅̅̅
̅ ̅, ̅ ̅ ̅
̅̅̅
̅ ̅ ̅, ̅ ̅ ̅ ̅
̅̅̅̅̅
Funkcja przekształcona do takiej postaci daje się przedstawić w postaci bramek NAND, tak
więc dalsze modyfikacje nie są konieczne. Jest to też minimalna postać tej funkcji.
1.2 Funckja b.
( ) ̅ ̅ ̅
̅̅̅̅̅̅̅̅̅̅̅̅̅,
Aby zminimalizować funkcję, korzystam z tablicy prawdy, aby sprawdzić jakie wartości mam
wpisać do tablicy Karnougha:
̅
̅ ̅
̅ ̅ ̅
̅ ̅ ̅
̅̅̅̅̅̅̅̅̅̅̅̅̅
0
0
0
0
0
0
1
0
0
1
0
1
1
0
0
1
1
0
0
0
1
1
1
1
0
0
0
1
1
1
0
1
0
1
0
1
0
0
0
0
0
1
1
0
1
0
0
0
1
0
1
0
0
0
0
1
5 |
S t r o n a
Odpowiednie wartości wpisuję do tablicy Karnougha:
a↓
bc→
00
01
11
10
0
1
0
1
1
1
1
1
1
0
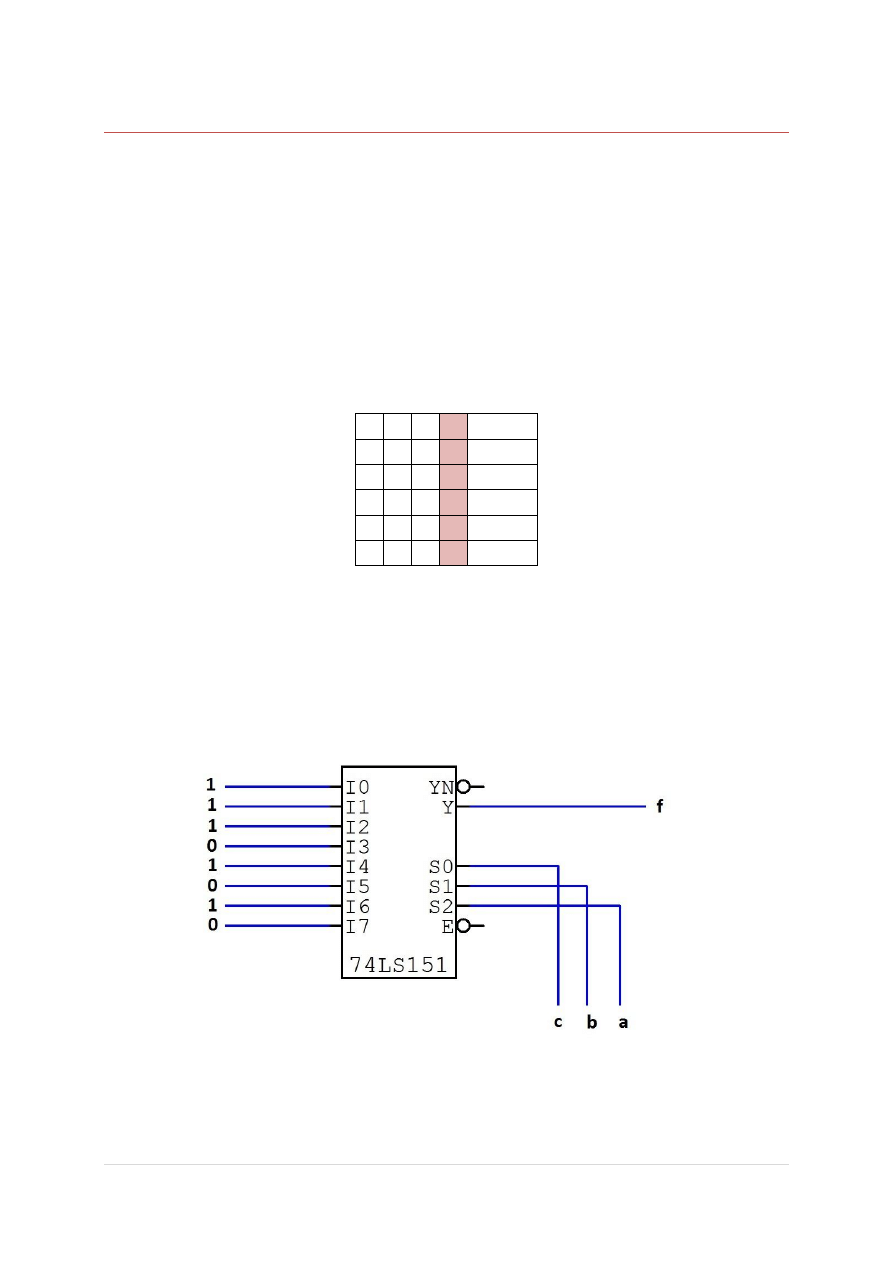
Trzy pary, które można ze sobą połączyć, zostały oznaczone różnymi kolorami. Tak
zminimalizowana funkcja będzie wyglądała w taki sposób:
( ) ̅ ̅( ̅) ( ̅) ̅ ( ̅) ̅ ̅ ̅
Aby przedstawić funkcję za pomocą bramek NAND, korzystam z praw de Morgana, tak więc:
( ) ̅ ̅ ̅
̿̿̿̿̿̿̿̿̿̿̿̿̿ ̅ ̅ ̅
̅̅̅̅̅̅̅̅̅̅
̅ ̅ ̅ ̅ ̅
̅̅̅
̅
̅̅̅
̅ ̅ ̅
̅̅̅̅
Funkcja przekształcona do takiej postaci, daje sie przedstawić w postaci bramek NAND, tak
więc dalsze modyfikacje nie są konieczne. Jest to też minimalna postać tej funkcji.
6 |
S t r o n a
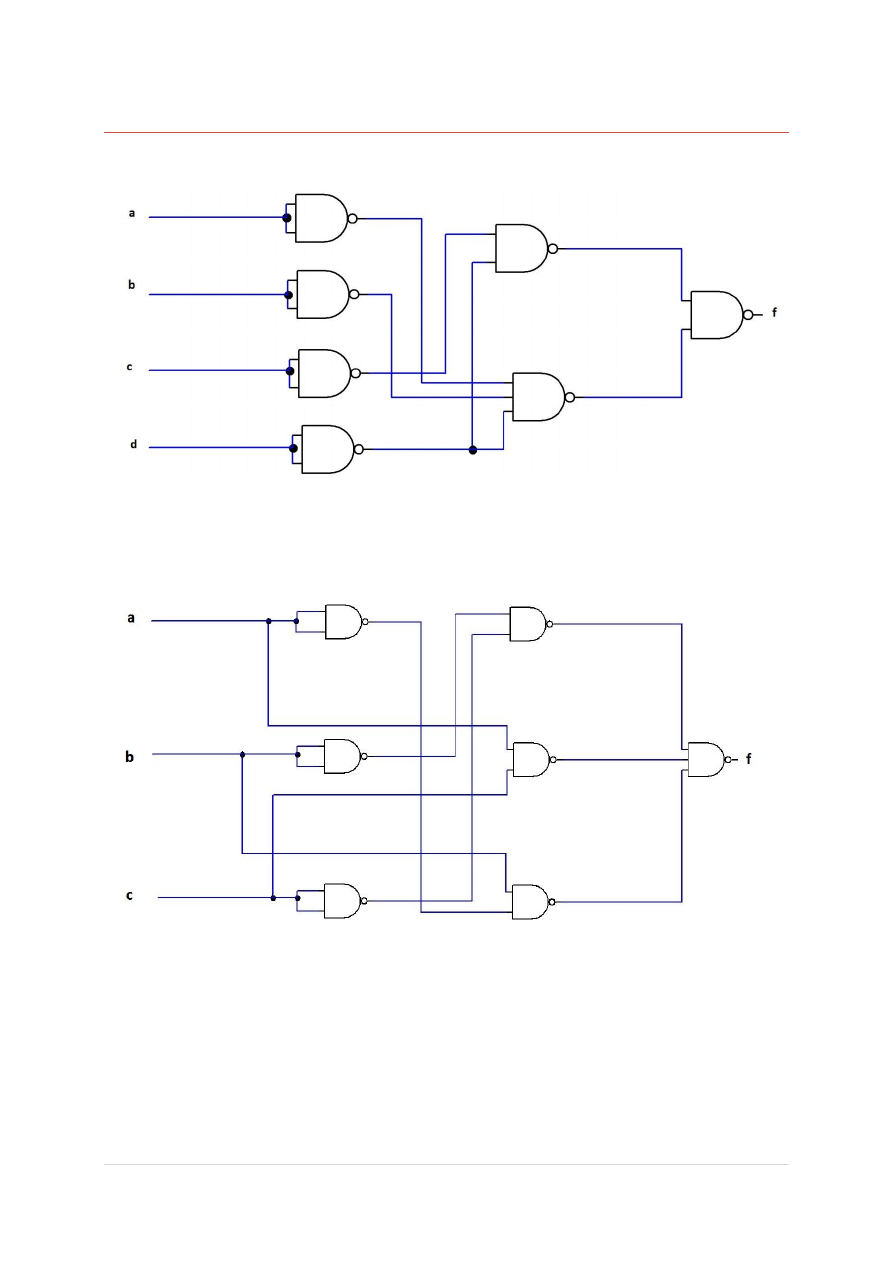
2. P
RZEDSTAWIENIE FUNKCJI ZA POMOCĄ BRAMEK
NAND
2.1 Funkcja a.
2.2 Funckja b.
7 |
S t r o n a
3.
PRZEDSTAWIENIE FUNKCJI ZA POMOCĄ
MUX
Aby przedstawić funkcję za pomocą multipleksera, muszę przedstawić fukcję w postaci
kanonicznej sumy. Do elementów sumy kanonicznej zaliczam wysokie wartości logiczne na
wyjsciu funkcji. A więc:
( ) (
̅̅̅̅̅̅̅ ̅
̅̅̅̅̅̅̅̅̅̅̅̅)
̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅̅,
( ) ( )
Następnie sprawdzam, jakie wartości zmiennych dają odpowiednie wartości na
wyjściu:
a b c d wynik
0 0 0 0
0
0 0 1 0
2
0 1 0 0
4
1 0 0 0
8
1 1 0 0
12
Z racji, że aby móc przekazać te wartości do multipleksera 74151, należy podać trzy wartości
sterujące, zauważam że wartość zmiennej d jest zawsze 0. Pomijam tą zmienną. Nowa postać
sumy kanonicznej to:
( ) ( )
8 |
S t r o n a
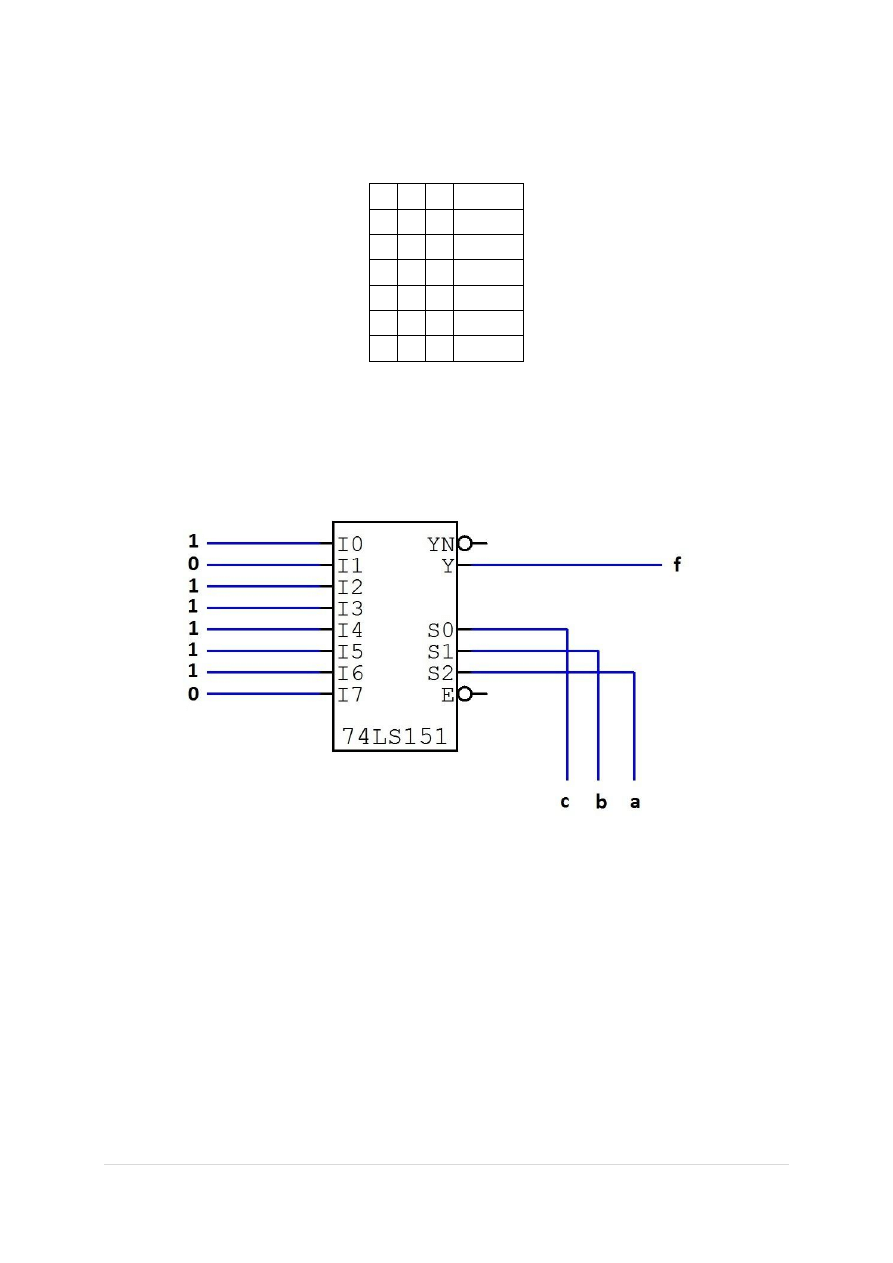
Analogicznie postępuję z drugą funkcją:
( ) ̅ ̅ ̅
̅̅̅̅̅̅̅̅̅̅̅̅̅,
a b c wynik
0 0 0
0
0 1 0
2
0 1 1
3
1 0 0
4
1 0 1
5
1 1 0
6
Funkcja nie wymaga modyfikacji, aby mogła zostać przekazana do multipleksera;
1 |
S t r o n a
4. O
DRĘCZNE RYSUNKI