
Architektura Systemów Komputerowych
Laboratorium
Nr ćwiczenia: 5
Temat ćwiczenia: Synteza układu synchronicznego.
Imię i nazwisko prowadzącego kurs: Maciej Huk
Wykonawca:
Jakub Bartusiak
Imię i Nazwisko
nr Indeksu, wydział
Jakub Bartusiak
197914, SKP
Termin zajęć: dzień tygodnia, godzina
Wtorek, 15
15
Data oddania sprawozdania:
27.03.2012
Ocena końcowa
Ewentualne adnotacje dotyczące wymaganych poprawek oraz daty otrzymania
poprawionego sprawozdania:

1 |
S t r o n a
S
PIS TREŚCI
2. SYNTEZA UKŁADU ZA POMOCĄ AUTOMATU MOORE’A ................................................. 2
? ................................................................ 2
............................................................................................... 3
3.SYNTEZA UKŁADU ZA POMOCĄ AUTOMATU MEALY’EGO ............................................... 5
? ......................................................... 5
............................................................................................. 5
2 |
S t r o n a
1.
C
EL ĆWICZENIA
Celem ćwiczenia jest zaprojektowanie własnego układu synchronicznego realizującego taką
funkcję, która parzyste jedynki z wejścia przekazywała będzie do wyjścia
, a nieparzyste do
wyjścia
, oraz analiza różnic jego działania w automacie Moore’a i Mealy’ego.
2.
S
YNTEZA UKŁADU ZA POMOCĄ AUTOMATU
M
OORE
’
A
2.1 Czym jest układ Moore’a i jak go zrealizować?
Układ Moore’a jest to taki układ, którego wyjście jest funkcją wyłącznie stanu wewnętrznego
układu. Układ taki mam zrealizować za pomocą dwóch przerzutników typu D, które
zachowują się w następujący sposób:
Q(t) Q(t+1) D
0
0
0
0
1
1
1
0
0
1
1
1
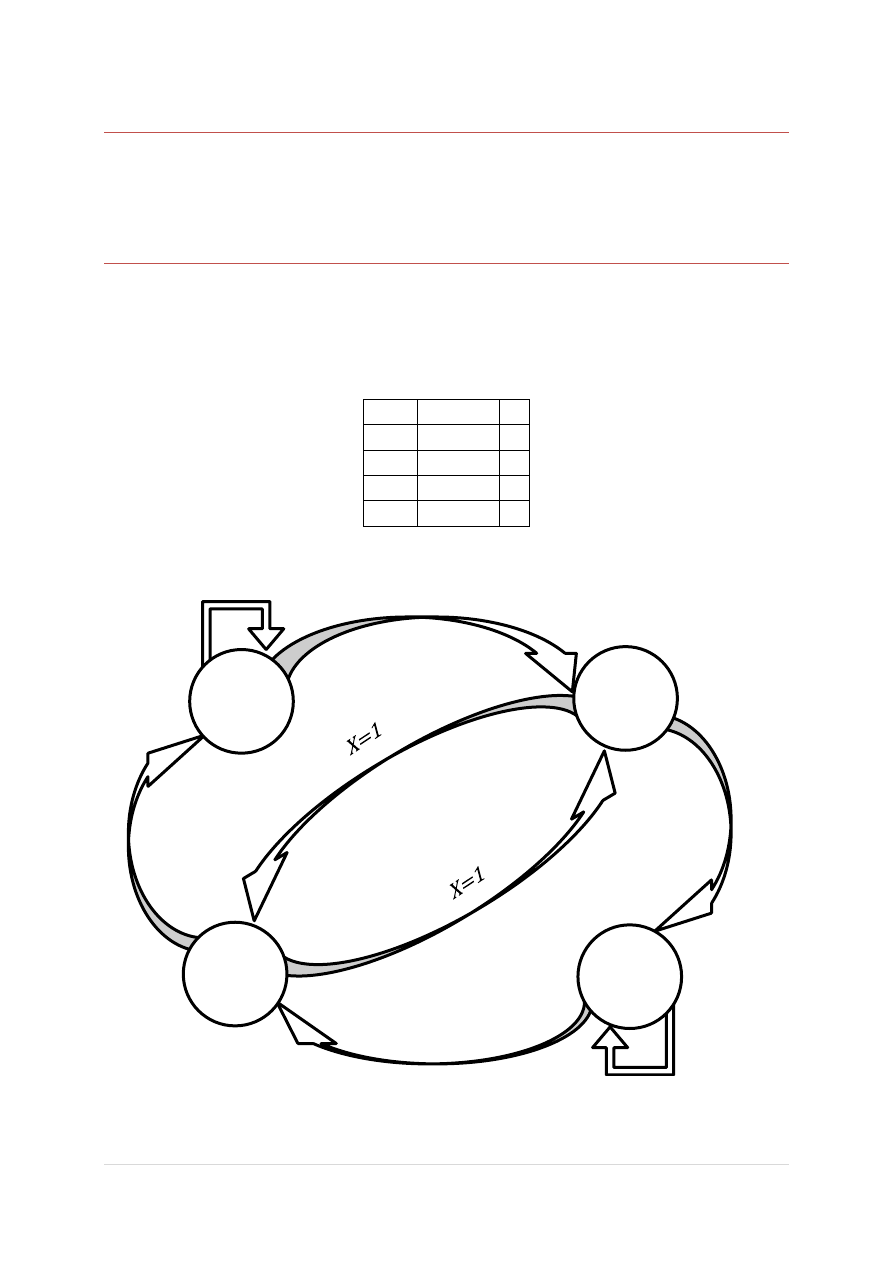
q
3
q
2
X=1
X=0
X=1
q
0
q
1
X=0
X=0
X=0
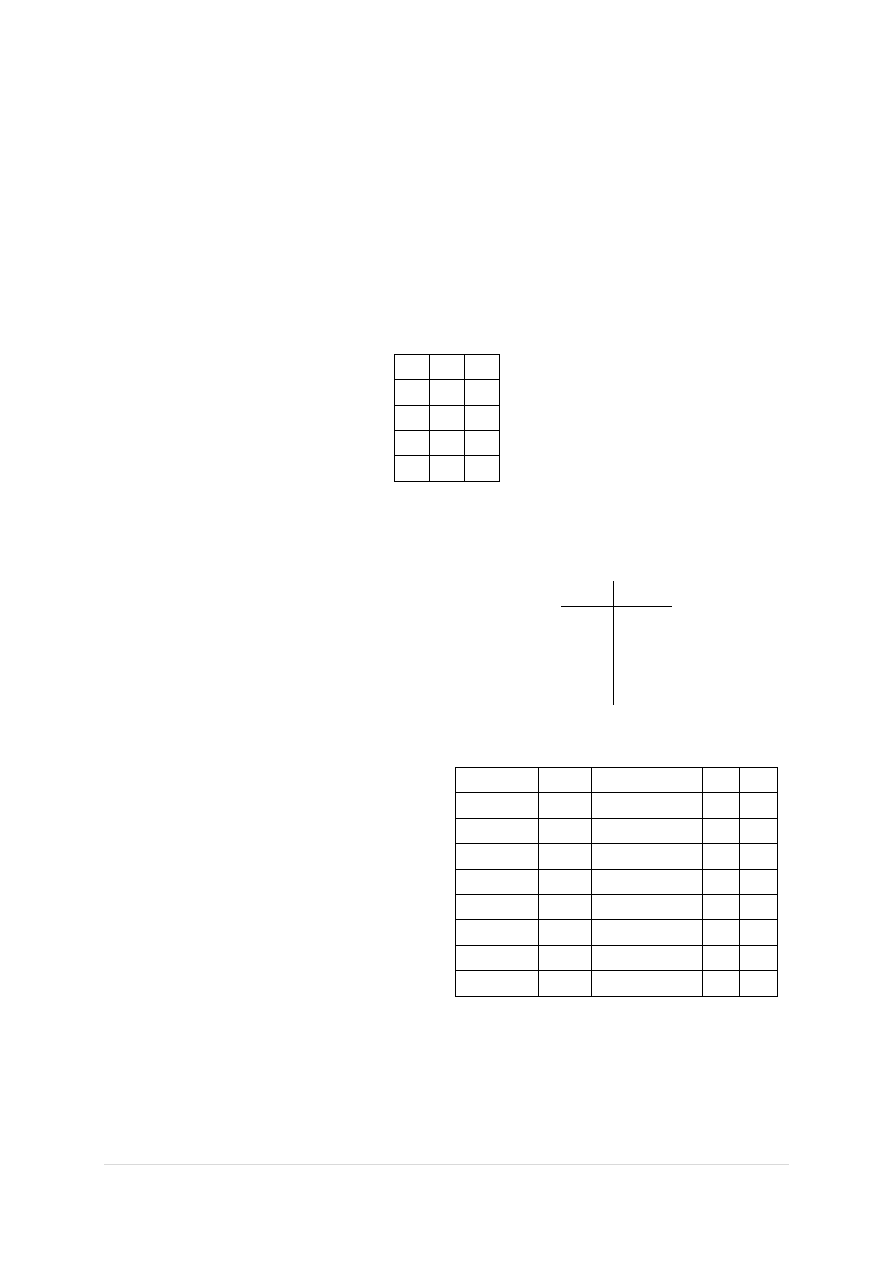
3 |
S t r o n a
Schemat przedstawiony na poprzedniej stronie reprezentuje zachowanie układu, gdzie:
q
0
- stan początkowy, który zapętla się gdy na wejściu jest jedynka, lub przechodzi do stanu
q
1
,
q
1
-kiedy pojawi sie nieparzysta jedynka na wejściu,
q
2
-kiedy pojawi sie parzysta jedynka na wejściu,
q
3
- stan po pojawieniu się nieparzystej jedynki, jednak wejście zmieniło się na zero.
Po takiej analizie, mogę zaprojektować tablicę wyjść:
Q Z
1
Z
2
q
0
0 0
q
1
1 0
q
2
0 1
q
3
0 0
Po czym przechodzę już do syntezy tego układu.
2.2 Synteza układu Moore’a
Pierwszym krokiem do syntezy układu jest
zakodowanie stanów. Ja zrobiłem to w ten
sposób:
Q Q
1
Q
0
q
0
00
q
1
01
q
2
10
q
3
11
Gdy zakodowałem już stany, rozpatrzam
osiem przypadków stanu poprzedniego i
wejścia, które mają wpływ na wartość
wyjściową przerzutnika D.
Q
1
Q
0
(t) X(t) Q
1
Q
0
(t+1) D
1
D
0
00
0
00
0 0
01
0
11
1 1
11
0
11
1 1
10
0
00
0 0
00
1
01
0 1
01
1
10
1 0
11
1
10
1 0
10
1
01
0 1
4 |
S t r o n a
Następnym krokiem jest kodowanie funckji wejść przerzutników, oraz ich minimalizacja:
Q
1
Q
0
x
0
1
00
0
1
01
1
0
11
1
0
10
0
1
Q
1
Q
0
x
0
1
00
0
0
01
1
1
11
1
1
10
0
0
̅
̅̅̅̅ ̅
̅̅̅̅̅
̅̅̅̅
̅̅̅̅̅
̅̅̅̅̅̅̅̅̅̅̅̅
Ostatnim krokiem jest określenie funkcji wyjść. Zauważam jednak, że oba stany wyjścia Z
przyjmują wartość 1 tylko przy jednej konfiguracji, co przedstawiają następujące tablice:
Q
1
Q
0
Z
1
00 0
01 1
11 0
10 0
̅̅̅̅
̅̅̅̅̅̅̅
Q
1
Q
0
Z
2
00 0
01 0
11 0
10 1
̅̅̅
̅̅̅̅̅̅̅̅̅̅
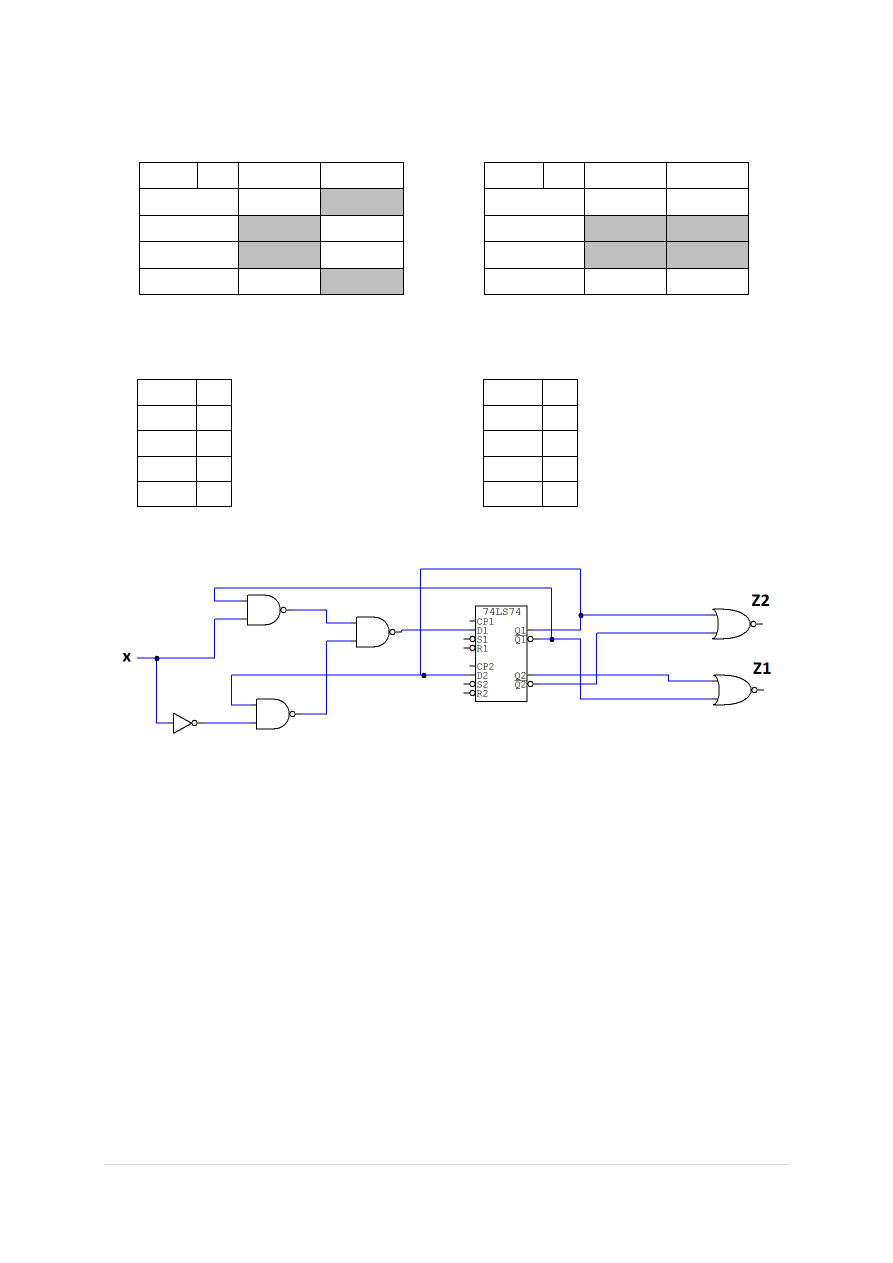
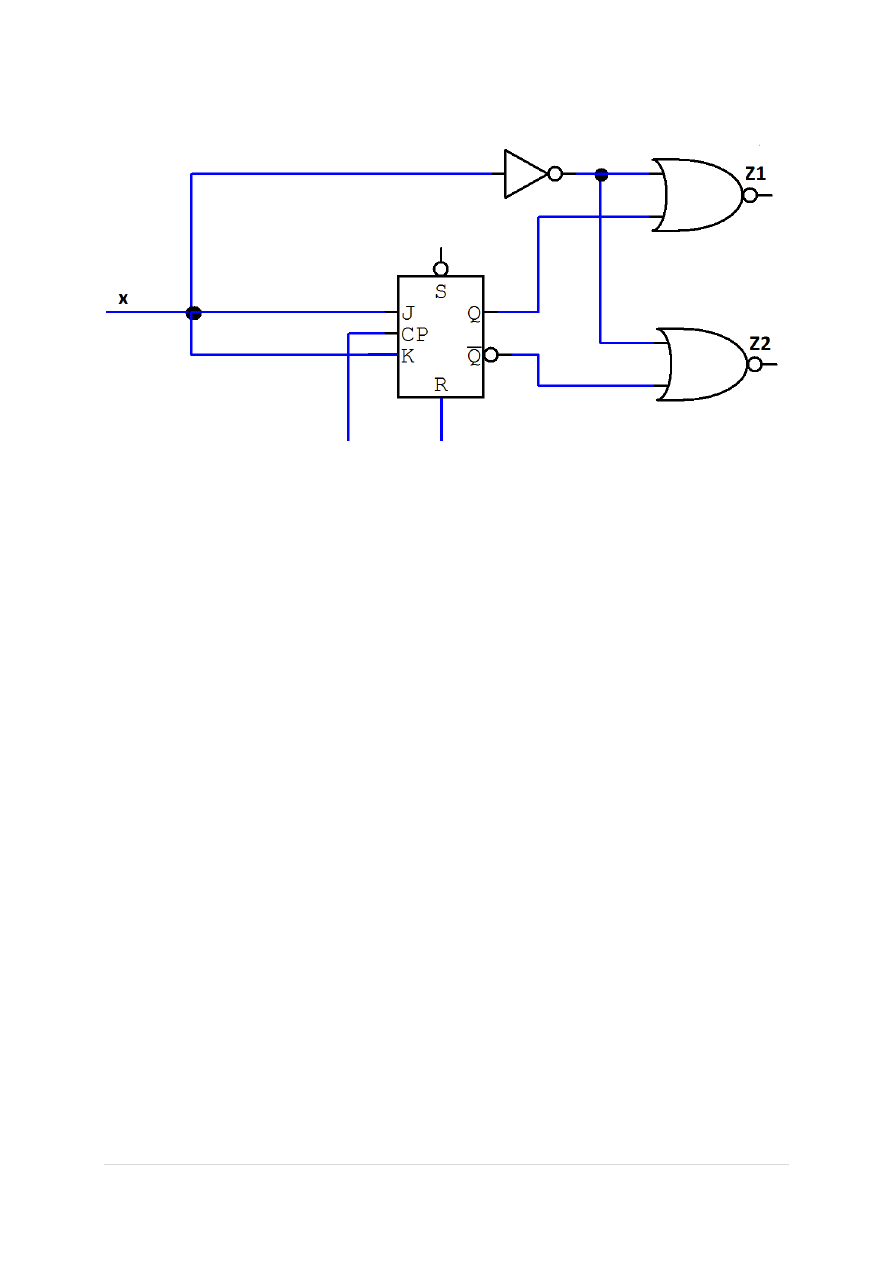
Teraz mogę przeprowadzić syntezę układu. Układ będzie wyglądał następująco:
To podsumowuje syntezę układu Moore’a.
5 |
S t r o n a
3.S
YNTEZA UKŁADU ZA POMOCĄ AUTOMATU
M
EALY
’
EGO
3.1 Czym jest automat Mealy’ego i jak go zrealizować?
Automat Mealy’ego jest to automat, którego wyjście jest funkcją stanu wewnętrznego i
sygnałów wejściowych. Automat Mealy’ego w tym zadaniu ma być realizowany poprzez
przerzutnik JK. Wykorzystując fakt, że funkcja wyjść jest zależna również od tego, co jest na
wejściu, maszynę możemy zredukować aż do dwóch stanów!
Problemem przy realizacji automatu Mealy’ego będzie fakt, że stan funkcji wyjściowej nie
zawsze będzie poprawny. Należy go odczytywać pomiędzy momentem ustalenia się
zmiennych wejściowych, a taktem zegara taktującego automat. Dla przykładu, jeśli automat
taktowany jest narastającym zboczem zegarowym, a dane są wprowadzana na opadającym
zboczu zegarowym, to wartość jest poprawna w momencie pomiędzy narastaniem a
opadaniem. Wynika to ze specyfikacji automatu, i nie można nic na to poradzić.
3.2 Synteza układu Mealy’ego
Postępuję w sposób analogiczny do
poprzedniego; najpierw określam
zachowanie wyjść dla odpowiedniego stanu
układu i wartości na wejściu:
Q x Z
1
Z
2
q
0
0 0 0
q
0
1 0 1
q
1
0 0 0
q
1
1 1 0
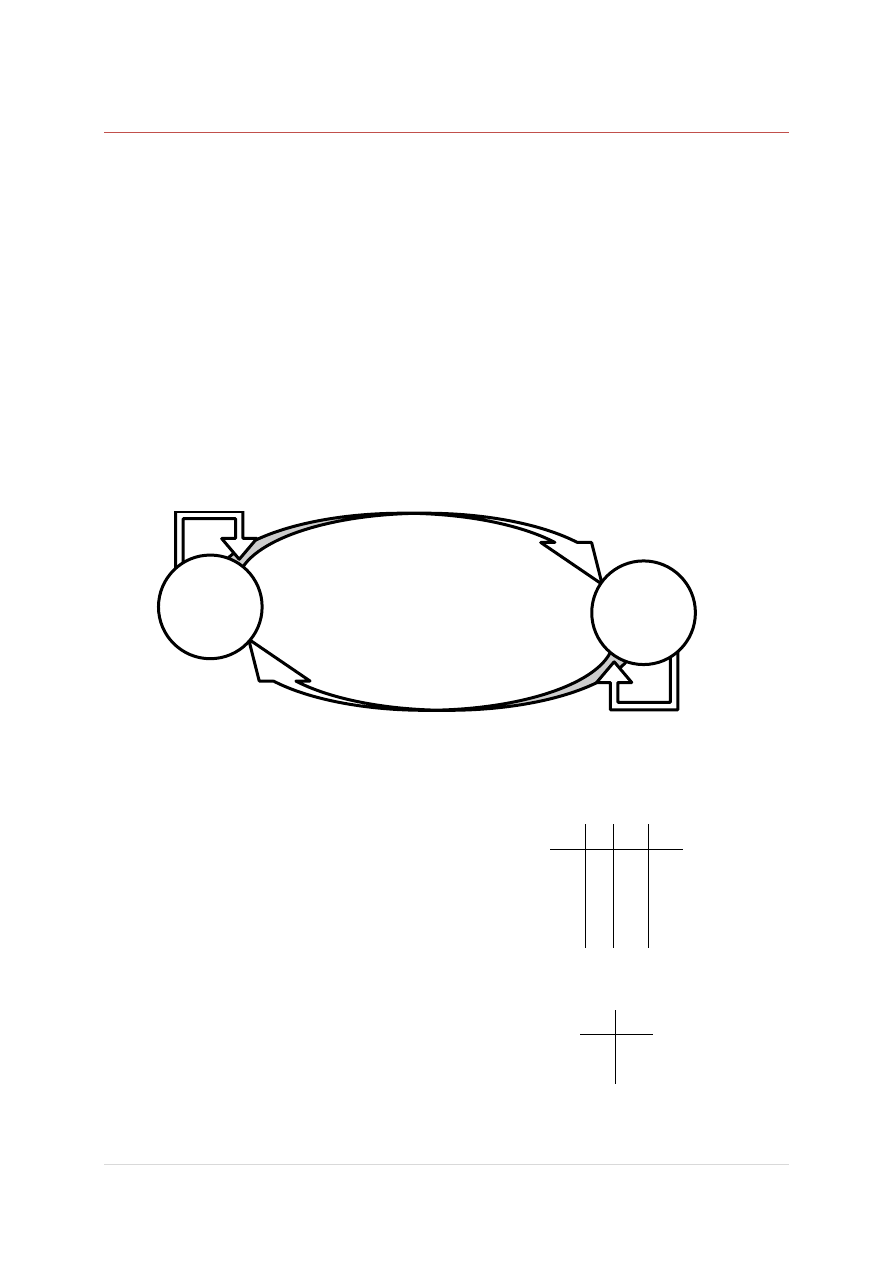
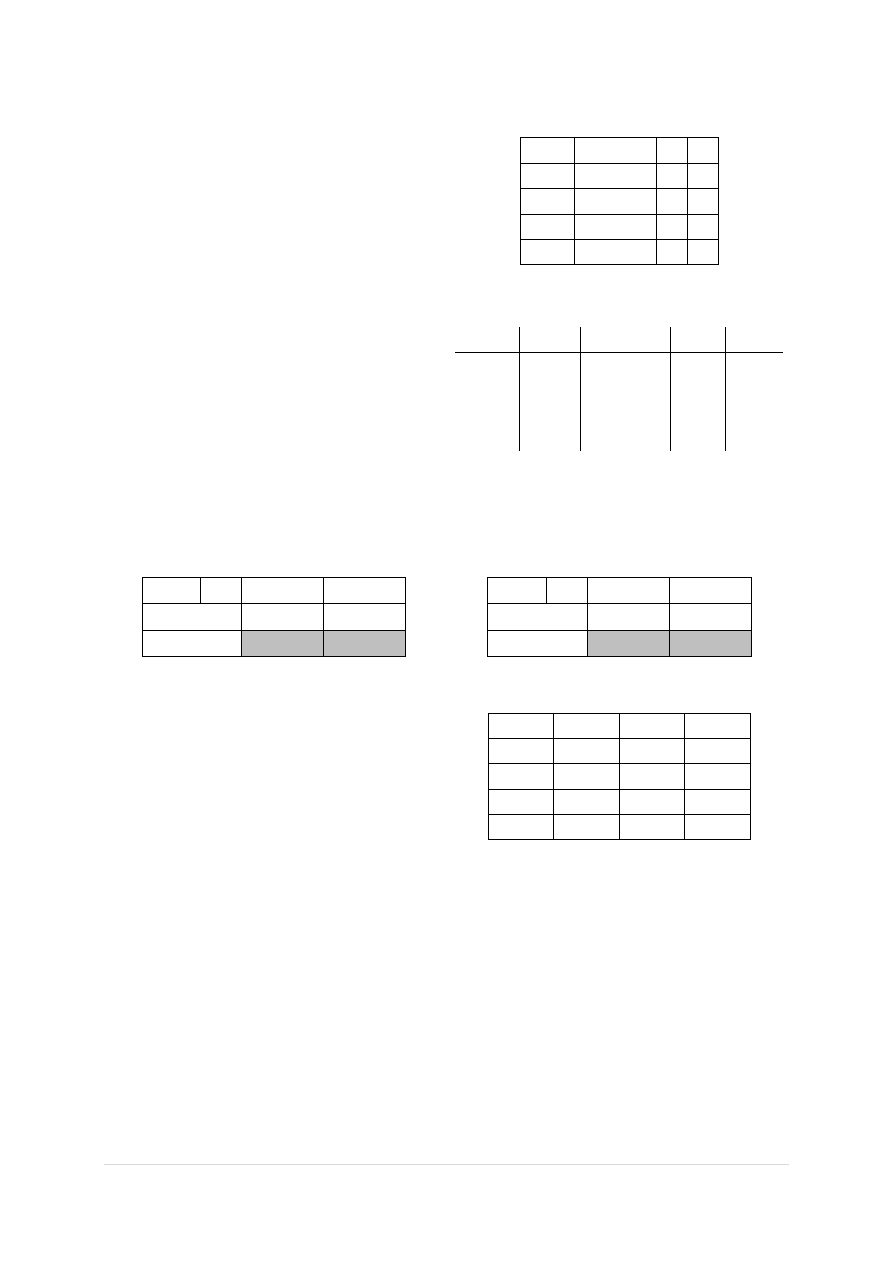
A następnie koduje stany:
Q Q
0
q
0
0
q
1
1
q
2
q
1
X=0
X=0
X=1
X=1
6 |
S t r o n a
Znając zachowanie przerzutnika typu JK,
mogę określić później tabele wzbudzeń
przerzutników. Oto jak zachowuje się
przerzutnik typu JK:
Q(t) Q(t+1) J K
0
0
0
0
1
1
1
0
1
1
1
0
Wykorzystując informację, konstruuję tabelę
wzbudzeń przerzutników:
Q
0
(t) x(t) Q
0
(t+1) J
0
K
0
0
0
0
0
0
1
1
1
1
0
1
0
1
1
0
1
Następnie konstruuje funkcje wejścia przerzutników, oraz minimalizuje je:
(
)
(
)
x
Q
0
0
1
0
0
1
1
x
Q
0
0
1
0
1
1
0
Kolejnym krokiem jest konstrukcja tabeli
wyjść:
Q
0
(t)
x
Z
1
Z
2
0
0
0
0
0
1
0
1
1
0
0
0
1
1
1
0
Ostatnim krokiem jest odczytanie funkcji wyjść:
̅̅̅̅ ̅
̅̅̅̅̅̅̅̅̅̅̅
̅
̅̅̅̅̅̅̅̅̅̅̅
7 |
S t r o n a
To podsumowuje syntezę układu. Układ będzie wyglądał w następujący sposób:
Schemat układu Moore’a
Diagram dla sekwencji 1
Diagram dla sekwencji 2

8 |
S t r o n a
Schemat układu Mealy’ego
Diagram dla sekwencji 1
Diagram dla sekwencji 2
Wyszukiwarka
Podobne podstrony:
Architekrura Systemow Lab4 id 6 Nieznany
09 Architektura systemow rozproszonychid 8084 ppt
Wstęp do informatyki z architekturą systemów kompuerowych, Wstęp
informatyczne systemy zarzadzan Nieznany
Ekologiczne podstawy systemu ws Nieznany
IMW W01 Wstepny System produkc Nieznany
Architekrura Systemów Lab1
Lab5 Analiza sygnalu mowy Lab5 Nieznany
66 251103 projektant architekt systemow teleinformatycznych
Architektura5 id 67923 Nieznany (2)
Architekrura Systemów Lab3
KOMPUTEROWE SYSTEMY STEROWANIA Nieznany
Po reinstalacji systemu Windows Nieznany
tranzystory mosfet(1), Architektura systemów komputerowych, Sentenza, Sentenza
więcej podobnych podstron