Dr inż. Michał Chłędowski

 PODSTAWY AUTOMATYKI I ROBOTYKI – 

LABORATORIUM

Ćw. S-II.2

CHARAKTERYSTYKI SKOKOWE 

ELEMENTÓW AUTOMATYKI

        

 

 Cel ćwiczenia

 

 

Celem   ćwiczenia   jest   zapoznanie   się

 

z   pojęciem  charakterystyki   skokowej   h(t), 

praktycznym  sposobem jej   otrzymywania   oraz  możliwościami  wykorzystania  do  identyfikacji 
parametrów badanych elementów. Dodatkowym celem jest zapoznanie się z metodami symulacji 
działania   elementów   automatyki,   w   tym   przypadku   poprzez   graficzne   przedstawianie 
charakterystyk skokowych wykorzystując programy Matlab lub SciLab.

        

 

 Program ćwiczenia

 

 

1. Cześć doświadczalna

 

 

Należy zarejestrować wykresy charakterystyk skokowych trzech termopar:

•

T1 – termopara typu J (żelazo-konstantan) w osłonie,

•

T2 – termopara typu J bez osłony,

•

T3 – termopara lotnicza (do pomiaru temperatury głowicy silnika lotniczego).

2. Opracowanie wyników

 

 

•

Dla   każdej   termopary   należy   napisać  G(s)   wyznaczajśc   uprzednio   z  otrzymanych 
wykresów charakterystyk skokowych wartości współczynników występujących w tych 
transformatach,

•

Narysować  wykresy charakterystyk skokowych elementów automatyki opisanych w/w 
transformatami   korzystając   z   dostępnego   oprogramowania.   Przeanalizować   wpływ 
parametrów na przebieg h(t).

        

 

 Podstawy teoretyczne

 

 

Analiza   i   synteza   układów   sterowania   automatycznego   opiera   się   na   wykorzystaniu 

charakterystyk dynamicznych. Charakterystyki te opisują zachowanie się

 

układu sterowania jako 

całości   lub   poszczególnych   jego   elementów   w   stanach   dynamicznych,   tj.   podczas   trwania 
procesów przejściowych.

Rozróżniamy dwa rodzaje charakterystyk dynamicznych:

1) charakterystyki czasowe,

1

2)

charakterystyki częstotliwościowe.

            

 

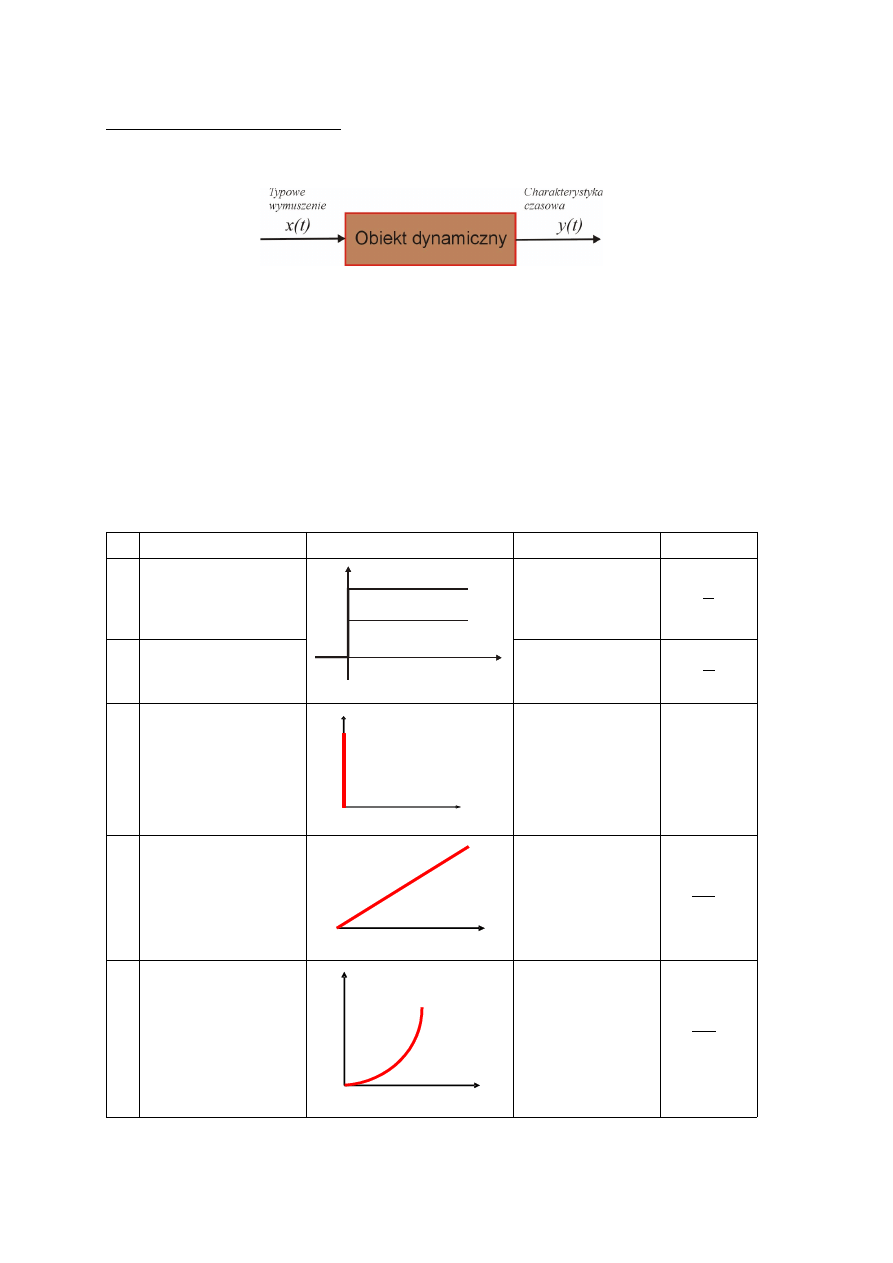
 Charakterystyka czasowa

 

 

Jest to przebieg w czasie odpowiedzi y(t) układu (elementu) dynamicznego (rys. 2.1) na 

określone wymuszenie x(t), zwane typowym wymuszeniem .

Rys. 2.1. Ilustracja definicji charakterystyki czasowej

W   celu   badania   właściwości   dynamicznych   elementów   należy   rozwiązać

 

równanie 

różniczkowe lub jakimś

 

pośrednim sposobem przebadać

 

jego rozwiązanie. Możliwe to jest pod 

warunkiem,   że   znana   jest   wielkość

 

wejściowa  x(t)  jako   funkcja   czasu.   W   warunkach 

rzeczywistych   przy   pracy   układu   sterowania   wielkość

 

wejściowa   każdego   elementu   jest 

właściwie   przypadkową

 

funkcją

 

czasu.   Dlatego   do   badania   elementów   przyjmuje   się

 

kilka 

typowych   (standardowych)   sygnałów   odzwierciedlających   różne   stany   zbioru   wejściowych 
sygnałów przypadkowych. Sygnały wejściowe nazywają

 

się

 

wymuszeniami, a sygnały wyjściowe 

powstające w wyniku ich oddziaływania - odpowiedzią

 

na te wymuszenia. Typowe wymuszenia 

przed tabela 2.1.

Tabela 2.1. Typowe wymuszenia

Lp. Nazwa

Wykres

f(t)

F(s)

1

Skok jednostkowy
(funkcja Heaviside'a)

1(t)

1

s

2

Wymuszenie 
skokowe

1t ⋅a

a

s

3

Funkcja Diraca
(wymuszenie 
impulsowe)

F(s) = 1

4

Wymuszenie   liniowo 
narastajśce

 

(skok 

prędkości)

a⋅t

5

Wymuszenie 
paraboliczne
(skok przyśpieszenia)

a⋅t

2

2

a1(t)

1(t)

t

x(t)

0

t



(t)

t

at

x

t

at

2

















0

0

0

)

(

t

przy

t

przy

t



2

s

a

3

2

s

a

            

 

 Charakterystyki skokowe

 

 

Najczęściej stosowanym wymuszeniem jest wymuszenie skokowe. Wymuszenie to osiąga 

skokowo w chwili t = 0 wartość

 

a = const i dalej pozostaje stałe. Znaczy to, że  x(t) = a przy t



0

 

i x(t) = 0 przy t < 0.

Często dla funkcji skokowej używa się

 

oznaczenia

x t =a⋅1t

Funkcja 1(t) nazywa się

 

jednostkową

 

funkcją

 

skokową

 

lub krótko skokiem jednostkowym. 

Jeśli   amplituda   skoku   jest   różna   od   jedności   i   wynosi  a,   to   takie   wymuszenie   nazywamy 
wymuszeniem skokowym (Tabela 2.1).

Powstawanie   skokowego   sygnału   wejściowego   jest   bardzo   typowe.   W   urządzeniach 

elektrycznych i elektromechanicznych sygnał

 

skokowy oznacza przyłączenie napięcia stałego na 

wejście elementu np. napięcia zasilania. W miernikach podanie na zaciski wejściowe mierzonej 
wielkości oznacza podanie wymuszenia skokowego. W rezultacie takiego wymuszenia miernik 
przejdzie do nowego stanu równowagi. Proces przechodzenia do nowego stanu równowagi przy 
wymuszeniu skokowym opisuje się

 

rozwiązaniem równania różniczkowego przy x(t) = a

⋅

 

1(t). 

Proces ten czyli odpowiedź

 

skokowa

 

(lub charakterystyka skokowa) - to odpowiedź

 

elementu

 

lub 

układu na skokowe wymuszenie wejściowe.

Transformata Laplace'a wymuszenia skokowego ma postać: 

L [a⋅1 t]=a

1

s

=

a

s

.

            

 

 Odpowiedzi skokowe podstawowych elementów automatyki

 

 

Odpowiedzią

 

y(t) na wymuszenie x(t) nazywamy przebieg w czasie wielkości wyjściowej 

y następujący po wprowadzeniu sygnału wejściowego x(t).

Z definicji transmitancji 

G s =

Y s 
X  s

=

b

m

s

m



b

m

−

1 s

m

−

1...b

o

a

n

s

n



b

n

−

1 s

n

−

1...a

o

=

M  s 

N  s

mamy 

Y s=G s ⋅X  s =

M  s 

N  s

X  s 

.

Ogólnie, odpowiedź

 

y(t) jest oryginałem transformaty Y(s) 

Odpowiedź

 

skokowa układu lub elementu - jest to odpowiedź

 

na funkcję

 

skokową

 

x(t) = a

⋅ 

1(t).

 

Charakteryzuje ona przejście układu z jednego stanu równowagi lub stanu ustalonego do 

drugiego. Jeśli równanie liniowe układu słuszne jest dla małych odchyleń, to wielkość

 

a funkcji 

skokowej powinna być

 

mała. Dla układów liniowych zwykle przyjmuje się

 

a = 1. Odpowiedź 

układu na jednostkowe wymuszenie skokowe przyjęto oznaczać

 

jako h(t).

W celu określenia odpowiedzi skokowej układu lub elementu liniowego należy rozwiązać 

równanie   niejednorodne   układu   (patrz   równanie   1.1   w   ćw.   1)   przy  założeniu,  że  na   wejście 
podamy wymuszenie skokowe x(t) = 1(t). Wówczas za y(t) możemy podstawić

 

h(t) i otrzymamy

a

n

d

n

h

dt

n

+

a

n−1

d

n−1

h

dt

n−1

+

...+a

2

d

2

h

dt

2

+

a

1

d h

dt

+

a

o

h=

¿

b

o

1(t)+b

1

d1(t)

dt

+

b

2

d

2

1(t)

dt

2

+

...+b

m

d

m

1(t)

dt

m

(2.1)

Rozwiązanie równania (2.1) jest równoważne określeniu oryginału transmitancji

3

H  s=G  s

1

s

=

M  s

N  s 

1

s

skąd

h t= L

−

1

[

H  s ]=c

o



∑

i =1

n

c

i

e

s

i

t

(2.2)

gdzie:

c

o

=

M 0

N 0

=

b

o

a

o

s

i

 

- pierwiastki równania charakterystycznego.

Wyrażenie   (2.2)   jest   słuszne   tylko   wtedy,   gdy  wielomian  N(s)  nie   ma   pierwiastków 

wielokrotnych ani pierwiastka równego zero.

Odpowiedź

 

skokowa  h(t),   charakteryzująca   proces  ustalania   wielkości   wyjściowej   przy 

skokowej zmianie wielkości wejściowej składa się

 

z dwóch składowych: c

o

 i 

∑

i=1

n

c

i

e

s

i

t

 . Druga 

składowa   przedstawia   sobą

 

całkę

 

równania   jednorodnego   (2.1),   tzn.   składową

 

przejściową 

procesu ustalania. Składowa ta jest nazywana uchybem dynamicznym. W układzie lub elemencie 
stabilnym składowa przejściowa dąży do zera z upływem czasu, tzn. że

lim

t ∞

∑

i =1

n

c

i

e

s

i

t

=

0

(2.3)

Składowa  

c

o

=

M 0

N 0

=

b

o

a

o

to   szczególne   rozwiązanie   równania   niejednorodnego 

(2.1), tzn. ustalona wartość

 

wielkości wyjściowej. Do tej wartości wielkość

 

wyjściowa dąży w 

miarę

 

zanikania składowej przejściowej czyli uchybu dynamicznego.

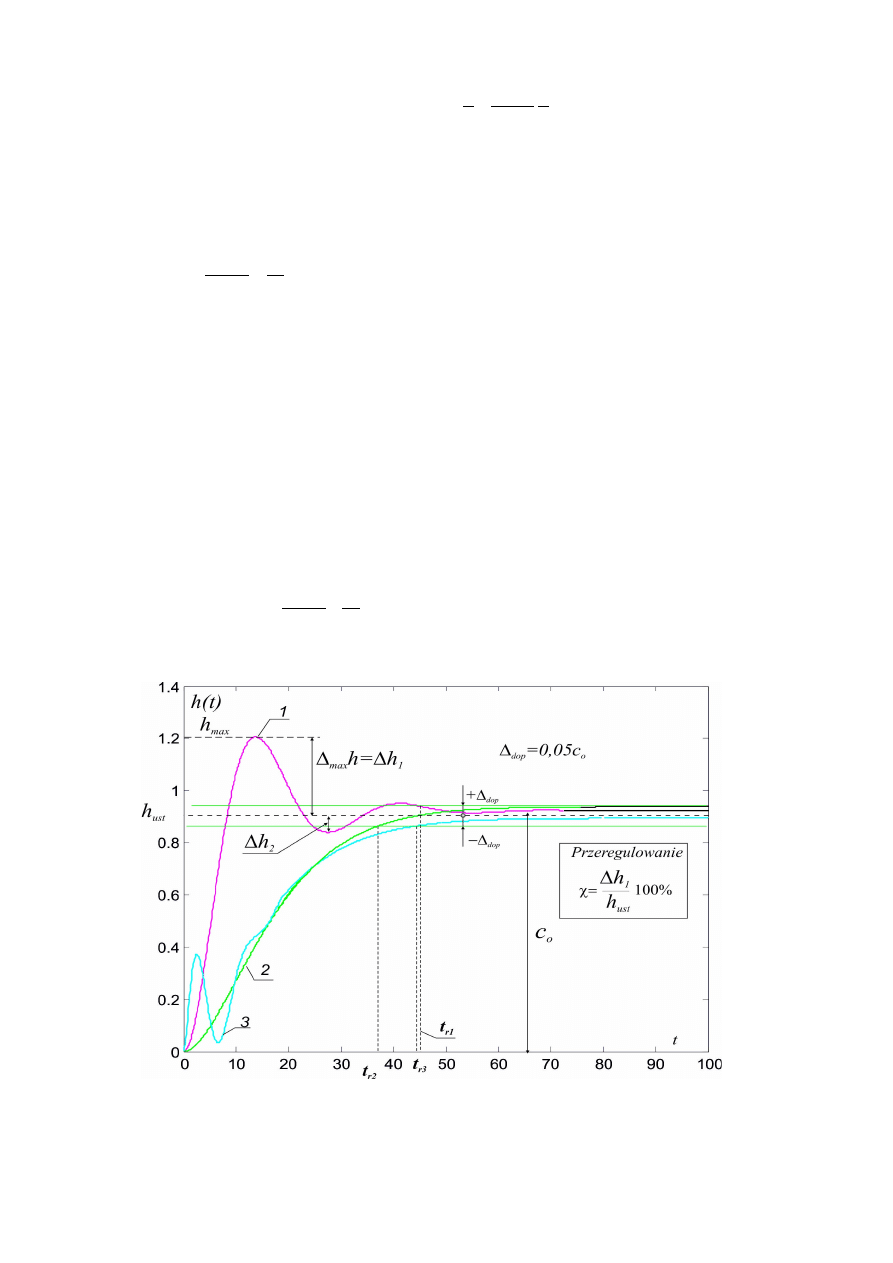
Rys. 2.3. Przykładowe charakterystyki skokowe

4

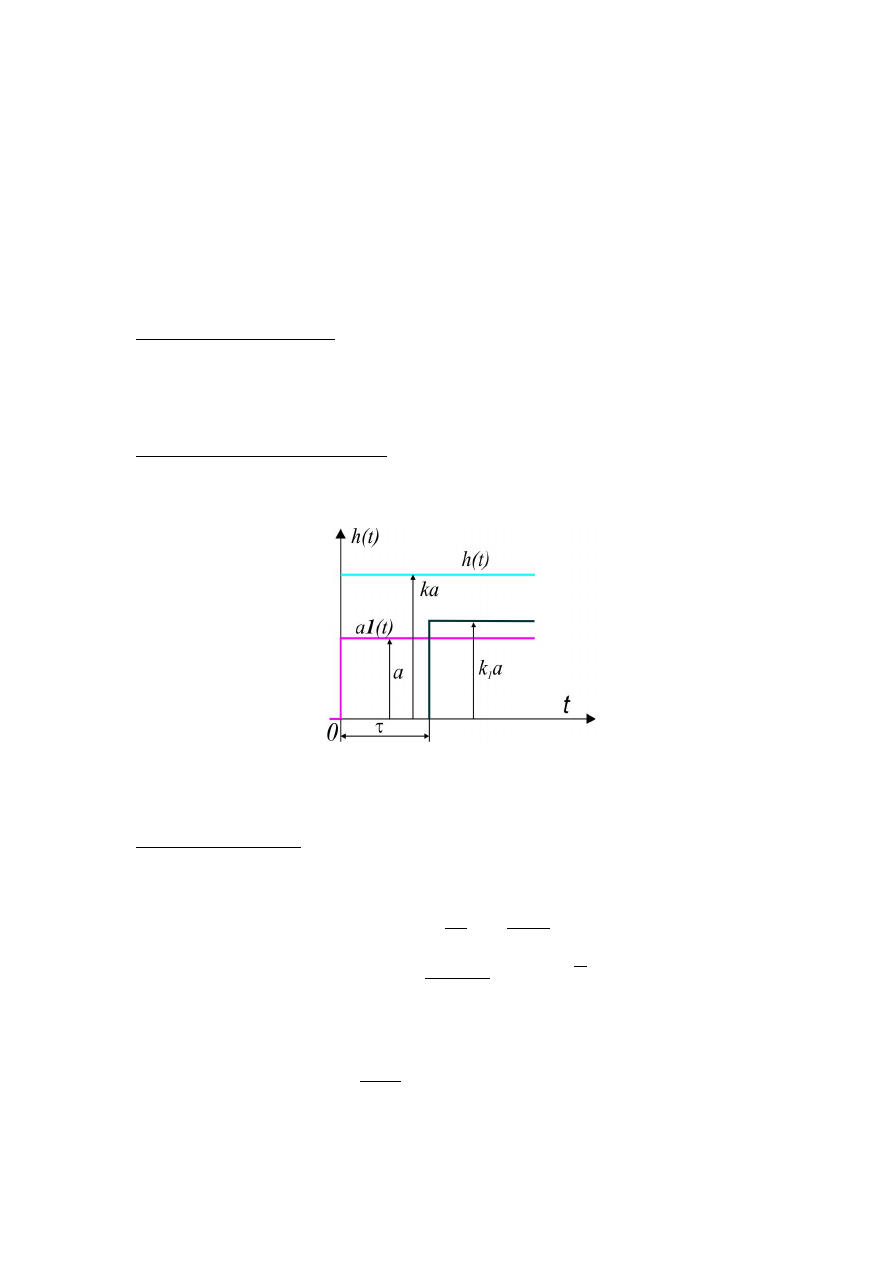
Odpowiedź

 

skokowa w ogólnym przypadku (rys. 2.3) charakteryzuje się

 

czasem regulacji 

t

r

,  wielkością

 

przekroczeń

 

Δh

1

,  Δh

2

 

i   ich   liczbą.    Δh

1

 

nazywa   się

 

przeregulowaniem.  Czas 

regulacji to czas, po upływie którego odpowiedź

 

skokowa pozostaje w granicach 0.95 c

o

 < h(t) < 

1.05 c

o

.  Praktycznie można uważać, że w czasie  t

r

  wielkość

 

wyjściowa osiąga swoją

 

wartość 

ustaloną. Teoretyczny czas ustalania w układzie liniowym dąży do nieskończoności zgodnie z 
wyrażeniem (2.3). Przeregulowanie - to przekroczenie przez wielkość

 

wyjściową

 

swojej wartości 

ustalonej w procesie ustalania. Przeregulowania zwykle są określane jako odchylenia procentowe 
od wartości c

o 

i w tej postaci oznaczane jako χ.

Rozpatrzymy   odpowiedzi   skokowe   podstawowych   członów   przyjmując   wymuszenie 

skokowe o amplitudzie równej a ( x(t)=a1(t)).

            

 

 Człon wzmacniający

 

 

Odpowiedź

 

skokowa członu wzmacniającego 

h t=k⋅a⋅1t

przedstawia sobą

 

funkcją

 

skokową

 

zwiększoną

 

k razy w stosunku do wejściowej.

            

 

 Człon o stałym opóźnieniu 

 

 τ  

Odpowiedź

 

skokowa będzie funkcją

 

skokową

 

przesuniętą

 

wzdłuż

 

osi czasu o wielkość

 

τ, tzn. 

h t=k

1

⋅

a⋅1t−

Rys.2.4. Charakterystyka skokowa członu wzmacniającego (proporcjonalnego)

i członu wzmacniającego z opóźnieniem

            

 

 Człon inercyjny

 

 

Transmitancja i wzór na charakterystykę

 

skokową

 

elementu inercyjnego I-go rzędu mają 

postać

G s = y



s 
x



s=

k

Ts1

;

h t= L

−

1

[

k



Ts1 s

]

=

ka



1−e

−

t

T



(2.4)

Odpowiedź

 

skokową

 

członu   można   otrzymać

 

także   z   rozwiązania   równania 

niejednorodnego opisującego człon inercyjny (2.5).

T

dht 

dt



ht=k⋅a⋅1t

(2.5)

Odpowiedź

 

skokowa posiada dwie składowe:  ka  i  - ka e

-t/T

. Druga składowa to całka 

5

jednorodnego równania (2.5), tzn. składowa przejściowa procesu ustalania (uchyb dynamiczny). 
Jak widać, uchyb dynamiczny zmniejsza się z upływem czasu według zależności wykładniczej. 
Składowa  ka  jest rozwiązaniem szczególnym równania pełnego (2.5). Przedstawia ona wartość 
ustaloną,   do   której   dąży   wielkość

 

wyjściowa   w   miarę

 

zanikania   składowej   przejściowej. 

Zauważmy, że rozwiązanie równania (2.5) we współrzędnych h i t jest funkcją

 

wykładniczą.  Na 

rys. 2.5 przedstawiono krzywe h(t) dla trzech wartości T (T

1

 < T

2

 < T

3

 ). Jak widać

 

z krzywych, 

czas   trwania   procesu   przejściowego   (ustalenia   wielkości   wyjściowej)   jest   tym   mniejszy,   im 
mniejsza jest stała czasowa. Przy  T = 0  funkcja wykładnicza zamienia się w funkcją

 

skokową 

ka1(t),   a   człon   inercyjny   staje   się   członem   wzmacniającym.   Odpowiedź

 

skokowa   członu 

inercyjnego   nie   ma   przeregulowania,   a   czas   regulacji   równy  jest   w   przybliżeniu   3÷4  stałym 
czasowym, tzn. 

t

r

=

3÷4

.

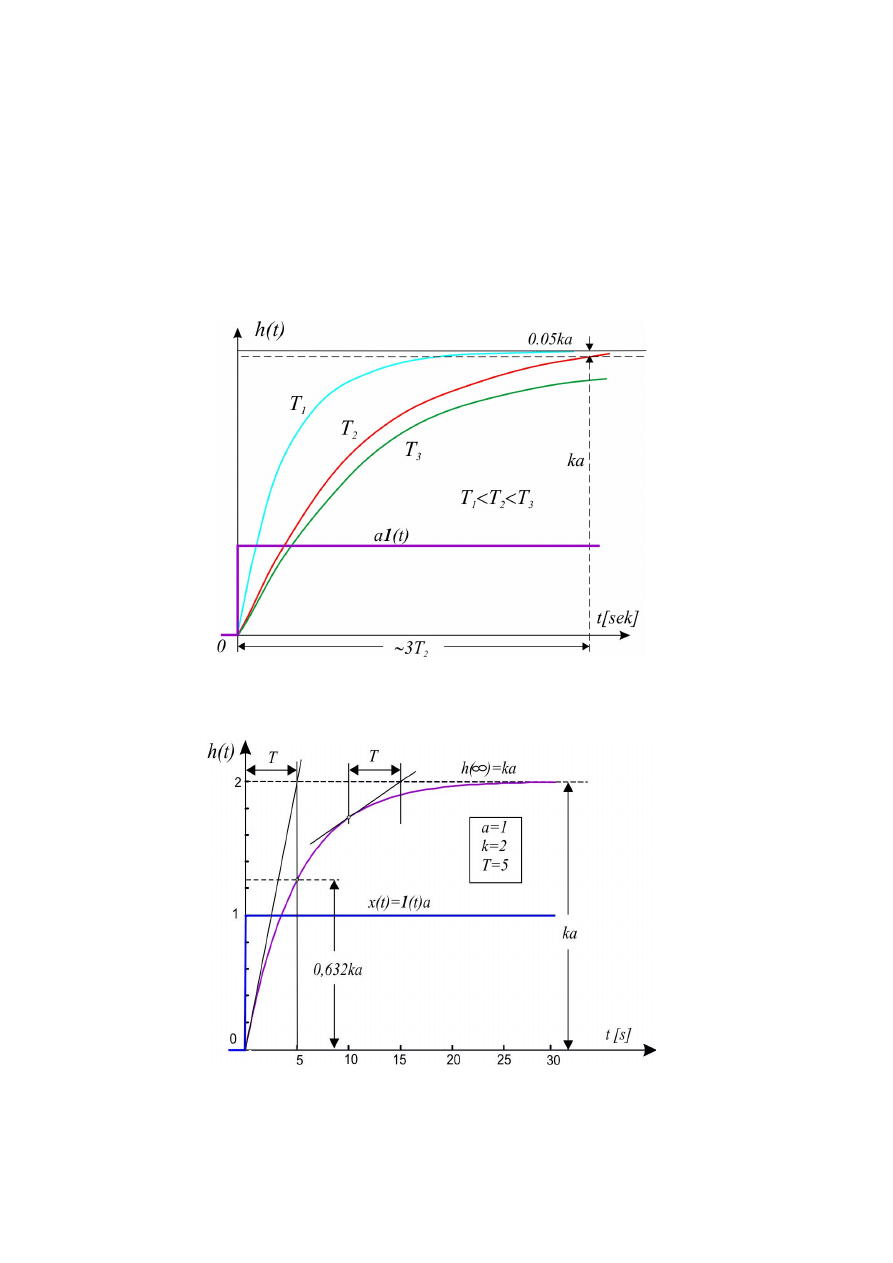
Rys. 2.5. Odpowiedzi skokowe członu inercyjnego przy rożnych stałych czasowych

Rys.   2.6.   Sposoby  wyznaczania   stałej   czasowej   z   wykresu   charakterystyki   skokowej 
członu inercyjnego

6

Odpowiedź

 

skokową  elementu   inercyjnego   (jak   i   innych)  można   otrzymać 

eksperymentalnie przykładając na wejście rzeczywistego elementu inercyjnego sygnał skokowy. 
Zarejestrowany przebieg zmian wielkości wyjściowej będzie właśnie odpowiedzią

 

skokową. Z 

zapisu eksperymentalnego  h(t)  można określić

 

parametry  k  i  T  odpowiedzi skokowej. W celu 

określenia  T  przeprowadza   się   styczną   do  h(t)  przy  t   =   0  (rys.   2.6).   Styczna   ta   odcina   na 
asymptocie krzywej wykładniczej (prosta ka) stałą

 

czasową

 

T. Jeżeli początek procesu na zapisie 

(oscylogramie) trudno jest ustalić, to styczną

 

można poprowadzić

 

z  dowolnego punktu krzywej 

wykładniczej przenosząc w ten punkt początek układu współrzędnych.

            

 

 Człon całkujący

 

 

Równanie członu ca

_

kującego przy wymuszeniu skokowym x(t) = a1(t) ma postać

dy

dt

=

ka⋅1 t

(2.6)

Odpowiedź

 

skokowa opisana jest wzorem

h t=

∫

0

t

kadt=kat

i przedstawia równanie linii prostej. Wielkość

 

wyjściowa nieprzerwanie wzrasta liniowo przy 

stałej wartości wielkości wejściowej. Jest to naturalne ponieważ

 

człon ten nie posiada równowagi 

statycznej. Pojęcie czasu regulacji nie ma tutaj sensu. 

            

 

 Człon drugiego rzędu

 

 

Odpowiedź

 

skokową

 

otrzymuje się

 

jako rozwiązanie równania

T

2

d

2

ht 

dt

2



2 T

dh t

dt



h t=k⋅1 t

przy zerowych warunkach początkowych lub jako oryginał

 

z wyrażenia

H  s=G  s

1

s

=

k

T

2

s

2



2 Ts1

1

s .

W   zależności   od   wartości  ζ

 

otrzymujemy   następujące   przypadki   i   związane   z   nimi 

wyrażenia odpowiedzi skokowej:

1.

ζ

 

> 1, oba pierwiastki są

 

liczbami ujemnymi rzeczywistymi

(typowy człon inercyjny drugiego rzędu)

h t=k

[

1−

r

2

r

2

−

r

1

e

−

r

1

t

T



r

1

r

2

−

r

1

e

−

r

2

t

T

]

(2.7)

gdzie: 

r

1

=−





2

−

1 , r

2

=∓





2

−

1

 .

2.

ζ

 

< 1, oba pierwiastki są

 

liczbami zespolonymi sprzężonymi; w tym przypadku 

człon nazywa się

 

oscylacyjnym a charakterystyka skokowa ma postać

h t=k

[

1−

e

−

t

T

r

sin



r

t

T





]

(2.8)

gdzie: 

r =



1−

2

, =arctg

r



.

7

3. ζ

 

= 0 - przypadek krytyczny (oscylacje niegasnące) 

h t=k

[

1−



1

t

T



e

−

t

T

]

(2.9)

W   celu   otrzymania   równania   (2.9)   należy   się   posłużyć

 

wzorem   rozkładu   funkcji 

wymiernej dla pierwiastków wielokrotnych lub szukać rozwiązania równania

T

2

d

2

h

1



t 

dt

2



2 T

dh

1



t 

dt



h

1



t=0

(2.10)

w postaci

h

1



t=c

1

e

−

t

T



c

2

t e

−

t

T

gdzie c

1

 i c

2

 - stałe.

Wyra

ε

ż nie (2.9) otrzymuje się

 

także drogą

 

przekształcenia granicznego z (2.7) lub (2.8) 

przy ζ

 

→

 

1. Przy ζ

 

< 1

 

(pierwiastki zespolone sprzężone) proces przejściowy jest oscylacyjnie 

gasnący (jak na rys. 2.3). Przy  ζ

 

> 1

 

proces jest aperiodyczny i przebiega bez oscylacji (jak 

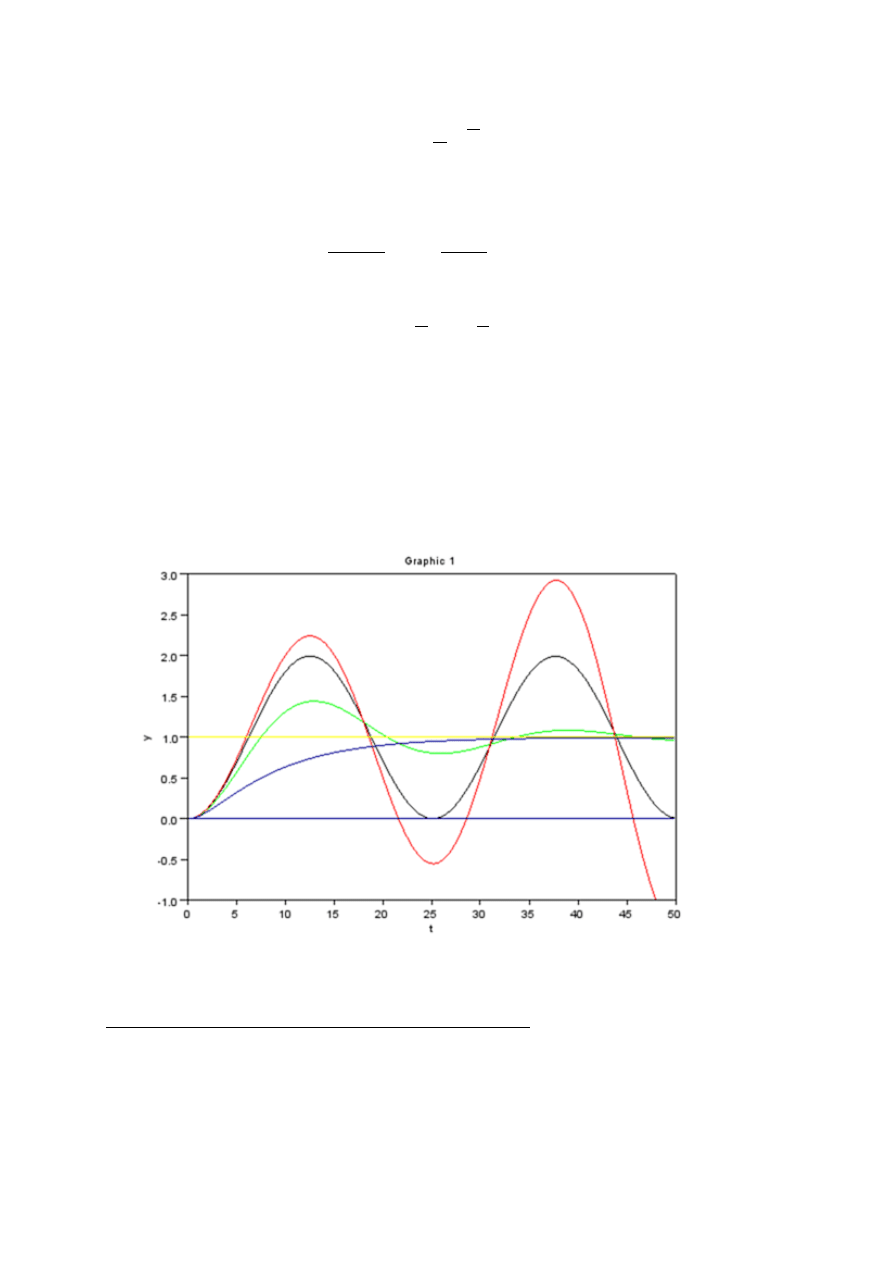
krzywa 2 na rys. 2.3). Na rys. 2.7 przedstawiono przebiegi charakterystyk skokowych członu 
opisanego równaniem (2.10) dla następujących danych: T = 4, ζ = 0; 0,25; 1,2;-0,07. Czytelnikowi 
pozostawimy dopasowanie poszczególnych krzywych do poszczególnych wartości ζ.

Rys. 2.7. Charakterystyki skokowe członu o równaniu (2.10)

            

 

 Termoelement (termopara) jako element automatyki

 

 

Dwa przewody z różnych metali zespawane na jednym końcu tworzą

 

termoelement. Jeżeli 

spoina   pomiarowa   ma   inną

 

temperaturę

 

nić

 

wolne   końce   w   termoelemencie   powstaje   siła 

termoelektryczna. Jeżeli temperatura wolnych końców jest stała i znana, wartość

 

powstającej siły 

termoelektrycznej jest miarę

 

temperatury spoiny pomiarowej.  Czujniki termoelektryczne  zwane 

8

potocznie  termoparami  są   elementami   pomiarowymi   często   wykorzystywanymi   w   układach 
automatycznej   regulacji.  Mierzą

 

 

 

  różnicę   temperatur   pomiędzy   gorącym   i   zimnymi   końcami

 

  

termopary.   Wielkością

 

wyjściową

 

jest   siła   termoelektryczna   mierzona   miliwoltomierzem. 

Charakteryzują

 

się   dużym   zakresem   pomiarowym,   dobrą

 

liniowością

 

charakterystyk   i 

dokładnością.

Termopary wykonywane są z różnymi typami osłon, zależnie od środowiska i temperatury 

pracy. Osłony z żelaza, żeliwa i stali są stosowane do 350

°

C, mosiądz i stale nierdzewne do 

800

°

C, specjalne stale żaroodporne do 1200

°

C i osłony ceramiczne do 2200

°

C.

Coraz   częściej   stosowane   są

 

obecnie   specjalne  czujniki   płaszczowe,   w   których 

termoelement w izolacji z tlenku magnezu jest zaprasowany w osłonie stalowej o średnicy 0.1

÷

6 

mm.  Czujniki te mają

 

bardzo małą

 

bezwładność

 

cieplną

 

i dają

 

się wyginać. W urządzeniach 

laboratoryjnych stosuje się często termoelementy bez osłony.

Przewody   kompensacyjne   służą

 

do   przedłużenia   termoelementu   od   głowicy   czujnika 

(zimnych   końców),   w   której   występują

 

duże   wahania   temperatury   do   miejsca,   w   którym 

utrzymuje   się   stałą   temperaturę

 

odniesienia.   Przewody  kompensacyjne,   zwłaszcza   w   zakresie 

0

÷

200

°

C,   mają

 

taką

 

samą

 

charakterystykę

 

termoelektryczną

 

jak   termoelement   z   którym 

współpracują, ale są

 

tańsze.

Najczęściej stosowanym i najtańszym układem termometru termoelektrycznego jest układ 

odchyłowy.   Schemat   takiego   układu   przedstawia   rys.   2.8.   Jego   wskazania   są

 

prawidłowe 

wówczas,   gdy  rezystancja   obwodu   zewnętrznego  miernika   jest   równa   wartości   znamionowej, 
podanej   na   mierniku.   Wartość   tę   dopasowuje   się   przez   odpowiednie   nastawienie   rezystora 
wyrównawczego R

k

.

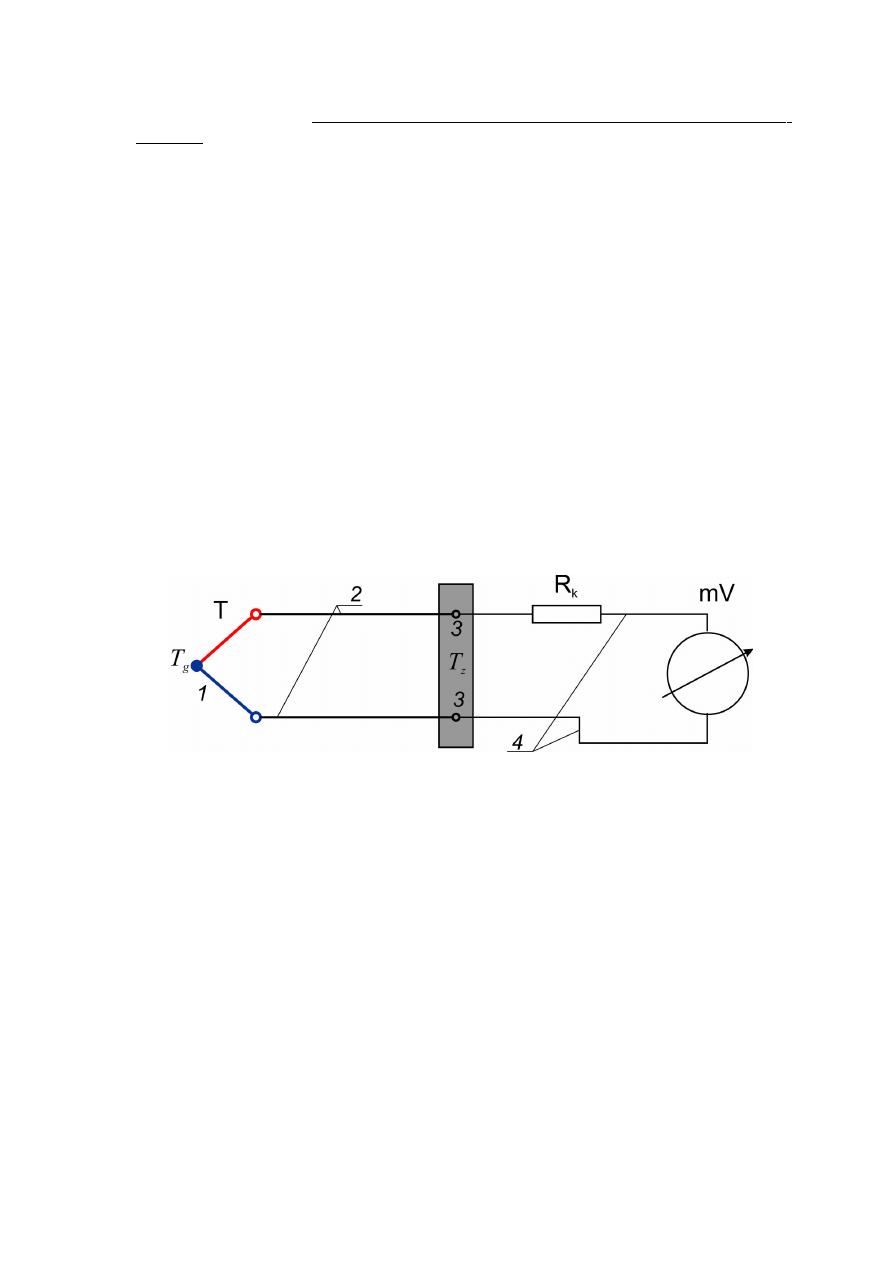
Rys. 2.8. Termometr termoelektryczny w układzie odchyłowym;  T  – termoelement,  1  – 

spoina pomiarowa, 2 – przewody kompensacyjne, 3 – wolne końce, 4 – przewody łączeniowe, T

z 

- temperatura odniesienia (zimnych końców), T

g

 – temperatura mierzona (złącza pomiarowego – 

gorących końców), R

k 

 - rezystor kompensacyjny, mV - miliwoltomierz         

Właściwości dynamiczne termoelementu bez osłony lub w osłonie o małej bezwładności 

cieplnej  (np.  termopary płaszczowe)  opisuje  się  równaniem charakterystycznym  dla  elementu 
inercyjnego   I-go   rzędu.   W   przypadku   masywnej   osłony   konieczne   jest   uwzględnienie   stałej 
czasowej   obudowy,   która   w   tym   przypadku   jest   dominująca.   Własności   dynamiczne   takiej 
termopary opisuje się przy pomocy równania charakterystycznego dla elementu inercyjnego II-go 
rzędu. W celu uproszczenia opisu często stosuje się opis własności dynamicznych termopary w 
obudowie  w  postaci  opisu dla  elementu  inercyjnego  I-go rzędu z   opóźnieniem.   Przykładowe 
charakterystyki termopar przedstawia rys. 2.9. Krzywa  1  charakterystyczna jest dla termopar o 
małej stałej czasowej (małej bezwładności – np. dla termopar płaszczowych lub termopar bez 
osłony). Krzywa 2 odpowiada charakterystyce skokowej termopary w masywnej osłonie.

Współczynnik   wzmocnienia  k  określamy  jako   stosunek   sygnału   wyjściowego   w   stanie 

ustalonym do amplitudy sygnału wejściowego. Stan ustalony symbolizować będziemy znakiem 

9

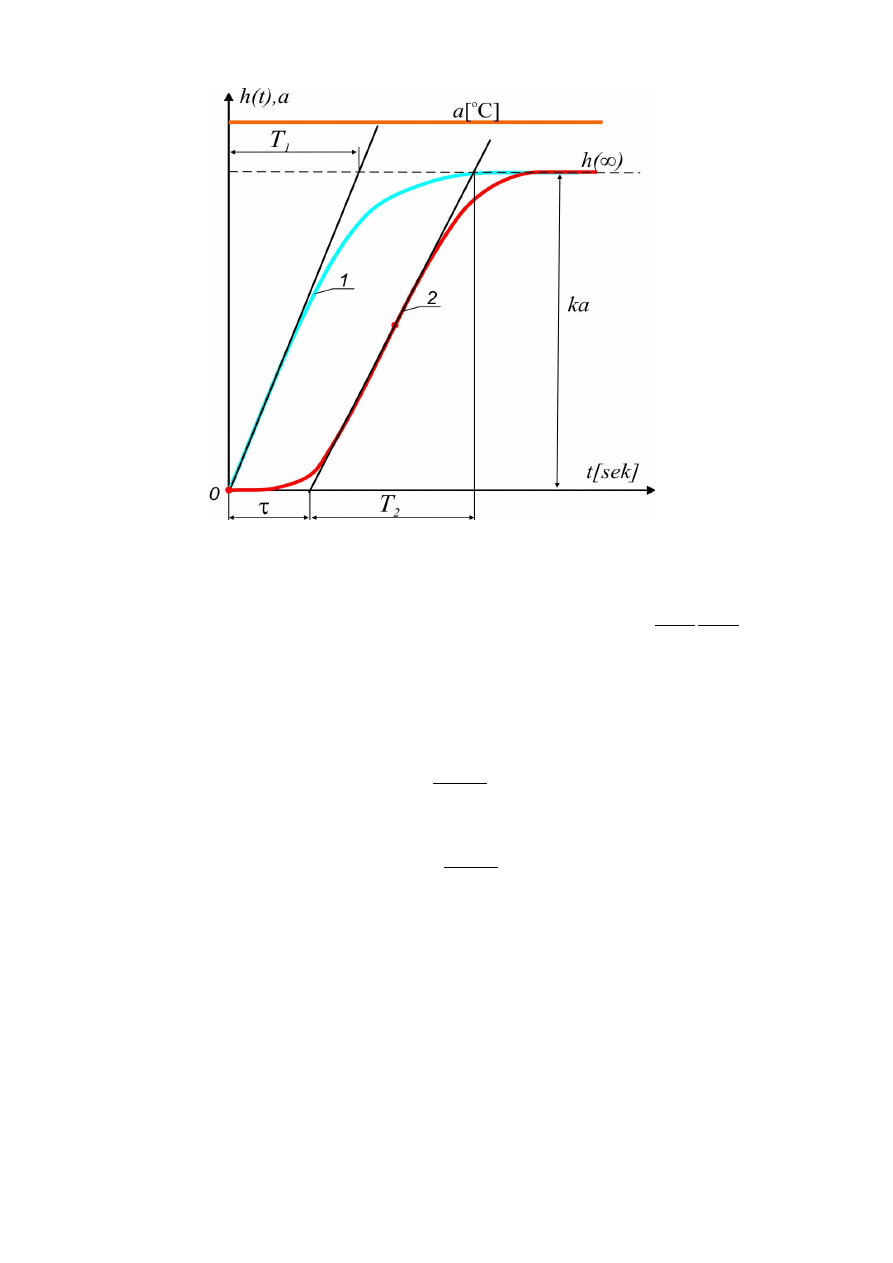
Rys. 2.9. Przykładowe charakterystyki skokowe termopar

nieskończoności.   Współczynnik   wzmocnie  k  wyznaczymy   ze   wzoru  

k =

h (∞)

a

[

mV ]

[

C

o

]

. 

Interpretacja   fizyczna   –   współczynnik   wzmocnienia   termoelementu   pokazuje   o   ile   wzrośnie 
wartość   sygnału   wyjściowego   (w   tym   przypadku   napięcia)   przy  wzroście   amplitudy  sygnału 
wejściowego o jedną jednostkę (w tym przypadku – o 1 stopień).

Transmitancję termopary 1 zapiszemy w postaci transmitancji elementu inercyjnego I-go 

stopnia czyli

G

1

(

s)=

k

1+T

1

s

Transmitancją

 

termopary 2 można w sposób przybliżony zapisać

 

następująco

G

2

(

s )=

k

1+T

2

s

e

−

τ

s

.

10

        

 

 Praktyczna realizacja ćwiczenia

 

 

            Część doświadczalna

Badaniu podlegać będą trzy termopary: T1, T2 i T3.

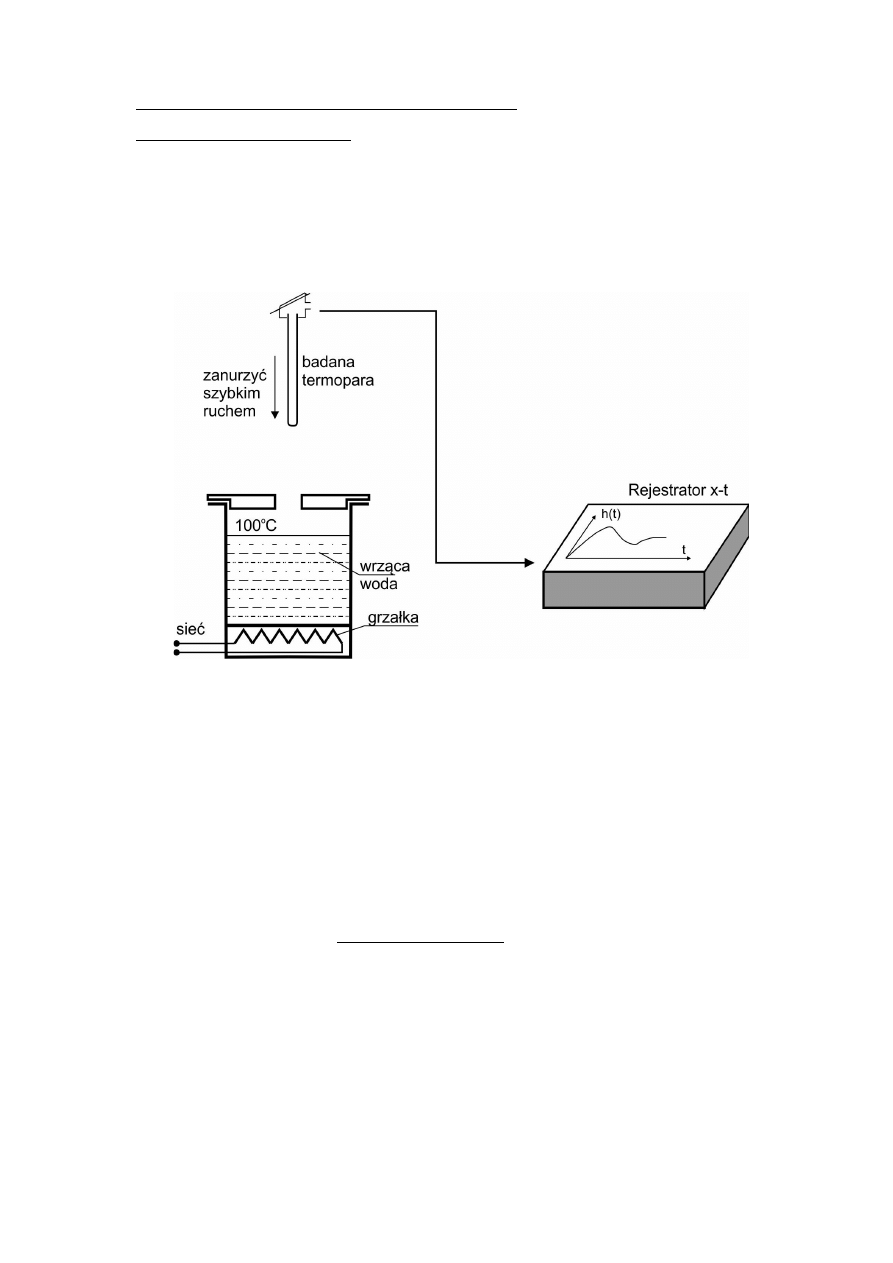
Schemat   stanowiska   do   rejestracji   charakterystyk   skokowych   termopar   przedstawiony 

jest   na   rys.   2.10   a   rzeczywisty  wygląd   prezentuje   foto   2.1.  Wymuszenie   skokowe,   które   dla 
termopar   ma   postać   różnicy  temperatur   pomiędzy  zimnymi   i   gorącym   końcami   termopary  , 
będziemy realizowali w następujący sposób:

Rys. 2.10. Schemat stanowiska laboratoryjnego do rejestracji charakterystyk skokowych 

termopar

W   kolbie   znajdującej   się   w   płaszczu   grzewczym   mamy   wrzącą   wodę.   Temperaturę 

wrzenia wody przyjmujemy równą   100

°

C. Zimne końce mają temperaturę równą temperaturze 

otoczenia. Wartość temperatury otoczenia odczytujemy z termometru cieczowego wiszącego w 
laboratorium   na   filarze.   Po   energicznym   zanurzeniu   badanej   termopary   do   wrzącej   wody 
będziemy   przyjmowali,   że   podaliśmy   na   nią   temperaturowe   wymuszenie   skokowe,   którego 
amplituda wynosi  100

°

C – temperatura otoczenia.

Końce termopary podłączymy do rejestratora X-t. Sposób podłączenia, wskazane zakresy 

pomiarowe  i ogólnie, obsługa techniczna rejestratora zostanie omówiona  przez prowadzącego 
bezpośrednio przed realizacją ćwiczenia.

Należy zarejestrować dwie pary charakterystyk (dwa razy po dwa wykresy). 

W   jednym   układzie   współrzędnych   należy   zarejestrować   charakterystyki   skokowe 

termopar T1 i T2. Są to termopary wykonane z tej samej pary metali (Fe-Konst). Pierwsza jest w 
osłonie,   druga   -     bez   osłony.   Należy   porównać   właściwości   metrologiczne   tych   termopar   i 
wyciągnąć wnioski.

W   drugim   układzie   współrzędnych   należy   zarejestrować   wykresy   charakterystyk 

skokowych termopar T1 i T3. Mają one zbliżone właściwości cieplne (stałe czasowe) natomiast 
inny współczynnik nachylenia charakterystyki. Poziom sygnału wyjściowego w stanie ustalonym 
dla tych termopar będzie inny.

11

Foto 2.1. Fotografia stanowiska do rejestrowania charakterystyk skokowych

            Część obliczeniowa

Cześć obliczeniowa w tym ćwiczeniu sprowadzać się będzie do dwóch zadań:

1. Identyfikacji badanych termopar jako elementów automatyki, czyli napisania dla 

każdej z badanych termopar ich transmitancji operatorowych.

2. Stworzenia   modeli   tych   termopar   i   narysowanie   wykresów   charakterystyk 

skokowych uzyskanych na podstawie tych modeli.

Ad.   1.    Na   podstawie   charakterystyki   skokowej   termopary  T1  zapisanej   w 

pierwszej parze wykresów oraz na podstawie charakterystyk skokowych termopar  T2  i 
T3  zapisanych   jako   druga   para   wykresów   można   przypisać   każdej   termoparze 
następujące postacie transmitancji operatorowych:

G

1

(

s)=

k

1

1+T

1

s

e

−

τ

s

;G

2

(

s)=

k

2

1+T

2

s

;G

3

(

s)=

k

3

1+T

3

s

.

Wykorzystując metody przedstawione na rys. 2.6  i 2.9 należy określić liczbowe 

parametry badanych termopar: k

1

 ,  k

2

 , k

3

 , T

1

 , T

2

 , T

3

 , τ  i napisać wyżej przedstawione 

transmitancje operatorowe wstawiając wyznaczone parametry.

Przeanalizować  wykresy oraz  transmitancje  operatorowe  i  wyciągnąć  rozsądne 

wnioski.

12

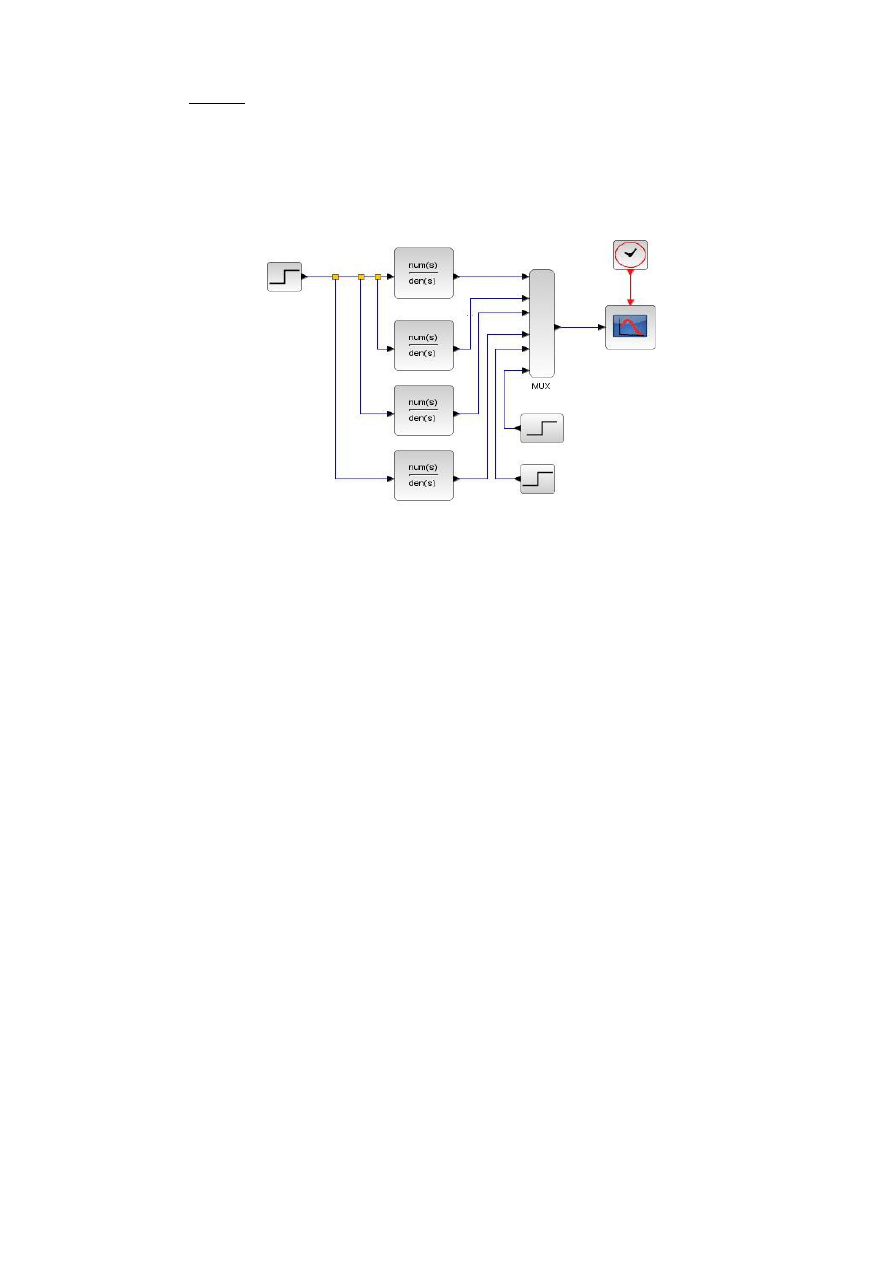
Ad. 2.    Ta część sprawozdania ma za zadanie poćwiczenie problemów symulacji 

elementów automatyki z wykorzystaniem programu symulacyjnego: Matlab lub SciLab.

Zadanie sprowadza się do narysowania charakterystyk skokowych  elementów o 

transmitancjach  G

1

(s), G

2

(s), G

3

(s). Można to zrobić na wiele sposobów. Jednym z nich 

jest poniższy schemat, przy pomocy którego zostały uzyskane wykresy na rys. 2.7 z 
wykorzystaniem programu SciLab.

Rys. 2.11. Schemat blokowy układu w programie SciLab (xcos) do rysowania 
charakterystyk skokowych

13