
Instytut Technologii Maszyn i Automatyzacji Produkcji
PK
Zakład Procesów Wytwarzania i Systemów Jakości
Pomoc dydaktyczna
Obliczanie naddatków na obróbkę
skrawaniem metodą analityczną
Na podstawie książki: Kowan W. M. „Obliczanie naddatków na obróbkę w budowie maszyn”
Opracował:
Mgr inż. Jacek Habel
Obliczanie naddatków na obróbkę
2
W. M. Kowan
Obliczanie naddatków na obróbkę w budowie maszyn
Obliczanie naddatków na obróbkę oraz tolerancji wymiarów międzyoperacyjnych ma
znaczenie techniczno-ekonomiczne. Zbyt duże naddatki często powodują usuwanie
najbardziej odpornych na zużycie powierzchni metalu i obniżenie własności mechanicznych
PO. Wskutek stosowania zbyt dużych naddatków wzrasta również zużycie metalu, energii
elektrycznej i narzędzi co powoduje wzrost kosztów własnych produkcji. Zbyt małe naddatki
nie zapewniają możliwości usuwania warstw powierzchniowych metalu oraz otrzymania
wymaganej dokładności i gładkości obrabianych powierzchni. Skutkiem stosowania zbyt
małych naddatków jest powstawanie dużej liczby braków, co również zwiększa koszt własny
produkcji.
Teoretyczne podstawy obliczeniowo-analitycznej metody określania
naddatków na obróbkę.
Terminologia, podstawowe określenia i pojęcia.
Usuwana w procesie obróbki warstwa materiału nazywa się naddatkiem na obróbkę.
Wielkość rzeczywistego naddatku na obróbkę określa się różnicą wymiarów przedmiotu
przed i po obróbce. Rozróżnia się międzyoperacyjne i całkowite naddatki na obróbkę.
Naddatkiem międzyoperacyjnym nazywamy warstwę materiału, niezbędną do wykonania
zabiegu technologicznego. Naddatek międzyoperacyjny określa się różnicą wymiarów,
otrzymywanych w dwóch kolejnych zabiegach procesu technologicznego obróbki danej
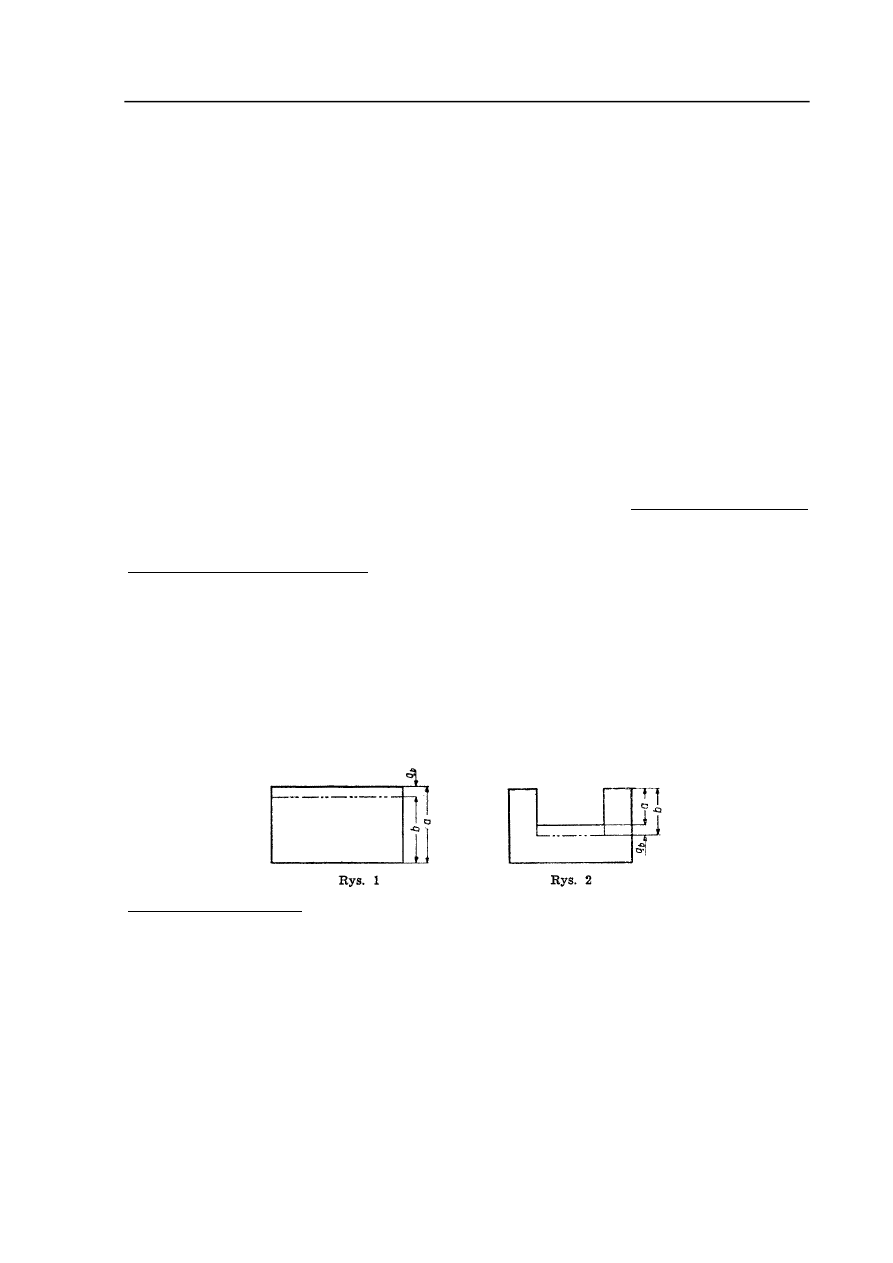
powierzchni elementarnej w zabiegu poprzedzającym i wykonywanym. Dla zewnętrznych
powierzchni PO (rys.1):
a - b = q
b
→
q
b
= b - a
gdzie:
q
b
- naddatek dla zabiegu wykonywanego,
a - wymiar otrzymany w poprzedzającym zabiegu,
b - wymiar otrzymywany w wykonywanym zabiegu.
Naddatkiem całkowitym nazywamy warstwę materiału, niezbędną do wykonania całokształtu
zabiegów technologicznych, to znaczy całego procesu obróbki elementarnej powierzchni.
Naddatek całkowity określa się różnicą wymiarów półwyrobu nie obrobionego i przedmiotu
gotowego. Dla powierzchni mamy:
q
o
= a
w
- a
p
gdzie:
q
o
- naddatek całkowity na obróbkę,
a
p
- wymiar nieobrobionego półwyrobu,
a
w
- wymiar gotowego wyrobu.
Naddatek całkowity na obróbkę równy jest sumie naddatków międzyoperacyjnych dla
wszystkich zabiegów obróbkowych od nieobrobionego półfabrykatu do gotowego przedmiotu
Obliczanie naddatków na obróbkę
3
q
q
o
i
i
n
=
=
∑
1
gdzie n - liczba zabiegów obróbkowych.
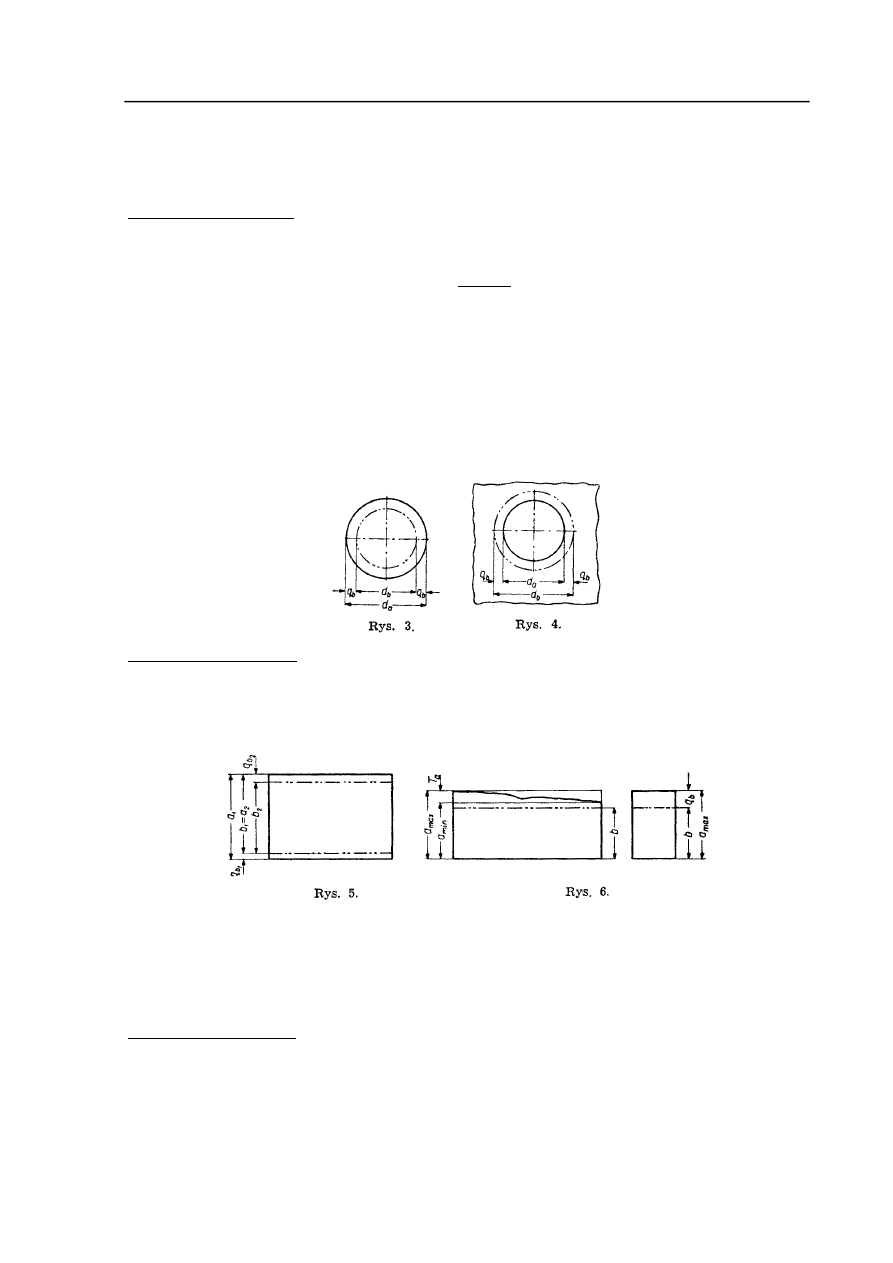
Rozróżnia się symetryczne i asymetryczne naddatki na obróbkę.
Naddatki symetryczne występują zawsze przy obróbce zewnętrznych i wewnętrznych
powierzchni obrotowych (rys. 3 i 4), a w niektórych wypadkach - przy równoległej obróbce
przeciwległych powierzchni płaskich
q
d
d
b
a
b
=
−
2
lub
2q
b
= d
a
- d
b
i 2q
b
= l
a
- l
b
gdzie:
2q
b
- naddatek na średnicy lub naddatek na obie strony przy równoległej obróbce
przeciwległych powierzchni płaskich;
d
a
i d
b
- wymiary średnic dla zabiegów poprzedzającego i wykonywanego;
l
a
i l
b
- wymiary między powierzchniami płaskimi, obrabianymi w dwóch kolejnych
zabiegach: poprzedzającym i wykonywanym.
Naddatki asymetryczne mają różne wielkości na przeciwległych powierzchniach w wypadku
ich kolejnej obróbki (rys.5)
q
b1
= a
1
- b
1
q
b2
= a
2
- b
2
Naddatki jednostronne stanowią szczególny przypadek naddatków asymetrycznych, gdy
przeciwległa ściana nie podlega obróbce.
Rozpatrując czynniki wpływające na wielkość naddatku, należy zaznaczyć, że
podobnie jak każdy półfabrykat zależnie od metody jego wykonania, ma określoną
dokładność i jakość powierzchni, tak samo również w wyniku wykonania każdego
technologicznego zabiegu obróbki otrzymuje się odpowiednią dokładność i określoną jakość
powierzchni.
Dokładność wykonania półfabrykatów i następnej ich obróbki zależy od:
1) odchyleń od założonych wymiarów,
2) błędów kształtu (odchylenia makrogeometryczne),
3) odchylenia od założonego położenia współzależnych elementów półfabrykatu lub
gotowego przedmiotu (odchylenia przestrzenne).
Obliczanie naddatków na obróbkę
4
Odchylenie od założonego wymiaru ograniczone jest tolerancją wymiaru. Błędy kształtów
geometrycznych (eliptyczność, stożkowość, baryłkowatość, wężkowatość, wklęsłość,
wypukłość, nierównoległość przeciwległych ścian itp.) powinny się mieścić w granicach pola
tolerancyjnego wymiaru.
Odchylenia przestrzenne (wygięcie, przesunięcie, zboczenie i nierównoległość osi,
nieprostopadłość osi i powierzchni, odchylenia od współosiowości stopni wałów i otworów,
mimośrodowość zewnętrznych powierzchni w stosunku do otworów itp.) nie są związane z
tolerancją wymiaru elementarnej powierzchni i powinny być uwzględniane oddzielnie przy
wyznaczaniu naddatków na obróbkę.
W celu usunięcia przy wykonywanym zabiegu błędów poprzedniej obróbki należy
uwzględnić tolerancję wymiaru i odchylenia przestrzenne, otrzymane w poprzedzającym
zabiegu technologicznym.
W przypadku gdy chodzi o usunięcie błędu nierównoległości ścian i innych błędów
kształtu powierzchni obrabianej, zawartych w granicach pola tolerancji wymiaru, naddatek
dla zabiegu wykonywanego przy obróbce partii przedmiotów powinien być (gdy nie ma
innych błędów) nie mniejszy od tolerancji wymiaru zabiegu poprzedzającego (rys. 6).
Przy usuwaniu błędów stożkowości, eliptyczności i innych błędów kształtu
(zawartych w granicach pola tolerancji wymiaru) naddatek dla zabiegu wykonywanego przy
obróbce partii przedmiotów stanowiących bryły obrotowe powinien być nie mniejszy od
tolerancji wymiaru zabiegu poprzedzającego (rys. 7).
2q
T
b
a
≥
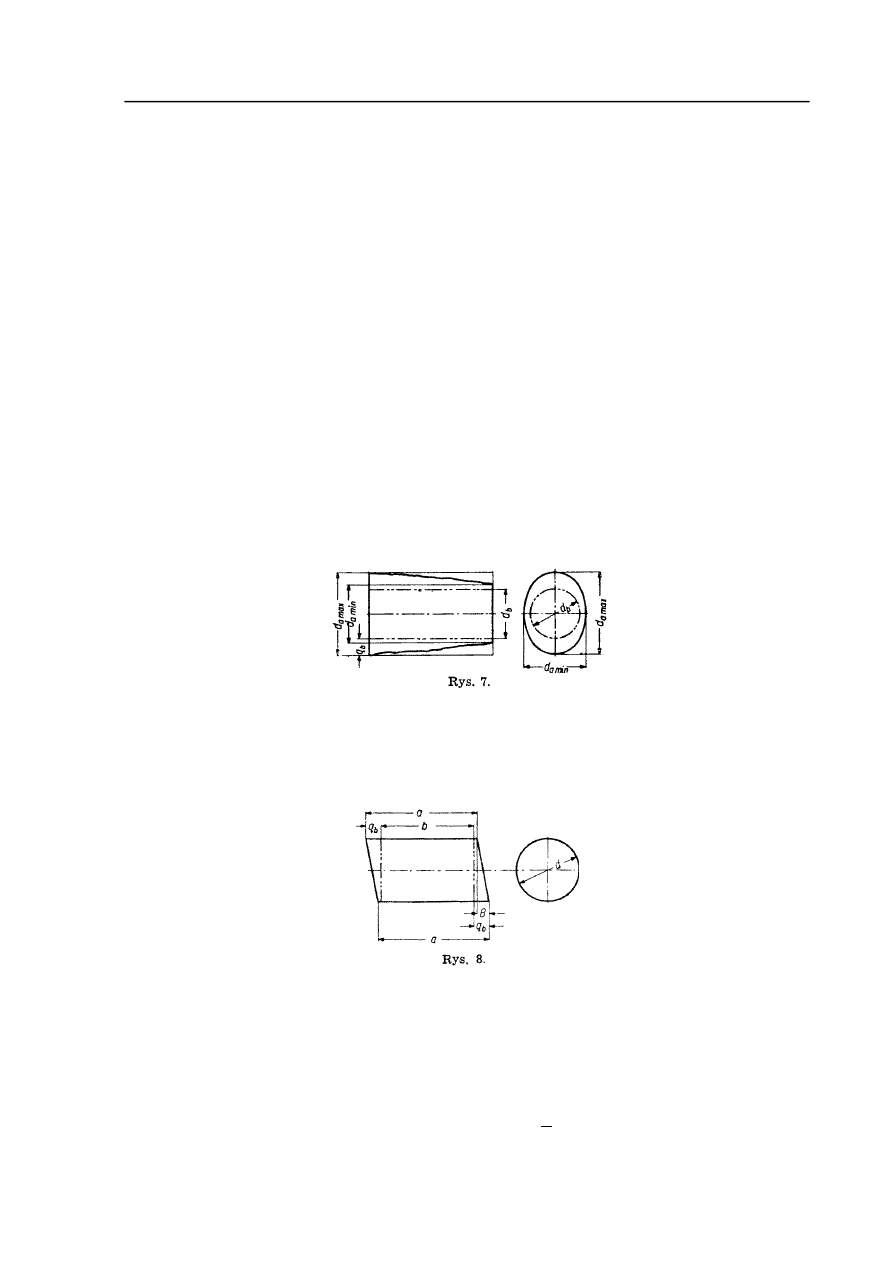
W celu usunięcia błędu nieprostopadłości naddatek na planowanie każdego czoła przedmiotu
walcowego (rys. 8) powinien być, (gdy nie ma innych błędów), nie mniejszy od odchylenia
od prostopadłości
q
B
b
≥
gdzie B - wielkość charakteryzująca odchylenie od prostopadłości.
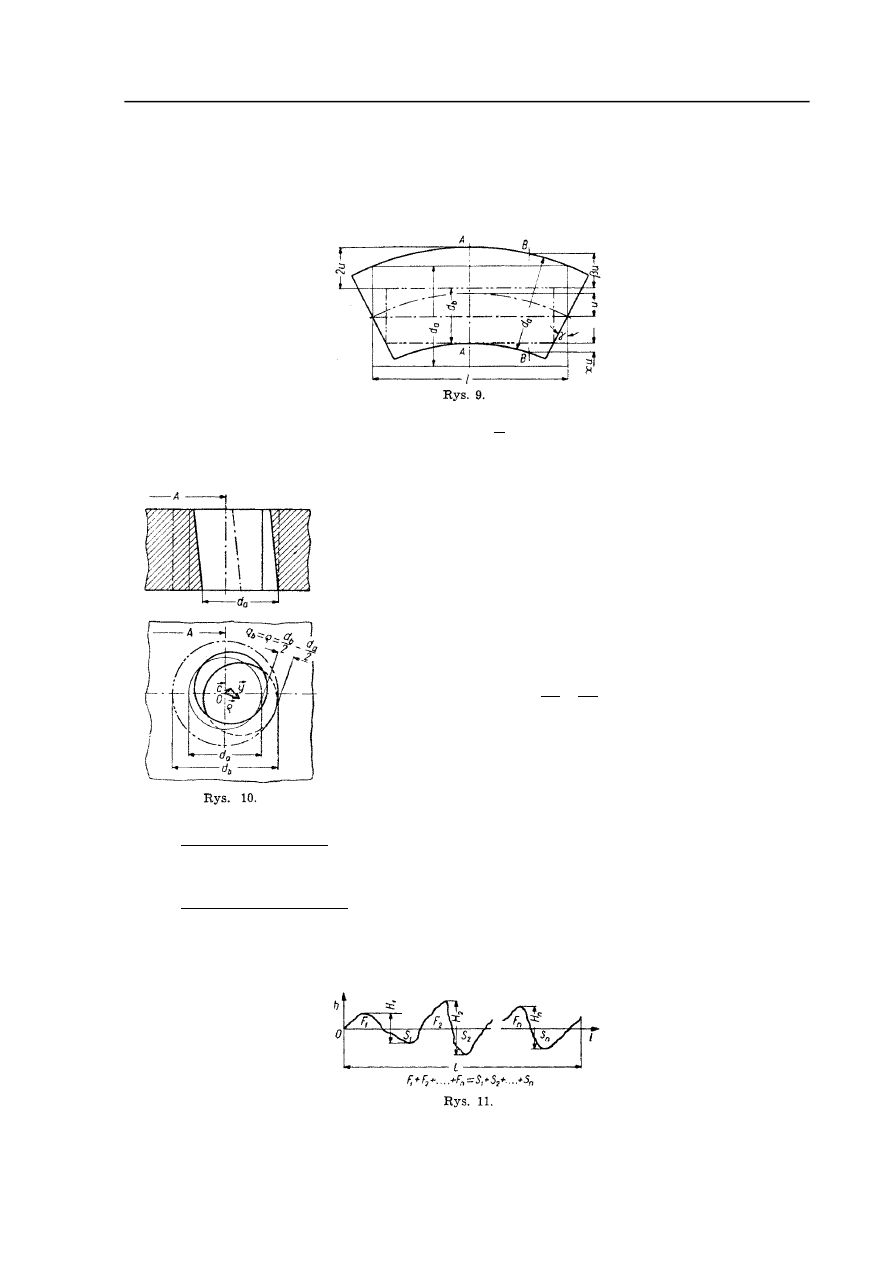
Naddatek na obróbkę półwyrobu wygiętego powinien być nie mniejszy od podwójnego
wygięcia (rys. 9)
2
2
q
u
b
≥
gdzie u - wielkość wygięcia.
W wyniku wygięcia półwyrobu otrzymuje się nierównoległość jego czół, zależną od
wielkości wygięcia; naddatek na obróbkę każdego czoła wyniesie
q
d tg
d
u
l
bc
b
b
≥
=
0 5
0 5
.
.
γ
Obliczanie naddatków na obróbkę
5
gdzie:
q
bc
- naddatek na obróbkę każdego czoła;
d
b
- średnica otrzymywana podczas wykonywanego zabiegu;
γ - kąt, charakteryzujący wygięcie;
u - wielkość wygięcia półwyrobu;
l - długość, na której określa się wygięcie (połowa długości półfabrykatu wg. rys.9).
Wielkość
tg
u
l
γ
=
można nazwać wygięciem jednostkowym.
Naddatek kompensujący odchylenia przestrzenne
wyznacza się przez dodanie ich wielkości wektorowych. Jeżeli
np. przy obróbce otworu w poprzedzającym zabiegu nastąpiło
przesunięcie i jednocześnie odchylenie osi otworu, to naddatek
wyrównujący te odchylenia w wykonywanym zabiegu powinien
być wyznaczony przez dodanie wektorów: przesunięcia osi r
c i
odchylenia osi (rys. 10).
ry
r
ρ
ρ
=
ρ
=
Wektor jako suma wektorów r
c i ry jest jednocześnie różnicą
promieni.
−
d
d
b
a
2
2
≤ q
b
lub
2
2
≤
d
d
b
a
q
b
−
Przytoczone przykłady wskazują wyraźnie, że przy wyznaczaniu
naddatków na obróbkę należy uwzględniać tolerancję wymiaru i
odchylenia przestrzenne.
Jakość powierzchni charakteryzuje się jej gładkością, tzn. jej mikrozarysem lub
chropowatością, jak również stanem i głębokością warstwy powierzchniowej, różniącej się
swoimi fizykalnymi własnościami od własności metalu zasadniczego.
Gładkość powierzchni części maszyn ma bezpośredni wpływ na ich własności
eksploatacyjne. W szczególności od gładkości powierzchni zależą: odporność na zużycie
połączeń ruchowych, wytrzymałość pasowań wciskanych oraz wytrzymałość dynamiczna
części maszyn przy obciążeniach obustronnie zmiennych.
Gładkość powierzchni określa się jednym z następujących parametrów:
Obliczanie naddatków na obróbkę
6
• średnią kwadratową wysokością chropowatości H
sk
,
• średnią wysokością chropowatości H
śr
.
Średnią kwadratową wysokością chropowatości H
sk
nazywamy pierwiastek kwadratowy ze
średniego kwadratu odległości punktów zarysu od jego prostej środkowej, tzn. od prostej,
dzielącej zarys w ten sposób, że sumy pól zawartych pomiędzy tą prostą i konturem profilu są
równe z obu stron tej prostej (rys. 11).
H
L
h dl
sk
L
=
∫
1
2
0
Średnią wysokość chropowatości H
śr
określa się jako średnią arytmetyczną wysokości
chropowatości H od wierzchołka do dna wgłębienia (rys. 11). Przy określaniu H
śr
nie
uwzględnia się poszczególnych wartości H, odbiegających znacznie od innych.
H
H
H
H
śr
n
n
=
+
+ +
1
1
2
(
)
K
Jakość powierzchni (gładkość powierzchni, stan i głębokość warstwy
powierzchniowej) zmienia się zależnie od własności materiału obrabianego, warunków
obróbki półfabrykatów oraz innych czynników (drgania, zjawiska cieplne itp.). Własności
mechaniczne powierzchniowej warstwy przedmiotu niekiedy znacznie pogarszają się po
obróbce, przekraczając granice odpowiadające wymaganym warunkom eksploatacyjnym
pracy części. W tych wypadkach w celu uniknięcia stopniowego nagromadzenia się w
warstwie powierzchniowej odchyleń od normalnej struktury metalu należy w wykonywanym
zabiegu usunąć całkowicie warstwę powierzchniową, otrzymaną podczas poprzedniego
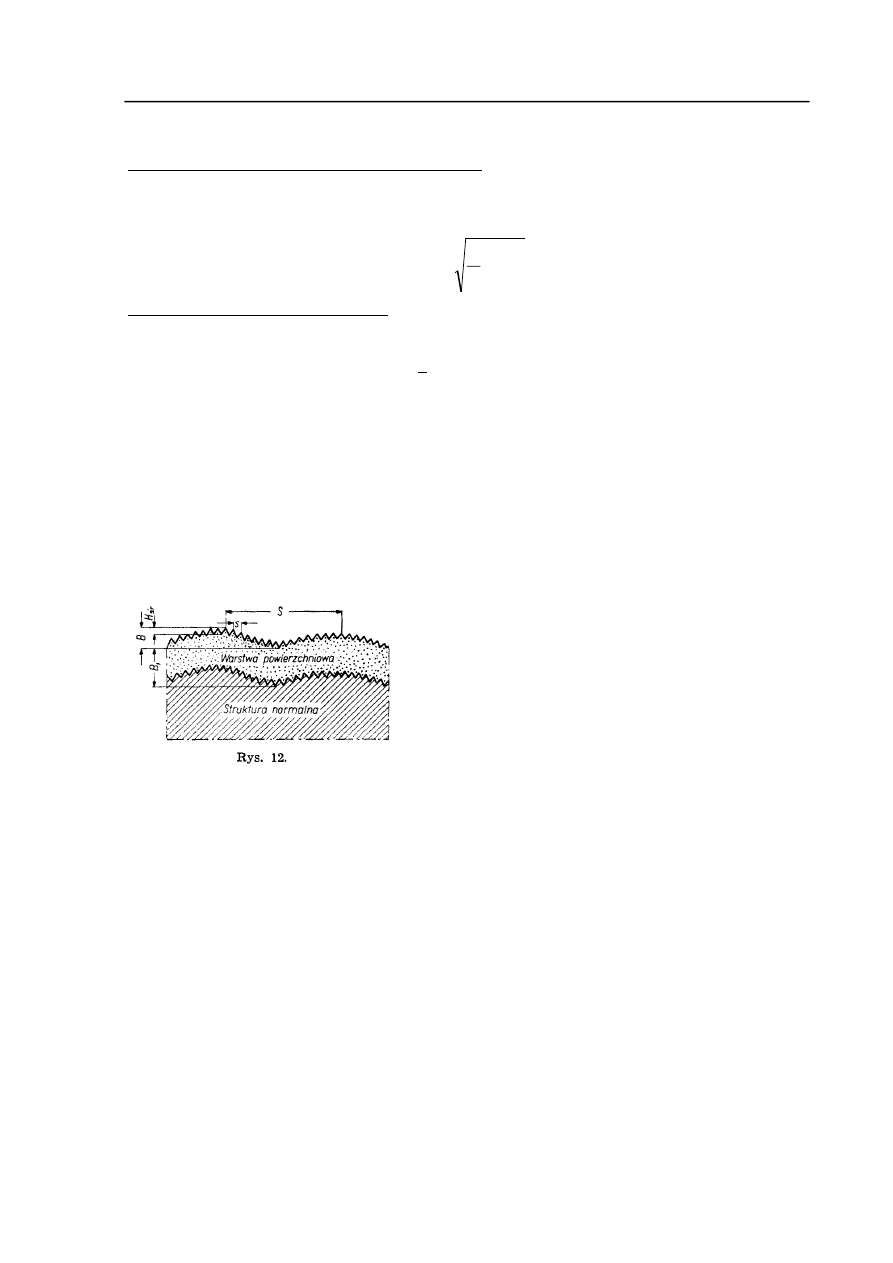
zabiegu technologicznego. Badania wykazały, że spód warstwy powierzchniowej ma podobne
makro- i mikronierówności, jak jej górna część (rys. 12).
Makronierówności mieszczą się w granicy tolerancji
wymiaru, natomiast mikronierówności i głębokość
warstwy powierzchniowej mają wpływ na wielkość
naddatków na obróbkę.
W celu usunięcia mikronierówności i warstwy
powierzchniowej, otrzymanych podczas zabiegu
poprzedzającego, należy dla następnego zabiegu (gdy
nie ma innych błędów) ustalić naddatek nie mniejszy
od sumy średniej wysokości chropowatości H
śra
i
głębokości warstwy powierzchniowej B
1a
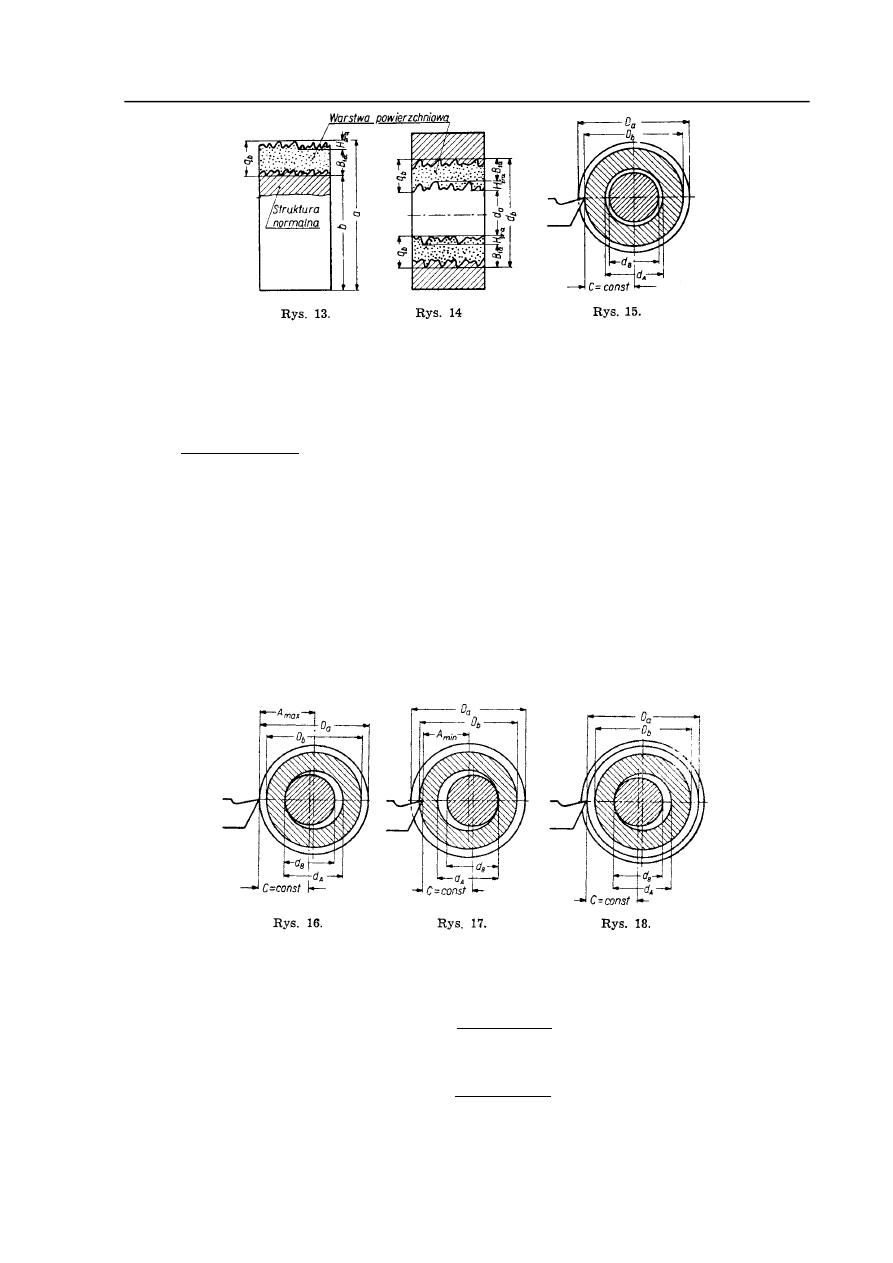
. Otrzymamy więc dla naddatku asymetrycznego
przy obróbce zewnętrznych powierzchni (rys. 13)
q
a b H
B
b
śra
a
= − ≥
+
1
dla naddatku symetrycznego przy obróbce wewnętrznych powierzchni (rys. 14)
2
2
1
q
d
d
H
B
b
b
a
śra
a
=
−
≥
+
(
)
W praktyce wystarczy jednak ograniczyć się do częściowego usunięcia warstwy
powierzchniowej.
Obliczanie naddatków na obróbkę
7
Z powyższego wynika, że wielkość naddatku dla wykonywanego zabiegu określa się
tolerancją wymiaru, sumą wektorową przestrzennych odchyleń oraz jakością powierzchni
otrzymanej podczas poprzedzającego zabiegu.
Naddatek ten może się jednak okazać nie wystarczający dla dokładnej obróbki, jeżeli nie
uwzględni się błędu ustawienia w wykonywanym zabiegu.
Błąd ustawienia
ε
u
składa się z błędu ustalenia (bazowania)
ε
b
i błędu zamocowania
ε
z
. Przypuśćmy, że przy obróbce partii przedmiotów obieramy za podstawę obróbkową (bazę)
otwór, którego wymiar dla różnych przedmiotów tej partii waha się w granicach
d
d
A
A
max
min
T
A
−
=
Obróbkę przeprowadzamy na różnych obrabiarkach, a więc na różnych trzpieniach, których
wymiar waha się w granicach
d
d
B
B
max
min
T
B
−
=
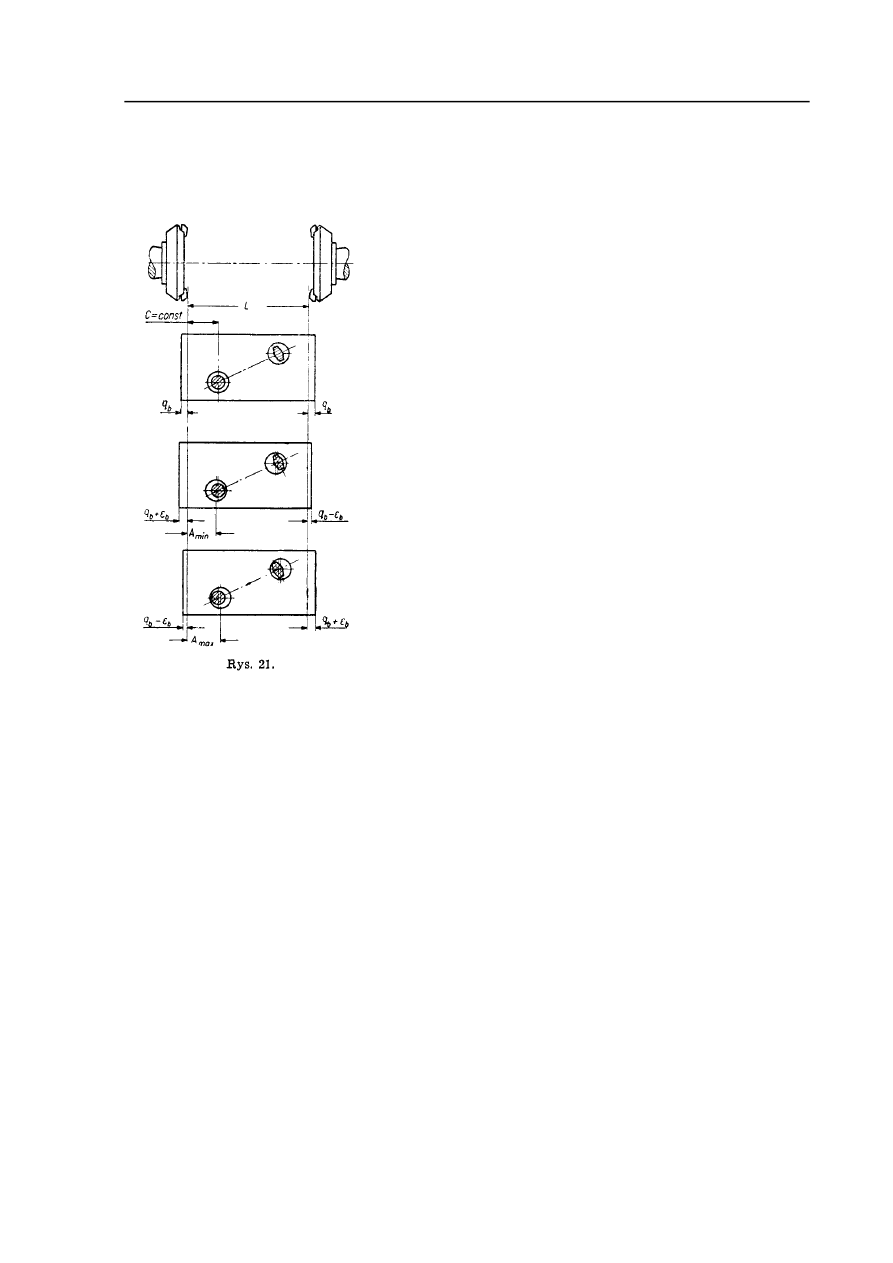
Przy zamocowaniu przedmiotu na trzpieniu z równomiernym luzem promieniowym, osie
trzpienia i otworu pokrywają się (rys. 15); błąd ustalenia w tym wypadku równa się zeru
(zgodność podstawy obróbkowej z pomiarową) i naddatek na obróbkę przedmiotu o
wymiarze D
a
na wymiar D
b
określony zostaje jako różnica tych wymiarów
2q
D
D
b
a
b
=
−
Jednak małe jest prawdopodobieństwo tak dokładnego dopasowania przedmiotu obrabianego
do trzpienia. W praktyce oś przedmiotu przesunie się w stosunku do nastawionego na wymiar
narzędzia w granicach od
A
C
d
d
A
B
max
max
min
= +
−
2
(rys. 16)
do
A
C
d
d
A
B
min
max
min
= −
−
2
(rys. 17)

Obliczanie naddatków na obróbkę
8
Błąd ustalenia (bazowania)
ε
b
będzie wtedy różnicą granicznych odchyleń podstawy
pomiarowej w stosunku do nastawionego na wymiar narzędzia skrawającego
ε
b
A
B
A
B
A
A
C
d
d
C
d
d
=
−
= +
−
− +
−
max
min
max
min
max
min
2
2
ε
b
A
L
L
L
L
T
=
+
=
=
+
+
max
max
max
min
2
2
B
T
gdzie:
L
max
- luz największy,
L
min
- zapewniony luz najmniejszy,
T
A
- tolerancja wymiaru otworu,
T
B
- tolerancja wymiaru trzpienia.
W związku z przesunięciem otworu przedmiotu w stosunku do ostrza skrawającego (błąd
ustalenia) nóż nie będzie skrawał w określonym położeniu przedmiotu (rys. 16). Stąd
wniosek, że w celu prawidłowego wykonania obróbki powierzchni obrotowej należy w
omawianym wypadku zwiększyć naddatek o podwójny błąd ustalenia (rys. 18)
(
)
2
2
ε
b
A
L
T
T
=
+
+
min
B
Jeżeli występujące siły są
niewielkie i nie powodują
przesunięcia kłów we wrzecionie
i koniku, to przy zamocowaniu
trzpienia w sztywnych kłach
błąd zamocowania
ε
z
= 0. W tym
wypadku błąd ustawienia równy
jest błędowi ustalenia.
Przy zamocowaniu
przedmiotu obrabianego na trzpieniu rozprężnym nie ma
luzu między trzpieniem i przedmiotem, a błąd ustalenia
można przyjąć równy zeru (
ε
b
=0), jednak przy
zamocowaniu trzpienia w uchwycie samocentrującym
należy brać pod uwagę błąd zamocowania w wyniku
przesunięcia się trzpienia w kierunku promieniowym w
związku z nierównomiernym odkształceniem szczęk
zaciskających uchwytu. W tym wypadku błąd ustawienia
równa się błędowi zamocowania
ε
z
(rys. 19).
Obliczanie naddatków na obróbkę
9
Wreszcie mogą zdarzyć się wypadki, kiedy występuje zarówno błąd ustalenia, jak i błąd
zamocowania. Na przykład przy zamocowaniu przedmiotu na trzpieniu walcowym powstanie
błąd ustalenia, a przy zamocowaniu tego trzpienia w trójszczękowym uchwycie - błąd
zamocowania. Błąd ustawienia jest w tym wypadku sumą wektorów wartości błędu ustalenia
ε
b
i błędu zamocowania
ε
z
(rys. 20)
r
r
r
ε
ε
ε
u
b
z
=
+
b
A
B
L
T
T
=
+
+
min
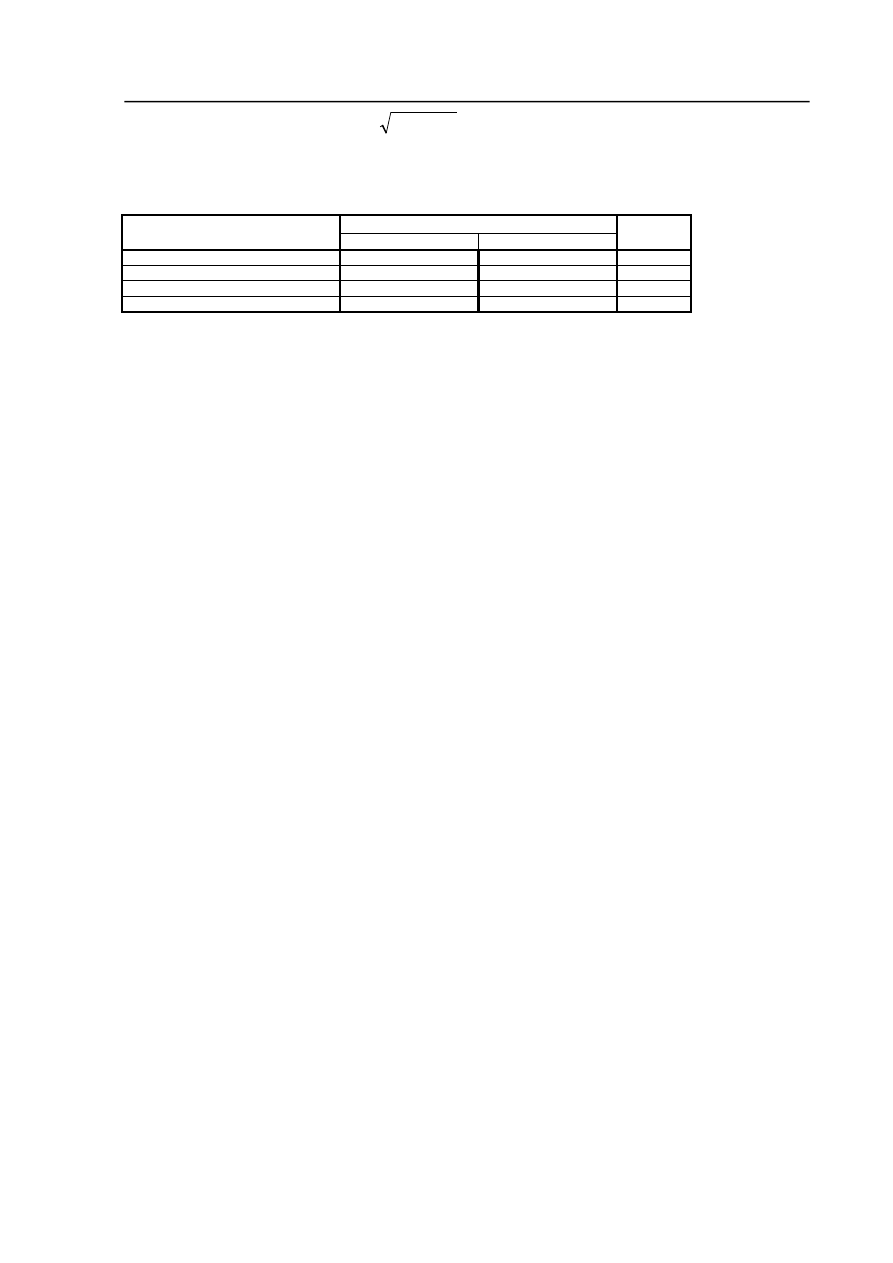
Na rys. 21 pokazano ustawienie korpusu do obróbki
płaskich, czołowych powierzchni. Przy znacznej odległości
między osiami na kołki ustalające można pominąć
skrzywienie przedmiotu przy wyznaczaniu naddatków i
błąd ustalenia można przyjąć z dostateczną dokładnością ze
wzoru
ε
Uwzględniając możliwość przesunięcia się przedmiotu
zarówno w jedną, jak i w drugą stronę, należy w
rozpatrywanym wypadku zwiększyć naddatek na obróbkę
powierzchni czołowej o wielkość równą błędowi ustalenia
ε
b
.

Obliczanie naddatków na obróbkę
10
Wzory do obliczania naddatków na obróbkę
W wyniku wykonywanych kolejno zabiegów błędy powstające przy obróbce
stopniowo się zmniejszają, a proces technologiczny kończy się zabiegiem, po wykonaniu
którego błąd obróbki osiąga wielkość dopuszczalną ze względu na wymagania techniczne
dotyczące PO. Podczas wykonywania każdego zabiegu technologicznego powinny być
usunięte błędy zabiegu poprzedzającego w tym celu, by błędy powstałe w tych zabiegach nie
sumowały się.
Ponieważ błąd ustawienia w wykonywanym zabiegu powstaje wskutek odchylenia
położenia podstawy pomiarowej w stosunku do nastawionego na wymiar narzędzia
skrawającego oraz przestrzenne odchylenia półfabrykatu otrzymane w poprzedzającym
zabiegu skierowane są względem siebie w wielu wypadkach pod kątem, dodawanie tych
błędów powinno się odbywać zgodnie z prawem dodawania wektorów.
Stąd wniosek, że naddatek na obróbkę można obliczyć według następujących wzorów:
• dla naddatków symetrycznych
(
) (
)
2
2
2
1
q
T
H
B
b
a
śra
a
a
ub
≥
+
+
+
+
r
r
ρ
ε
$
• dla naddatków asymetrycznych
(
) (
)
q
T
H
B
b
a
śra
a
a
ub
≥
+
+
+
+
1
r
r
ρ
ε
$
gdzie:
q
b
- naddatek na stronę w zabiegu wykonywanym,
T
a
- tolerancja wymiaru, otrzymanego podczas poprzedzającego zabiegu,
H
śra
- średnia wysokość chropowatości (mikronierówności powierzchniowych)
otrzymanych podczas poprzedzającego zabiegu,
B
1a
- głębokość warstwy powierzchniowej, otrzymana podczas poprzedzającego
zabiegu,
r
ρ
a
- suma wektorowa odchyleń przestrzennych wzajemnie związanych powierzchni
obrabianego przedmiotu, otrzymana podczas poprzedzającego zabiegu,
r
ε
ub
- suma wektorowa błędów ustalenia i zamocowania, tj. błąd ustawienia powstały
w zabiegu wykonywanym,
indeks a - zabieg poprzedzający,
indeks b - zabieg wykonywany (bieżący).
Odchylenia przestrzenne powierzchni elementarnych mają różny charakter, zależny od
kształtu i tolerancji wymiarów, czyli od klasy przedmiotu. Na przykład zewnętrzne
powierzchnie walcowe wałów stopniowych mogą mieć wygięcie i niewspółosiowość stopni;
czołowe powierzchnie wałów - nieprostopadłość do osi wału; otwory - przesunięcie i
odchylenie osi otworu; płaskie powierzchnie korpusów - odchylenia od prostopadłości tych
powierzchni itp.
Zależnie od klasy przedmiotu, jego ustalenia i zamocowania, wzajemne położenie
wektorów
r
ρ
a
i
r
ε
ub
zmienia się w szerokich granicach - od kierunków zgodnych do
przeciwnych w skrajnych położeniach.
Oznaczając przez sumę geometryczną wektorów
rc
r
ρ
a
i
r
ε
ub
przez - większy, a przez
- mniejszy z tych wektorów, otrzymamy
ra
r
b
r r r
c
a b
= +
( )
c
a
b
ab
ab
=
+
+
2
2
2 cos r
r
r
r
gdzie
(
- kąt zawarty między wektorami
)
r r
a b
,
a i b .
Wzór ten przekształca się:

Obliczanie naddatków na obróbkę
11
1) w wypadku zgodnych kierunków wektorów (kąt
( )
r r
a b
,
równy 0
°)
c a b
= +
r
2) dla przeciwnych kierunków wektorów (kąt
( )
ra b
,
równy 180
°)
c a b
= −
3) w wypadku, gdy kąt
nie może być dokładnie ustalony, przyjmujemy, że wartość
jego wynosi 90
° (średnie położenie wektorów)
(
r r
a b
,
)
c
a
b
=
+
2
2
W przybliżeniu otrzymamy
a
b
a
2
2
0 96
0 4
+
≈
+
.
b
.
b
dla a b
≥
Dla
mamy
a
≥ 4
a
b
a
a
a
a
a a
2
2
2
2
2
2
4
16
103075
+
=
+
=
+
=
≈
.
a więc a
b
2
2
+
≈ a
ub
dla a
b
≥ 4
Błąd rachunku w obu wypadkach nie przekracza 4% rzeczywistej wielkości.
Posługując się takimi przybliżeniami możemy przyjąć, że:
(
)
r
r
ρ
ε
ρ
ε
a
ub
a
$
.
.
+
≈
+
0 96
0 4
dla
ρ
ε
a
u
>
b
b
r
r
(
)
ρ
ε
ρ
ε
a
ub
a
u
$
.
.
+
≈
+
0 4
0 96
dla
ρ
ε
a
ub
<
Tak samo oblicza się
r
ρ
a
jako geometryczną sumę wektorów odchyleń przestrzennych i
r
ε
ub
jako sumę geometryczną wektorów błędów ustalenia i zamocowania.
Przykładowo dla dwu różnych odchyleń przestrzennych
ρ
1
i
ρ
2
, wartość
ρ
a
oblicza się tak:
(
)
r
r
r
ρ
ρ ρ
ρ
a
=
+
≈
+
1
2
1
0 96
0 4
$
.
.
ρ
2
dla
ρ
ρ
1
2
>
Przy istnieniu trzech odchyleń przestrzennych, np. wygięcia, odchylenia od współosiowości
poszczególnych stopni oraz błędu nakiełkowania dla wałów stopniowanych, otrzymamy
(
)
r
r
r
r
ρ
ρ ρ
ρ
ρ
ρ
a
=
+
+
≈
+
+
1
2
3
1
2
0 94
0 39
0 3
.
.
.
ρ
3
dla
ρ
ρ
ρ
1
2
>
>
3
l
Przykładowo wygięcie jednostkowe
∆u dla nieobrobionych kutych wałów o średnicy
ponad 500 [mm] wynosi:
∆u = 1÷2 [mm/m] długości. Ugięcie dla dowolnego przekroju wału
wyniesie
u
u
u
=
⋅
∆
[mm]
gdzie l
u
- odległość od przekroju, dla którego oblicza się ugięcie, do najbliższego czoła w [m].
Ponadto należy zaznaczyć, że całkowity naddatek na obróbkę powierzchni
elementarnej jest sumą naddatków międzyoperacyjnych. Przykładowo dla stopnia wału
φ22k6
należy przeprowadzić obróbkę zgrubną, dokładną (kształtującą), szlifować zgrubnie i
wykańczająco, stąd wzór na całkowity naddatek przyjmie postać
2
2
2
2
2
q
q
q
q
q
b
bzgr
bdok
bszlzgr
bszlwyk
=
+
+
+
a po jego obliczeniu otrzymamy: 2q
b
= 4.6 [mm].
Średnicę pręta (półfabrykatu) oblicza się ze wzoru:
′ =
+
′
D
D
q
p
w
2
b
gdzie:
′
D
p
- największy obliczony wymiar graniczny półwyrobu,
D
w
- największy wymiar graniczny przedmiotu wg. rysunku,
2
′
q
b
- całkowity obliczony naddatek na obróbkę (na średnicy).
Przyjmuję się najbliższą średnicę
′′
D
p
pręta w danym asortymencie. Całkowity naddatek na
obróbkę
wynosi wtedy
2
′′
q
b

Obliczanie naddatków na obróbkę
12
2
′′ = ′′ −
q
D
D
b
p
w
m
Czyli średnica wału przed obróbką zgrubną powinna wynosić co najmniej
φ26.6. Dobierając
półfabrykat np. z pręta walcowanego należy wybrać średnicę pierwszą większą z dostępnych,
tu
φ28.
W przypadku obliczania naddatku na obróbkę zgrubną wartości T
a
, (H
śra
+B
1a
) i
ρ
a
odnoszą się
do półfabrykatu.
Przykład 1
Przykład ten przedstawia sposób wyliczania tolerancji wg. wzorów zawartych w
książce w rozdziale 5. Posługując się tablicami zawartymi w tej książce określimy tolerancję
dla toczenia wstępnego, dokładnego i bardzo dokładnego przy obróbce sztywnych wałków
(L<5d) ze stali walcowanej zwykłej dokładności o średnicy 50 i 150 mm.
Przy obliczeniach przyjmujemy dla stali 20:
H
B
n
max
= 24330 ,
(str. 204 tabl. I-12)
H
B
n
min
= 19600
1. Obliczenia dla średnicy 50 mm dają następujące wyniki:
wartość całkowita odchyleń przestrzennych nie obrobionego półfabrykatu: wygięcie
u
= ⋅
=
2 125 250
µ
(tabl. 18); błąd nakiełkowania
ε
µ
n
m
= 425
(tabl. 18);
r
r r
ρ
ε
µ
a
n
u
m
= +
=
⋅
+
⋅
=
$
.
.
0 96 425 0 4 250 508
błąd ustawienia w sztywnych kłach
ε
u
= 0 .
Głębokość skrawania równa się połowie naddatku na obróbkę
(
)
g
T
H
B
m
a
śra
a
a
u
max
.
.
(
)
=
+
+
+
+
=
⋅
+
+
+
=
=
0 5
0 5 1600
150 150
500 1600
16
1
ρ
ε
µ
mm
.
(tabl.18).
g
g
T
a
min
max
.
.
.
=
−
=
−
=
2
16
16
2
0 8 mm
Sztywność obrabiarki:
a) w położeniu suportu przy koniku
′ =
j
obr
kG
mm
1000
b) w środkowym położeniu suportu
′′ =
j
obr
kG
mm
1333
Podatność obrabiarki:
a) w położeniu suportu przy koniku
′ =
=
m
kG
1000
1000
1
µ
W
b) w środkowym położeniu suportu
′′ =
=
m
kG
1000
1333
0 75
.
µ
W
P
C
g
p H
y
y
x
y
B
n
max
max max
max
.
.
.
.
.
=
=
⋅
⋅
⋅
0 0027 16
0 35
24330 45 5
0 9
0 75
,
≈
,
≈
kG
P
C
g p H
y
y
x
y
B
n
min
min min
min
.
.
.
.
.
=
=
⋅
⋅
⋅
0 0019 0 8
0 35
19600 13 9
0 9
0 75
kG
Podatność układu w położeniu suportu przy koniku równa się podatności obrabiarki
[ ]
′ = ′ =
=
W
W
W
uk
m
kG
ł
max
1
µ
Podatność układu w środkowym położeniu suportu
′′ = ′′ +
W
W
W
uk
p
ł
Sztywność półwyrobu w środkowym położeniu suportu
j
EJ
l
p
=
=
⋅ ⋅
⋅
⋅
=
4 8
4 8 2 10 0 05 5
25
19200
3
6
4
3
.
.
.
kG
W
j
p
p
m
kG
=
=
=
1000
1000
19200
0 05
.
µ
Podatność układu w środkowym położeniu suportu
W
W
W
uk
p
m
kG
ł
.
.
.
= ′′ +
=
+
=
0 75 0 05 0 8
µ
W
m
kG
min
.
= 0 8
µ

Obliczanie naddatków na obróbkę
13
∆y P
W
P
W
m
y
y
=
−
=
⋅ −
⋅
≈
max
max
min
min
.
.
.
.
45 5 1 139 0 8 34 4
µ
Błąd nastawienia obrabiarki
∆n
m
= 50
µ
Wielkość zużycia noża
∆z = 60 m
µ
(tabl. 43)
Bicie wrzeciona powodujące stożkowatość - 5
µm.
Błąd obrotu wrzeciona powodujący owalność - 8
µm.
Σ∆
obr
m
= + =
5 8 13
µ
Przy zgrubnym toczeniu wymiar może być utrzymany z tolerancją
(
) (
)
T
y
n
z
obr
≈
+
+
+
≈
+
+
+
≈
2
2 34 4
50
60 13
280
2
2
2
2
∆
∆
∆
Σ∆
.
.
µ
m
Przy dokładnym toczeniu mamy
(
)
[
]
(
)
[
]
ρ
ρ
=
+
−
=
⋅
⋅
+
−
C
p H
g
g
W
y
y
B
n
a
x
x
max
max
min
min
max
.
.
.
.
.
.
.
.
.
0 0027 0 35
24330 0 8 0 5
0 8
1 133
0 75
0 9
0 9
µ
⋅ =
(
)
g
max
.
.
.
.
=
⋅
+
+
+
=
≈
0 5 280
50 50
133 2533 0 25
mm
g
min
.
=
−
=
=
250
110 011
280
2
mm
P
C
g
p H
y
y
x
y
B
n
max
max max
max
.
.
.
.
.
=
=
⋅
⋅
⋅
0 0025 0 25
0 2
24330 5 3
0 9
0 75
.
≈
.
≈
kG
P
C
g p H
y
y
x
y
B
n
min
min min
min
.
.
.
.
.
=
=
⋅
⋅
⋅
0 00215 011
0 2
19600 17
0 9
0 75
kG
∆y P
W
P
W
m
y
y
=
−
=
⋅ −
⋅
=
max
max
min
min
.
.
.
.
5 3 1 17 0 8 39
µ
Błąd nastawienia
∆n
m
= 20
µ
.
Wielkość zużycia narzędzia
∆z = 40 m
µ
(tabl. 47).
Przy dokładnym toczeniu wymiar może być utrzymany z tolerancją
(
)
T
m
≈
+
+
+
=
≈
2 39
20
40 13
146 150
2
2
.
µ
Dla bardzo dokładnego toczenia wartość
ρ jako małą pomijamy.
g
m
max
.
(
)
.
=
mm
⋅
+
+
=
=
0 5 150
15 25
115
011
µ
g
m
min
.
=
−
=
=
115
40
0 04
150
2
µ
mm
.
.
P
y max
.
.
.
.
.
=
⋅
⋅
⋅
≈
0 0036 011
0 08
24300 2 4
0 9
0 75
kG
P
y min
.
.
.
.
.
=
⋅
⋅
⋅
≈
0 0031 0 04
0 08
19600 0 9
0 9
0 75
kG
∆y
m
=
⋅ −
⋅
≈
2 4 1 0 9 0 8 17
.
.
.
.
µ
Błąd nastawienia
∆n
m
= 15
µ
.
Wielkość zużycia narzędzia
∆z
m
= 20
µ
.
Przy bardzo dokładnym toczeniu wymiar może być utrzymany z tolerancją
(
)
T
m
≈
+
+
+
=
≈
2 17
15
20 13
96 100
2
2
.
µ
Obliczenia dla średnicy 150 mm dają następujące wyniki:
Wygięcie półwyrobu nieobrobionego: u
m
= ⋅
=
2
750
750
2
µ
(tabl. 18);
błąd nakiełkowania:
ε
µ
n
m
= 820
(tabl. 18)
r
r
r
r
r
ρ ε
µ
=
+ ≈
+
≈
n
u
m
820 750 1090
g
max
.
(
)
=
⋅
+
+
+
=
≈
0 5 3200
150 150
1090 2990 3mm (tabl. 18)
g
min
.
.
= −
=
3
1
3 2
2
4 mm
Sztywność obrabiarki:
a) w położeniu suportu przy koniku:
′ =
j
obr
kG
mm
1500
;
′ =
W
m
kG
0 66
.
µ
b) w środkowym położeniu suportu:
′′ =
j
obr
kG
mm
2000
;
′′ =
m
kG
0 5
.
µ
W
Sztywność układu obrabiarka-przedmiot obrabiany:

Obliczanie naddatków na obróbkę
14
a) w położeniu suportu przy koniku:
′ =
j
obr
kG
mm
1500
;
′ =
W
m
kG
0 66
.
µ
; W
m
kG
max
.
= 0 66
µ
b) w środkowym położeniu suportu:
j
EJ
l
p
kG
mm
=
=
⋅ ⋅
⋅
⋅
=
4 8
4 8 2 10 0 05 15
75
57600
3
6
4
.
.
.
W
m
p
= 0 017
.
µ
Podatność układu w środkowym położeniu suportu
W
W
W
uk
obr
p
m
kG
ł
.
.
.
=
+
=
+
=
0 5 0 017 0 517
µ
W
m
kG
min
.
= 0 52
µ
P
y max
.
.
.
.
=
⋅
⋅
⋅
=
0 00305 3
0 4
24330 100 4
0 9
0 75
.
.
kG
P
y min
.
.
.
.
.
=
⋅
⋅
⋅
=
0 00215 14
0 4
19600 28 7
0 9
0 75
kG
∆y P
W
P
W
m
y
y
=
−
=
⋅
−
⋅
=
max
max
min
min
.
.
.
.
.
100 4 0 66 28 7 0 52 5134
µ
Błąd nastawienia
∆n
m
= 50
µ
.
Wielkość zużycia narzędzia
∆z = 80 m
µ
(tabl. 43).
Bicie wrzeciona: 10
µm.
Błąd obrotu wrzeciona: 10
µm. Stąd Σ∆
obr
m
=
+
=
10 10 20
µ
Przy toczeniu zgrubnym wymiar może być utrzymany z tolerancją
(
)
T
m
≈
+
+
+
=
≈
2 5134
50
80 20
338 6 340
2
2
.
.
µ
Dla dokładnego toczenia mamy
[
]
ρ
µ
=
⋅
⋅
+
−
=
0 0035 0 4
24330 14 11
14
0 66 23
0 75
0 9
0 9
.
.
( .
. )
.
.
.
.
.
m
g
m
max
.
(
)
.
=
m
⋅
+
+
+
=
≈
0 5 340
50 50
23 293 0 3
g
m
min
.
=
−
=
=
300
130 013
340
2
m
.
.
P
y max
.
.
.
.
.
=
⋅
⋅
⋅
=
0 00292 0 3
0 25
24330 8 8
0 9
0 75
kG
P
y min
.
.
.
.
.
=
⋅
⋅
⋅
=
0 0025 013
0 25
19600 2 7
0 9
0 75
kG
∆y
m
=
⋅
−
⋅
=
8 8 0 66 2 7 0 52 4 4
.
.
.
.
.
µ
Błąd nastawienia:
∆n
m
= 20
µ
.
Wielkość zużycia narzędzia
∆z = 40 m
µ
(tabl. 47).
Przy dokładnym toczeniu wymiar może być utrzymany z tolerancją
(
)
T
m
≈
+
+
+
=
2 4 4
20
40 20
160
2
2
.
µ
Dla bardzo dokładnego toczenia mamy
[
]
ρ
µ
=
⋅
⋅
+
−
⋅
=
0 00292 0 25
24330 013 0 023
013
0 66 0 5
0 75
0 9
0 9
.
.
( .
.
)
.
.
.
.
.
.
m
g
m
max
.
(
)
.
.
.
=
⋅
mm
+
+
+
=
≈
0 5 160
15 25
0 5 120 5
012
µ
g
m
min
.
=
−
=
=
120
40
0 04
160
2
µ
mm
.
.
P
y max
.
.
.
.
.
=
⋅
⋅
⋅
=
0 0042 012
01
24330 2 5
0 9
0 75
kG
P
y min
.
.
.
.
.
=
⋅
⋅
⋅
=
0 0036 0 04
01
19600 0 74
0 9
0 75
kG
∆y
m
=
⋅
−
⋅
=
2 5 0 66 0 74 0 52 13
.
.
.
.
.
µ
Błąd nastawienia:
∆n
m
= 15
µ
.
Wielkość zużycia narzędzia
∆z
m
= 20
µ
.
Błędy geometryczne obrabiarki
Σ∆
obr
m
= 20
µ
.
Przy bardzo dokładnym toczeniu wymiar może być utrzymany z tolerancją
Obliczanie naddatków na obróbkę
15
(
)
T
m
≈
+
+
+
=
2 13
15
20 20
110
2
2
.
µ
Tolerancje wymiarów średnic półwyrobów nie obrobionych oraz półwyrobów obrobionych
wstępnie, dokładnie i bardzo dokładnie podane są w tabeli 1.
Tabela 1
Metody obróbki
Tolerancje na średnicy w µm
Stosunek
50 mm
150 mm
Walcowanie zwykłej dokładności 1600 3200
2,0
Toczenie zgrubne
280
340
1,2
Toczenie dokładne 150
160
1,1
Toczenie bardzo dokładne 100
110
1,1
Przykład 2
Dany jest np. wałek, którego wymiar rysunkowy wynosi 27.35
-0.014
, a całkowita
długość - 100 mm. Wyjściowym półfabrykatem jest w tym wypadku stal kalibrowana
ciągniona o wysokiej dokładności (3 klasa). Naddatek na szlifowanie bezkłowe po obcięciu
(przed obróbką cieplną) oblicza się wg. wzoru
(
) (
)
2
2
2
1
q
T
H
B
b
a
śra
a
a
ub
=
+
+
+
+
r
r
ρ
ε
$
Ponieważ jednak przy obróbce na szlifierce bezkłowej nie występuje błąd zamocowania, więc
powyższy wzór przyjmie postać
(
)
2
2
1
q
T
H
B
b
a
śra
a
a
=
+
+
+
ρ
2
Zgodnie z tablicą 14 obliczamy wartość
ρ
a
ρ
µ
a
u
u l
m
=
⋅ =
⋅
=
∆
15 50 75
.
Podstawiając do wzoru tę wartość oraz odpowiednie wartości pozostałych składników
naddatku podane w tej tablicy, otrzymamy
2
45 2 40 40
2 75 355
q
m
b
=
+
+
+ ⋅
=
(
)
µ
Naddatek na szlifowanie bezkłowe po obróbce cieplnej (tabl. 54) wynosi
2
2
q
T
H
b
a
śra
a
2
=
+
+
ρ
2
45 2 10 2 0 9 50 155
q
m
b
=
+ ⋅
+ ⋅
⋅
=
.
µ
Naddatek na szlifowanie bardzo dokładne
2
21 2 3 2 0 06 50 33
q
m
b
=
+ ⋅ + ⋅
⋅
=
.
µ
Całkowity naddatek na obróbkę
2
355 155 33 543
′ =
+
+
=
q
m
b
µ
Największy wymiar półwyrobu wyniesie
′ =
+
=
D
m
p
27 35 0 543 27 893
.
.
.
m
m
Przyjmując
, otrzymamy całkowity naddatek na obróbkę
′′ =
D
m
p
28
2
28 27 35 0 65
′′ =
−
=
q
m
b
.
.
m
Przykład 3
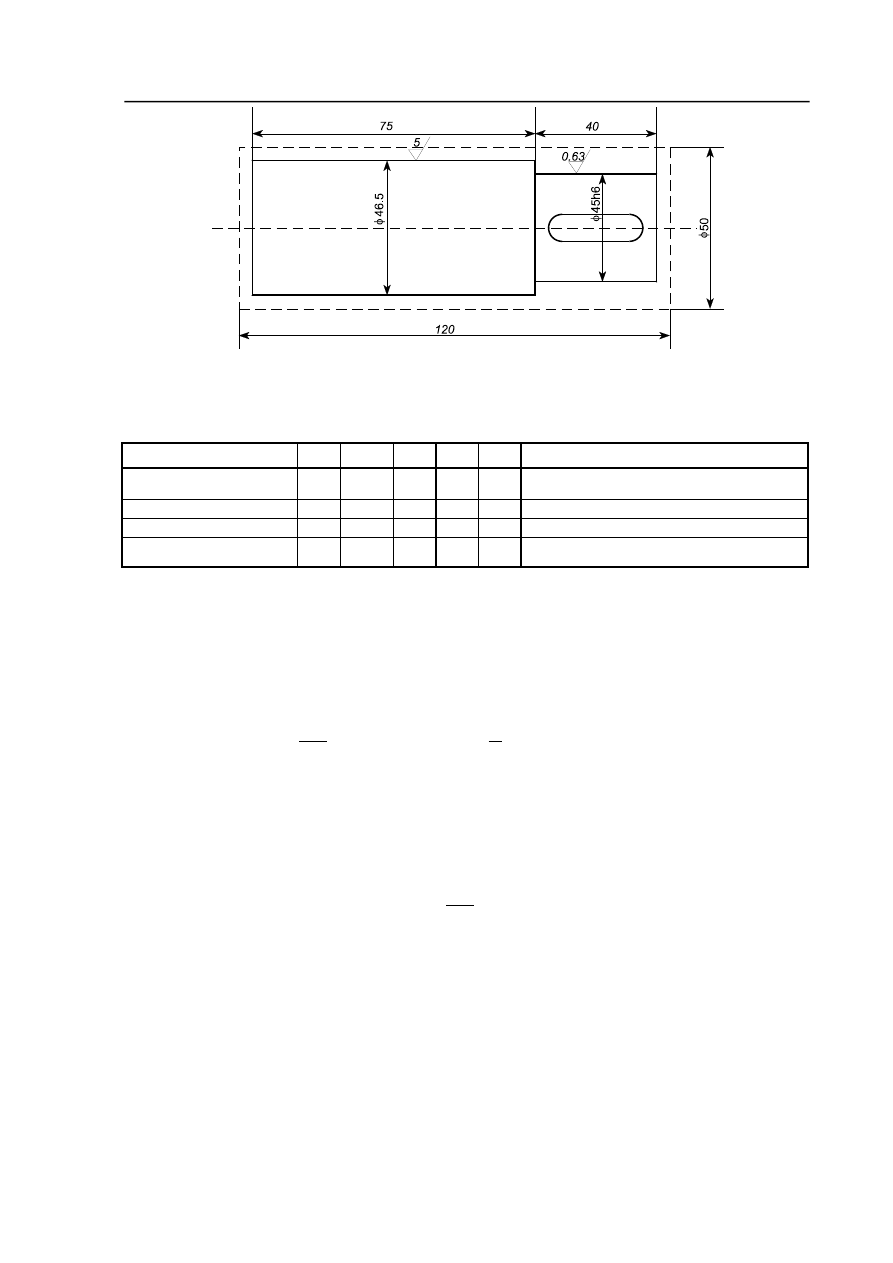
Dla przedmiotu podanego na rysunku 1 należy dla powierzchni
φ45h6 obliczyć
całkowity naddatek. Za wyjściowy półfabrykat przyjmijmy pręt walcowany zwykłej
dokładności ze stali. Dla wykonania tej powierzchni należy przeprowadzić obróbkę zgrubną,
dokładną (kształtującą), szlifować zgrubnie i wykańczająco, stąd wzór na całkowity naddatek
przyjmie postać
2
2
2
2
2
q
q
q
q
q
b
bzgr
bdok
bszlzgr
bszlwyk
=
+
+
+
Obliczanie naddatków na obróbkę
16
Rysunek 1
Zestawmy potrzebne do obliczeń parametry w tabeli.
Tabela 2
Oznaczenia
T
a
H
śra
B
a
1
ρ
a
ε
ub
Uwagi
Toczenie zgrubne
1600 150 150
861.2 120
∆u=12µm bez prostowania (∆u=2µm. po prostowaniu)
błąd nakiełkowania
ε
n
=425
µm
Toczenie kształtujące
340 50 50 25 0
Szlifowanie zgrubne
170 15 25 0 0
Szlifowanie wykańczające
50 10 25
(50?)
1.2 0
∆u=0.03µm
1. Naddatek na toczenie zgrubne
Ponieważ parametry we wzorze mają indeks a (z operacji poprzedzającej), to
parametry te należy odczytać dla półfabrykatu. Dla pręta walcowanego normalnej
dokładności odczytujemy z tablicy 18 dla
φ50 i długości 120. W zależności od
sposobu ustalenia mamy:
• dla ustalenia w uchwycie szczękowym samocentrującym
ρ
=
⋅ =
⋅
=
∆u l
m
u
12
120
2
720
µ
, gdzie l
L
u
=
2
, L - długość przedmiotu obrabianego
Błędy ustalenia odczytujemy z tablic 9, 10, 11. Z tablicy 9 błąd bazowania
ε
b
=0, z
tablicy 10 błąd zamocowania
ε
z
=120
µm (?), stąd
ρ
µ
a
m
= 720
,
ε
µ
ub
m
= 120
.
Naddatek na obróbkę zgrubną
2
1600 2 150 150
2 0 96 720 0 4 120
3678 4
36784
q
m
bzgr
=
+ ⋅
+
mm
+ ⋅
⋅
+
⋅
=
=
(
)
( .
.
)
.
.
µ
• dla ustalenia w kłach stałych
ρ
ε
a
u
n
u l
m
=
⋅
⋅ +
⋅
=
⋅ ⋅
+
⋅
=
0 96
0 4
0 96 12
120
2
0 4 425 8612
.
.
.
.
∆
µ
.
Z tablicy 9 błąd bazowania
ε
b
=0, z tablicy 10 błąd zamocowania
ε
z
=0
µm, stąd
ε
µ
ub
m
= 0
. Naddatek na obróbkę zgrubną
2
1600 2 150 150
2 8612 3922 4
39224
q
m
bzgr
=
+ ⋅
+
mm
+ ⋅
=
=
(
)
.
.
.
µ
2. Naddatek na toczenie kształtujące
Tu odczytujemy wartości parametrów z poprzedniej operacji, czyli po toczeniu
zgrubnym z tabeli 44 (lub tabeli 43). Dla toczenia w kłach z zabierakiem
ε
µ
ub
m
= 0
.
Naddatek na toczenie kształtujące
2
340 2 50 50
2 25 590
0 59
q
m
bdok
=
mm
+ ⋅
+
+ ⋅
=
=
(
)
.
µ

Obliczanie naddatków na obróbkę
17
3. Naddatek na szlifowanie zgrubne kłowe
Tu odczytujemy wartości parametrów z poprzedniej operacji, czyli po toczeniu
kształtującym z tabeli 47. Dla szlifowania kłowego
ε
µ
ub
m
= 0
. Naddatek na
szlifowanie zgrubne
2
170 2 15 25
250
0 25
q
m
bszlzgr
=
+ ⋅
+
mm
=
=
(
)
.
µ
4. Naddatek na szlifowanie wykańczające
Tu odczytujemy wartości parametrów z poprzedniej operacji, czyli po szlifowaniu
zgrubnym z tabeli 54.
ρ
µ
a
u
u l
m
=
⋅ =
⋅
=
∆
0 03 40 12
.
.
Naddatek na szlifowanie wykańczające
2
50 2 10 25
2 12 122 4
01224
q
m
bszlwyk
=
mm
+ ⋅
+
+ ⋅
=
=
(
)
.
.
.
µ
Naddatek całkowity
2
3922 4 590 250 122 4 4884 8
4885
q
m
b
=
+
m
+
+
=
≈
.
.
.
µ
µ
(dla zgrubnej w kłach)
2
3678 4 590 250 122 4 4640 8
4641
q
m
b
=
+
m
+
+
=
≈
.
.
.
µ
µ
(dla zgrubnej w uchwycie)
Wyszukiwarka
Podobne podstrony:
07 naddatki
Naddatki na szlifowanie otworów
Naddatki
przykladowy projekt 3, naddatki, Obliczam naddatki na obróbkę
6 Rodzaje naddatków
OPTYMALIZACJA NADDATKÓW OBRÓBKOWYCH
Naddatki na wytaczanie
naddatki międzyoperacyjne
TABELA NADDATKOW czysta, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Semest
naddatki
Naddatki na szlifowanie klowe
Naddatki na toczenie kształtujące
odlew naddatkizgóry
Dobór naddatków na obróbkę elementu odlewanego - Projekt, Uczelnia, Technologia budowy maszyn
Naddatki na obróbkę powierzchni zewnętrznych, OPERATOR OSN CNC, Obróbka skrawaniem, Obróbka skrawani
TABELA NADDATKOW, Studia, ZiIP, SEMESTR VI, Technologia maszyn
Dobór naddatków i program obróbki wałka wielostopniowego, Projektowanie procesów technologicznych
NADDATKI OPERACYJNE
TABELA NADDATKOW, POLITECHNIKA ŚLĄSKA Wydział Mechaniczny-Technologiczny - MiBM POLSL, Semestr 6, Se
więcej podobnych podstron