Algorytmy i struktury danych
Ćwiczenie 4
Algorytmy rekurencyjne
1. F
UNKCJE W JĘZYKU
C++
W języku C++ istnieje możliwość posługiwania się podprogramami, które możemy
traktować jako małe programy w programie głównym. W języku C++ wszystkie
podprogramy nazywane są funkcjami. Funkcję wywołuje się poprzez podanie jej nazwy
oraz argumentów, które umieszczamy w nawiasach. Każda funkcja ma swoją nazwę,
która ją identyfikuje. Tak samo jak nazwy zmiennych, wszelkie nazwy – przed pierwszym
odwołaniem się do nich – muszą zostać zadeklarowane.
A) Deklaracja funkcji
B) Wywołanie funkcji w programowe głównym
int main(int argc, char *argv[])
{
float Wynik;
Wynik = suma(1.0, 13.23);
cout << ”suma wynosi:” << Wynik << endl;
return EXIT_SUCCESS;
}
C) Definicja funkcji
float suma(float a, float b)
{
float s;
s = a+b;
return s;
}
float suma (float a, float b);
Algorytmy i struktury danych
Ćwiczenie 4
Algorytmy rekurencyjne
2. F
UNKCJE REKURENCYJNE
Funkcję nazywamy rekurencyjną, jeśli wywołuje ona sama siebie.
Z
ADANIE
Zaproponuj rekurencyjny algorytm obliczania silni dla dowolnej liczby całkowitej
dodatniej n.
Wskazówka:
n
n
n
n
n
1
dla
)!
1
(
0
dla
1
!
R
OZWIĄZANIE
//Program glowny:
int main(int argc, char *argv[])
{
int n;
cout<<"Podaj liczbe naturalna: ";
cin>>n;
co
ut<<"Silnia wynosi: "<<silnia(n)<<"\n";
return EXIT_SUCCESS;
}
#
include <iostream>
using namespace std;
//Funkcja rekurencyjna:
long silnia(int n)
{
long s;
if(n==0)
{
s=1;
}
else
{
s=n*silnia(n-1);
}
return s;
}
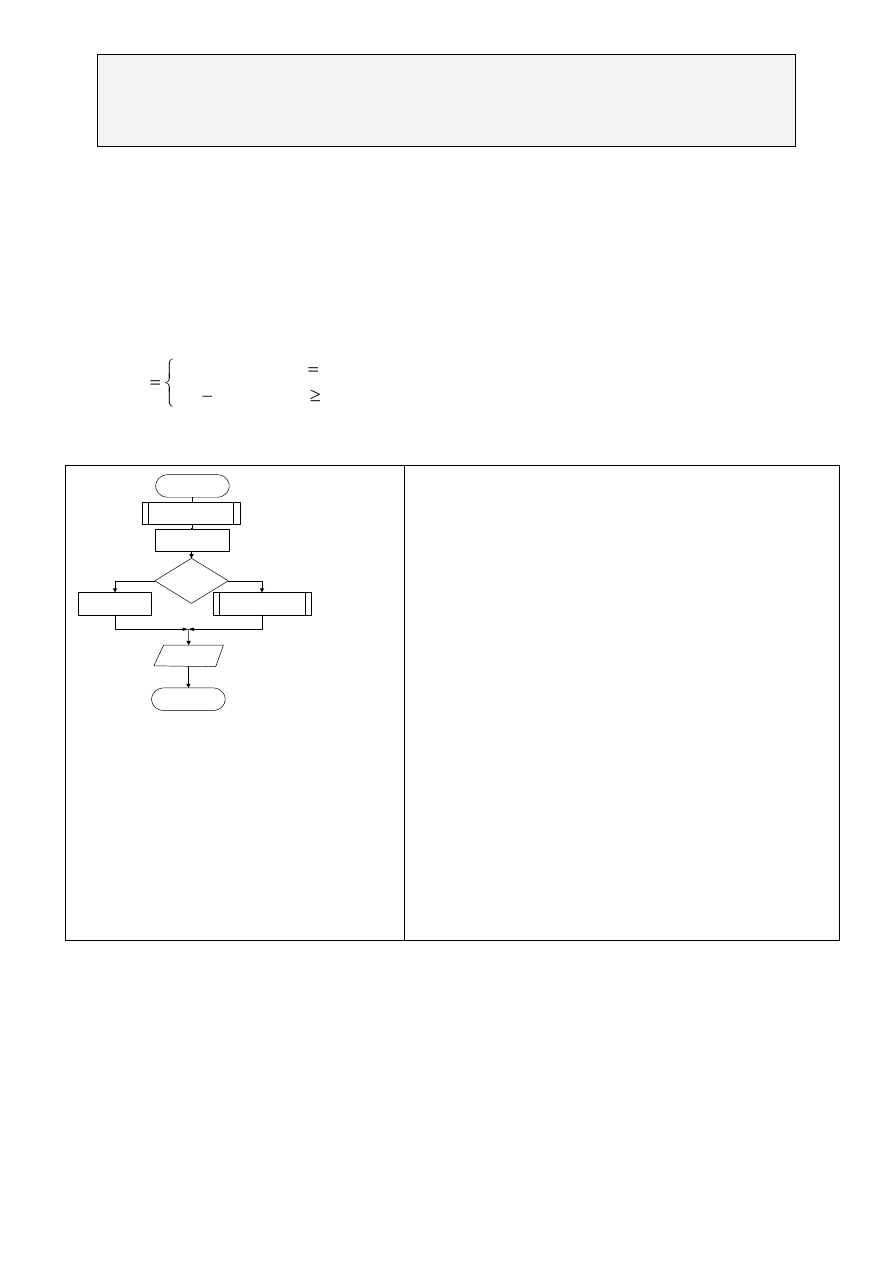
START
n==0
s=1
s= n *silnia(n-1)
zwracaj(s)
STOP
T
N
long s
long silnia( int n)
Rys. Schemat blokowy dla funkcji rekurencyjnej
silnia.
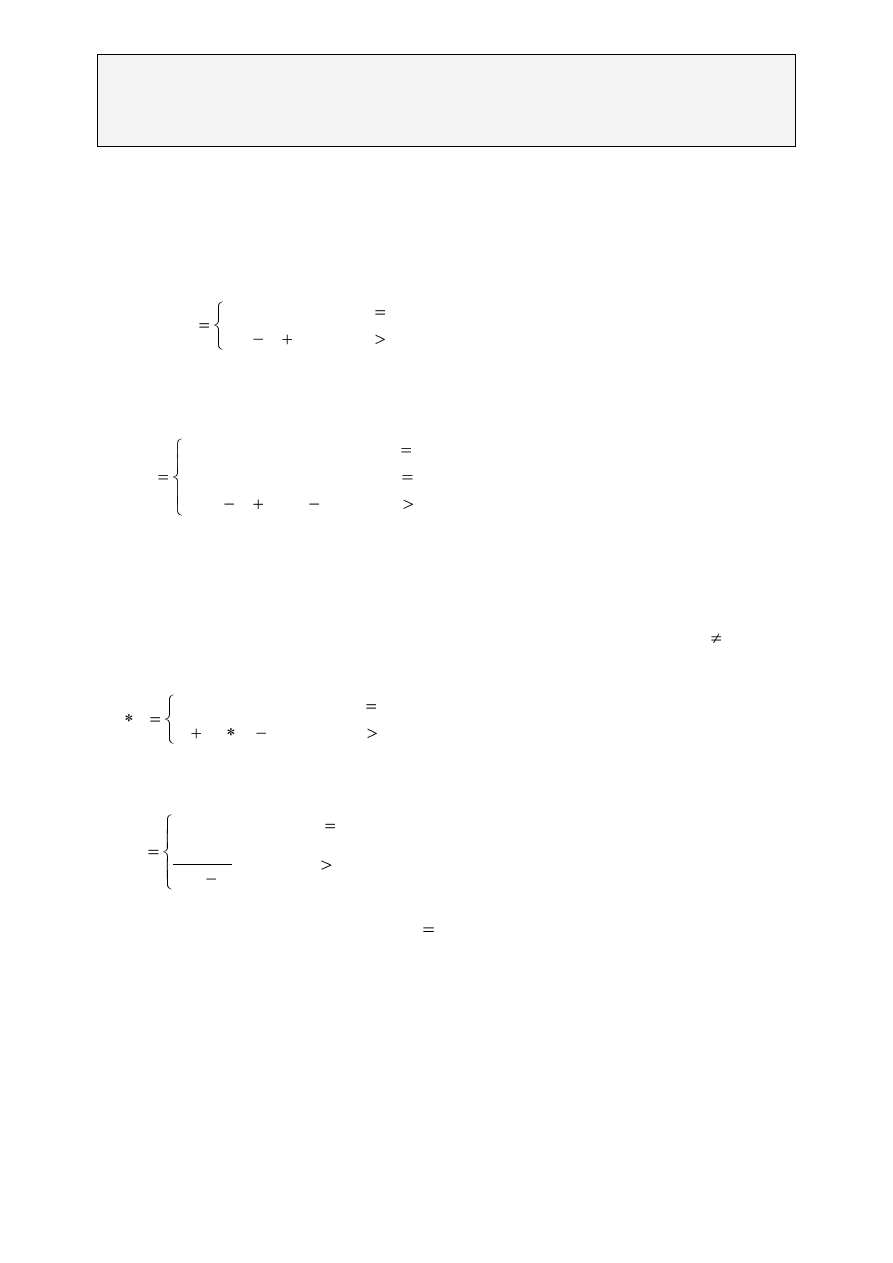
Algorytmy i struktury danych
Ćwiczenie 4
Algorytmy rekurencyjne
Z
ADANIA
Zadanie 1.
Dany jest ciąg o wyrazie ogólnym
)
(n
L
zdefiniowany rekurencyjnie:
.
0
dla
)
1
(
,
0
dla
1
)
(
n
n
n
L
n
n
L
Zaproponuj rekurencyjny algorytm obliczania n-tego wyrazu ciągu L(n).
Zadanie 2.
Zaproponuj rekurencyjny algorytm obliczania elementów ciągu Fibonacciego:
1
dla
)
2
(
)
1
(
1
dla
1
0
dla
0
)
(
n
n
fib
n
fib
n
n
n
fib
Narysuj drzewo wywołań funkcji rekurencyjnej
)
(n
fib
dla n=5.
Co można powiedzieć o efektywności rekurencyjnego rozwiązania powyższego problemu?
Zadanie 3.
Napisz rekurencyjny algorytm mnożenia dwóch liczb naturalnych m i n (gdzie
0
, n
m
).
Wskazówka: Korzystamy z definicji mnożenia:
n
n
m
m
n
m
n
m
1
dla
)]
1
(
[
1
dla
Zadanie 4.
Dany jest ciąg
)
(n
Q
zdefiniowany rekurencyjnie:
0
dla
)
1
(
0
dla
1
)
(
n
n
Q
n
n
n
Q
Napisz rekurencyjny algorytm obliczania n-tego wyrazu ciągu
)
(n
Q
. Narysuj drzewo
wywołań funkcji rekurencyjnej
)
(n
Q
dla
4
n
.
Zadanie 5.
Zaproponuj rekurencyjne rozwiązanie algorytmu Euklidesa obliczającego największy
wspólny dzielnik dwóch liczb naturalnych.