III.

A

RYTMETYKA LICZB DWÓJKOWYCH

Są dwa podstawowe problemy arytmetyki komputera: sposób reprezentowania liczb (w formacie

binarnym) oraz algorytmy podstawowych operacji arytmetycznych (dodawania, odejmowania, mnożenia,

dzielenia). Obydwa te problemy dotyczą zarówno arytmetyki stałoprzecinkowej (calkowitoliczbowej), jak

i zmiennoprzecinkowej (zmiennopozycyjnej) – wyrażane jako liczba (mantysa) pomnożona przez stałą

(podstawę) podniesioną do pewnej potęgi (wykładnik) i implementowane normą IEEE-754.

Kluczowym problemem arytmetyki komputerowej jest wybór dwóch bardzo różnych

reprezentacji liczb: stałoprzecinkowych i zmiennoprzecinkowych.

3.1.

P

ODSTAWOWE POJĘCIA

.

ARYTMETYKA LICZB STAŁOPRZECINKOWYCH

3.1.1.

D

ODAWANIE

W stosunku do liczb dziesiętnych arytmetyka dwójkowa jest istotnie łatwiejsza ponieważ mamy do

czynienia tylko z czterma kombinacjami wartości dwóch (a nie dziesięciu) cyfr z którymi mogą

wypełniać się operacji arytmetyczne: 0 i 0, 0 i 1, 1 i 0 oraz 1 i 1. Dodawanie tych cyfr (0+0, 1+0, 0+1,

1+1) pokazano w tabl. 3.1, a z uzgodnieniem przeniesienia – w tabl. 3.2.

Tabl.

3.1

Tabl.

3.2

A B C

in

C

out

A+B

Jak jest pokazane wyżej, przedstawione liczby np.: 8-bitowe jako słowa w kodzie prostym wartości tych

liczb są tak naprawdę zapisane na 7 bitach, bowiem najbardziej znaczący bit służy do przechowywania

informacji o znaku (+ → 0, – → 1), a pozostałe bity – to wartość bezwzlędna liczby. Oznacza to, że

największą liczbą całkowitą 8-bitowego słowa jest

1

2

7

−

, czyli + 127 → 01111111, a najmnięszą liczbą,

czyli – 127 → 11111111.

Np.

+22

10

⇒ 00010110

2

natomiast

–22

10

⇒ 10010110

2

.

Dodawanie liczb dwójkowych zapisanych w kodzie prostym odbywa się podobnie jak przy dodawaniu

liczb w systemie dziesiętnych. Np. 26

10

+ 27

10

odpowiednio 00011010

2

+ 00011011

2

:

2

1

6

10

0

0

0

1

1

1

10

1

1 0

2

2 7

10

0 0 0 1 1 0 1 1

2

53

10

0 0 1 1 0 1 0 1

2

A B

A+B

0 0

00

0 0 0
0 0 1

0 0

0 1
1 0
1 1

01
01
10

0 1

0 1 0

0 1

0 1 1

1 0

1 0 0

0 1

1 0 1
1 1 0
1 1 1

1 0
1 0
1 1

+ +

Błąd przepełnienia wystąpi dopiero gdy pojawi się 1 przeniesienia na 8-j pozycji tzn. pozycji znaku. Taki

błąd wystąpi również przy odejmowaniu gdy zachodzi pożyczka z odejmnej albo gdy odjemnik jest

większy od odjemnej (wtedy konieczna jest zmiana znaku) i w wyniku otrzymujemy nieprawidłową

różnicę. Podobne kłopoty znikają przy zastosowaniu metod kodowania opartych na dopełnieniu do

podstawy systemu liczbowego.

Dla dodawania operandów dwójkowych z dowolnym znakiem wykorzystuje się odwrotne

(uzupełnienie do 1) i uzupełnieniowe (uzupełnienie do 2) kodowanie.

Odwrotny kod

2

A ujemnej liczby

otrzymuje się w sposób negacii (inwertowania) wszystkich cyfr w

każdej pozycji danej liczby czyli przez zamiany 0 na 1, a 1 na 0 oprócz znakowej cyfry. Np. odwrotny

kod

2

A

2

A

ujemnej liczby

= 1.010110

2

A

2

równa się

2

A

= 1.101001

2

.

Przy operacji odejmowania

2

2

2

2

B

A

B

A

+

=

−

, może się pojawić 1 przeniesienia do następnej wyższej

znakowej pozycji (gdzie może być tylko jedna pozycja) co wymusza do wykonania tz. przeniesienia

cyklicznego – dodawania tej 1 do LSB liczby otrzymanej sumy. Przeniesienie cykliczne jest technicznie

nie wygodne, poniewaz zabiera zbyt dużo czasu na realizację operacji dodawania. Zatem w wypadku

dodawania liczb ujemnych przewagę ma kod uzupełnieniowy

, który wyprowadza się z kodu

odwrotnego

2

~

A

2

A w sposób dodawania 1 do LSB, a mianowicie jako

1

~

2

2

+

= A

A

. Więc operacja

odejmowania liczb dwójkowych przeprowadza się następująco:

2

2

~

2

2

2

2

2

2

~

1

)

(

2

2

B

A

B

A

B

A

B

A

B

B

+

⇒

+

+

⇒

−

+

=

−

,

2

B

⇒

i

– operatory przetwarzania w kod odwrotny i kod uzupełnieniowy, odpowiednio.

2

~

B

⇒

Jeśli w znakowej pozycji mamy 1 przepełnienia, to ją poprostu pomijamy. Jeśli suma okaże się

ujemna (w znakowej pozycji mamy 1), to znaczy że wynik jest w kodzie uzupełnieniowym, a jeśli 0, to

wynik jest w kodzie prostym. Taka sytuacja zawsze wynika przy ujemnych liczbach sumy, tzn. że jest w

kodzie uzupełnieniowym, a także gdy udejmna jest mniejsza od odjemnika. Ostateczny wynik dodawania

w kodzie prostym otrzymuje się po wypełnieniu wstecznego przetwarzania: do ujemnej sumy

trzeba

dodać (–1) w kodzie uzupełnieniowym (czyli liczbę 1.11

⋅⋅⋅1), a każdą pozycję otrzymanej ujemnej sumy

w kodzie odwrotnym

2

~

S

2

S przeinwertować z czego wyniknie poszukiwana liczba w kodzie zwykłym

.

2

S

Prz.

Znaleźć sumę liczb

i

1010

.

0

2

=

A

0100

.

1

2

=

B

(tutaj kropka umownie rozdziela znak liczby

półbajtowej)

1100

.

1

1011

.

1

0100

.

1

2

2

~

2

B

B

B

⇒

⇒

=

0.

1

1010

1.1100
Odp.

.

0110

.

0

2

2

=

+ B

A

10.0110

Prz.

Znaleźć sumę liczb

i

1010

.

1

2

=

A

0100

.

0

2

=

B

.

0110

.

1

0101

.

1

1010

.

1

2

2

~

2

A

A

A

⇒

⇒

=

1.0

1

110

Otrzymaną sumę

w kodzie uzupełnieniowym przetwarzamy w kod odwrotny,

dodawając do niej liczbę

1.1111:

1010

.

1

2

2

=

+ B

A

Otrzymaną sumę

1001

.

1

2

2

=

+ B

A

w kodzie

odwrotnym przetwarzamy w kod zwykły: 1.1001

⇒ 1.0110.

Odp.

0110

.

1

2

2

=

+ B

A

Prz.

Znaleźć sumę liczb

i

1010

.

1

2

=

A

0100

.

1

2

=

B

.

Z poprzednich przykładów

mamy

liczby

0110

.

1

~

2

=

A

i

, a więc

otrzymujemy:

1.

1100

.

1

~

2

=

B

1

0

1

110 1.

1

0

1

0

1

10

1. 1 1 0 0

1. 1 1 1 1

Postępując tak samo z liczbą 1.0001

⇒ 1.1110

11. 0 0 1 0

11. 0 0 0 1

0.0100
1.1010

1

Odp.

1110

.

1

2

2

=

+ B

A

3.1.2.

M

NOŻENIE

W porównaniu z dodawaniem i odejmowaniem mnożenie jest operacją złożoną niezależnie od tego, czy jest

realizowane sprzętowo, czy przez oprogramowanie. W różnych komputerach wykorzystywano wiele różnych

algorytmów.

Rozpoczniemy od prostego mnożenia dwóch bezznakowych (nieujemnych) liczb całkowitych.

Wykonuje się tak, jak zwykle robi się to za pomocą ołówka i kartki papieru.

Zauważmy: 1) wynikiem mnożenia dwóch n-bitowych binarnych liczb całkowitych jest liczba o

długości do 2n bitów (np. 11x11 = 1001); 2) dla każdej 1 mnożnika są wymagane operacje

sumowania i przesunięcia, jednak dla każdego 0 potrzebne jest tylko przesunięcie.

3.1.3.

D

ZIELENIE

Dzielenie jest nieco bardziej złożone niż mnożenie, jednak opiera się na takich samych zasadach ogólnych.

Jak poprzednio, podstawą algorytmu jest rozwiązanie stosowane przy obliczeniach za pomocą ołówka i

1. 10

1

10

1. 1 1 1 1
11.1 0 0 1

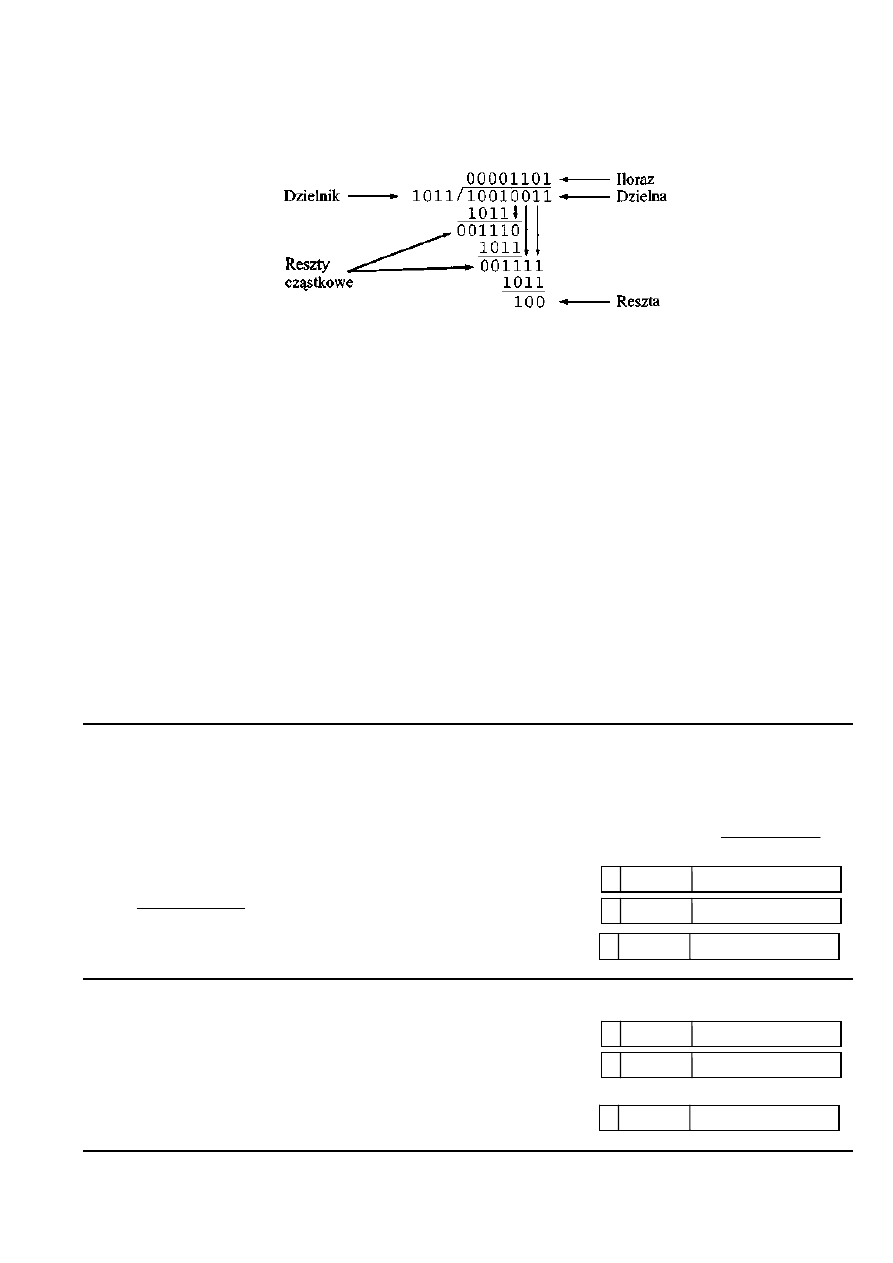
papieru, a sama operacja obejmuje powtarzające się przesuwanie oraz dodawanie lub odejmowanie. Niżej

pokazano przykład długiego dzielenia bezznakowych binarnych liczb całkowitych.

3.2.

A

RYTMETYKA LICZB ZMIENNOPRZECINKOWYCH

W przypadku dodawania i odejmowania konieczne jest zapewnienie, żeby oba argumenty miały taki sam

wykładnik. Może to wymagać przesunięcia przecinka pozycyjnego w jednym z argumentów. Mnożenie i

dzielenie są pod tym względem prostsze. Ponieważ wynikiem którejkolwiek z tych operacji może być utrata

cyfr, przesuwa się raczej mniejszą liczbę; ewentualne stracone cyfry mają stosunkowo małe znaczenie.

Wyrównanie jest osiągane przez powtarzające się przesuwanie mantysy o jedną cyfrę w prawo i odpowiednie

zwiększanie wykładnika, aż do zrównania się wykładników.

Jeśli dodawać za pomocą kartki i ołówka dwie liczby zmiennoprzecinkowe, które mają różne

wartości wykładnika, to musimy najpierw zmienić jedną z nich w taki sposób, aby obie liczby miały taki

sam wykładnik, tzn. znormalizować. Np. 0,5

× 10

2

+ 2,0

× 10

3

= 0,5

× 10

2

+ 20,0

× 10

2

= 20,5

× 10

2

.

Dodawanie i odejmowanie liczb zmiennoprzecinkowych przebiega w taki sam sposób.

Prz.

Znależć sumę

liczb A

2

2

B

A

+

10

= 10,5 i B

B

10

= 2,05.

Dokonując normalizacji z zachowaniem większego wykładnika mamy

A : 10,5

10

⇒ 1010,1

2

; A

2

= 1010,1 = 0,1010100000

× 2

4

1010,1

B: 2,05

10

⇒ 10,000011

2

; B

B

2

= 10,000011

⇒ 0,0010000011 × 2

10,000011

4

wykładnik:

16

+

4

=

20

1100,100011

+

0,1010100000

0 1 0 1 0 0

1 0 1 0 1 0 0 0 0 0

0,0010000011

0,1100100011

+

+

0 1 0 1 0 0

0 0 1 0 0 0 0 0 1 1

0 1 0 1 0 0

1 1 0 0 1 0 0 0 1 1

=

Odp.

= 0,1100100011

× 2

2

2

B

A

+

4

⇒ 12,55

10

Prz.

Znależć iloczyn

2

2

B

A

× liczb A

10

= 10,5 i B

B

10

= 2,05.

A

2

= 1010,1 = 0,1010100000

× 2

4

(16 + 4 = 20)

B

B

2

= 10,000011 = 0,1000001100

× 2 (16

+

2

=

18)

2

0 1 0 1 0 0

1 0 1 0 1 0 0 0 0 0

×

0 1 0 0 1 0

0 0 1 0 0 0 0 0 1 1

0 1 0 1 0 1

1 0 1 0 1 0 0 0 0 1

=

Odp.

= 0,1010100001

× 2

2

2

B

A

×

5

⇒ 21,525

10