2014-01-10
1
1
Architektura Systemów Komputerowych
Wykład 2
Algebra Boole’a, operatory i bramki logiczne.
Logika Boole’a
działania Boolowskie to działania na obiektach, które
mogą przyjmować tylko dwie wartości: PRAWDA lub
FAŁSZ (1 i 0). Ponieważ budowa komputera oparta jest
głównie na systemie binarnym, algebra Boole’a jest
naturalnym sposobem przetwarzania informacji cyfrowej.
wyrażenie boolowskie składa się z jednej lub więcej
zmiennych (argumentów) oraz operatorów
funkcja boolowska składa się z danych wejściowych a
wynik funkcji przyjmuje jeden z dwu stanów: 0 lub 1
Operatory logiczne - proste
AND (i) – koniunkcja, iloczyn logiczny
OR (lub) – alternatywa lub suma logiczna
NOT (nie) – negacja
Operatory boolowskie można charakteryzować
przy pomocy tablicy prawdy lub przy pomocy
działania na dwóch zbiorach
X
Y
Operator AND, iloczyn logiczny
x
y
xy
1
1
1
1
0
0
0
1
0
0
0
0
Obie zmienne muszą być prawdziwe aby
zaistniała prawda
xy
y
x
y
x
y
x
∧
∧
∩
•
X
Y
2014-01-10
2
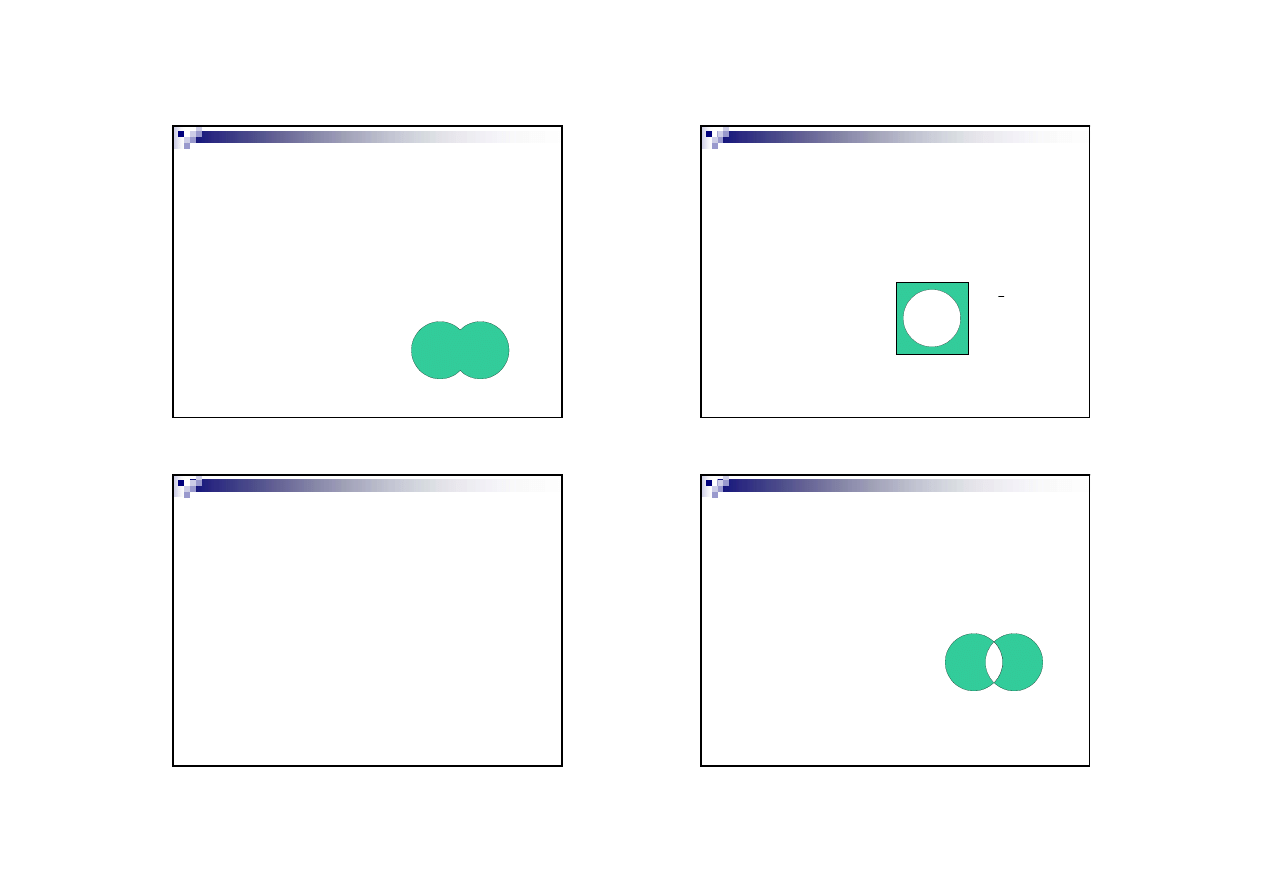
Operator OR, suma logiczna
Przynajmniej jeden argument musi być
prawdziwy aby zaistniała prawda
x
y
x+y
1
1
1
1
0
1
0
1
1
0
0
0
xy
y
x
y
x
y
x
∨
∨
∪
+
X
Y
Operator NOT - zaprzeczenie
jest to przeciwieństwo
x
NOT x
1
0
0
1
x
x
¬
X
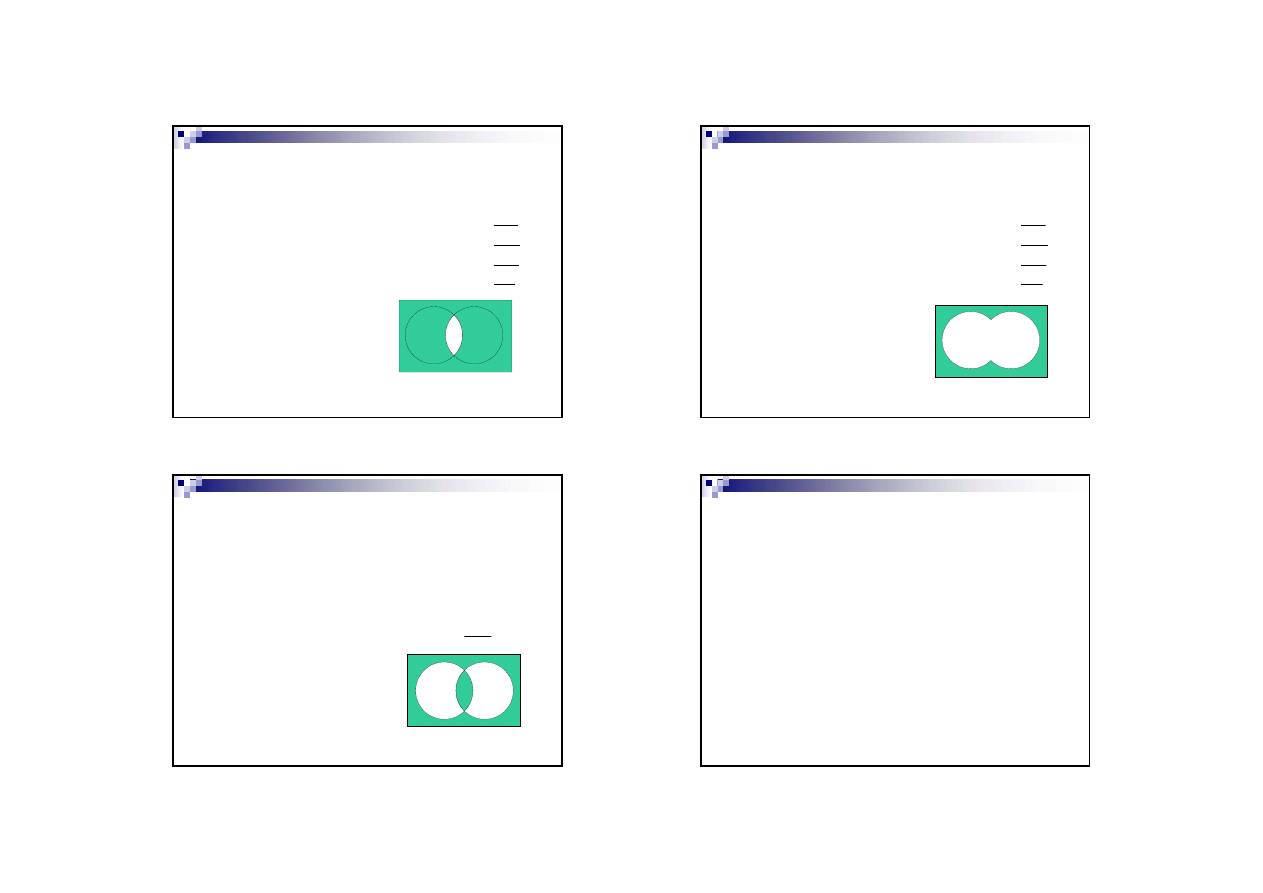
Operatory złożone
XOR - różnica symetryczna, suma rozłączna
NAND – zaprzeczenie iloczynu
NOR – zaprzeczenie sumy
XNOR – zaprzeczenie różnicy symetrycznej
Operator XOR
x
y
xy
1
1
0
1
0
1
0
1
1
0
0
0
X
Y
jeżeli oba argumenty są takie same to wynikiem jest
fałsz
y
x
⊕
2014-01-10
3
Operator NAND
Oznacza działanie: NOT x
•y
NOT AND
x
y
xy
NOT xy
1
1
1
0
1
0
0
1
0
1
0
1
0
0
0
1
X
Y
xy
y
x
y
x
y
x
∨
∨
∪
+
Operator NOR
Oznacza działanie: NOT x
+y
NOT OR
x
y
x+y
NOT x+y
1
1
1
0
1
0
1
0
0
1
1
0
0
0
0
1
xy
y
x
y
x
y
x
∨
∨
∪
+
X
Y
Operator XNOR
Zarówno X i Y ale NIE X lub Y
jeżeli oba argumenty są takie same to wynikiem jest
prawda
x
y
x+y
NOT x+y
1
1
1
1
1
0
1
0
0
1
1
0
0
0
0
1
X
Y
y
x
⊕
Zalety stosowania operatorów złożonych
są szybsze niż stosowanie kilku operatorów prostych
operatory prostsze i złożone wyczerpują cały zakres
możliwych stanów wyjściowych dla dwóch zmiennych o
dowolnych wartościach
x
y
AND
OR
NOT
XOR
NAND NOR
XNOR
1
1
1
1
0
1
0
0
0
1
0
0
1
0
0
1
0
1
0
1
0
1
1
0
1
0
1
0
0
0
0
1
1
1
1
0
2014-01-10
4
Aksjomaty algebry Boole’a i prawa de Morgana
1. Przemienność
2. Łączność
3. Rozdzielczość
4. Tożsamość
5. Komplementarność
A
B
B
A
A
B
B
A
+
=
+
⋅
=
⋅
C)
(B
A
C
B)
(A
C)
(B
A
C
B)
(A
+
+
=
+
+
⋅
⋅
=
⋅
⋅
BC
A
C)
B)(A
(A
C
A
B
A
C)
A(B
+
=
+
+
⋅
+
⋅
=
+
A
A
A
A
A
A
1
1
A
A
1
A
A
0
A
0
0
A
=
+
=
⋅
=
+
=
⋅
=
+
=
⋅
1
A
A
0
A
A
=
+
=
⋅
B
A
B
A
B
A
B
A
+
=
⋅
⋅
=
+
Prawa de Morgana
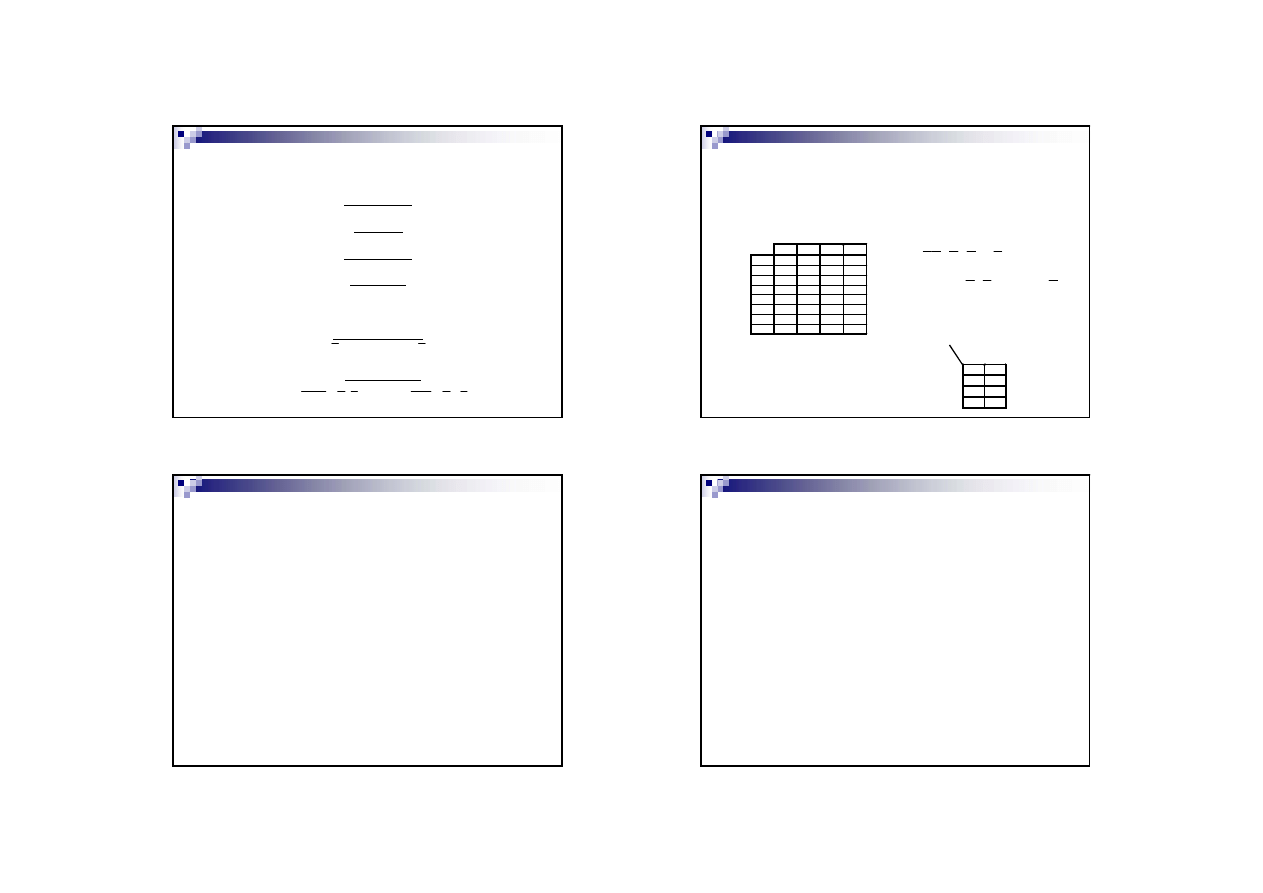
FUNKCJE BOOLE’OWSKIE
Istnieją cztery sposoby przedstawienia tych funkcji:
• tablica prawdy
• postać kanoniczna funkcji
• dziesiętny zapis funkcji
• mapa Karnaugha
)
x
x
)(x
x
x
x
)(
x
x
(x
y
lub
x
x
x
x
x
x
x
x
x
x
x
x
y
2
1
0
2
1
0
2
1
0
2
1
0
2
1
0
2
1
0
2
1
0
+
+
+
+
+
+
=
+
+
+
=
(
)
(
)
∏
∑
=
=
0,4,3
y
lub
1,2,5,6,7
y
X
0
X
1
X
2
f
0
0
0
0
0
1
1
0
0
1
2
0
1
0
1
3
1
1
0
0
4
0
0
1
0
5
1
0
1
1
6
0
1
1
1
7
1
1
1
1
∏
∑
- wskazanie na postać alternatywną
- wskazanie na postać koniunkcyjną
1.
2.
3.
4.
X
2
X
0
X
1
0
1
0
0
0
0
0
1
1
1
1
1
0
1
1
0
1
1
Algebra Boole'a
Algebra Boole'a jest to struktura matematyczna złożona z
uniwersum X, trzech funkcji: działań binarnych +, * i
działania unarnego ~ oraz wyróżnionych elementów 0, 1
spełniających następujące aksjomaty:
Podstawowe aksjomaty Algebry
Boola
Tożsamość
koniunkcja
alternatywa
el. neutralny
1x=x
0+x=x
własność 0 i 1
0x=0
1+x=1
idempotentność
xx=x
x+x=x
uzupełnienie
x¬x=0
x+ ¬x=1
przemienność
xy=yx
x+y=y+x
podwójne zaprzeczenie
¬ ¬ x=x
prawo De Morgana
¬(xy)= ¬x+ ¬y
¬(x+y)= ¬(xy)
Łączność
(xy)z=x(yz)
x+(y+z)=(x+y)+z
Rozdzielność
x+yz=(x+y)(x+y) x(y+z)=xy+xz
Adsorpcja
x(x+y)=x
x+xy=x
UWAGA:
¬(xy) ≠ ¬x¬y
2014-01-10
5
przykłady algebry Boola
Algebra zbiorów. X jest w tym przypadku jakimś ciałem zbiorów.
Działanie + jest to suma zbiorów, * - przekrój zbiorów, a ~ -
dopełnienie. 0 to zbiór pusty, a 1 - cały zbiór X
Rachunek zdań. X to w tym przypadku zbiór formuł logicznych,
działanie * to koniunkcja, + - alternatywa, zaś ~ - negacja. Wreszcie
1 to formuła zawsze prawdziwa, a 0 - zawsze fałszywa (tak
naprawdę elementami X nie są same formuły logiczne, a klasy
abstrakcji ze względu na relację: formuła f jest równoważna formule
g, jeśli dla tych samych podstawień zmiennych ich wartość logiczna
jest taka sama).
Podstawowe działania logiczne i
ich własności
Bramki logiczne
element konstrukcyjny maszyn i mechanizmów (dziś zazwyczaj: układ
scalony, choć podobne funkcje można zrealizować również za pomocą
innych rozwiązań technicznych, np. hydrauliki czy pneumatyki), realizujący
fizycznie pewną prostą funkcję logiczną, której argumenty (zmienne
logiczne) oraz sama funkcja mogą przybierać jedną z dwóch wartości, np. 0
lub 1
Podstawowymi elementami logicznymi, stosowanymi powszechnie w
budowie układów logicznych, są elementy realizujące funkcje logiczne:
sumy (alternatywy), iloczynu (koniunkcji) i negacji. Są to odpowiednio
bramki OR, AND i NOT. Za pomocą dwóch takich bramek (np. OR i NOT
lub AND i NOT) można zbudować układ, realizujący dowolną funkcję
logiczną.
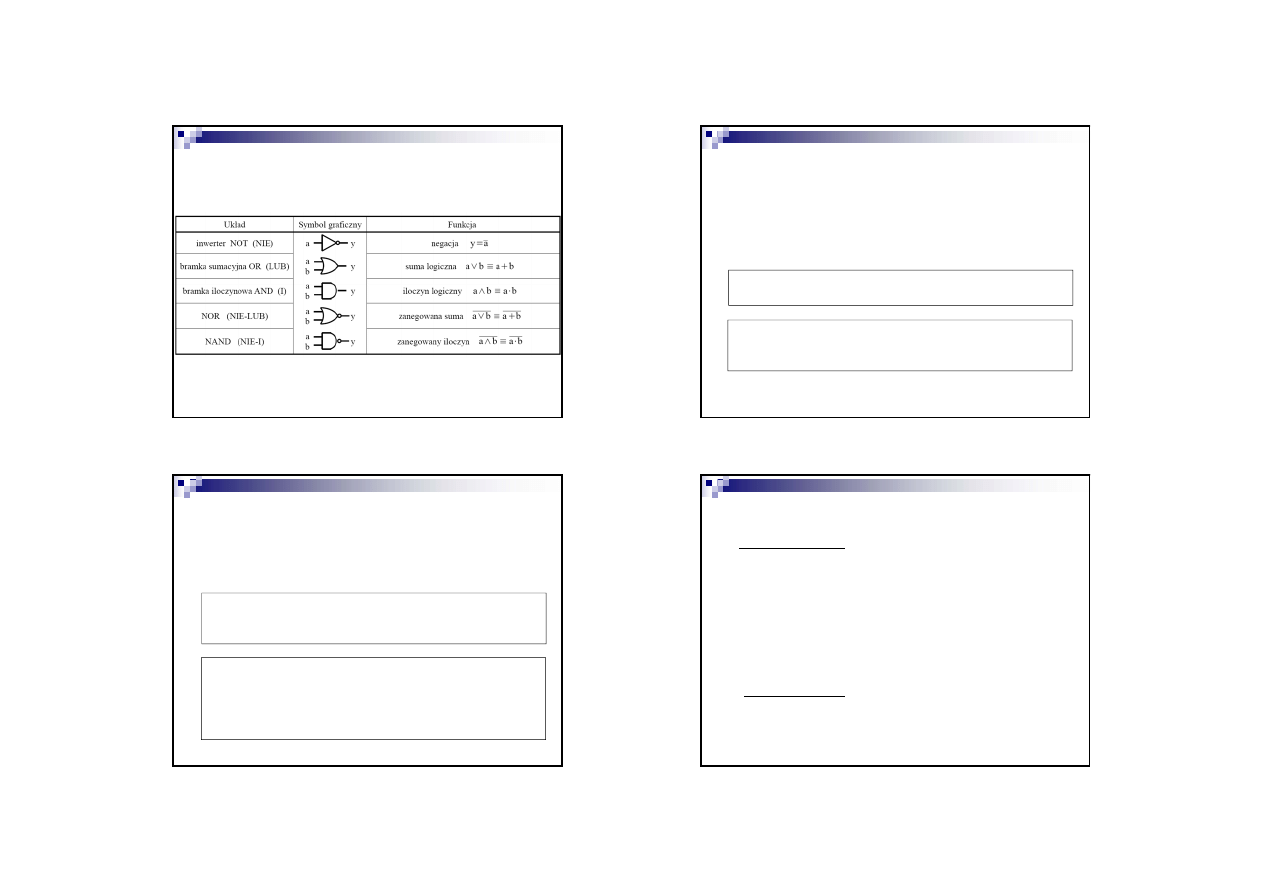
Wzory bramek
x
y
xy
x
y
x+y
x
y
x+y
x
x
x
y
xy
x
y
x+y
x
y
x+y
AND
OR
NOT
NAND
NOR
XOR
XNOR
2014-01-10
6
Zestawienie układów logicznych
Układy logiczne
Układy logiczne można podzielić (w zależności od
przyjętego kryterium) na:
•układy kombinacyjne
•układy sekwencyjne
Układ kombinacyjny to taki układ cyfrowy, w którym stan
wejść jednoznacznie określa stan wyjść układu.
Układem sekwencyjnym nazywamy taki układ cyfrowy, w
którym stan wyjść zależy od stanu wejść oraz od
poprzednich stanów układu.
Układy logiczne
•układy asynchroniczne
•układy synchroniczne
Układem asynchronicznym nazywamy taki układ cyfrowy,
dla którego w dowolnym momencie jego działania stan
wejść oddziaływuje na stan wyjść.
Układem synchronicznym nazywamy taki układ cyfrowy,
dla którego stan wejść wpływa na stan wyjść w pewnych
określonych odcinkach czasu zwanych czasem czynnym,
natomiast w pozostałych odcinkach czasu zwanych
czasem martwym stan wejść nie wpływa na stan wyjść..
Podział układów logicznych
Układy kombinacyjne:
– sumatory
– komparatory
– dekodery, kodery, transkodery
– multipleksery, demultipleksery
– .....
• układy matrycowe
• ........
• układy zbudowane z bramek
• bloki kombinacyjne
Układy sekwencyjne:
• przerzutniki
• rejestry
• liczniki
• .....
2014-01-10
7
Informacja cyfrowa
Zmienna binarna – zmienna o wartościach 1 i 0
Wektor informacji cyfrowej (w.i.c.) – wektor o
elementach binarnych, np.: 0111
Informacja cyfrowa – informacja przedstawiona
za pomocą ciągu wektorów informacji cyfrowej
Adresowanie wektora informacji cyfrowej-
wzajemnie jednoznaczne przypisanie każdemu
wektorowi innego w.i.c. zwanego adresem
Reprezentacja czasowa w.i.c.
Bitowo-równoległa – wszystkie bity wektor są dostępne
jednocześnie (na równoległych liniach magistrali lub w
rejestrze)
Bitowo-szeregowa – poszczególne bity pojawiają się na
tej samej linii lub w tym samym przerzutniku, w kolejnych
„okienkach czasu”
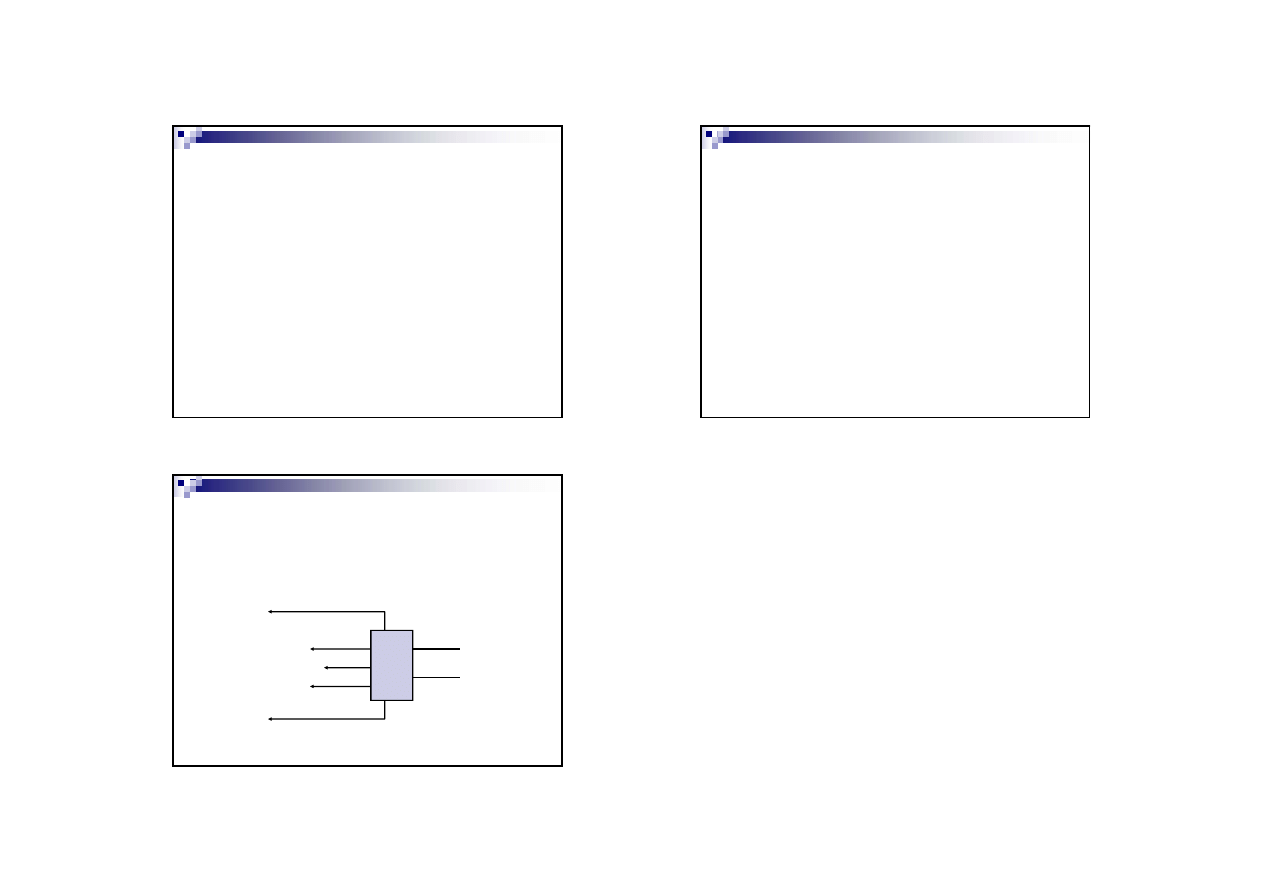
Przerzutniki
Posiada co najmniej dwa wejścia i z reguły dwa wyjścia
we
jś
c
ia
pr
ogr
a
m
uj
ą
ce
we
jś
ci
a
infor
m
a
c
yjne
wejście
zegarowe
wy
jś
ci
a
Przerzutniki są podstawowymi elementami układów
sekwencyjnych, których zasadniczym zadaniem jest
pamiętanie jednego bitu informacji.