Ewelina Dudek
6.05.2008 r.
Rok I, chemia podstawowa
dr Tomasz Greczyło
wtorek, 12
45
-15
00
60. Wyznaczanie współczynnika załamania światła ciał stałych i cieczy
1.
Pomiary
1.1
Pomiar współczynnika załamania przy użyciu refraktometru
Abbego
A.
Dla wody destylowanej
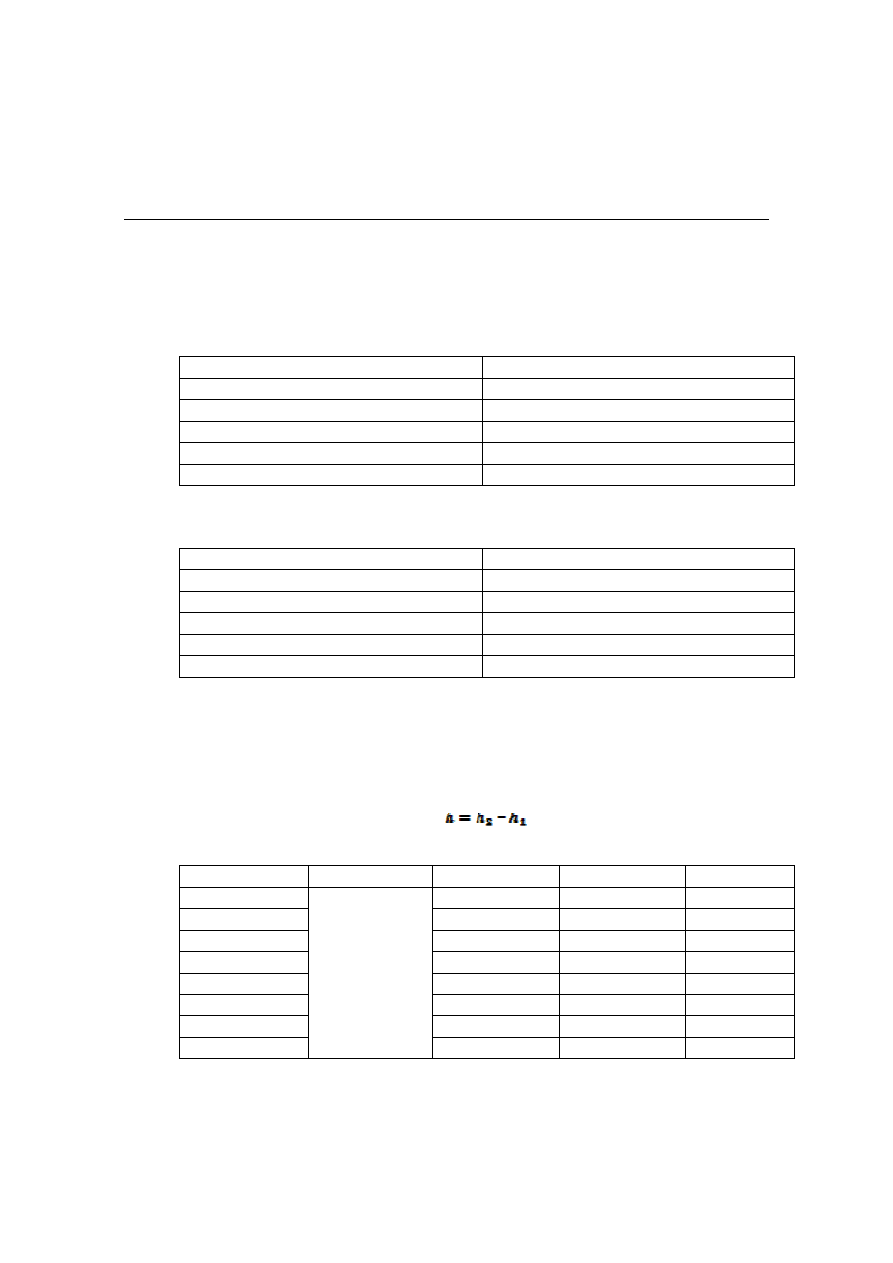
Tabela 1.1.1
Pomiar
Wartość współczynnika załamania, n
1
1,323
2
1,325
3
1,325
4
1,324
5
1,325
B.
Dla alkoholu
Tabela 1.1.2
Pomiar
Wartość współczynnika załamania, n
1
1,366
2
1,366
3
1,367
4
1,366
5
1,366
1.2
Pomiar współczynnika załamania przy użyciu mikroskopu
d- grubość „geometryczna” płytki
h
1
- odległość pomiędzy mosiężnymi bolcami dla kreski dolnej
h
2
- odległość pomiędzy mosiężnymi bolcami dla kreski górnej
h- grubość „optyczna” płytki
A.
Dla płytki szklanej
Tabela 1.2.1
Pomiar
d[mm]
h
1
[mm]
h
2
[mm]
h[mm]
1
61,32
72,22
10,90
2
61,34
72,82
11,48
3
61,26
72,92
11,66
4
61,35
72,50
11,15
5
61,50
72,24
10,74
6
61,36
72,50
11,14
7
61,40
72,51
11,11
8
19,90
61,28
72,34
11,06
B.
Dla płytki z pleksiglasu
Tabela 1.2.2
Pomiar
d[mm]
h
1
[mm]
h
2
[mm]
h[mm]
1
71,90
66,54
5,36
2
72,38
65,82
6,56
3
72,44
65,10
7,34
4
73,06
66,00
7,06
5
72,42
67,00
5,42
6
72,36
66,10
6,26
7
72,26
66,00
6,26
8
10,40
73,00
66,10
6,90
2.
Opis teoretyczny
2.1
Zachowanie promienia świetlnego na granicy dwóch ośrodków –
prawo odbicia i załamania
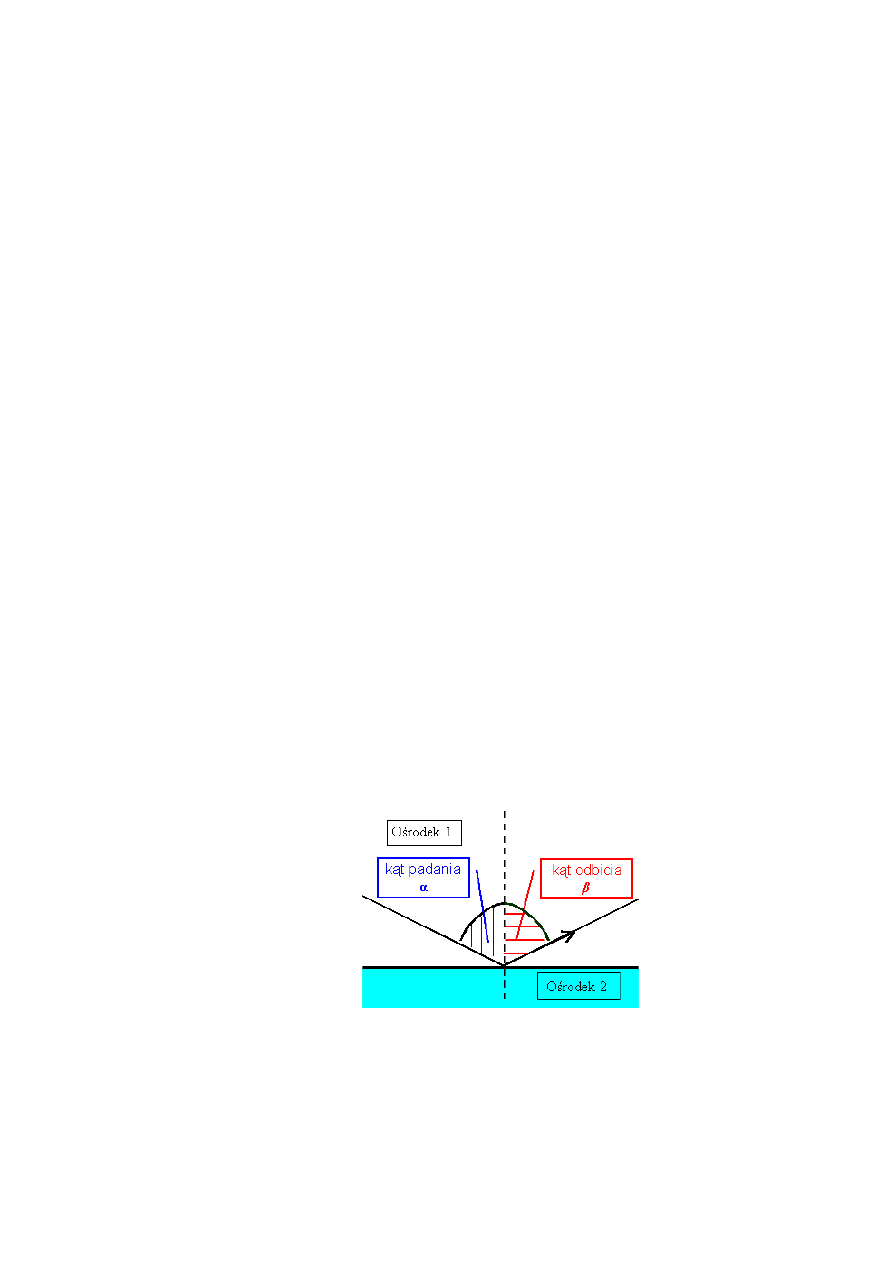
Prawo odbicia – odbicie światła jest zjawiskiem zachodzącym wówczas, gdy
światło pada na granicę dwóch ośrodków, w których prędkości rozchodzenia
się światła mają różną wartość. Na powierzchni granicznej, zwanej
powierzchnią odbijającą, następuje rozdzielenie wiązki padającej na dwie
wiązki: odbitą i załamaną. W przypadku odbicia od powierzchni
nieprzezroczystej wiązka załamana ulega pochłonięciu. Światło odbija się od
powierzchni granicznej zgodnie z prawem odbicia, tak samo jak fala
mechaniczna. Pierwsze prawo odbicia mówi, że kąt padania jest równy kątowi
odbicia. Drugie prawo odbicia brzmi następująco: promień padający, promień
odbity i normalna wystawiona z powierzchni w punkcie padania leżą w jednej
płaszczyźnie, zwanej płaszczyzną padania. Obydwa prawa odbicia wynikają z
zasady Fermata. Podczas prostopadłego odbicia światła następuje zmiana fazy
fali o π, jeśli odbicie następuje od ośrodka, w którym prędkość światła ma
większą wartość. W innym przypadku następuje odbicie bez zmiany fazy.
Rozróżniamy odbicie zwierciadlane(regularne) i rozproszone (dyfuzyjne).
Odbicie zwierciadlane jest to odbicie światła od gładkiej, wypolerowanej
powierzchni, podczas którego równoległa wiązka światła nadal pozostaje
wiązką równoległą. Rozproszone odbicie światła zachodzi na chropowatej
powierzchni, np. kartce papieru. Równoległa wiązka światła po odbiciu
rozchodzi się we wszystkich możliwych kierunkach, przy czym każdy z
promieni z osobna spełnia prawa odbicia(kąty padania dla poszczególnych
promieni są różne). To, czy odbicie jest zwierciadlane, czy rozproszone, zależy
od rozmiaru powierzchni odbijającej. Odbicie światła charakteryzowane jest
przez współczynnik odbicia. Promień odbity od powierzchni dielektryka jest
częściowo spolaryzowany.
Rys.1
Prawo załamania –załamania fali zachodzące dla światła na granicy dwu
ośrodków o różnych współczynnikach załamania. Na powierzchni granicznej
następuje rozdzielenie wiązki światła na wiązkę odbitą i wiązkę załamaną.
Podczas załamania światła nie zmienia się częstotliwość fali świetlnej,
natomiast długość i prędkość zmieniają się w zależności od gęstości optycznej
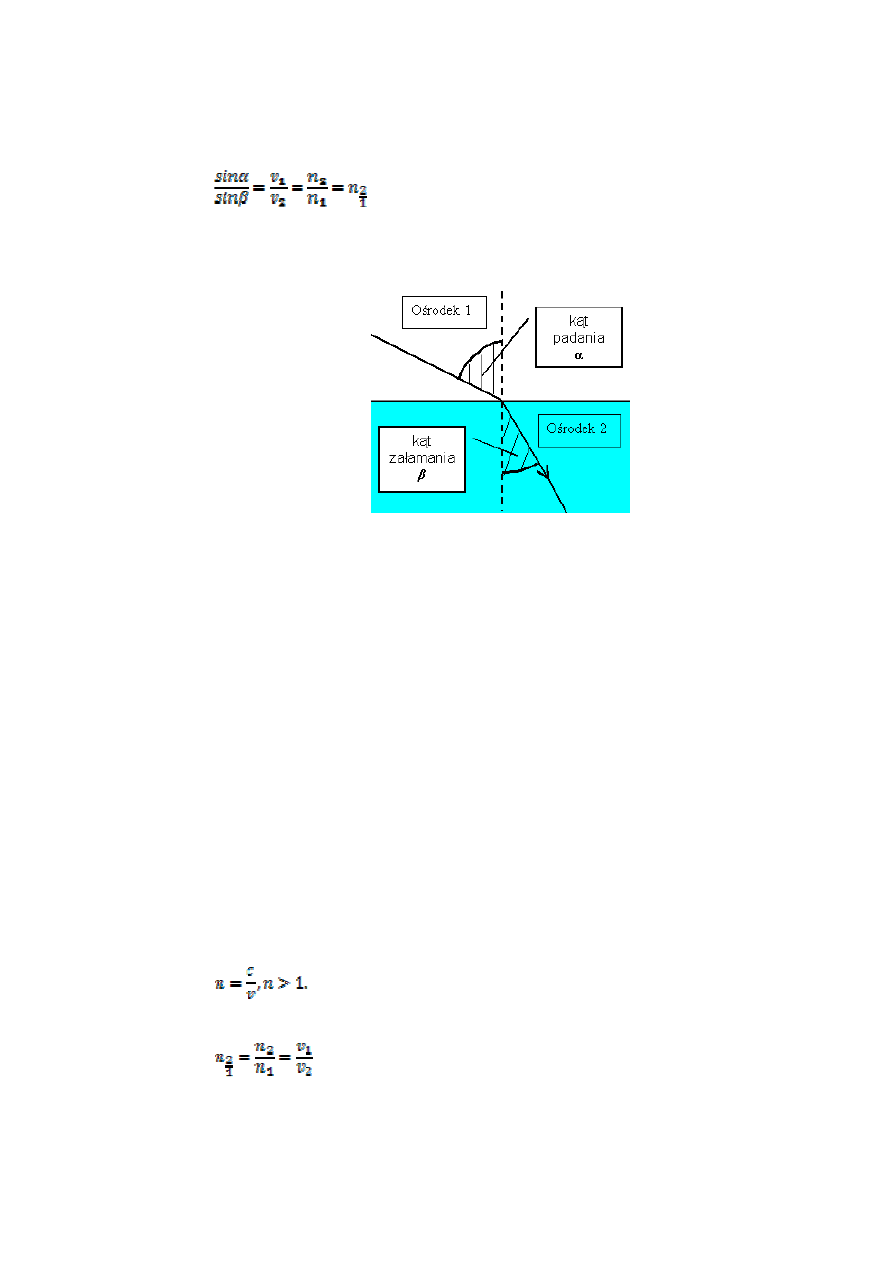
ośrodka. Związek między kątami padania α i załamania β wyraża prawo Snella
(Snelliusa):
gdzie:
v
1
,v
2
- prędkości światła w ośrodku pierwszym i drugim,
n
1
,n
2
-współczynniki załamania światła w obu ośrodkach,
n
2/1
- względny współczynnik załamania światła w obu ośrodkach.
Rys.2
2.2
Kąt graniczny i całkowite wewnętrzne odbicie
Promień świetlny biegnący w ośrodku optycznie gęstym (np. szkle) pada na
powierzchnię odgradzającą ten ośrodek od drugiego ośrodka o mniejszej
gęstości optycznej (np. powietrza). Jeżeli kąt padania θ wzrasta, dochodzimy
do sytuacji, w której promień załamany biegnie równolegle do powierzchni
łamiącej, czyli kąt załamania wynosi 90º. Dla kątów padania większych od
tego kąta granicznego θ
g
nie otrzymamy promienia załamanego, natomiast
zajdzie zjawisko zwane całkowitym wewnętrznym odbiciem. Całkowite
odbicie nie może mieć miejsca, gdy światło przechodzi z ośrodka o mniejszym
współczynniku do ośrodka o większym współczynniku.
2.3
Bezwzględny i względny współczynnik załamania
Współczynnik załamania światła, n jest wielkością charakteryzującą
oddziaływanie fali elektromagnetycznej z atomami ośrodka, w którym ta fala
się rozchodzi.
Bezwzględny współczynnik załamania światła, n – jest równy stosunkowi
prędkości światła w próżni c do prędkości v rozchodzenia się światła w danym
ośrodku
Względny współczynnik załamania światła, n
2/1
- jest równy stosunkowi
prędkości światła w ośrodkach sąsiadujących
.
W ośrodkach izotropowych współczynnik załamania światła nie zależy od
kierunku rozchodzenia się światła. Przykładowe wartości współczynnika
załamania światła dla kilku ośrodków:
n
powietrza
=1,0002,
n
wody
=1,32,
n
diamentu
=2,42,
2.4
Metody pomiarowe wyznaczania współczynnika załamania światła
A.
Wyznaczanie współczynnika załamania płytek szklanych za pomocą
mikroskopu
Na granicy dwóch ośrodków światło ulega załamaniu. Załamaniem rządzą
następujące prawa: kąt padania i kąt załamania leżą w jednej płaszczyźnie,
a współczynnik załamania n jest stosunkiem sinusów kąta padania α i
załamania β. Jeżeli kąt α jest bardzo mały, to zachodzi
i
podobnie
. Korzystając z tych upraszczających założeń na
podstawie rysunku możemy napisać:
oraz
,
stąd,
Grubość płytki d mierzymy mikromierzem, a pozorną grubość h za pomocą
mikroskopu. Na przedniej i tylnej powierzchni badanej płytki znajdują się
rysy. Mikroskop nastawia się na ostrość widzenia rysy górnej i odczytuje
położenie tubusa a
g
. Podobnie odczytuje się położenie tubusa a
d
, gdy
mikroskop jest nastawiony na ostrość widzenia rysy dolnej. Większość
mikroskopów ma wzorcowane obroty pokrętła precyzyjnego przesuwu
tubusa i jeden obrót tego pokrętła odpowiada przesunięciu 0,1 mm. Na
pokrętle znajduje się podziałka pozwalająca odczytać położenie tubusa z
dokładnością do 0,001 lub 0,01 mm. Gdy brak jest takiej podziałki, wtedy
zastosować można zwykły czujnik mikrometryczny, opierając stopę jego
żerdzi o ruchomą część mikroskopu.
B.
Wyznaczanie współczynnika załamania przy użyciu refraktometru
Abbego
Do wyznaczania współczynnika załamania wykorzystuje się zjawisko
całkowitego wewnętrznego odbicia. Do oświetlenia stosuje się naturalne
lub sztuczne białe światło rozproszone. Okienko podziałki się otwiera i
nastawia się lunetkę na ostrość widzenia podziałki i krzyża z nici
pajęczych. Podnosi się pryzmat a powierzchnie pryzmatów przeciera się
watką zwilżoną w wodzie destylowanej i osusza suszarką elektryczną. W
celu wykonania pomiaru za pomocą zaokrąglonego pręcika szklanego na
powierzchnię pryzmatu wprowadza się kilka kropel badanej cieczy i
pryzmat pierwszy dociska się do pryzmatu drugiego. Pryzmaty się oświetla
i za pomocą pokręteł doprowadza się do przecięcia linii podziału pola
widzenia z punktem skrzyżowania nici pajęczych i kompensuje się
zabarwienie linii podziału. Na koniec odczytuje się współczynnik
załamania.
3.
Opis doświadczenia
3.1
Pomiar współczynnika załamania przy użyciu refraktometru
Abbego
Wprowadzamy kilka kropel wody destylowanej do wgłębienia pomiędzy pryzmatami.
Przez obrót pryzmatów ustawiamy w polu widzenia lunety granicę cienia na środku
tego pola. Jeśli granica części jasnej i ciemnej jest nieostra, pokręcamy gałką
kompensatora. Odczytujemy wartość współczynnika załamania. Pomiar powtarzamy
kilka razy. Ten sam pomiar wykonujemy dla alkoholu, przy wcześniejszym osuszeniu
pryzmatów z wody destylowanej.
3.2
Pomiar współczynnika załamania przy użyciu mikroskopu
Przy pomocy specjalnej suwmiarki mierzymy grubość „geometryczną” płytki
szklanej. Umieszczamy płytkę na stolik mikroskopu i ustawiamy tubus na ostre
widzenie kreski zaznaczonej na dolnej powierzchni płytki. Za pomocą suwmiarki
mierzymy odległość pomiędzy bolcami zamocowanymi do tubusa i do stolika
mikroskopu. Następnie ustawiamy tubus na ostre widzenie kreski zaznaczonej na
górnej powierzchni płytki i za pomocą suwmiarki mierzymy odległość między tymi
samymi bolcami. Pomiar powtarzamy 8-10 razy. Tę samą czynność wykonujemy dla
płytki z pleksiglasu.
4.
Pomiary
4.1
Obliczenie średniej arytmetycznej otrzymanych wartości
współczynnika załamania dla danej cieczy
4.2
Obliczenie niepewności standardowej
4.3
Obliczenie średniej arytmetycznej otrzymanych wartości grubości
„optycznej” płytki dla danego materiału
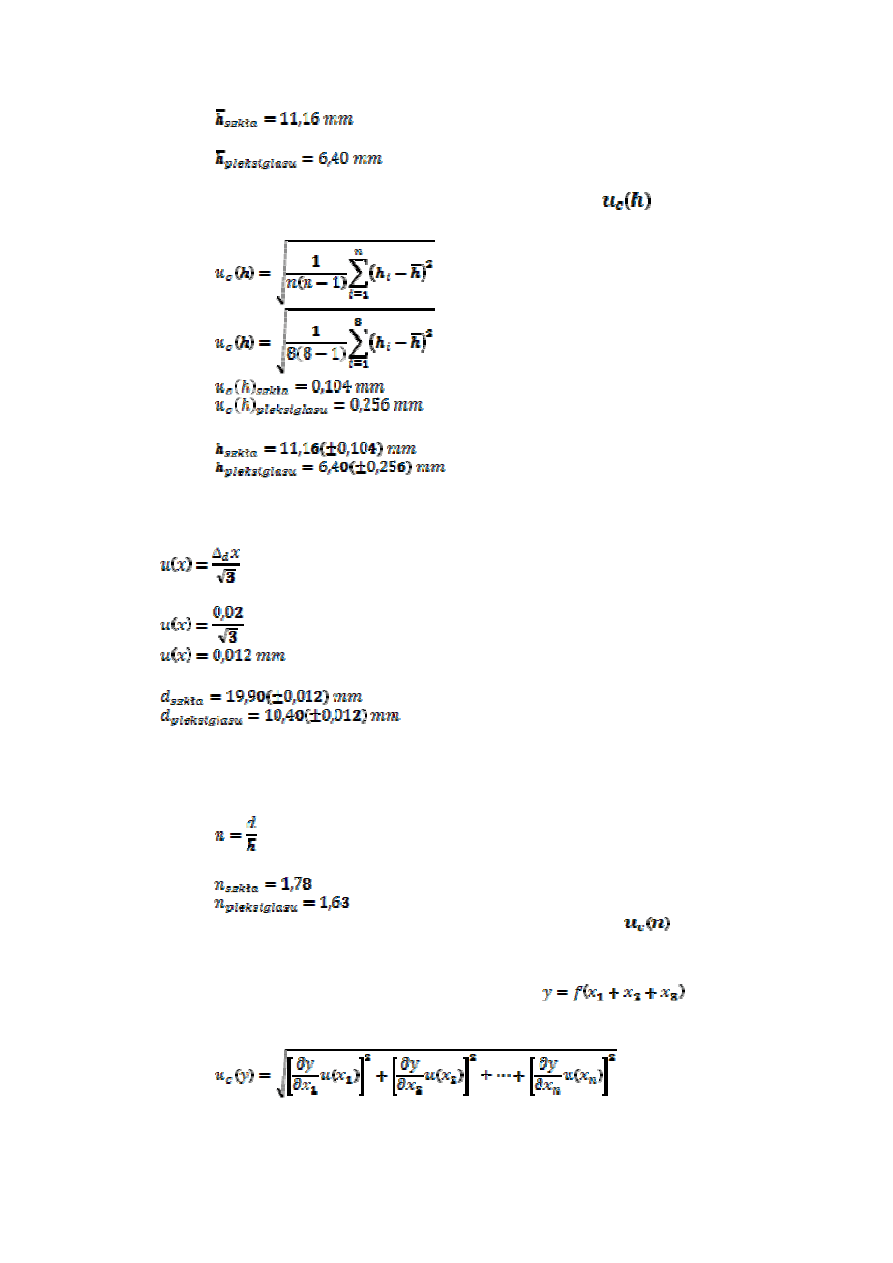
4.4
Obliczenie złożonej niepewności standardowej
4.5
Obliczenie niepewności standardowej grubości „geometrycznej”
danej płytki
4.6
Wyznaczenie wartości współczynnika załamania n dla danego
materiału
4.7
Wyznaczenie złożonej niepewności standardowej
z prawa
przenoszenia niepewności standardowych
Niepewność standardową wielkości złożonej
obliczamy z
tzw. prawa przenoszenia niepewności, jako sumę geometryczną różniczek
cząstkowych
gdzie:
- pochodna cząstkowa funkcji f względem zmiennej
, zwana
współczynnikiem wrażliwości,
– niepewność standardowa zmiennej niezależnej.
Tak więc, dla
mamy
Podstawiając dane liczbowe otrzymujemy:
a)
dla szkła
b)
dla pleksiglasu
5.
Wnioski
W ćwiczeniu zapoznano się z metodami pomiaru współczynnika załamania światła za
pomocą mikroskopu i refraktometru Abbego. Uzyskane wyniki pomiarów nie różnią
się praktycznie od wartości tablicowych. Należy jednak zaznaczyć, że posługując się
drugą z metod, musimy wykonać więcej czynności pomiarowych, takich jak pomiar
grubości „d” płytki oraz złożony odczyt grubości „optycznej” „h” za pomocą
mikroskopu. Tak więc, dokładność niniejszej metody jest mniejsza, niż dla
refraktometru Abbego, gdzie wartość współczynnika załamania może zostać
odczytana natychmiast, co znacząco skraca czas pomiarów. Warto dodać, że zjawisko
całkowitego wewnętrznego odbicia wykorzystane w refraktometrze Abbego znalazło
obecnie szerokie zastosowanie przede wszystkim w światłowodach.