
Algorytmy i struktury danych - wykład 4. strona: 1
Listy, stosy i kolejki
W tym wykładzie zostaną przedstawione struktury danych, należące do
tzw. abstrakcyjnych struktur danych - ADT (ang. Abstract Data Type),
które są wykorzystywane prawie w każdej aplikacji. W projektowaniu
programu definicja ADT wymaga specyfikacji zbiorów danych i działań na
tych zbiorach.
Listy, podobnie jak tablice używane są jako struktury bazodanowe do
przechowywania kartotek osobowych, danych finansowych, katalogów i
tym podobnych danych, które odpowiadają rzeczywistym obiektom. Ich
charakterystyczną cechą jest ułatwienie dostępu do danych, czyli operacji
wstawiania, usuwania i wyszukiwania.
Stosy i kolejki częściej używane są jako narzędzia programisty.
Stanowią raczej pomoc konceptualną przy rozwiązywaniu różnych
problemów i są tworzone na czas wykonania pewnego zadania i po jego
wykonaniu są niepotrzebne. W przypadku tych struktur dostęp do
elementów jest ograniczony. Tylko jeden element może zostać pobrany
lub usunięty w danej chwili. Definicja tych struktur zakłada, że dostęp do
pozostałych elementów jest niemożliwy.
ADT: LISTA
Jest to skończony ciąg elementów ustalonego typu ElementType
a
1
, a
2
, . . . , a
n
, ,
n >= 0
przy czym ElementType może być np. typem struktury, int, string itp.
Terminologia:
•
n – długość listy
•
a
1
– pierwszy element listy, a
n
– ostatni
•
a
i
poprzedza a
i+1
,
•
a
i
jest na pozycji i-tej

Algorytmy i struktury danych - wykład 4. strona: 2
Przykładowy zestaw operacji struktury LISTA
1.
END(L) - zwraca pozycję następną po ostatnim elemencie listy
„pierwsze wolne miejsce")
2.
FIRST(L) - zwraca pierwszą pozycję w L, wynik równy END(L) gdy
L pusta
3.
MAKENULL(L) - powoduje że L staje się listą pustą (lub utworzenie
nowej pustej listy)
4.
INSERT(x, p, L) - wstawia element x typu ElemType na pozycję p
w liście L, przesuwając elementy z pozycji p i wyższych o jedną
pozycję dalej (czyli lista się wydłuża)
przed: a
1
, a
2
, ..., a
p-1
,
a
p
, ..., a
n
po: a
1
, a
2
, ..., a
p-1
,
x
, a
p
, ..., a
n
je
ś
li p=END(L) to wynik:
a
1
, a
2
, ..., a
p-1
, a
p
, ..., a
n
,
x
jeśli w liście L nie istnieje pozycja p to wynik niezdefiniowany
5.
LOCATE(x, L) - oblicza pozycję ‘x’ w liście L jeśli x więcej niż raz w
liście L to zwraca pierwszą pozycję, jeśli x nie ma w liście to zwraca
END(L)
6.
RETRIEVE(p, L) - zwraca element na pozycji p w liście rezultat
niezdefiniowany jeśli nie ma pozycji p w liście
7.
DELETE(p, L) - usuwa element na pozycji p (czyli lista się skraca)
przed: a
1
, a
2
, ..., a
p-1
,
a
p
,
a
p+1
, ..., a
n
po: a
1
, a
1
, ..., a
p-1
,
a
p+1
, ..., a
n
wynik niezdefiniowany jeśli w L nie ma pozycji p
8.
NEXT(p, L), PREVIOUS(p, L) - podają pozycję następną i
poprzednią do p, niezdefiniowane gdy nie ma pozycji p w L,
NEXT niezdefiniowane gdy p=END(L), PREVIOUS niezdefiniowane
gdy p=1
9.
PRINTLIST(L) - drukuj w kolejności występowania na liście
Mając zrealizowaną strukturę listy jak wyżej możemy zrealizować na
przykład następujące zadanie: usunąć wszystkie powtarzające się
elementy z listy L.
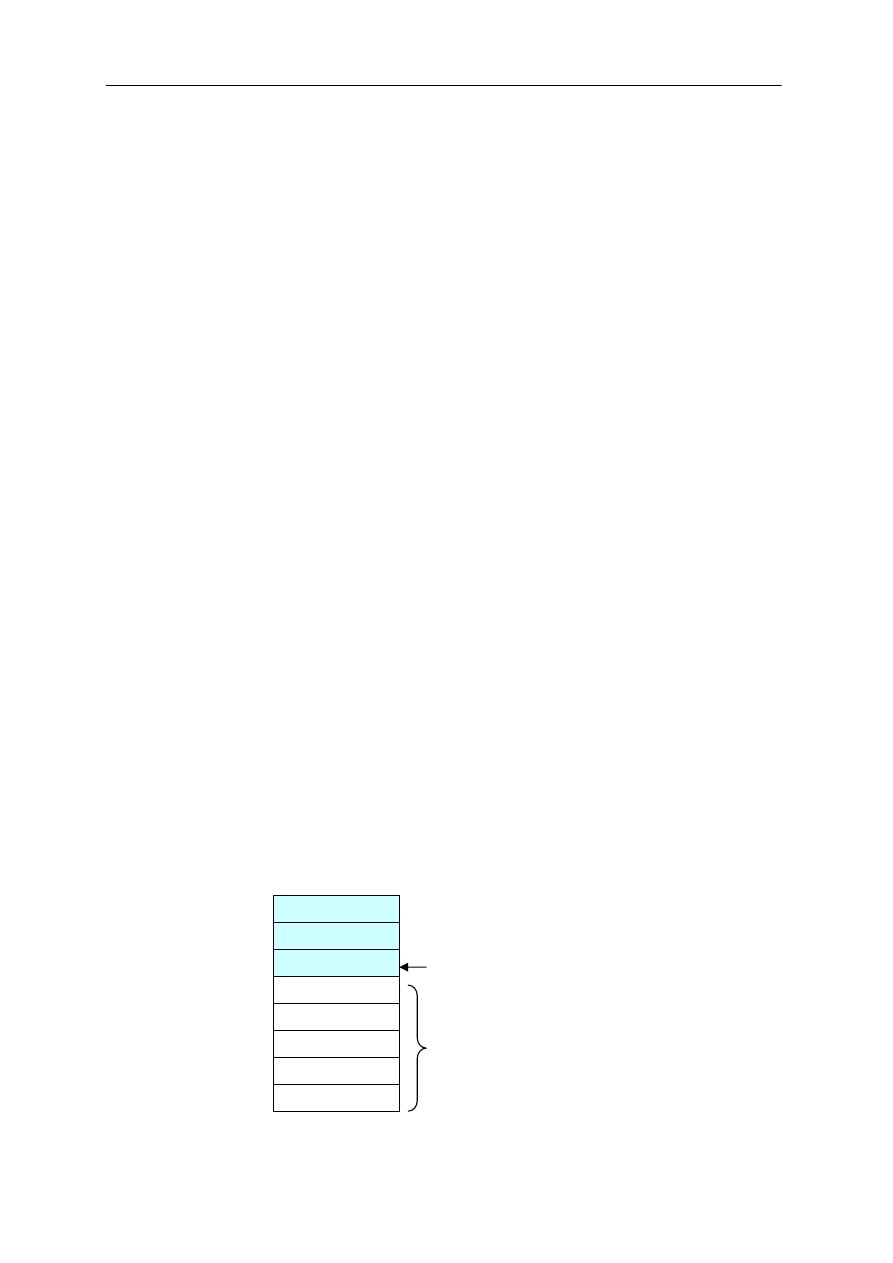
Algorytmy i struktury danych - wykład 4. strona: 3
lista L ; // L jest list
ą
noDups() // usuwa duplikaty z listy L
{ p,q typu pozycja // p – b
ę
dzie 'aktualn
ą
' pozycj
ą
// q b
ę
dzie szuka
ć
takich samych elementów
p = L.FIRST();
while ( p != L.END() )
{ q = L.NEXT (p)
while ( q
!=
L.END() )
if (L.Retrieve(p) == L.RETRIEVE(q))
then L.DELETE(q);
else q = L.NEXT(q);
p = L.NEXT(p);
}
} // noDups()
Implementacja abstrakcyjnych struktury danych w ustalonym języku
opisu algorytmów (w szczególności może to być konkretny język
programowania) polega na deklaracji typów danych, zmiennych tych
typów oraz deklaracji metod, których działanie spełnia warunki definicji
struktury.
Zalety wyraźnego rozdzielenia definicji abstrakcyjnej od realizacyjnej
to, łatwiejsza modyfikowalność programu – zmieniamy tylko szczegóły
implementacyjne w jednym miejscu programu, postać operacji i sposób
ich wykorzystania są bez zmian.
Tablicowa implementacja listy w Javie.
maxSize -1
a
0
a
1
a
2
last
0
wolne

Algorytmy i struktury danych - wykład 4. strona: 4
class listArray
{ private int maxSize; // rozmiar tablicy zawieraj
ą
cej liste
private long[] list; // tablica zawieraj
ą
ca liste
private int last; // liczba elementów listy
//----------------------------------------------------------
public listArray(int Size) // konstruktor
{ // MakeList(L)
maxSize = Size;
list = new long[maxSize]; // tworzymy list
ę
pust
ą
last = 0; // na razie brak elementów
}
//----------------------------------------------------------
public int End(){ // zwraca pozycje za ostatnim elementem
return last;
} // end()
//----------------------------------------------------------
public int First() // zwraca pierwsza pozycj
ę
na li
ś
cie
{
return 0;
}
//----------------------------------------------------------
public int Locate(long searchElem)
{ // szukanie okre
ś
lonej warto
ś
ci
int j;
for(j=0; j<last; j++) // dla ka
ż
dego elementu...
if(list[j] == searchElem) // czy znaleziono?
return j; // tak, zwraca pozycje
return last; // nie, zwraca pozycje za
} // end Locate() // ostatnim elementem
//----------------------------------------------------------
public void Insert(long x, int p) // wstawienie x do listy
// na pozycj
ę
p
{
if (last >= maxSize) error ("lista pelna");
else
if ( (p > last) || ( p < 0) )
error ("pozycja nie istnieje");
else
{
for(int q =last; q > p; q--)
list[q] = list[q-1];
list[p] = x;
last++;
}
} //end Insert()
//----------------------------------------------------------
public void Delete(int p) // usuni
ę
cie elementu listy
{
if (last == 0) error("lista pusta");
else
if ( (p >= last) || ( p < 0) )
error ("pozycja nie istnieje");
else
{

Algorytmy i struktury danych - wykład 4. strona: 5
for(int q = p; q < last; q++) // przesuwamy pozostałe
// elementy
list[q] = list[q+1];
last--; // zmniejszamy licznik
// elementów
}
} // koniec delete()
//----------------------------------------------------------
public void printList() // wypisuje zawarto
ść
listy
{
if (last == 0) error("lista pusta");
else{
for(int j=0; j<last; j++) // dla ka
ż
dego elementu...
System.out.print(list[j] + ", "); // ...wypisujemy
// jego warto
ść
System.out.println("");
}
}
//----------------------------------------------------------
public void error(String ms) // wypisuje informacje o bł
ę
dzie
{
System.out.println(ms); // ...wypisujemy
}
//----------------------------------------------------------
public long Retrieve(int p) // zwraca element z pozycji p
{
if ( (p >= last) || ( p < 0) )
{ error ("pozycja nie istnieje");
return -1; //
}
else
return list[p];
}
//----------------------------------------------------------
public int Next(int p) // zwraca nast
ę
pn
ą
pozycj
ę
po p
{
if ( (p > last-1) || ( p < 0) )
{ error ("pozycja nie istnieje");
return -1;
}
else
return p+1;
}
//----------------------------------------------------------
public int Previous(int p) // zwraca pozycj
ę
poprzedni
ą
dla p
{
if ( (p > last) || ( p < 1) )
{ error ("pozycja nie istnieje");
return -1;
}
else
return p-1;
} // koniec Previous()
} // koniec klasy listArray
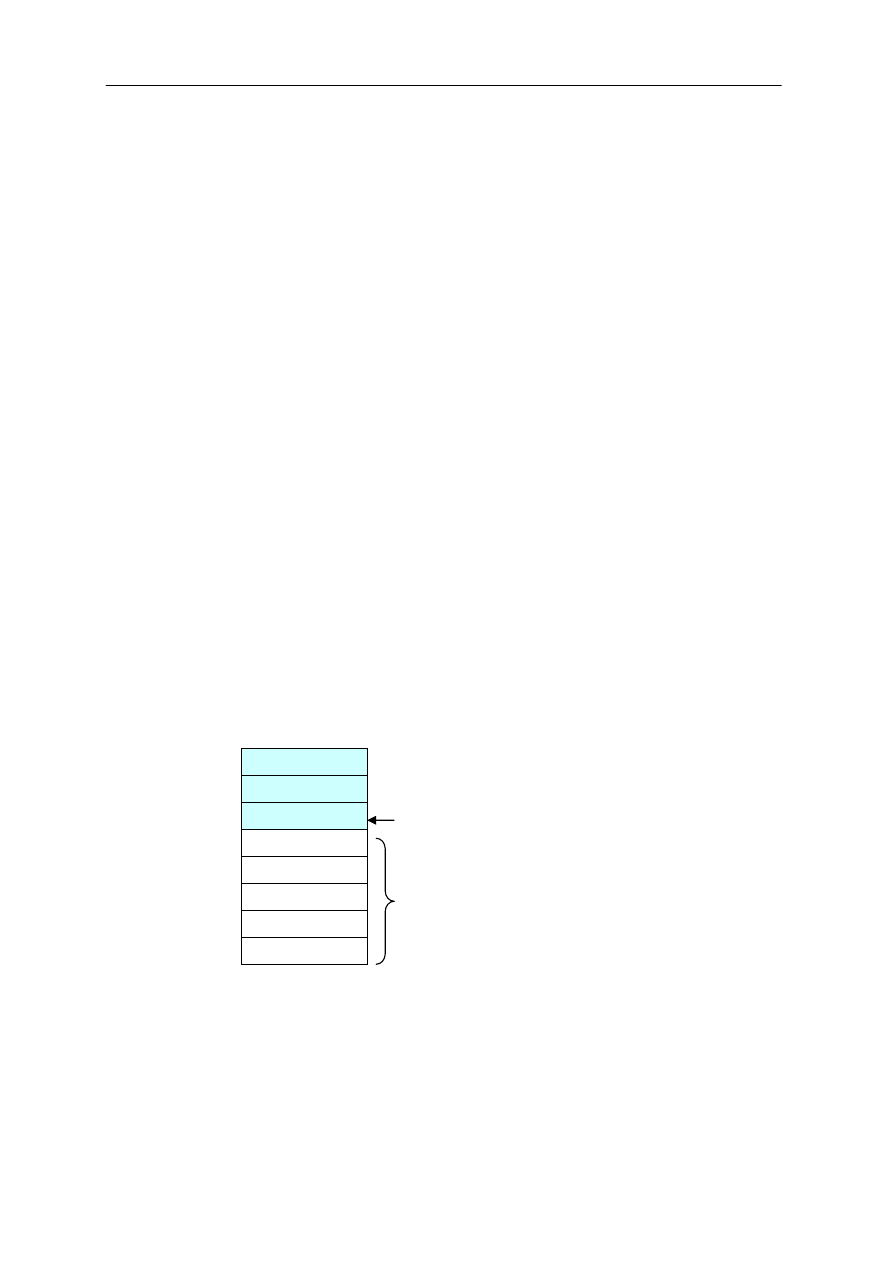
Algorytmy i struktury danych - wykład 4. strona: 6
Dodajmy na koniec, że złożoność operacji Insert(), Delete(), Locate() oraz
PrintList() jest liniowo zależna od liczby elementów listy, czyli T(n)=O(n).
NS 4.04.09
ADT: STOS
czasami nazywany kolejką LIFO (last in first out).
Jest to lista z wyróżnionym jednym końcem, nazywanym wierzchołkiem,
na którym wykonywane są operacje:
1.
Top() -odczytuje element na stosie
2.
Pop() - usuwa element ze stosu i zwraca go
3.
Push(x) - wstawia element x na stos
oraz na ogół
4.
Create() - twórzy pusty stos
5.
isEmpty() - sprawdza czy stos jest pusty
Realizacja stosu za pomocą tablicy w Javie
class StackType{
private int maxSize; // rozmiar tablicy zawieraj
ą
cej stos
private long[] stackArray; // tablica zawieraj
ą
ca stos
private int top; // indeks szczytu stosu
//-------------------------------------------------------------
maxSize -1
a
b
c
top
0
wolne

Algorytmy i struktury danych - wykład 4. strona: 7
public StackType(int size) { // konstruktor - Create()
maxSize = size; // ustawiamy rozmiar tablicy
stackArray = new long[maxSize]; // tworzymy tablic
ę
top = -1; // na razie brak elementów
}
//-------------------------------------------------------------
public void push(long x) { / odkłada element na szczyt stosu
if(isFull()) System.out.println("stos jest pelny");
else stackArray[++top] = x; // zwi
ę
kszamy top,
// odkładamy element
}
//-------------------------------------------------------------
public long pop(){ // pobiera element ze szczytu stosu
if(isEmpty())
{ System.out.println("stos jest pusty");
return -1;
}
else return stackArray[top--]; // pobieramy element,
// zmniejszamy top
}
//-------------------------------------------------------------
public long top(){ // podgl
ą
da warto
ść
na szczycie stosu
if ( isEmpty() )
{ System.out.println("stos jest pusty");
return –1;
}
else
return stackArray[top];
}
//------------------------------------------------------------
public boolean isEmpty(){ // zwraca true, je
ż
eli stos pusty
return (top == -1);
}
//-------------------------------------------------------------
public boolean isFull(){ // zwraca true, je
ż
eli stos pełny
return (top == maxSize-1);
}
//------------------------------------------------------------
} // koniec klasy Stack

Algorytmy i struktury danych - wykład 4. strona: 8
Wykorzystanie stosu do odwracania słowa.
Poniższy program przedstawia wykorzystanie stosu do odwracania
kolejności znaków. Znaki najpierw są pobierane z wejścia i odkładane na
stosie. Następnie są zdejmowane ze stosu i wypisywane na wyjściu.
// Plik: reverse.java
import java.io.*; // operacje wej
ś
cia-wyj
ś
cia
class Stack
{
private int maxSize;
private char[] stackArray;
private int top;
//-------------------------------------------------------------
public Stack(int max) // konstruktor
{
maxSize = max;
stackArray = new char[maxSize];
top = -1;
}
//-------------------------------------------------------------
public void push(char j) // odkłada element na stos
{
stackArray[++top] = j;
}
//-------------------------------------------------------------
public char pop() // zdejmuje element ze stosu
{
return stackArray[top--];
}
//-------------------------------------------------------------
public char top() // podgl
ą
da element na szczycie stosu
{
return stackArray[top];
}
//-------------------------------------------------------------
public boolean isEmpty() // zwraca true je
ż
eli stos pusty
{
return (top == -1);
}
//-------------------------------------------------------------
} // koniec klasy Stack
class Reverser
{
private String input; // napis wej
ś
ciowy
private String output; // napis wyj
ś
ciowy
//-------------------------------------------------------------
public Reverser(String in) // konstruktor
{ input = in; }
//-------------------------------------------------------------
public String doRev() // odwraca napis

Algorytmy i struktury danych - wykład 4. strona: 9
{
int stackSize = input.length(); // pobiera długo
ść
napisu
Stack theStack = new Stack(stackSize); // tworzy stos o
// takiej pojemno
ś
ci
for(int j=0; j<input.length(); j++)
{
char ch = input.charAt(j); // pobiera kolejny znak z
// wej
ś
cia...
theStack.push(ch); // ...i odkłada na stosie
}
output = "";
while( ! theStack.isEmpty() )
{
char ch = theStack.pop(); // zdejmuje znak ze stosu...
output = output + ch; // ...i doł
ą
cza do napisu
// wyj
ś
ciowego
}
return output;
} // koniec doRev()
//-------------------------------------------------------------
} // koniec klasy Reverser
class ReverseApp
{
public static void main(String[] args) throws IOException
{
String input, output;
while(true)
{
System.out.print("Wprowad
ź
napis: ");
input = getString(); // wczytujemy napis z
// klawiatury
if( input.equals("") ) // koniec, je
ż
eli sam [Enter]
break;
// tworzymy obiekt
// odwracaj
ą
cy słowa
Reverser theReverser = new Reverser(input);
output = theReverser.doRev(); // u
ż
ywamy go
System.out.println("Odwrócony: " + output);
} // koniec while
} // koniec main()
//-------------------------------------------------------------
public static String getString() throws IOException
{
InputStreamReader isr = new InputStreamReader(System.in);
BufferedReader br = new BufferedReader(isr);
String s = br.readLine();
return s;
}
//-------------------------------------------------------------
} // koniec klasy ReverseApp
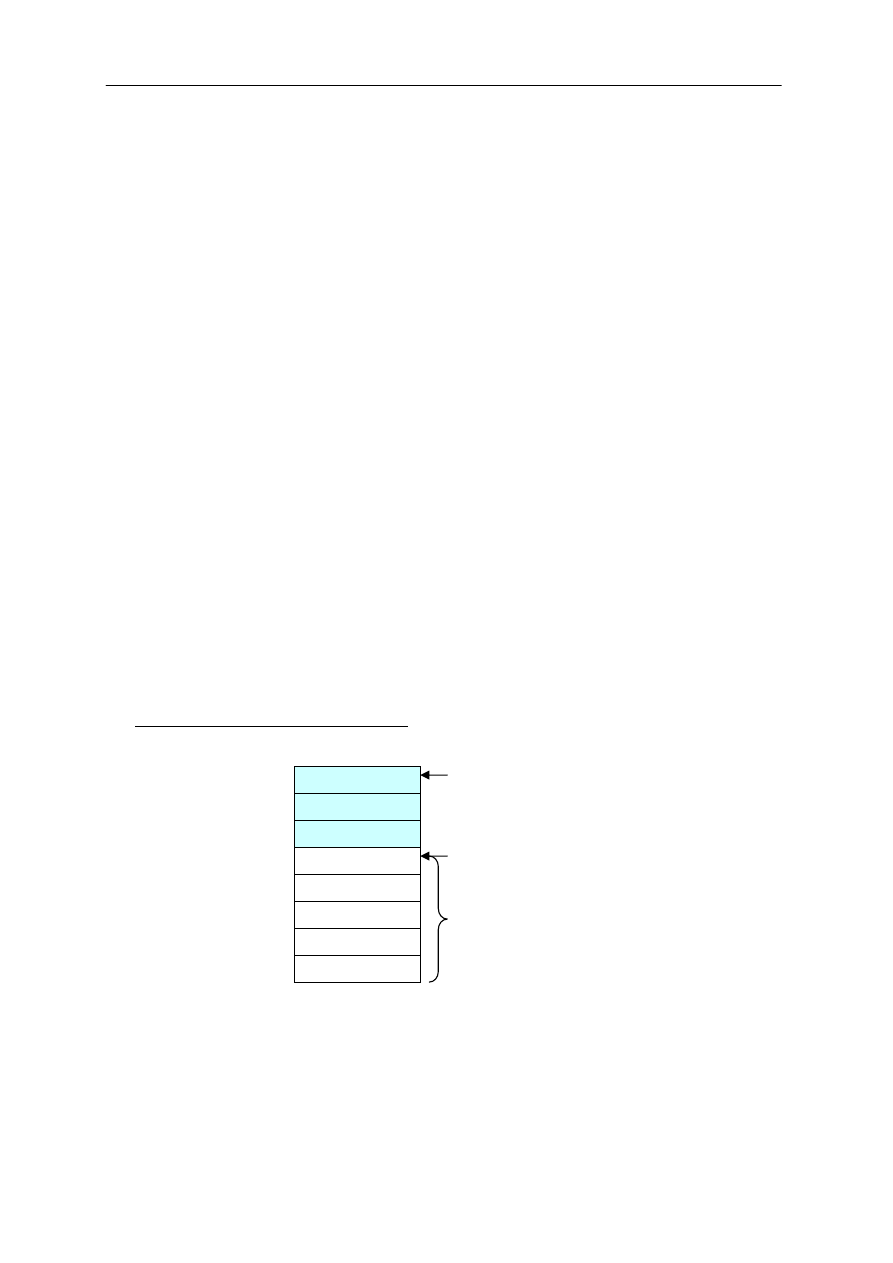
Algorytmy i struktury danych - wykład 4. strona: 10
ADT : KOLEJKA
czyli kolejka FIFO (first in first out).
Jest to lista, w której operacja wstawiania nowego elementu odbywa
się na jednym z góry ustalonym końcu (koniec kolejki - rear), przy czym
rear oznacza pierwszą wolną komórkę, do której będzie wstawiony nowy
element, a odczytywanie i usuwanie odbywa się na drugim końcu
(początek kolejki – front, który wskazuje pierwszy element w kolejce).
Operacje:
1.
Create() - twórzy pustą kolejkę
2.
isEmpty() - sprawdza czy kolejka pusta
3.
enQueue(x)- wstawia nowy element x
4.
Front()- odczytuje pierwszy element w kolejce
5.
deQueue() - usuwa pierwszy element w kolejce i go zwraca
Efektywna realizacja tablicowa kolejki (tablica cykliczna):
Najprostszą i nieefektywną realizacją kolejki w tablicy jest przyjęcie,
że początek kolejki front będzie zawsze równy 0, a rear będzie indeksem
do pierwszego wolnego elementu tablicy.
W tej reprezentacji operacja usuwania elementu z kolejki wymaga
każdorazowo przesuwania elementów kolejki w górę.
W przypadku gdy front będzie się zwiększać o jeden podczas
operacji usuwania elementu, powstaje problem, braku miejsca przy
maxSize -1
a
b
c
rear
0
wolne
front
Algorytmy i struktury danych - wykład 4. strona: 11
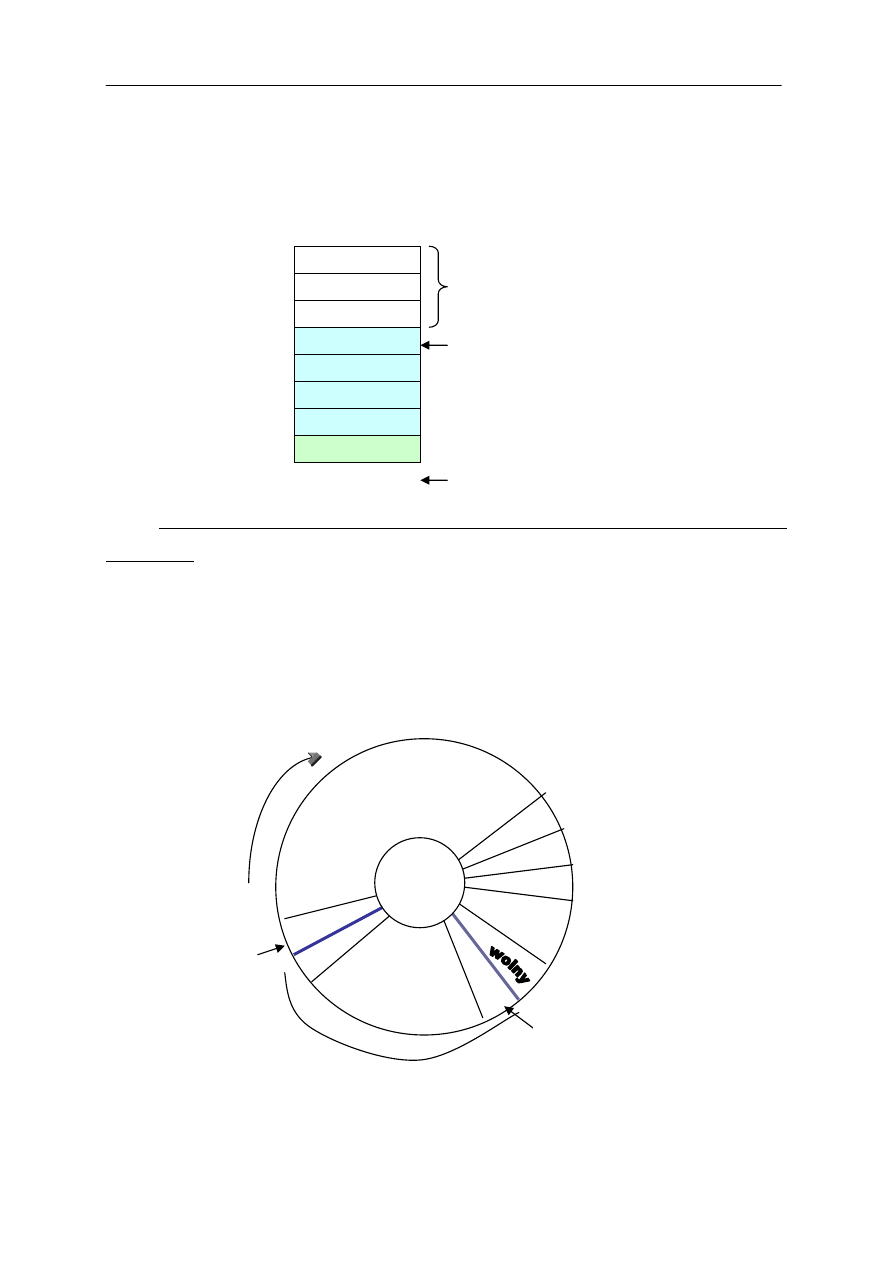
wstawianiu elementu na koniec kolejki, podczas gdy będzie wolne miejsce
na początku kolejki.
Poniżej przedstawiono kolejkę po usunięciu trzech elementów i
wstawieniu pięciu.
Najlepszym rozwiązaniem jest reprezentacja kolejki w tablicy
cyklicznej. Wstawianie i usuwanie zwiększają pozycje końca i początku o 1
modulo rozmiar tablicy.
Ponieważ za pomocą tylko indeksu końca i początku kolejki nie da się
odróżnić kolejki pustej od kolejki zajmującej całą tablicę, więc nie
dopuszczamy do wypełnienia całej tablicy (operacja enQUEUE).
maxSize -1
d
e
f
g
front
0
h
wolne
rear
0
1
maxSize
-1
rear
kolejka
front

Algorytmy i struktury danych - wykład 4. strona: 12
DZ 27.03.09
class queueArray
{
private int maxSize;
private long[] queArray;
private int front; //front = indeks pocz
ą
tku
private int rear; //rear = indeks nast
ę
pny za ko
ń
cem
// czyli pierwszy wolny
//-------------------------------------------------------------
private int Addone (int i) //pomocnicza
{
return (i+1) % maxSize; // reszta z dzielenia
}
//-------------------------------------------------------------
public queueArray(int size) // konstruktor
{
maxSize = size;
queArray = new long[maxSize];
front = 0;
rear = 0;
}
//-------------------------------------------------------------
public void enQueue(long x) // wstawia element na koniec
// kolejki
{
if (isFull()) error ("queue is full");
else{
queArray[rear] = x;
rear = Addone(rear);
}
}
//-------------------------------------------------------------
public long deQueue() // usuwa element z pocz
ą
tku kolejki
{
if(isEmpty()){
front
front
rear
rear
rear
front
Pusta
Jedno-elemenetowa
Pełna

Algorytmy i struktury danych - wykład 4. strona: 13
error("queue is empty");
return -1;
}
else {
long temp = queArray[front]; // pobieramy element
front = Addone(front);
return temp;
}
}
//-------------------------------------------------------------
public long Front() // podgl
ą
da element na pocz
ą
tku kolejki
{
if(isEmpty()){
error("queue is empty");
return -1;
}
else return queArray[front];
}
//-------------------------------------------------------------
public boolean isEmpty() // zwraca true, je
ż
eli kolejka
// pusta
{
return (rear == front);
}
//-------------------------------------------------------------
public boolean isFull() // zwraca true, je
ż
eli kolejka
// pełna
{
return (Addone(rear) == front);
}
//-------------------------------------------------------------
public void error(String ms) // wypisuje informacje
// o bł
ę
dzie
{
System.out.println(ms); // ...wypisujemy
}
//-------------------------------------------------------------
} // koniec klasy queueArray
Złożoność każdej operacji na stosie lub kolejce:
Θ
(1) – stała.

Algorytmy i struktury danych - wykład 4. strona: 14
ADT: Kolejka priorytetowa
to struktura danych przechowująca zbiór elementów ustalonego typu z
następującymi operacjami:
•
Insert(x, q) – wstawienie elementu ‘x’ do kolejki q
•
Max(q) – odczyt największego elementu w kolejce (element ten jest
zwracany jako wynik operacji, kolejka się nie zmienia)
•
Delete_max (q) – usunięcie największego elementu z kolejki q
oraz operacje utworzenia nowej (pustej) kolejki i sprawdzania czy dana
kolejka jest pusta. W niektórych zastosowaniach pojawia się osobna
operacja tworzenia kolejki zawierającej zadany zbiór elementów.
Analogicznie (w zależności od potrzeb) definiuje się i realizuje kolejkę
priorytetową z zamianą Max na Min.
Zastosowanie m.in. do sortowania, w algorytmach grafowych.
Realizacja kolejki priorytetowej:
najprostsza: za pomocą listy realizowanej w tablicy.
Wariant A: tablica nieuporządkowana.
Atrybuty struktury:
Size – aktualna długość kolejki
maxSize – wielkość tablicy
A[0] ... A[maxSize-1] – tablica zawierająca elementy kolejki
Inicjalizacja – tworzenie pustej kolejki: Size = 0
Wstawianie:
dopisanie elementu na koniec listy i powiększenie Size o 1
Max:
znalezienie elementu największego spośród
A[0], . . . ,A[maxSize-1]

Algorytmy i struktury danych - wykład 4. strona: 15
Delete_Max:
znalezienie położenia (indeksu p) elementu największego, a
następnie przesunięcie elementów o indeksach większych niż p o 1
pozycję w dół oraz Size zmniejsza się o 1.
Wariant B: tablica uporządkowana rosnąco.
Zmienne – jak wyżej.
Max: ostatni element w liście, tj. A[0], ... ,A[maxSize-1]
Delete_Max:
skrócenie listy o ostatni element, tj. Size = Size – 1
Insert(x, q):
znajdź położenie elementu ‘x’ w tablicy algorytmem bisekcji;
wstaw element ‘x’ w to miejsce (z rozsunięciem);
Size = Size +1
Jako ćwiczenie oceń, które operacje w poszczególnych wariantach
realizacji kolejki priorytetowej są wykonywane szybko a które wolniej ?
Kolejki dwustronne (deque)
Kolejka dwustronna pozwala wstawiać i usuwać elementy zarówno z
początku, jak i z końca kolejki.
Posiada, zatem operacje:
•
InsertLeft() – wstaw z lewej strony
•
InsertRight()-wstaw z prawej strony
•
RemoveLeft()- usuń z lewej strony
•
RemoveRight()- usuń z prawej strony
Kolejka dwustronna jest bardziej uniwersalną strukturą danych niż stosy i
zwykłe kolejki.

Algorytmy i struktury danych - wykład 4. strona: 16
Zastosowanie stosu
Bardzo interesującym algorytmem, który w istotny sposób korzysta z
właściwości stosu jest algorytm przekształcenia wyrażenia arytmetycznego
z postaci infiksowej (zwykłej) do postaci ONP.
Przypomnijmy algorytm.
Wejście: input - wyrażenie w postaci zwykłej
Wyjście: output - wyrażenie w ONP
Pomocniczo: stos
Infix_To_Onp(){ // przekształca wyrażenie z input do output
DO {
wez_kolejny_element_z_wejścia;
IF ( element_jest_operandem )
dopisz_element_na_wyjscie ;
ELSE // element jest operatorem lub nawiasem
IF
(
element_jest_operatorem ) {
WHILE ( nie_pusty_stos && prior_operatora_na_stosie >= prior_elementu )
przepisz_operator_ze_stosu_na_wyjscie ;
wstaw_element_na_stos;
}
ELSE
IF ( element = ‘(‘ ) wstaw_element_na_stos;
ELSE
IF ( element = ‘)’ ) // przepisuj ze stosu do output aż do '('
WHILE ( na_stosie_operator )
przepisz_operator_ze_stosu_na_wyjscie ;
wyrzuc_ze_stosu_( ; // zapomnij o ')'
WHILE ( ! koniec_danych);
WHILE ( niepusty_stos )
przepisz_operator_ze_stosu_na_wyjscie ;
}
Poniżej plik: infix.java prezentuje realizację tego algorytmu w Javie.
// infix.java

Algorytmy i struktury danych - wykład 4. strona: 17
// przekształca wyra
ż
enia infiksowe na ONP
//--------------------------------------------------------------
import java.io.*; // operacje wejscia-wyjscia
class StackX // klasa stosu
{
private int maxSize;
private char[] stackArray;
private int top;
//--------------------------------------------------------------
public StackX(int s) // konstruktor
{
maxSize = s;
stackArray = new char[maxSize];
top = -1;
}
//--------------------------------------------------------------
public void push(char ch) // odkłada znak na stosie
{ stackArray[++top] = ch;
displayStack("stos: "); // *diagnostyka*
}
//--------------------------------------------------------------
public char pop() // zdejmuje znak ze stosu
{ char ch = stackArray[top--];
displayStack("stos: "); // *diagnostyka*
return ch;
}
//--------------------------------------------------------------
public char top() // podglada znak na szczycie stosu
{ return stackArray[top]; }
//--------------------------------------------------------------
public boolean isEmpty() // zwraca true, je
ż
eli stos pusty
{ return (top == -1); }
//-------------------------------------------------------------
public int size() // zwraca ilosc elementów na stosie
{ return top+1; }
//--------------------------------------------------------------
public void displayStack(String s)
{
System.out.print(s);
for(int j=0; j<size(); j++)
{
System.out.print(stackArray[j]);
System.out.print(' ');
}
System.out.println("");
}
//--------------------------------------------------------------
} // koniec klasy StackX
class InToONP // przekształca do ONP
{
private StackX theStack;
private String input;
private String output = "";
//--------------------------------------------------------------
public InToONP(String in) // konstruktor
{
input = in;
int stackSize = input.length();
theStack = new StackX(stackSize);
}
//--------------------------------------------------------------
public String doONP() // wykonuje przekształcenie
{

Algorytmy i struktury danych - wykład 4. strona: 18
for(int j=0; j<input.length(); j++) // dla ka
ż
dego znaku...
{
char ch = input.charAt(j); // ...pobieramy go z wejscia
switch(ch)
{
case '+': // + albo -
case '-':
gotOper(ch, 1); // zdejmujemy operatory o priorytecie
// wi
ę
kszym ni
ż
1
break;
case '*': // * albo /
case '/':
gotOper(ch, 2); // zdejmujemy operatory o priorytecie
// wi
ę
kszym ni
ż
2
break;
case '(': // nawias otwierajacy...
theStack.push(ch); // ...odkładamy na stosie
break;
case ')': // nawias zamykajšcy...
gotParen(ch); // zdejmujemy operatory
break;
default: // argument...
output = output + ch; // ...kopiujemy na wyjscie
break;
} // koniec switch
} // koniec for
while( !theStack.isEmpty() ) // zdejmujemy pozostałe na stosie
// operatory...
{
output = output + theStack.pop(); // ...i kopiujemy na wyjscie
}
theStack.displayStack("stos: empty "); // *diagnostyka*
return output; // zwracamy wyra
ż
enie przyrostkowe
} // koniec doONP()
//--------------------------------------------------------------
public void gotOper(char opThis, int prec1)
{ // pobrano operator z wejscia
while( !theStack.isEmpty() )
{
char opTop = theStack.pop();
if( opTop == '(' ) // je
ż
eli to '('
{
theStack.push(opTop); // odkładamy '('
break;
}
else // to operator
{
int prec2; // priorytet zdj
ę
tego operatora
if(opTop=='+' || opTop=='-') // okreslamy priorytet zdj
ę
tego
// operatora
prec2 = 1;
else
prec2 = 2;
if(prec2 < prec1) // je
ż
eli priorytet zdj
ę
tego mniejszy...
{ // ...ni
ż
wczytanego z wejscia
theStack.push(opTop); // odkładamy na stosie zdj
ę
ty operator
break;
}
else // priorytet zdj
ę
tego operatora...
output = output + opTop; // ...nie mniejszy ni
ż
wczytanego
} // koniec else (to operator)
} // koniec while
theStack.push(opThis); // odkładamy nowy operator na stosie
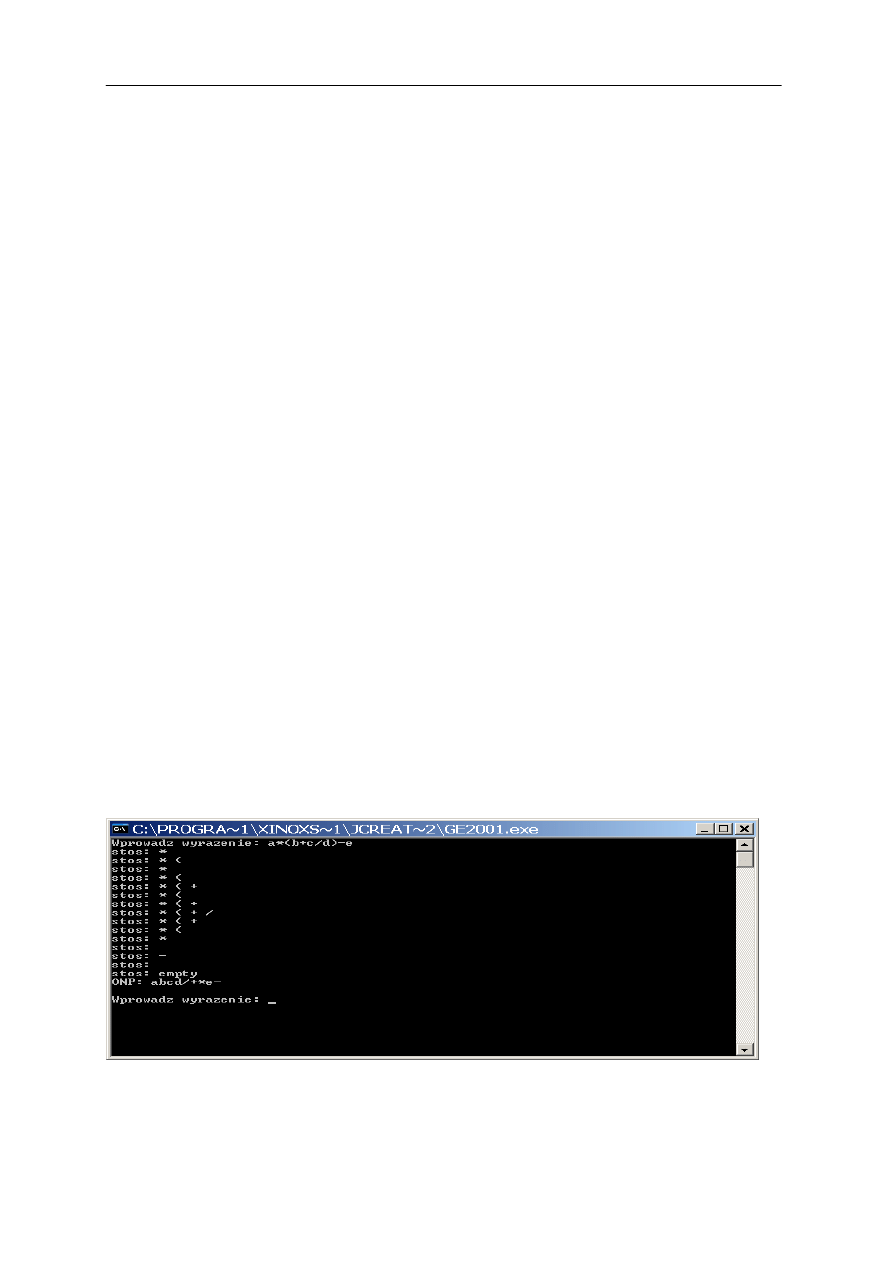
Algorytmy i struktury danych - wykład 4. strona: 19
} // koniec gotOper()
//--------------------------------------------------------------
public void gotParen(char ch)
{ // wczytano nawias zamykajacy
while( !theStack.isEmpty() )
{
char chx = theStack.pop(); // chx - symbol na wierzcholku stosu
if( chx == '(' ) // je
ż
eli zdj
ę
to '('...
break; // ...koniec p
ę
tli
else // je
ż
eli to operator...
output = output + chx; // ...kopiujemy go na wyjscie
} // koniec while
} // koniec gotParen()
//--------------------------------------------------------------
} // end class Infix_To_ONP
class InfixApp
{
public static void main(String[] args) throws IOException
{
String input, output;
while(true)
{
System.out.print("Wprowadz wyrazenie: ");
System.out.flush();
input = getString(); // wczytujemy napis z klawiatury
if( input.equals("") ) // koniec je
ż
eli sam [Enter]
break;
// tworzymy obiekt tłumaczacy
InToONP theONP = new InToONP(input);
output = theONP.doONP(); // wykonujemy tłumaczenie
System.out.println("ONP: " + output + '\n');
} // koniec while
} // koniec main()
//--------------------------------------------------------------
public static String getString() throws IOException
{
InputStreamReader isr = new InputStreamReader(System.in);
BufferedReader br = new BufferedReader(isr);
String s = br.readLine();
return s;
}
//--------------------------------------------------------------
} // koniec klasy InfixApp
Wyszukiwarka
Podobne podstrony:
APP Stosy Kolejki Listy 2011
APP Stosy Kolejki Listy
APP ZO 006 Stosy Kolejki Listy
zadania na stosy i kolejki
algorytmy listy stos kolejki
listy zadan, rach3
FM listy id 178271 Nieznany
Listy o A. Lisowskim, W, Rozmaitości
Lk Gabinet zabiegowy, Listy-Kontrolne-DOC
LISTY PAWLA-NOWY TESTMENT, Staropolka
Listy Biotechnologia2010-2011, Biotechnologia Enzymatyczna
więcej podobnych podstron