WOJSKOWA AKADEMIA TECHNICZNA

LABORATORIUM FIZYCZNE

prowadząca(y)

...............................................................

grupa

.....................

podgrupa

..........

zespół

..........

student(ka)

...............................................................

SPRAWOZDANIE Z PRACY LABORATORYJNEJ nr .....................

..............................................................................................................................................

pomiary wykonano dnia

.....................

jako ćwiczenie

.....................

z obowiązujących

.....................

OCENA ZA TEORIĘ

data

podejście

1 (zasadnicze)

2 (poprawa)

3

OCENA KOŃCOWA

data

Uwagi:

Strona 1 z 14

WOJSKOWA AKADEMIA TECHNICZNA

LABORATORIUM FIZYCZNE

prowadzący

dr inż. Konrad ZUBKO

grupa

F0x1s1

podgrupa

2

zespół

3

grupa szkoleniowa (1-3) (1-6)

student

Hordebert EKSPERYMENTATOR

Imię i Nazwisko

SPRAWOZDANIE Z PRACY LABORATORYJNEJ nr

0

nr zgodnie ze skryptem

RUCH W POLU GRAWITACYJNYM

temat zgodnie ze skryptem

pomiary wykonano dnia

13.09.2008

jako ćwiczenie

1

z obowiązujących

8

dd.mm.rrrr nr kolejny ilość prac

OCENA ZA TEORIĘ

data

podejście

1 (zasadnicze)

2 (poprawa)

3

OCENA KOŃCOWA

data

Uwagi:

•

tą stronę można pobrać z

www.wtc.wat.edu.pl

lub wykonać samodzielnie,

•

poniżej przedstawiony jest przykładowy schemat wykonania sprawozdania wraz z uwagami.

Strona 2 z 14

2. ISTOTA ĆWICZENIA nr 0

2.1 Celem ćwiczenia jest:

•

wyznaczenie wartości przyspieszenia ziemskiego

g w miejscu wykonywania doświadczenia,

z

pomiarów pośrednich;

•

wyznaczenie charakterystyki wagi sprężynowej

metodą regresji liniowej (kwadratów Gaussa),

•

.......... .

2.2 Wyznaczanie wielkości (

metody pomiaru i wyznaczania niepewności):

•

długość wahadła podana, jako stała stanowiska wraz z niepewnością standardową;

•

masa podwieszana do sprężyny podana, jako stała stanowiska bez niepewności;

•

okres drgań wahadła wyznaczam

metodą bezpośredniego odczytu z niepewnością określaną

metodą typu B;

•

przemieszczenia swobodnego końca sprężyny wyznaczam

metodą bezpośredniego odczytu z

niepewnością określaną

metodą typu A;

W metodzie

bezpośredniego odczytu (odchyleniowej), wartość wielkości mierzonej określona jest na

podstawie:

•

czasu – stopera, odchylenia wskazówki lub wskazania cyfrowego narzędzia pomiarowego,

•

długości – linijki, przyłożenia narzędzia pomiarowego do mierzonego obiektu.

Niepewność pomiaru wykonywanego tą metodą wynika głównie z:



istnienia dopuszczalnej systematycznej niepewności narzędzia pomiarowego określonego jego

klasą dokładności



lub niepewności maksymalnej określonej działką jednostkową.

2.3 Inne informacje

Oprócz metod bezpośredniego odczytu, istnieją też metody porównawcze:

a) różnicowa, b) przez podstawienie, c) zerowe

[ c1) mostkowa oraz c2) kompensacyjna ],

które nie są wykorzystane w tym ćwiczeniu.

Należy pamiętać o ograniczeniu: 1-2 strony A4 wykonane odręcznie!

Strona 3 z 14

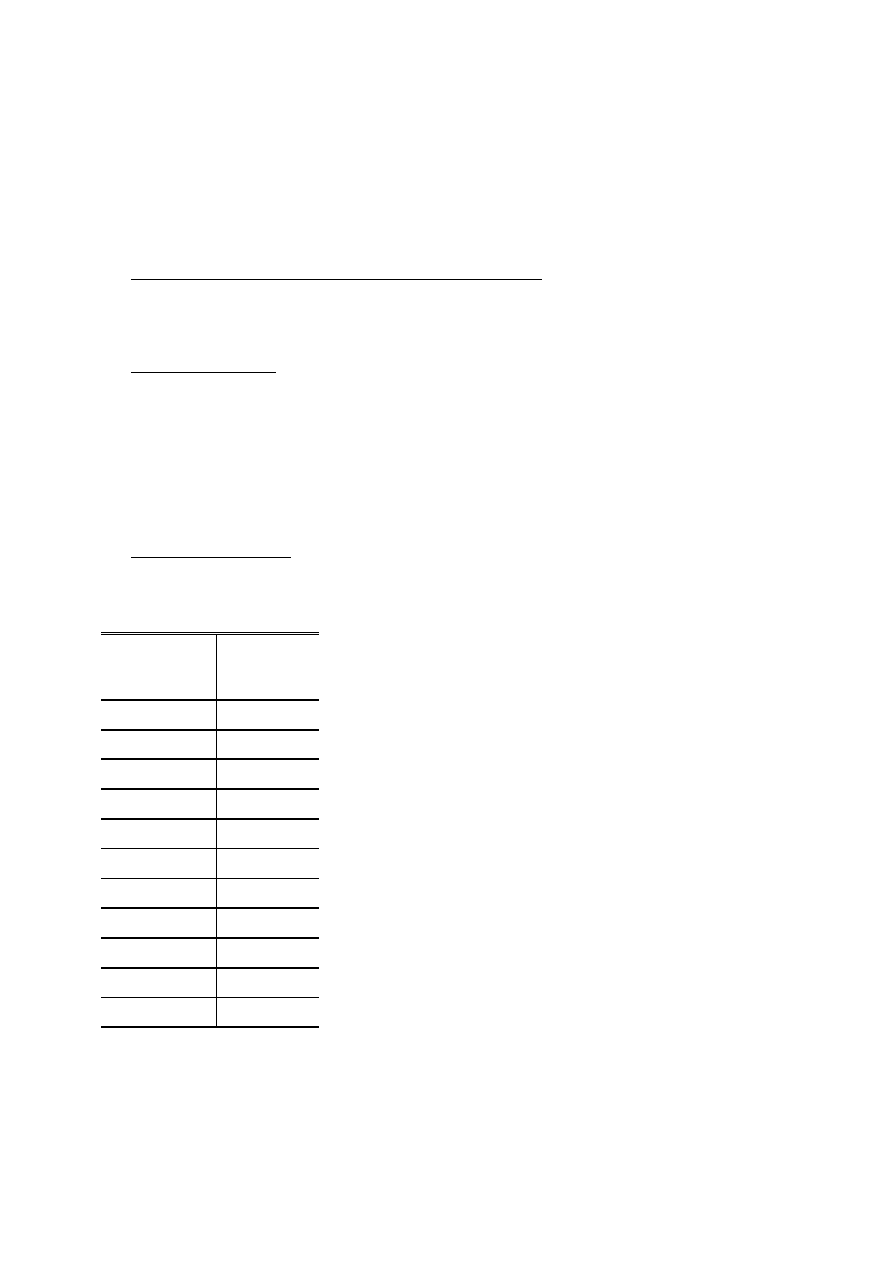
3. KARTA POMIARÓW DO ĆWICZENIA nr 0

Hordebert EKSPERYMENTATOR, F0x1s1

Zespół można wykonać jedną Kartę Pomiarów, ale do sprawozdania każda osoba ćwicząca musi

dołączyć czytelną kopię.

3.1 Wartości teoretyczne wielkości wyznaczanych lub określanych:

•

przyspieszenie ziemskie dla Warszawy g = 9,81225 m/s

2

(wg GUM, bez niepewności).

3.2 Parametry stanowiska:

•

długość wahadła d = 1 m, niepewność standardowa u(d) = 0,01 m;

•

masa każdego z 9-ciu odważników m

O

= 200 g, bez niepewności;

•

niepewność okresu drgań wahadła

T przy zastosowaniu stopera elektronicznego sprężonego z

fotokomórką wynosi u(T) = 0,02 s.

3.3 Pomiary i uwagi do nich:

3.3.1 Tabela pomiarów okresu drgań wahadła.

Pomiar czasu wykonano stoperem ręcznym w zastępstwie

uszkodzonego urządzenia.

Niepewność standardowa zostanie wyznaczona metodą typu B.

Niepewność maksymalna wyznaczenia okresu drgań wahadła za

pomocą stopera ręcznego silnie zależy od czasu reakcji

fizjologicznych eksperymentatora.

Kilkukrotne włączenie i wyłączenie stopera pozwoliło określić, że

czynności te zajmują do 0,2 s.

Na podstawie osądu eksperymentatora jako niepewność

maksymalną przyjęto

T

∆

= 0,2 s.

Strona 4 z 14

Numer próby

Okres drgań

i

T

[s]

Niepewność

0,20 [s]

1

2,00

2

1,91

3

2,09

4

1,99

5

2,01

6

1,98

7

2,02

8

1,97

9

2,03

10

2,00

3.3.2 Tabela pomiarów do testu wagi sprężynowej.

3.4 Inne:

........

13,09,2008

Konrad Zubko

Strona 5 z 14

Numer próby

Przemieszczenie swobodnego

końca sprężyny

i

x

[cm]

Masa podwieszana do swobodnego

końca sprężyny

i

m

[kg]

niepewność

1 [mm]

brak

1

0

0

2

2,9

0,2

3

6,0

0,4

4

9,0

0,6

5

11,8

0,8

6

14,8

1,0

7

17,8

1,2

8

20,7

1,4

9

24,0

1,6

10

26,0

1,8

4. OPRACOWANIE ĆWICZENIA nr 0

4.1 Wyznaczenie średniego okresu drgań wahadła matematycznego

Na podstawie danych z tabeli 3.3.1 wyznaczam wartość średnią okresu drgań wahadła

matematycznego:

∑

∑

=

=

=

=

10

1

1

10

1

1

i

i

n

i

i

T

T

n

T

[s]

(1)

skąd

T

= 2,00 s.

4.2 Wyznaczenie niepewności standardowej średniego okresu drgań wahadła matematycznego

4.2.1 Gdyby okres drgań wahadła matematycznego był wyznaczany za pomocą stopera

elektronicznego sprzężonego z fotokomórką, to niepewność standardowa wyznaczona metodą typu A

na podstawie danych z tabeli 3.3.1 i punktu 4.1 wynosiłaby:

( )

(

)

(

)

(

)

(

)

10

1

10

1

10

1

2

1

2

−

−

=

−

−

=

=

∑

∑

=

=

i

i

n

i

i

T

T

T

n

n

T

T

T

u

σ

[s]

(2)

skąd

( )

T

u

= 0,01453 s, a po zaokrągleniu

( )

T

u

= 0,015 s.

4.2.2 Okres drgań wahadła matematycznego był wyznaczany w pomiarze bezpośrednim za pomocą

stopera ręcznego i dlatego niepewność standardowa zostanie wyznaczona metodą typu B.

Niepewność maksymalna wyznaczenia okresu za pomocą stopera ręcznego silnie zależy od czasu

reakcji fizjologicznych eksperymentatora. Jako niepewność maksymalną przyjęto

T

∆

= 0,2 s.

Zakładam, że rozkład statystyczny tych wyników ma charakter jednorodny, a wtedy niepewność

standardowa:

( )

3

T

T

u

∆

=

[s]

(3)

skąd

( )

T

u

= 0,13867 s, a po zaokrągleniu

( )

T

u

= 0,14 s.

4.2.3 Ponieważ do niepewności standardowej okresu drgań wahadła mają wkład niepewności

wyznaczone ze wzorów (2) i (3), to łączna niepewność wynosi:

( )

( )

(

) (

)

2

2

2

2

13867

,

0

01453

,

0

3

+

=

∆

+

=

T

T

u

T

σ

(4)

skąd

( )

T

u

= 0,139429 s, a po zaokrągleniu

( )

T

u

= 0,14 s.

Strona 6 z 14

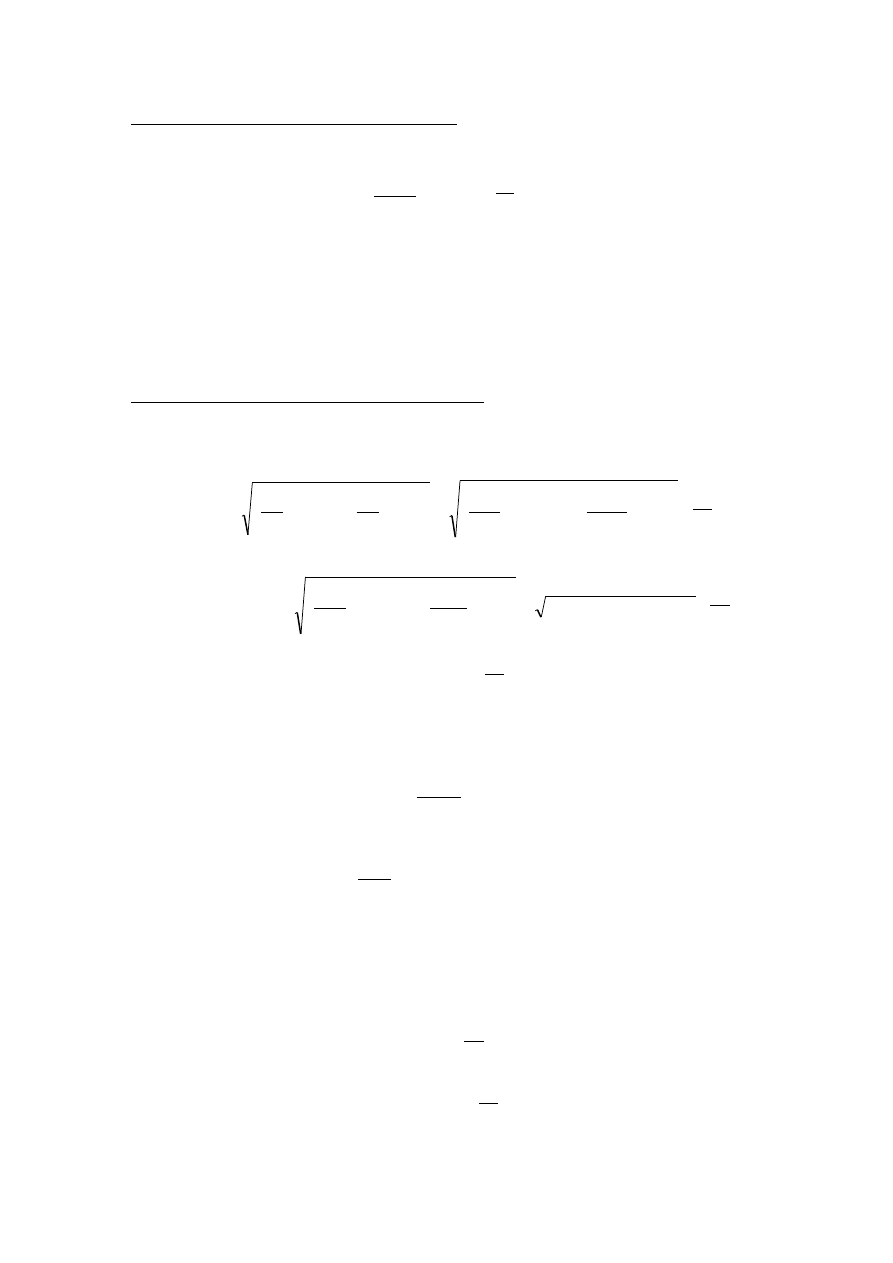
4.3 Wyznaczenie wartości przyspieszenia ziemskiego

Związek pomiędzy okresem wahań wahadła, jego długością i przyspieszeniem ziemskim:

2

2

4

T

d

g

π

=

[ ]









=

2

s

m

g

(5)

gdzie:

•

d - długość wahadła, wartość z punktu 3.2;

•

T - okres drgań wahadła, wyznaczony w punkcie 4.1;

stąd

=

g

9,8696 m/s

2

.

4.4 Wyznaczenie niepewności przyspieszenia ziemskiego

4.4.1 Niepewność złożona bezwzględna przyspieszenia ziemskiego wynosi:

( )

( )

( )

( )

( )

2

3

2

2

2

2

2

2

4

4













−

+













=









∂

∂

+









∂

∂

=

T

u

T

d

d

u

T

T

u

T

g

d

u

d

g

g

u

c

π

π









2

s

m

(6)

czyli

( )

477305

,

0

009741

,

0

14

,

0

2

1

4

01

,

0

2

4

2

3

2

2

2

2

+

=













−

+













=

π

π

g

u

c









2

s

m

(7)

stąd

( )

6987

,

0

=

g

u

c

, a po zaokrągleniu

( )

70

,

0

=

g

u

c









2

s

m

.

4.4.2 Niepewność złożona względna przyspieszenia ziemskiego wynosi

( )

( )

g

g

u

g

u

c

r

c

=

,

(8)

podstawiając zaokrąglone wartości mamy

( )

070922

,

0

87

,

9

70

,

0

,

=

=

g

u

r

c

(9)

a po zaokrągleniu

( )

071

,

0

,

=

g

u

r

c

.

4.4.3 Niepewność rozszerzona przyspieszenia ziemskiego wynosi

( )

( )

g

u

k

g

U

c

⋅

=









2

s

m

(10)

gdzie współczynnik rozszerzenia k=2, stąd

( )

4

,

1

=

g

U









2

s

m

.

Strona 7 z 14

4.4.4 W analizowanym przypadku zachodzi nierówność

)

(g

U

g

g

tablica

<

−









2

s

m

(11)

gdyż

05735

,

0

81225

,

9

86960

,

9

=

−









2

s

m

jest mniejsze niż 1,4









2

s

m

co oznacza, że zachodzi zgodności wyznaczonej wartości przyspieszenia ziemskiego z wartością

tabelaryczną.

4.5 Test wagi sprężynowej

Badano, jaką masą należy obciążyć wagę, aby osiągnąć żądane rozciągnięcie sprężyny. Związek

pomiędzy masą a ugięciem sprężyny dany jest:

x

g

k

m

=

























=

m

s

m

s

kg

kg

2

2

(12)

gdzie:

 m – masa powieszona do swobodnego końca sprężyny;

 x – ugięcie swobodnego końca sprężyny;

 g – przyspieszenie grawitacyjne;

 k – współczynnik sprężystości sprężyny.

Zależność

( )

x

g

k

x

m









=

można przedstawić jako prostą

b

ax

m

+

=

o nachyleniu

g

k

a

=

,

dla której

0

=

b

w przypadku idealnym.

4.6 Wyznaczenie charakterystyki wagi metodą najmniejszych kwadratów Gaussa

Otrzymane punkty eksperymentalne z tabeli 3.3.1 oraz obliczenia pomocnicze zestawiam w tabeli

4.6.1.

Otrzymana seria pomiarowa okresów wahadła wykazuje powtarzalność wyników,

gdyż spełniona jest relacja

)

(

min

max

T

U

T

T

<

−

(13)

gdzie

18

,

0

91

,

1

09

,

2

=

−

[s]

natomiast

( )

23

,

0

23094

,

0

3

2

,

0

2

3

2

≈

=

=

∆

=

T

T

U

[s].18,091,109,2

=−

Strona 8 z 14

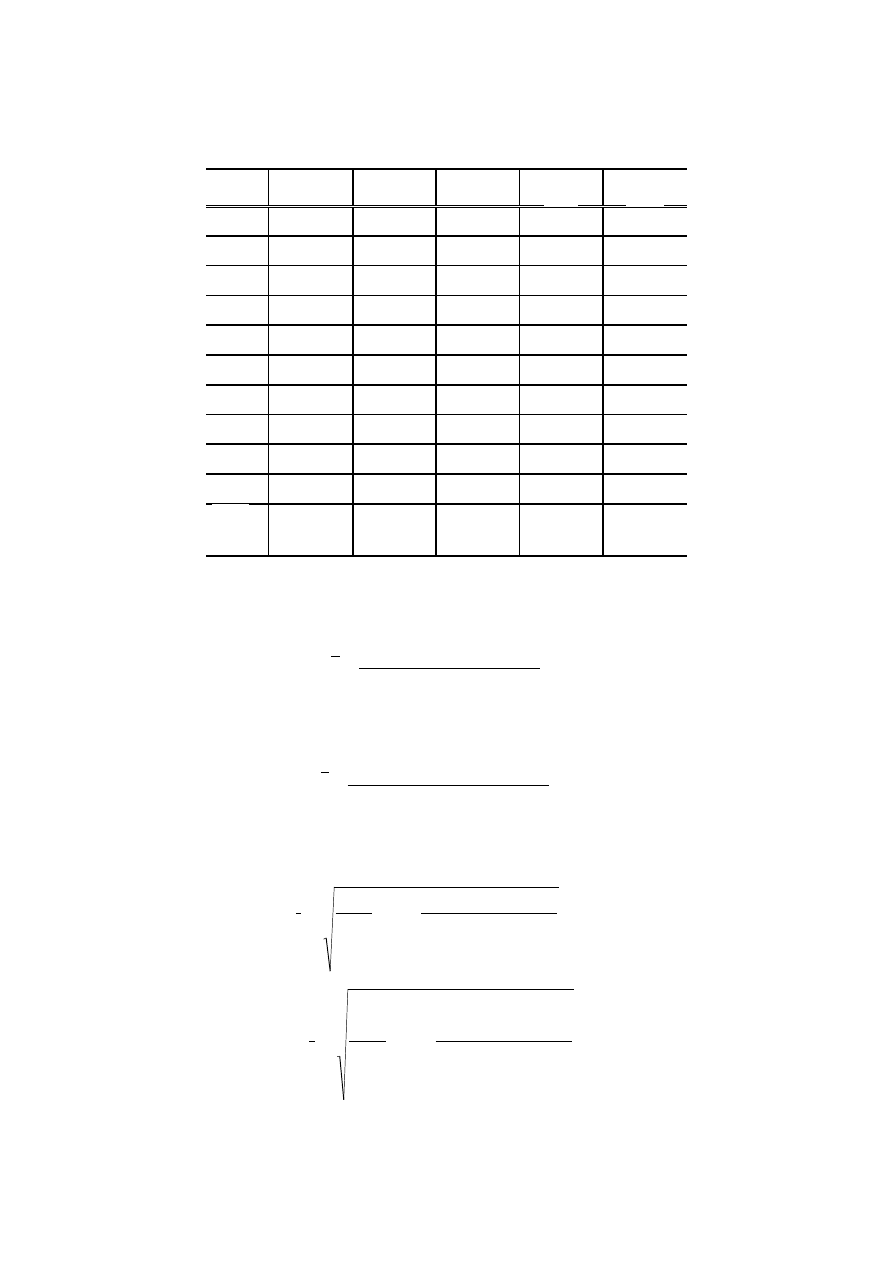
Tabela 4.6.1

Nr

i

x

[cm]

i

m

[kg]

i

i

m

x

2

i

x

2

i

m

1

0

0

0

0

0

2

2,90

0,2

0,58

8,41

0,04

3

6,00

0,4

2,40

36,00

0,16

4

9,00

0,6

5,40

81,00

0,36

5

11,80

0,8

9,44

139,24

0,64

6

14,80

1,0

14,80

219,040

1,00

7

17,80

1,2

21,36

316,840

1,44

8

20,70

1,4

28,98

428,50

1,96

9

24,00

1,6

38,40

576,00

2,56

10

26,00

1,8

46,80

676,00

3,24

∑

=

=

10

1

i

133,00

9,0

168,16

2481,00

11,40

Z tabeli wyznaczam parametry prostej:

∑

∑

∑

∑

∑

=

=

=

=

=

−













−

=

n

i

i

n

i

i

n

i

i

i

n

i

i

n

i

i

x

n

x

m

x

n

m

x

a

1

2

2

1

1

1

1

)

(

(14)

∑

∑

∑

∑

∑

∑

=

=

=

=

=

=

−













−

=

n

i

i

n

i

i

n

i

i

n

i

i

n

i

i

i

n

i

i

x

n

x

x

m

m

x

x

b

1

2

2

1

1

2

1

1

1

(15)

oraz ich odchylenia standardowe:

∑

∑

∑

=

=

=









−

ε

−

=

σ

n

i

n

i

i

n

i

i

i

a

x

x

n

n

n

1

2

1

1

2

2

2

1

(16)

∑

∑

∑

∑

=

=

=

=









−

ε

−

=

σ

n

i

n

i

i

n

i

i

n

i

i

i

b

x

x

n

x

n

1

2

1

1

2

1

2

2

2

1

(17)

Strona 9 z 14

gdzie:

∑

∑

∑

∑

=

=

=

=

−

−

=

n

i

n

i

n

i

i

i

i

n

i

i

i

m

b

m

x

a

m

1

1

1

1

2

2

ε

(18)

oraz współczynnik korelacji (0<R

2

<1), którego wartość bliska 1 świadczy o zgodności rozkładów

punktów eksperymentalnych z wyznaczoną prosta

(

)(

)

(

)

(

)

2

1

2

1

2

1

2

∑

∑

∑

=

=

=

−

−









−

−

=

n

i

i

n

i

i

n

i

i

i

m

m

x

x

m

m

x

x

R

(19)

W efekcie otrzymuję wartości:

 parametru

1

680

0

−

=

kgcm

a

,

oraz jego niepewności

1

0014

,

0

−

=

kgcm

a

σ

;

 parametru

kg

b

005

0,

−

=

oraz jego niepewności

kg

b

022

0,

=

σ

;

 parametru R

2

= 0,9993.

Końcowy efekt obliczeń przedstawiam w postaci wykresu (rys. 1) zaznaczając na nim punkty

eksperymentalne, ich niepewności pomiarowe, oraz wyznaczoną prostą.

4.7 Wyznaczenie współczynnika sprężystości sprężyny

Związek współczynnika sprężystości sprężyny ze współczynnikiem kierunkowym prostej oraz

przyspieszeniem grawitacyjnym dany jest wyrażeniem:

g

a

k

⋅

=









2

s

kg

(20)

gdzie:

 a - współczynnik kierunkowy prostej;

 g - przyspieszenie grawitacyjne.

Wartość współczynnika sprężystości sprężyny wynosi

16

,

671

87

,

9

68

=

⋅

=

k









2

s

kg

(21)

Strona 10 z 14

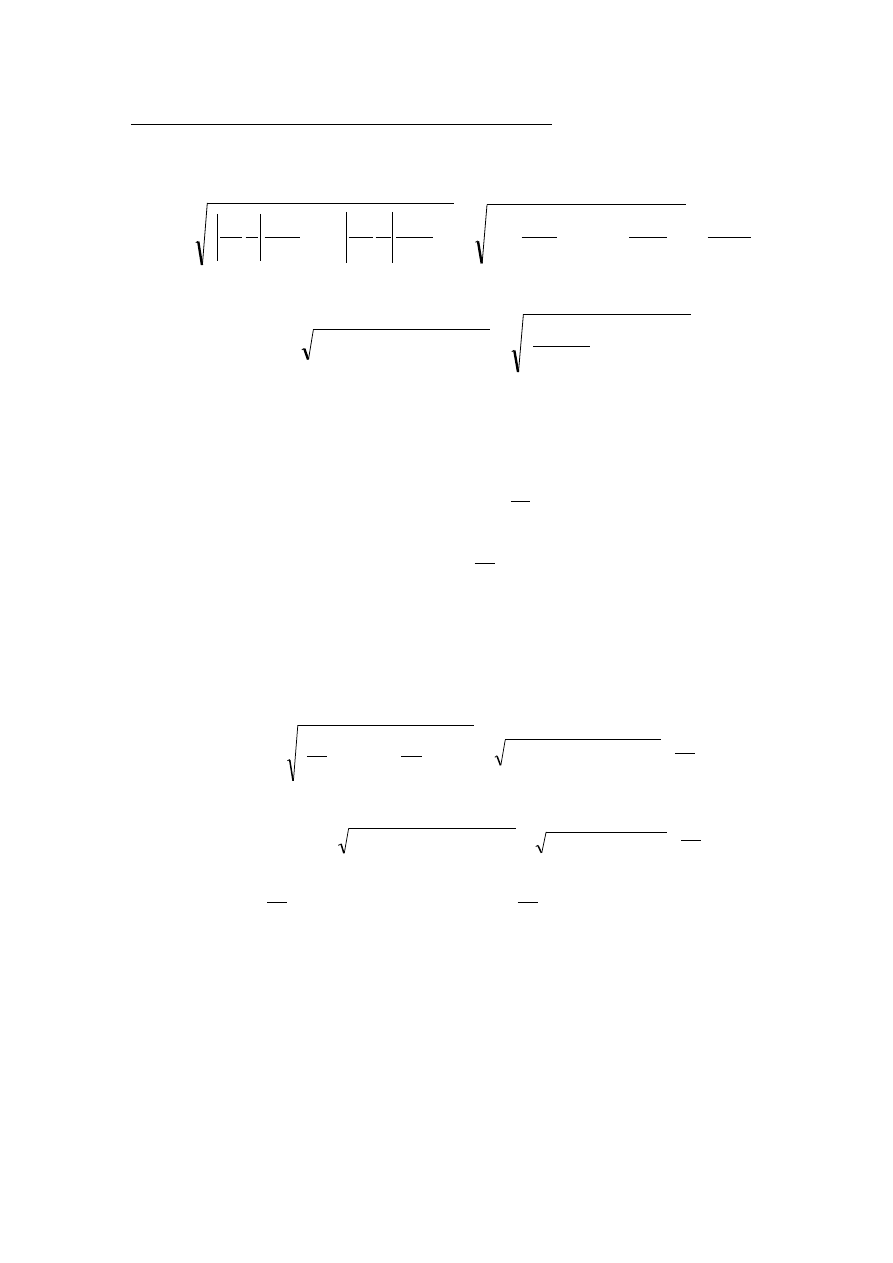
4.8 Wyznaczenie niepewności współczynnika sprężystości sprężyny

4.8.1 Niepewność złożona względna (liczona z użyciem wag) wynosi

( )

( )

( )

( )

( )

( )

k

k

u

g

g

u

w

a

a

u

w

g

g

u

k

g

g

k

a

a

u

k

a

a

k

k

u

c

g

a

r

c

=













+









=













∂

∂

+













∂

∂

=

2

2

2

2

,

(22)

ponieważ wagi dla funkcji klasy y(x)=Cx

n

wynoszą |n|, to

( )

( )

[

]

( )

[

]

[

]

2

2

2

2

,

071

,

0

6800

,

0

0014

,

0

1

1

+









=

⋅

+

⋅

=

g

u

a

u

k

u

g

c

r

c

(23)

stąd

( )

07153

,

0

,

=

k

u

r

c

, a po zaokrągleniu

( )

072

,

0

,

=

k

u

r

c

.

4.8.2 Niepewność rozszerzona wynosi

( )

( )

k

u

k

k

U

c

⋅

=









2

s

kg

(24)

gdzie współczynnik rozszerzenia k=2, stąd

( )

96

=

k

U









2

s

kg

.

Nie jest znana wartość teoretyczna współczynnika sprężystości sprężyny, więc nie można sprawdzać,

czy wyznaczona wartość jest zgodna z wartością tabelaryczną.

4.8.3 Niepewność złożona bezwzględna wynosi:

( )

( )

( )

( )

[

]

( )

[

]

2

2

2

2

g

u

a

a

u

g

g

u

g

k

a

u

a

k

k

u

c

⋅

+

⋅

=













∂

∂

+









∂

∂

=









2

s

kg

(25)

czyli

( )

[

] [

]

76

,

2265

9094

,

1

7

,

0

68

14

,

0

87

,

9

2

2

+

=

⋅

+

⋅

=

k

u

c









2

s

kg

(26)

stąd

( )

6201

,

47

=

k

u

c









2

s

kg

, a po zaokrągleniu

( )

48

=

k

u

c









2

s

kg

.

Strona 11 z 14

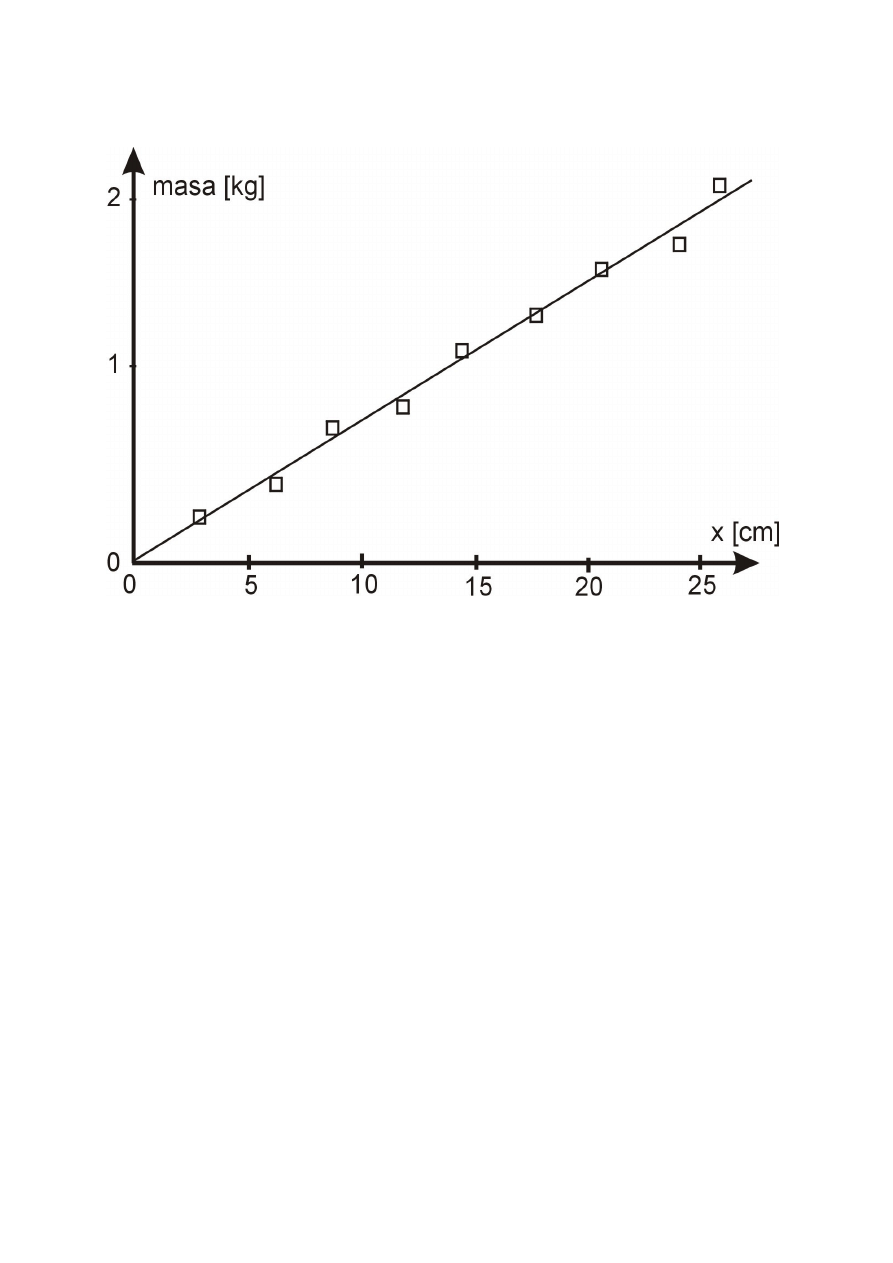
Charakterystyka wagi sprężynowej m = 0,680 x - 0,005

Wykresy należy wykonać zgodnie z opisem w skrypcie, uwzględniając w szczególności:

•

wykonanie odręcznie na arkuszach A4 papieru milimetrowego,

•

podanie tytuły wykresów z podaniem znaczenia ewentualnie użytych symboli,

•

opis osi (wartości, symbole, jednostki),

•

dobranie zakresów zmiennych tak, by przedstawiane funkcje obejmowały większość

powierzchni wykresu (skale dobrać tak by było widać istotne zależności),

•

naniesienie niepewności wartości przedstawianych na wykresach,

•

przybliżenie przebiegu funkcji krzywą znaną z teorii analizowanego zjawiska:

o

odręcznie dla funkcji innych niż prosta,

o

metodą regresji liniowej dla prostych y=ax+b (naniesienie na wykres),

•

wykreślenie rodziny porównywanych funkcji na oddzielnym arkuszu,

•

wyznaczając wartości parametrów graficznie należy na wykresie pozostawić odpowiednie linie

pomocnicze (proste, okręgi, zaznaczając istotne punkty przecięć) .

Nie wykonywać wykresów „giełdowych”- łącząc punkty pomiarowe odcinkami!

Strona 12 z 14

5. OCENA REZULTATÓW I WNIOSKI

5.1 Zestawienie wartości:

•

wynik i niepewność standardowa (możliwe są 3 równoważne sposoby zapisu):

•

przyspieszenie ziemskie jest równe 9,87 ms

-2

, a niepewność standardowa pomiaru 0,70 ms

-2

,

•

g=9,87 ms

-2

, u(g)=0,70 ms

-2

•

g=9,87(70) ms

-2

lub g = 9,87(0,70) ms

-2

•

niepewność względna (możliwe są 2 równoważne sposoby zapisu)

•

niepewność względna pomiaru 0,071

•

( )

=

g

u

r

c,

0,071

•

wynik i niepewność poszerzona (możliwe są 3 równoważne sposoby zapisu):

•

przyspieszenie ziemskie jest równe 9,87 ms

-2

, a niepewność rozszerzona pomiaru 1,4 ms

-2

,

•

g=9,87 ms

-2

, U(g)=1,4 ms

-2

•

g=(9,87

±1

,4) ms

-2

•

wartość teoretyczna dla Warszawy g = 9,81225 ms

-2

wyznaczona przez GUM.

Wyniki pomiarów i obliczeń należy podawać w jednostkach, dla których wartość liczbowa zawarta jest w

przedziale od 0,1 do 1000, dodając d symbolu odpowiedniej jednostki właściwy przedrostek.

Analogicznie należy zestawić wyniki dla współczynnika sprężystości sprężyny.

5.2 Ocena rezultatów:

•

wpływu wielkości mierzonych bezpośrednio lub parametrów stanowiska na niepewność wyniku

końcowego:

W przypadku przyspieszenia grawitacyjnego (punkt 4.4.1, wzór 7) widać, że największy wpływ na

niepewność złożoną ma niepewność pomiaru bezpośredniego z użyciem stopera ręcznego.

•

wartości niepewności względnej, pod kątem rodzaju popełnianych błędów (Grubych,

Przypadkowych, Systematycznych):

W przypadku przyspieszenia grawitacyjnego (punkt 4.4.2, wzór 9) widać, że niepewność względna

wynosząca 0,071 jest mniejsza od 0,12, co przy wykonaniu 10-ciu pomiarów okresu stanowi, że

wpływ błędów grubych i systematycznych na wynik końcowy nie jest znaczący.

•

relacji wartości teoretycznej i przedziału (wartość wyznaczona +/- niepewność poszerzona) pod

kątem rodzaju popełnianych błędów (G, P, S):

W przypadku przyspieszenia grawitacyjnego (punkt 4.4.4, wzór 11) widać, że zachodzi zgodności

wyznaczonej wartości przyspieszenia ziemskiego z wartością tabelaryczną, czyli wpływ błędów

grubych i systematycznych na wynik końcowy nie jest znaczący.

Strona 13 z 14

•

Uwzględniając uwagę (punkt 4.4.4) iż otrzymana seria pomiarowa okresów wahadła wykazuje na

powtarzalność wyników, oraz powyższe uwagi należy przyjąć, że nie popełniono błędów grubych, a

niepewności wyników zależą głownie od błędów przypadkowych.

Analogicznie należy przedstawić ocenę dla współczynnika sprężystości sprężyny. Należy się

zastanowić, czy lepiej jest wykonać oddzielne analizy dla przyspieszenia grawitacyjnego i

współczynnika sprężystości, czy jedną łączną.

•

wyników przedstawionych na wykresach, w tym pod kątem rodzaju popełnianych błędów (G, P, S):

Charakter rozkładu punktów pomiarowych wokół wyznaczonej prostej na rysunku 1 oraz wartość

współczynnika korelacji (punkt 4.6, wzór 19 ) świadczą, że nie popełniono błędów grubych.

•

............ .

5.3 Wnioski:

•

wykazanie czy cel ćwiczenia (został / nie został) osiągnięty:

Cel ćwiczenia: wyznaczenie wartości przyspieszenia ziemskiego g oraz wyznaczenie

charakterystyki wagi sprężynowej został osiągnięty gdyż uzyskano wyniki obarczone akceptowalną

niepewnością.

•

uwagi na temat możliwości dokładniejszego wykonania i opracowania ćwiczenia w przyszłości

(niedoskonałości wynikają z działań eksperymentatora, przyrządów pomiarowych, metod

pomiarowych, mierzonych obiektów):

Celem podniesienia dokładności pomiarów okresu wahadła należy wyeliminować udział

eksperymentatora z pomiaru czasu i zastąpić go pomiarem automatycznym o mniejszej

niepewności.

•

............ .

Należy także przedstawić wnioski dla współczynnika sprężystości sprężyny.

Strona 14 z 14