6. Dopasowywanie modeli do danych

W procesie dopasowywania modelu matematycznego y

m

= g

m

(u,θ) do dodanych

eksperymentalnych wyodrębnić można dwa podstawowe etapy:

• identyfikację strukturalną, czyli dobór g

m

– odpowiedniego do problemu typu równań

matematycznych i powiązań między nimi (może się ona odbywać na drodze analizy
struktury fizycznej obiektu lub empirycznie);

• estymację parametrów, polegająca na doborze takich wartości parametrów modelu θ , aby

jak najdokładniej opisywał on posiadane dane (poza przypadkiem stosowania praw lub
teorii fizycznych, w których wartości parametrów są określone, ma ona charakter
empiryczny).

6.1. Estymacja parametrów jako zadanie odwrotne

Estymacja parametrów modelu jest zadaniem odwrotnym drugiego rodzaju. Na podstawie
skutku, jakim są dane wyjściowe y (uzyskane dla pewnego pobudzenia u) wyznaczana jest
przyczyna takiej, a nie innej ich postaci, a są nią wartości parametrów modelu θ. Rozwiązanie
tego zadania wymaga formalnego odwrócenia związku przyczynowo-skutkowego
wyrażonego przez model g

m

, jego struktura mus być zatem znana.

Estymacja parametrów modeli fizykomatematycznych, gdzie odzwierciedlają one
właściwości fizyczne modelowanego obiektu, jest równoważna z pośrednim pomiarem
złożonym tych właściwości.

Można się zastanawiać, czy estymacja parametrów danego modelu (o znanej strukturze g

m

) jest jednakowo

efektywna dla dowolnego pobudzenia u, czy też istnieje pewne u optymalne, dające najdokładniejsze
oszacowanie θ. Na pytanie to odpowiada teoria planowania eksperymentów (rozdz. 8).

6.2. Estymacja parametrów modeli liniowych

Model może być liniowy np. względem wejść, parametrów, zmiennych stanu itd. W rozdziale
tym pod pojęciem „model liniowy” rozumiane będą modele liniowe względem parametrów
(LP), gdyż właśnie ta cecha determinuje postać algorytmów estymacji.

Przypomnijmy, że model liniowy musi spełniać zasadę superpozycji:













2

1

2

1

,

,

,

θ

u

θ

u

θ

θ

u

y

m

m

m

m

bg

ag

b

a

g









,

gdzie a i b są skalarami, a całkowity wektor parametrów to θ





T

T
2

T

1

θ

θ



. Model taki,

uwzględniając przekształcenie pobudzenia u przez funkcję (liniową lub nieliniową) f

i

, można

ogólnie zapisać jako:

 

 

θ

u

θ

u

y

i

m

m

f

g





,

,

2

Techniki eksperymentu

(© A.G. Polak 2014)

lub posługując się macierzą eksperymentu (tożsamą z macierzą wrażliwości):

Xθ

y



m

,

gdzie dla N próbek i p parametrów:

 

 

 

 





























N

p

N

p

m

u

f

u

f

u

f

u

f











1

1

1

1

θ

y

X

.

Zwykle liczba obserwacji (danych w spróbkowanych sygnałach u i y) jest większa od liczby
parametrów θ, tj. N > p.

Przykładem może być model w postaci szeregu potęgowego 3-go rzędu:

 

 

 

 

.

3

4

2

3

2

1

4

4

3

3

2

2

1

1

u

u

u

1

u

u

u

u

y

































f

f

f

f

m

Wtedy macierz eksperymentu przyjmie postać:























3

3

1

1

1

1

N

N

u

u

u

u













X

.

Ostatecznie zarejestrowane dane wyjściowe y to (w uproszczeniu) wyjście modelu y

m

zakłócone addytywnym szumem v:

v

y

y





m

.

6.2.1. Podstawowe założenia

Podczas estymacji parametrów modelu w oparciu o dane eksperymentalne najczęściej zakłada
się, że można je traktować jako realizację zmiennej losowej y opisanej funkcją gęstości
prawdopodobieństwa p(y,θ), co wypływa ze stochastycznego charakteru wektora parametrów

θ :

 

θ

u

y

,

0

g



lub szumu v:





ν

θ

u

y





0

0

,

g

.

4. Wsadowe metody estymacji parametrów modeli liniowych

3

Prawdziwy (hipotetyczny) model związku przyczynowo-skutkowego o charakterze
deterministycznym oznaczony jest tu jako g

0

, a θ

0

to prawdziwe wartości parametrów tego

modelu.

Wektor v traktowany jest jako realizacja zmiennej losowej v. Jeżeli szum jest skorelowany, to
macierz jego kowariancji wynosi

 

 

R

νν

ν





T

cov

E

.

W szczególności, gdy szum jest nieskorelowany, macierz kowariancji ma postać:









2

2

2

2

1

diag

N











R

,

lub dodatkowo dla szumu stacjonarnego:

I

R

2

v





.

Często zakłada się też, że addytywne zakłócenia losowe mają charakter szumu białego
(gaussowskiego):

e

ν



, gdzie e to realizacja szumu białego o wariancji

2

e



.

Koncepcja wyjaśniająca losowy charakter danych wynikający z ich zakłócenia addytywnym
szumem pozwala następująco scharakteryzować właściwości statystyczne y:

 





 

R

y

θ

u

y







cov

,

0

0

g

E

.

Natomiast w przypadku losowego charakteru wektora parametrów, θ

0

należy interpretować

jako

 

θ

E

.

6.2.2. Metody wsadowe

Metody wsadowe pozwalają na obliczenie estymatorów parametrów modelu matematycznego
na podstawie wcześniej zarejestrowanych danych pomiarowych (off-line). W przypadku
modeli liniowych realizujące je algorytmy są jednokrokowe i stosunkowo nieskomplikowane.
Wadą ich jednak jest to, że estymacja może być przeprowadzona dopiero po zakończeniu
eksperymentu, a nie w czasie jego trwania.

6.2.2.1. Metody bayesowskie

Metody bayesowskie wykorzystują prawdopodobieństwa warunkowe. Do ich grona należy
metoda maksymalnego prawdopodobieństwa a posteriori (MAP). Dane eksperymentalne y
traktowane są w niej jako znane, natomiast θ jako wektor losowy. Estymator

MAP

θˆ

uzyskuje

się maksymalizując prawdopodobieństwo tego, że pochodzi on z systemu o zarejestrowanym
(ustalonym) y:





y

θ

θ

θ

|

max

arg

ˆ

f

MAP



,

4

Techniki eksperymentu

(© A.G. Polak 2014)

gdzie funkcja gęstości prawdopodobieństwa a posteriori

 

y

θ |

f

na podstawie wzoru Bayesa

wynosi:







  

 

y

θ

θ

y

y

θ

f

f

f

f

|

|



.

Funkcja gęstości prawdopodobieństwa

 

θ

y |

f

znajdująca się w liczniuku nazywana jest

funkcją

wiarygodności

L(y,θ).

Ponieważ

y

jest

ustalone,

maksymalizacja

prawdopodobieństwa a posteriori sprowadza się do maksymalizacji licznika:

   

θ

θ

y

θ

θ

f

L

MAP

,

max

arg

ˆ



.

W celu wyznaczenia wartości estymatora

MAP

θˆ

konieczna jest zatem aprioryczna znajomość

funkcji gęstości prawdopodobieństwa wektora parametrów f(



), co jednak rzadko ma miejsce.

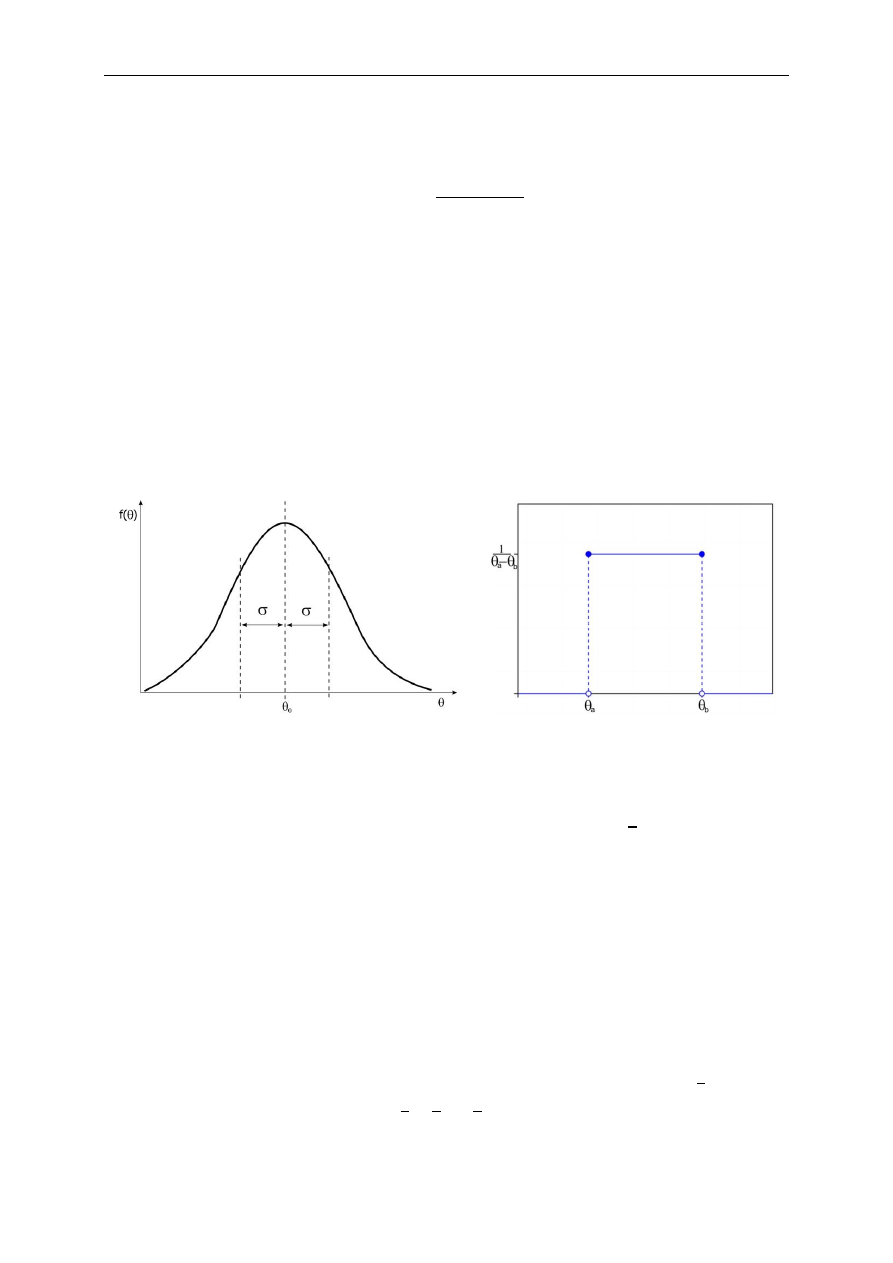
W sprzyjających okolicznościach dostępne są typy poszczególnych rozkładów (rys.) oraz
estymaty ich dwóch pierwszych momentów, tj. wartości oczekiwanej i wariancji [Nied’09].

Rys. Przykładowe rozkłady gęstości prawdopodobieństwa parametru: normalny (lewy panel) i jednostajny

(prawy panel)

6.2.2.2. Metoda największej wiarygodności

W metodzie największej wiarygodności (ML) dane eksperymentalne y traktowane są jako
zmienna losowa, a



jako nieznany, lecz ustalony wektor parametrów. Estymację można

interpretować jako wybór takiego wektora parametrów, dla którego zarejestrowane dane są
najbardziej prawdopodobne (wg funkcji wiarygodności L).

Przy maksymalizacji prawdopodobieństwa wystąpienia zaobserwowanych wartości y (tzn. ich
wiarygodności) postępuje się analogicznie jak przy dopasowaniu odpowiedzi modelu do
pomiarów tyle, że tym razem model odpowiedzi ma charakter statystyczny, podany w postaci
funkcji gęstości prawdopodobieństwa wystąpienia ich określonych wartości.

Funkcja gęstości prawdopodobieństwa ciągu próbek

N

y

y ,...,

1

sygnału odpowiedzi na znane

pobudzenie ma postać wielowymiarową, a wartości próbek zależą od poszukiwanych
parametrów modelu θ. Każda z próbek jest realizacją pewnej zmiennej losowej y

i

, a funkcja

gęstości opisuje cały wektor zmiennych





N

y

y ,...,

1



y

w sposób łączny.

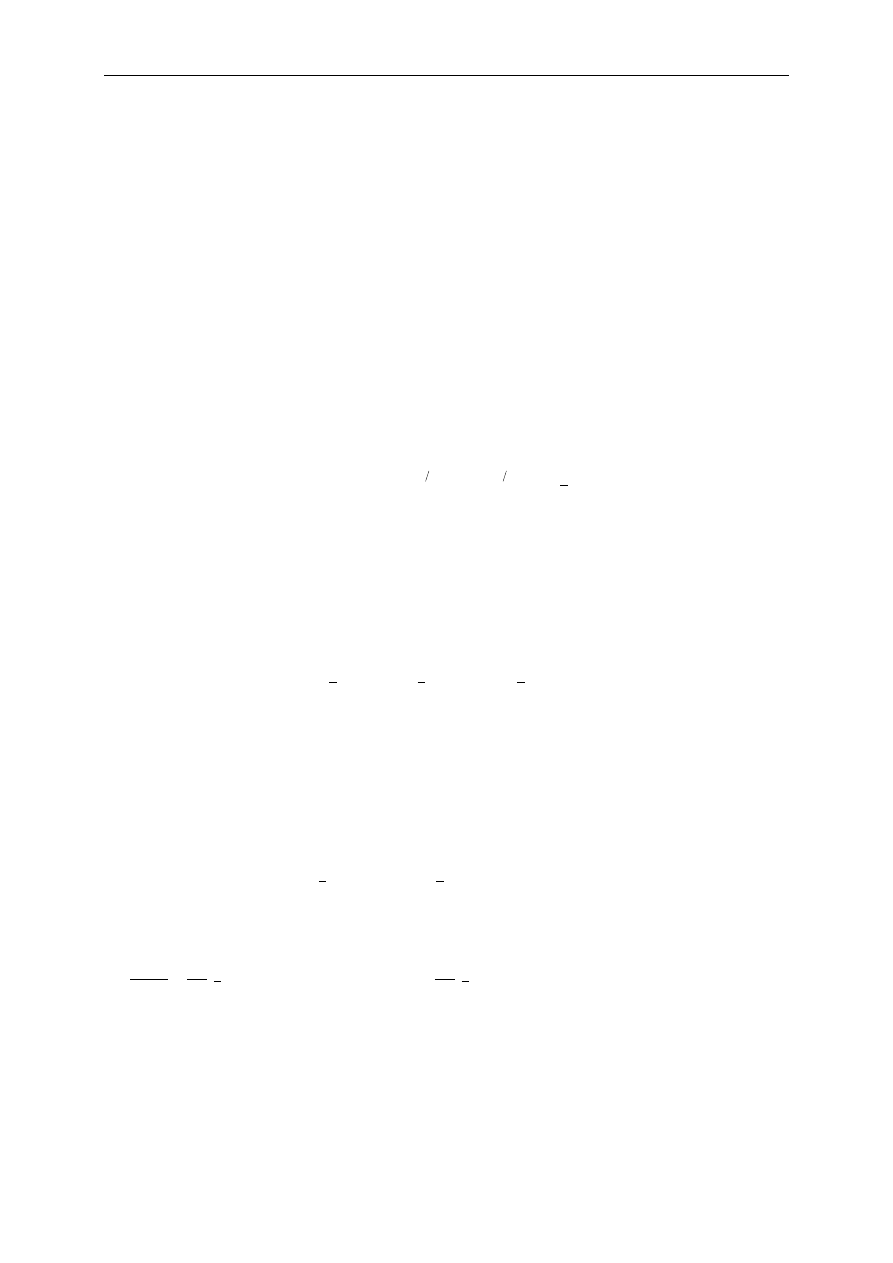
4. Wsadowe metody estymacji parametrów modeli liniowych

5

Estymator

ML

θˆ

maksymalizuje funkcję wiarygodności L(y,θ) ≡ f(y|θ):

 

θ

y

θ

θ

,

max

arg

ˆ

L

ML



.

Maksymalizacja może być przeprowadzona tylko przy znajomości postaci funkcji
wiarygodności. Zatem, aby obliczyć

ML

θˆ

, należy znać lub założyć na podstawie posiadanej

wiedzy jej jawną postać zależną od θ.

W ogólności poszukiwanie ekstremum nieliniowej funkcji L sprowadza się do problemu
optymalizacyjnego (patrz rozdz. 3.4). W przypadku pewnych rozkładów gęstości
prawdopodobieństwa zadanie upraszcza się jednak do estymacji liniowej. Takim
przypadkiem, najczęściej też stosowanym w praktyce, jest opis addytywnych zakłóceń
pomiaru poprzez rozkład normalny, a w szczególności przez ich macierz kowariancji R.
Wtedy wielowymiarowy rozkład łączny ma funkcję gęstości prawdopodobieństwa (funkcję
wiarygodności) postaci:



 

  

 





 

 





θ

ε

R

θ

ε

R

R

θ

y

θ

y

1

T

2

1

2

1

2

exp

det

2

,

,

|













N

L

f

π

,

gdzie wektor rezyduów (reszt):

ε(θ) = y – y

m

(θ).

Korzystając z faktu, iż logarytm jest funkcją monotoniczną, poszukiwanie maksimum funkcji
wiarygodności sprowadza się do poszukiwaniu maksimum jej logarytmu naturalnego postaci:

 

 





 

 

θ

ε

R

θ

ε

R

1

T

2

1

2

1

2

1

det

ln

π

2

ln

ln











N

L

,

co upraszcza obliczenia. Ponieważ pierwsze dwa składniki maksymalizowanego wyrażenia
nie zależą od estymowanych parametrów, to ostatecznie maksymalizacja funkcji
wiarygodności prowadzi do minimalizacji (znak minus przy ostatnim czynniku) funkcjonału

 

θ

ML

V

:

 

 





 

 

 

 





 





.

,

min

arg

ln

max

arg

ˆ

1

T

2

1

1

T

2

1

θ

y

y

R

θ

y

y

θ

ε

R

θ

ε

θ

θ

θ

θ

θ

m

m

ML

ML

ML

V

V

L

















Różniczkując macierzowo funkcję kryterialną V

ML

(θ) względem θ

 





 

























Xθ

y

R

X

Xθ

y

R

Xθ

y

θ

θ

y

y

R

θ

y

y

θ

θ





































1

T

1

T

2

1

1

T

2

1

m

m

ML

V

i przyrównując pochodną do zera:





y

R

X

θ

X

R

X

θ

X

R

X

y

R

X

θ

X

y

R

X

1

T

1

T

1

T

1

T

1

T

ˆ

,

0

ˆ

,

0

ˆ

























ML

ML

ML

6

Techniki eksperymentu

(© A.G. Polak 2014)

Znajduje się minimum V

ML

dla estymatora postaci:





y

R

X

X

R

X

θ

1

T

1

1

T

ˆ









ML

o macierzy kowariancji S

ML

:

 





1

1

T

ˆ

cov









X

R

X

θ

S

ML

ML

.

Warto zauważyć, że estymator ML jest szczególnym przypadkiem estymatora MAP wtedy,
gdy rozkłady gęstości prawdopodobieństwa parametrów modelu są jednostajne:

 

t

f

MAP

ML

cons





θ

θ

θ

ˆ

ˆ

,

gdyż wtedy:

   

 

ML

MAP

L

f

L

θ

θ

y

θ

θ

y

θ

θ

θ

ˆ

,

max

arg

,

max

arg

ˆ







.

6.2.2.3. Metoda najmniejszych kwadratów

W metodzie najmniejszych kwadratów (LS), wprowadzonej przez Legendre’a i Gaussa,
zakłada się addytywny charakter szumu będącego realizacją nieskorelowanych zmiennych
losowych o rozkładzie normalnym, zerowej wartości oczekiwanej i jednakowej wariancji (co
w wielu wypadkach jest uzasadnione dzięki centralnemu twierdzeniu granicznemu). Podejście
to wymaga zatem niewielkiej wiedzy apriorycznej.

Estymator

LS

θˆ uzyskuje się minimalizując odległość modelu y

m

(θ) od danych

eksperymentalnych y w przestrzeni l

2

(odległość euklidesowa):

 

θ

θ

θ

LS

LS

V

min

arg

ˆ



,

gdzie funkcjonał V

LS

ma postać:

 

 











 



.

,

T

2

2

1

2

2

2

Xθ

y

Xθ

y

Xθ

y

θ

θ

y

y

θ























N

i

i

m

i

m

LS

u

y

y

V

Zauważmy, że podejście to stosowane jest przy założeniu, że addytywne błędy pomiarowe e
występują tylko w zmiennej zależnej (zarejestrowany sygnał wyjściowy y), natomiast
zmienna niezależna (pobudzenie u) znana jest bezbłędnie (rys).

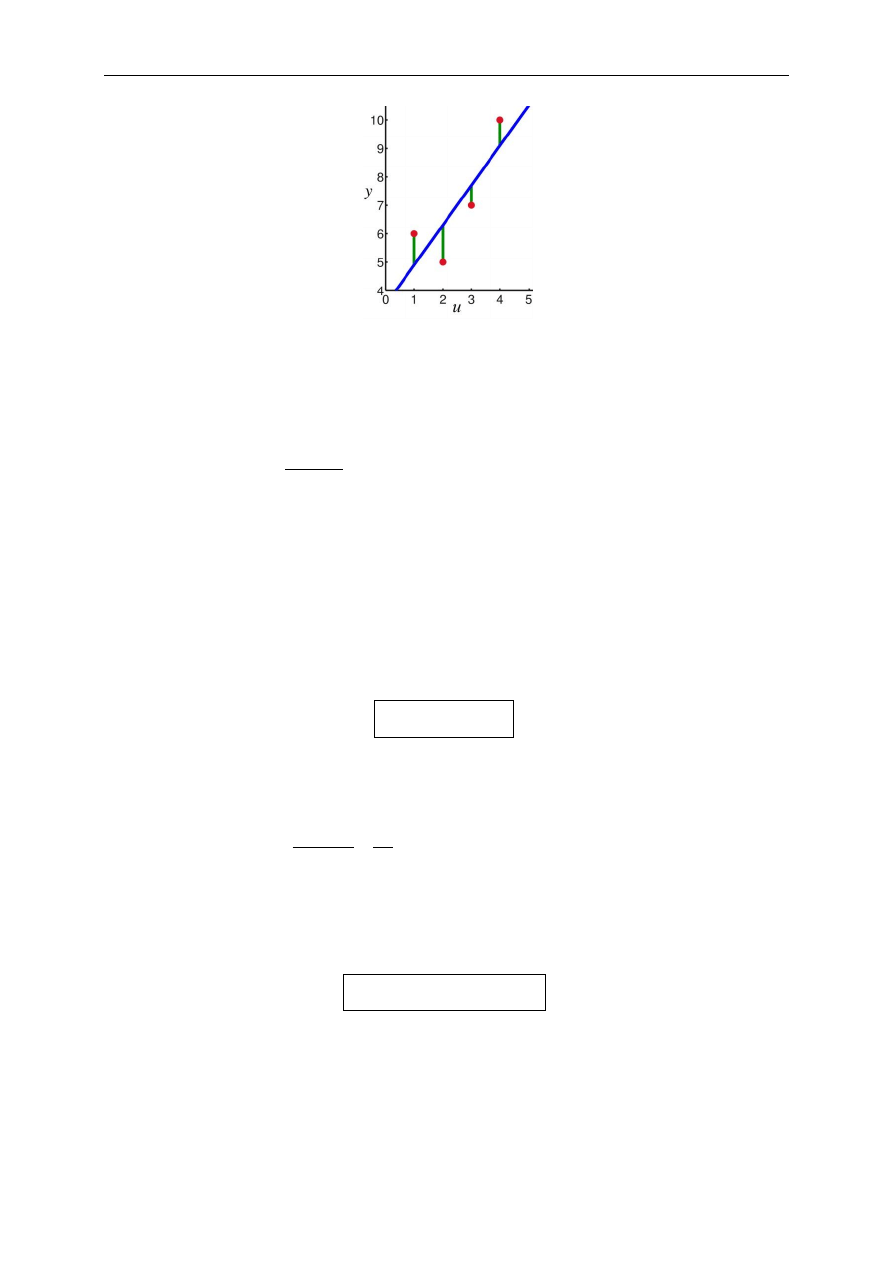
4. Wsadowe metody estymacji parametrów modeli liniowych

7

Rys. Ilustracja błędów zmiennej zależnej y w metodzie najmniejszych kwadratów

W celu znalezienia wektora parametrów dającego minimum funkcjonału należy
zróżniczkować V

LS

względem θ:





Xθ

X

y

X

Xθ

y

X

θ

θ

T

T

T

2

2

2

)

(

















LS

V

i uzyskane wyrażenie na pochodną przyrównać do zera:

.

ˆ

,

0

ˆ

2

2

T

T

T

T

y

X

θ

X

X

θ

X

X

y

X









LS

LS

Macierz X

T

X o wymiarze p



p (gdzie p to liczba parametrów) jest kwadratowa i jeżeli jest

nieosobliwa, to można ją odwrócić uzyskując wyrażenie na estymator:

 

y

X

X

X

θ

T

1

T

ˆ





LS

.

Warunkiem na to, że wyznaczone ekstremum to minimum, jest dodatnio określony hessian,
czyli macierz drugich pochodnych:

 





X

X

Xθ

X

y

X

θ

θ

θ

T

T

T

2

2

2

2

2

















LS

V

.

Macierz X

T

X jest dodatnio określona, zatem znalezione ekstremum to minimum.

Macierz kowariancji estymatora LS dana jest przez:

 

 

1

T

2

ˆ

cov







X

X

θ

S

e

LS

LS



,

gdzie

2

e



, dla przypomnienia, jest wariancją addytywnego szumu białego. Ponieważ metodę

LS stosuje się w sytuacjach, w których nieznane są właściwości statystyczne zakłóceń, nie
można wyznaczyć odchyleń standardowych estymatorów bezpośrednio z powyższego wzoru
(wartość

2

e



nie jest znana). Wariancję szumu można jednak oszacować na podstawie

8

Techniki eksperymentu

(© A.G. Polak 2014)

rezyduów, zakładając bezbłędność modelu. Wtedy błąd średniokwadratowy V

MSE

dopasowania modelu do danych wynosi [Sjöberg’95]:

 

 





2

2

2

ˆ

1

ˆ

e

e

e

LS

LS

LS

LS

MSE

σ

N

p

N

N

p

σ

σ

V

E

N

V











θ

θ

.

Pamiętając, że jednocześnie

 

 





 





θ

y

y

θ

y

y

ε

ε

θ

m

m

LS

LS

N

N

V

N









T

T

1

1

ˆ

1

,

otrzymuje się znane wyrażenie pozwalające oszacować wariancję szumu na podstawie
wyznaczonych rezyduów:

ε

ε

T

2

1

N

N

p

N

e







i ostatecznie [Hocking’76]:

   

 





p

N

p

N

LS

LS

e













y

X

X

X

X

I

y

θ

ε

θ

ε

T

1

T

T

T

2

ˆ

ˆ

ˆ



.

Estymator LS jest szczególnym przypadkiem estymatora ML (a tym samym MAP) w sytuacji,
gdy addytywne zakłócenia mają charakter stacjonarny (tj.

2

2

2

2

2

1

e

N



















) i są

realizacją niezależnych zmiennych losowych (tzn. macierz kowariancji jest diagonalna):

I

R

θ

θ

2

ˆ

ˆ

e

ML

LS







,

gdyż wtedy:









 

 

LS

e

e

e

e

ML

θ

y

X

X

X

y

X

X

X

y

X

X

X

y

R

X

X

R

X

θ

ˆ

ˆ

T

1

T

2

T

1

T

2

2

T

1

2

T

1

T

1

1

T





































.

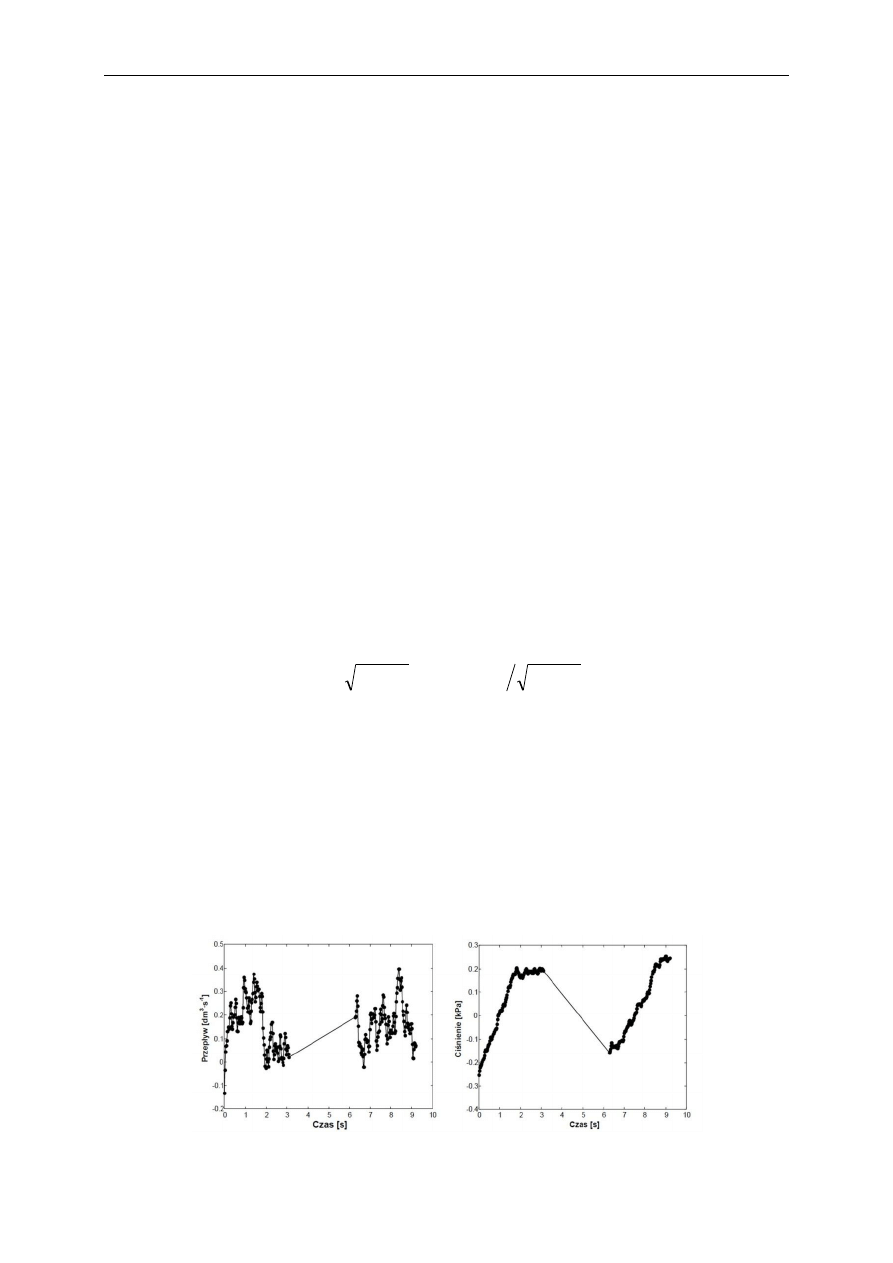
Przykład: Estymacja parametrów układu oddechowego podczas sztucznej wentylacji

W uproszczeniu układ oddechowy można zamodelować jako szeregowe połączenie dwóch parametrów: oporu
R

rs

i podatności C

rs

(rezystor i kondensator w elektrycznym modelu zastępczym – rys.).

Rys. Elektryczny model zastępczy procesu sztucznej wentylacji płuc

Z II prawa Kirchhoffa otrzymuje się związek (model MISO) między wyjściem (ciśnienie P

rs

mierzone w

respiratorze) i wejściem modelu (przepływ Q mierzony w respiratorze oraz obliczana na jego podstawie objętość
powietrza wprowadzonego do płuc V = ∫Qdt ):

 

 

 

0

P

t

V

E

t

Q

R

t

P

rs

rs

rs







,

4. Wsadowe metody estymacji parametrów modeli liniowych

9

który w zapisie macierzowym przyjmuje postać (przez P

0

oznaczając ciśnienie na początku pomiarów):

0

P

E

R

rs

rs

rs







v

q

p

.

Wektor parametrów modelu to θ = [R

rs

, E

rs

, P

0

]

T

. Macierz eksperymentu wynosi:





1

v

q

θ

p

X

,

,









rs

,

zatem estymaty parametrów (w tym mechanicznych właściwości układu oddechowego) oblicza się następująco:









rs

rs

rs

P

E

R

p

X

X

X

T

1

T

T

0

ˆ

,

ˆ

,

ˆ





.

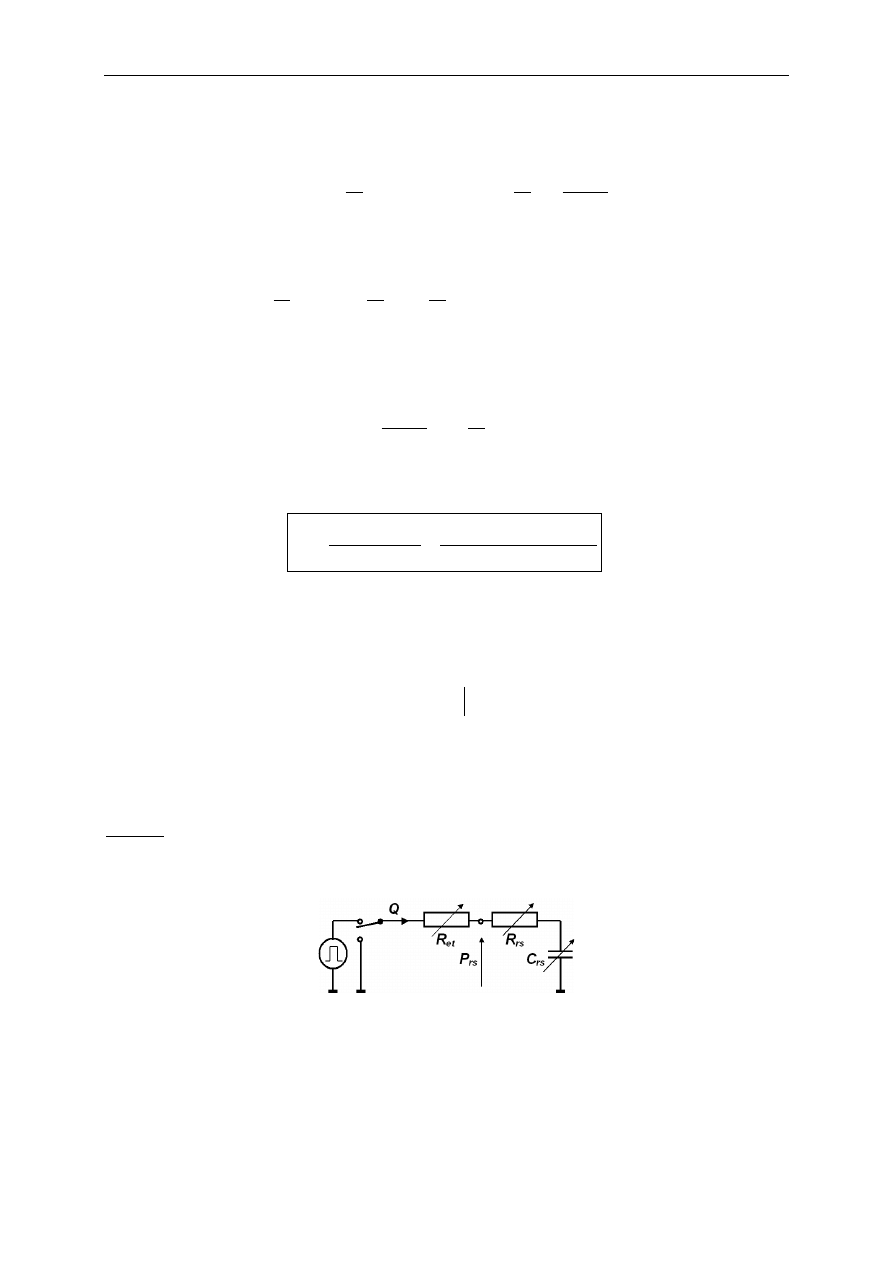
Przykładowy przepływ wentylacyjny Q oraz wynik dopasowania modelu do danych ciśnienia P

rs

pokazano na

rys.

Rys. Przykładowe dopasowanie modelu sztucznej wentylacji płuc do danych

6.2.2.3. Metoda ważonych najmniejszych kwadratów

Często stosowanym, uogólnionym podejściem do estymacji, jest metoda ważonych
najmniejszych kwadratów (WLS), w której estymatory

WLS

θˆ

wyznacza się minimalizując

funkcjonał V

WLS

:

 

θ

θ

θ

WLS

WLS

V

min

arg

ˆ



,

w postaci ważonego błędu średniokwadratowego (odległości modelu od danych w l

2

):

 

 





 



 

 



Xθ

y

W

Xθ

y

θ

y

y

W

θ

y

y

θ













T

T

m

m

WLS

V

,

gdzie W jest różnie w poszczególnych metodach dobieraną, dodatnio określoną, symetryczną
macierzą wag (najczęściej diagonalną). Wyrażają one posiadaną wiedzę aprioryczną o
poszczególnych danych pomiarowych, np. ich dokładność czy szczególne znaczenie.

Wektor estymatorów i macierz kowariancji dane są w tym przypadku wzorami [VBos’88]:

0

0.5

1

1.5

2

2.5

3

3.5

4

-1

-0.5

0

0.5

Model 1

Fl

o

w

Q

(

L

/s

)

0

0.5

1

1.5

2

2.5

3

3.5

4

-0.1

0

0.1

0.2

0.3

0.4

Time (s)

P

re

s

s

u

re

P

rs

(

k

P

a

)

Data
Model

10

Techniki eksperymentu

(© A.G. Polak 2014)





Wy

X

WX

X

θ

T

1

T

ˆ





WLS

i

 









1

T

T

1

T

ˆ

cov









WX

X

WRWX

X

WX

X

θ

S

WLS

WLS

,

gdzie R, przypomnijmy, jest dodatnio określoną macierzą kowariancji zakłóceń addytywnych
o zerowej wartości oczekiwanej.

Nietrudno zauważyć, że zarówno ML jak i LS są szczególnymi przypadkami metody
ważonych najmniejszych kwadratów. Można to sprawdzić podstawiając W = R

–1

w przypadku

metody największej wiarygodności (wagi są wtedy odwrotnie proporcjonalne do niepewności
poszczególnych danych) lub W = I w przypadku metody najmniejszych kwadratów
(wszystkie wagi są jednakowe i wynoszą 1).

Zależność estymatora od wyjścia modelu i szumu pomiarowego
Na przykładzie metody WLS warto przyjrzeć się, w jaki sposób estymator parametrów
budowany jest przez wyjście modelu y

m

(tożsame z niezakłóconym wyjściem obiektu w

przypadku bezbłędnego modelu), a w jakim stopniu przez konkretną realizację szumu
pomiarowego e (pamiętając, że w przypadku szumu addytywnego obowiązuje relacja
y = y

m

+ e):

































,

ˆ

T

1

T

0

T

1

T

0

T

1

T

T

1

T

0

T

1

T

0

T

1

T

T

1

T

We

X

WX

X

θ

We

X

WX

X

WXθ

X

WX

X

We

X

WX

X

Wy

X

WX

X

e

y

W

X

WX

X

Wy

X

WX

X

θ

































WLS

gdzie θ

0

oznacza wektor parametrów o prawdziwych wartościach (tj. takich, które miał model

generujący wyjście y

m

= Xθ

0

). Widać stąd, że wpływ obu czynników (y

m

i e) jest analogiczny

– są one tak samo przetworzone przez operator





W

X

WX

X

T

1

T



. W efekcie estymator

WLS

θˆ

ma charakter zmiennej losowej (także w innych metodach), a obliczane jego wartości tym
bardziej są zbliżone do wartości oczekiwanej, im mniejsza jest energia zakłóceń losowych
zawartych w danych empirycznych (im większy stosunek sygnału do szumu – SNR).

6.2.3. Estymacja z ograniczeniami

6.2.3.1. Estymacja z ograniczeniami liniowymi

W rzeczywistych sytuacjach parametry odpowiadające fizycznym właściwościom obiektu
mogą przyjmować tylko pewne wartości, zazwyczaj należące do znanego przedziału [a, b],
lub np. nie mogą być ujemne. W procesie wyznaczania ich wartości należy wykorzystać tę
informację aprioryczną, a stosowane metody noszą nazwę estymacji z ograniczeniami.

4. Wsadowe metody estymacji parametrów modeli liniowych

11

Zdanie estymacji z ograniczeniami jest złożone i zaproponowano wiele metod jego
rozwiązania. Do najpopularniejszych należą metody liniowe (opierające się o LS), w których
ograniczenia nałożone na θ przyjmują postać układu równań liniowych:

g

Gθ



,

gdzie G

(q×p)

(q < p) jest znaną macierzą więzów, a g jest znanym wektorem współczynników

liniowych. Należy zatem rozwiązać typowe zadanie LS ale tak, aby estymatory parametrów
spełniały powyższe równanie:



 



















.

ˆ

,

min

arg

ˆ

T

g

θ

G

Xθ

y

Xθ

y

θ

θ

W tym celu stosuje się jedną z dwóch metod: metodę mnożników Lagrange’a (typowo gdy
q < p/2) lub metodę elementów (q > p/2).

Metoda elementów
Metoda elementów wykorzystuje fakt, że skoro p parametrów jest skojarzonych ze sobą za
pośrednictwem q równań liniowych, to niezależnych jest tylko q z nich, a inne można wyrazić
jako kombinacje liniowe pozostałych. Ostatecznie wystarczy wyestymować wartości p – q
parametrów, a q następnych obliczyć na ich podstawie. Prowadzi to do redukcji liczby
estymowanych parametrów i stąd metoda ta zwana jest również metodą redukcji zmiennych.

Pierwszym krokiem jest przedstawienie macierzy G jako macierzy blokowej, podzielonej na
macierz prostokątną G

1

((p–q)×q)

oraz macierz kwadratową G

2

(q×q)

: G [G

1

|G

2

], a wektora

parametrów odpowiednio jako [θ

1

θ

2

]

T

. Wtedy układ równań więzów przyjmuje postać:





g

θ

θ

G

G















2

1

2

1

|

.

Stąd:

g

θ

G

θ

G





2

2

1

1

,

a rozwiązanie względem θ

2

:





1

1

1

2

2

θ

G

g

G

θ







.

Pozwala to na wyeliminowanie q parametrów z równania modelowego, przy czym macierz
eksperymentu również dzieli się na odpowiednie bloki:





2

2

1

1

2

1

2

1

|

θ

X

θ

X

θ

θ

X

X

y



















m

.

Podstawiając teraz wyprowadzoną zależność na θ

2

, otrzymuje się następujące równanie z

niewiadomym wektorem p – q parametrów:





1

1

1

2

2

1

1

θ

G

g

G

X

θ

X

y









m

.

12

Techniki eksperymentu

(© A.G. Polak 2014)

Można je uporządkować do podstawowej postaci liniowej (przenosząc na lewo znane
wartości) i pamiętając, że posiadane dane y = y

m

+ e, zapisać:





e

θ

X

G

G

X

X

y

g

G

X

y













1

1

1

2

2

1

1

2

2



 



 









r

r

,

a następnie znaleźć estymator θ

1

metodą najmniejszych kwadratów. Ostatecznie uzyskuje się:



























.

ˆ

ˆ

,

ˆ

1

1

1

2

2

T

1

T

1

θ

G

g

G

θ

y

X

X

X

θ

r

r

r

r

6.2.4. Estymacja parametrów modeli fourierowskich

Analiza właściwości danych powiązanych z ich widmem nie musi być przeprowadzana w
dziedzinie częstotliwości. W wielu sytuacjach znane są częstotliwości składowe
analizowanych sygnałów, a poszukiwane jedynie ich amplitudy i przesunięcia fazowe.
Przydatne okazuje się wtedy wykorzystanie modelu matematycznego badanego sygnału
analogicznego do szeregu Fouriera (częstotliwości nie muszą być harmoniczne):

 





































p

k

i

k

k

p

k

i

k

k

p

k

k

i

k

k

i

m

t

f

b

t

f

a

t

f

t

y

1

1

0

1

0

π

2

sin

π

2

cos

π

2

sin









,

gdzie:

2

2

k

k

k

b

a







i

2

2

sin

k

k

k

k

b

a

a







.

Ponieważ w tym przypadku nieznanymi parametrami są α

0

, a i b, dopasowywanie tego

modelu do danych sprowadza się do estymacji modelu LP w dziedzinie czasu (rys.), a
macierz eksperymentu przyjmuje postać:











































































N

p

N

p

N

N

p

p

p

p

t

f

t

f

t

f

t

f

t

f

t

f

t

f

t

f

t

f

t

f

t

f

t

f

π

2

sin

π

2

cos

π

2

sin

π

2

cos

1

π

2

sin

π

2

cos

π

2

sin

π

2

cos

1

π

2

sin

π

2

cos

π

2

sin

π

2

cos

1

1

1

2

2

2

1

2

1

1

1

1

1

1

1



















X

.

4. Wsadowe metody estymacji parametrów modeli liniowych

13

Rys. Dopasowanie modelu Fouriera do danych składających się z 7 sinusoid przesuniętych w fazie [Polak’06].

Potencjalnie analogicznie można próbować rozwiązać problem dodatkowej estymacji
częstotliwości powyższego szeregu, jednakże wtedy model staje się NLP i, co gorsze, posiada
dużą liczbę minimów lokalnych.