E. Michlowicz: Badania operacyjne – Programowanie liniowe (1)
1
Wykład 2
PROGRAMOWANIE LINIOWE
OPTYMALIZACJA GRAFICZNA
1. Ogólna postać zadania optymalizacyjnego
Należy zoptymalizować funkcję z(x):
z(x) = f(x
1
, x
2
, ....x
i
.... x
n
) max, min
gdzie:
x = (x
1
, x
2
, ....x
i
.... x
n
) – zmienne decyzyjne
przy ograniczeniach:
g
i
( x
1
, x
2
, x
j
,.... x
m
)
0
x
i
0; i = 1, 2, ....n
x
j
0; j = 1, 2, ....m
2. Elementy programowania liniowego
Z
matematycznym
liniowym
modelem
optymalizacyjnym
problemu
decyzyjnego mamy do czynienia wtedy, kiedy
równania i nierówności modelu
opisujące rozpatrywany problem mają charakter liniowy.
Zadaniem programowania liniowego
nazywa się problem decyzyjny polegający na
wyznaczeniu warunkowego ekstremum (minimum lub maksimum) funkcji celu
modelu liniowego, którego zmienne decyzyjne przyjmują nieujemne wartości.
Ogólna postać zadania programowania liniowego
Wyznaczyć wartość ekstremalną funkcji celu z ( x ):
x
c
x
z
T
)
(
przy warunkach (ograniczeniach):
b
Ax
0
x
gdzie:
z(x) - funkcja celu (kryterium),
x - wektor kolumnowy zmiennych decyzyjnych,
A -
macierz współczynników przy zmiennych decyzyjnych o wymiarach:
m x n; przy czym m < n,
E. Michlowicz: Badania operacyjne – Programowanie liniowe (1)
2
c - n
wymiarowy wektor kolumnowy współczynników funkcji celu,
b - m
wymiarowy wektor kolumnowy wyrazów wolnych ograniczeń, zwany prawymi
stronami ograniczeń,
-
oznacza relację typu:
,
lub =
Zagadnienie programowania liniowego posiada cztery postaci
w zależności od
występujących relacji:
(1) Postać standardowa I typu, jeżeli zależność jest opisana wzorem:
b
Ax
(2) Postać standardowa II typu dla przypadku, gdy:
b
Ax
(3) Postać kanoniczna dla:
b
Ax
(4) Postać mieszana dla zależności:
3
3
2
2
1
1
b
x
A
b
x
A
b
x
A
gdzie:
macierz A jest
macierzą blokową postaci:
3
2
1
A
A
A
A
a wektor b jest postaci:
3
2
1
b
b
b
b
Rozwiązaniem dopuszczalnym zadania programowania liniowego jest n –
wymiarowy wektor :
x = [ x
1
, x
2
,
…, x
n
]
spełniający warunki ograniczające i brzegowe.
Rozwiązanie dopuszczalne, przy którym funkcja celu osiąga wartość ekstremalną
nazywamy
rozwiązaniem optymalnym.
E. Michlowicz: Badania operacyjne – Programowanie liniowe (1)
3
W przypadku poszukiwania maksimum funkcji celu, typowy zwrot nier
ówności
ograniczeń to
(nie większe) oraz
(nie mniejsze) dla zadań na minimum.
Jeśli ten warunek nie jest spełniony, mnożymy daną nierówność ograniczenia
przez wartość „–1” zmieniając tym samym zwrot tej nierówności.
W zadaniach programowania
liniowego stosuje się dwa rodzaje optymalizacji
(minimalizację i maksymalizację).
Zawsze jedno z kryterium optymalizacji można zastąpić kryterium przeciwnego
rodzaju poprzez zmianę wartości współczynników funkcji celu na przeciwne.
I tak zadanie programowania liniowego postaci:
0
4
2
18
6
3
2
1
2
1
2
1
2
1
x
x
x
x
x
x
x
x
x
z
,
max,
)
(
jest
równoważne zadaniu postaci:
0
4
2
18
6
3
2
1
2
1
2
1
2
1
x
x
x
x
x
x
x
x
x
z
,
min,
)
(
3. Optymalizacja – metoda graficzna
Rozwiązanie zadania programowania liniowego, które posiada dwie zmienne
decyzyjne x
1
i x
2
,
można przedstawić graficznie.
Zadanie przyjmuje postać:
0
2
1
2
2
1
1
2
2
22
1
21
1
2
12
1
11
2
2
1
1
x
x
b
x
a
x
a
b
x
a
x
a
b
x
a
x
a
eks trem um
x
c
x
c
x
z
n
n
n
,
........
..........
..........
,
)
(
W układzie współrzędnych Ox
1
x
2
,
wyznacza się zbiór rozwiązań dopuszczalnych
X. Jest
to iloczyn wszystkich prostych i półpłaszczyzn odpowiadających równaniom
i nierównościom kolejnych ograniczeń zadania. Jeżeli ograniczenia są podane tylko w
postaci nierówności, obszarem rozwiązań dopuszczalnych będzie wielobok wypukły.
Rozwiązaniem dopuszczalnym będą współrzędne wierzchołka wieloboku, dla
których funkcja celu przyjmuje wartość ekstremalną – tzw. wierzchołka optymalnego.
E. Michlowicz: Badania operacyjne – Programowanie liniowe (1)
4
W celu odnalezienia wierzchołka optymalnego wykreśla się w układzie
współrzędnych Ox
1
x
2
gradient
z(x)
funkcji celu z(x)
„ zaczepiając go” w początku
układu współrzędnych.
Kierunek wskazywany przez gradient jest niezależny od zmiennych decyzyjnych:
(x
1
, x
2
, …, x
n
).
Następnie rysujemy prostą prostopadłą do gradientu funkcji celu, przechodzącą
przez początek układu współrzędnych, czyli prostą o równaniu:
2
2
1
1
0
x
c
x
c
x
L
)
(
Nadając funkcji L(x) coraz większe wartości przesuwa się ona równolegle wzdłuż
kierunku wyznaczonego przez gradient, przecinając wielobok będący zbiorem
rozwiązań dopuszczalnych. Otrzymane proste równoległe dla różnych wartości funkcji
L(x)
są nazywane liniami izocelowymi.
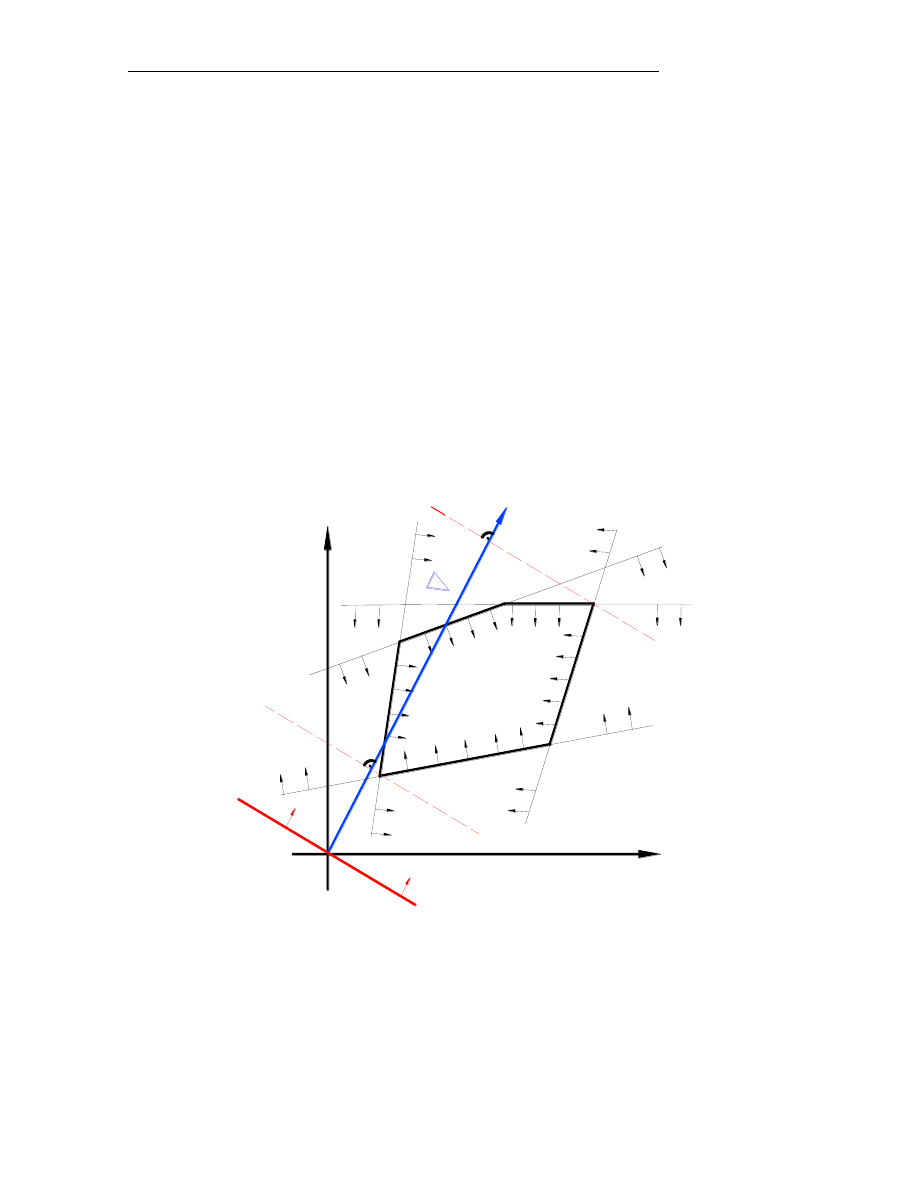
Na rysunku 1
przedstawiono opisane postępowanie dla przykładowego zbioru
rozwiązań zadania programowania liniowego dla dwóch zmiennych x
1
i x
2
.
A
B
C
D
E
X
2
X
1
z(x)
L(x)
Rys. 1. Interpretacja graficzna zadania programowania liniowego
dwóch zmiennych
W momen
cie „zerwania kontaktu” prostej ze zbiorem rozwiązań, ostatni punkt
wspólny zbioru i prostej jest wierzchołkiem optymalnym. Rozwiązanie to będzie
maksymalizować funkcje celu z(x). W przypadku poszukiwania minimum, postępuje się
E. Michlowicz: Badania operacyjne – Programowanie liniowe (1)
5
podobnie, przesuwając prostą prostopadłą do gradientu, w kierunku przeciwnym do tego
jaki wskazuje gradient.
Na rysunku 1
pole wieloboku ABCDE to zbiór rozwiązań zadania programowania
liniowego. Współrzędne wierzchołków wieloboku reprezentują dopuszczalne
rozwiązania bazowe. Współrzędne wierzchołka A stanowią rozwiązanie optymalne
minimalizujące funkcję celu z(x), natomiast współrzędne wierzchołka D maksymalizuję
funkcje celu. A i D są wierzchołkami optymalnymi.
W przypadku
kiedy jedna z prostych izocelowych będzie równoległa do jednego
z boków wieloboku wypukłego będzie to oznaczać, że rozwiązanie optymalne znajduje
się w dwóch punktach wierzchołkowych. Sytuację taką przedstawia rysunek 2.
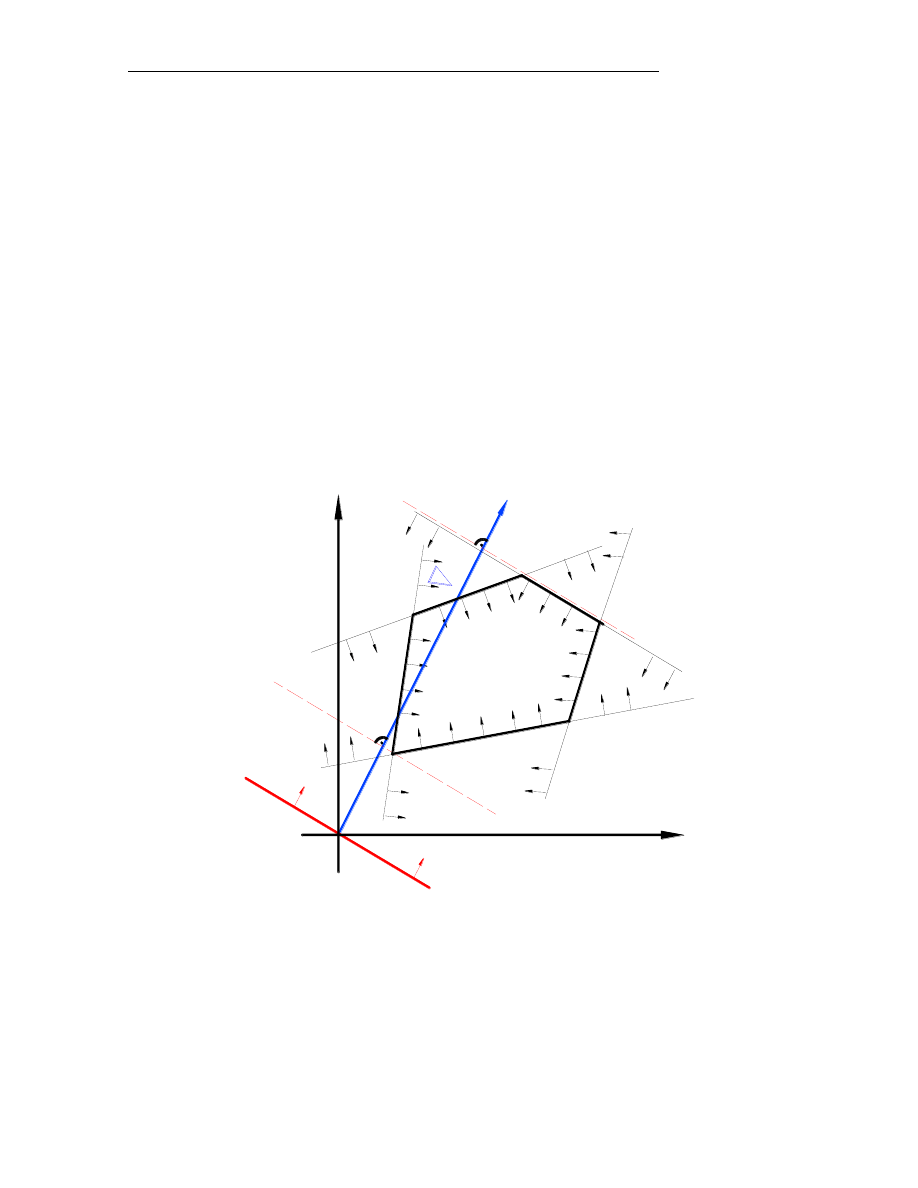
Dla przypadku z rysunku 2
wierzchołkami optymalnymi maksymalizującymi
funkcję celu z(x) są wierzchołki C i D. Rozwiązaniami optymalnymi będą również
wszystkie punkty boku CD.
A
B
C
D
E
X
2
X
1
z(x)
L(x)
Rys.2.
Przypadek z nieskończenie wielką liczbą rozwiązań zadania liniowego
Dochodzenie do rozwiązania zadania programowania liniowego w metodzie
graficznej przebiega dwuetapowo:
1. W
ykreślenie zbioru rozwiązań dopuszczalnych.
2. W
yznaczenie w tym zbiorze rozwiązania optymalnego.
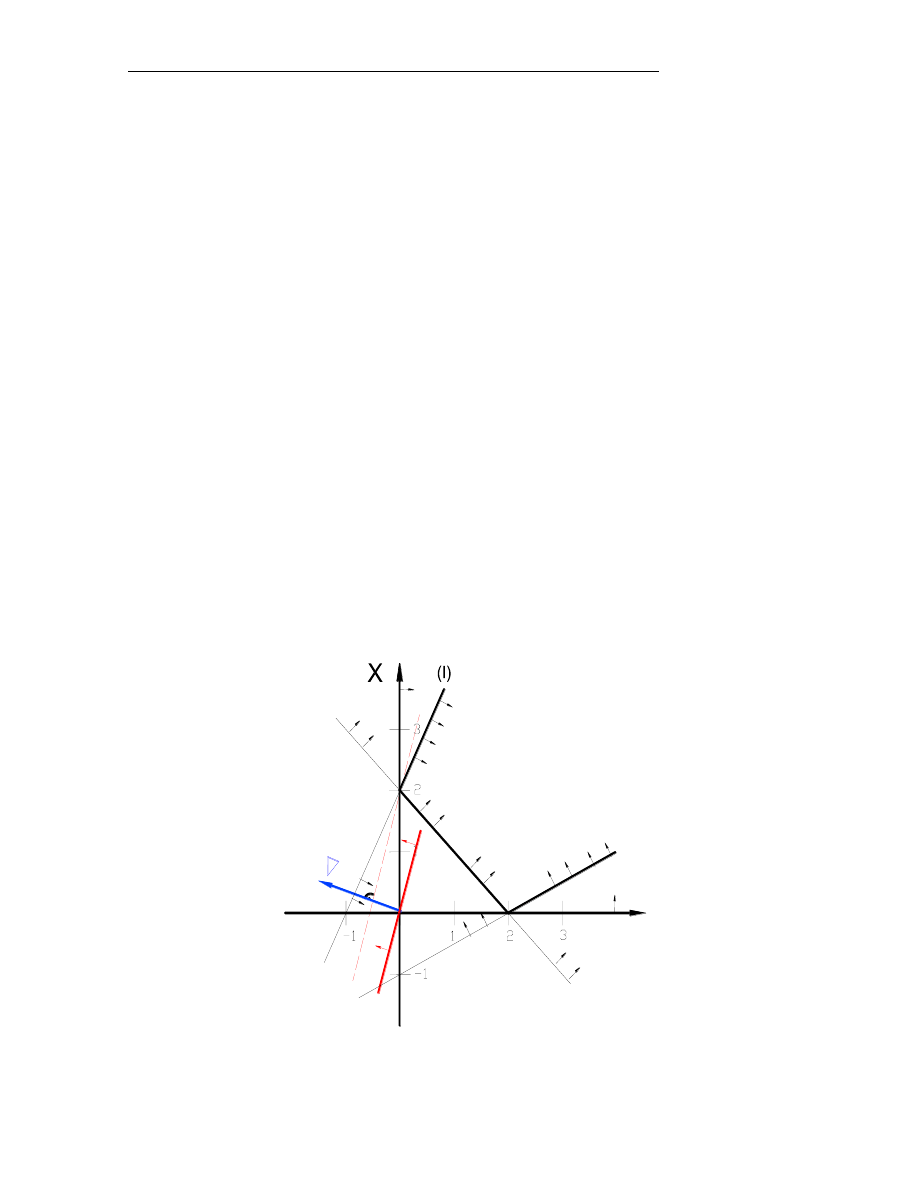
E. Michlowicz: Badania operacyjne – Programowanie liniowe (1)
6
Przy wykreślaniu zbioru rozwiązań może wystąpić jeden z czterech przypadków:
rozwiązanie zadania posiada dokładnie jedno rozwiązanie optymalne,
rozwiązanie zadania posiada wiele rozwiązań optymalnych,
rozwiązanie zadania programowania liniowego jest sprzeczne,
rozwiązanie zadanie nie posiada skończonego rozwiązania
optymalnego.
Przypadek 1 -
rozwiązanie zadania posiada dokładnie jedno rozwiązanie optymalne
Maksymalizujemy funkcję celu postaci:
max
)
(
2
1
3
x
x
x
z
przy ograniczeniach:
0
2
2
2
2
2
2
1
2
1
2
1
2
1
x
x
III
x
x
II
x
x
I
x
x
,
)
(
)
(
)
(
Rysunek 3
przedstawia geometryczną interpretację rozwiązania przypadku. Istnieje
prosta izocelowa
, która przecina zbiór rozwiązań dopuszczalnych dokładnie w
jednym punkcie
. Punkt ten jest wierzchołkiem optymalnym, a jego współrzędne
maksymalizują funkcję celu.
2
X
1
z(x)
L(x)
(II)
(III)
Rys.3. Interpretacja geometryczna
skończonego jednoznacznego rozwiązania
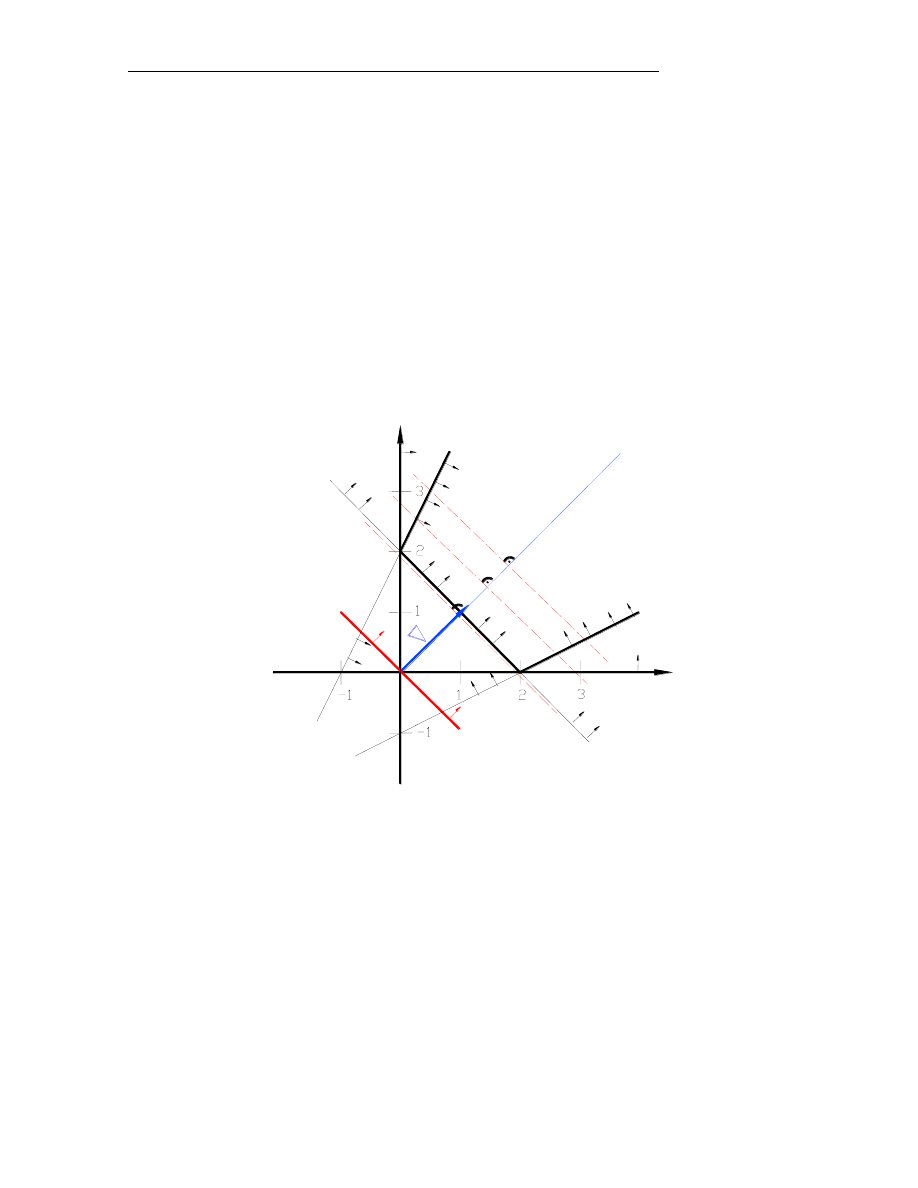
E. Michlowicz: Badania operacyjne – Programowanie liniowe (1)
7
Przypadek 2 -
rozwiązanie zadania posiada wiele rozwiązań optymalnych
Rozwiązaniami optymalnymi są współrzędne skrajnych punktów boku oraz każde
współrzędne będące liniową wypukłą ich kombinacją. Sytuację tą przedstawia rys. 4.
Dotyczy ona minimalizacji funkcji celu postaci:
min
)
(
2
1
2
2
x
x
x
z
przy ograniczeniach:
0
2
2
2
2
2
2
1
2
1
2
1
2
1
x
x
III
x
x
II
x
x
I
x
x
,
)
(
)
(
)
(
X
2
X
1
z(x)
L(x)
(I)
(II)
(III)
Rys.4. Interpretacja geometryczne niejednoznacznego rozwiązania
Przypadek 3 -
rozwiązanie zadania programowania liniowego jest sprzeczne
Maksymalizujemy funkcję celu postaci:
max
)
(
2
1
x
x
x
z
przy ograniczeniach:
0
2
2
2
2
2
2
1
2
1
2
1
2
1
x
x
III
x
x
II
x
x
I
x
x
,
)
(
)
(
)
(
E. Michlowicz: Badania operacyjne – Programowanie liniowe (1)
8
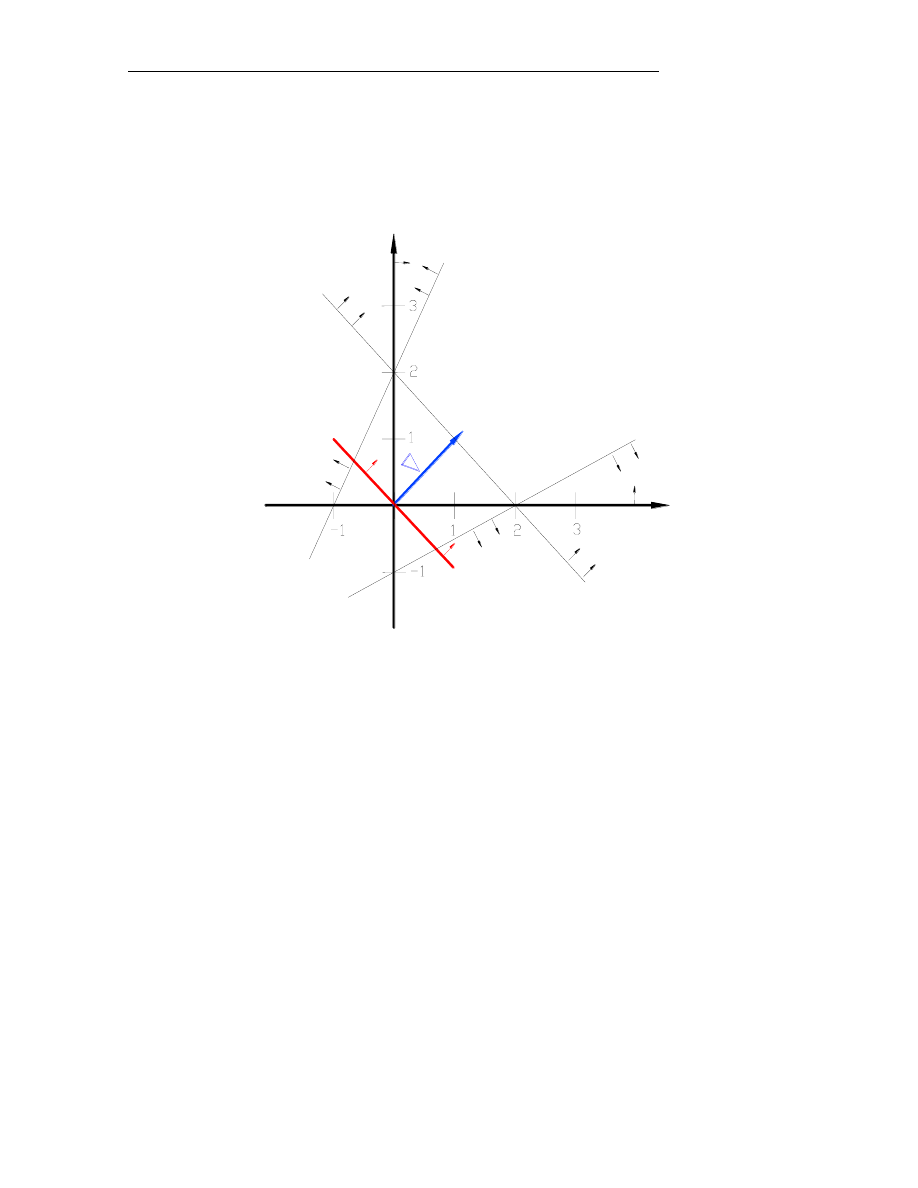
Rysunek 5
przedstawia geometryczną interpretację rozwiązania przypadku. Zbiór
rozwiązań dopuszczalnych jest pusty (X=
).
Układ warunków ograniczających jest
sprzeczny.
X
2
X
1
z(x)
L(x)
(I)
(II)
(III)
Rys.5. Interpretacja geometryczne przypadku zadania sprzecznego
Geometrycznie można rozwiązać również zadanie programowania liniowego
posiadające trzy zmienne decyzyjne.
Obszarem rozwiązań dla takiego zadania będzie wielościan wypukły w
przestrzeni trójwymiarowej R
3
.
W przypadku wystąpienia trzech i więcej zmiennych
decyzyjnych, do rozwiązania zadania stosuje się różnego rodzaju algorytmy ułatwiające
poszukiwanie rozwiązań optymalnych.