J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
1
WSTĘP
Optymalizacja = wybór najlepszego spośród dopuszczalnych rozwiązao (wariantów).
Rozwiązanie dopuszczalne = rozwiązanie spełniające przyjęte warunki – ograniczenia,
Rozwiązanie najlepsze = rozwiązanie, dla którego przyjęte kryterium wyboru – funkcja celu ma
ekstremum.
ZADANIE OPTYMALIZACJI
rozwiązywany problem da się opisad w sposób sformalizowany za pomocą tzw. modelu
matematycznego,
cechy problemu, których wartości należy wyznaczyd, są uporządkowad w formie wektora
zmiennych decyzyjnych
1
, , , ,
T
i
n
x
x
x
x
należącego do przestrzeni stanu, tzn.
n
x
R
,

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
2
możliwe są tylko takie wektory
x
, które należą do zbioru dopuszczalnego
x
, okre-
ślonego za pomocą układu ograniczeo
0,
1, ,
j
g
j
m
x
, tzn.
:
0,
1, ,
j
g
j
m
x
x
, przy czym
zawiera więcej niż jeden wektor
x
,
rozwiązywaniem zadania – wektorem optymalnym
ˆx
jest ten spośród dopuszczalnych
wektorów
x
, dla którego funkcja celu – kryterium wyboru osiąga ekstremum
Q
ext
x
.

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
3
MATEMATYCZNY SENS ZADANIA OPTYMALIZACJI
Q x
ma minimum lokalne w
ˆx
, jeśli
ˆ
, Q
Q
x
U
x
x
, gdzie
n
U
R
jest
otoczeniem
ˆx
.
Q x
ma minimum globalne w
ˆx
, jeśli
ˆ
,
n
Q
Q
x
R
x
x
.
Q x
ma warunkowe minimum globalne w
ˆ
x
, jeśli
ˆ
, Q
Q
x
x
x
.
Wniosek:
Zadanie optymalizacji polega na szukaniu wa-
runkowego globalnego minimum funkcji celu.

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
4
SYSTEMATYKA ZADAO OPTYMALIZACJI
Z UWAGI NA WYSTĘPOWANIE OGRANICZEO
zadanie z ograniczeniami – w którym zmienne decyzyjne muszą przyjmowad wartości nale-
żące do zbioru dopuszczalnego,
zadanie bez ograniczeo – w którym zmienne decyzyjne mogą przyjmowad dowolne wartości.
Z UWAGI NA CHARAKTER ZMIENNYCH
DECYZYJNYCH
zadanie statyczne (parametryczne) – które polega na wyznaczeniu wartości zmiennych de-
cyzyjnych, dla których funkcja celu osiąga ekstremum,
zadanie dynamiczne – w którym zmienne decyzyjne zadania są funkcjami tej samej innej
zmiennej (np. czasu), zatem poszukiwad będziemy ekstremum pewnego funkcjonału.
Z UWAGI NA TYP FUNKCJI CELU ORAZ OGRANICZEO
zadanie programowania liniowego (optymalizacji liniowej) – w którym zarówno funkcja ce-
lu jak i ograniczenia są liniowymi kombinacjami zmiennych decyzyjnych.

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
5
zadanie programowania nieliniowego (optymalizacji nieliniowej) – w którym przynajmniej
jedna spośród funkcji występujących w zadaniu (ograniczenia, funkcja celu) jest nieliniowa
względem zmiennych decyzyjnych.
Z UWAGI NA WARTOŚCI, JAKIE MOGĄ PRZYJMOWAD ZMIENNE DECYZYJNE
programowanie w zbiorach ciągłych – kiedy to zmienne decyzyjne mogą przyjmowad do-
wolne wartości należące do zbioru dopuszczalnego (np. zbioru liczb rzeczywistych),
programowanie w zbiorach dyskretnych – kiedy to zmienne decyzyjne muszą przyjmowad
tylko określone wartości (muszą należed do zbioru dyskretnego).
Z UWAGI NA LICZBĘ FUNKCJI CELU
programowanie jednokryterialne – w którym optymalizacja przebiega w oparciu o jedną
funkcję celu (kryterium),
programowanie wielokryterialne – w którym występuje wiele funkcji celu (kryteriów) a
optymalizacja przebiega z uwzględnieniem ich wszystkich jednocześnie.

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
6
RÓŻNICE POMIĘDZY POSZCZEGÓLNYMI RODZAJAMI ZADANIA OPTYMALIZACJI
POWODUJĄ, IŻ NIE MA JEDNEJ EFEKTYWNEJ METODY ROZWIĄZYWANIA WSZYSTKICH
JEGO RODZAJÓW. POSZCZEGÓLNE RODZAJE ZADANIA ROZWIĄZUJE SIĘ ZA POMOCĄ
WYSPECJALIZOWANYCH METOD (ALGORYTMÓW) ODPOWIEDNICH DLA KAŻDEGO
RODZAJU.

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
7
PROGRAMOWANIE LINIOWE
WPROWADZENIE DO PROGRAMOWANIA LINIOWEGO
PRZESTRZENIE LINIOWE, ZBIORY WYPUKLE
Elementami tworzącymi
n
-wymiarową unormowaną przestrzeo Euklidesową
n
R
są punkty
(wektory) będące uporządkowanymi zbiorami liczb rzeczywistych (współrzędnych)
i
x R
,
które można przedstawid w formie jednokolumnowej macierzy (wektora):
1
1
T
n
i
i
n
n
x
x
x
x
x
x
x
x
R
(1.1)

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
8
Liniową kombinacją wektorów jest wyrażenie:
1 1
1
,
k
n
i
i
k
k
i
i
i
i
i
R
x
x
x
x
x
R
(1.2)
Hiperpłaszczyzną w przestrzeni
n
R
nazywamy zbiór punktów
n
x
R
takich, że:
:
T
b
x a x
(1.3)
W przestrzeni dwuwymiarowej równanie (1.3) jest równaniem prostej
1 1
2 2
a x
a x
b
,
a w przestrzeni trójwymiarowej – równaniem płaszczyzny
1 1
2 2
3 3
a x
a x
a x
b
.
Zastępując znak równości w wyrażeniu (1.3) znakiem nierówności, otrzymamy półprzestrzeo
domkniętą w przestrzeni
n
R
:
:
T
b
x a x
(1.4)
lub półprzestrzeo otwartą w przestrzeni
n
R
:
:
T
b
x a x
(1.5)

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
9
Zbiór równao liniowych (1.3) tworzy układ równao:
11 1
1
1
1
1 1
1 1
i i
n n
j
ji i
jn n
j
m
mi i
mn n
m
a x
a x
a x
b
a x
a x
a x
b
a x
a x
a x
b
(1.6)
którego rozwiązaniem jest przecięcie
m
hiperpłaszczyzn:
1 1
dla
1
j
ji i
jn n
j
a x
a x
a x
b
j
m
jeżeli dla każdego
j
co najmniej jedna z liczb
0
ji
a
.

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
10
Podobnie zbiór nierówności (1.5) tworzy układ nierówności:
11 1
1
1
1
1 1
1 1
i i
n n
j
ji i
jn n
j
m
mi i
mn n
m
a x
a x
a x
b
a x
a x
a x
b
a x
a x
a x
b
(1.7)
Rozwiązaniem każdej z nierówności
1 1
j
ji i
jn n
j
a x
a x
a x
b
jest półprze-
strzeo domknięta, jeśli co najmniej jedna z liczb
0
ji
a
.
Wektor
1
T
j
j
ji
jn
a
a
a
a
jest wektorem normalnym do hiperpłaszczyzny
1 1
j
ji i
jn n
j
a x
a x
a x
b
.
Zbiór rozwiązao układu nierówności (1.7), będący częścią wspólną półprzestrzeni domkniętych
1 1
j
ji i
jn n
j
a x
a x
a x
b
tworzy wielościan wypukły
n
R
.
J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
11
0
:
T
j
j
b
x a x
0
:
T
j
j
b
x a x
0
:
T
j
j
b
x a x
0
x
j
a
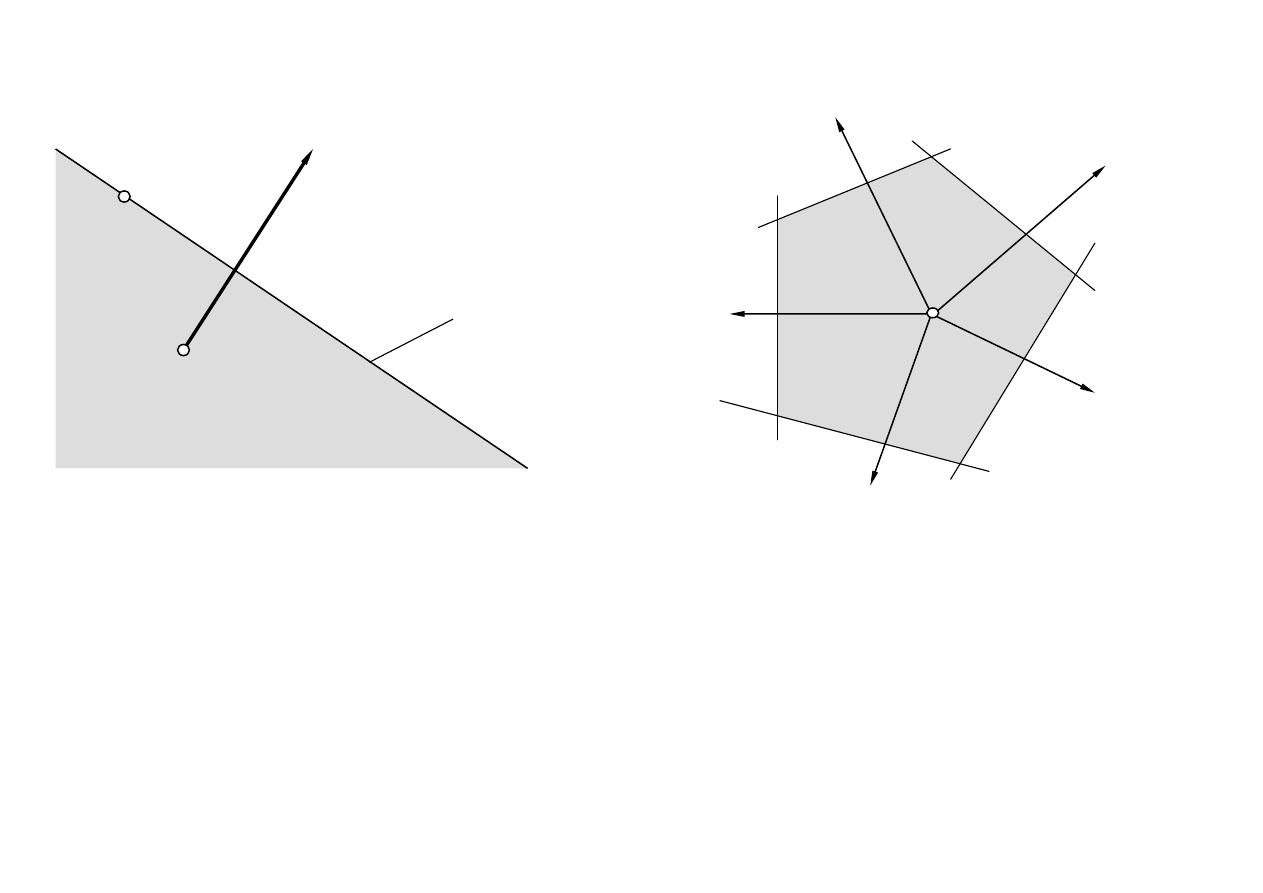
Półprzestrzenie i hiperpłaszczyzna wyznaczo-
ne przez punkt i wektor normalny
1
a
2
a
3
a
4
a
5
a
Wielościan wypukły – część wspólna półprze-
strzeni domkniętych

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
12
Wprowadzając oznaczenia:
1
11
1
1
1
1
1
T
i
n
T
j
ji
jn
j
j
T
m
mi
mn
m
m
a
a
a
b
a
a
a
b
a
a
a
b
a
a
A
b
a
liniowe układy równao (1.6) i nierówności (1.7) można zapisad w postaci macierzowej:
A x
b
(1.8)
A x
b
(1.9)

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
13
EKSTREMUM WARUNKOWE FUNKCJI LINIOWEJ
Rozpatrzymy układ nierówności
A x
b
, którego zbiorem rozwiązao jest wielościan wypu-
kły
Φ
oraz liniową funkcję:
1
gdzie
T
T
i
n
Q
c
c
c
x
c x
c
(1.10)
Funkcja
Q x
ma ekstremum warunkowe w zbiorze określonym układem nierówności
:
x A x
b
w wierzchołkach wielościanu wypukłego
.
To stwierdzenie ma również duże znaczenie praktyczne w rozwiązywaniu zadao programowa-
nia liniowego. Zadanie poszukiwania ekstremum warunkowego w zbiorze rozwiązao
spro-
wadza się bowiem do przeszukania skooczonego zbioru wierzchołków tego zbioru.

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
14
POSTAD OGÓLNA, STANDARDOWA I KANONICZNA ZADANIA PROGRAMOWANIA LINIOWEGO
Terminologia i notacja:
ł
1
1
11
1
1
1
1
wektor zmiennych
macierz wspó czynników
decyzyjnych
T
i
n
T
i
j
ji
jn
j
T
n
m
mi
mn
m
x
a
a
a
x
a
a
a
x
a
a
a
a
a
x
A
a

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
15
ń
1
1
1
funkcja celu
wektor prawych
wektor funkcji
stron ogranicze
celu (kosztów)
ograniczenie
T
j
j
j
i
n
T
i i
i
m
n
b
c
b
b
c
Q
c x
b
c
a x
b
c
x
c x
Zbiór
:
,
x A x
b x
0
- zbiór dopuszczalny.
Punkt
x
,
1
T
i
n
x
x
x
x
- rozwiązanie dopuszczalne.

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
16
Rozwiązanie dopuszczalne
ˆx
, dla którego funkcja celu
ˆ
Q
ext
x
(osiąga wartośd ekstre-
malną), jest rozwiązaniem optymalnym zadania, a wartośd
ˆ
Q x
optymalną wartością zada-
nia.
POSTAD OGÓLNA ZADANIA PROGRAMOWANIA LINIOWEGO
Zadanie:
min
T
Q
x
c x
A x
b
x
0
(1.11)
określamy mianem postaci ogólnej zadania programowania liniowego.
Ograniczenie równościowe może byd zastąpione układem ograniczeo nierównościowych:
T
j
j
T
T
j
j
j
j
b
b
a x
a x
b
a x
(1.12)

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
17
Również zadanie poszukiwania maksimum funkcji celu można zastąpid zadaniem poszukiwania
minimum:
max
min
T
T
Q
Q
x
c x
x
c x
(1.13)
POSTAD STANDARDOWA ZADANIA PROGRAMOWANIA LINIOWEGO
Każdą z nierówności:
1 1
T
j
j
j
ji i
jn n
j
b
a x
a x
a x
b
a x
można zastąpid równością:
1
1 1
1
T
j
n
j
j
ji i
jn n
n
j
x
b
a x
a x
a x
x
b
a x
(1.14)
dodając po lewej stronie zmienną uzupełniającą
1
0
n
x
.

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
18
Jeśli nierównośd ma zwrot przeciwny:
1 1
T
j
j
j
ji i
jn n
j
b
a x
a x
a x
b
a x
zmienną uzupełniająca należy odjąd:
1
1 1
1
T
j
n
j
j
ji i
jn n
n
j
x
b
a x
a x
a x
x
b
a x
(1.15)
Zastępując wszystkie ograniczenia nierównościowe w zadaniu ograniczeniami równościowymi,
można sprowadzid zadanie programowania liniowego do postaci standardowej:
min
T
Q
x
c x
A x
b
x
0
(1.16)
Sprowadzając zadanie programowania liniowego z postaci ogólnej do standardowej, zwiększy-
liśmy wymiar zadania dodając
m
zmiennych uzupełniających.

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
19
Postad ogólna:
11 1
1
1
1
1 1
1 1
i i
n n
j
ji i
jn n
j
m
mi i
mn n
m
a x
a x
a x
b
a x
a x
a x
b
a x
a x
a x
b
Postad standardowa:
11 1
1
1
1
1
1 1
1 1
i i
n n
n
j
ji i
jn n
n j
j
m
mi i
mn n
n m
m
a x
a x
a x
x
b
a x
a x
a x
x
b
a x
a x
a x
x
b
(1.17)

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
20
lub po wprowadzeniu dodatkowych oznaczeo:
1
1
T
T
N
i
n
B
n
n j
n m
x
x
x
x
x
x
A
N
I
B
x
x
w postaci macierzowej:
,
N
N
B
B
x
N x
B x
b
N B
b
x
(1.18)
Wtedy funkcja celu przyjmie postad:
,
T
N
T
T
N
B
N
N
B B
B
Q
x
x
c c
c x
c x
x
(1.19)

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
21
POSTAD KANONICZNA ZADANIA PROGRAMOWANIA LINIOWEGO
Przekształcając zadanie programowania liniowego z postaci ogólnej do standardowej, otrzy-
muje się macierz
B
I
.
Zadanie, w którym w macierzy współczynników
A
można wyodrębnid kwadratową
n
-wymiarową podmacierz jednostkową, nazywamy kanoniczną postacią zadania programowa-
nia liniowego.
Jeśli jednak ograniczenia w zadaniu mają formę równości, to zastępowanie ich nierównościami
– postad ogólna, którą dalej sprowadza się do postaci standardowej, jest niecelowe, bowiem
przez wprowadzanie zmiennych uzupełniających powiększa się wymiar zadania. Układ ograni-
czeo nierównościowych może byd sprowadzony do postaci kanonicznej bezpośrednio, eliminu-
jąc zmienne
i
x
ze wszystkich równao układu (eliminacja Gaussa).

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
22
ROZWIĄZYWANIE ZADANIA PROGRAMOWANIA LINIOWEGO
Jeżeli rozwiązanie jest jednoznaczne, to leży w jednym z wierzchołków wielościanu wypukłego
(zbioru dopuszczalnego)
. Zatem należy przeszukad skooczony zbioru wierzchołków i wybrad
ten, w którym funkcja celu ma najmniejszą wartośd.
Przykład
1
2
1
2
1
2
1
2
1
2
,
2
max
2
2
4
6
,
0
Q x x
x
x
x
x
x
x
x x
Sprowadźmy zadanie do postaci standardowej:

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
23
1
2
1
2
3
1
2
4
1
2
3
4
2
min
2
2
4
6
, , ,
0
Q
x
x
x
x
x
x
x
x
x x x x
x
1° Dla
1
1
2
3
4
0
2
6
0
x
x
x
x
Q
x
przy czym
1
2
3
4
, , ,
0
x x x x
,
zatem
1
0
0
x
jest rozwiązaniem dopuszczalnym.
Rozwiązanie
1
x
możemy poprawid wtedy, gdy znajdziemy inne wierzchołki zbioru
Φ
, w któ-
rych
1
i
Q
Q
x
x
.
2° Dla
1
3
2
4
0
2
14
x
x
x
x
punkt nie jest rozwiązaniem dopuszczalnym, gdyż
2
0
x
.

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
24
3° Dla
2
1
4
2
3
3
7
0
3
2
2
x
x
x
x
Q
x
przy czym
1
2
3
4
, , ,
0
x x x x
,
zatem
2
0
3
2
x
jest rozwiązaniem dopuszczalnym.
4° Dla
3
2
3
1
4
0
1
7
1
x
x
x
x
Q
x
przy czym
1
2
3
4
, , ,
0
x x x x
,
zatem
3
1
0
x
jest rozwiązaniem dopuszczalnym, lecz
3
2
Q
Q
x
x
.
5° Dla
2
4
1
3
0
6
14
x
x
x
x
punkt nie jest rozwiązaniem dopuszczalnym, gdyż
1
0
x
,
J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
25
6° Dla
4
3
4
1
2
0
2
2
6
x
x
x
x
Q
x
przy czym
1
2
3
4
, , ,
0
x x x x
,
zatem
4
2
2
x
jest rozwiązaniem opty-
malnym, bo
4
min
i
Q
Q
x
x
.
Ostatecznie:
ˆ
2,2
6
Q
Q
x
.
Wnioski:
kolejnośd sprawdzania ma wpływ na to, w
którym kroku uzyskamy rozwiązanie,
od wartości współczynników funkcji
Q x
zależy, jaki wpływ mają odpowiadające im zmienne na wartośd
Q x
.
1
x
2
x
6
Q
x
1
0
1
3
2
2
2
1
x
2
x
3
x
4
ˆ
x
x
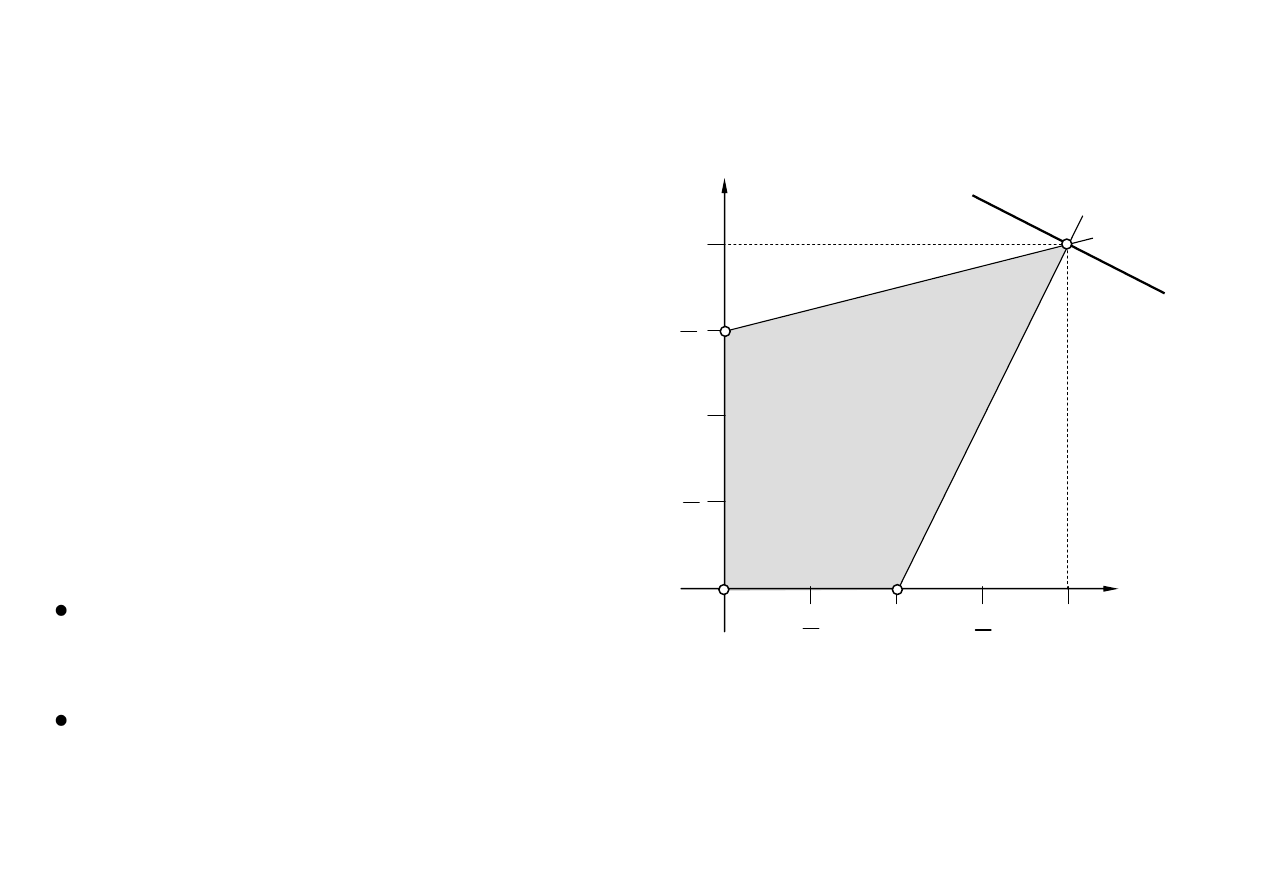
Graficzne rozwiązanie przykładu
1
2
3
2
1
2

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
26
ALGORYTM SYMPLEKS
Zrewidowany algorytm sympleks - jedna z odmian podstawowej wersji algorytmu.
Rozwiązaniem zadania jest jeden z wierzchołków zbioru dopuszczalnego
, lecz nie potrafimy
ich wszystkich wyznaczyd.
Rozpatrzymy zadanie:
min
T
Q
x
c x
A x
b
x
0
Rozwiązanie zaczniemy od przekształcenia zadania do postaci kanonicznej:
,
N
N
B
B
x
A x
b
N x
B x
b
N B
b
x
(1.20)
Macierz
B
jest macierzą jednostkową a o wektorze prawych stron
b
założymy, że jest nie-
ujemny (
,
B
I b
0
).

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
27
ETAP 1: ZNAJDOWANIE BAZOWEGO ROZWIĄZANIA DOPUSZCZALNEGO
Przyjmijmy:
N
x
0
Rozwiązaniami pozostałego układu
B
B x
b
Są wierzchołki zbioru dopuszczalnego opowiadającego bazie
B
.
Zbiór (obszar) wyznaczony przez te wierzchołki (wielościan wypukły) nazywamy symlpeksem.
1
0
B
x
x
B
b
(1.21)
Jeżeli macierz
B
jest nieosobliwa
1)
a rozwiązanie bazowe jest nieujemne
B
x
0
, to jest to
bazowe rozwiązanie dopuszczalne.
1)
Macierz kwadratowa n n, której wszystkie wyznaczniki główne (minory) są różne od zera jest macierzą nieosobliwą.

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
28
ETAP 2: POPRAWA BAZOWEGO ROZWIĄZANIA DOPUSZCZALNEGO
Dotychczasowe rozwiązanie
B
x
daje wartośd funkcji celu:
0
0
,
T
B
T
T
B
N
B
B
Q
x
x
c x
c c
c x
0
(1.22)
n
- elementowy zbiór wierzchołków wielościanu wypukłego
, jest liczniejszy niż
n
m
-
elementowy zbiór wierzchołków sympleksu, którego wierzchołki są bazowymi rozwiązaniami
dopuszczalnymi.
Pomysł:
Zamiast przeszukiwad kolejne wierzchołki zbioru
, w celu znalezienia tego, w którym funkcja
celu ma minimum, można wybierad po jednym spośród tych , które dotąd nie były wierzchoł-
kami sympleksu i zastępowad nimi dotychczasowe wierzchołki. Przy każda zamiana powinna
poprawiad (zmniejszad) wartośd funkcji celu.

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
29
Realizacja:
Trzeba odpowiedzied na dwa pytania:
1°którym z wierzchołków wielościanu
powinniśmy z najlepszym skutkiem zastąpid jeden z
dotychczasowych wierzchołków sympleksu?
(inaczej dokonad wyboru zmiennej niebazowej wprowadzanej do bazy),
2° który z wierzchołków sympleksu powinien byd z najlepszym skutkiem zastąpiony przez je-
den z wierzchołków wielościanu
?
(inaczej wybór zmiennej bazowej wyprowadzanej z bazy).
1 ° WYBÓR ZMIENNEJ NIEBAZOWEJ WPROWADZANEJ DO BAZY
Należy wybrad ten wierzchołek, który najbardziej zmniejsza wartośd funkcji
Q x
.
Z (1.20) mamy:

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
30
1
1
B
N
x
B
b
B
N x
1
1
1
1
T
T
T
T
B
B
N
N
B
N
N
N
T
T
T
T
B
N
B
N
N
Q
x
c x
c x
c
B
b
B
N x
c x
c B
b
c
c B
N x
q
p x
(1.23)
gdzie:
1
T
B
q
c B
b
,
(1.24)
1
T
T
T
T
T
N
B
N
p
c
c B
N
c
N
λ
,
(1.25)
λ
– wektor mnożników sympleksowych.
Równanie (1.23) wyraża funkcję celu zależną tylko od zmiennych niebazowych
N
x
. Wartośd
N
Q
Q
x
x
zależy zatem od wektora
p
, bowiem
N
x
0
. Rozwiązanie można popra-
wid (zmniejszyd dotychczasową wartośd funkcji celu), jeżeli wśród składowych wektora
p
są
składowe ujemne.
J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
31
I.
p
0
,
Wszystkie składowe wektora
p
są dodatnie, nie można zmniejszyd wartości
Q x
, do-
tychczasowe rozwiązanie jest rozwiązaniem optymalnym
ˆ
B
x
x
.
II.
0
k
p
,
W wektorze
p
istnieje zerowa składowa o indeksie
k
, rozwiązanie jest niejednoznaczne,
przechodząc do następnego wierzchołka nie zmieniamy wartości
Q x
2
)
.
III.
0
k
p
,
W wektorze
p
istnieje co najmniej jedna ujemna składowa
k
p
, można zmniejszyd wartośd
Q x
przechodząc do następnego wierzchołka. Jeśli składowych ujemnych jest więcej,
wybieramy najmniejszą z nich.
2)
Istnieje niebezpieczeostwo powstania cyklu polegającego na powrocie do tego samego wierzchołka po pewnej liczbie iteracji.

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
32
Spośród
1
(
)
k
n
m
kolumn podmacierzy
N
wybieramy kolumnę
k
a
i wprowa-
dzamy ją do bazy
B
w następnej iteracji. Jest to równoważne wybraniu jednego z wierz-
chołków wielościanu
, którym zostanie zastąpiony jeden z dotychczasowych wierzchołków
sympleksu.
2° WYBÓR ZMIENNEJ BAZOWEJ WYPROWADZANEJ Z BAZY
Zamiana wierzchołków powinna przynieśd jak największą poprawę (zmniejszenie) wartości
Q x
. Nowe rozwiązanie bazowe powinno byd dopuszczalne
B
x
0
.
1
1
k
B
k
N
x
B
b
B
a x
0
(1.26)
Oznaczając:
1
0
B
B
b
x
– bieżące rozwiązanie bazowe,
1
k
B
a
d
,
mamy:
0
k
B
B
N
x
x
dx

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
33
Jeżeli
d
0
, to zwiększenie
k
N
x
powoduje zmniejszenie
B
x
, co pociąga zmniejszenie funkcji
celu.
Indeks
l
kolumny wyprowadzanej z bazy to ten, dla którego
(
) 1
n
m
l
n
zachodzi
0
min
Bl
l
x
d
przy
l
d
0
.
Kolumna bazy odpowiadające zmiennej
0
Bl
x
jest wyprowadzana z bazy do części niebazowej.
W przeciwnym przypadku wartośd funkcji celu może byd pomniejszona do
, czyli że zbiór
bazowych rozwiązao dopuszczalnych jest nieograniczony .
J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
34
PRZYKŁAD
1
2
1
2
1
2
3
1
2
4
1
2
3
4
,
2
min
2
2
4
6
, , ,
0
Q x x
x
x
x
x
x
x
x
x
x x x x
Iteracja 1:
1
1
1
1
2
0
0
0
0
2
3
4
0
2
0
1 0 2 0 0
6
2
6
B
B
x
x
x
Q
x
x
x
x
B
b
I
b
x
0
x
x
1
2
3
4
1
2
3
4
2
1
1
0
2
1
2
0
0
1
4
0
1
6
T
T
T
N
B
x
x
x
x
x
x
x
x
A
b
c
N
B
c
c

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
35
1
1
1
4
4
I
k
d
B
a
I
4
3
1
4
2
2
6
2
3
mi
4
n
0
2
1
2
l
x
x
d
x
x
l
d
d
1
1
2
2
1
1
2
2
0 0
1
4
1
2
T
T
I
N
B
x
k
x
p
c
c
B
N
I
J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
36
Iteracja 2:
1
1
2 0
1
4
1 0
0 2
1
1
1 1
1
2
2
0
4
II
k
p
1
x
4
x
4
1
3
4
1
2
0
0
T
I
T
T
NI
BI
x
x
x
x
c
c
c
2
1
3
7
1
1
3
4
2
1
3
4
4
4
2
1
2
1
1
2
1
0
4
0
1
0
6
BI
I
I
I
I
x
x
x
x
x
x
A
x
B
b
0
N
B
1
3
2
7
3
2
2
4
0
0
B
I
N
x
x
x
x
x
x
x
3
1 0
2
3
2
I
Q
x
7
1
4
4
1
1
4
4
1
2
0
1
II
d

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
37
4 1
1
0
2
1
2
2
7 7
0
1
1
4
1 2 6
2
7 7
BII
II
A
x
0
2
3
1
4
x
x
x
x
II
N
II
B
1
x
2
x
1
2
d
d
3
4
x
x
3
1
3
2
min
0
2
1
1
4
7
2
7
4
l
x
l
x
d
2
2
1 2 2 2
6
0 0
1
2
0
0
T
II
II
II
Q
x
x
c
3
x
B
x
N
x
T
N
c
T
B
c
4
x
1
x
2
x
1
x
4
x
3
x
2
x

J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
38
III iteracja:
4 1
1 0
6 6
7 7
0 0
1
2
0
1 2 0 1
7 7
7 7
III
p
Wektor
p
nie ma ujemnych składowych, rozwiązanie otrzymane w II iteracji jest rozwiązaniem
optymalnym:
2
ˆ
ˆ
,
6
2
Q
x
x
.
ODWRACANIE MACIERZY W ALGORYTMIE SYMPLEKS
Zauważmy, że w każdej iteracji macierz bazowa
B
różni się od macierzy
B
z poprzedniej
iteracji tylko jedną kolumną:
1
1
k
n
l
n
B
a
a
a
B
a
a
a
.
J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
39
Jeśli oznaczyd:
1
1
T
l
k
n
B
a
y
y
y
to można wykazad, że:
1
1
B
E B
, gdzie
1
1
0
1
0
0
0
1
k
k
n
k
y
y
E
y
y
y
J.Stadnicki Optymalizacja- wykład dla Informatyki, częśd 1: PROGRAMOWANIE LINIOWE
40
Dla macierzy z przykładu
1 0
1
1
i
0 1
0
4
B
B
,
1
0
i
4
1
l
k
a
a
1
1
1
1
1 0
1
4
1 4
0 1
4
1
0
4
T
l
B
a
B
Wyszukiwarka
Podobne podstrony:
Opracowanie Programowanie liniowe metoda sympleks
BO WYK2 Program liniowe optymalizacja
programowanie liniowe teoria
PL (programowanie liniowe), semestr 8, Matematyka, Teoria i praktyka decyzji ekonomicznych
konspekt cw 3 1 programowanie liniowe
programowanie liniowe zadanie 1 wmzghak5ktjjzelzmpatqlx6iahqoqrauoxjgtq WMZGHAK5KTJJZELZMPATQLX6IA
badania operacyjne, w3 Zagadnienia Dualne Programowania Liniowego
Rozwiązywanie zadań programowania liniowego metoda geometryczna, Zadania
6 2 Zadania programowania liniowego
programowanie liniowe zadania
AM, Liniowe zadanie decyzyjne, Model matematyczny zadania programowania liniowego
badania operacyjne w3-Zagadnienia Dualne Programowania Liniowego
Badania operacyjne - programowanie liniowe, lista3
13 Projektowanie układów sekwencyjnych procesowo–zależnych o programach liniowych na przykładzie uk
programowanie liniowe
,programowanie liniowe, zadania
Programowanie liniowe zagadnienia dualne
6.4 Dualizm w programowaniu liniowym
więcej podobnych podstron