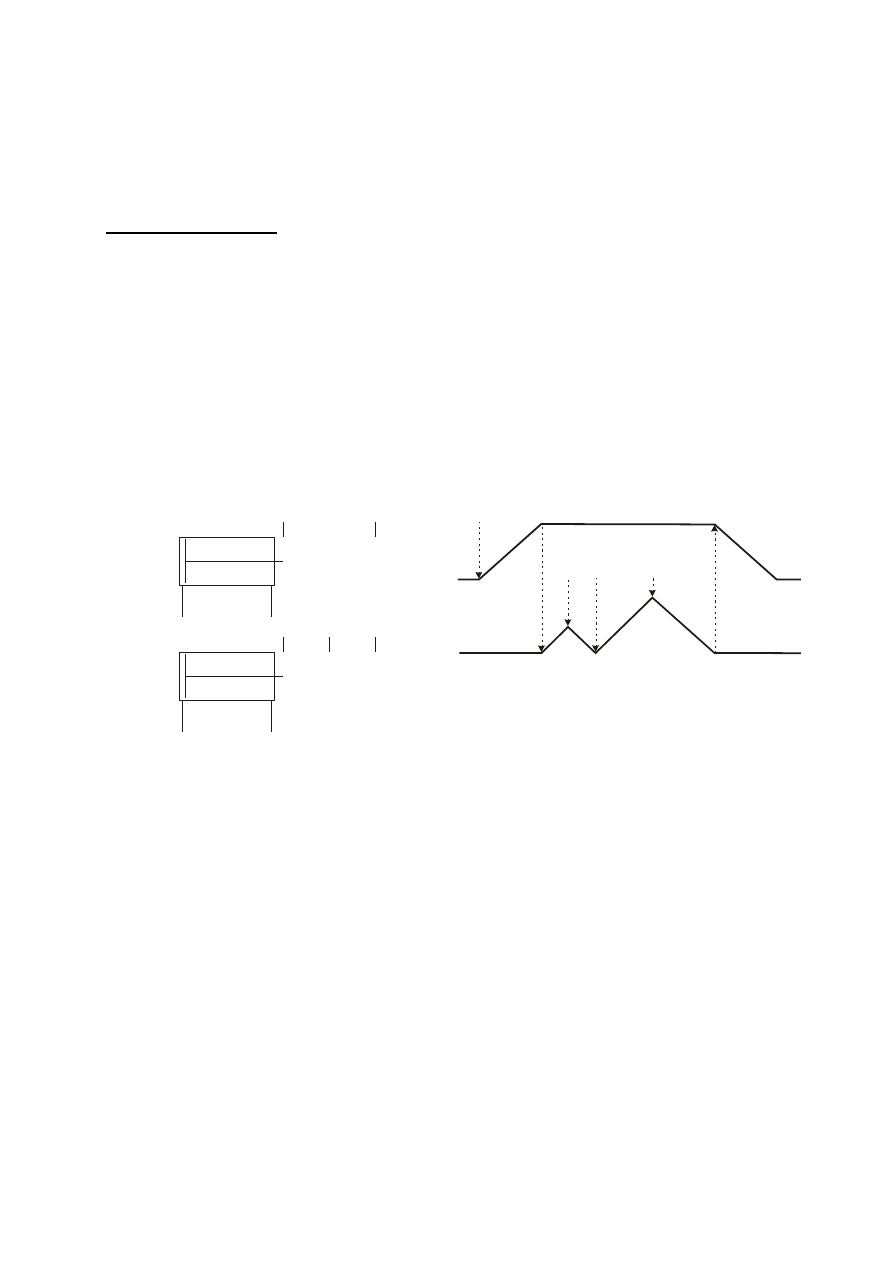
Strona 1
13. Projektowanie
układów
sekwencyjnych
procesowo–
zależnych o programach liniowych na przykładzie układów
elektropneumatycznych.
Przykładowy problem
Zaprojektować układ sterowania dwoma siłownikami pneumatycznymi A i B dwustronnego
działania, wyposażonymi w przekaźniki położenia a, b, c, d, e, usytuowane jak na rysunku.
Układ sterowania winien zapewnić wykonanie cyklu ruchów:
1 – całkowite wysunięcie siłownika A,
2 – częściowe wysunięcie siłownika B do przekaźnika d,
3 – wycofanie siłownika B,
4 – całkowite wysunięcie siłownika B,
5 – wycofanie siłownika B,
6 – wycofanie siłownika A.
Cykl pracy jest inicjowany przez podanie impulsu z przycisku START (x). Układ winien
umożliwić rozpoczęcie cyklu pracy tylko w przypadku gdy obydwa siłowniki są wycofane.
a)
b)
A
B
a
b
e
c
d
Usytuowanie przekaźników położenia
Cyklogram pracy siłowników
Należy rozważyć:
- wykorzystanie zaworów roboczych monostabilnych (układ sterowania o dwóch
sygnałach wyjściowych y
1
i y
2
),
- wykorzystanie zaworów roboczych bistabilnych (układ sterowania o czterech
sygnałach wyjściowych A+, A-, B+, B-),
Zrealizować układ sterowania jako:
- układ Moore’a i Mealy’ego,
- do kodowania stanów wewnętrznych zastosować kod ze stałym odstępem i kod
„1 z n”
Zostaną zrealizowane warianty:
1. układ Moore’a – kod ze stałym odstępem – zawory robocze monostabilne,
2. układ Moore’a – kod ze stałym odstępem – zawory robocze bistabilne,
3. układ Moore’a – kod „1 z n” – zawory robocze monostabilne,
4. układ Moore’a – kod „1 z n” – zawory robocze bistabilne,
5. układ Mealy’ego – kod ze stałym odstępem – zawory robocze monostabilne,
6. układ Mealy’ego – kod ze stałym odstępem – zawory robocze bistabilne,
7. układ Mealy’ego – kod „1 z n” – zawory robocze monostabilne,
x·a·c
d
c
e
b
c
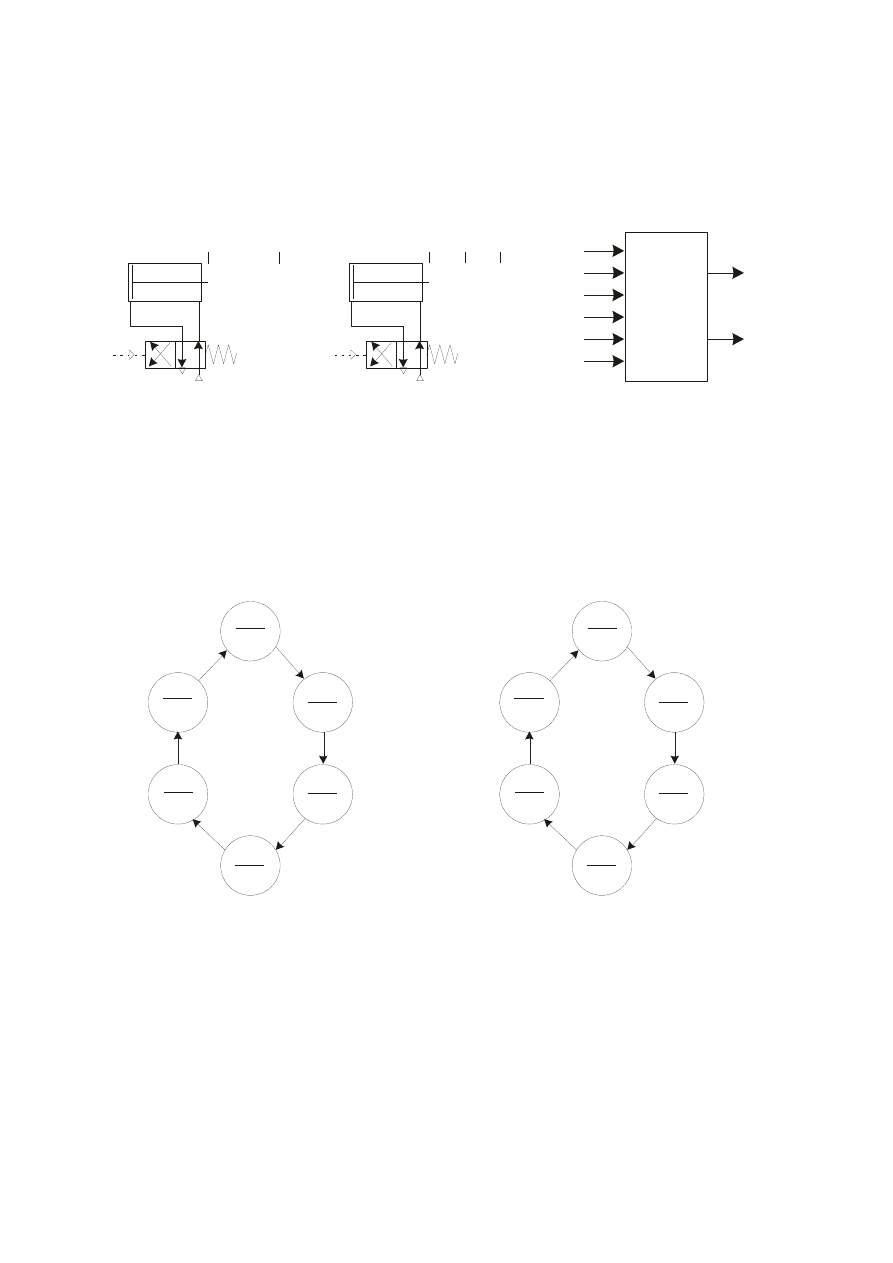
Strona 2
8. układ Mealy’ego – kod „1 z n” – zawory robocze bistabilne.
Należy zbudować schematy logiczne układów sterowania dla poszczególnych
wariantów oraz realizacje elektropneumatyczne i pneumatyczne.
Wariant 1 - układ Moore’a – kod ze stałym odstępem – zawory robocze
monostabilne
A
B
a
b
e
c
d
y
1
y
2
a
b
c
d
e
x
y
1
y
2
Schemat układy napędowego i schemat blokowy projektowanego układu
W przypadku układu Moore’a liczba stanów wewnętrznych jest równa liczbie
kolejnych stanów sygnałów wyjściowych (stanów wyjść) wyjść w cyklu pracy.
Na podstawie opisu procesu tworzymy graf układu, numerujemy stany wewnętrzne i
przyporządkowujemy im stany wyjść (w biegunach grafu). Strzałki reprezentują stany wejść,
które powinny spowodować przejście do następnego stanu wewnętrznego. Opis jest
symboliczny, np.
c
a
x
przy strzałce oznacza, że zmiana stanu winna wystąpić kiedy
zaistnieje
1
c
a
x
. Graf jest syntetyczną formą zapisu działania układu.
1
10
2
11
0
00
5
10
3
10
4
11
b
c
e
c
x·a·c
d
1
10
2
11
0
00
5
10
3
10
4
11
b
c
e
c
x·a·c
d
000
100
110
111
011
001
Graf – opis działania układu
Kodowanie stanów wewnętrznych
y
1
y
2
Q
1
Q
2
Q
3
Strona 3
W
2
Z
2
Q
2
Q
2
W
1
Q
1
Q
1
Z
1
W
3
Z
3
Q
3
Q
3
1
10
2
11
0
00
5
10
3
10
4
11
b
c
e
c
x·a·c
d
Q
1
2
3
Q Q
000
100
110
111
011
001
w
2
w
1
z
3
z
2
z
1
w
3
y
1
2
y
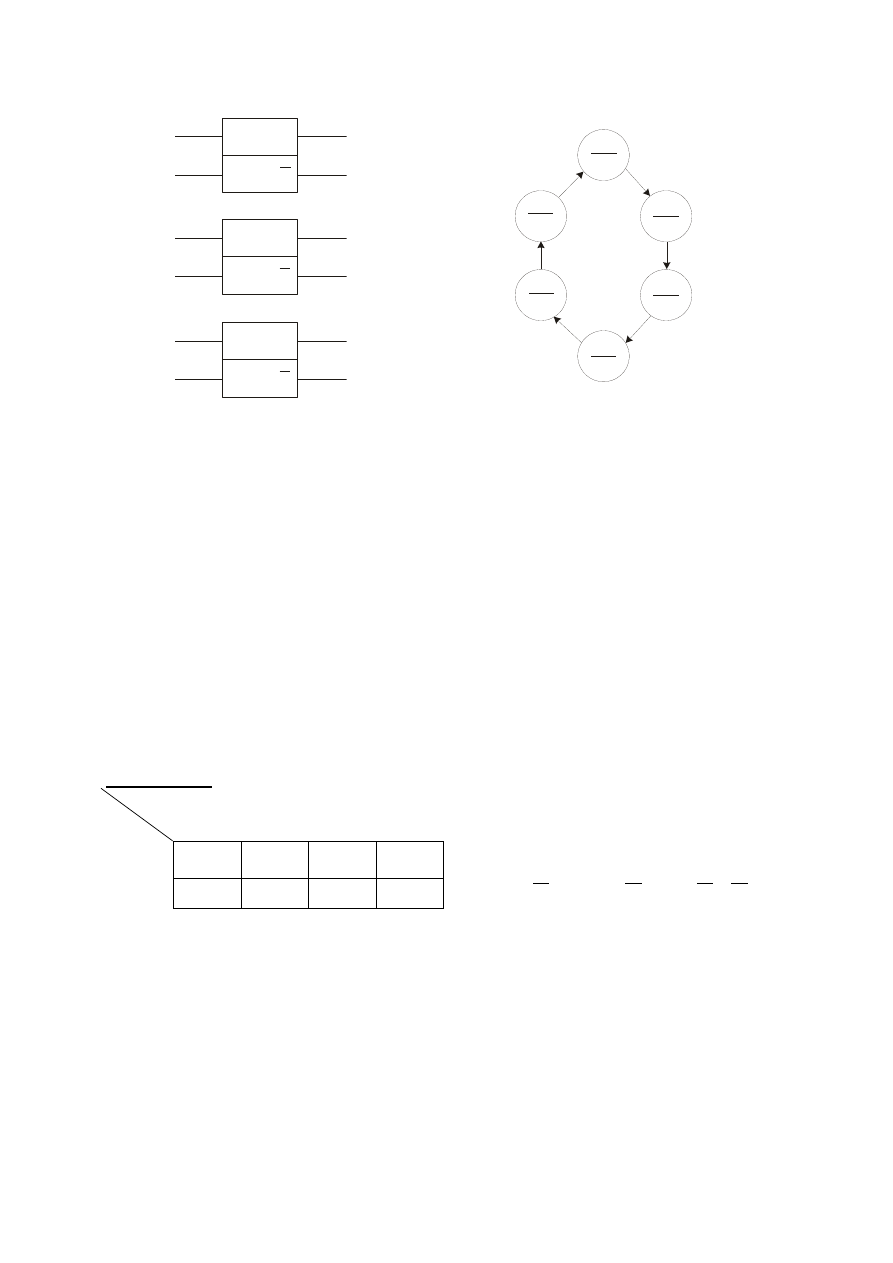
Oznaczenia sygnałów przerzutników
Wzbudzenia powodujące zmiany stanów wewnętrznych
Drugim etapem jest kodowanie stanów wewnętrznych – ustalamy potrzebną liczbę
zmiennych kodowych, oznaczamy te zmienne, np.
3
2
1
,
,
Q
Q
Q
i przypisujemy poszczególnym
stanom wewnętrznym zestawy wartości tych zmiennych (kody). W danym przypadku
zastosowano kod pseudopierścieniowy.
Ponieważ każda zmienna kodowa reprezentuje stan jednego przerzutnika, to wiadomo już ile
jest potrzebnych przerzutników w projektowanym układzie – rys. powyżej. Pozostaje
wyznaczyć funkcje wyjść i funkcje wzbudzeń przerzutników.
W układach Moore’a sygnały wyjściowe zależą tylko od sygnałów reprezentujących stan
wewnętrzny. Funkcje wyjść mają więc postać:
)
,
,
(
3
2
1
1
1
Q
Q
Q
f
y
oraz
)
,
,
(
3
2
1
2
2
Q
Q
Q
f
y
.
Zależności te są zdefiniowane w zakodowanym grafie. Aby uzyskać ich postać
analityczną należy je przepisać do odpowiedniej tablicy Karnaugha (lub przeprowadzić
syntezę funkcji wykorzystując inne metody) - tablicy wyjść i utworzyć postać alternatywną
(sklejanie jedynek) lub koniunkcyjną (sklejanie zer). W dalszych działaniach są tworzone
tylko postacie alternatywne funkcji.
Tablica wyjść
3
2
Q
Q
1
Q
00
01
11
10
0
00
10
11
--
3
1
1
Q
Q
y
1
10
--
10
11
)
(
3
1
2
3
2
2
1
2
Q
Q
Q
Q
Q
Q
Q
y
2
1
, y
y
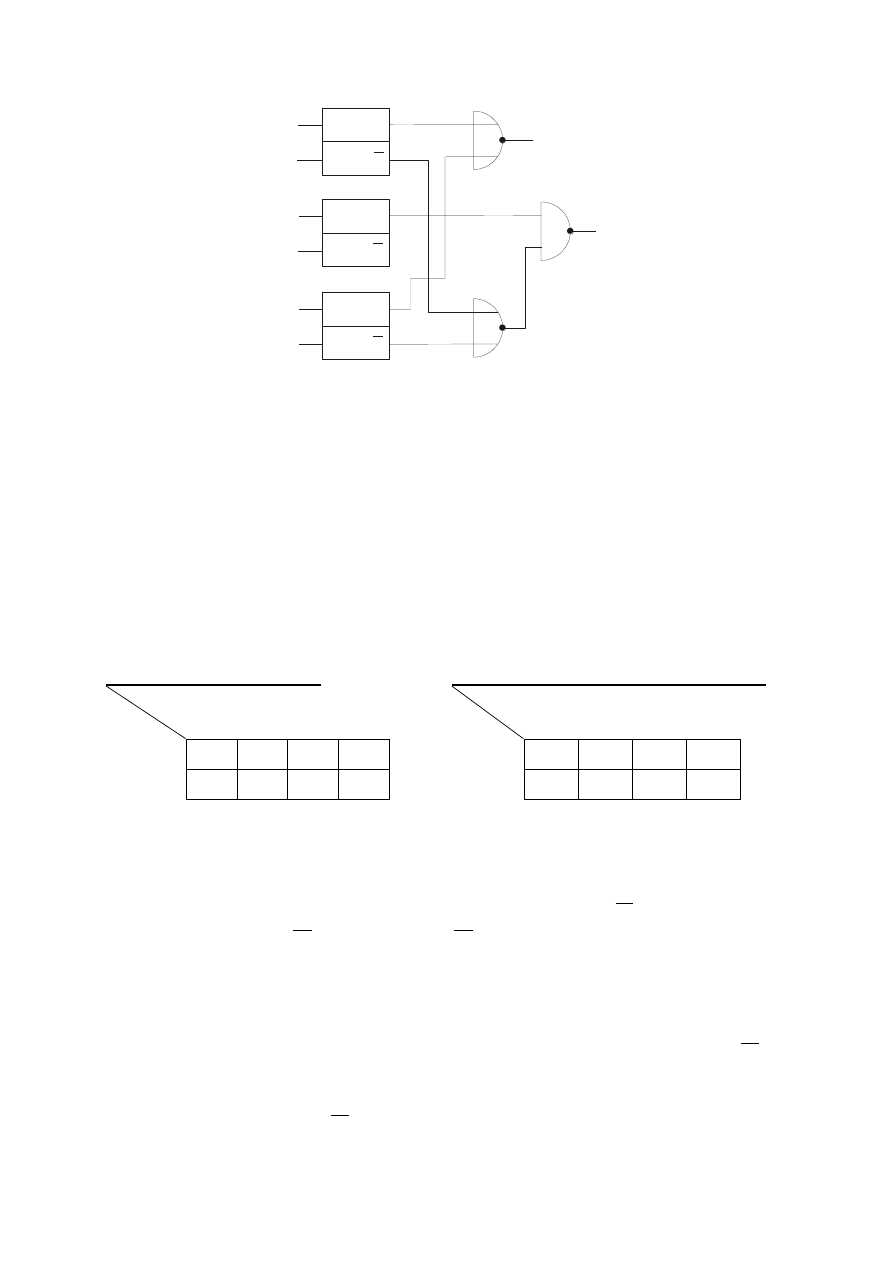
Do układu przerzutników można już dołączyć schemat układu realizującego funkcje
wyjść.
Strona 4
W
2
Z
2
Q
2
Q
2
W
1
Q
1
Q
1
Z
1
W
3
Z
3
Q
3
Q
3
y
1
y
2
Funkcje wzbudzeń przerzutników wyznacza się dwuetapowo. Układ realizujący
funkcje wzbudzeń winien zapewnić uzyskanie założonej kolejności zmian stanów
wewnętrznych oraz to, że zmiany te będą następować z chwilą pojawienia się odpowiednich
stanów wejść (zgodnie z ustaleniami zapisanymi w grafie).
W pierwszej kolejności ustala się wzbudzenia zapewniające uzyskanie założonej
kolejności zmian stanów wewnętrznych. Służy do tego uproszczona tablica przejść –
wymienione są w niej kody stanów następnych
'
i
Q
względem stanów aktualnych
i
Q .
Funkcje wzbudzeń można wyznaczyć albo tworząc na podstawie uproszczonej tablicy przejść
i macierzy przejść zastosowanych przerzutników tablice wzbudzeń poszczególnych
przerzutników albo bezpośrednio na podstawie tzw. uniwersalnej uproszczona tablica
przejść. W dalszym ciągu wzbudzenia będą wyznaczane na podstawie tablic uniwersalnych.
Uniwersalną uproszczoną tablicę przejść tworzymy na podstawie uproszczonej tablicy
przejść przez pogrubienie tych wartości
'
i
Q
, które są inne niż
i
Q .
Uproszczona tablica przejść
3
2
Q
Q
1
Q
00
01
11
10
0
001
011
111
---
1
000
---
110
100
3
2
1
,
,
Q
Q
Q
Uniwersalna uproszczona tablica przejść
3
2
Q
Q
1
Q
00
01
11
10
0
001
011
111
---
1
000
---
110
100
3
2
1
,
,
Q
Q
Q
Posługując się wzorami do ustalania wzbudzeń (ich postaci alternatywnych) na
podstawie tablicy uniwersalnej
w
F1(F1,F-) oraz
z
F0(F0,F-), otrzymuje się
wyrażenia:
2
1
2
1
Q
z
Q
w
3
2
3
2
Q
z
Q
w
1
3
1
3
Q
z
Q
w
Wzbudzenia zgodne z powyższymi równaniami zapewniają uzyskanie właściwej
kolejności zmian stanów wewnętrznych, jednakże bez oczekiwania na wykonanie
zamierzonej czynności w danym stanie wewnętrznym. Na przykład, w stanie wewnętrznym
000 przejście do kolejnego stanu 001 powoduje pojawienie się w stanie 000 wzbudzenia
1
3
w
. Z chwilą osiągnięcia stanu 000, wyznaczone wzbudzenie
1
1
3
Q
w
spowodowałoby natychmiastowe przejście do stanu 001, itd. Zmiana stanu wewnętrznego z
000 na 001 powinna nastąpić dopiero po pojawieniu się koniunkcji
1
c
a
x
, zatem
ostatecznie powinno być
c
a
x
Q
w
3
3
.
Strona 5
Analogicznie należy skojarzyć wyznaczone na podstawie uniwersalnej uproszczonej
tablicy przejść wzbudzenia przerzutników z odpowiednimi sygnałami wejściowymi,
powodującymi pożądane zmiany stanów wewnętrznych. Ułatwia to dokonany opis grafu.
Ostatecznie więc wzbudzenia przerzutników mają postać:
c
Q
z
d
Q
w
2
1
2
1
e
Q
z
b
Q
w
3
2
3
2
c
Q
z
c
a
x
Q
w
1
3
1
3
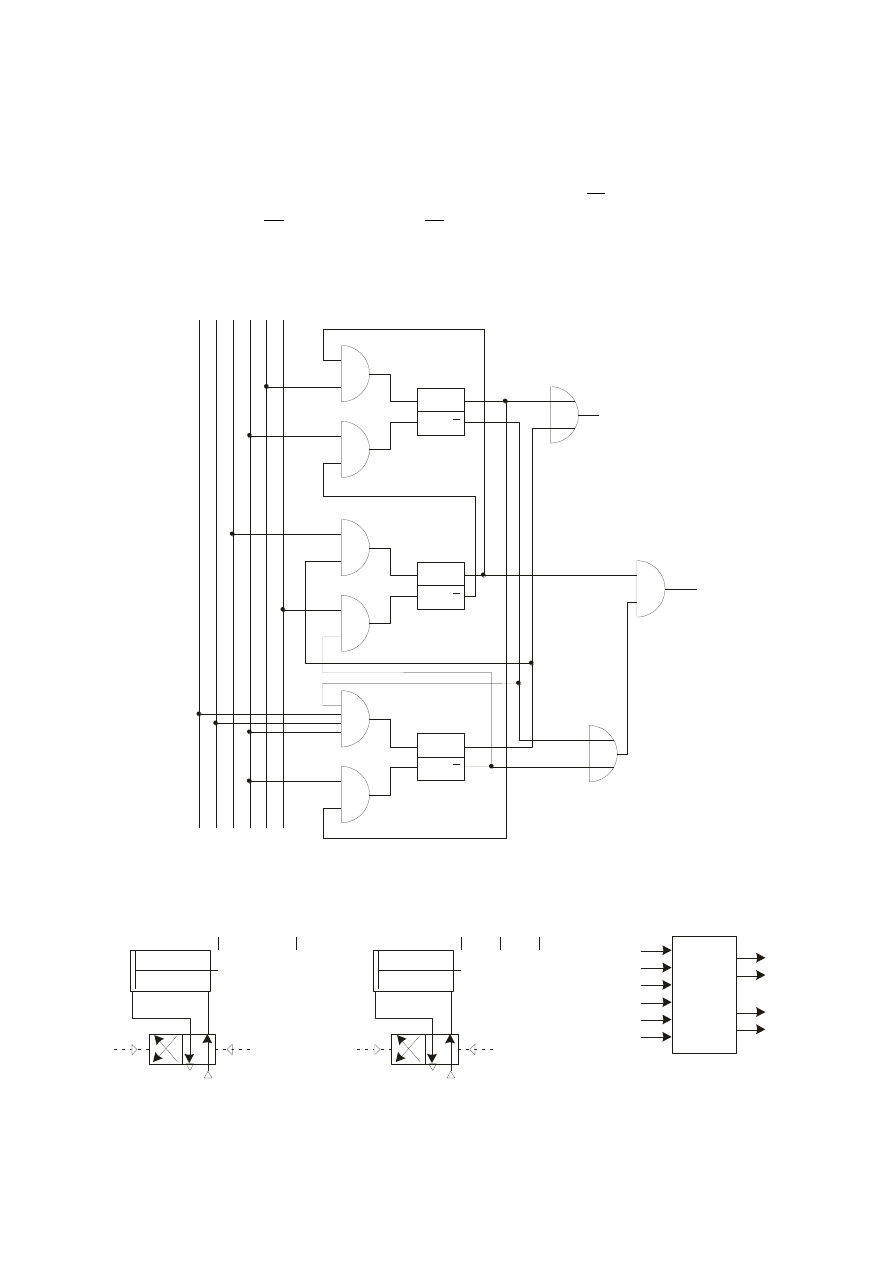
Uwzględniając powyższe równania, można zbudować kompletny schemat logiczny
projektowanego układu.
W
1
Q
1
Q
1
Z
1
W
2
Q
2
Q
2
Z
2
W
3
Q
3
Q
3
Z
3
x
a
b
c d
e
y
1
y
2
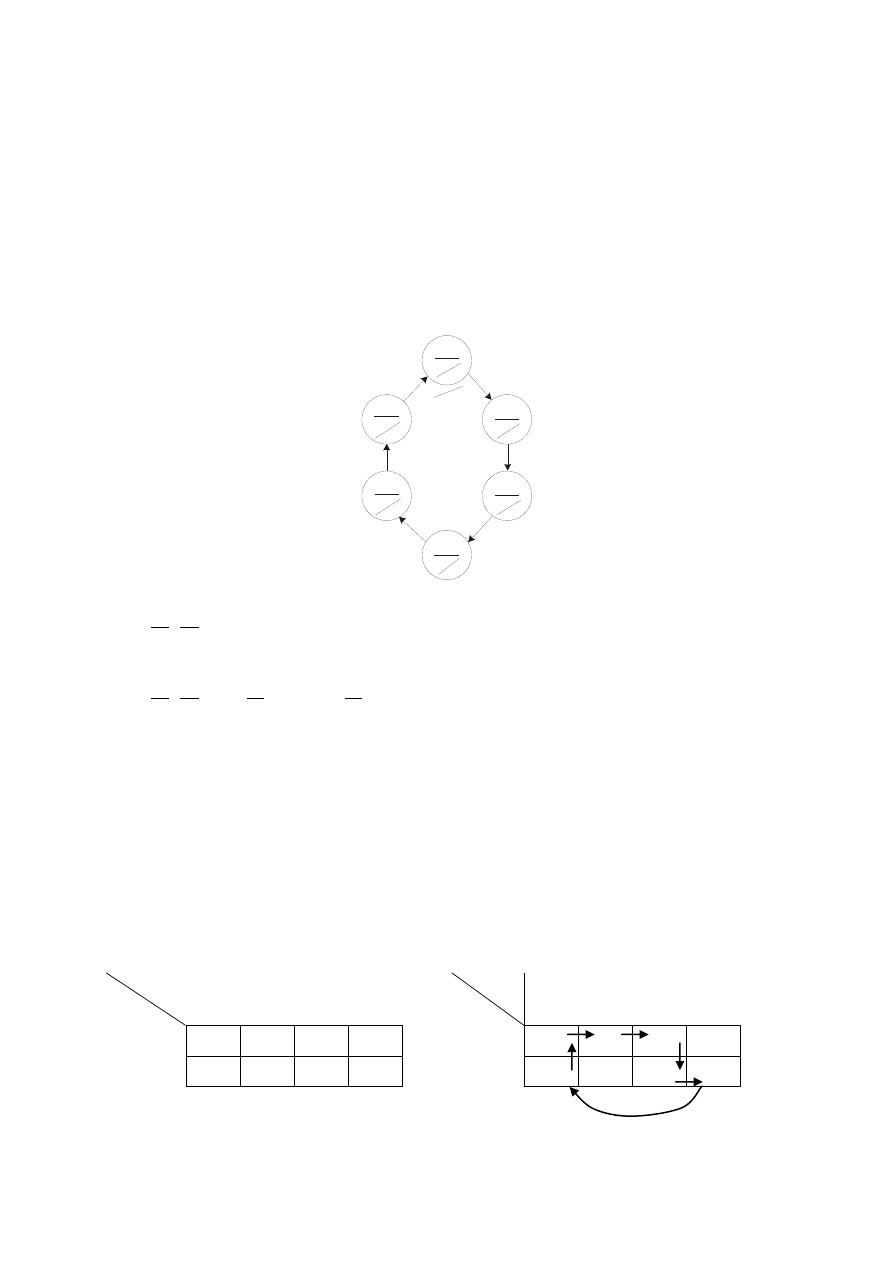
Wariant 2 - układ Moore’a – kod ze stałym odstępem – zawory robocze bistabilne
A
B
a
b
e
c
d
a
b
c
d
e
x
A+
B+
A-
B-
A+
A-
B+
B-
Schemat układy napędowego i schemat blokowy projektowanego układu
Strona 6
W tym przypadku zadaniem projektowanego układu sterującego jest wytwarzanie
czterech sygnałów sterujących zaworami roboczymi napędu. Sygnał
A
powoduje
wysuwanie siłownika A, sygnał
A
wycofanie siłownika A. Analogicznie sygnały
B
i
B
.
Projektowany układ różni się od poprzedniego tylko budową części wytwarzającej sygnały
wyjściowe. Poniżej przedstawiono zatem tylko tok postępowania zmierzający do
wyznaczenia funkcji wyjść.
W tym wariancie, aby uzyskać zamierzone ruchy siłowników, w stanie 1 trzeba wytworzyć
sygnał
1
A
, w stanie 2 sygnał
1
B
, itd., co pokazano na grafie.
1
10
2
11
0
00
5
10
3
10
4
11
Q
1
2
3
Q Q
000
100
110
111
011
001
y y
1
2
A+
B+
B-
B+
B-
A-
Aby wytworzyć sygnał
1
A
w stanie 1, należałoby zrealizować funkcję
3
2
1
Q
Q
Q
A
. Sygnał
1
A
mógłby bez zmiany działania układu istnieć także w stanach
2, 3, 4 i 5. Gdyby np. utrzymywać go w stanach 1 i 2, to uprościłoby to funkcję wyjść, bo
byłoby
3
1
3
2
1
3
2
1
Q
Q
Q
Q
Q
Q
Q
Q
A
Do uzyskania najprostszych postaci funkcji wyjść prowadzi opisana poniżej
procedura.
Zawory bistabilne są przerzutnikami. Traktując sygnały
A
i
B
jako sygnały
włączające tych przerzutników (zaworów), tablicę wyjść z wariantu poprzedniego można
potraktować jako tablicę stanów tych zaworów. Stan 1 zaworu sterującego siłownikiem A to
stan, w którym siłownik wysuwa się.
W tablicy stanów zaworów można pokazać za pomocą strzałek kolejność zmian stanu
tych zaworów, zgodnie z kolejnością zmian stanów wewnętrznych. Dzięki temu tablicę
można przekształcić do postaci tablicy uniwersalnej, przez pogrubienie tych wartości, które
różnią się od wartości poprzedniej.
Tablica stanów bistabilnych zaworów
roboczych
3
2
Q
Q
1
Q
00
01
11
10
0
00
10
11
--
1
10
--
10
11
A,B
Tablica stanów bistabilnych zaworów
roboczych ostrzałkowana
3
2
Q
Q
1
Q
00
01
11
10
0
00
10
11
--
1
10
--
10
11
A,B
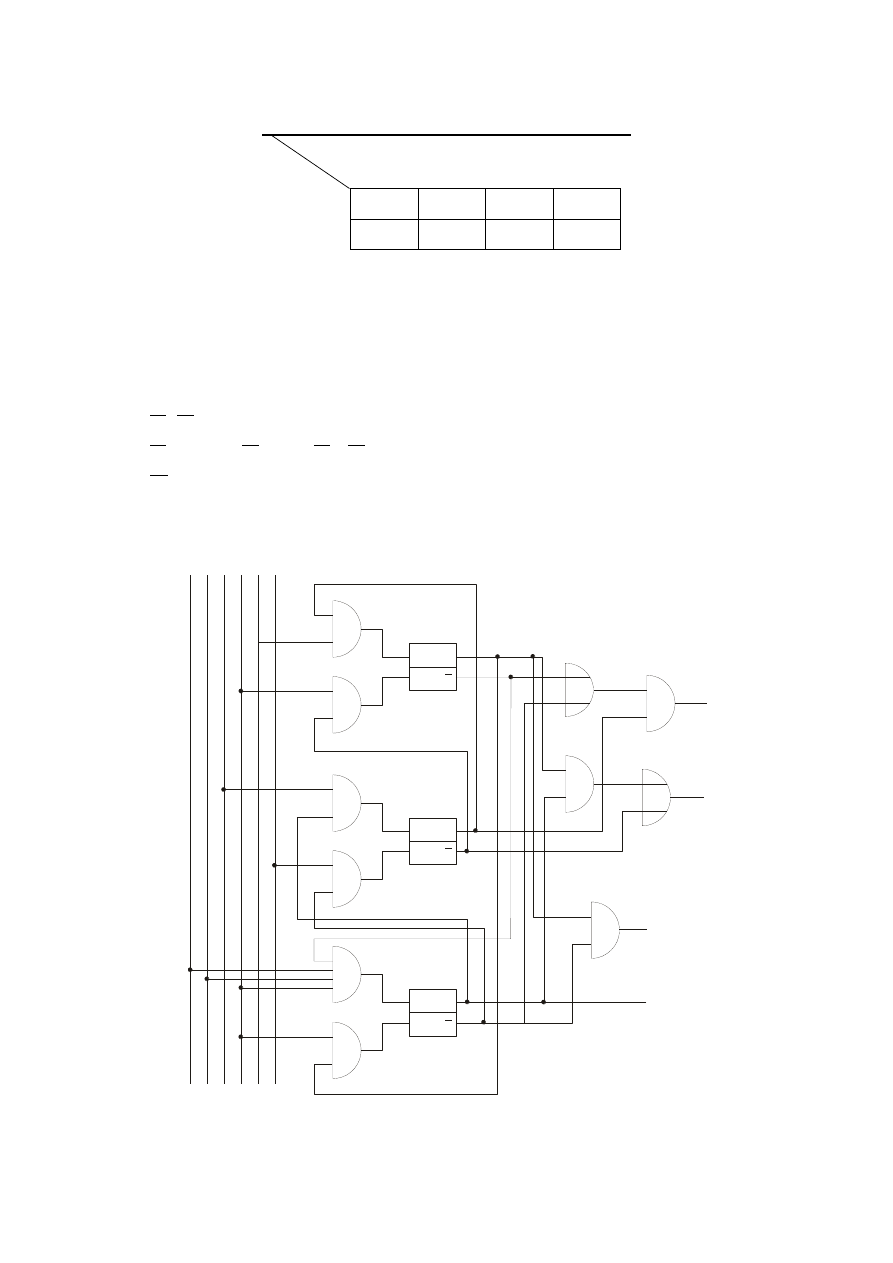
Strona 7
Uniwersalna tablica stanów zaworów roboczych
3
2
Q
Q
1
Q
00
01
11
10
0
00
10
11
--
1
10
--
10
11
A,B
Na podstawie tablicy uniwersalnej, zgodnie z wzorami
A
F1(F1,F-)
A
F0(F0,F-)
i podobnie dla sygnałów
B
i
B
, otrzymuje się poszukiwane funkcje wyjść
3
Q
A
3
1
Q
Q
A
)
(
3
1
2
3
2
2
1
Q
Q
Q
Q
Q
Q
Q
B
3
1
2
Q
Q
Q
B
Wykorzystując z poprzedniego wariantu część układy realizującą funkcję przejść można
wykreślić schemat logiczny układu
W
1
Q
1
Q
1
Z
1
W
2
Q
2
Q
2
Z
2
W
3
Q
3
Q
3
Z
3
x
a
b
c d
e
B+
B-
A-
A+
Schemat logiczny układu sterującego wg wariantu 2
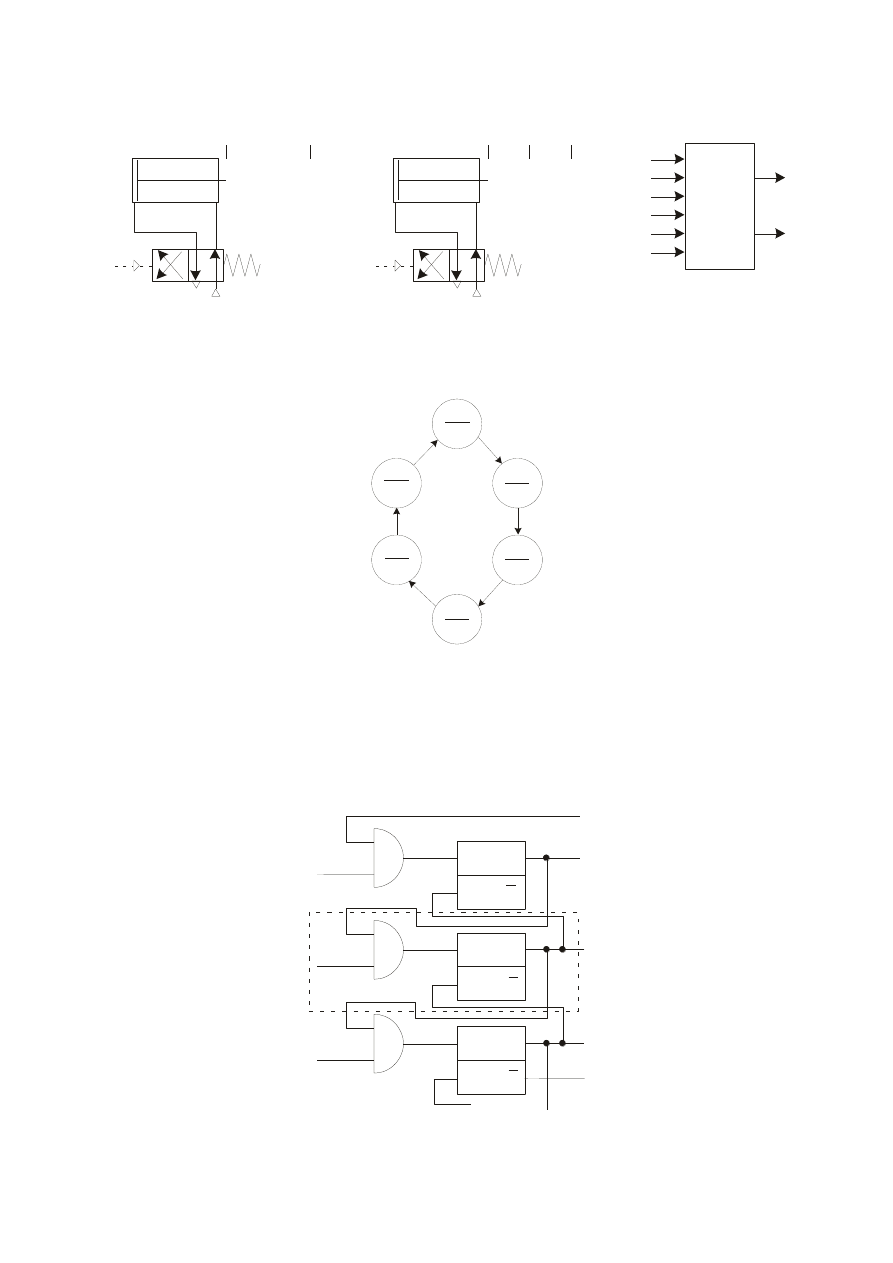
Strona 8
Wariant 3 - układ Moore’a – kod „1 z n” – zawory robocze monostabilne
A
B
a
b
e
c
d
a
b
c
d
e
x
y
1
y
2
y
1
y
2
Schemat układy napędowego i schemat blokowy projektowanego układu
1
10
2
11
0
00
5
10
3
10
4
11
100000
000001
000010
000100
001000
010000
y y
1
2
b
c
e
c
x·a·c
d
Q
Q Q
0
4
5
Q
1
2
3
Q Q
Graf układy ze stanami wewnętrznymi zakodowanymi w kodzie „1 z 6”
W tym wariancie liczba zmiennych kodowych jest równa liczbie stanów
wewnętrznych. Do budowy części układu realizującej funkcję przejść (część odpowiedzialną
za zmiany stanu wewnętrznego) należy więc wykorzystać w tym przypadków 6
przerzutników. Projektowanie formalne tej części prowadzi do układu składającego się z
jednakowych segmentów. Pojedynczy segment został na rysunku poniżej obwiedziony linią
przerywana
W
i
Z
i
Q
i
Q
i
W
i-1
Q
i-1
Q
i-1
Z
i-1
W
i+1
Z
i+1
Q
i+1
Q
i+1
x
i-1
x
i
x
i+1
Strona 9
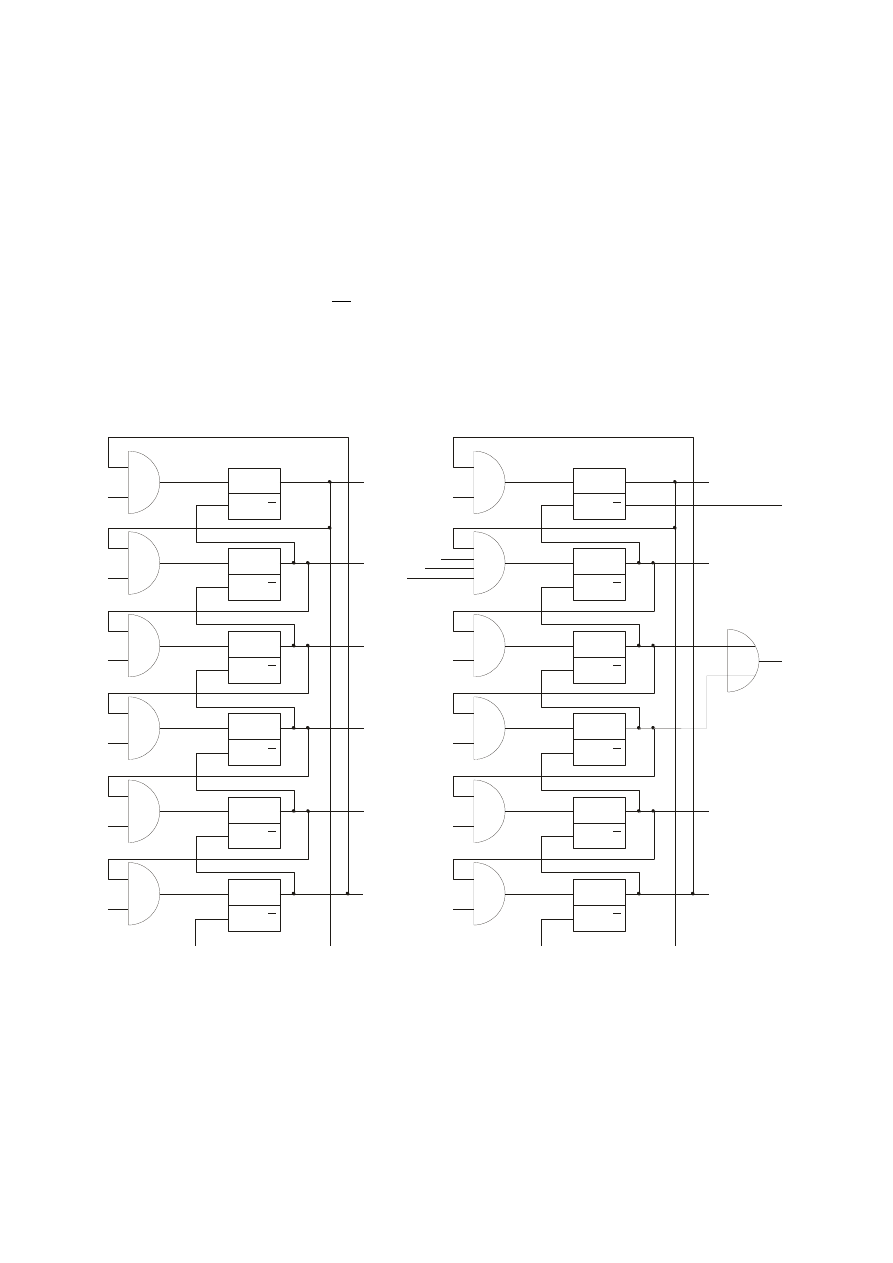
Budowa segmentu układów realizujących funkcje przejść w przypadku zastosowania
kodu „1 z n”
Sygnał
i
x to sygnał wejściowy powodujący zmianę stanu wewnętrznego – włączenie
przerzutnika
i
Q . Po jego włączeniu następuje wyłączenie przerzutnika włączonego w stanie
dotychczasowym i podanie sygnału
i
Q na wejście elementu koniunkcji członu następnego.
Pojawienie się sygnału wejściowego
1
i
x
powoduje przejście do kolejnego stanu
wewnętrznego.
Funkcje wyjść ustala się bezpośrednio na podstawie zakodowanego grafu:
0
5
4
3
2
1
1
Q
Q
Q
Q
Q
Q
y
4
2
2
Q
Q
y
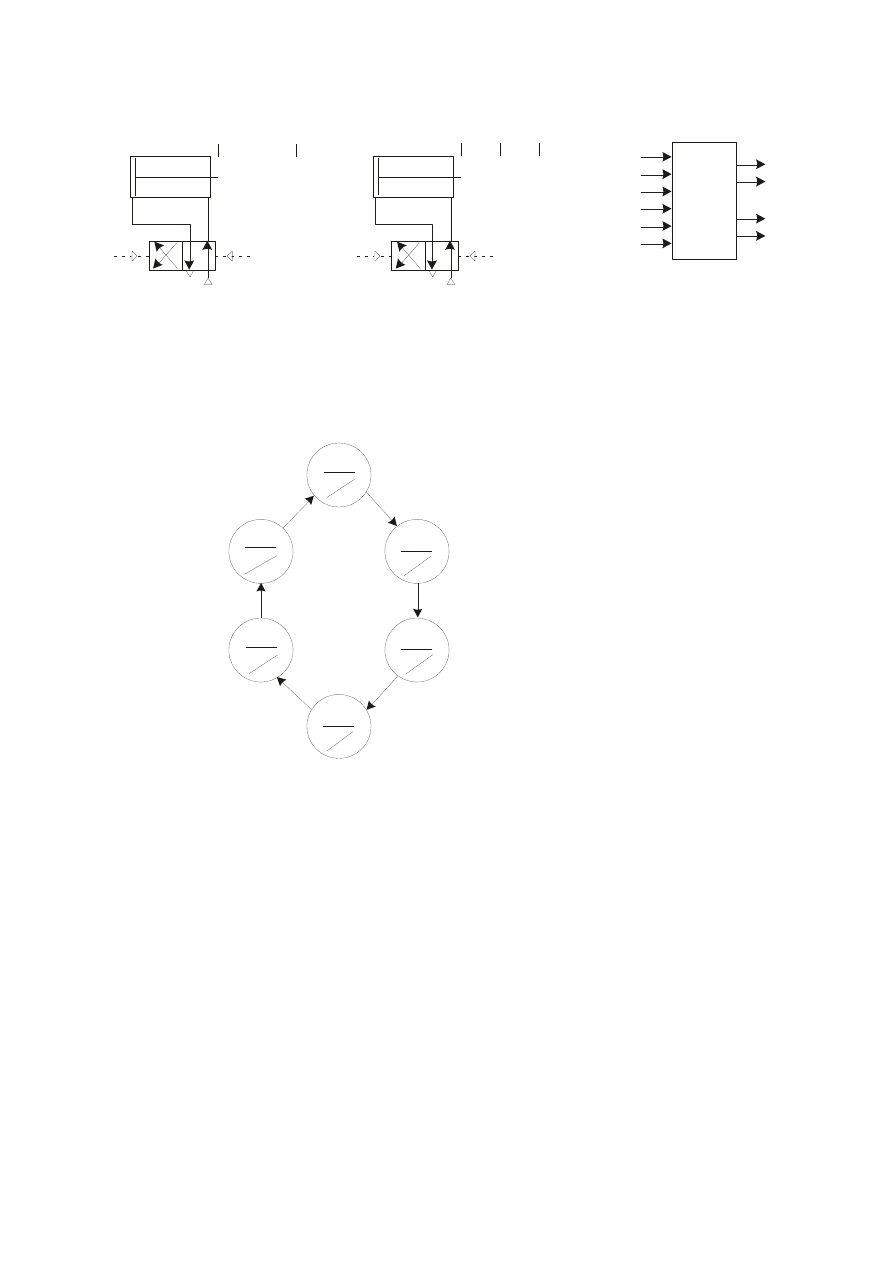
Na rysunkach poniżej pokazano strukturę układu o sześciu stanach wewnętrznych,
zakodowanych w kodzie „1 z 6”, realizującego funkcję przejść oraz kompletny schemat
układu wg wariantu 3.
W
0
Q
0
Q
0
Z
0
W
1
Q
1
Q
1
Z
1
W
2
Q
2
Q
2
Z
2
W
3
Q
3
Q
3
Z
3
W
4
Q
4
Q
4
Z
4
W
5
Q
5
Q
5
Z
5
W
0
Q
0
Q
0
Z
0
W
1
Q
1
Q
1
Z
1
W
2
Q
2
Q
2
Z
2
W
3
Q
3
Q
3
Z
3
W
4
Q
4
Q
4
Z
4
W
5
Q
5
Q
5
Z
5
e
c
a
x
b
d
y
1
y
2
c
c
Strona 10
Wariant 4 - układ Moore’a – kod „1 z n” – zawory robocze bistabilne
A
B
a
b
e
c
d
a
b
c
d
e
x
A+
B+
A-
B-
A+
A-
B+
B-
Schemat układy napędowego i schemat blokowy projektowanego układu
1
10
2
11
0
00
5
10
3
10
4
11
100000
000001
000010
000100
001000
010000
b
c
e
c
x·a·c
d
A-
B+
A+
B-
B-
B+
Q
Q Q
0
4
5
Q
1
2
3
Q Q
5
3
4
2
0
1
Q
Q
B
Q
Q
B
Q
A
Q
A
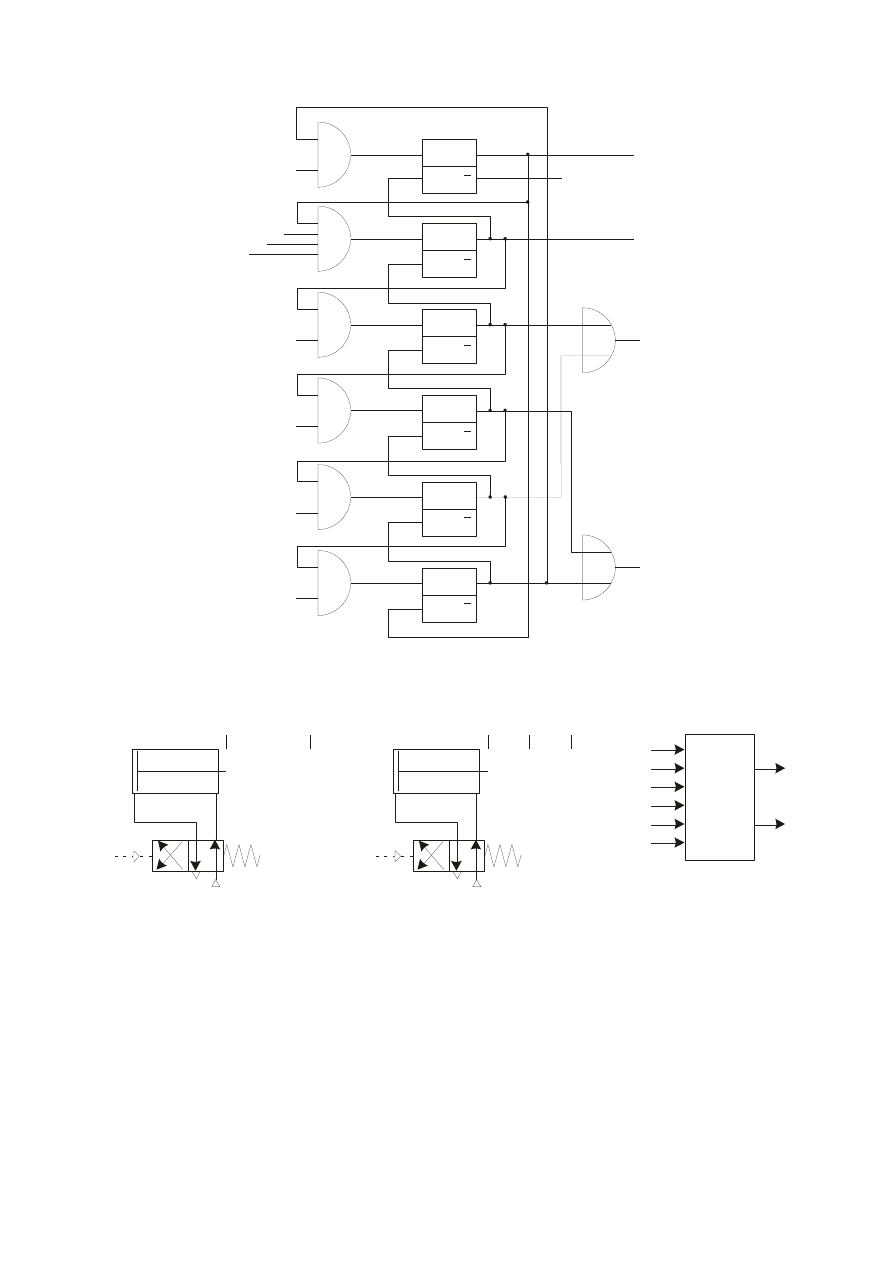
Graf układu z kodem „1 z 6”
Funkcje wyjść
Strona 11
W
0
Q
0
Q
0
Z
0
W
1
Q
1
Q
1
Z
1
W
2
Q
2
Q
2
Z
2
W
3
Q
3
Q
3
Z
3
W
4
Q
4
Q
4
Z
4
W
5
Q
5
Q
5
Z
5
e
c
a
x
b
d
B+
B-
A+
A-
c
c
Schemat logiczny układu
Wariant 5 - układ Mealy’ego – kod ze stałym odstępem – zawory robocze monostabilne
A
B
a
b
e
c
d
a
b
c
d
e
x
y
1
y
2
y
1
y
2
Schemat układy napędowego i schemat blokowy projektowanego układu
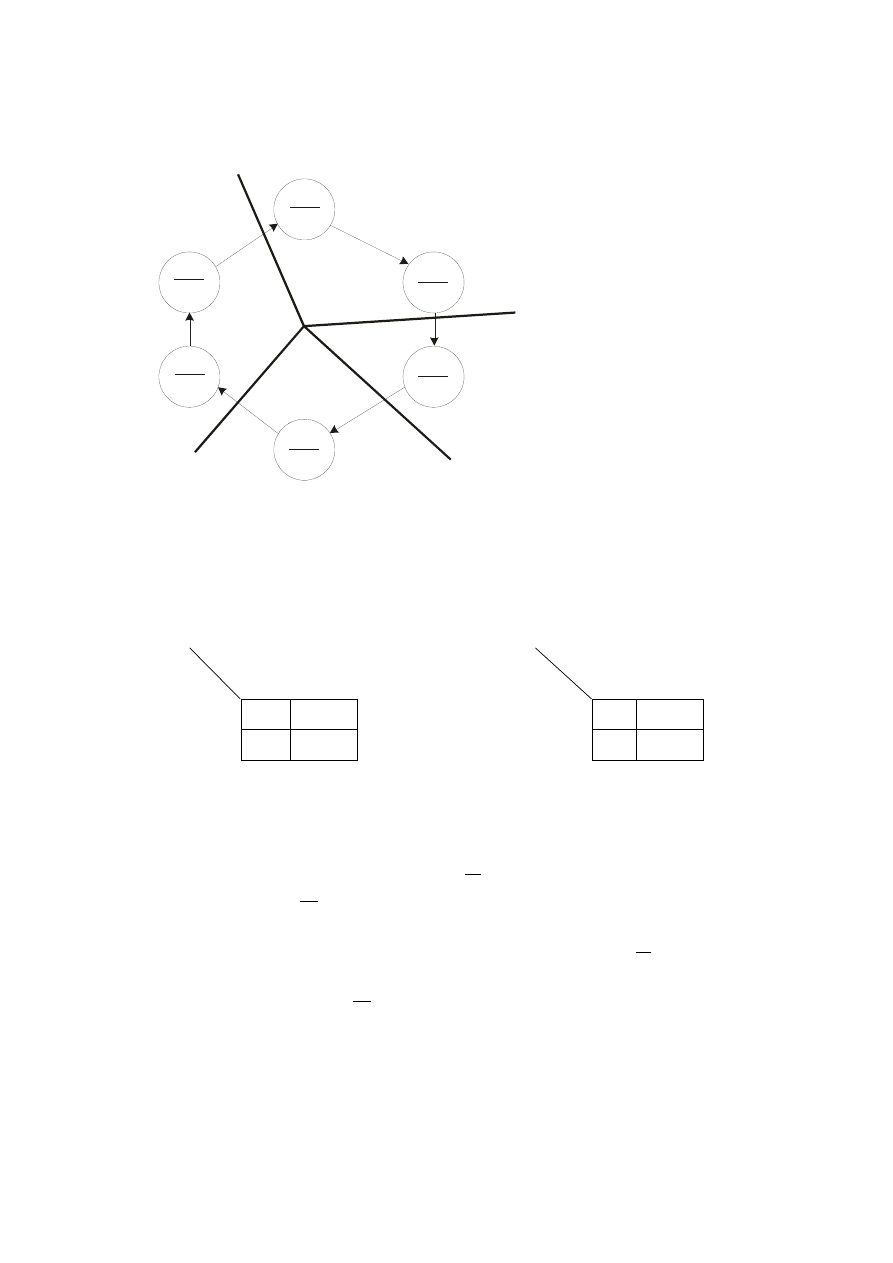
Badanie możliwości realizacji układu jako układu Mealy’ego polega na poszukiwaniu
sąsiednich stanów wewnętrznych, w których wykonywane czynności nie są przeciwne. Dla
ułatwienia tej czynności oznaczamy na grafie, przy każdym stanie wewnętrznym układu
Moore’a, wykonywaną czynność, np.
A
oznacza w tym przypadku wysuwanie siłownika
A,
A
oznacza wycofanie siłownika A.
Strona 12
1
10
2
11
0
00
5
10
3
10
4
11
b
c
e
c
x·a·c
d
A-
B+
A+
B-
B-
B+
Q Q
1
2
01
11
10
00
y y
1
2
Czynności wykonywane w stanach
1 i 2, tj.
A
i
B
są nie są
przeciwne, zatem te dwa stany
można w układzie Mealy’ego
traktować jako jeden stan
wewnętrzny. Nowe stany
oddzielamy od innych liniami
wychodzącymi promieniście ze
środka grafu i wprowadzamy kody
nowych stanów wewnętrznych.
W tym przypadku układ Mealy’ego
ma tylko cztery stany wewnętrzne,
zatem do ich zakodowania
wystarczą dwie zmienne (dwa
przerzutniki)
1
Q i
2
Q .
W celu ustalenia wzbudzeń przerzutników zostanie wykorzystana metodyka jak w wariancie
1. Na podstawie uproszczonej tablicy przejść zostaje utworzona uniwersalna uproszczona
tablica przejść.
2
Q
1
Q
0
1
0
01
11
1
00
10
2
1
,Q
Q
2
Q
1
Q
0
1
0
01
11
1
00
10
2
1
,Q
Q
Uproszczona tablica przejść
Uniwersalna uproszczona tablica przejść
Na podstawie uniwersalnej uproszczonej tablicy przejść wyznacza się wzbudzenia
zapewniające uzyskanie właściwej kolejności zmian stanów wewnętrznych:
2
1
2
1
Q
z
Q
w
1
2
1
2
Q
z
Q
w
Aby spowodować zmianę stanu wewnętrznego z 00 na 01 należy w sytuacji gdy zaistnieje
stan wejść
1
c
a
x
, wytworzyć sygnał
1
2
w
, zatem ostatecznie
c
a
x
Q
w
1
2
.
Podobnie na podstawie grafu otrzymuje się ostateczną postać pozostałych wzbudzeń:
d
Q
w
2
1
e
Q
z
2
1
c
Q
z
1
2
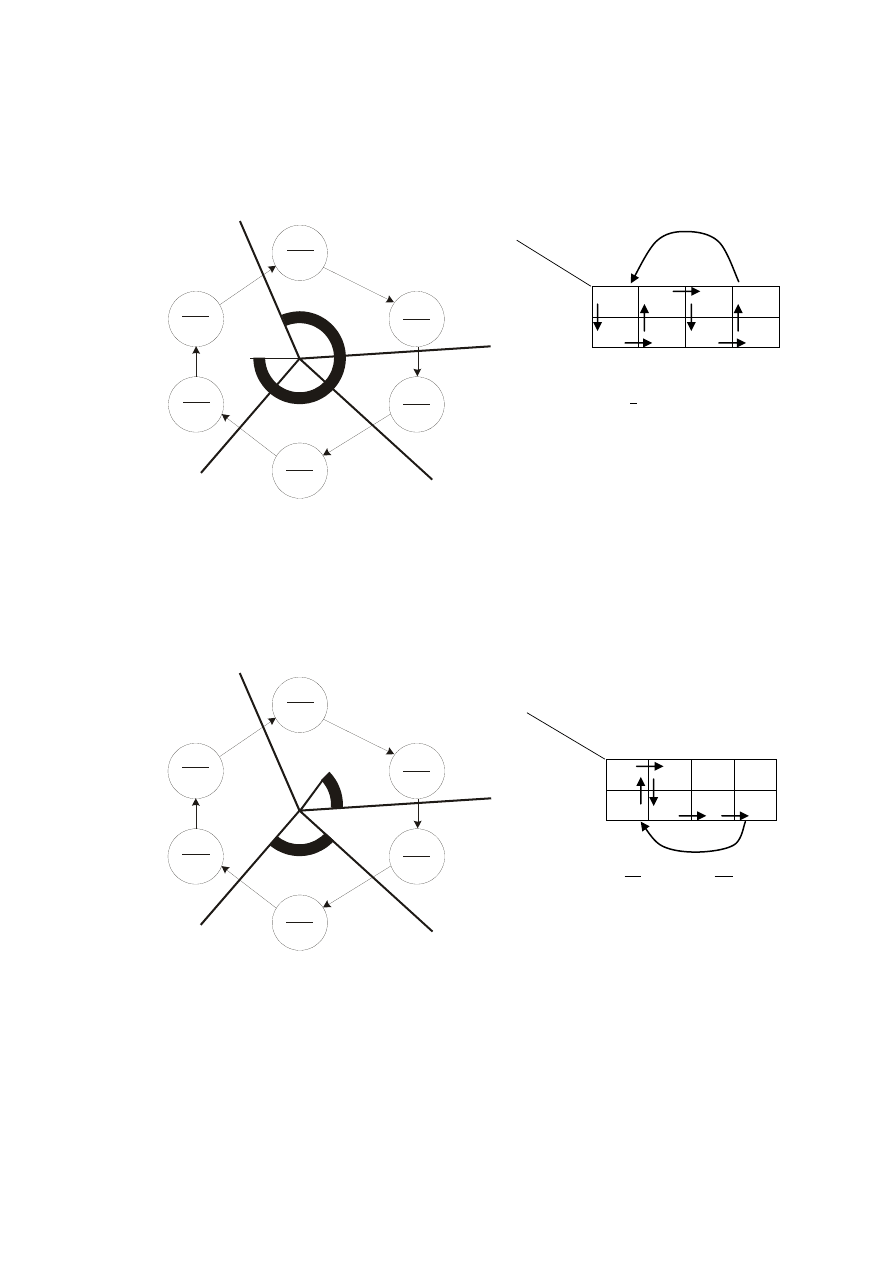
Kolejnym problemem jest wyznaczenie funkcji wyjść układu Mealy’ego.
Z grafu układu Moore’a wynika, że układ winien wytwarzać sygnał
1
1
y
w stanach 1, 2, 3,
4 i 5, a w układzie Mealy’ego w stanach 01, 11, 10 i w stanie 00 do chwili pojawienia się
sygnału
1
c
, co zaznaczono na poniższym grafie. Zatem sygnał
1
y zależy od sygnałów
1
Q ,
Strona 13
2
Q i c . Na podstawie grafu można zbudować tablicę Karnaugha funkcji wyjść
)
,
,
(
2
1
1
c
Q
Q
f
y
1
10
2
11
0
00
5
10
3
10
4
11
b
c
e
c
x·a·c
d
Q Q
1
2
01
11
10
00
y
1
y y
1
2
2
1
Q
Q
c
00
01
11
10
0
1
1
1
1
1
0
1
1
1
1
y
2
1
1
Q
Q
c
y
Analogicznie z grafu wynika, że sygnał
1
2
y
powinien być wytworzony w stanie 01 od
chwili pojawienia się sygnału
1
b
oraz w stanie 10. Zatem
)
,
,
(
2
1
2
b
Q
Q
f
y
.
1
10
2
11
0
00
5
10
3
10
4
11
b
c
e
c
x·a·c
d
Q Q
1
2
01
11
10
00
y
2
y
2
y y
1
2
2
1
Q
Q
b
00
01
11
10
0
0
0
-
-
1
0
1
0
1
2
y
2
1
2
1
2
Q
Q
Q
Q
b
y
Strona 14
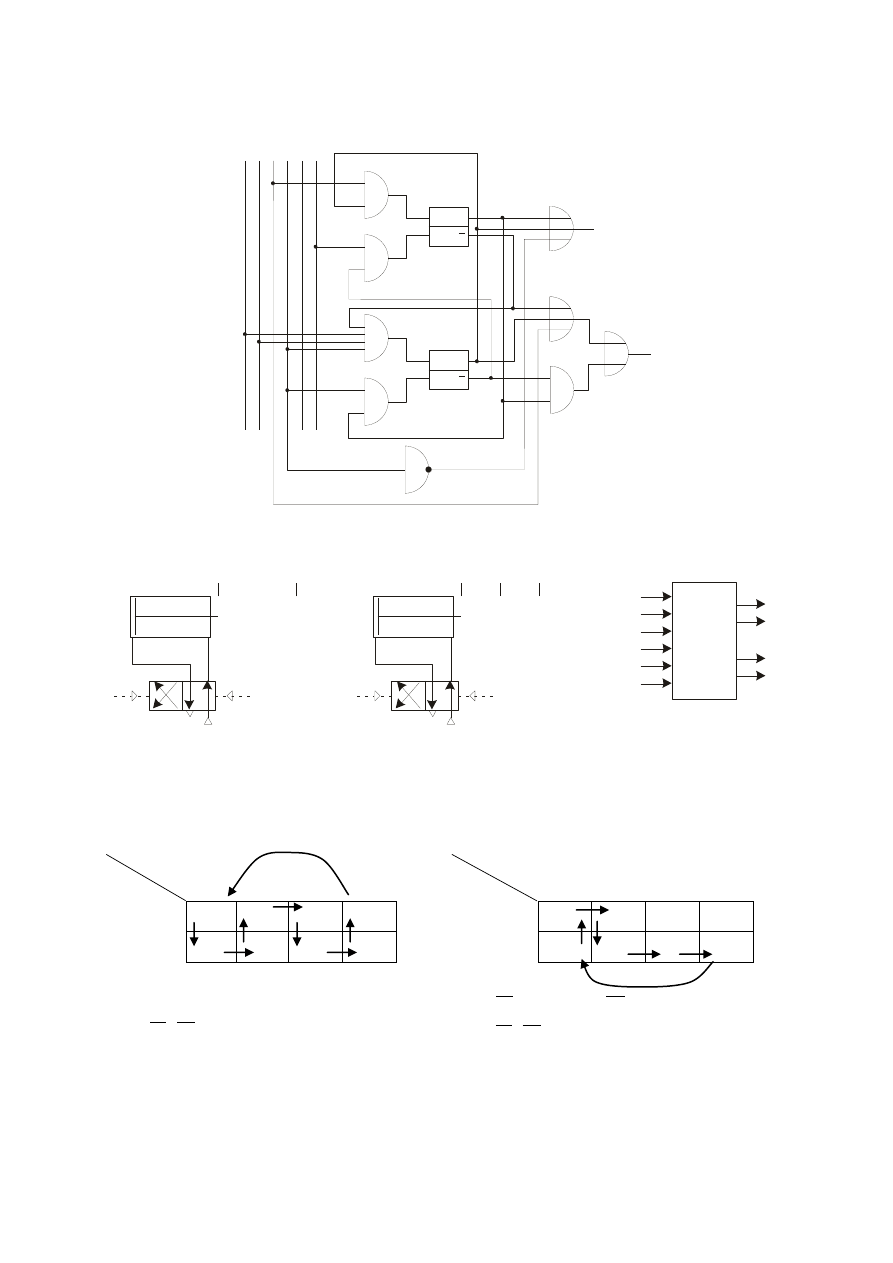
Schemat układu – wariant 5
W
1
Q
1
Q
1
Z
1
W
2
Q
2
Q
2
Z
2
x
a
b
c d
e
y
1
y
2
Wariant 6 - układ Mealy’ego – kod ze stałym odstępem – zawory robocze bistabilne
A
B
a
b
e
c
d
a
b
c
d
e
x
A+
B+
A-
B-
A+
A-
B+
B-
Schemat układy napędowego i schemat blokowy projektowanego układu
Część układu realizująca funkcję przejść pozostaje jak w wariancie 5. Zmienia się część
układy realizująca funkcję wyjść.
Analogicznie jak w wariancie 2, tablice wyjść przekształcamy w uniwersalne tablice stanów
zaworów roboczych, na podstawie których wyznacza się sygnały
A
,
A
,
B
i
B
.
2
1
Q
Q
c
00
01
11
10
0
1
1
1
1
1
0
1
1
1
A
2
1
Q
Q
b
00
01
11
10
0
0
0
-
-
1
0
1
0
1
B
2
Q
A
c
Q
Q
A
2
1
2
1
2
1
Q
Q
b
Q
Q
B
2
1
2
1
Q
Q
Q
Q
B
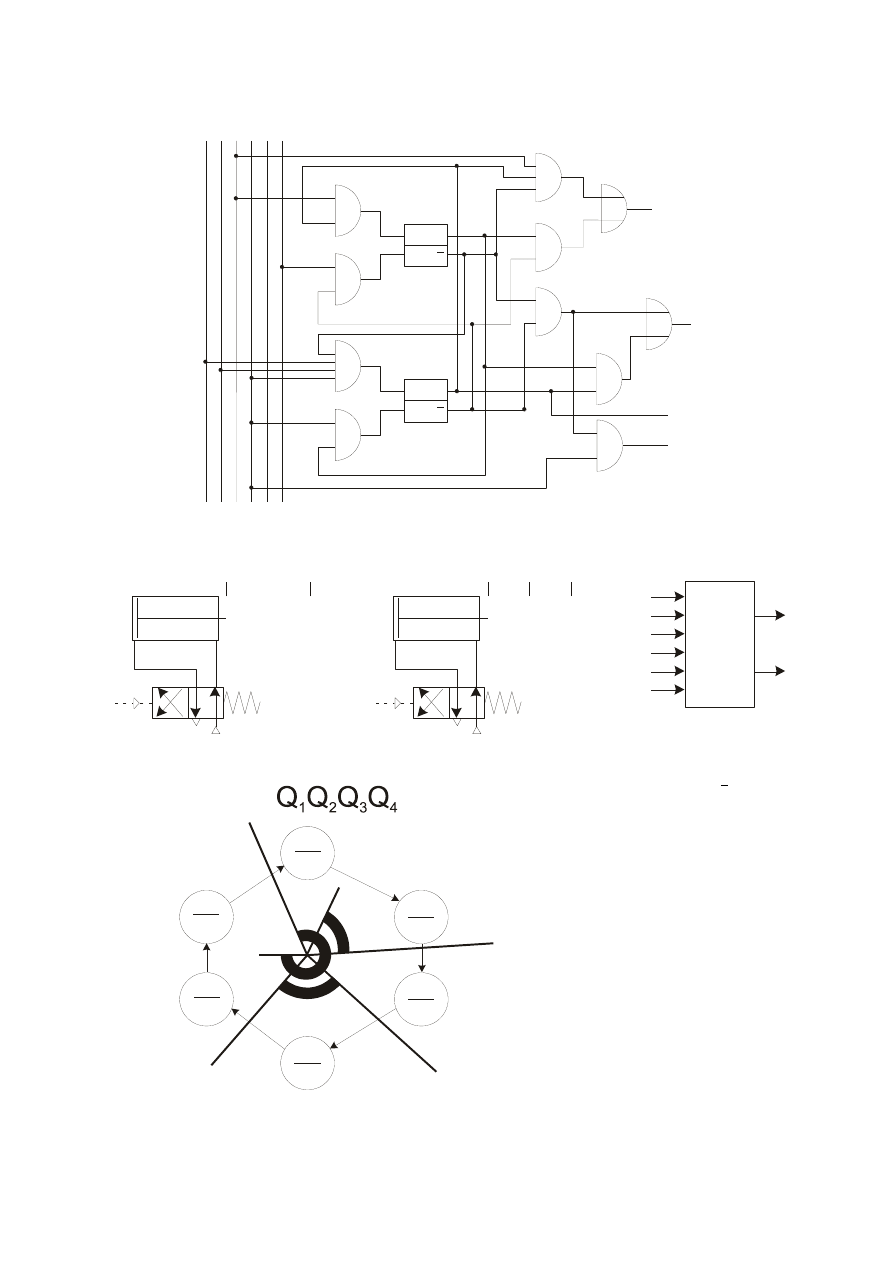
Schemat logiczny układu
Strona 15
W
1
Q
1
Q
1
Z
1
W
2
Q
2
Q
2
Z
2
x
a
b
c d
e
B+
B-
A+
A-
Wariant 7 - układ Mealy’ego – kod „1 z n” – zawory robocze monostabilne
A
B
a
b
e
c
d
a
b
c
d
e
x
y
1
y
2
y
1
y
2
Schemat układy napędowego i schemat blokowy projektowanego układu
Graf zakodowany
Funkcje wyjść
1
10
2
11
0
00
5
10
3
10
4
11
b
c
e
c
x·a·c
d
1000
0100
0010
0001
y
2
y
2
y y
1
2
y
1
c
Q
Q
Q
Q
y
4
3
2
1
1
3
1
2
Q
b
Q
y
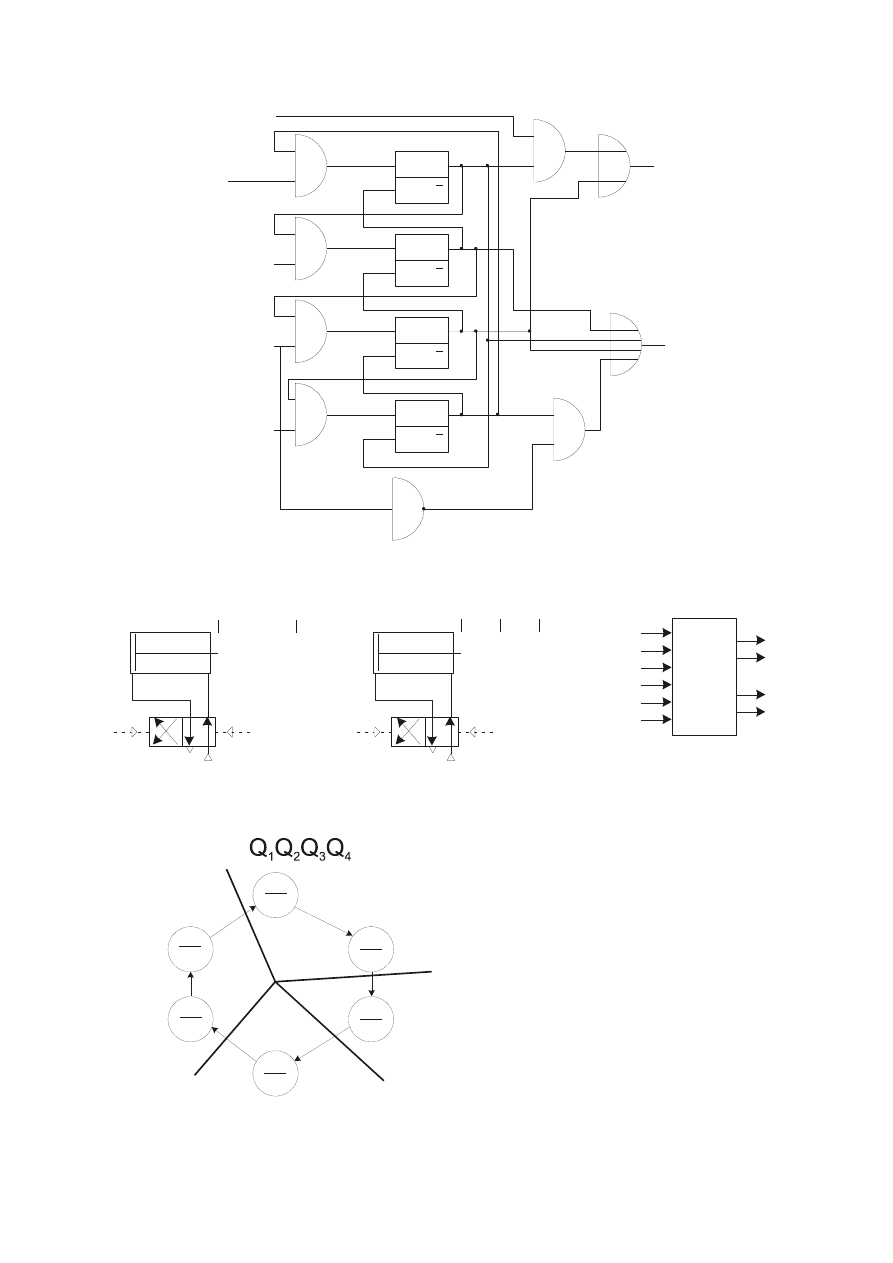
Schemat układu
Strona 16
W
1
Q
1
Q
1
Z
1
W
2
Q
2
Q
2
Z
2
W
3
Q
3
Q
3
Z
3
W
4
Q
4
Q
4
Z
4
x·a·c
d
c
b
b
y
1
y
2
Wariant 8 - układ Mealy’ego – kod „1 z n” – zawory robocze bistabilne
A
B
a
b
e
c
d
a
b
c
d
e
x
A+
B+
A-
B-
A+
A-
B+
B-
Schemat układy napędowego i schemat blokowy projektowanego układu
Graf zakodowany
Funkcje wyjść
1
10
2
11
0
00
5
10
3
10
4
11
b
c
e
c
x·a·c
d
1000
0100
0010
0001
A+
B+
B-
B+
B-
A-
1
Q
A
c
Q
A
4
3
1
Q
b
Q
B
4
2
Q
Q
B
Strona 17
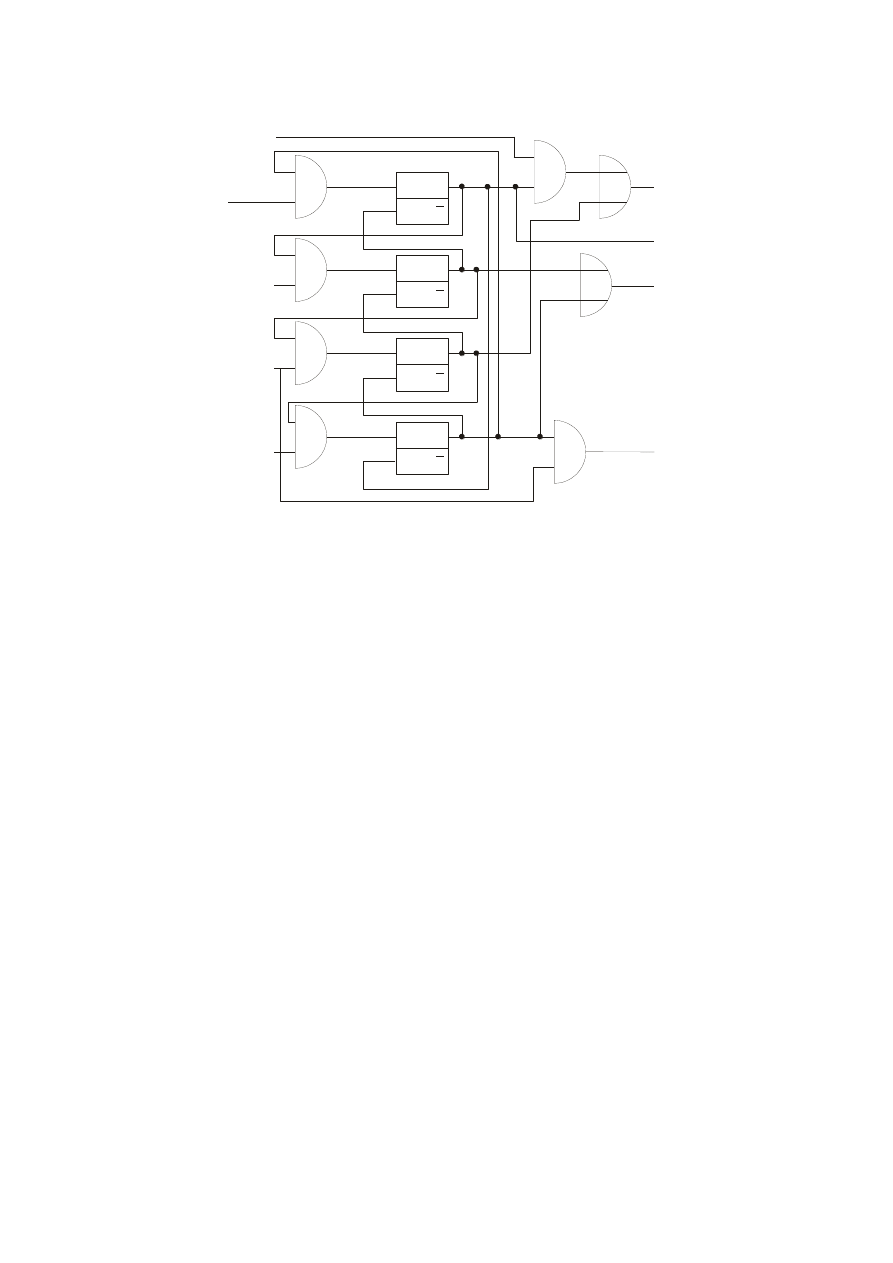
Schemat układu
W
1
Q
1
Q
1
Z
1
W
2
Q
2
Q
2
Z
2
W
3
Q
3
Q
3
Z
3
W
4
Q
4
Q
4
Z
4
x·a·c
d
c
b
b
B+
A+
B-
A-