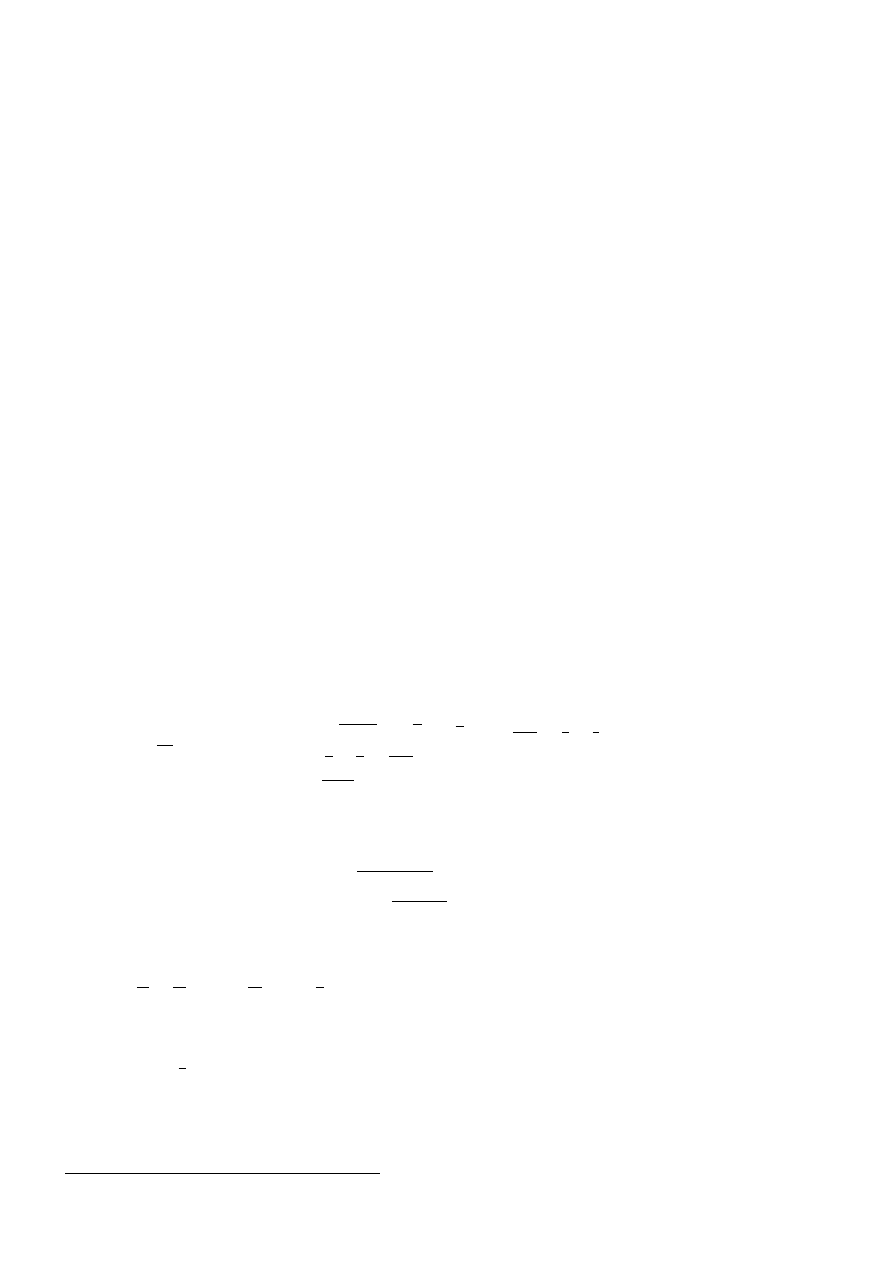
ALGEBRA Z GEOMETRI ¾

A ANALITYCZN ¾

A

ALGEBRA LINIOWA 1

Kursy MAP1029, 1039, 1070, 1140, 1141, 3046, 3055

Lista zda´n obejmuje ca÷

y materia÷kursu oraz okre´sla rodzaje i przybli·

zony stopie´n trudno´sci zada´n, które

pojawi ¾

a si ¾

e na kolokwiach i egzaminach. Na ´cwiczeniach nale·

zy rozwi ¾

aza´c 1-2 podpunkty z ka·

zdego zadania.

Wyj ¾

atkiem s ¾

a zadania oznaczone liter ¾

a (p) oraz symbolem (*). Zadania oznaczone liter ¾

a (p) s ¾

a proste i nale·

zy

je rozwi ¾

aza´c samodzielnie. Z kolei zadania oznaczone gwiazdk ¾

a (*) s ¾

a trudne. Te nieobowi ¾

azkowe zadania

kierujemy do ambitnych studentów. Za kilkana´scie dni na ko´ncu listy umieszczone zostan ¾

a po 4 przyk÷

adowe

zestawy zada´n z obu kolokwiów oraz egzaminu podstawowego i poprawkowego.

Uzdolnionym studentom proponujemy udzia÷w egzaminach na ocen ¾

e celuj ¾

ac ¾

a z algebry i analizy. Zadania

z tych egzaminów z kilku ubieg÷

ych lat mo·

zna znale´z´c na stronie internetowej

http://im.pwr.edu.pl/StudenciCelujace.php

Przed sprawdzianami warto zapozna´c si ¾

e z zestawieniem b÷¾

edów, które studenci cz ¾

esto pope÷

niaj ¾

a na kolok-

wiach i egzaminach z matematyki.

http://prac.im.pwr.edu.pl/

~skoczylas/typowe_bledy_studentow.pdf

Opracowanie: doc. dr Zbigniew Skoczylas

Lista zada´n

1. (p) Poda´c przyk÷

ady liczb rzeczywistych, dla których nie zachodz ¾

a

równo´sci:

a)

(x + y)

2

= x

2

+ y

2

; b)

p

x + y =

p

x + py; c)

1

x+y

=

1
x

+

1
y

;

d)

p

x

2

= x;

e)

x
y

+

u
v

=

x+u

y+v

;

f )

sin 2x = 2 sin x;

h)

jx + yj = jxj + jyj ;

i)

log

2

a

log

2

b

= log

2

(a

b) ;

j)

a

n

a

m

= a

n m

:

2. Za pomoc ¾

a indukcji matematycznej uzasadni´c, ·

ze dla ka·

zdej liczby naturalnej n zachodz ¾

a to·

zsamo´sci:

a)

1 + 3 + : : : + (2n

1) = n

2

;

b)

1 2 + 2 3 + : : : + n (n + 1) =

n(n+1)(n+2)

3

;

c)

cos x cos 2x cos 4x : : : cos 2

n

x =

sin 2

n+1

x

2

n+1

sin x

(x 6= k ) :

3. Korzystaj ¾

ac z indukcji matematycznej uzasadni´c nierówno´sci:

a)

2

n

> n

2

dla n

> 5;

b)

1

1

2

+

1

2

2

+ : : : +

1

n

2

6 2

1

n

dla n 2 N;

c)

n! > 2

n

dla n

> 4;

d)

(1 + x)

n

> 1 + nx dla x > 1 oraz n 2 N (nierówno´s´c Bernoulliego);

e)

n! <

n

2

n

dla n

> 6:

4. Metod ¾

a indukcji matematycznej pokaza´c, ·

ze dla ka·

zdej liczby naturalnej n liczba:

a)

n

5

n jest podzielna przez 5;

b)

4

n

+ 15n

1 jest podzielna przez 9:

0

Zadania z listy pochodz ¾

a z ksi ¾

a·

zek „Algebra i geometria analityczna. De…nicje, twierdzenia, wzory”, „AiGA. Przyk÷

ady i

zadania”, „AiGA. Kolokwia i egzaminy” oraz „Wst ¾

ep do analizy i algebry”.

1

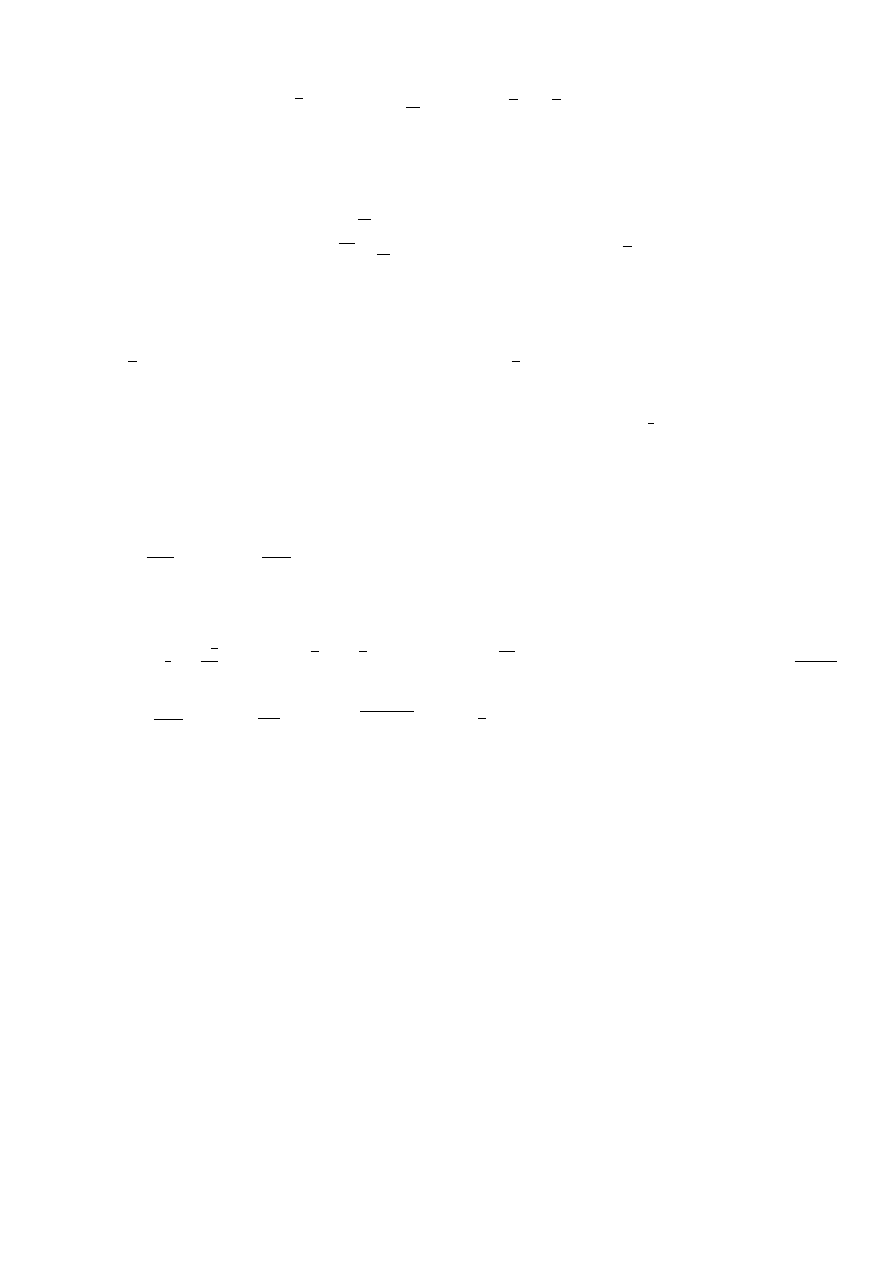
5. (*) Uzasadni´c, ·

ze n kwadratów mo·

zna podzieli´c na cz ¾

e´sci, z których da si ¾

e z÷

o·

zy´c kwadrat.

6. Zastosowa´c wzór dwumianowy Newtona do wyra·

ze´n:

a)

(2x + y)

4

;

b)

c

p

2

6

;

c)

x +

1

x

3

5

;

d)

(

p

u

4

p

v)

8

:

7. (*) Korzystaj ¾

ac ze wzoru dwumianowego Newtona obliczy´c sumy:

a)

n

P

k=0

n
k

;

b)

n

P

k=0

n
k

2

k

;

c)

n

P

k=0

n
k

( 1)

k

:

8. a) W rozwini ¾

eciu wyra·

zenia a

3

+

1

a

2

15

znale´z´c wspó÷

czynnik przy a

5

;

b)

W rozwini ¾

eciu wyra·

zenia

4

p

x

5

3

x

3

7

znale´z´c wspó÷

czynnik przy

4

p

x:

FFF

9. Porównuj ¾

ac cz ¾

e´sci rzeczywiste i urojone obu stron równa´n znale´z´c ich rozwi ¾

azania:

a)

z = (2

i)z; b) z

2

+ 4 = 0; c) (1 + 3i) z + (2

5i) z = 2i

3; d*) z

3

= 1:

10. Na p÷

aszczy´znie zespolonej narysowa´c zbiory liczb zespolonych spe÷

niaj ¾

acych warunki:

a)

Re (z + 1) = Im (2z

4i) ; b) Re z

2

= 0;

c)

Im z

2

6 8; d) Re

1
z

> Im (iz) :

11. Korzystaj ¾

ac z interpretacji geometrycznej modu÷

u ró·

znicy liczb zespolonych wyznaczy´c i narysowa´c zbiory

liczb zespolonych spe÷

niaj ¾

acych warunki:

a)

jz + 2

3ij < 4; b) jz + 5ij > j3

4ij ; c) jz

1j = j1 + 5i

zj ;

d)

jz + 3ij < jz

1

4ij ; e) jiz + 5

2ij < j1 + ij ; f) jz + 2

3ij < 5;

g)

z 3i

z

> 1; h)

z

2

+4

z 2i

6 1; i) z

2

+ 2iz

1 < 9; (j*)

2 jz

1j < z

2

z + 2

6 3 jz 2j

12. Korzystaj ¾

ac ze wzoru de Moivre’a obliczy´c:

a)

1
2

+ i

p

3

2

6

; b)

5

p

2

i

5

p

2

15

;

c)

2i

p

12

9

; d*)

(i

2)

24

(13 + 9i)

8

;

e*)

(7+i)

11

(2+i)

22

:

13. Wyznaczy´c i narysowa´c na p÷

aszczy´znie zespolonej elementy pierwiastków:

a)

4

p

16;

b)

3

p

27i;

c*)

4

q

(2

i)

8

;

d)

6

p

8:

14. W zbiorze liczb zespolonych rozwi ¾

aza´c równania:

a)

z

2

2z + 10 = 0;

b)

z

2

+ 3iz + 4 = 0;

c)

z

4

+ 5z

2

+ 4 = 0;

d)

z

2

+ (1

3i) z

2

i = 0;

e)

z

6

= (1

i)

12

;

f )

(z

i)

4

= (z + 1)

4

:

FFF

15. (p) Znale´z´c pierwiastki ca÷

kowite wielomianów:

a)

x

3

+ 3x

2

4;

b)

x

4

2x

3

+ x

2

8x

12;

c)

x

4

x

2

2:

16. Znale´z´c pierwiastki wymierne wielomianów:

a)

12x

3

+ 8x

2

3x

2;

b)

3x

3

2x

2

+ 3x

2;

c)

6x

4

+ 7x

2

+ 2:

17. (p) Wyznaczy´c pierwiastki rzeczywiste lub zespolone wraz z krotno´sciami wielomianów:

a)

(x

1) (x + 2)

3

;

b)

(2x + 6)

2

(1

4x)

5

;

c)

z

2

1

z

2

+ 1

3

z

2

+ 9

4

:

18. Nie wykonuj ¾

ac dziele´n wyznaczy´c reszty z dzielenia wielomianu P przez wielomian Q; je·

zeli:

a)

P (x) = x

8

+ 3x

5

+ x

2

+ 4; Q (x) = x

2

1;

b)

P (x) = x

47

+ 2x

5

13; Q (x) = x

3

x

2

+ x

1;

c)

P (x) = x

99

2x

98

+ 4x

97

; Q (x) = x

4

16;

d*)

P (x) = x

2006

+ x

1002

1; Q (x) = x

4

+ 1;

e*)

P (x) = x

444

+ x

111

+ x

1; Q (x) = x

2

+ 1

2

:

2

19. Pokaza´c, ·

ze je·

zeli liczba zespolona z

1

jest pierwiastkiem wielomianu rzeczywistego P , to liczba z

1

tak·

ze jest

pierwiastkiem wielomianu P: Korzystaj ¾

ac z tego faktu znale´z´c pozosta÷

e pierwiastki zespolone wielomianu

P (x) = x

4

4x

3

+ 12x

2

16x + 15 wiedz ¾

ac, ·

ze jednym z nich jest x

1

= 1 + 2i:

20. Podane wielomiany roz÷

o·

zy´c na nierozk÷

adalne czynniki rzeczywiste:

a) x

3

27;

b) x

4

+ 16;

c) x

4

+ x

2

+ 4;

d*) x

6

+ 1:

21. Podane funkcje wymierne roz÷

o·

zy´c na rzeczywiste u÷

amki proste:

a)

2x+5

x

2

x 2

;

b)

x+9

x(x+3)

2

;

c)

3x

2

+4x+3

x

3

x

2

+4x 4

;

d)

x

3

2x

2

7x+6

x

4

+10x

2

+9

:

FFF

22. Niech ~

a

= (3;

3; 0; 9) ; ~

b

= (1; 2; 1; 4) b ¾

ed ¾

a wektorami z przestrzeni R

4

:

Wyznaczy´c wektory:

a)

~

x

= 2~

a

~

b

;

b)

~

x

=

1
3

~

b

+ 3~

a:

23. Obliczy´c:

a)

Odleg÷

o´s´c punktów A = (1;

2; 3; 0; 0) ; B = (0; 1;

2; 3;

4) w przestrzeni R

5

;

b)

Obliczy´c k ¾

at mi ¾

edzy wektorami ~

a

= ( 1; 0; 2; 2) ;~

b

= (0;

2; 1;

2) w przestrzeni R

4

;

FFF

24. (p) Trójk ¾

at jest rozpi ¾

ety na wektorach ~

a

;~

b

: Wyrazi´c ´srodkowe trójk ¾

ata przez wektory ~

a

; ~

b

:

25. (p) Przek ¾

atnymi równoleg÷

oboku s ¾

a wektory ~

a

= ( 3; 4) ;~

b

= (1; 2). Wyznaczy´c k ¾

at ostry mi ¾

edzy bokami

równoleg÷

oboku.

26. D÷

ugo´sci wektorów ~

a

;~

b

wynosz ¾

a odpowiednio 3; 5: Znamy iloczyn skalarny ~

a ~

b

=

2: Obliczy´c ~

a

~

b

2~

a

+ 3~

b

:

27. (p) Wyznaczy´c równanie prostej, która przechodzi przez punkt P = ( 1; 3) i tworzy k ¾

at 120

o

z dodatni ¾

a

cz ¾

e´sci ¾

a osi Ox:

28. (p) Napisa´c równania prostej (normalne, kierunkowe, parametryczne) przechodz ¾

acej przez punkty P

1

=

(2; 3) ; P

2

= ( 3; 7) :

29. (p) Znale´z´c punkty przeci ¾

ecia prostej

l :

x = 4

2t;

y =

6 + t;

gdzie t 2 R;

z osiami uk÷

adu wspó÷

rz ¾

ednych. Czy punkt P = (4; 7) nale·

zy do prostej l?

30. Znale´z´c punkt przeci ¾

ecia prostych:

k :

x = 1

t;

y = 3 + t;

gdzie t 2 R; l :

x = 2t;

y = 3

t;

gdzie t 2 R;

31. (p) Znale´z´c równanie prostej, która przechodzi przez punkt P = ( 1; 2) i jest

a)

równoleg÷

a do prostej 3x

y + 2 = 0;

b)

prostopad÷

a do prostej x + y = 0:

32. Dla jakiej warto´sci parametru m; odleg÷

o´s´c punktów P = (1; 0) i Q = (m + 3;

2) jest równa 4?

33. (p) Wyznaczy´c odleg÷

o´s´c punktu P

0

= ( 4; 1) od prostej l o równaniu 3x + 4y + 12 = 0:

34. (p) Znale´z´c odleg÷

o´s´c prostych równoleg÷

ych l

1

; l

2

o równaniach odpowiednio x 2y = 0;

3x+6y 15 = 0:

3

35. Obliczy´c wysoko´s´c trójk ¾

ata o wierzcho÷

kach A = (0; 0) ; B = ( 1; 3) ; C = (2; 5) opuszczon ¾

a z wierzcho÷

ka

C:

36. (*) Znale´z´c równania dwusiecznych k ¾

atów wyznaczonych przez proste o równaniach 3x + 4y

2 = 0; 4x

3y + 5 = 0:

FFF

37. a) Dla jakich warto´sci parametrów p; q wektory ~

a

= (1

p; 3;

1) ; ~

b

= ( 2; 4

q; 2) s ¾

a równoleg÷

e?

b)

Dla jakich warto´sci parametru s wektory ~

p

= (s; 2; 1

s) ; ~

q

= (s; 1;

2) s ¾

a prostopad÷

e?

38. (p) Znale´z´c wersor, który jest prostopad÷

y do wektorów ~

u

= ( 1; 3; 0) ; ~

v

= (0; 1; 1) :

39. (p) Wyznaczy´c cosinus k ¾

ata mi ¾

edzy wektorami ~

p

= (0; 3; 4) ; ~

q

= (2; 1;

2) :

40. a) Obliczy´c pole równoleg÷

oboku rozpi ¾

etego na wektorach ~

u

= ( 1; 2; 5) ; ~

v

= (0; 3; 2) :

b)

Obliczy´c pole trójk ¾

ata o wierzcho÷

kach A = (0; 0; 1) ; B = (3; 0; 0) ; C = (0;

5; 0) :

c)

Trójk ¾

at ma wierzcho÷

ki A = (0; 0; 1) ; B = (2; 3;

2) ; C = (1; 1; 4) : Obliczy´c wysoko´s´c trójk ¾

ata

opuszczon ¾

a z wierzcho÷

ka C:

41. a)

Obliczy´c obj ¾

eto´s´c równoleg÷

o´scianu rozpi ¾

etego na wektorach: ~

a

= (1; 2; 3) ;

~

b

= (0; 4; 1) ; ~

c

=

( 1; 0; 2) :

b)

Obliczy´c obj ¾

eto´s´c czworo´scianu o wierzcho÷

kach: A = (1; 1; 1) ; B = (1; 2; 3) ; C = (0; 4; 1) ; D =

(2; 2; 2) :

c)

Dla czworo´scianu z punktu b) obliczy´c wysoko´s´c opuszczon ¾

a z wierzcho÷

ka A:

42. Znale´z´c równania normalne i parametryczne p÷

aszczyzny:

a)

przechodz ¾

acej przez punkty P = (1;

1; 0) ; Q = (2; 3; 7) ; R = (4; 0; 1) ;

b)

przechodz ¾

acej przez punkt A = ( 2; 5; 4) oraz zawieraj ¾

ac ¾

a o´s Oz;

c)

przechodz ¾

acej przez punkt A = ( 2; 5; 4) oraz prostopad÷

ej do osi Oy:

43. Pokaza´c, ·

ze równania parametryczne:

8

<

:

x = 3

t + 2s;

y =

1 + t;

z = 2 + t

3s;

8

<

:

x = 4 + 3t + 3s;
y = t

s;

z =

2t

4s

przedstawiaj ¾

a t ¾

e sam ¾

a p÷

aszczyzn ¾

e.

44. a) P÷

aszczyzn ¾

e

: 2x + y

z

7 = 0 zapisa´c w postaci parametrycznej.

b)

P÷

aszczyzn ¾

e

:

8

<

:

x =

s + t;

y

=

2

2t;

z

=

3 + 3s

t

przekszta÷

ci´c do postaci normalnej.

45. Znale´z´c równanie parametryczne i kraw¾

edziowe prostej:

a)

przechodz ¾

acej przez punkty A = ( 3; 4; 1) ; B = (0; 2; 1) :

b)

przechodz ¾

acej przez punkt P = (3;

1; 2) i przecinaj ¾

acej prostopadle o´s Oy:

46. Pokaza´c, ·

ze równania:

8

<

:

x = 1

t;

y = 2

3t;

z = 4t;

8

<

:

x = 2t;
y =

1 + 6t;

z = 4

8t

przedstawiaj ¾

a t ¾

e sam ¾

a prost ¾

a.

47. a) Prost ¾

a l :

x + y

3

= 0

y + z

1 = 0

zapisa´c w postaci parametrycznej.

b)

Prost ¾

a l : x = 3; y = 2

2t; z = t zapisa´c w postaci kraw¾

edziowej.

4

48. Wyznaczy´c punkt przeci ¾

ecia:

a)

prostej l : x = t; y = 1

2t; z =

3 + 2t oraz p÷

aszczyzny

: 3x

y

2z

5 = 0;

b)

p÷

aszczyzn

1

: x + 2y

z

5 = 0;

2

: x + 2y + 2 = 0;

3

: x + y + z = 0;

c)

prostych l

1

: x = 1

t; y = 1; z =

3 + 2t; l

2

: x = t; y = 3

2t; z = 2

5t:

49. Obliczy´c odleg÷

o´s´c:

a)

punktu P = (0; 1;

2) od p÷

aszczyzny

: 3x

4y + 12z

1 = 0;

b)

p÷

aszczyzn równoleg÷

ych

1

: x

2y + 2z

3 = 0;

2

:

2x + 4y

4z + 18 = 0;

c)

punktu P = (2;

5; 1) od prostej l : x = t; y = 1

2t; z =

3 + 2t;

d)

prostych równoleg÷

ych

l

1

:

x + y + z

3

= 0

x

2y

z

1 = 0

; l

2

:

x + y + z

3

= 0

x

2y

z + 4 = 0

;

e)

prostych sko´snych l

1

: x = 1

t; y = 1; z =

3 + 2t; l

2

: x = s; y = 3

2s; z = 1

5s:

50. Wyznaczy´c rzut prostopad÷

y punktu P = (1;

2; 0) na:

a)

p÷

aszczyzn ¾

e

: x + y + 3z

5 = 0;

b)

prost ¾

a l : x = 1

t; y = 2t; z = 3t:

51. Obliczy´c k ¾

at mi ¾

edzy:

a)

p÷

aszczyznami

1

: x

y + 3z = 0;

2

:

2x + y

z + 5 = 0;

b)

prost ¾

a l :

x + y + z

3

= 0

x

2y

z

1 = 0

i p÷

aszczyzn ¾

a

: x + y = 0;

c)

prostymi l

1

: x =

t; y = 1 + 2t; z =

3; l

2

: x = 0; y =

2s; z = 2 + s:

FFF

52. We wskazanej przestrzeni zbada´c liniow ¾

a niezale·

zno´s´c uk÷

adów wektorów:

a)

R

2

; ~

a

1

= (2; 3) ; ~

a

2

= ( 1; 0) ;

b)

R

3

; ~

b

1

= (1; 2; 3) ; ~

b

2

= (3; 2; 1) ; ~

b

3

= (1; 1; 1) ;

c)

R

4

; ~

c

1

= (1; 0; 0; 0) ; ~

c

2

= ( 1; 1; 0; 0) ; ~

c

3

= (1;

1; 1; 0) ; ~

c

4

= ( 1; 1;

1; 1) :

53. Zbada´c, czy uk÷

ady wektorów s ¾

a bazami wskazanych przestrzeni liniowych R

n

:

a)

f(1; 2; 0) ; ( 1; 0; 3) ; (0; 2; 3)g ; R

3

;

b)

f(1; 0; 0; 0) ; (1; 1; 0; 0) ; (1; 1; 1; 0) ; (1; 1; 1; 1)g ; R

4

;

c)

f(1; 1; 0; 2) ; (1; 0; 3; 0) ; (0; 1; 3; 0) ; (0; 0; 0; 1)g ; R

4

:

54. Znale´z´c bazy i wymiary podprzestrzeni:

a)

A = (x; y; z) 2 R

3

: 3x + 2y

z = 0 ;

b)

B = (x; y; z; t) 2 R

4

: x = 2y =

t ;

c)

C = (u; v; x; y; z) 2 R

5

: u + v = 0; x + y + x = 0 :

55. Zbada´c, czy przekszta÷

cenia s ¾

a liniowe:

a)

F : R

2

! R; F (x

1;

x

2

) = x

1

3x

2

;

b)

F : R

3

! R

3

; F (x; y; z) = ( x; 5x + y; y

2z) ;

c)

F : R ! R

4

; F (x) = 0; x

2

; 0;

3x ;

d)

F : R

4

! R

2

; F (x

1

; x

2

; x

3

; x

4

) = (x

1

x

2

; x

3

x

4

) :

5

56. Znale´z´c macierze przekszta÷

ce´n liniowych w standardowych bazach:

a)

F : R

2

! R

3

;

F (x; y) = (x; y; x

y) ;

b)

F : R

3

! R

4

;

F (x; y; z) = (y; z; x; x + y + z) ;

d)

F : R

4

! R

2

;

F (x; y; z; t) = (x + y + z + t; y

t; ) :

57. a) Uzasadni´c, ·

ze obrót na p÷

aszczy´znie R

2

wokó÷pocz ¾

atku uk÷

adu wspó÷

rz ¾

ednych o kat ' jest przeksz-

ta÷

ceniem liniowym. Znale´z´c macierz tego obrotu w bazach standardowych.

b)

Pokaza´c, ·

ze symetria wzgl ¾

edem osi Oz w przestrzeni R

3

jest przekszta÷

ceniem liniowym. Znale´z´c

macierz tej symetrii w bazach standardowych.

FFF

58. (p) Dla par macierzy A; B wykona´c (je´sli to jest mo·

zliwe) dzia÷

ania 3A

1
2

B; A

T

; AB; BA; A

2

:

a)

A =

1

4

2 0

; B =

0

6

8

2

;

b)

A = 1

3 2 ; B = 2

4 0 ;

c)

A =

2

6

6

4

1
0
3
0

3

7

7

5 ; B =

2 1 0 5 ;

d)

A =

2

4

1

0

1

2

1

4

3 0

2

3

5 ; B =

2

4

2 0

4

1

0

3

3

5 :

59. (p) Rozwi ¾

aza´c równanie macierzowe

3

0

@

2

4

1

0

3 3

2

5

3

5 X

1

A = X+

2

4

4

3

0

6

1 2

3

5 :

60. (p) Znale´z´c niewiadome x; y; z spe÷

niaj ¾

ace równanie

2

x + 2 y + 3

3

0

=

3

6

y

z

T

:

61. Poda´c przyk÷

ady macierzy kwadratowych A; B; które spe÷

niaj ¾

a warunki:

a)

AB 6= BA;

b)

AB = 0; ale A 6= 0; B 6= 0;

c)

A

2

= 0; ale A 6= 0:

62. (*) Pokaza´c, ·

ze ka·

zd ¾

a macierz kwadratow ¾

a mo·

zna przedstawi´c jednoznacznie jako sum ¾

e macierzy sym-

etrycznej A

T

= A i antysymetrycznej A

T

=

A . Napisa´c to przedstawienie dla macierzy

B =

2

6

6

4

0

1

4

2

3 5

2

8

2

4

3

4

6

0

0

1

3

7

7

5 :

63. Dane s ¾

a przekszta÷

cenia liniowe: L : R

2

! R

3

okre´slone wzorem L (x; y) = (x; y; x + y) oraz K : R

3

! R

okre´slone wzorem K (u; v; w) = u w: Korzystaj ¾

ac z twierdzenia o postaci macierzy z÷

o·

zenia przekszta÷

ce´n

znale´z´c macierz przekszta÷

cenia K

L:

FFF

64. Napisa´c rozwini ¾

ecia Laplace’a wyznaczników wg wskazanych kolumn lub wierszy (nie oblicza´c wyz-

naczników w otrzymanych rozwini ¾

eciach):

a)

1 4

3

3 1

0

2

5

2

; trzecia kolumna;

b)

1

4

3

7

2

4

2

0

5

4

1

6

2

0

0

3

;

czwarty wiersz.

6

65. Obliczy´c wyznaczniki:

a)

2

5

3

7

;

b)

1

1

2

3

2

4

2

2

1

;

c)

2

0

0

0

3

3 5

7

4

0

1

4

5

0

2

2

:

66. Korzystaj ¾

ac z w÷

asno´sci wyznaczników uzasadni´c, ·

ze macierze s ¾

a osobliwe:

a)

2

4

2

4

4

1

2

2

3

5

6

3

5 ; b)

2

4

1 2 3
4 4 4
3 2 1

3

5 ;

c)

2

6

6

4

1 5 2

2

7 5 2

5

5 7 4

4

3 3 0

3

3

7

7

5 :

67. a) Wiadomo, ·

ze det

2

4

a

b

0

c

d

0

5

2 3

3

5 = 24: Obliczy´c det

a

b

c

d

;

b)

Wiadomo, ·

ze det

2

6

6

4

3

0

0

0

1

x

y

0

5

z

t

0

7

4

5

2

3

7

7

5 = 18: Obliczy´c det

x

y

z

t

:

68. Jakie s ¾

a mo·

zliwe warto´sci wyznacznika macierzy kwadratowej A stopnia n spe÷

niaj ¾

acej warunki:

a)

A

3

= 4A

dla n = 3; 4;

b)

A

T

=

A

2

dla n = 3; 4 ?

69. Obliczy´c det (2A) ; je·

zeli det (3A) = 54 i det (4A) = 128:

70. a) Obliczy´c pole równoleg÷

oboku rozpi ¾

etego na wektorach: ~a = (2;

4) ;~b = (3; 7) ;

b)

Obliczy´c obj ¾

eto´s´c równoleg÷

o´scianu rozpi ¾

etego na wektorach: ~a = (1; 1; 0), ~b = (0; 1; 1), ~c = (1; 0; 1) :

71. (*) Obliczy´c wyznaczniki macierzy:

a)

2

6

6

6

6

4

1

2

3

4

5

2

2

3

4

5

3

3

3

4

5

4

4

4

4

5

5

5

5

5

5

3

7

7

7

7

5

;

b)

2

6

6

6

6

4

2

1

0

0

0

0

2

1

0

0

0

0

2

1

0

0

0

0

2

1

1

0

0

0

2

3

7

7

7

7

5

;

c)

2

6

6

6

6

6

4

5

3

0

: : :

0

2

5

3

: : :

0

0

2

5

: : :

0

..

.

..

.

..

.

. .. 3

0

0

0

: : : 5

3

7

7

7

7

7

5

n n

:

FFF

72. Korzystaj ¾

ac z twierdzenia o postaci macierzy odwrotnej wyznaczy´c macierze odwrotne do :

a)

A =

2 5
3 8

;

b)

A =

2

4

1

0

0

3

1

0

2

5

1

3

5 ; c)

2

6

6

4

0 1 0 0
2 0 0 0
0 0 0 3
0 0 4 0

3

7

7

5 :

73. Korzystaj ¾

ac z metody do÷¾

aczonej macierzy jednostkowej znale´z´c macierze odwrotne do :

a)

A =

1

2

3

1

;

b)

A =

2

4

1

4

12

0

2

0

0

2

6

3

5 ; c) A =

2

6

6

4

1

0

1 0

4

1

0

0

0

2

1

3

0

0

0

1

3

7

7

5 :

74. Wiadomo, ·

ze

(A)

1

=

2

4

4

0

0

8

2

0

10

12

6

3

5 :

Wyznaczy´c

1
2

A

1

:

75. Macierze A; B maj ¾

a stopie´n 3: Ponadto det (A) = 4 oraz det (B) =

3: Obliczy´c:

a)

det

h

A (6B)

1

i

;

b)

det

h

A

1

(2B)

3

A

2

i

:

7

76. Znale´z´c rozwi ¾

azania równa´n macierzowych:

a)

3 5
1 2

X =

0

3

1

4

2 0

;

b)

X

2

6

6

6

6

4

1 2

0

1 1

1

2 6

1

3

7

7

7

7

5

=

3 1 2 ;

c)

X

2

4

3 0 4

1

1 1

2 0 3

3

5 =

5 1 2

1

2 3

;

d)

2 1
3 2

X

3

2

5

3

=

2 8
0 5

;

e)

X

2

4

2 0 3

1

1 1

3 0 4

3

5

1

=

2 1 3 ;

f )

1

1

1

2

X

1

5 6
4 5

=

2 7
1 4

:

77. Korzystaj ¾

ac ze wzorów Cramera wyznaczy´c wskazan ¾

a niewiadom ¾

a z uk÷

adów równa´n liniowych:

a)

2x

y

= 0

3x + 2y

= 5

; niewiadoma y;

b)

8

<

:

x

+ y

+ 2z

=

1

2x

y

+ 2z

=

4

4x + y

+ 4z

=

2

; niewiadoma x;

c)

8

>

>

<

>

>

:

2x + 3y

+ 11z

+ 5t =

2

x

+

y

+

5z

+ 2t =

1

2x +

y

+

3z

+ 2t =

3

x

+

y

+

3z

+ 4t =

3

; niewiadoma z:

FFF

78. Korzystaj ¾

ac z interpretacji geometrycznej przekszta÷

ce´n liniowych znale´z´c ich j ¾

adra, obrazy i rz ¾

edy:

a)

L : R

2

! R

2

; obrót o k ¾

at

=

3

wokó÷pocz ¾

atku uk÷

adu.

b)

L : R

2

! R

2

; rzut prostok ¾

atny na prost ¾

a x + y = 0:

c)

L : R

3

! R

3

; symetria wzgl ¾

edem p÷

aszczyzny y = z:

d)

L : R

3

! R

3

; obrót wokó÷osi Oy o k ¾

at

2

:

79. Wyznaczy´c j ¾

adra, obrazy oraz rz ¾

edy przekszta÷

ce´n liniowych:

a)

L : R

2

! R; F (x

1;

x

2

) = x

1

3x

2

;

b)

L : R

2

! R

2

; F (x; y) = (x + y; 2x + 2y) ;

c)

L : R

3

! R

3

; F (x; y; z) = ( x; 5x + y; y

2z) ;

d)

L : R ! R

4

; F (x) = (0; x; 0;

x) :

80. Metod ¾

a eliminacji Gaussa rozwi ¾

aza´c uk÷

ady równa´n:

a)

8

<

:

x

+ y

+ 2z

=

1

2x

y

+ 2z

=

4

4x + y

+ 4z

=

2

;

b)

8

>

>

<

>

>

:

3x

2y

5z

+

t

=

3

2x

3y

+

z

+ 5t =

3

x

+ 2y

4t =

3

x

y

4z

+ 9t =

22

:

8

81. a) Znale´z´c trójmian kwadratowy, który przechodzi przez punkty ( 1; 2) ; (0; 1) ; (2; 4) :

b)

Wyznaczy´c wspó÷

czynniki a; b; c funkcji y = a2

x

+ b3

x

+ c4

x

; która w punktach

1; 0; 1 przyjmuje

odpowiednio warto´sci

3
4

; 1; 1:

c)

Funkcja y (x) = A cos 2x + B sin 2x spe÷

nia równanie ró·

zniczkowe y

00

6y

0

+ 13y = 25 sin 2x:Wyznaczy´c

wspó÷

czynniki A; B:

82. a) Dla jakich warto´sci parametru m; podany uk÷

ad jednorodny ma niezerowe rozwi ¾

azanie

8

<

:

mx + y

+

2z

= 0

2x

y

+ mz

= 0

mx + y

+

4z

= 0

?

b)

Dla jakich warto´sci parametrów a; b; c; d; podany uk÷

ad równa´n liniowych jest sprzeczny

8

>

>

<

>

>

:

x + y

= a

z

+ t =

b

x

+ z

=

c

y

+ t = d

?

c)

Znale´z´c warto´sci parametru p; dla których podany uk÷

ad równa´n liniowych ma tylko jedno rozwi ¾

azanie

8

<

:

x

+ 2y

3z

=

1

2x

py

+

z

=

3

2x +

y

pz

=

5

:

FFF

83. Korzystaj ¾

ac z de…nicji wyznaczy´c wektory i warto´sci w÷

asne przekszta÷

ce´n liniowych:

a)

symetria wzgl ¾

edem osi Oy w przestrzeni R

2

;

b)

obrót w przestrzeni R

3

wokó÷osi Ox o k ¾

at

6

;

c)

symetria w przestrzeni R

3

wzgl ¾

edem p÷

aszczyzny yOz;

d)

rzut prostok ¾

atny na o´s Oy w przestrzeni R

3

:

84. Znale´z´c warto´sci i wektory w÷

asne przekszta÷

ce´n liniowych:

a)

L : R

2

! R

2

; F (x; y) = (x + y; 2x + 2y) ;

c)

L : R

3

! R

3

; F (x; y; z) = ( x; 5x + y; y

2z) ;

d)

L : R

4

! R

4

; F (x; y; z; t) = (0; x; 0; y) :

FFF

85. (p) Napisa´c równanie okr ¾

egu, którego ´srednic ¾

a jest odcinek o ko´ncach A = ( 1; 3), B = (5; 7) :

86. (p) Wyznaczy´c wspó÷

rz ¾

edne ´srodka i promie´n okr ¾

egu x

2

4x + y

2

+ 6y + 2 = 0:

87. (p) Znale´z´c równanie okr ¾

egu opisanego na trójk ¾

acie ABC o wierzcho÷

kach A = (0; 0), B = (8; 0), C =

(0; 6).

88. Wyznaczy´c równanie okr ¾

egu, o ´srodku S = (3; 4) ; który jest styczny do prostej l : 3x

4y

12 = 0:

89. Znale´z´c równanie okr ¾

egu, który przechodzi przez punkty P = (3; 4), Q = (5; 2) i ma ´srodek na osi Ox.

90. Dolna po÷

owa okr ¾

egu x

2

+ 8x + y

2

10y + 2 = 0 jest wykresem funkcji f zmiennej x: Wyznaczy´c funkcj ¾

e

f oraz okre´sli´c jej dziedzin ¾

e.

91. (*) Znale´z´c równanie okr ¾

egu, który jest styczny do obu osi uk÷

adu wspó÷

rz ¾

ednych oraz przechodzi przez

punkt A = (5; 8): Ile rozwi ¾

aza´n ma zadanie?

9

92. Znale´z´c równanie stycznej okr ¾

egu x

2

+ y

2

= 25:

a)

w punkcie ( 3; 4);

b)

przechodz ¾

acej przez punkt ( 5; 10);

c)

równoleg÷

ej do prostej x

y

4 = 0;

d)

prostopad÷

ej do prostej x + 2y = 0:

93. (p) Wyznaczy´c osie, wspó÷

rz ¾

edne ognisk oraz mimo´sród elipsy

x

2

16

+

y

2

9

= 1:

94. Punkty F

1

= ( 5; 0) ; F

2

= (5; 0) s ¾

a ogniskami elipsy. Znale´z´c równanie tej elipsy, je·

zeli jednym z jej

wierzcho÷

ków jest punkt W = (0;

3) :

95. Naszkicowa´c elips ¾

e o równaniu 4x

2

8x + 9y

2

+ 36y + 4 = 0:

96. Lewa po÷

owa elipsy 4x

2

+ 25y

2

= 100 jest wykresem funkcji f zmiennej y: Znale´z´c funkcj ¾

e f oraz okre´sli´c

jej dziedzin ¾

e.

97. (p) Wyznaczy´c osie, wspó÷

rz ¾

edne ognisk oraz równania asymptot hiperboli

x

2

144

y

2

25

= 1:

98. Narysowa´c hiperbol ¾

e wraz z ogniskami i asymptotami:

a)

9 (y + 5)

2

16 (x

2)

2

= 144;

b)

4x

2

25y

2

+ 8x = 0:

99. Wyznaczy´c wspó÷

rz ¾

edne ogniska, wierzcho÷

ka oraz poda´c równanie kierownicy paraboli o równaniu: a)

y

2

= 12x;

b)

y = x

2

+ 6x:

100. Napisa´c równanie paraboli, której:

a)

kierownic ¾

a jest prosta y =

2; a punkt W = ( 1; 6) - wierzcho÷

kiem;

b)

kierownic ¾

a jest prosta x = 1; a punkt W = (5; 1) - wierzcho÷

kiem.

101. Jakie krzywe przedstawiaj ¾

a równania:

a)

x

2

y

2

+ 4 = 0;

b)

(x

y)

2

= 1;

c)

x

2

+ y

2

= 2xy?

10