
SIŁY WEWNETRZNE
Siły wewnętrzne w słupie wyznacza się w układzie poprzecznym obejmującym słupy oraz
podciąg. Dla wyznaczonych w schemacie ramy sił przeprowadza się wymiarowanie
zbrojenia.
Jeżeli podciąg był obliczany metodą uproszczoną - jako belka wieloprzęsłowa – słupy
środkowe można traktować jako obciążone osiowo, natomiast w słupach skrajnych należy
uwzględnić moment wynikający z zamocowania podciągu zgodnie ze wzorem:
h
I
I
l
l
M
M
col
c
col
col
A
+
=
0
gdzie: M
0
– moment w p. A wyznaczony przy założeniu obustronnego utwierdzenia przęsła A
na podporach.
PROJEKTOWANIE SŁUPA
DŁUGOŚĆ OBLICZENIOWA
Jeśli w ustroju konstrukcyjnym stropu występuje przynajmniej 8 słupów połączonych
monolitycznie za pomocą rygli z płytą stropową, to ustrój możemy traktować jako
nieprzesuwny. Długość obliczeniowa wynosi:
col
l
l
7
,
0
0
=
col
l - odległość górnej płaszczyzny stopy fundamentowej od geometrycznego środka podciągu
W pozostałych przypadkach
col
l
l
⋅
β
=
0
1
5
1
1
+
+
=
β
A
k
col
col
cm
eff
c
cm
A
l
I
E
l
I
E
k
2
=
gdzie:
eff
c
cm
l
I
E
sztywność giętna podciągu,
col
col
cm
l
I
E
sztywność giętna słupa
WYZNACZENIE MIMOŚRODÓW
Mimośród statyczny (konstrukcyjny)
Sd
Sd
e
N
M
e
=
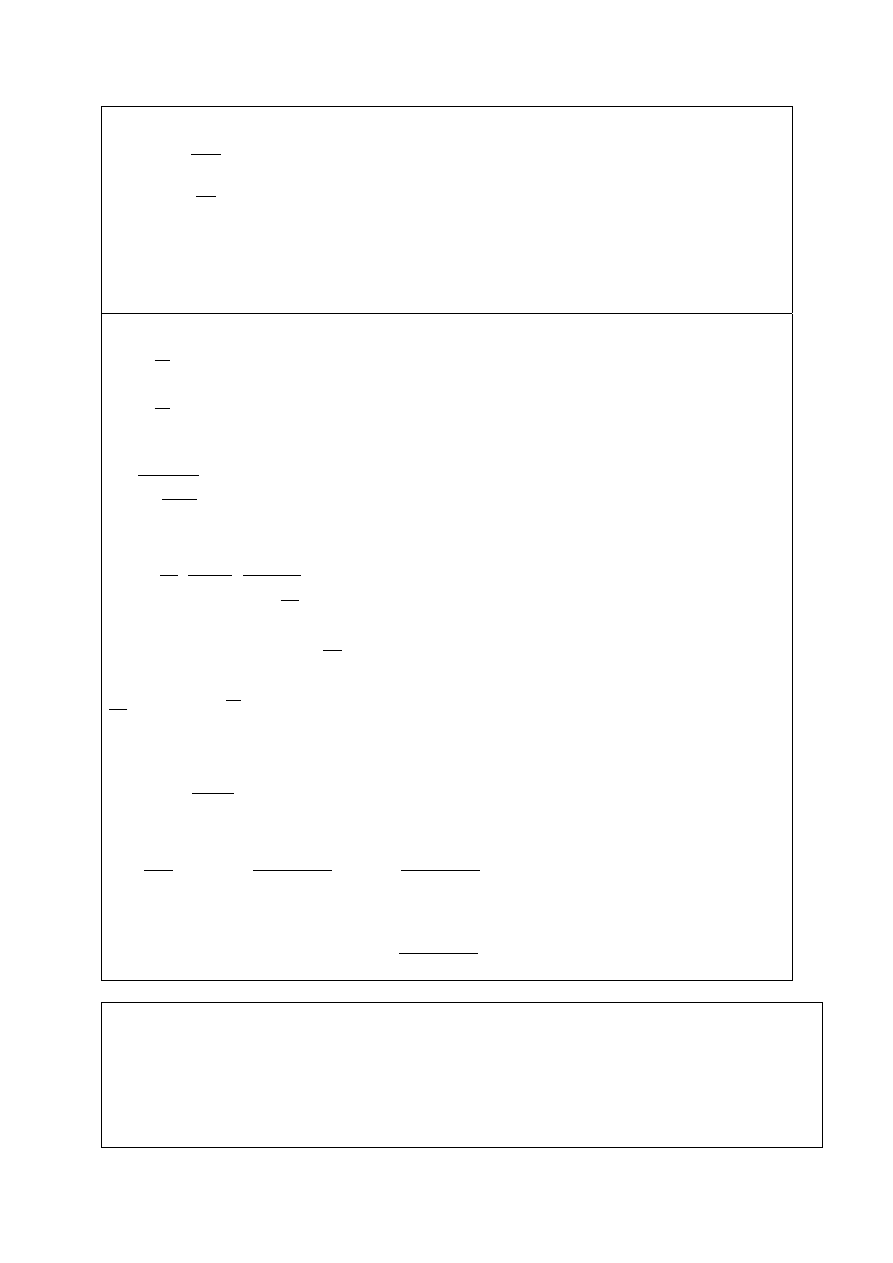
Mimośród niezamierzony
=
mm
h
l
e
col
a
10
30
600
max
Mimośród początkowy
a
e
o
e
e
e
+
=
WPŁYW SMUKŁOŚCI I OBCIĄŻEŃ DŁUGOTRWAŁYCH
Jeżeli
7
0
≤
h
l
słup jest krępy, mimośród całkowity e
o
tot
e
=
Jeżeli
7
0
>
h
l
słup jest smukły, mimośród całkowity e
o
tot
e
⋅
η
=
Gdzie:
crit
Sd
N
N
−
=
η
1
1
+
+
+
=
s
s
o
lt
c
cm
crit
I
E
h
e
k
I
E
l
N
1
,
0
1
,
0
11
,
0
2
9
2
0
wstawiona do wzoru wartość
h
e
o
powinna być nie mniejsza niż:
[
]
−
−
≥
05
,
0
01
,
0
01
,
0
5
,
0
0
MPa
f
h
l
h
e
cd
o
współczynnik k
lt
wyraża wpływ oddziaływania długotrwałego:
(
0
,
,
5
,
0
1
t
N
N
k
Sd
lt
Sd
lt
∞
ϕ
+
=
)
)
, gdzie
końcowy współczynnik pełzania betonu wg
załącznika A Normy
(
0
,t
∞
ϕ
12
3
bh
I
c
=
,
2
2
1
2
2
2
1
1
2
2
−
−
+
−
−
=
a
a
h
A
a
a
h
A
I
s
s
s
można przyjąć wstępnie stopień zbrojenia
%
1
=
ρ
L
, wtedy moment bezwładności przekroju
stalowego dany jest wzorem
2
ρ
=
h
bd
I
L
s
2
1
2
−
−
a
a
PROJEKTOWANIE ZBROJENIA
Mimośrody względem zbrojenia
1
1
5
,
0
a
h
e
e
tot
−
+
=
(dla zbrojenia rozciąganego lub „mniej” ściskanego)
2
2
5
,
0
a
h
e
e
tot
+
−
=
(dla zbrojenia ściskanego)
Graniczna wysokość strefy ściskanej
d
x
eff
eff
⋅
ξ
=
lim
,
lim
,
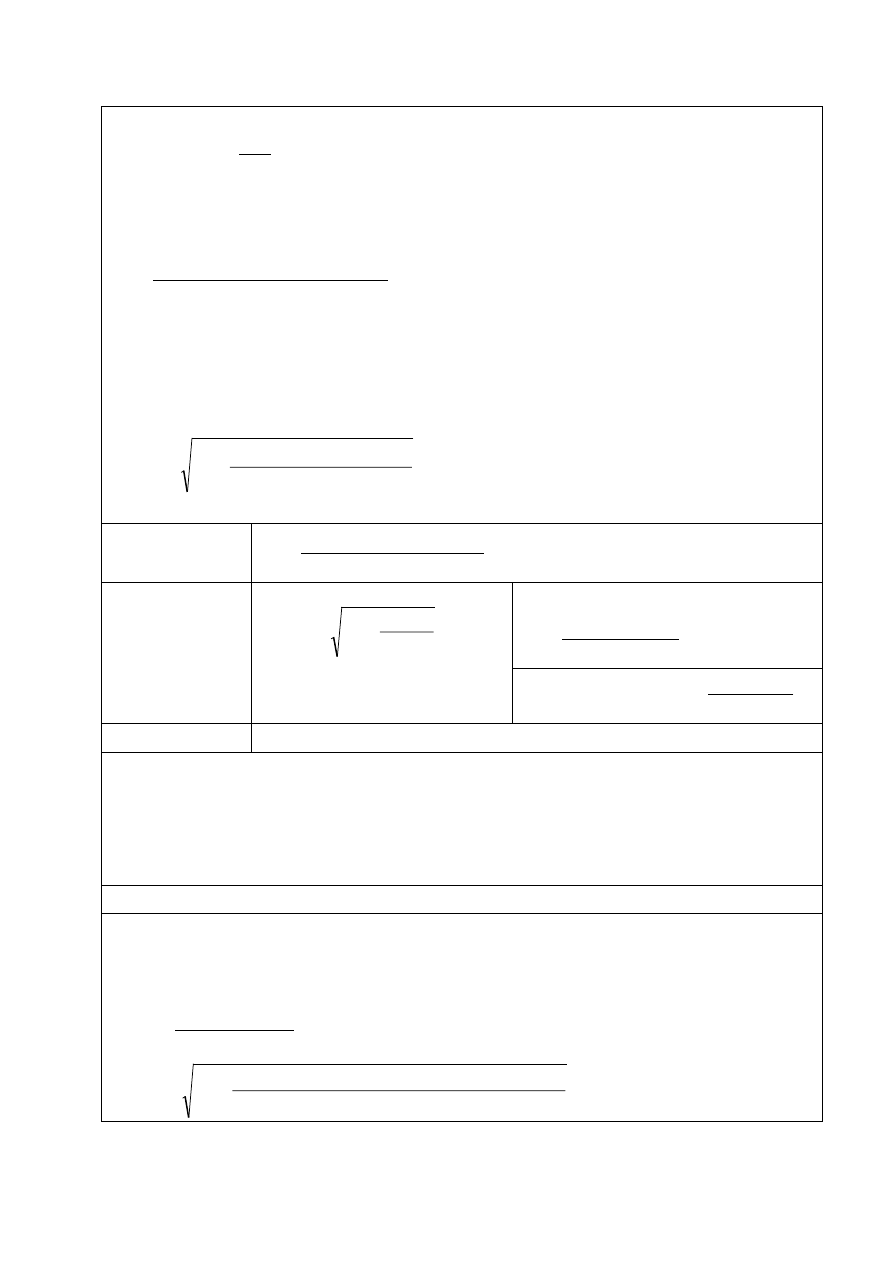
Zbrojenie minimalne (całkowite)
=
c
yd
Sd
s
A
f
N
A
003
,
0
15
,
0
max
min
,
Wstępnie należy założyć przypadek dużego mimośrodu
Pole potrzebnej powierzchni zbrojenia
2
s
A
(
)
(
)
2
lim
,
lim
,
1
2
5
,
0
a
d
f
x
d
bx
f
e
N
A
yd
eff
eff
cd
Sd
s
−
−
−
=
Przyjęcie zbrojenia:
≥
min
,
2
2
5
,
0
s
s
r
s
A
A
A
dla przyjętej średnicy zbrojenia należy wyznaczyć odległość od krawędzi a
r
2
Skorygowana wysokość strefy ściskanej
(
)
[
]
b
f
a
d
A
f
e
N
d
d
x
cd
r
r
s
yd
Sd
eff
2
2
1
2
2
−
−
−
−
=
obliczenie potrzebnego zbrojenia
1
s
A
Jeżeli
lim
,
2
2
eff
eff
r
x
x
a
≤
≤
yd
r
s
yd
eff
cd
Sd
s
f
A
f
bx
f
N
A
2
1
+
+
−
=
Dla
pole:
r
eff
a
x
2
2
≤
yd
Sd
f
N
eff
cd
s
bx
f
A
+
−
=
1
Jeżeli
r
eff
a
x
2
2
<
Ponownie należy obliczyć:
b
f
e
N
d
d
x
cd
Sd
eff
1
2
2
−
−
=
Dla
pole:
r
eff
a
x
2
2
>
)
(
2
2
1
a
d
f
e
N
A
yd
s
Sd
s
−
=
lim
,
eff
eff
x
x
>
Przypadek małego mimośrodu
Jeśli obliczone
to należy przyjąć i rozmieścić zbrojenie:
0
1
≥
s
A
≥
min
,
1
1
5
,
0
s
s
r
s
A
A
A
dla przyjętej średnicy zbrojenia należy wyznaczyć odległość od krawędzi a
r
1
KONIEC
Jeśli należy wyznaczyć zbrojenie dla przypadku małego mimośrodu
0
1
<
s
A
Przypadek małego mimośrodu
Należy przyjąć wstępnie zbrojenie:
min
,
1
5
,
0
s
s
A
A
=
wyznaczenie wysokości strefy ściskanej:
(
)
(
)
bd
f
a
d
A
f
a
A
cd
eff
s
yd
lim
,
2
1
2
1
2
ξ
−
−
−
=
(
)
(
)
(
)
[
]
(
)
b
f
a
d
A
f
e
N
A
A
x
cd
eff
s
yd
eff
Sd
eff
eff
lim
,
2
1
lim
,
2
lim
,
2
1
1
1
2
ξ
−
−
ξ
+
−
ξ
−
−
+
=
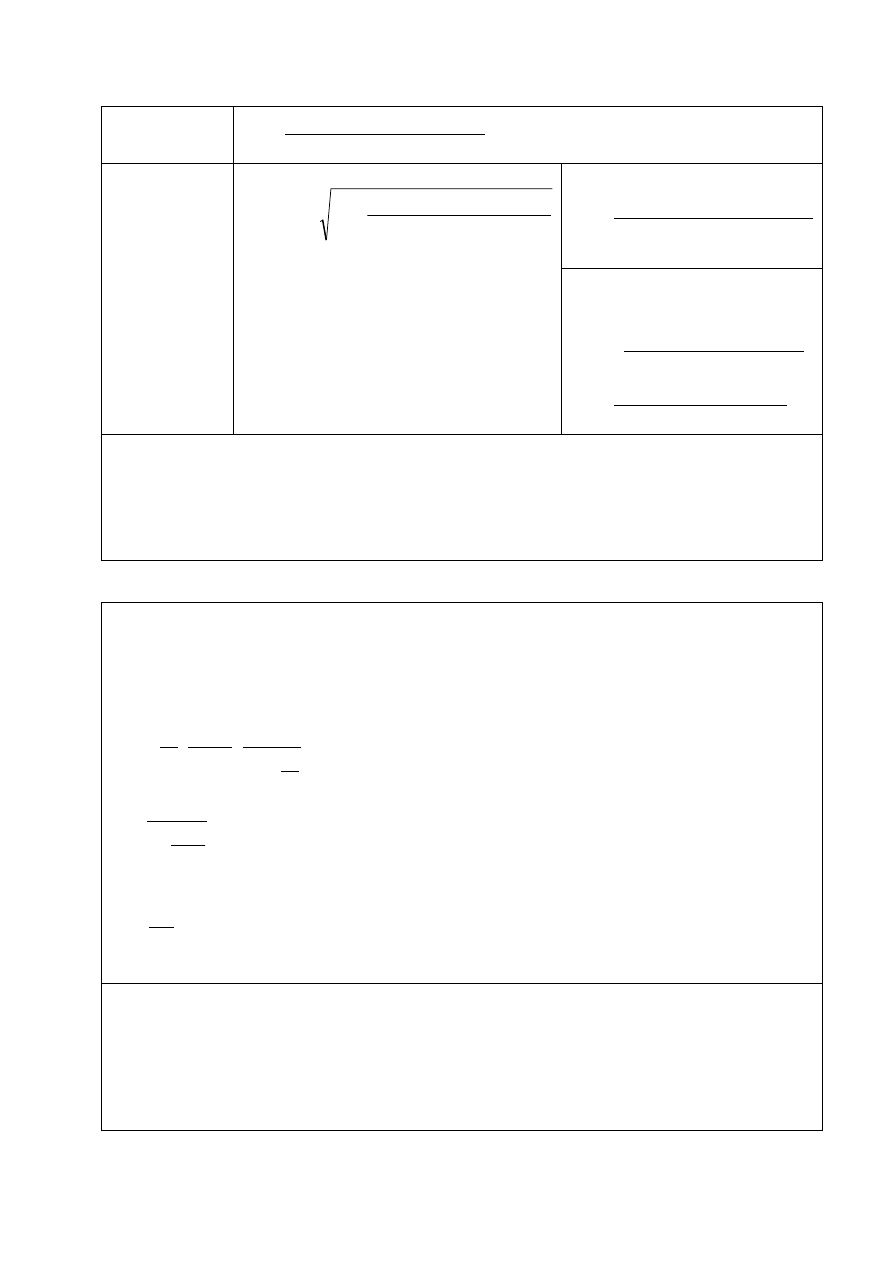
Jeżeli
d
x
x
eff
eff
≤
<
lim
,
(
)
(
)
2
1
2
5
,
0
a
d
f
x
d
bx
f
e
N
A
yd
eff
eff
cd
Sd
s
−
−
−
=
jeżeli
to oblicza się
h
x
eff
≤
(
)
(
)
2
1
2
5
,
0
a
d
f
x
d
bx
f
e
N
A
yd
eff
eff
cd
Sd
s
−
−
−
=
Jeżeli
d
x
eff
>
Ponownie należy obliczyć
(
)
[
]
b
f
a
d
A
f
e
N
a
a
x
cd
s
yd
Sd
eff
2
1
2
2
2
2
2
−
+
−
+
=
jeżeli
to należy założyć
h
x
eff
>
h
x
eff
=
(
)
(
)
2
2
2
1
5
,
0
a
d
f
a
h
bh
f
e
N
A
yd
cd
Sd
s
−
−
+
−
=
(
)
(
)
2
2
2
5
,
0
a
d
f
h
d
bh
f
e
N
A
yd
cd
Sd
s
−
−
−
=
Przyjęcie i rozmieszczenie zbrojenia:
≥
min
,
1
1
5
,
0
s
s
r
s
A
A
A
dla przyjętej średnicy zbrojenia należy wyznaczyć odległość od krawędzi a
r
1
KONIEC
SPRAWDZENIE POPRAWNOŚCI PRZYJĘTYCH ZAŁOŻEŃ DLA WYBOCZENIA:
Na podstawie przyjętych powierzchni zbrojenia górnego i dolnego wyznacza się rzeczywisty
moment bezwładności dla stali:
(
)
(
)
2
2
2
2
1
1
5
,
0
5
,
0
r
r
s
r
r
s
r
s
a
h
A
a
h
A
I
−
+
−
=
+
+
+
=
r
s
s
o
lt
c
cm
r
crit
I
E
h
e
k
I
E
l
N
1
,
0
1
,
0
11
,
0
2
9
2
0
r
crit
Sd
r
N
N
−
=
η
1
1
o
r
r
tot
e
e
⋅
η
=
03
,
1
8
,
0
≤
≤
tot
r
tot
e
e
, jeśli warunek nie jest spełniony to należy ponownie obliczyć zbrojenie dla
skorygowanej wartości mimośrodu
r
tot
e
SPRAWDZENIE NOŚNOŚCI PRZEKROJU
Obliczenia przeprowadza się dla przyjętej powierzchni i rozmieszczenia zbrojenia:
r
r
a
h
d
1
−
=
r
r
tot
r
a
h
e
e
1
1
5
,
0
−
+
=
r
r
tot
r
a
h
e
e
2
2
5
,
0
+
−
=
dla przypadku dużego mimośrodu:

b
f
A
f
A
f
N
x
cd
r
s
yd
r
s
yd
Sd
r
eff
1
2
+
−
=
Jeżeli
lim
,
2
2
eff
r
eff
r
x
x
a
≤
≤
warunek nośności przekroju:
(
)
(
)
r
r
s
yd
r
eff
r
r
eff
cd
Rd
Sd
a
d
A
f
x
d
bx
f
M
e
N
2
2
1
5
,
0
−
+
−
=
≤
jeśli
r
r
eff
a
x
2
2
≤
(
)
r
eff
r
r
eff
cd
Rd
Sd
x
d
bx
f
M
e
N
5
,
0
1
−
=
≤
Jeżeli
r
r
eff
a
x
2
2
<
Ponownie należy obliczyć
b
f
A
f
N
x
cd
r
s
yd
Sd
r
eff
1
+
=
jeśli
r
r
eff
a
x
2
2
>
(
)
r
r
r
s
yd
Rd
Sd
a
d
A
f
M
e
N
2
1
2
−
=
≤
Należy ponownie obliczyć:
(
)(
)
(
)
r
s
yd
eff
r
cd
r
s
yd
eff
r
s
yd
r
s
yd
Sd
eff
A
f
bd
f
A
f
A
f
A
f
N
d
x
1
lim
,
1
lim
,
2
1
2
1
2
1
+
ξ
−
+
ξ
−
−
−
=
jeśli
r
r
eff
d
x
≤
(
)
(
)
r
r
s
yd
r
eff
r
r
eff
cd
Rd
Sd
a
d
A
f
x
d
bx
f
M
e
N
2
2
1
5
,
0
−
+
−
=
≤
Jeżeli
lim
,
eff
r
eff
x
x
>
mały mimośród
jeśli
ponownie oblicza się:
r
r
eff
d
x
>
b
f
A
f
A
f
N
x
cd
r
s
yd
r
s
yd
Sd
eff
2
1
−
−
=
jeśli
h
x
r
eff
≤
(
)
(
)
r
r
s
yd
r
eff
r
r
eff
cd
Rd
Sd
a
d
A
f
x
d
bx
f
M
e
N
2
2
1
5
,
0
−
+
−
=
≤
jeśli
nośność strefy ściskanej niewystarczająca
h
x
r
eff
>
W przypadku gdy warunek nośności nie jest spełniony należy:
Dla
dozbroić strefę rozciąganą
lim
,
eff
r
eff
x
x
≤
Dla
dozbroić strefę ściskaną
lim
,
eff
r
eff
x
x
>
SZCZEGÓŁY ZBROJENIA
Średnica strzemion
∅
(
∅
- średnica zbrojenia głównego)
∅
≥ 2
,
0
s
Rozstaw strzemion
∅
=
m
b
s
4
,
0
15
min
max
POŁĄCZENIE SŁUPA Z FUNDAMENTEM
(połączenie zbrojenia na zakład w miejscu przerwy technologicznej, patrz p. 8.1.4.3 PN)
min
,
1
s
bd
s
l
l
l
≥
α
=
min
,
b
r
s
s
b
a
bd
l
A
A
l
l
≥
α
=
1
=
α
a
(dla prętów prostych)
mm
l
l
b
b
100
lub
10
3
,
0
min
,
∅
≥
=
(dla prętów rozciąganych) l
mm
l
b
b
100
lub
10
6
,
0
min
,
∅
≥
=
(dla
prętów ściskanych)
bd
yd
b
f
f
l
4
∅
=
1
1
=
α
(dla prętów ściskanych),
(dla prętów rozciąganych)
4
,
1
1
=
α
Na długości zakładu rozstaw strzemion należy zagęścić do 1/2
POŁĄCZENIE SŁUPA Z PODCIĄGIEM
długość zakotwienia zbrojenia słupa w podciągu
min
,
b
r
s
s
b
a
bd
l
A
A
l
l
≥
α
=
(oznaczenia jak we wzorach powyżej)
STOPA FUNDAMENTOWA
ODPÓR GRUNTU POD FUNDAMENTEM
fund
fund
W
M
A
D
N
q
±
γ
+
=
min
max,
2
B
A
fund
=
,
6
3
B
fund
=
W
odpowiednio
powierzchnia i wskaźnik zginania podstawy
stopy fund.)
N
,
M - reakcja ze słupa, D – głębokość
posadowienia,
γ
– uśredniona gęstość stopy i
zasypki, można przyjąć
3
/
20
m
kN
=
γ
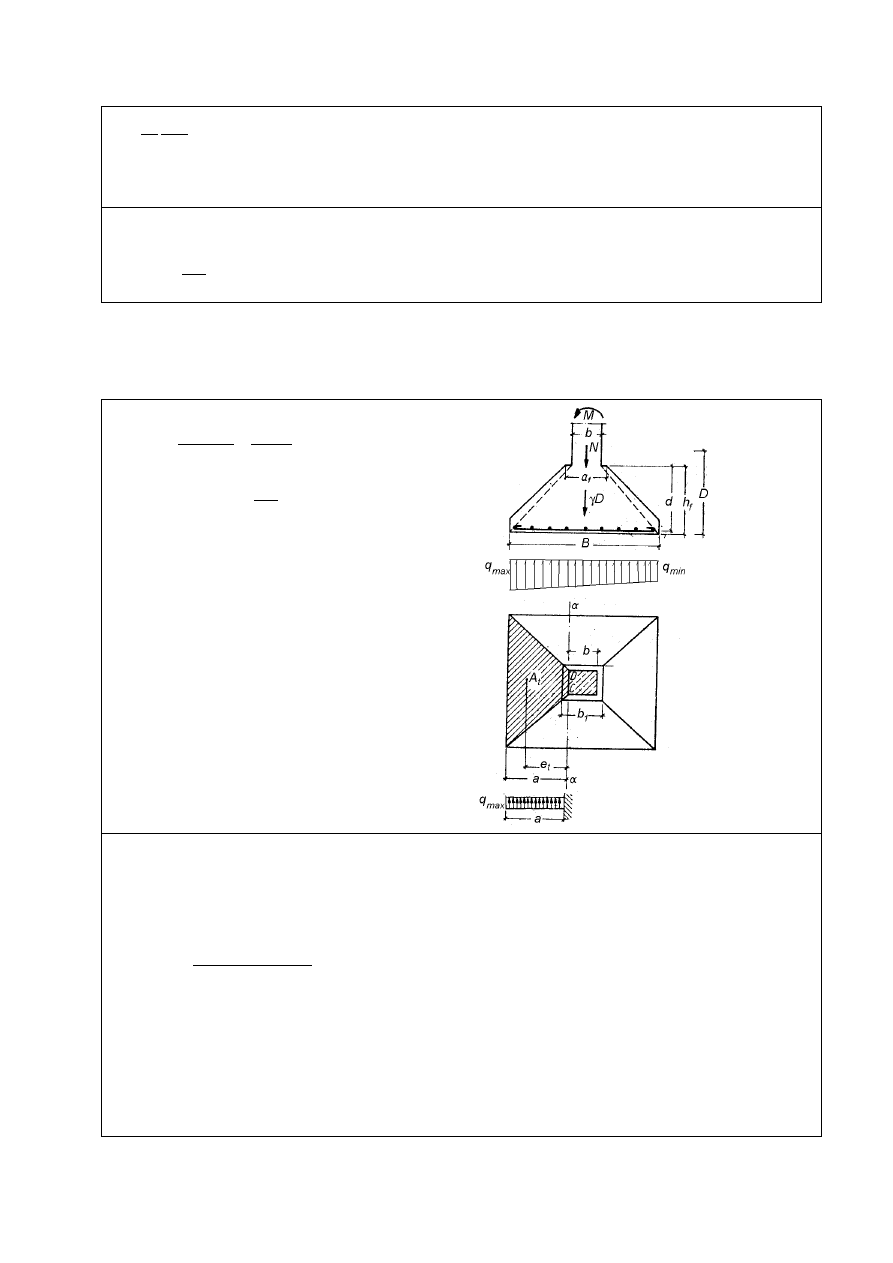
WYMIAROWANIE STOPY NA ZGINANIE
(metoda wsporników trapezowych)
jeżeli jest niewielka różnica pomiędzy
q
max
i
q
min
można do wymiarowania zbrojenia przyjąć
uproszczony model wspornika obciążonego maksymalnym odporem, wtedy wzór na moment
zginający pole trapezu wg rys. przybierze postać:
(
) (
)
24
2
2
max
b
B
b
B
q
M
Sd
+
−
≈
w przypadku dużej różnica pomiędzy
q
max
i
q
min
należy wyznaczyć moment dla wspornika
obciążonego trapezowo.
średnica zbrojenia (wstępnie można przyjąć
mm
f
12
=
∅
)
f
h
c
a
∅
+
∆
+
=
5
,
1
1
(minimalna otulina
mm
c 50
=
,
)
mm
h 10
=
∆
1
a
h
d
f
−
=
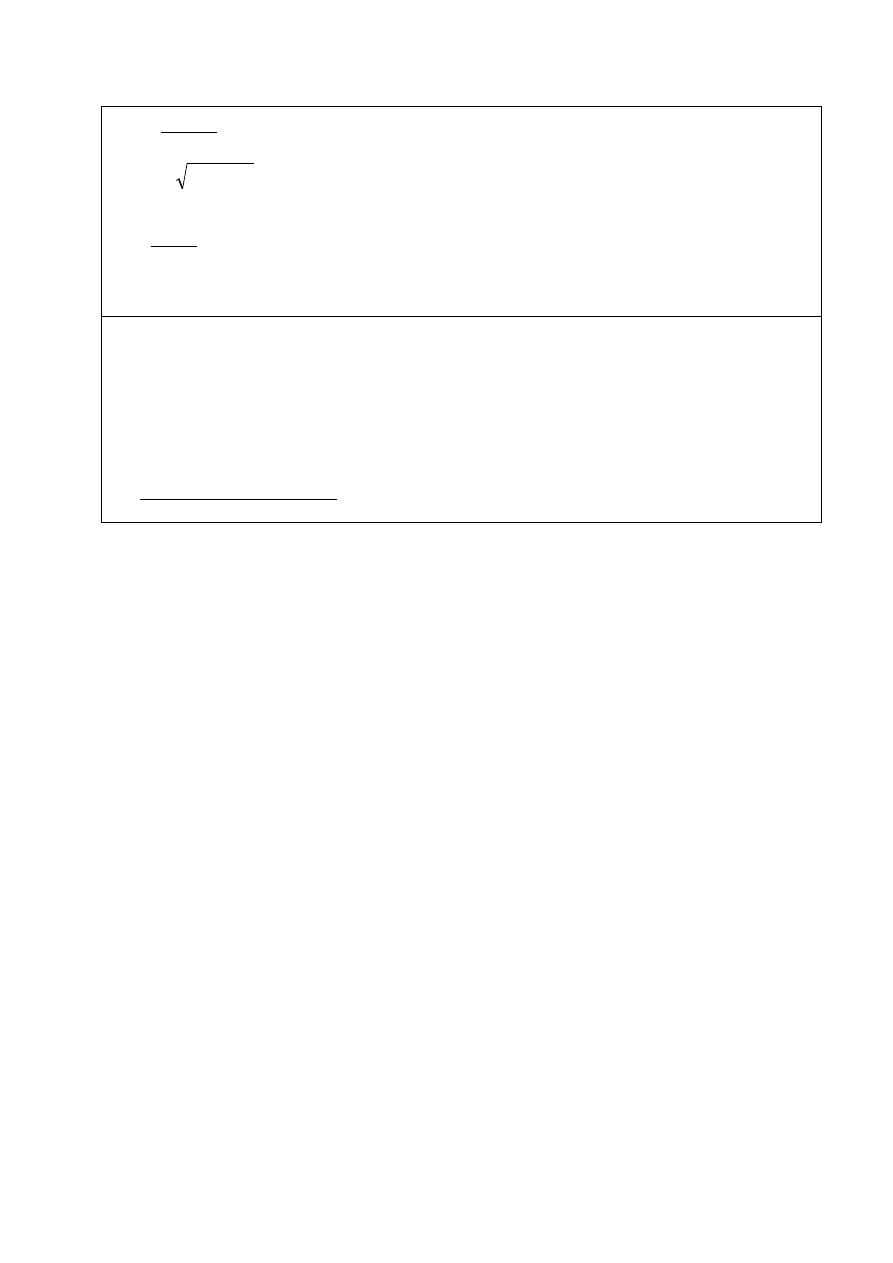
2
Bd
f
M
s
cd
Sd
cceff
=
cceff
eff
s
2
1
1
−
−
=
ξ
eff
ξ
−
=
ζ
5
,
0
1
d
f
M
A
yd
Sd
s
ζ
=
1
Przyjmując zbrojenie fundamentu należy pamiętać, że maksymalny rozstaw wkładek wynosi
30cm)
WYMIAROWANIE STOPY NA PRZEBICIE
Nośność na przebicie należy sprawdzać dla fundamentów w których
d
b
B
2
+
>
Zgodnie ze wzorem (87) PN nośność fundamentu mimośrodowo obciążonego powinna spełniać
warunek:
d
b
f
N
A
q
m
ctd
Rd
=
≤
max
d
b
b
m
+
=
obciążenie zbierane jest z powierzchni:
(
) (
)
(
)
2
5
,
0
2
d
b
B
B
d
b
A
−
−
+
+
=
Document Outline
Wyszukiwarka
Podobne podstrony:
Oszacowanie redystrybucji naprężeń w przekroju słupa żelbetowego, ściskanego siłą osiową
Autodesk Robot Structural Analysis 2010 Projekt moj zelbet analiza słupa Wyniki MES aktualne
14 TIOB W14 zelbet i klasyfikacja deskowan
przekroj podłużny przez most żelbetowy
Żelbet obliczenia
Druk podania o rejestrację na semestr letni 2010-2011, Nauka, budownictwo, żelbet EC przykłądy
Studia zaoczne - pytania VII, SEMESTR VII, ŻELBET
zelbet test, Skrypty, PK - materiały ze studiów, I stopień, SEMESTR 7, Konstrukcje Betonowe II, egza
ściana2, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 4, Semestr VII, Żel
ściana3, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 4, Semestr VII, Żel
Monier paten na żelbet
styś, podstawy konstrukcji?tonowych, Projektowanie?lek żelbetowych
żelbet
więcej podobnych podstron