Z

arówno inwestorzy indy-
widualni, jak i maklerzy
trudniàcy si´ zawodowo

obrotem gie∏dowym i walutowym

wiedzà – dziÊ lepiej ni˝ kiedykolwiek

– ˝e notowania na wszelkich rynkach fi-

nansowych cz´sto zmieniajà si´ z szybkoÊcià,

która mo˝e przyprawiç obserwatora o atak serca.

W chwilach goràczkowej aktywnoÊci na gie∏dzie, kie-

dy obroty rosnà, a skoki kursów stajà si´ coraz gwa∏tow-

niejsze, rodzà si´ i przepadajà fortuny. Na przyk∏ad we wrze-
Êniu ub. r. ceny akcji francuskiej firmy Alcatel, produkujàcej
sprz´t telekomunikacyjny, spad∏y w ciàgu jednego dnia
o mniej wi´cej 40%, przez dwa nast´pne jeszcze o 6%, by
czwartego wzrosnàç o 10%.

Klasyczne modele finansowe, pozostajàce w u˝yciu przez

wi´kszà cz´Êç naszego stulecia, nie przewidujà tak gwa∏tow-
nych zmian. Kamieniem w´gielnym funkcjonowania rynków
finansowych jest tzw. wspó∏czesna teoria portfela, zoriento-
wana na maksymalizacj´ zysku przy za∏o˝onym poziomie
ryzyka. Le˝àcy u podstaw tej teorii model matematyczny
traktuje sytuacje ekstremalne po macoszemu: zak∏ada, ˝e
wi´ksze ruchy cen sà albo zbyt ma∏o prawdopodobne, by od-
grywaç jakàkolwiek rol´, albo niemo˝liwe do uwzgl´dnie-
nia. Prawdà jest, ˝e teoria portfela trafnie opisuje zachowanie
si´ rynku nawet przez 95% czasu. Jednak ukazywany przez
nià obraz nie odzwierciedla rzeczywistoÊci, jeÊli uÊwiadomi-
my sobie, ˝e pozosta∏e 5% to w∏aÊnie okres najwa˝niejszych
wydarzeƒ na rynku. Wr´cz narzuca si´ tu analogia z ˝egla-
rzem na morzu. Gdy umiarkowane warunki pogodowe utrzy-
mujà si´ przez 95% rejsu, czy mo˝e on tym samym pozwoliç
sobie na ignorowanie ewentualnoÊci nadejÊcia tajfunu?

Kryjàce si´ za teorià portfela wzory matematyczne s∏u˝àce

do minimalizacji ryzyka opierajà si´ na licznych daleko idà-
cych za∏o˝eniach, które w ostatecznym rachunku okazujà si´
bezpodstawne. Po pierwsze, przyjmuje si´, ˝e zmiany cen –
statystycznie rzecz ujmujàc – sà niezale˝ne od siebie: na przy-

k∏ad dzisiejsza nie ma wp∏ywu na zmiany, które nastàpià do
jutra. Przewidywanie reakcji rynku staje si´ wi´c niemo˝li-
we. Po drugie, mamy za∏o˝enie dotyczàce zgodnoÊci rozk∏a-
du zmian cen ze standardowà krzywà Gaussa. Jest to krzywa
o kszta∏cie dzwonu, którego szerokoÊç (mierzona wartoÊcià

σ,

czyli odchylenia standardowego) okreÊla, jak bardzo zmia-
ny cen odbiegajà od Êredniej – wielkoÊci ekstremalne uznawa-
ne sà za niezwykle rzadkie. W efekcie przyjmuje si´ wi´c, ˝e
tajfuny nie istniejà.

Czy dane finansowe spe∏niajà takie za∏o˝enia? OczywiÊcie,

˝e nie. Wykresy notowaƒ gie∏dowych lub kursów walut istot-
nie ukazujà sta∏e drobne wahania cen, nie majà one jednak
charakteru tak jednorodnego, jak nale˝a∏oby oczekiwaç, gdy-
by rozk∏ad zmian cen odpowiada∏ krzywej Gaussa. Tego ro-
dzaju regularnoÊci to jednak tylko jeden aspekt wykresu. Na
tle zaburzeƒ wzgl´dnie umiarkowanych wyró˝nia si´ znacz-
na liczba nag∏ych du˝ych zmian. Z wykresu strzela co pewien
czas nieoczekiwanie w gór´ lub w dó∏ „iglica” – jest to obraz
znany z historii notowaƒ akcji Alcatela. Co wi´cej, mo˝e si´
zdarzyç, ˝e amplituda wahaƒ (tych drobnych i tych znacz-
nych) utrzymuje si´ na zbli˝onym poziomie przez ca∏y rok,
po czym nagle wzrasta na d∏u˝szy okres. Du˝e skoki cen wy-
st´pujà cz´Êciej w warunkach pog∏´biajàcego si´ zamieszania
na rynku – na wykresie pojawiajà si´ wtedy ca∏ymi grupami.

Zgodnie z teorià portfela prawdopodobieƒstwo tak znacz-

nych fluktuacji by∏oby rz´du bilionowych cz´Êci jednej bilio-
nowej (fluktuacje przekraczajà dziesi´ciokrotnoÊç odchylenia
standardowego). A jednak na wykresach stale obserwuje si´
„iglice” – nierzadko w ka˝dym miesiàcu – prawdopodobieƒ-
stwo zaÊ ich wystàpienia jest rz´du setnych. Zauwa˝my, ˝e
krzywà Gaussa okreÊla si´ cz´sto jako krzywà normalnà bàdê
te˝, mówiàc ÊciÊlej, rozk∏ad normalny. Czy oznacza to, ˝e ryn-
ki finansowe nale˝y uznaç za nienormalne? Z ca∏à pewnoÊcià
nie – sà takie, jakie sà, zawodzi natomiast teoria portfela.

Wspó∏czesna teoria portfela wystawia na niebezpieczeƒ-

stwo osoby, które zbyt mocno w nià wierzà, a dla teoretyków
stanowi powa˝ne wyzwanie. Jej zwolennicy przyznajà cza-
sem, i˝ obecne podejÊcie nie jest doskona∏e, ale twierdzà przy
tym, ˝e ˝adnych innych za∏o˝eƒ nie da si´ ujàç w ramy mate-
matyczne. Rodzi si´ zatem pytanie, czy mo˝na w ogóle po-
daç Êcis∏y opis iloÊciowy choçby niektórych aspektów znacz-
niejszych zaburzeƒ na rynkach finansowych. PesymiÊci
odpowiadajà, ˝e wszystkie powa˝niejsze zawirowania ryn-

64 Â

WIAT

N

AUKI

Kwiecieƒ 1999

M

ultifraktale rzàdzà na

W

all

S

treet

Geometria opisujàca kszta∏t linii brzegowych
i rozmieszczenie galaktyk we WszechÊwiecie
pomaga wyjaÊniç nieoczekiwane spadki
i zwy˝ki notowaƒ gie∏dowych

Benoit B. Mandelbrot

LAURIE GRACE

kowe to anomalie, jednostkowe przy-

padki dzia∏ania „si∏y wy˝szej”, które nie pozwalajà zaobser-
wowaç ˝adnej regularnoÊci. Reformatorzy próbujà modyfi-
kowaç budzàce wàtpliwoÊci za∏o˝enia wspó∏czesnej teorii
portfela, dokonujàc drobnych poprawek, które nie sà jednak
podyktowane ˝adnà myÊlà przewodnià i nie dajà zadowala-
jàcych rezultatów. Natomiast badania, które prowadz´ od
wielu lat, przynoszà zdecydowanie bardziej optymistycznà
odpowiedê.

Jestem zdania, ˝e wahania notowaƒ na rynkach finanso-

wych t∏umaczyç mo˝e model oparty na wynikach moich prac
z dziedziny geometrii fraktalnej. Nie twierdz´, ˝e fraktale –
a mówiàc ÊciÊlej, pewne uogólnienie tego poj´cia, tzw. mul-
tifraktale – pozwolà przewidywaç przysz∏oÊç z ca∏kowità
pewnoÊcià. Dajà one jednak bli˝szy rzeczywistoÊci obraz za-
gro˝eƒ rynkowych. Majàc w pami´ci niedawne k∏opoty,
w które popad∏y du˝e konsorcja inwestycyjne zwane fundu-
szami hedgingowymi*, nale˝a∏oby uznaç za nader nierozsàd-
nà rezygnacj´ z badania modeli umo˝liwiajàcych precyzyj-
niejszà ocen´ ryzyka.

Co ∏àczy multifraktale z rynkiem?

Podstawy matematyczne badaƒ nad fraktalami i multifrak-

talami sà ju˝ ugruntowane. Obiekty o w∏asnoÊciach fraktali
opisujà nie tylko zmiennoÊç notowaƒ papierów wartoÊcio-
wych, ale równie˝ rozk∏ad galaktyk we WszechÊwiecie czy
przebieg linii brzegowych na kuli ziemskiej; pojawiajà si´
tak˝e w niezliczonych grafikach dekoracyjnych generowa-
nych przez rozmaite programy komputerowe.

Fraktal to figura geometryczna, którà mo˝na podzieliç na

cz´Êci o takiej w∏asnoÊci, ˝e ka˝da z nich stanowi pomniej-
szonà kopi´ ca∏oÊci. W dziedzinie finansów koncepcja ta nie
jest zawieszonà w pró˝ni abstrakcjà. Pozwala ujàç w katego-
riach teoretycznych pewnà dobrze znanà z praktyki gie∏do-
wej prawid∏owoÊç: graficzny obraz wahaƒ kursów papierów
wartoÊciowych lub walut zawsze wyglàda podobnie, nieza-
le˝nie od tego, czy wykres powi´kszymy, czy te˝ pomniej-
szymy, by dopasowaç go do okreÊlonej skali czasu i cen. Ob-
serwator nie jest wi´c w stanie stwierdziç, czy dany przebieg
ilustruje zmiany cen zachodzàce z tygodnia na tydzieƒ, z dnia
na dzieƒ, czy mo˝e z godziny na godzin´. Ta cecha pozwala
zaliczyç badane wykresy do kategorii krzywych fraktalnych,
dzi´ki czemu mo˝liwe staje si´ zastosowanie do ich analizy
wielu mocnych narz´dzi matematycznych i numerycznych.

Tego typu zwiàzek mi´dzy cz´Êcià a ca∏oÊcià okreÊla si´

w j´zyku fachowym mianem samopowinowactwa. Cecha ta
nawiàzuje do bardziej znanego ze Êwiata fraktali poj´cia sa-
mopodobieƒstwa, z którym stykamy si´ wtedy, gdy ka˝dy
element obrazu zostaje pomniejszony lub powi´kszony w ta-
kim samym stosunku – dzieje si´ tak na przyk∏ad podczas
sporzàdzania odbitki fotograficznej. Wykresom notowaƒ na
rynkach finansowych daleko jednak do samopodobieƒstwa.

Je˝eli na wykresie amplituda oscylacji jest wi´ksza ni˝ ich

szerokoÊç – a tak w∏aÊnie dzieje si´ w przypadku poszcze-

gólnych cykli wzrostu i

spadku notowaƒ – transfor-

macja, która przekszta∏ca ca∏oÊç wy-

kresu na jego cz´Êç, musi skracaç oÊ po-

ziomà w wi´kszym stopniu ni˝ pionowà. Na

wykresie notowaƒ gie∏dowych skal´ czasu (oÊ pozio-

ma) nale˝y wi´c „Êcisnàç” bardziej ni˝ skal´ cen (oÊ piono-

wa). W j´zyku geometrii powiedzielibyÊmy, ˝e mi´dzy ca∏o-
Êcià a jej cz´Êciami zachodzi relacja samopowinowactwa.

Wi´kszoÊç statystyków nie przywiàzuje zbytniej wagi do ist-

nienia w∏asnoÊci niezmienniczych. Ich badaniu oddajà si´ na-
tomiast z upodobaniem fizycy i matematycy, w tym tak˝e ja.
OkreÊlamy je mianem niezmienników i najbardziej lubimy
modele, które majà jakàÊ interesujàcà w∏asnoÊç tego rodza-
ju. Dobrym przyk∏adem jest prosty wykres ilustrujàcy zmia-
ny cen od chwili 0 do (póêniejszej) chwili 1, zachodzàce w ko-
lejnych przedzia∏ach czasowych. D∏ugoÊç tych przedzia∏ów nie
odgrywa roli – równie dobrze mo˝e to byç sekunda, jak go-
dzina, dzieƒ czy nawet rok.

Punktem wyjÊcia jest okreÊlona cena – na wykresie ilustru-

je jà prosta zwana linià trendu [

ilustracja 1

]. Nast´pnie wpro-

Â

WIAT

N

AUKI

Kwiecieƒ 1999 65

LINIA TRENDU

CENA

GENERATOR

GENERATOR

PO PRZESKALOWANIU

CZAS

Odcinek 1

Odcinek 2

Odcinek 3

0

0

1

1

1

Z¸O˚ONY Z TRZECH ODCINKÓW generator fraktalny

(wy-

kres górny) zast´puje w kolejnych krokach (po odpowiednim
przeskalowaniu) ka˝dy z odcinków tworzàcych poprzedni wy-
kres

(trzy dolne wykresy). Obraz, który zaczyna si´ wy∏aniaç, co-

raz bardziej przypomina oscylacje cen na rynku. (W przypadku
odcinków opadajàcych generator zast´puje si´ jego symetrycz-
nym odbiciem.)

LAURIE GRACE

wadzana jest oznaczona linià przerywanà ∏amana, którà okre-
Êla si´ jako generator. Odpowiada ona wahaniom ceny noto-
wanej na rynkach finansowych. Generator sk∏ada si´ z trzech
odcinków, którymi w pierwszym kroku zast´puje si´ lini´
trendu. (Generator z∏o˝ony z mniej ni˝ trzech odcinków nie
nadawa∏by si´ do symulowania ceny, która mo˝e i wzrastaç,
i spadaç.) Po narysowaniu generatora zast´pujemy ka˝dy z je-
go trzech odcinków trzema krótszymi. Powtarzajàc t´ pro-
cedur´ w toku kolejnych iteracji, odtwarzamy raz po raz kszta∏t
generatora, czyli krzywej ceny, poddajàc go jednak coraz sil-
niejszej kompresji. Zarówno oÊ pozioma (czas), jak i pionowa
(cena) ulegajà skróceniu, tak by kraƒcowe punkty generatora
pokry∏y si´ z koƒcami danego odcinka.

Iteracje, iteracje...

Ilustracja ukazuje tylko poczàtkowe kroki, ale opisany pro-

ces trwa nadal. Teoretycznie nie ma on koƒca, choç w praktyce
nie mia∏oby sensu powtarzanie kolejnych kroków d∏u˝ej ni˝ do
chwili, gdy przedzia∏ czasowy staje si´ krótszy od odst´pu mi´-
dzy poszczególnymi transakcjami gie∏dowymi. Mo˝e on wyno-
siç, powiedzmy, minut´ lub mniej. Jasne jest, ˝e ka˝dy fragment
wykresu przybierze w koƒcu kszta∏t zbli˝ony do kszta∏tu ca∏o-
Êci. Innymi s∏owy, niezmienniczoÊç wzgl´dem skali wynika z sa-
mej konstrukcji naszego modelu. Natomiast rezultatem nowym
(i zaskakujàcym) jest to, ˝e tego rodzaju samopowinowate krzy-
we fraktalne charakteryzujà si´ bogatà strukturà – która stano-
wi podstaw´ zarówno geometrii fraktalnej, jak i teorii chaosu.

Niektóre specjalnie dobrane generatory dajà poczàtek tzw.

krzywym unifraktalnym. Odpowiada im model stosunkowo
spokojnego zachowania si´ rynków we wspó∏czesnej teorii
portfela. Ale spokój utrzymuje si´ tylko w bardzo specyficz-
nych warunkach, które zapewniajà wy∏àcznie generatory
o szczególnych w∏asnoÊciach. Za∏o˝enia przyjmowane w tym
nadmiernie uproszczonym modelu stanowià jeden z kardy-
nalnych b∏´dów teorii portfela. Przypomina ona teori´ fal
morskich, która nie dopuszcza∏aby mo˝liwoÊci ich wypi´-
trzania si´ powy˝ej 2 m.

Pi´kno fraktalnej geometrii polega na tym, ˝e udost´pnia ona

model na tyle ogólny, ˝e mo˝na go zastosowaç do opisu zarów-
no stabilnych rynków, które przewiduje teoria portfela, jak i go-
ràczki gie∏dowej ostatnich miesi´cy. Opisanà metod´ modelo-
wania cen za pomocà fraktali da si´ zmodyfikowaç w sposób
uwzgl´dniajàcy wahania poziomu intensywnoÊci transakcji ryn-
kowych – a wi´c istot´ zmiennoÊci rynków. To w∏aÊnie t´ zmien-
noÊç podkreÊla przedrostek „multi-” dodany do s∏owa „fraktal”.

Przekszta∏cenie fraktala w multifraktal polega na wyd∏u-

˝aniu bàdê skracaniu odcinków osi poziomej (czasu), przez
co sà równie˝ Êciskane lub rozciàgane poszczególne odcinki
tworzàce generator. OÊ pionowà (ceny) mo˝na pozostawiç
bez zmian. Pierwszy odcinek generatora unifraktalnego jest
coraz bardziej skracany, dzi´ki czemu zwalnia si´ miejsce na
wyd∏u˝enie odcinka drugiego [

ilustracja 2

].

Po dokonaniu tych zmian generator zmienia si´ w multi-

fraktalny (M1 do M4). IntensywnoÊç transakcji na rynku wzra-
sta w przedziale czasowym odpowiadajàcym pierwszemu
odcinkowi generatora, a obni˝a si´ w przedziale odpowia-
dajàcym odcinkowi drugiemu [

ilustracja 3

].

Taka modyfikacja generatora pozwala przeprowadziç pe∏-

nà symulacj´ fluktuacji cen w okreÊlonym czasie z zastoso-
waniem opisanej wczeÊniej konstrukcji iteracyjnej. Za ka˝-
dym razem, kiedy pierwszy odcinek generatora skraca si´
jeszcze bardziej, wykres uzyskany w wyniku takiego zabie-
gu – po wykonaniu kolejnych iteracji – coraz bardziej przypo-
mina obraz znany z rynków o du˝ej zmiennoÊci [

ilustracja 4

].

Wykres unifraktalny (U), przedstawiony na ilustracji przed do-

konaniem jakiegokolwiek skrócenia, odpowiada modelowi
spokojnych rynków postulowanemu przez teori´ portfela.
Ka˝dy kolejny wykres (M1 do M4) odbiega od tego modelu
coraz bardziej – pojawiajà si´ gwa∏towne chwilowe skoki cen
oraz okresy ich zwi´kszonej zmiennoÊci, co przypomina sy-
tuacj´ panujàcà ostatnio na gie∏dach. Aby tego rodzaju mode-
le rynków o du˝ej zmiennoÊci mog∏y osiàgnàç konieczny po-
ziom realizmu, kolejnoÊç trzech odcinków sk∏adajàcych si´
na ka˝dy generator jest w sposób losowy zmieniana, co na
ilustracjach nie zosta∏o uwidocznione. Zrozumiemy ten me-
chanizm, gdy wyobrazimy sobie kostk´, której ka˝da ze Êcian
odpowiada jednej z szeÊciu permutacji odcinków generatora.
Przed zastàpieniem ka˝dego kolejnego odcinka przez gene-
rator stosujemy permutacj´ wskazanà przez rzut kostkà.

66 Â

WIAT

N

AUKI

Kwiecieƒ 1999

M4

M3

M2

M1

U

4

...Przesuni´cie generatora w lewà stron´ sprawia, ˝e intensyw-
noÊç transakcji na rynku staje si´ coraz bardziej zmienna.

4/9

4/9

5/9

5/9

1

1

INTENSYWNOÂå TRANSAKCJI

0

1

0

U
M1
M2
M3
M4

Odcinek 1

Odcinek 2

Odcinek 3

CZAS

3

...powoduje, ˝e czas realizacji tego samego wolumenu transak-

cji skraca si´ dla pierwszego odcinka, a wyd∏u˝a dla drugiego...

0

4/9

5/9

1

CZAS

GENERATOR

CENA

1/3

2/3

1

0

Odcinek 1

Odcinek 2

Odcinek 3

U = unifraktal

M1 = multifraktal 1

M2 = multifraktal 2

M3 = multifraktal 3

M4 = multifraktal 4

2

PRZESUNI¢CIE ODCINKA generatora fraktali w lewà stron´...

BENOIT B. MANDELBROT

LAURIE GRACE

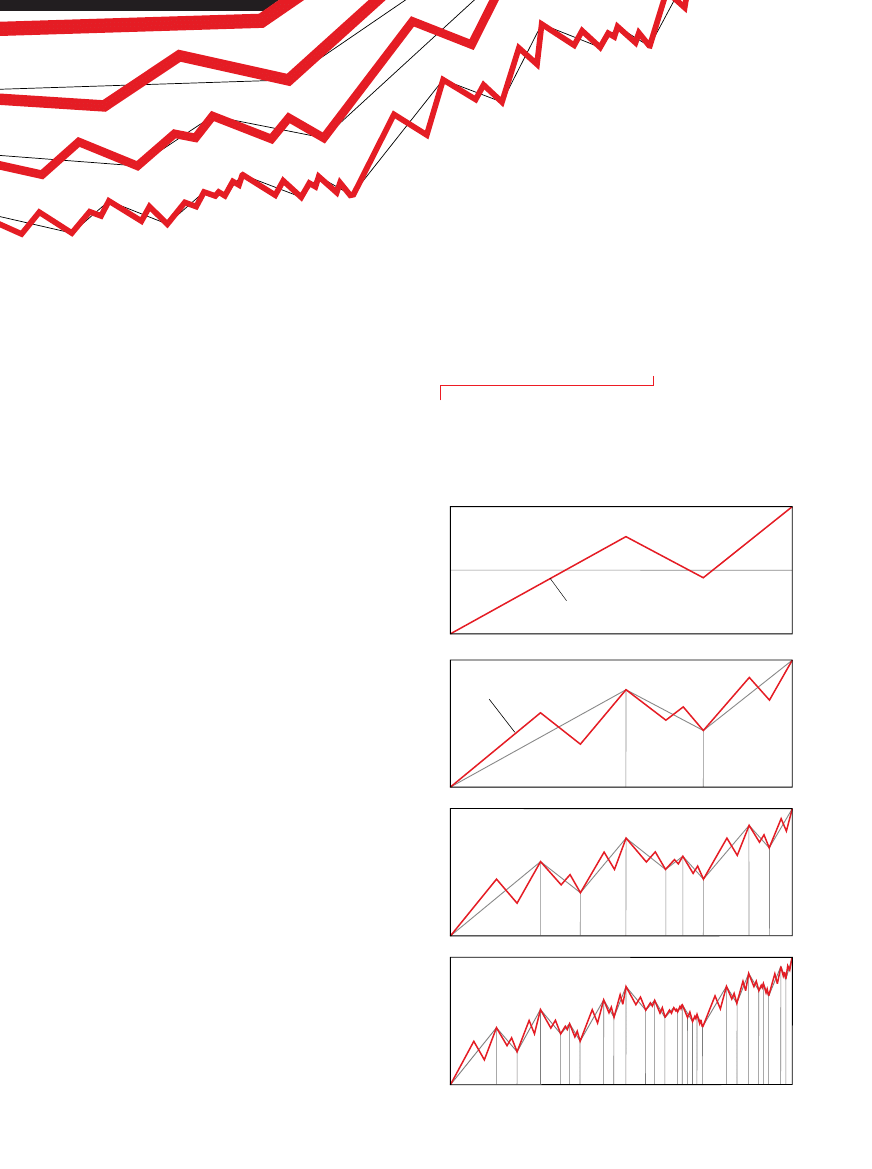
J

ak si´ majà multifraktale do faktycznych zmian cen notowanych na ryn-
kach finansowych? Aby oceniç, w jakim stopniu sprawdzajà si´ poszcze-

gólne modele, porównajmy ich przewidywania z kilkoma seriami auten-
tycznych danych gie∏dowych. Zachowania rzeczywistych rynków z ca∏à
pewnoÊcià nie oddaje wykres 1, przedstawia-
jàcy niezwykle monotonny i statyczny obraz
drobnych fluktuacji cen, który przypomina szum
s∏yszalny w radioodbiorniku nie nastrojonym
na ˝adnà stacj´. ZmiennoÊç utrzymuje si´ na
sta∏ym poziomie, bez ˝adnych gwa∏townych
skoków. Gdyby ceny rzeczywiÊcie zachowy-
wa∏y si´ w ten sposób, przebieg poszczegól-
nych dni na gie∏dzie móg∏by si´ ró˝niç, ale ob-
raz ka˝dego miesiàca by∏by bardzo podobny.
Wykres 2, o doÊç prostym przebiegu, jest nie-
co bli˝szy rzeczywistoÊci, gdy˝ pojawiajà si´
na nim liczne „iglice” – sà to jednak odosob-
nione przypadki wyró˝niajàce si´ z niezró˝nico-
wanego t∏a, w którego obr´bie zmiennoÊç po-
zostaje wartoÊcià sta∏à. Wykres 3 ukazuje
naprzemienne okresy zwy˝ki i spadku cen, któ-
re nigdy nie dokonujà si´ w sposób skokowy.

Intuicja podpowiada nam, ˝e wszystkie te

trzy wykresy sà zbyt proste, by uznaç je za
realistyczne. Mog´ teraz ujawniç, skàd pocho-
dzà: wykres 1 ilustruje fluktuacje cen w mo-
delu, który przedstawi∏ w roku 1900 francuski

matematyk Louis Bachelier. Zmiany cen podlegajà tu losowym zmianom
opisywanym krzywà Gaussa. Jest to model le˝àcy u podstaw wspó∏cze-
snej teorii portfela. Wykresy 2 i 3 ukazujà czàstkowe ulepszenia mode-
lu Bacheliera: zaproponowane przeze mnie rozwiàzanie (oparte na sta-

bilnych procesach losowych Lévy’ego) z roku
1963 oraz mojà w∏asnà wersj´ (opartà na u∏am-
kowych ruchach Browna) opublikowanà w roku
1965. Poprawki te nie rozwiàzujà jednak proble-
mu, z wyjàtkiem przypadków odnoszàcych si´ do
pewnych szczególnych warunków rynkowych.

Wa˝niejszà rol´ w naszych rozwa˝aniach od-

grywa pi´ç dolnych wykresów. Co najmniej jeden
z nich ukazuje rzeczywiste dane, a co najmniej je-
den inny zosta∏ wygenerowany przez komputer na
podstawie mojego najnowszego modelu multifrak-
talnego. Spróbujcie przyporzàdkowaç pi´ç wykre-
sów do odpowiednich kategorii. Mam nadziej´, ˝e
fa∏szerstwa zostanà ocenione jako bardzo przeko-
nujàce. Tak naprawd´ tylko dwa wykresy przed-
stawiajà rzeczywiste rynki finansowe. Wykres 5
ukazuje zmiany notowaƒ akcji IBM, a wykres 6 –
fluktuacje kursu dolara w stosunku do marki nie-
mieckiej. Pozosta∏e (4, 7 i 8) wykazujà du˝e podo-
bieƒstwo do swych z ˝ycia wzi´tych pierwowzo-
rów. Sà to jednak twory ca∏kowicie sztuczne,
uzyskane dzi´ki pewnej bardziej wyrafinowanej
wersji mojego modelu multifraktalnego.

Który fa∏szywy?

Co wynika z tego wszystkiego dla dyrektora finansowego

spó∏ki, maklera walutowego czy analityka gie∏dowego? Roz-
bie˝noÊci mi´dzy przewidywaniami wspó∏czesnej teorii port-
fela a rzeczywistymi ruchami cen sà oczywiste. Ceny nie zmie-
niajà si´ w sposób ciàg∏y; niezale˝nie od przyj´tej skali czasu
podlegajà nieregularnym wahaniom o znacznej amplitudzie.
Ich zmiennoÊç nie jest w ˝adnym razie zjawiskiem statycz-
nym, którego wp∏yw mo˝na pominàç lub wyeliminowaç po-
przez wprowadzenie jakiejÊ prostej poprawki – stanowi ona
samà istot´ funkcjonowania rynków finansowych. NiegdyÊ
osoby zarzàdzajàce aktywami finansowymi przyjmowa∏y
podstawowe za∏o˝enia wspó∏czesnej teorii portfela – doty-
czàce ciàg∏oÊci zmian cen i ich ograniczonej skali – po prostu
dlatego, ˝e nie by∏o przekonujàcych rozwiàzaƒ alternatyw-
nych. Obecnie jednak finansiÊci nie muszà ju˝ bezkrytycznie
akceptowaç wszystkiego, co przewidujà modele.

Dzi´ki multifraktalom mo˝liwe sta∏o si´ obecnie poddanie

portfela inwestycyjnego „próbie wytrzyma∏oÊci”. Stosowa-
na technika polega na tym, ˝e próbuje si´ uzyskaç – za po-
mocà regu∏ okreÊlajàcych w∏asnoÊci multifraktali – takie same
formy zmiennoÊci, jakie wynikajà z nie znanych nam regu∏
rzàdzàcych rzeczywistymi rynkami. Multifraktale dok∏adnie
opisujà zale˝noÊç mi´dzy kszta∏tem generatora a charakte-
rystykà wahaƒ faktycznych cen na rynku. Odkrycie to suge-
ruje, ˝e pos∏ugujàc si´ historycznymi danymi rynkowymi,

mo˝emy w praktyce znaleêç odpowiedni generator fraktali.
Model faktycznie stosowany nie ogranicza si´ do wykorzysty-
wania danych o zachowaniu si´ rynku, powiedzmy, w dniu
wczorajszym czy te˝ w ciàgu minionego tygodnia. Stanowi on
w rzeczywistoÊci bardziej realistyczny opis fluktuacji rynku,
zwanych u∏amkowymi ruchami Browna. Wykresy otrzymy-
wane za pomocà tego rodzaju generatorów mogà symulo-
waç alternatywne scenariusze, bazujàce na dotychczasowych
reakcjach rynku.

Techniki takie nie przybli˝ajà nas do prognozowania na

konkretny dzieƒ spadku lub wzrostu cen na podstawie da-
nych historycznych. Pozwalajà one jednak oszacowaç praw-
dopodobieƒstwo okreÊlonych zachowaƒ rynku i przygoto-
waç si´ do nieuchronnych zmian gie∏dowej pogody. Nowe
techniki modelowania stanowià drogowskazy u∏atwiajàce
poruszanie si´ po bardzo trudnym terenie rynków finanso-
wych. Potwierdzajà one równie˝ znanà wszystkim maryna-
rzom prawd´, o której – jak dowiod∏y niedawne wydarzenia
– zawsze nale˝y pami´taç: nawet przy najpi´kniejszej pogo-
dzie huragan mo˝e byç tu˝ za horyzontem.

T∏umaczy∏

Krzysztof KwaÊniewicz

* Istotà poj´cia „hedgingu” jest takie dobranie sk∏adu portfela inwestycyjnego,
by ewentualny spadek notowaƒ jednego waloru by∏ kompensowany przez wzrost
notowaƒ innego, na przyk∏ad przez lokowanie Êrodków w ró˝nych walutach
[patrz: Gary Stix, „Rachunek ryzyka”; Âwiat Nauki, lipiec 1998] (przyp. t∏um.).

Â

WIAT

N

AUKI

Kwiecieƒ 1999 67

Informacje o autorze

BENOIT B. MANDELBROT zajmuje si´ wieloma dziedzinami nauk Êcis∏ych

i humanistycznych. Z wykszta∏cenia matematyk od roku 1987 kieruje Kate-

drà Nauk Matematycznych im. Abrahama Robinsona w Yale University

i zajmuje stanowisko IBM Fellow Emeritus (Physics) w Thomas J. Watson Re-

search Center w Yorktown Heights (stan Nowy Jork), gdzie pracowa∏ w la-

tach 1958–1993. Jest cz∏onkiem American Academy of Arts and Sciences

i cz∏onkiem zagranicznym U.S. National Academy of Sciences oraz Akade-

mii Norweskiej. Jest laureatem m.in. Nagrody Wolfa w dziedzinie fizyki za

rok 1993, nagród Science for Art, Harveya, Humboldta i Hondy oraz posia-

daczem medali Barnarda, Franklina i Steinmetza.

Literatura uzupe∏niajàca

THE FRACTAL GEOMETRY OF NATURE

. Benoit B. Mandelbrot; W. H.

Freeman and Company, 1982.

FRACTALS AND SCALING IN FINANCE: DISCONTINUITY, CONCENTRATION,

RISK

. Benoit B. Mandelbrot; Springer-Verlag, 1997.

THE MULTIFRACTAL MODEL OF ASSET RETURNS

. Materia∏y dyskusyj-

ne Cowles Foundation for Economics, nr 1164-1166. Laurent

Calvet, Adlai Fisher i Benoit B. Mandelbrot; Cowles Founda-

tion, Yale University, 1997.

MULTIFRACTALS AND 1/F NOISE: WILD SELF-AFFINITY IN PHYSICS

. Be-

noit B. Mandelbrot; Springer-Verlag, 1999.

BENOIT B. MANDELBROT

1

2

3

4

5

6

7

8