1

Podstawowe charakterystyki

niezawodno

ś

ci

sem. 8. Niezawodno

ść

elementów i systemów, Komputerowe systemy pomiarowe

2

Niezawodno

ść

R (t) to prawdopodobie

ń

stwo pewnych zdarze

ń

Intensywno

ść

uszkodze

ń λ

(t) wyra

ż

a prawdopodobie

ń

stwo wyst

ą

pienia

uszkodzenia w ci

ą

gu jednostki czasu pracy w okre

ś

lonych warunkach

Statystyka matematyczna daje nam mo

ż

liwo

ść

wyznaczenia jedynie

estymatorów,

a jak jest warto

ść

rzeczywista nie wiemy

Estymator intensywno

ś

ci uszkodze

ń

- przedział ufno

ś

ci, który z okre

ś

lonym prawdopodobie

ń

stwem

β

zawiera warto

ść

rzeczywist

ą λ

β

λ

λ

λ

=

≤

≤

}

{

g

d

P

Wst

ę

p

3

β

λ

λ

λ

=

≤

≤

}

{

g

d

P

g

d

λ

λ

,

- dolna i górna granica przedziału ufno

ś

ci,

β

- poziom ufno

ś

ci, zwykle 0,6 lub 0,9

0,01

0,001

0,1 – 2

0,05

0,02

0,08 – 0,8

0,3

0,1

Poł

ą

czenia lutowane

Poł

ą

czenia owijane

Kondensatory

Rezystory obj

ę

to

ś

ciowe

Rezystory warstwowe

Tranzystory krzemowe

Mikroukłady analogowe

Mikroukłady cyfrowe

λ

[x 10

-6

1/h]

Rodzaj elementu

4

Podstawowe charakterystyki niezawodno

ś

ci

- liczbowe,
- funkcyjne.

Liczbowe

Obiekty nienaprawialne

FIT –

ś

redni czas pracy do uszkodzenia

→

uszkodzenie/10

9

godzin

/10

6

godzin

Failured in time

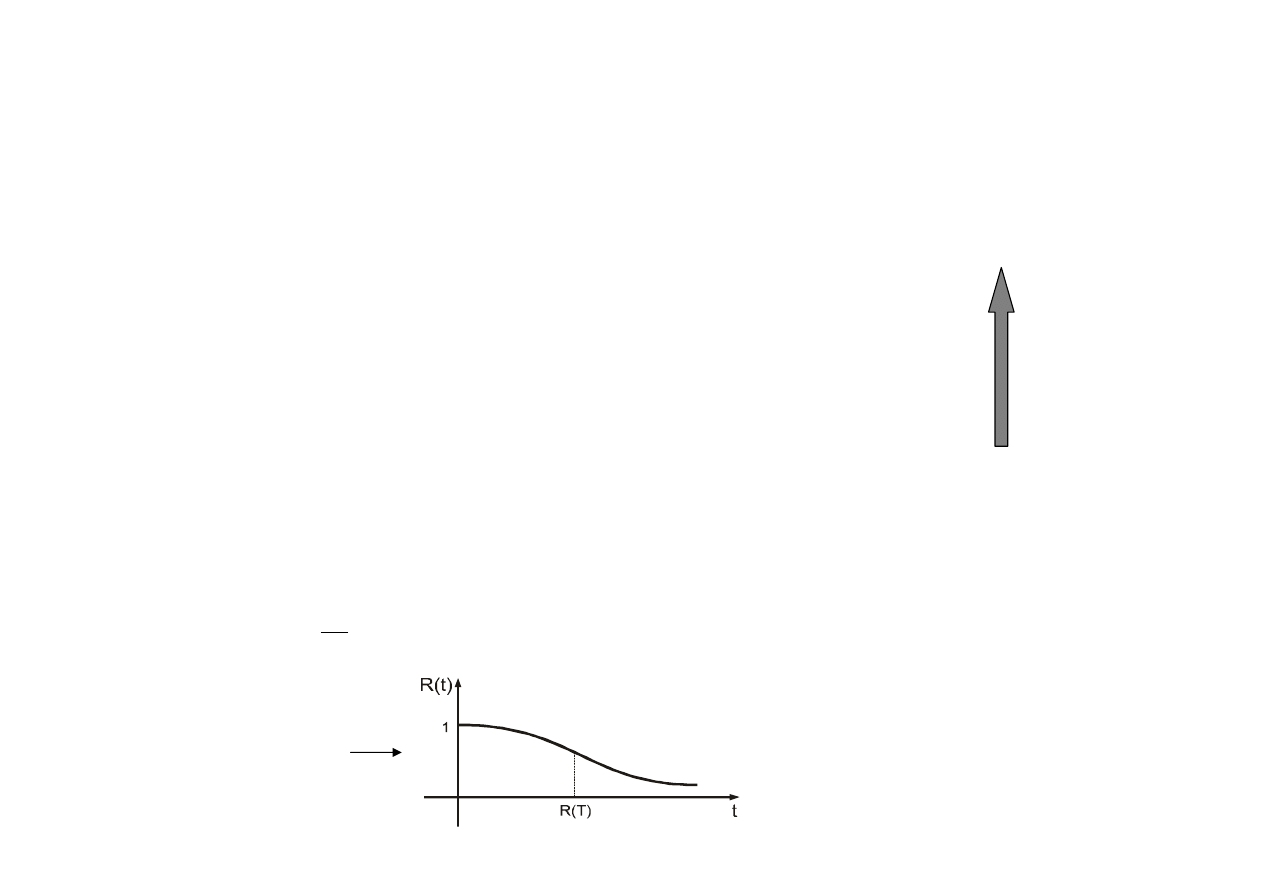
R (T) – niezawodno

ść

jako prawdopodobie

ń

stwo

n

m

T

R

=

)

(

m – liczba poprawnie pracuj

ą

cych wyrobów czasie T,

n – liczba wyrobów, które rozpocz

ę

ły prac

ę

w momencie t = 0

wykres

Reliability

10

6

godzin

41 666,6 dni
117,04 lat

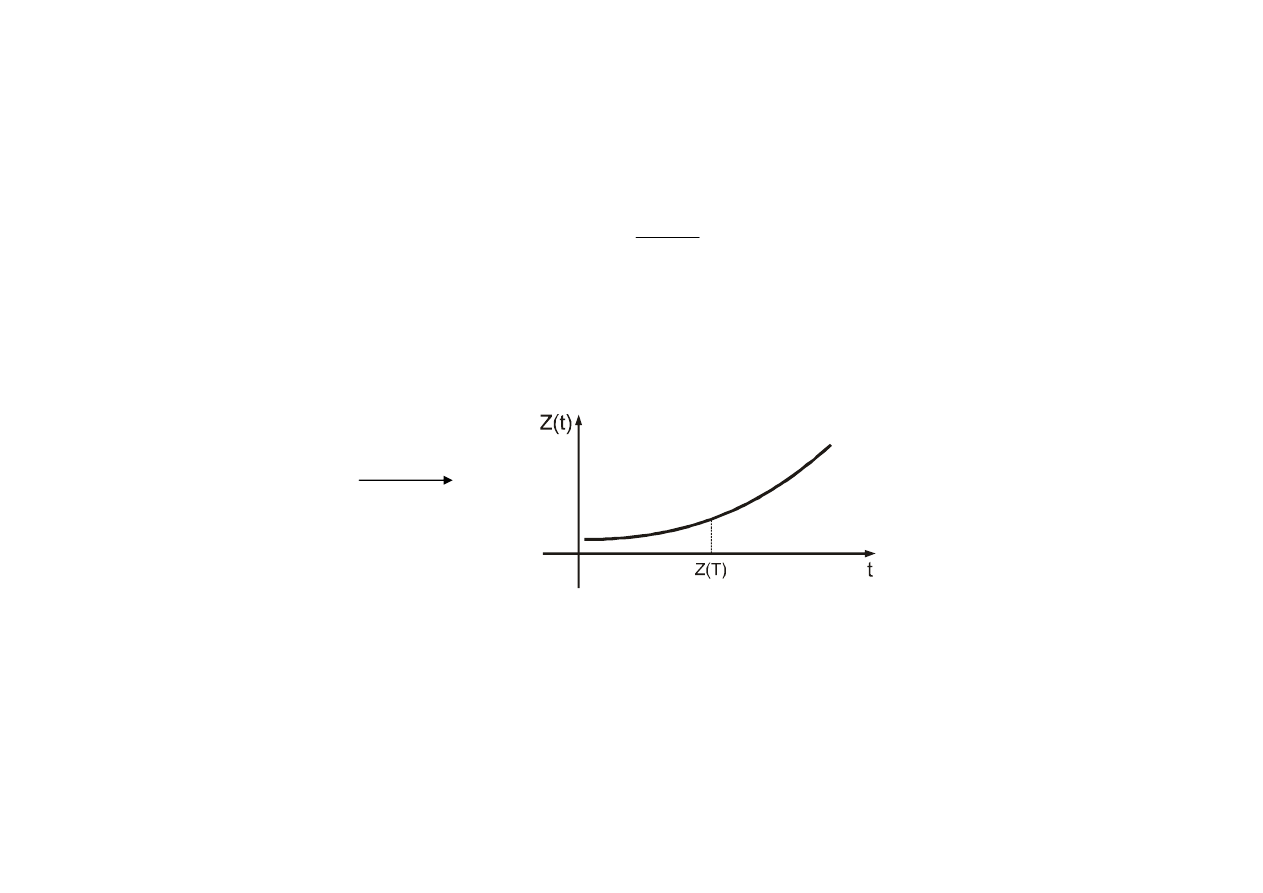
5

Z (T) – wska

ź

nik uszkodze

ń

n

m

n

T

Z

−

=

)

(

m – liczba poprawnie pracuj

ą

cych wyrobów czasie T,

n – liczba wyrobów, które rozpocz

ę

ły prac

ę

w momencie t = 0

wykres

Liczba uszkodze

ń

odniesiona do czasu

→

% uszkodze

ń

/10

6

godzin

/10

9

godzin

Failure rate

6

W normach podawane s

ą

Wadliwo

ść

dopuszczalna – AQL/1000 h

Liczba uszkodze

ń

, która mo

ż

e wyst

ą

pi

ć

po 1000 godzin

Accepted quality limit

Wadliwo

ść

dyskwalifikuj

ą

ca – LTPD/1000 h

Liczba uszkodze

ń

, która dyskwalifikuje oszacowany wska

ź

nik

Lot Tolerance Percent Defective

Badania kontrolne

Mil-S-19500
Mil-M-38510

7

Rzadziej stosowane wska

ź

niki

Ś

rednie ryzyko uszkodzenia w czasie eksploatacji

∑

=

=

n

i

i

t

n

1

*

1

µ

n - liczba obiektów,

t

i

* - czasy kolejnych uszkodze

ń

.

Wariancja i odchylenie standardowe

2

2

1

*

2

)

(

1

1

σ

σ

µ

σ

=

−

−

=

∑

=

n

i

i

t

n

8

Przykład

n = 10

132

116

107

101

84

63

48

41

36

33

t

i

*

10

9

8

7

6

5

4

3

2

1

i

37

1135

76

2

=

=

=

σ

σ

µ

9

Wska

ź

niki funkcyjne

- dystrybuanta czasu poprawnej pracy F (t),
- funkcja g

ę

sto

ś

ci uszkodze

ń

f (t),

- funkcja intensywno

ś

ci uszkodze

ń

– funkcja ryzyka

λ

(t),

- funkcja niezawodno

ś

ci R (t).

Dystrybuanta czasu poprawnej pracy F (t)

F (t) = P [t < t

1

]

uszkodzenie wyrobu nast

ą

pi

nie pó

ź

niej ni

ż

w chwili t

1

Funkcja g

ę

sto

ś

ci uszkodze

ń

f (t)

dt

t

dR

dt

t

dF

t

f

)

(

)

(

)

(

−

=

=

Funkcja niezawodno

ś

ci R (t)

R (t) = P [t

≥

t

1

]

uszkodzenie wyrobu nast

ą

pi

nie wcze

ś

niej ni

ż

w chwili t

1

R (t) = 1 – F (t)

okre

ś

la szybko

ść

zmian liczby uszkodzonych

wyrobów w obserwowanej populacji

10

Dystrybuanta i funkcja niezawodno

ś

ci mog

ą

by

ć

wyra

ż

one

przez funkcj

ę

g

ę

sto

ś

ci uszkodze

ń

∫

∫

∞

=

=

t

t

du

u

f

t

R

du

u

f

t

F

)

(

)

(

)

(

)

(

0

Prawdopodobie

ń

stwo,

ż

e wyrób uszkodzi si

ę

w przedziale [t, t +

∆

t]

wynosi f (t) ·

∆

t, przy zało

ż

eniu,

ż

e

∆

t jest małe

t

t

f

t

t

t

t

P

∆

⋅

≈

∆

+

≤

<

)

(

]

[

11

Funkcja intensywno

ś

ci uszkodze

ń

– funkcja ryzyka

λ

(t)

Pobieramy do bada

ń

prób

ę

reprezentatywn

ą

składaj

ą

c

ą

si

ę

z n wyrobów

Nale

ż

y znale

źć

prawdopodobie

ń

stwo zdarzenia,

ż

e wyrób, który pracował

od rozpocz

ę

cia bada

ń

(t = 0) uległ uszkodzeniu w przedziale czasu [t, t +

∆

t]

P [t,

∆

t]

Z definicji – prawdopodobie

ń

stwo jest stosunkiem liczby zdarze

ń

elementarnych

do ogólnej liczby zdarze

ń

Liczba zdarze

ń

elementarnych - n·f (t)·

∆

t

ka

ż

dy z wyrobów mo

ż

e ulec uszkodzeniu w przedziale [t, t +

∆

t]

Ogólna liczba zdarze

ń

elementarnych - n·R (t)

12

Wobec tego prawdopodobie

ń

stwo zdarzenia mo

ż

na zapisa

ć

jako:

t

t

R

t

f

t

R

n

t

t

f

n

t

t

P

∆

=

⋅

∆

⋅

⋅

=

∆

)

(

)

(

)

(

)

(

]

,

[

Funkcja intensywno

ś

ci uszkodze

ń

jest definiowana jako prawdopodobie

ń

stwo

zdarzenia losowego (uszkodzenia wyrobu) w przedziale czasu [t, t +

∆

t]

odniesione do czasu trwania przedziału

∆

t

)

(

)

(

)

(

)

(

]

,

[

)

(

t

R

t

f

t

t

t

R

t

f

t

t

t

P

t

=

∆

∆

=

∆

∆

=

λ

13

Zale

ż

no

ś

ci

dt

t

dR

dt

t

dF

t

f

)

(

)

(

)

(

−

=

=

)

(

)

(

)

(

t

R

t

f

t

=

λ

)

(

)

(

)

(

)

(

)

(

t

R

dt

t

dR

t

R

t

f

t

−

=

=

λ

dt

t

t

R

t

dR

)

(

)

(

)

(

λ

=

−

)

(

)

(

)

(

)

(

t

R

t

f

t

R

dt

t

dR

=

−

przy zało

ż

eniu,

ż

e R (0) = 1

]

)

(

exp[

)

(

0

∫

−

=

t

du

u

t

R

λ

14

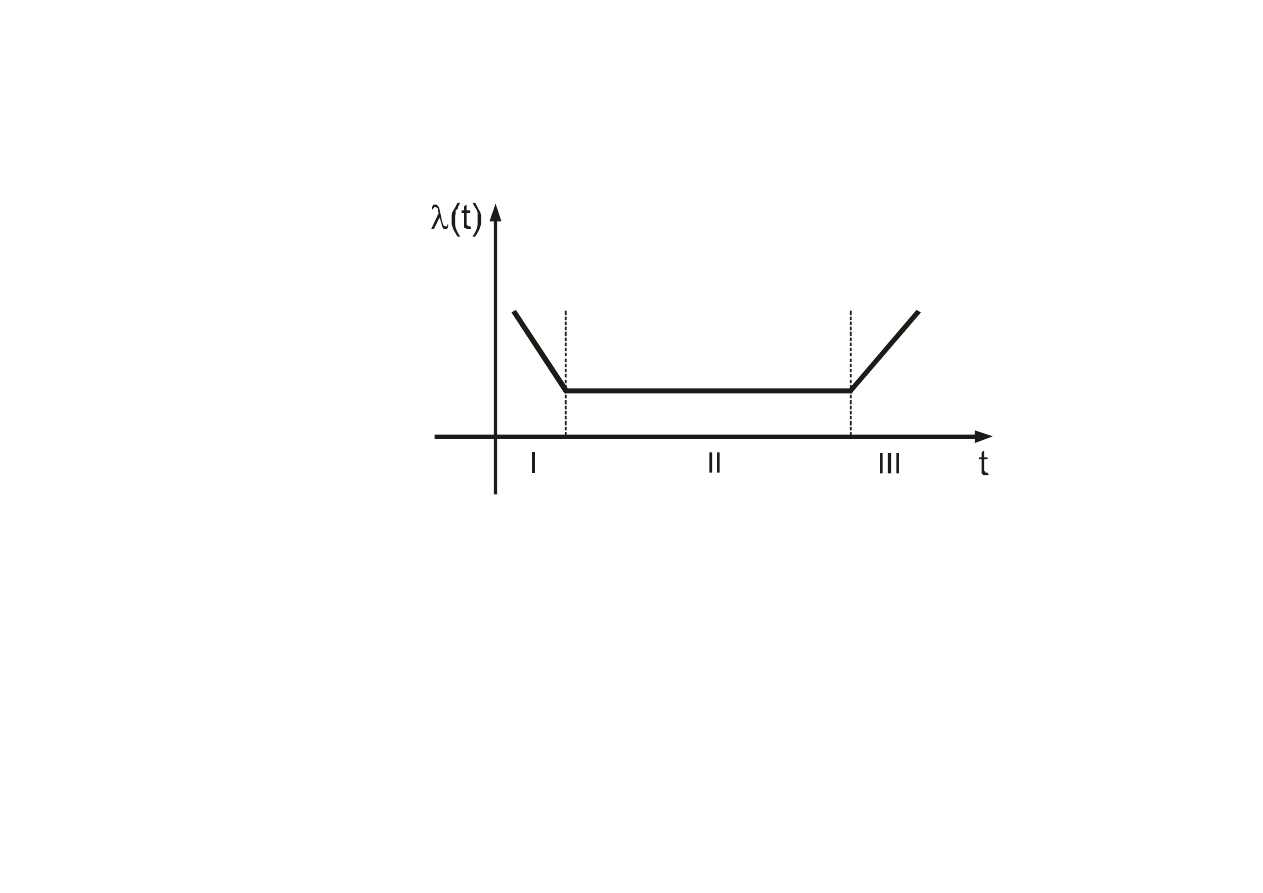
Okres

ż

ycia wyrobów (obiektów) nienaprawialnych

Krzywa „siodłowa”
Krzywa „wannowa”

Krzywa stosowana od lat 50. XX wieku –

na podstawie analizy czasu

ż

ycia

lamp elektronowych i pierwszych
maszyn cyfrowych

Trzy okresy

ż

ycia:

I – okres uszkodze

ń

wczesnych, uszkodzeniu ulegaj

ą

wyroby o złej jako

ś

ci, wadliwe,

II - okres normalnej eksploatacji, liczba uszkodze

ń

jest stała, uszkodzenia s

ą

przypadkowe, wynikaj

ą

ce z przeci

ąż

e

ń

, niepoprawnych warunków pracy,

III – okres zu

ż

ycia

15

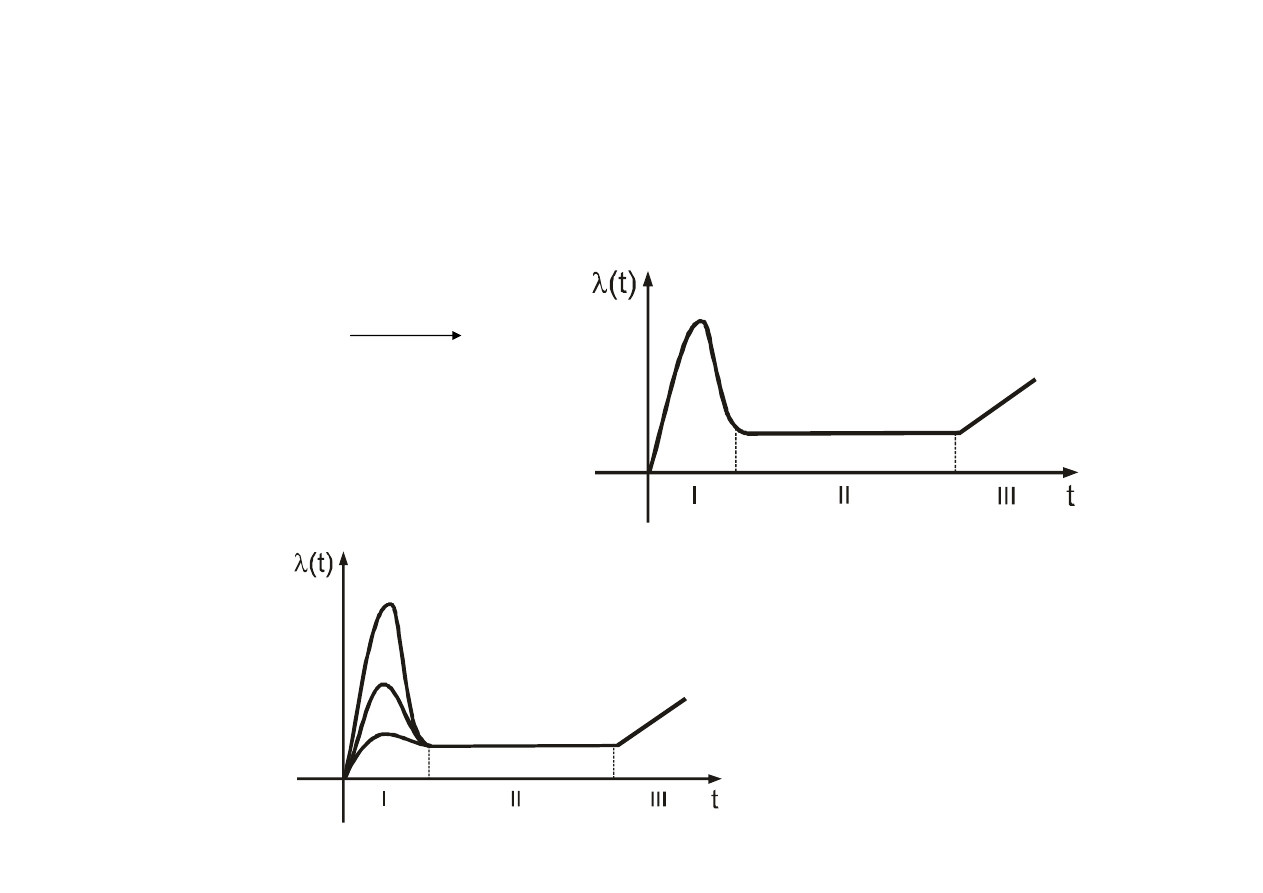
Obecnie wzorem okre

ś

laj

ą

cym przebieg funkcji ryzyka jest krzywa „grzbietowa”

Podział jest podobny, ale okres uszkodze

ń

wczesnych mo

ż

e mie

ć

ró

ż

ny przebieg

wykres

16

Charakterystyki obiektów naprawialnych (odnawialnych)

1. Obiekty z pomijalnym czasem odnowy
2. Obiekty z istotnym czasem odnowy

1. Obiekty z pomijalnym czasem odnowy

Liczbowe

Ś

redni czas pracy mi

ę

dzy uszkodzeniami (w okre

ś

lonym czasie T)

MTBF

Mean Time between Failure

Ś

redni czas pracy do uszkodze

ń

(w okre

ś

lonym czasie T)

MTTF

Mean Time to Failure

m

t

t

t

MTTF

m

+

+

+

=

...

2

1

gdzie: m – liczba uszkodze

ń

w czasie T,

t

i

- i - ty czas do uszkodzenia

17

MTBF

Ś

redni czas mi

ę

dzyawaryjny

Przykład

Zastosowanie do okre

ś

lenia

ż

ywotno

ś

ci twardych dysków

MTBF wynosi 200 000 godzin – okre

ś

lony dla danej serii dysków

MTBF – 200 tysi

ę

cy godzin, czyli prawdopodobie

ń

stwo uszkodzenia dysku

w ci

ą

gu roku jest równe około 4,5%

200 000 godzin: 24 = 8333.3 dni : 356 = 23,4 lat

23,4 – 100%

1 - 4,27%

Mamy 22 dyski – 1 dysk w ci

ą

gu roku mo

ż

e ulec uszkodzeniu, - pracuje 24 godziny

Je

ż

eli pracuje mniej, to ….

18

2. Obiekty z istotnym czasem odnowy

Współczynnik gotowo

ś

ci technicznej (dyspozycyjno

ś

ci)

MRT

MTBF

MTBF

t

k

k

g

t

g

+

=

=

∞

→

)

(

lim

gdzie: MRT –

ś

redni czas napraw

Mean Repair Time

k – prawdopodobie

ń

stwo,

ż

e w danej chwili t wyrób (obiekt)

b

ę

dzie zdatny do pracy,

t

i

– i –ty czas do uszkodzenia, czyli zmienna losowa t

19

Funkcyjne

Charakterystyka niezawodno

ś

ci wyrobów (obiektów) odnawialnych

– funkcja odnowy H (t)

Definiowana jest jako oczekiwana liczba m odnów wyrobu (obiektu) od momentu

rozpocz

ę

cia jego pracy do chwili t

G

ę

sto

ść

odnowy

Λ

(t) – szybko

ść

narastania liczby dokonywanych odnów

z upływem czasu pracy t

dt

t

dH

t

)

(

)

(

=

Λ

Zwi

ą

zek mi

ę

dzy H (t) i

Λ

(t) mo

ż

na zapisa

ć

:

∫

Λ

=

t

du

u

t

H

0

)

(

)

(

20

Charakterystyki niezawodno

ś

ciowe wyrobów (obiektów) pracuj

ą

cych na

żą

danie

Wyroby pracuj

ą

ce na

żą

danie:

- nieodnawialne,
- odnawialne.

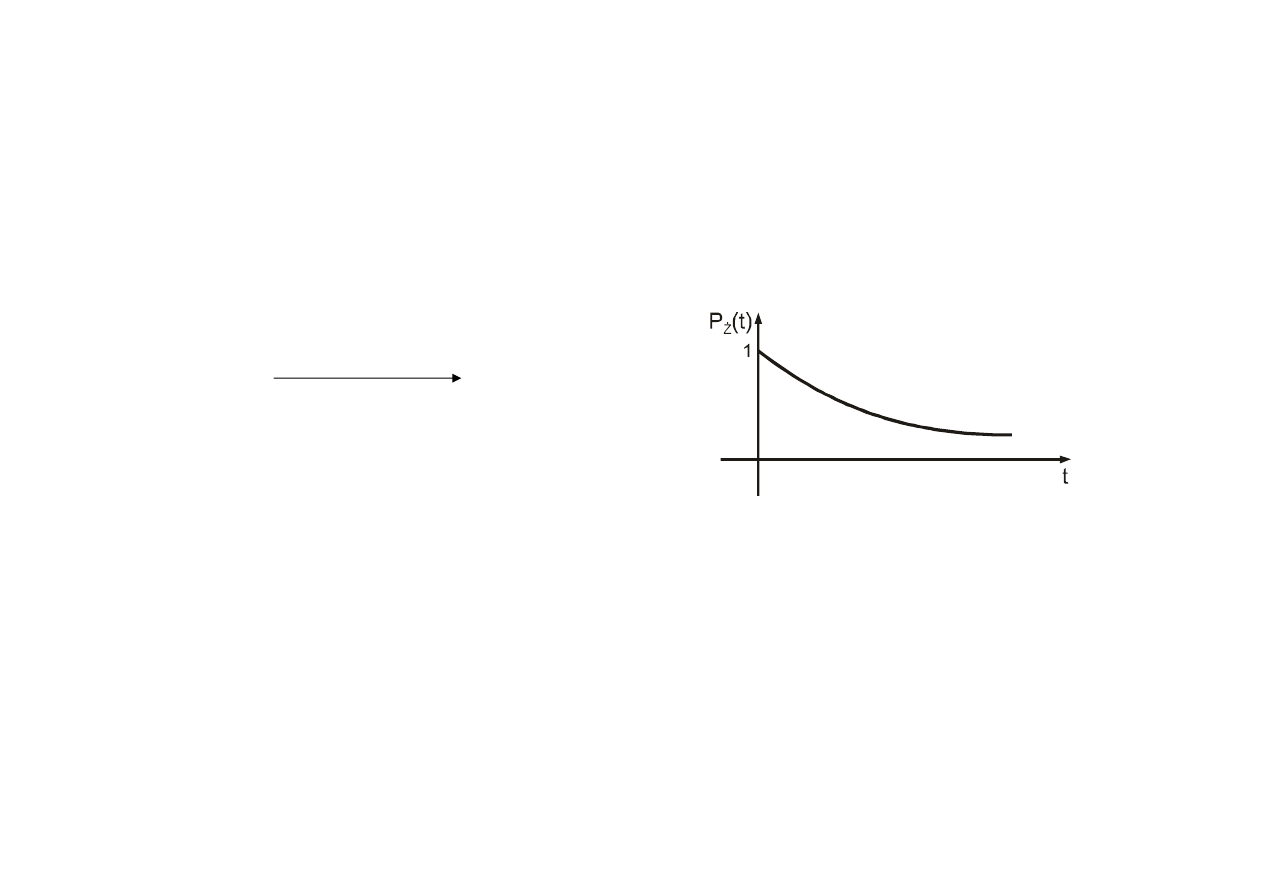
Wyroby nieodnawialne

wykres

P

ż

(t) jest zwykle funkcj

ą

monotonicznie malej

ą

c

ą

, bo w wyrobie (obiekcie) zachodz

ą

zmiany zwi

ą

zane z procesami starzenia, nawet je

ż

eli wyrób nie pracuje.

P

ż

(t) wyrobu (obiektu) odnawialnego jest funkcj

ą

okresow

ą

. Dzi

ę

ki naprawom

uszkodzenia s

ą

usuwane, a wi

ę

c i procesy starzenia nie wyst

ę

puj

ą

w sposób oczywisty.

P

ż

(t) – prawdopodobie

ń

stwo pracy na

żą

danie

21

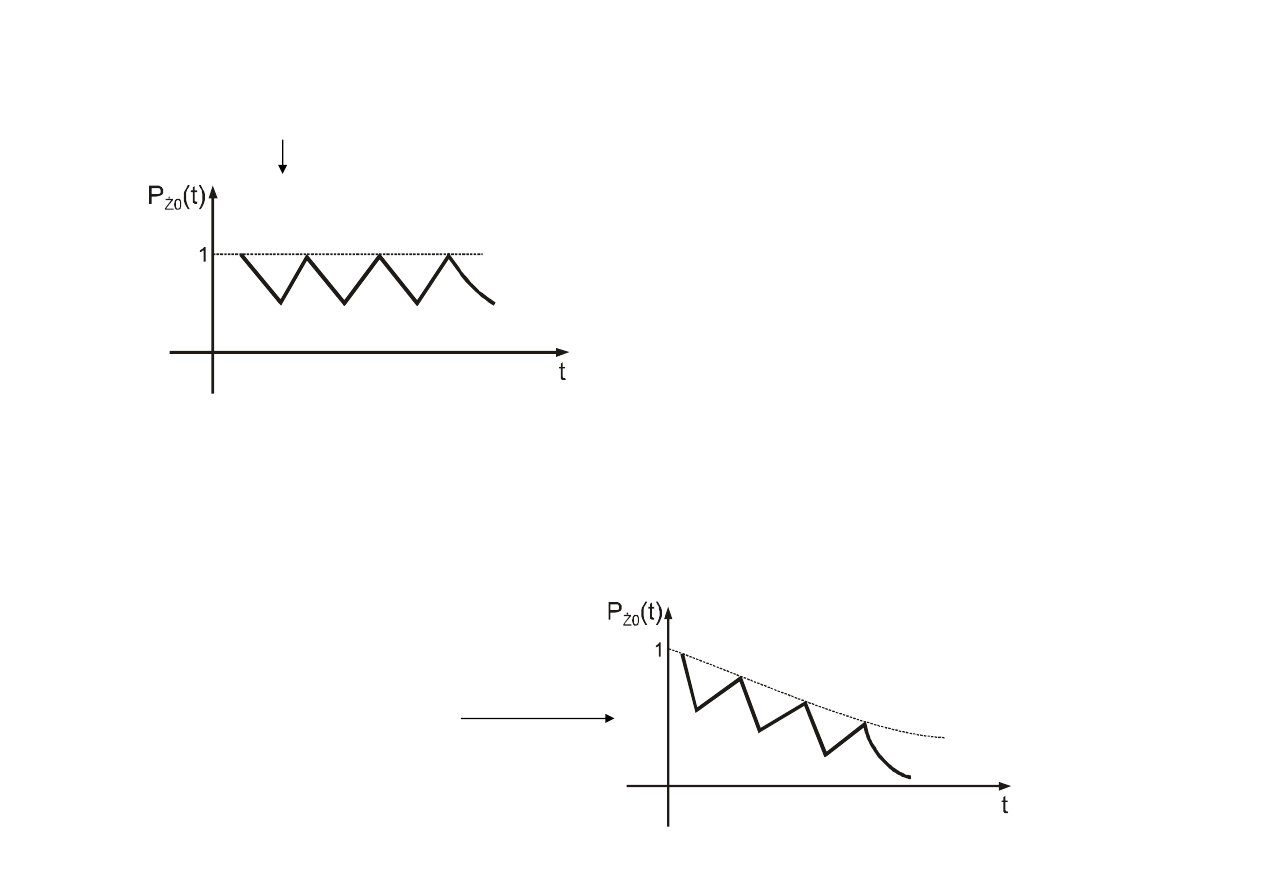
W rzeczywisto

ś

ci efekty starzenia mimo napraw te

ż

wyst

ę

puj

ą

i funkcja P

ż

o

(t)

jest funkcj

ą

okresow

ą

, malej

ą

c

ą

.

Wyroby odnawialne

wykres

Odnowa usuwa skutki uszkodzenia i P

ż

o

(t) po

odnowie = 1,

P

ż

o

(t) wyrobu (obiektu) odnawialnego jest funkcj

ą

okresow

ą

. Dzi

ę

ki naprawom

uszkodzenia s

ą

usuwane, a wi

ę

c i procesy starzenia nie wyst

ę

puj

ą

w sposób oczywisty.

wykres

P

ż

o

(t) – prawdopodobie

ń

stwo odmowy pracy