
MINIMALIZACJA FUNKCJI LOGICZNYCH
Funkcja logiczna może być w ogólnym przypadku przedstawiona za pomocą
wielu różnych mniej lub bardziej skomplikowanych funkcji logicznych.
Zagadnienie minimalizacji polega na wyznaczeniu dla danej funkcji tej formuły
która jest najprostsza. Zagadnienie to formułuje się też inaczej – dla danej
funkcji logicznej należy wyznaczyć możliwą najprostszą funkcję równoważną.
Minimalizacja funkcji logicznej wiąże się z porównaniem stopnia
skomplikowania funkcji. Dla porównania funkcji wprowadza się pojęcie
współczynnika skomplikowania definiowanego w rożny sposób. Jedna z
możliwych definicji współczynnika skomplikowania brzmi:
Współczynnikiem skomplikowania W funkcji logicznej i (and), lub (or),
nie (not) nazywamy sumę liczby wyrażeń (pojedynczych liter lub ich
kombinacji) podlegających mnożeniu i liczby wyrażeń podlegających
dodawaniu.
Metody minimalizacji funkcji logicznych można podzielić na dwie grupy.
Do pierwszej grupy należą metody przekształceń algebraicznych. Metody te nie
są zbyt przydatne w praktyce. Do drugiej grupy należą metody algorytmiczne.
Metoda Quine’a McCluskeya
Algorytm wprowadzimy rozważając następujący przykład.
Wyznaczyć minimalną funkcję logiczną równoważną funkcji:
F
1
=
x
1
x
2
x
3
x
+ x
1
x
2
x
3
x
4
+ x
1
x
2
x
3
x
4
+ x
1
x
2
x
3
x
4
+ x
1
x
2
x
3
x
4
+ x
1
x
2
x
3
x
4
+ x
1
x
2
x
3
x
4
+
+ x
1
x
2
x
3
x
4
1. Wypisujemy kombinacje zer i jedynek odpowiadające kolejnym pełnym
iloczynom. Iloczynom tym przyporządkowujemy numery w sposób analogiczny
do przyjętego poprzednio.
2 0010
3 0011
6 0110
7 0111
12 1100
13 1101
14 1110
15 1111
2. Szeregujemy te kombinacje według liczby jedynek. Otrzymujemy w ten
sposób grupy n = 0, 1, 2 ... jedynek
1
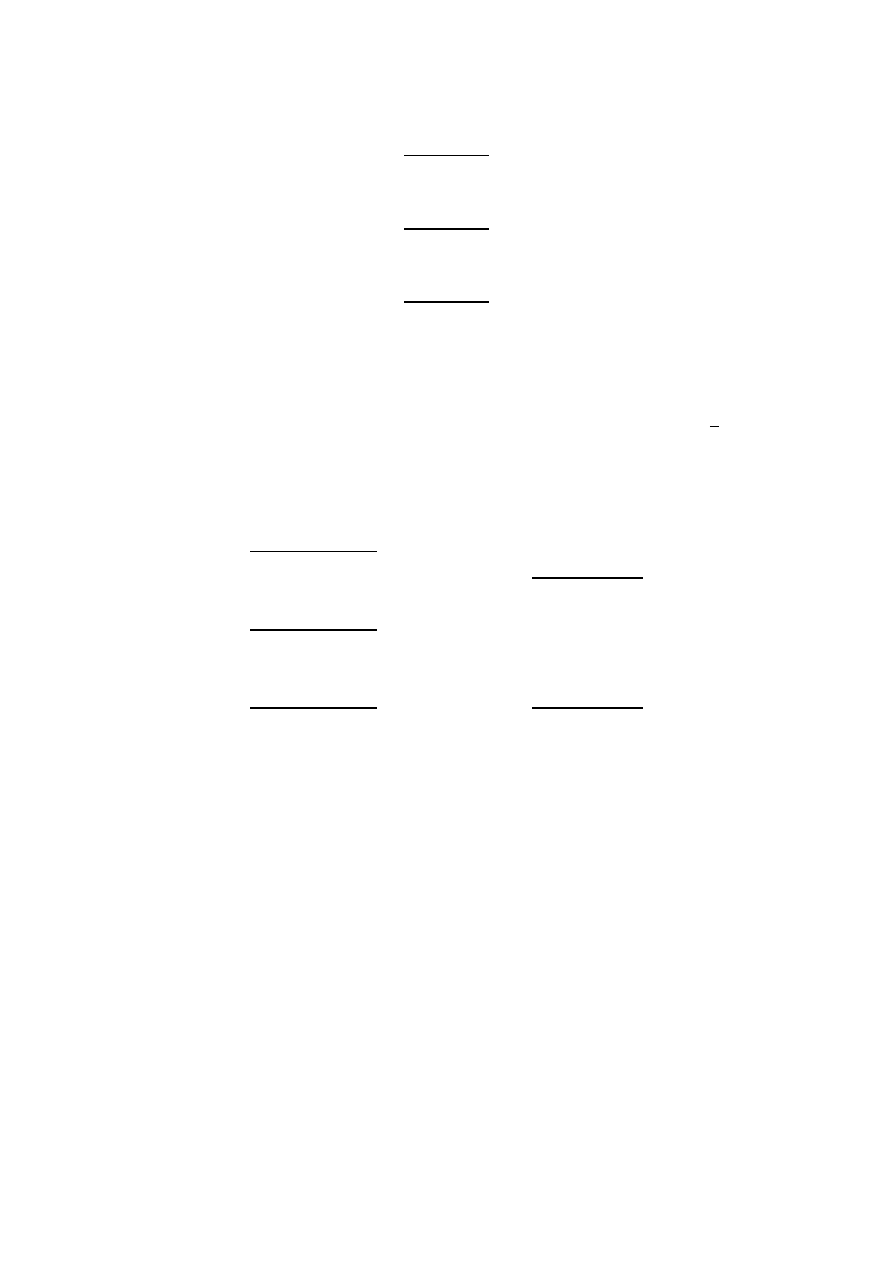
2 0010
3 0011
6 0110
12 1100
7 0111
13 1101
14 1110
15 1111
3. Porównujemy każdą kombinację należącą do grupy i-tej z każdą kombinacją
należącą do grupy i + 1. Jeżeli dwie takie kombinacje różnią się tylko na jednej
pozycji to kombinacje te sklejamy w jedną nową kombinację zastępując pozycje
różniące się symbolem
φ
. Wykorzystujemy tu związek xy
+
x
y
=x. W
poprzedniej tablicy odznaczamy (
∨
) kombinacje używane przy dokonywaniu
sklejeń i tworzymy nową tabelę.
2 0010
∨
2,3 001
φ
3 0011
∨
2,6 0
φ
10
6 0110
∨
3,7 0
φ
11
12 1100
∨
6,7 011
φ
7 0111
∨
6,14
φ
110
13 1101
∨
12,13 110
φ
14 1110
∨
12,14 11
φ
0
15 1111
∨
7,15
φ
111
13,15 11
φ
1
14,15 111
φ
4. Kontynuujemy procedurę usuwając kombinacje powtarzające się i łącząc
kombinacje różniące się na jednej pozycji
5. Procedurę kończymy, gdy nie ma już możliwości dokonania dalszych sklejeń.
W rozważanym przykładzie otrzymujemy ostatecznie:
2, 3, 6, 7, 0
φ
1
φ
6, 7, 14, 15,
φ
11
φ
12, 13, 14, 15, 11
φφ
W tabeli pomijamy zestawy numerów nie prowadzących do nowych kombinacji
– np. 2, 6, 3, 7 w stosunku do uwzględnionego 2, 3, 6, 7.
2

6. Tworzymy zbiór kombinacji nie mogących podlegać dalszemu sklejaniu. Do
zbioru tego należą te kombinacje, które znalazły się w tablicy końcowej oraz te,
które nie mogły być zastosowane do dalszego sklejania.
Punkt 6 kończy pierwszą część minimalizacji. Do jej kontynuowania
potrzebna jest następująca definicja:
Formułę G nazywamy implikantem formuły F, gdy (G
→
F) =1 albo
G
+ F=1
Oznacza to, że jeżeli G = 1, to F = 1, ale nie musi być odwrotnie. Implikantami
formuły kanonicznej sumy są więc wszystkie iloczyny pełne i wszystkie ich
połączenia typu x
1
x
2
x
3
+ x
1
x
2
x
3
= x
1
x
2
.
Formułę G
1
nazywamy prostym implikantem formuły F, gdy G
1
jest
implikantem formuły F oraz gdy nie istnieje formuła G
2
taka, że
(G
1
→
G
2
) = 1 oraz (G
2
→
F) = 1
Prostymi implikantami są więc wszystkie iloczyny, których kombinacje zer i
jedynek należą do zbioru otrzymanego w p. 6. Dla formuły x
1
x
2
x
3
+ x
1
x
2
x
3
+
+
x
1
x
2
x
3
wszystkie trzy iloczyny pełne są implikantami, a iloczyny x
1
x
2,
x
1
x
2
x
3
są prostymi implikantami. Można więc powiedzieć, że prostym implikantem jest
taki implikant, który nie może być połączony z żadnym innym implikantem bez
utraty swojej podstawowej własności.
Pojęcie implikantu sformułowane dla wyrażeń może być także odniesione
do funkcji tym wyrażeniom odpowiadającym. Niech wyrażeniom logicznym F i
G odpowiadają funkcje f
1
i g
1
. G jest wtedy implikantem F, jeżeli g
1
⊆
f
1
, czyli
zbiór jedynek G zawiera się w zbiorze jedynek F.
Poszukiwana formuła minimalna F
2
równoważna formule początkowej F
1
może być otrzymana w postaci sumy wyselekcjonowanych implikantów
prostych. Selekcji dokonuje się w taki sposób, aby wszystkie pełne iloczyny
występujące w formule F
1
były reprezentowane w wybranych implikantach
prostych; liczba wybranych implikantów powinna być jak najmniejsza. Jeżeli
istnieje kilka takich zestawów implikantów prostych, wybieramy ten, w którym
występuje najmniejsza łączna liczba liter.
Zagadnienie selekcji wyjaśnimy na podanym przykładzie.
Proste implikanty rozważanej formuły możemy zapisać w sposób
następujący:
x
1
x
3
= G
1
(2,3,6,7);
x
2
x
3
= G
2
(6,7,14,15);
3
x
1
x
2
= G
3
(12,13,14,15)
Oznacza to, że np. implikant x
1,
x
3
powstał w wyniku połączenia pełnych
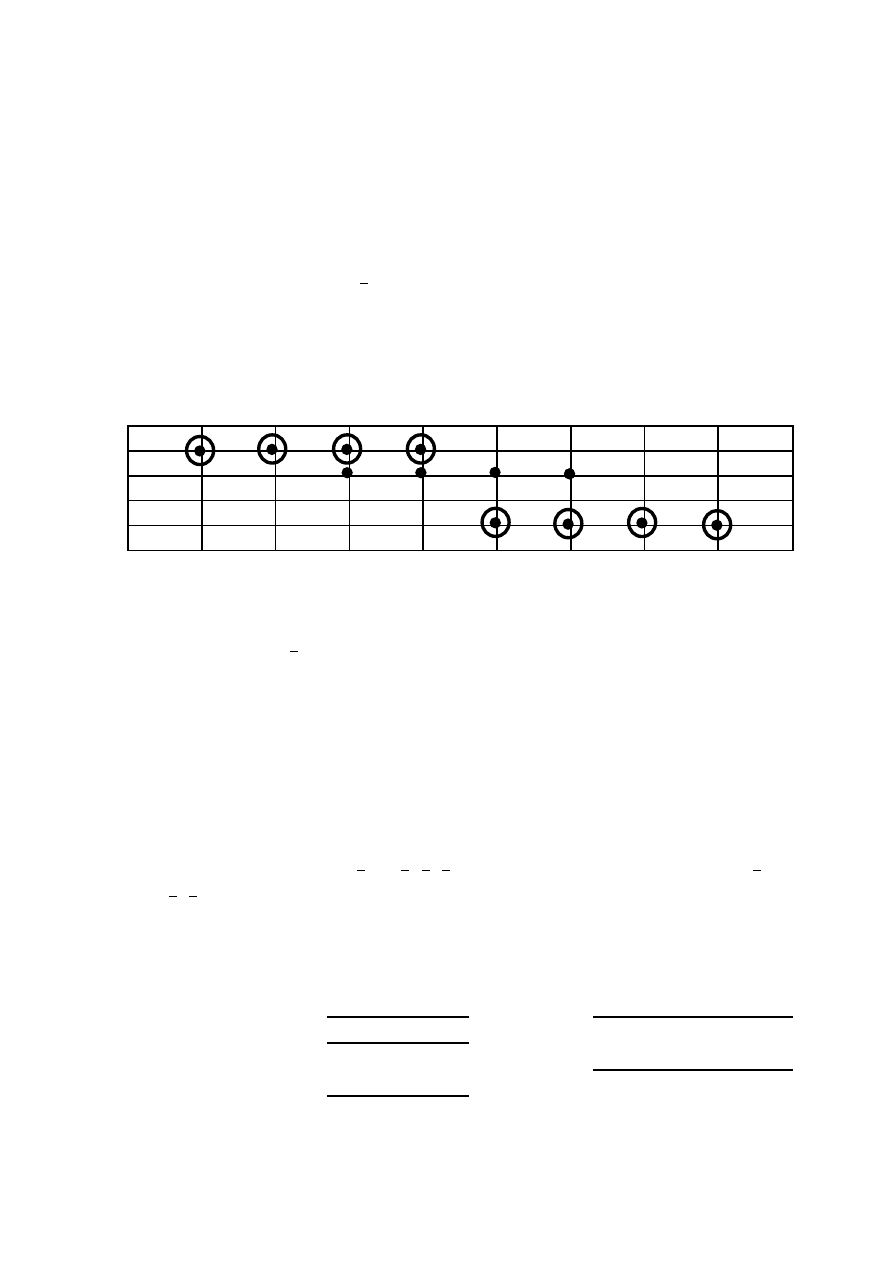
iloczynów o indeksach 2, 3, 6, 7. Selekcję wykonujemy, korzystając z tablicy
implikantów prostych.
x
1
x
3
2, 3, 6, 7
x
2
x
3
6, 7, 14, 15
x
1
x
2
12, 13, 14, 15
2
3 6
7
12
13
14
15
Wybieramy taki zestaw implikantów, aby w każdej kolumnie występował co
najmniej jeden znaczek selekcji (kółeczko) i aby liczba wybranych
implikantów była jak najmniejsza. W rozważanym przykładzie mamy
ostatecznie F
2
=
x
1
x
3
+ x
1
x
2
. Współczynnik skomplikowania dla F
1
i F
2
wynoszą odpowiednio 12 i 6.
Jeżeli funkcja, której formuła podlega redukcji nie jest określona dla
pewnych wyrazów n-tych danej funkcji, to odpowiednie iloczyny kanoniczne
są stosowane w procesie wyznaczania implikantów prostych, ale nie
występują w tablicy implikantów przeznaczonej do selekcji. Przykład:
Należy wyznaczyć formułę minimalną, która będzie równoważna
formule: F
1
= x
1
x
2
x
3
+ x
1
x
2
x
3
+
x
1
x
2
x
3
z dodatkowymi warunkami x
1
x
2
x
3
= x
1
x
2
x
3
= 0
Proces minimalizacji:
0 000
0 000
∨
0, 4
φ
00
x4 100
x4 100
∨
4, 5
10
φ ∨
x5 101
x5 101
∨
4, 6
1
φ
0
∨
6 110
6 110
∨
5, 7
1
φ
1
∨
7 111
7 111
∨
6, 7
11
φ ∨
4
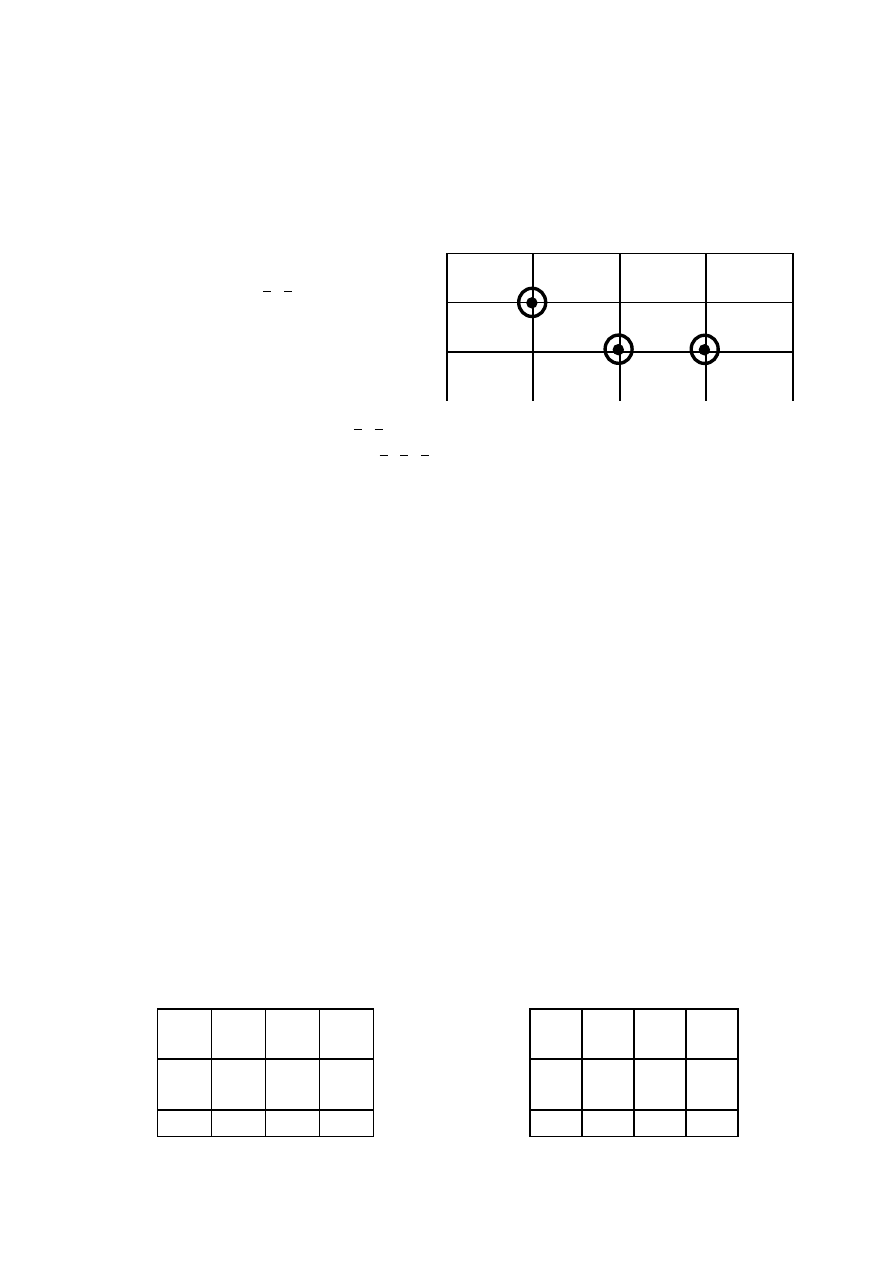
4, 5, 6, 7, 1
φφ
0
6
7
x
2
x
3
0,4
x
1
4, 5, 6, 7
Otrzymujemy F
2
= x
1
+
x
2
x
3
. Formule F
1
bez warunków dodatkowych
odpowiada formuła F
3
= x
1
x
2
+
x
1
x
2
x
3
Współczynniki skomplikowania dla F
1
,
F
2
, F
3
wynoszą odpowiednio 12, 5, 7.
Rozważana metoda w podanej postaci nadaje się do minimalizacji formuł
przedstawionych w postaci sumy pełnych iloczynów (formuł kanonicznych
sumy).
Minimalizacja formuł przedstawionych w postaci iloczynów pełnych sum
kanonicznych (formuł kanonicznych iloczynu) można dokonać przez przejście
od danej postaci iloczynu do jej negacji (postaci sumy); formuła ta jest
minimalizowana w podany sposób a następnie znowu wyznaczana jest negacja.
Metoda Veitcha-Karnaugh
Metoda Veitcha-Karnaugha polega na zastosowaniu tzw. diagramów Veitcha
lub tablic Karnaugha. Tablica taka – kwadratowa lub prostokątna – dla m
zmiennych składa się z 2
m
ponumerowanych kratek. W każdej kratce jest
wpisany numer kombinacji odpowiadający kratce (np. w prawym, dolnym rogu)
oraz wartość funkcji 0, 1 albo symbol – lub x, jeżeli wartość funkcji jest
nieokreślona.
Przykład przedstawienia funkcji czterech zmiennych za pomocą tablic
Karnaugha:
Funkcja zupełna funkcja niezupełna
00
01
11
10 x
3
x
4
00
01
11
10
x
3
x
4
00
0
0
1
1
0
3
0
2
00
0
0
1
1
3
0
2
01
0
4
0
5
1
7
0
6
01
4
5
1
7
0
6
11
0
1
1
1
11
1
1
1
5
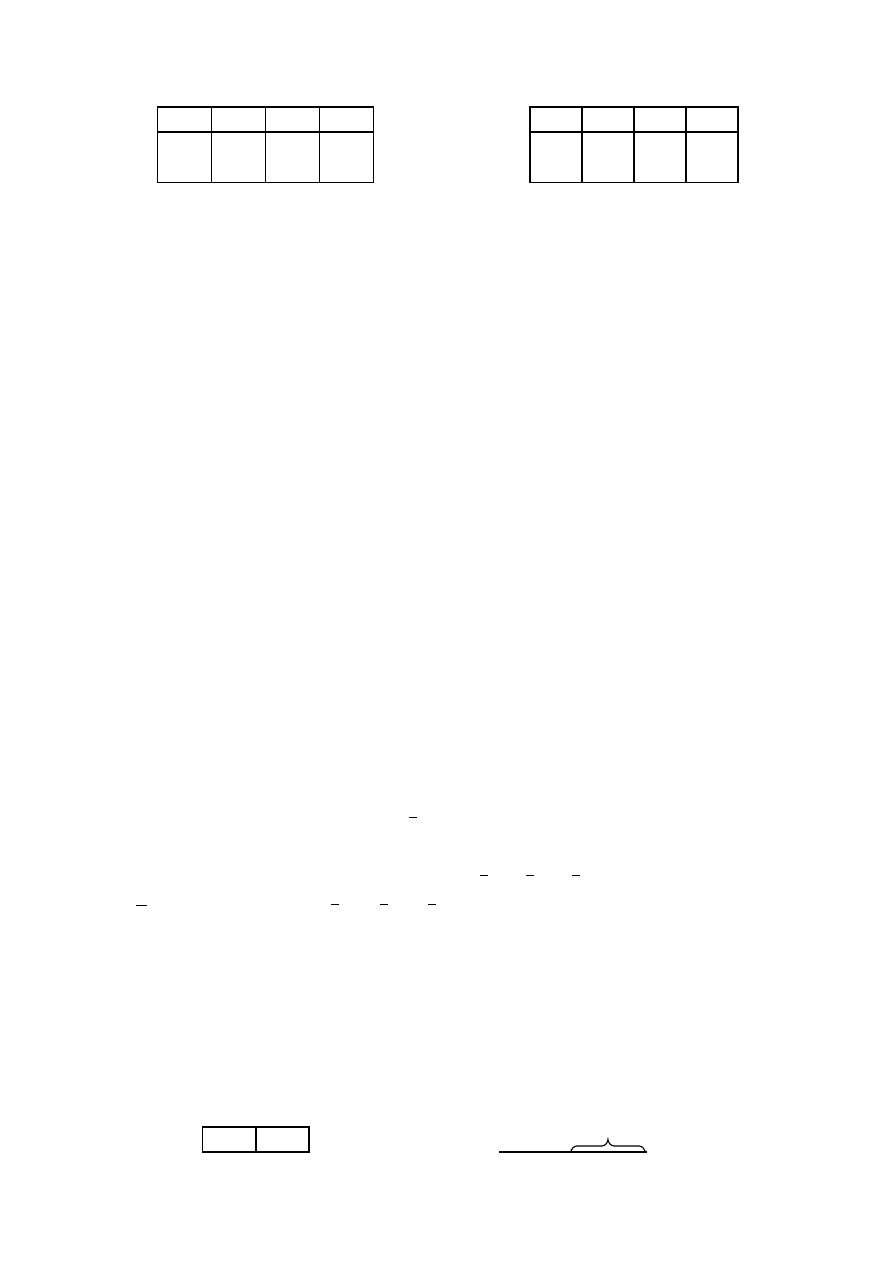
12
13
15
14
12
13
15
14
10
0
8
0
9
1
11
0
10
10
8
0
9
11
0
10
x
1
x
2
x
1
x
2
Każda kratka tablicy Karnaugha odpowiada kombinacji (wektorowi) zmiennych.
Można więc powiedzieć że kombinacja tych zmiennych tworzy adres kratki.
Kratki są ponumerowane, przy czym jak już pokazano numer (i) jest liczbą
dziesiętną odpowiadającą kombinacji zmiennych (wektorowi
zerojedynkowemu) traktowanej jako liczba dwójkowa. W poszczególnych
kratkach są wpisane – obok numerów – wartości funkcji (tj. 0 lub 1)
przyjmowane przez funkcję dla tej kombinacji, symbol – lub x, jeżeli funkcja
nie jest określona. Można też powiedzieć, że kratka o numerze i zawierająca 1
odpowiada iloczynowi pełnemu P
i
w kanonicznej postaci sumy dla danej
funkcji. Natomiast kratka o numerze i zawierająca 0 odpowiada sumie pełnej S
i
w kanonicznej postaci iloczynu.
Diagram Veitcha jest tworem analogicznym do tablicy Karnaugha; różni
się sposobem opisu tablicy. Można powiedzieć, że tablica Karnaugha ma opis
analityczny, a diagram Veitcha ma opis rysunkowy.
Zasada tworzenia diagramu Veitcha:
1) sumie wszystkich pełnych iloczynów (równej jedności) albo iloczynowi
wszystkich pełnych sum (równej zeru) odpowiada powierzchnia całego
kwadratu (prostokąta);
2) każdej zmiennej odpowiada połowa powierzchni kwadratu; druga połowa
odpowiada tej zmiennej zanegowanej; powierzchnie odpowiadające
dwom różnym zmiennym nie mogą być identyczne;
3) każdemu iloczynowi P
j
odpowiada kratka (mały kwadrat) stanowiący
wspólną powierzchnię powierzchni odpowiadających zmiennym (prostym
lub zanegowanym), które występują w tym iloczynie; ta sama kratka
odpowiada sumie S
j
.
Dla przykładu iloczynowi x
1
x
2
x
3
= P
6
dla trzech zmiennych odpowiada
kratka stanowiąca wspólną część „połowy x
1
”, „połowy x
2
” i „połowy nie x
3
”;
ta sama kratka odpowiada pełnej sumie
x
1
+
x
2
+
x
3
= S
6
(oczywiście S
6
=
P
6
). Inaczej - sumie
x
1
+
x
2
+
x
3
odpowiada kratka stanowiąca wspólną
część „połowy x
1
”, „połowy x
2
” i „połowy nie x
3
”; należy tu zwrócić uwagę
na odmienną konwencję przy przyporządkowywaniu kratek
odpowiadających pełnym sumom.
Tablice Karnaugha i diagramy Veitcha dla:
- dwóch zmiennych
Tablice Karnaugha
Diagramy Veitcha
x
2
0
1
x
2
6
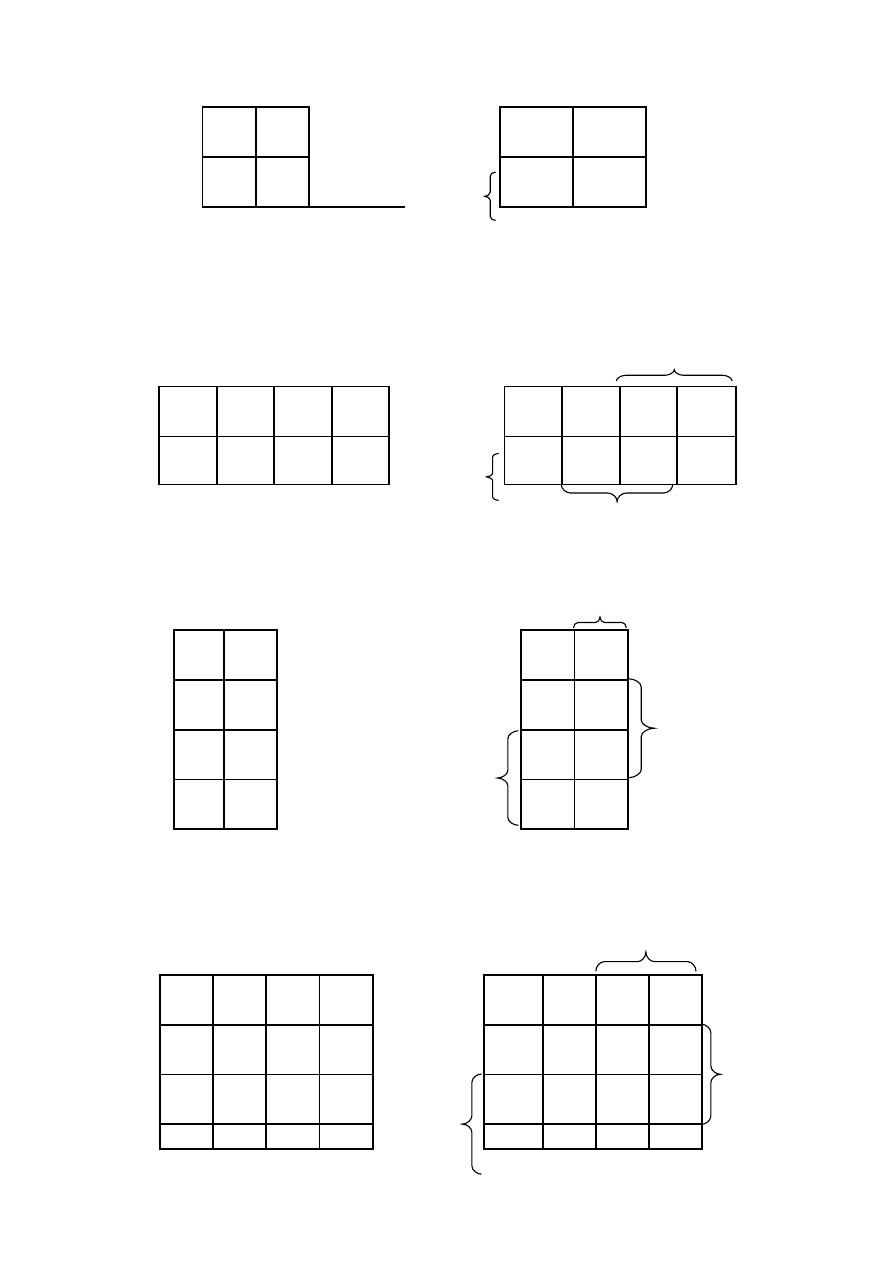
0
0
1
0
1
1
2
3
x
1
2
3
x
1
- trzech zmiennych
Tablice Karnaugha
Diagramy Veitcha
x
2
00
01
11
10
x
2
x
3
0
0
1
3
2
0
1
3
2
1
4
5
7
6
x
1
4
5
7
6
x
1
x
3
Inny wariant
x
3
0
1
x
3
00
0
1
0
1
01
2
3
2
3
x
2
11
6
7
6
7
x
1
10
4
5
4
5
x
1
x
2
- czterech zmiennych
x
3
00
01
11
10
x
2
x
3
00
0
1
3
2
0
1
3
2
01
4
5
7
6
4
5
7
6
x
2
11 12
13
15
14
12
13
15
14
x
1
10
8
9
11
10
8
9
11
10
7
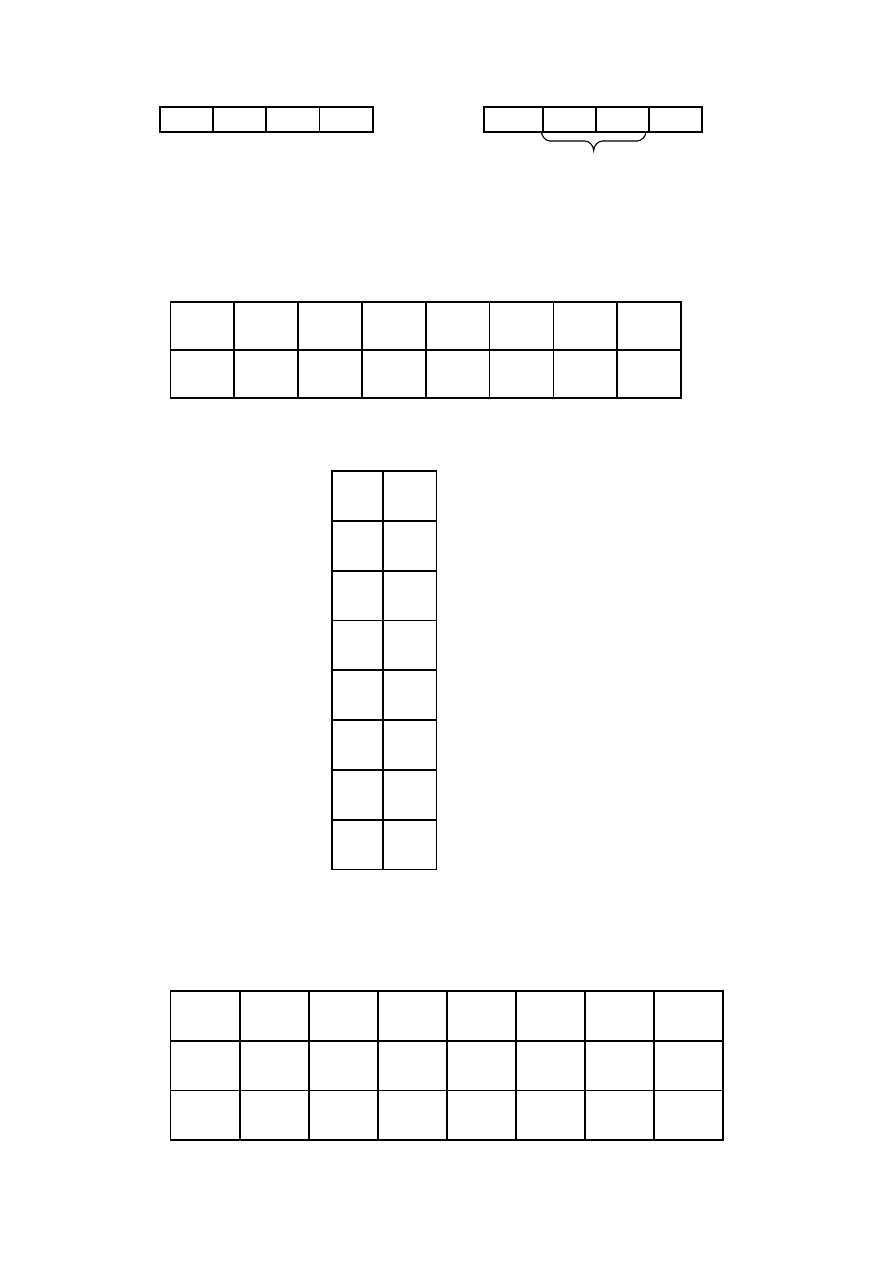
x
1
x
2
x
4
Inny wariant
000
001
011
010
110
111
101
100
x
2
x
3
x
4
0
0
1
3
2
6
7
5
4
1
8
9
11
10
14
15
13
12
x
1
0
1
x
4
000
0
1
001
2
3
011
6
7
010
4
5
110 12
13
111 14
15
101 10
11
100
8
9
x
1
x
2
x
3
- pięciu zmiennych
000
001
011
010
110
111
101
100
x
3
x
4
x
5
00
0
1
3
2
6
7
5
4
01
8
9
11
10
14
15
13
12
11
24
25
27
26
30
31
29
28
8
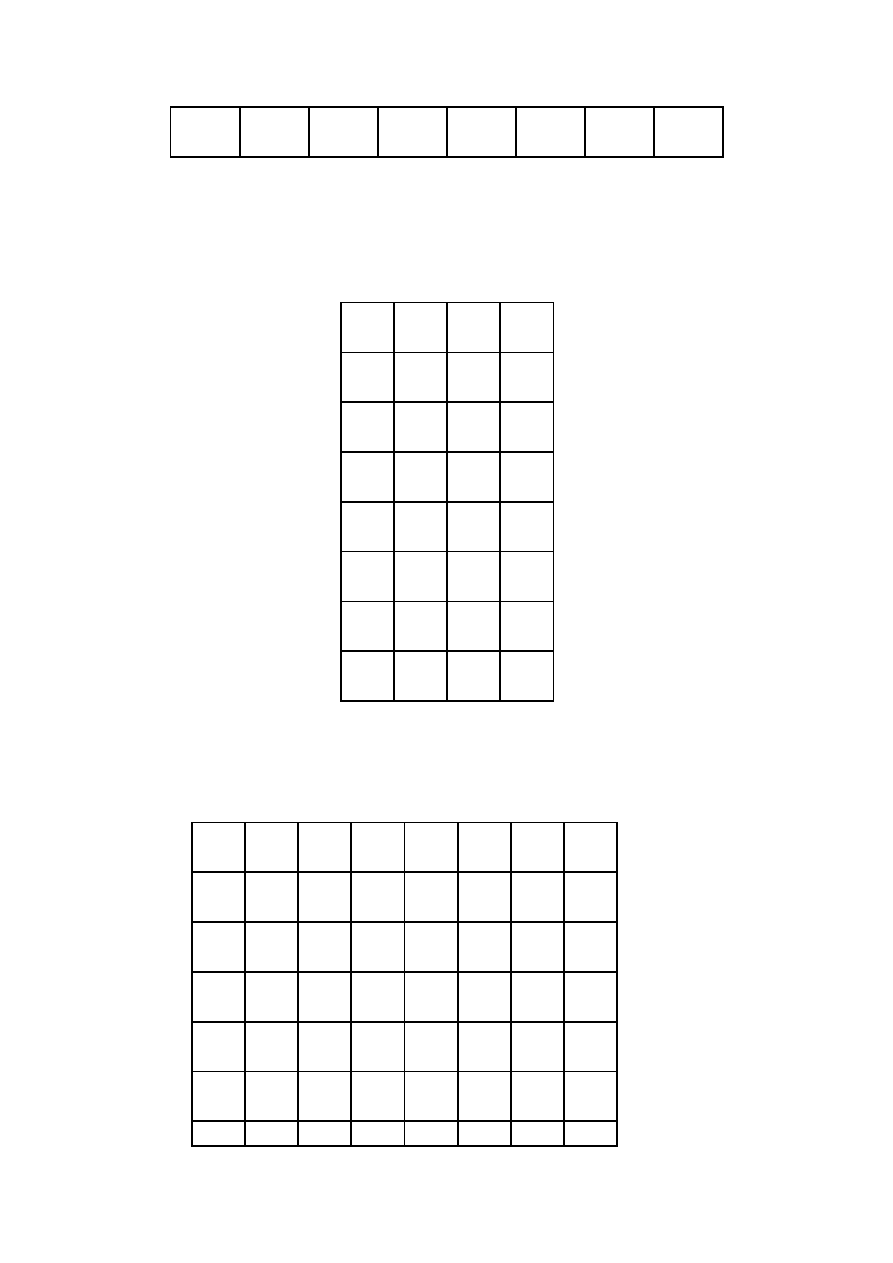
10
16
17
19
18
22
23
21
20
x
1
x
2
Inny wariant
00
01
11
10 x
4
x
5
000
0
1
3
2
001
4
5
7
6
011 12
13
15
14
010
8
9
11
10
110 24
25
27
26
111 28
29
31
30
101 20
21
23
22
100 16
17
19
18
x
1
x
2
x
3
- sześciu zmiennych
000 001 011 010 110 111 101 100 x
4
x
5
x
6
000
0
1
3
2
6
7
5
4
001
8
9
11
10
14
15
13
12
011 24
25
27
26
30
31
29
28
010 16
17
19
18
22
23
21
20
110 48
49
51
50
54
55
53
52
111 56
57
59
58
62
63
61
60
101 40
41
43
42
46
47
45
44
9
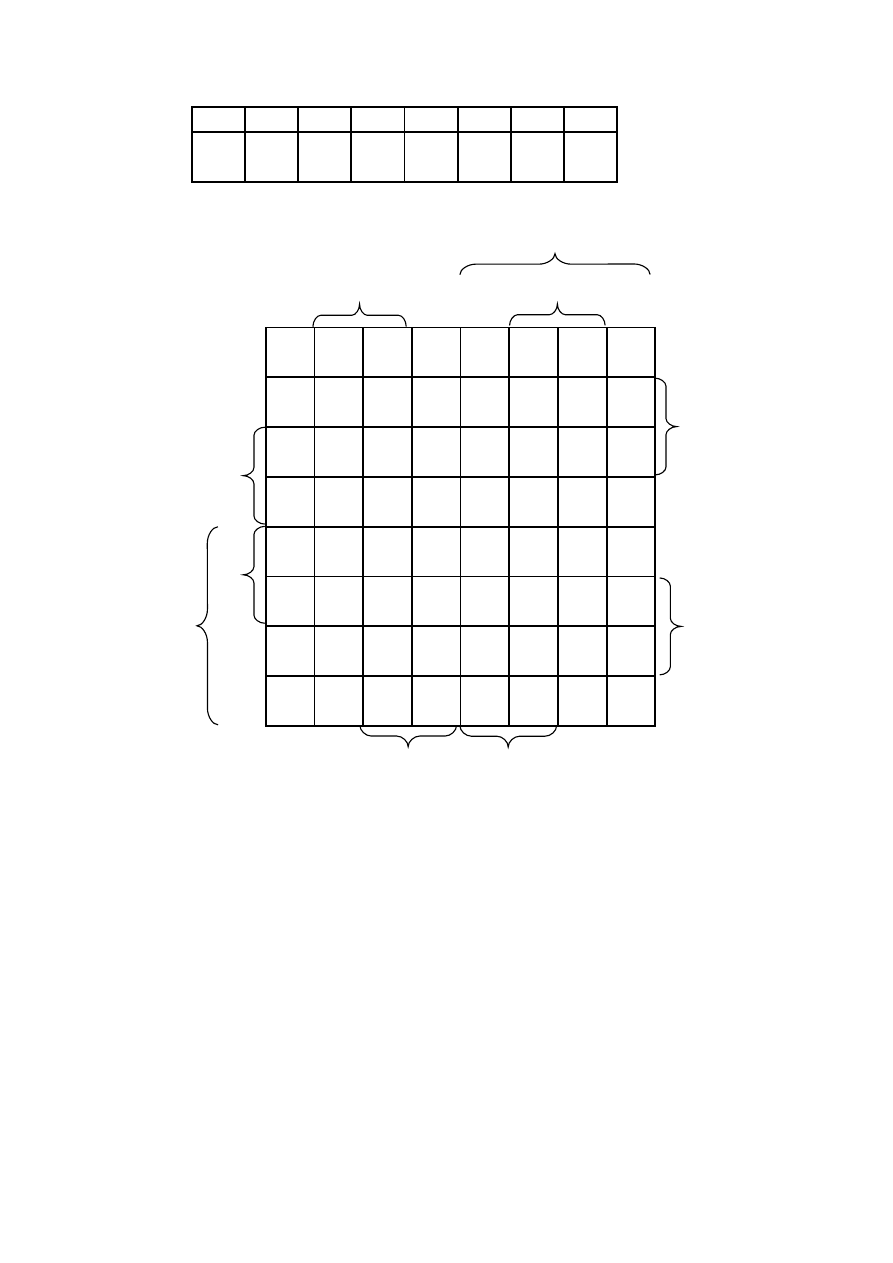
100 32
33
35
34
38
39
37
36
x
1
x
2
x
3
x
4
x
6
x
6
0
1
3
2
6
7
5
4
8
9
11
10
14
15
13
12
x
3
24
25
27
26
30
31
29
28
x
2
16
17
19
18
22
23
21
20
48
49
51
50
54
55
53
52
x
2
56
57
59
58
62
63
61
60
x
1
x
3
40
41
43
42
46
47
45
44
32
33
35
34
38
39
37
36
x
5
x
5
Tablice Karnaugha i diagramy Veitcha mają następujące zastosowania:
1) przedstawienie funkcji logicznej
2) wyznaczenie negacji
3) sprowadzenie formuł logicznych do postaci kanonicznej
4) uproszczenie formuł logicznych
5) synteza funkcji logicznych
Punktem wyjścia do minimalizacji jest najczęściej funkcja zadana tablicą
prawdy lub tablicą Karnaugha, lub w postaci zbiorów f
1
i f
0
. Odpowiada to
oczywiście kanonicznej postaci sumy lub iloczynu; jednak operowanie tymi
wyrażeniami jest w praktyce niewygodne zwłaszcza dla funkcji niezupełnych.
Minimalizacja formuły logicznej przedstawionej w postaci sumy iloczynów
(nie koniecznie pełnych) za pomocą diagramów Veitcha sprowadza się do
następujących czynności:
10
1) Przedstawienie formuły za pomocą diagramu Veitcha (jeżeli jest to
potrzebne).
2) Wyznaczenie prostych implikantów przez sklejenie możliwie jak
największych grup (par, czwórek, ósemek, ...) kratek zawierających
jedynki bądź też jedynki i krzyżyki według podanych reguł
W diagramie dwóch, trzech, czterech zmiennych sklejać można
a) pary kratek przylegające do siebie „wewnętrznie” (np. 9-11 lub 14-
10 na wykresie czterech zmiennych) lub „zewnętrzne” (np. 8-0 lub
8-10)
b) „kwadraty” wewnętrzne (np. 9-11-15-13) lub zewnętrzne (np. 9-8-
1-0, 8-10-0-2
c) pary wierszy lub kolumn przylegających do siebie wewnętrznie lub
zewnętrznie.
W diagramach pięciu lub sześciu zmiennych można sklejać grupy
kratek leżące symetrycznie względem osi symetrii w dwóch
częściach diagramu (np. dla pięciu zmiennych), z których każda jest
diagramem składowym (np. dla czterech zmiennych); dla pięciu
zmiennych można np. skleić kratki 5 i 7 z kratkami 21 i 23.
3) Wybranie niektórych grup z grup otrzymanych w p. 2 oraz
pojedynczych kratek (zawierających jedynki), które nie mogły być
sklejone, zgodnie z następującymi zasadami:
a) każda jedynka musi być co najmniej jeden raz reprezentowana w
zbirze wybranych grup
b) liczba wybranych grup powinna być możliwie jak najmniejsza
Suma iloczynów odpowiadających wybranym grupom stanowi
formułę minimalną równoważną formule pierwotnej.
Punkt 3 omawianej procedury odpowiada drugiej części procedury
Quine’a. W przypadkach bardziej złożonych może być celowe dokonanie
pierwszej części minimalizacji metodą Veitcha, a drugiej Quine’a z użyciem
tablicy implikantów.
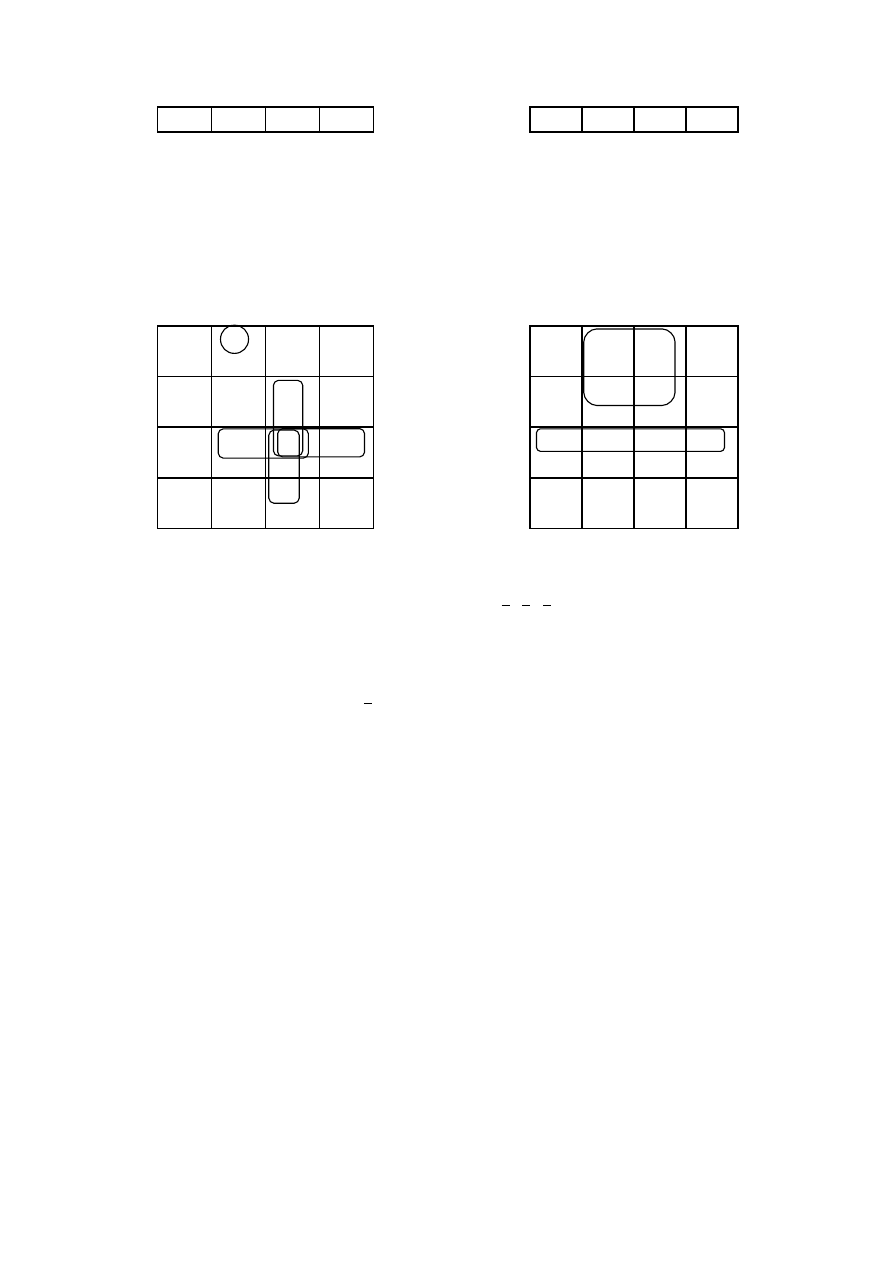
Przykład: należy podać formuły minimalne dla funkcji f
1
i f
2
podanych w
tablicach
00
01
11
10 x
3
x
4
00
01
11
10
x
3
x
4
00
0
0
1
1
0
3
0
2
00
0
0
1
1
3
0
2
01
0
4
0
5
1
7
0
6
01
4
5
1
7
0
6
11
0
12
1
13
1
15
1
14
11
12
1
13
1
15
1
14
10
0
0
1
0
10
0
0
11
8
9
11
10
8
9
11
10
x
1
x
2
x
1
x
2
Otrzymujemy:
00
01
11
10 x
3
x
4
00
01
11
10
x
3
x
4
00
0
0
1
1
0
3
0
2
00
0
0
1
1
3
0
2
01
0
4
0
5
1
7
0
6
01
4
5
1
7
0
6
11
0
12
1
13
1
15
1
14
11
12
1
13
1
15
1
14
10
0
8
0
9
1
11
0
10
10
8
0
9
11
0
10
x
1
x
2
x
1
x
2
Wyrażenie minimalne dla funkcji f
1
ma postać
F
1min
= x
1
x
2
x
3
+ x
1
x
2
x
4
+ x
1
x
3
x
4
+ x
2
x
3
x
4
+
x
1
x
2
x
3
x
4
14-15 13-15 11-15 7-15 1
Liczby pod wyrażeniami oznaczają numery sklejonych kratek. Dla funkcji f
2
będzie to:
F
2min
= x
1
x
2
+
x
1
x
4
12.13.14.15
1-3-5-7
Należy zwrócić uwagę że użycie kresek do uproszczenia ma istotne znaczenie.
Kreski sklejone z jedynkami „stają się” jedynkami. Kreski niesklejane „stają
się” zerami. Tak więc otrzymane wyrażenie interpretowane w pełnym zbiorze
{0, 1}
3
odpowiada funkcji zupełnej.
F
1
2
= {1, 3, 5, 7, 12, 13, 14, 15}
F
0
2
= {0, 2, 4, 6, 8, 9, 10, 11}
Natomiast dla funkcji niezupełnej mamy
F
1
2
= {1, 7, 13, 14, 15}
F
0
2
= {0, 2, 6, 9, 10}
Oczywiście
F
1
2
⊆
F
/
1
2
oraz
F
0
2
⊆
F
/
0
2
12

Natomiast wyrażenie F
2min
odpowiada funkcji f
2
w zbiorze jej określoności, tj.
dla
F
1
2
∪
F
0
2
W wyrażeniach logicznych minimalnych lub częściowo zminimalizowanych
występują także iloczyny niepełne, tj. nie zawierające wszystkich zmiennych.
Takie iloczyny mogą być jednoznacznie powiązane z odpowiednimi wektorami.
Trzeba przyjąć
WL(e
1
) =
x
e1
1
...
x
ej
j
...
x
em
m
przy czym
x
j
dla e
j
= 0
x
ej
j
= x
j
dla e
j
= 1
1 dla e
j
= *
Funkcja f może być wtedy zapisana jako
f :
D
m*
→
{0,1}
przy czym
D
m*
⊆
{0, 1, *}
m
Przykład:
Korzystając z wprowadzonego aparatu formalnego możemy napisać dla f
1
i f
2
e
1
e
2
e
3
e
4
1 1 1 x
1 1 x 1
f
1
= WL
-1
(F
1min
1 x 1 1
x 1 1 1
0 0 0 1
e
1
e
2
e
3
e
4
f
2
= WL
-1
(F
2min
)
1 1 x x
0 x x 1
Funkcje f
1
i f
2
przyporządkowują podanym wyżej wektorom wartość 1.
Przykład:
Funkcja zupełna f (x
1
, x
2
, x
3
, x
4
, x
5
, x
6
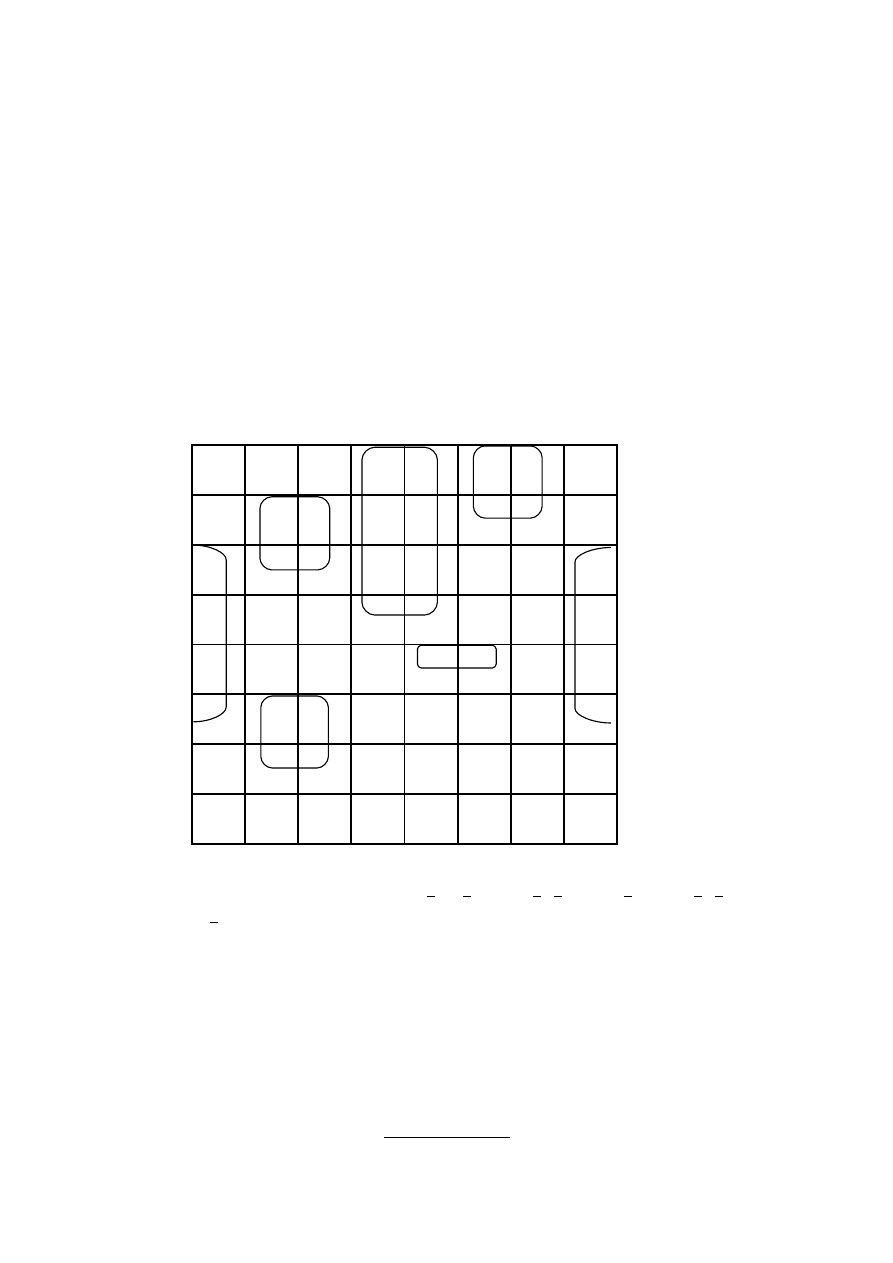
) jest dana w postaci F
1
= {2, 5, 6, 7, 9, 10,
11, 13, 14, 15, 16, 18, 20, 22, 24, 25, 26, 27, 28, 30, 41, 43, 48, 52, 54, 55, 56,
57, 59, 60}. Funkcja ta jest podana za pomocą tablicy Karnaugha.
13
000 001 011 010 110 111 101 100 x
4
x
5
x
6
000
0
0
0
1
0
3
1
2
1
6
1
7
1
5
0
4
001
0
8
1
9
1
11
1
10
1
14
1
15
1
13
0
12
011
1
24
1
25
1
27
1
26
1
30
0
31
0
29
1
28
010
1
16
0
17
0
19
1
18
1
22
0
23
0
21
1
20
110
1
48
0
49
0
51
0
50
1
54
1
55
0
53
1
52
111
1
56
1
57
1
59
0
58
0
62
0
63
0
61
1
60
101
0
40
1
41
1
43
0
42
0
46
0
47
0
45
0
44
100
0
32
0
33
0
35
0
34
0
38
0
39
0
37
0
36
x
1
x
2
x
3
Wyrażenie minimalne z tablicy Karnaugha ma postać
F
min
(x
1
, x
2
, x
3
, x
4
, x
5
, x
6
) =
x
1
x
5
x
6
+ x
2
x
5
x
6
+ x
3
x
4
x
6
+
x
1
x
2
x
4
x
6
+
+ x
1
x
2
x
3
x
4
x
5
Przykład
Należy zminimalizować funkcję f
1
przedstawioną w tabeli, podając minimalną
sumę iloczynów i minimalny iloczyn sum. Zastosować tablice Karnaugha.
Funkcja f
1
i x
1
x
2
x
3
f
1
14
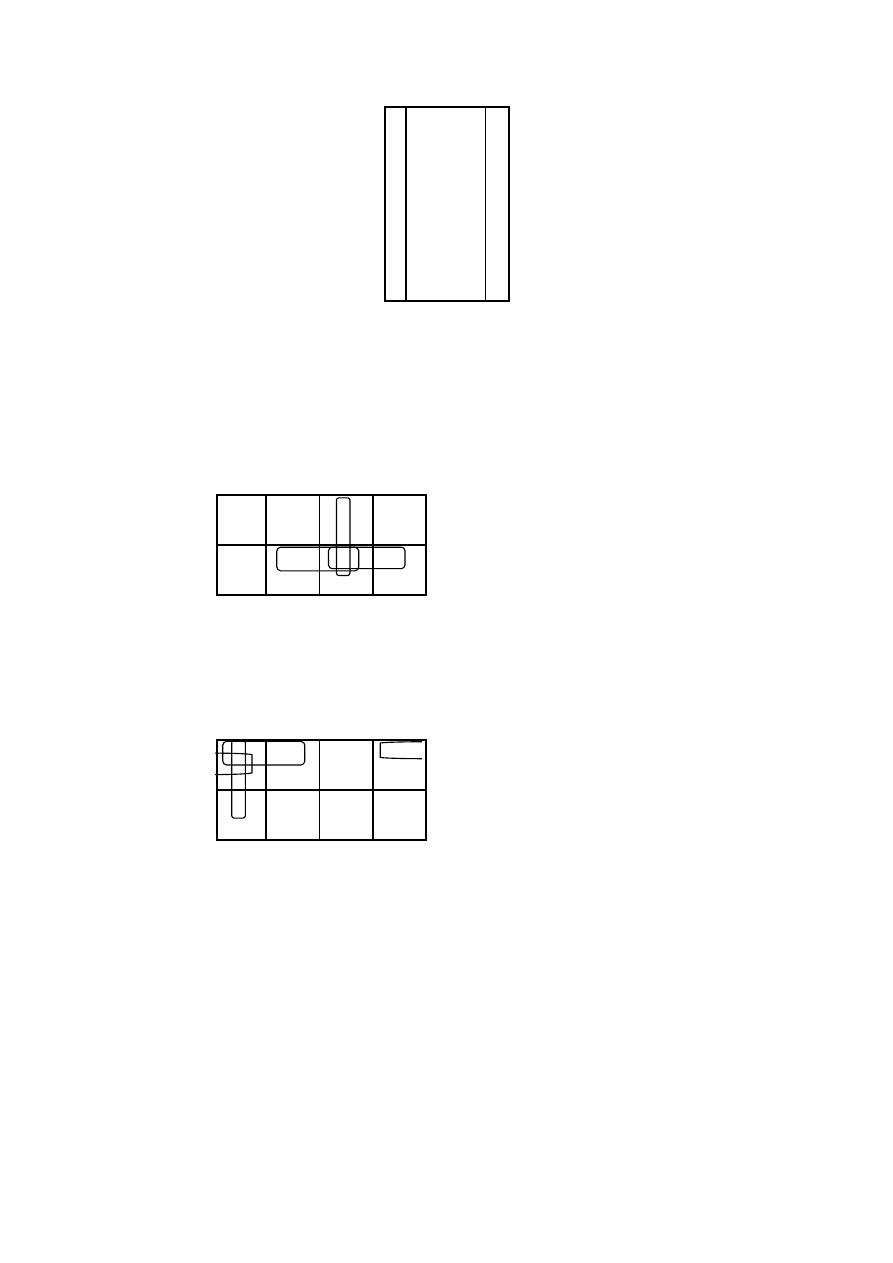
0 0 0 0 0
1 0 0 1 0
2 0 1 0 0
3 0 1 1 1
4 1 0 0 0
5 1 0 1 1
6 1 1 0 1
7 1 1 1 1
Po sklejeniu jedynek otrzymujemy
00
01
11
10
x
2
x
3
0
0
0
0
1
1
3
0
2
1
0
4
1
5
1
7
1
6
x
1
Otrzymujemy: F
1
= x
1
x
2
+ x
2
x
3
+ x
3
x
1
6-7 3-7 5-7
Natomiast sklejenie zer
00
01
11
10
x
2
x
3
0
0
0
0
1
1
3
0
2
1
0
4
1
5
1
7
1
6
x
1
prowadzi do par kratek 0-1, 0-2, 0-4, co odpowiada operacjom na wektorach
〈
000
〉
*
〈
001
〉
=
〈
00x
〉
→
x
1
+ x
2
〈
000
〉
*
〈
010
〉
=
〈
0x0
〉
→
x
1
+ x
3
〈
000
〉
*
〈
100
〉
=
〈
x00
〉
→
x
2
+ x
3
Otrzymujemy w wyniku sklejenia podane wyżej wektory i odpowiadające im
sumy (inna konwencja niż dla iloczynów). Ostatecznie
F
1
= (x
1
+ x
2
)(x
2
+ x
3
)(x
3
+ x
1
)
15
Tablice Karnaugha i diagramy Veitcha znajdują zastosowanie nie tylko do
minimalizacji.
Przykład:
Funkcję f zapisaną za pomocą formuły F = x
1
x
2
+ x
2
x
3
+ x
3
należy przedstawić w
kanonicznej postaci sumy, stosując diagram Veitcha. Jest to zagadnienie
odwrotne do minimalizacji.
x
3
0
0
1
1
1
3
0
2
x
1
0
4
1
5
1
7
1
6
x
2
Otrzymujemy F = P
1
+ P
3
+ P
5
+ P
6
+ P
7
Przykład
Funkcję f zapisaną za pomocą formuły F = (x
1
+ x
2
)(x
2
+ x
3
) należy
przedstawić w kanonicznej postaci iloczynu, stosując diagram Veitcha.
x
3
0
0
0
1
1
3
1
2
x
1
0
4
1
5
1
7
1
6
x
2
Otrzymujemy F = S
0
S
1
S
4
Przedstawione metody minimalizacji wyrażeń logicznych nadają się dla
niezbyt dużej liczby zmiennych – w przypadku tablic Karnaugha praktycznie
do 6. Metoda Quine’a-McCluskeya daje tu nieco większe możliwości, ale
staje się mało efektywna w przypadku tzw. funkcji słabookreślnych, dla
których zbiór D
m
jest małą częścią zbioru {0, 1}
m
. Znane są metody [20], [3],
umożliwiające wyznaczenie wyrażeń minimalnych i zminimalizowanych (tj.
16

nieoptymalnych) także dla funkcji słabookreślnych. Istnieją też metody
umożliwiające minimalizację zespołów wyrażeń logicznych.
17
Document Outline
Wyszukiwarka
Podobne podstrony:
minimalizacja funkcji logicznych
02 Minimalizacja funkcji logicznyc (2)
Algorytmy genetyczne w minimalizacji funkcji logicznych 5 część 2
Minimalizacja funkcji logicznych 3
Algorytmy genetyczne w minimalizacji funkcji logicznych 5 część 1
Algorytmy genetyczne w minimalizacji funkcji logicznych 5 część 3
minimalizacja funkcji logicznych
Algorytmy genetyczne w minimalizacji funkcji logicznych Karina Murawko
Instrukcja do zad proj 10 Podstawowe funkcje logiczne z z
cw 6 Synteza układów kombinacyjnych- realizacja sprzętowa funkcji logicznych
Pomiary wielkosci elektrycznych Minimalizacja funkcji tablica
Porównać metody realizacji funkcji logicznych
Badanie Funkcji Logicznych
Porównać metody realizacji funkcji logicznych, cwiczenie 2
Minimalizacja funkcji
Podstawowe funkcje logiczne
więcej podobnych podstron