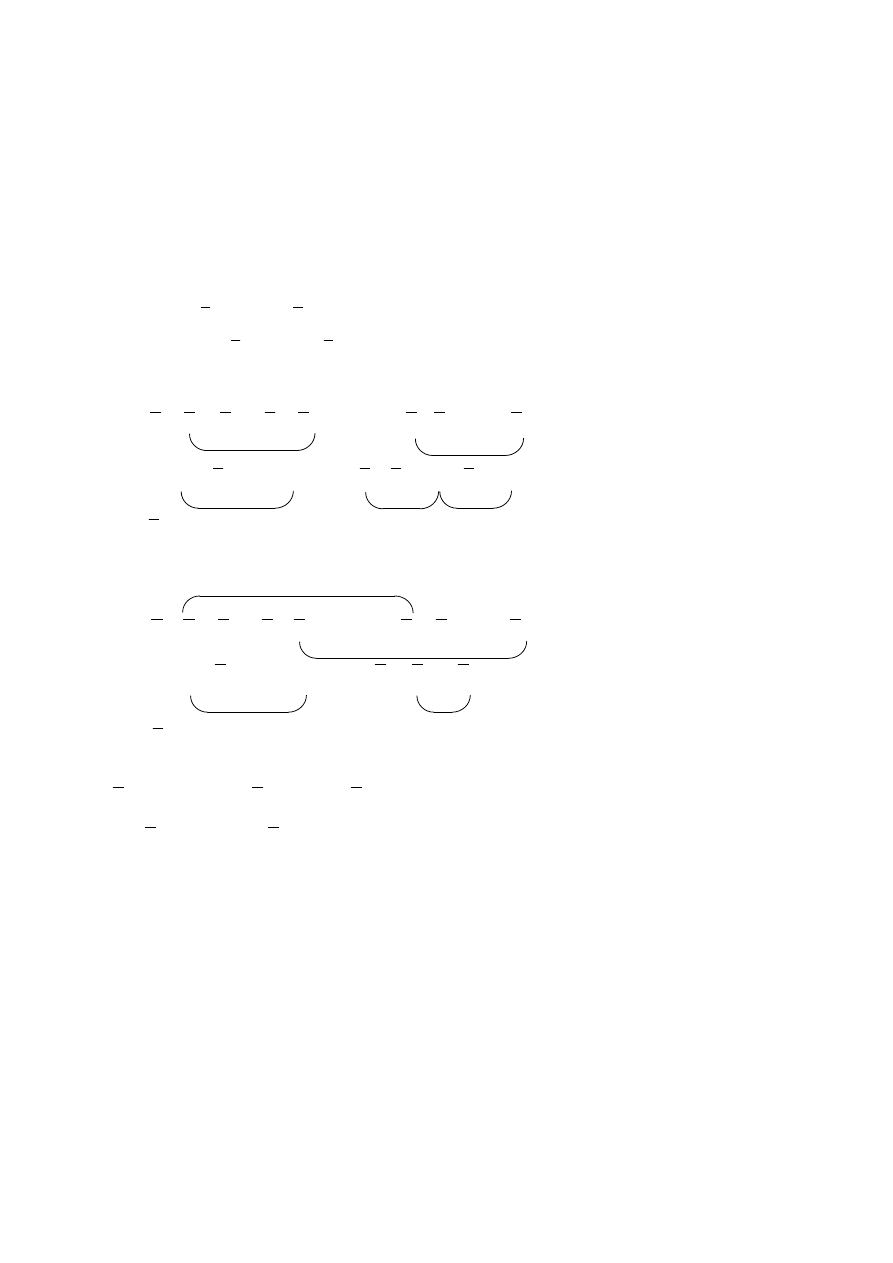
1
6. Minimalizacja funkcji logicznych
Metody minimalizacji funkcji logicznych:
- metoda przekształceń algebraicznych,
- metoda Quine’a – McCluskey’a,
- metoda tablic Karnaugha.
6.1. Metoda przekształceń algebraicznych
polega na wykonywaniu tzw. operacji
sklejania.
a
a
b
b
a
b
a
b
a
a
a
b
b
a
b
a
b
a
0
)
(
)
(
1
)
(
Zminimalizujmy postacie kanoniczne przykładowej funkcji
3
2
1
3
2
1
3
2
1
3
2
1
x
x
x
x
x
x
x
x
x
x
x
x
y
2
1
2
1
2
1
3
2
1
3
2
1
x
x
x
x
x
x
x
x
x
x
x
x
1
2
x
x
Nie zawsze znajdujemy najkorzystniejszy sposób sklejania, np.:
3
2
1
3
2
1
3
2
1
3
2
1
x
x
x
x
x
x
x
x
x
x
x
x
y
2
1
3
2
3
2
3
2
1
3
2
1
x
x
x
x
x
x
x
x
x
x
x
x
2
1
2
x
x
x
Rezultat ten można doprowadzić do najprostszej postaci dokonując przekształcenia:
)
(
)
(
2
2
1
2
2
1
2
x
x
x
x
x
x
x
1
2
1
2
1
)
(
x
x
x
x
Niekiedy, po wykonaniu wszystkich możliwych sklejeń, można zmniejszyć liczbę operacji
logicznych przez wyłączenie przed nawias wspólnego czynnika. Operacja taka nazywa się
faktoryzacją.
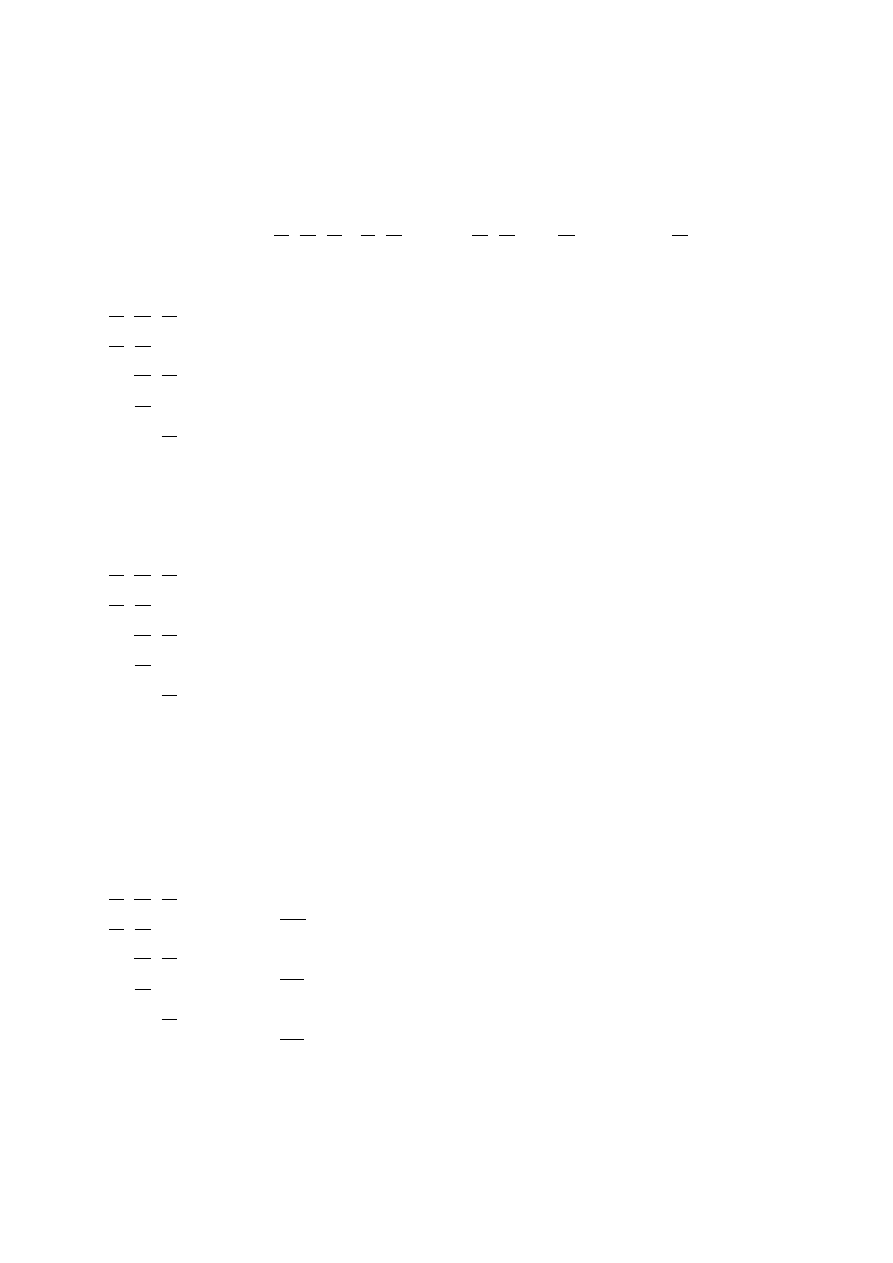
2
6.2. Metoda Quine’a – McCluskey’a
Metoda Quine’a – McCluskey’a polega na wykonaniu nad postacią kanoniczną wszystkich
możliwych sklejeń, przy czym stosuje się specyficzny, uporządkowany sposób postępowania,
co zostanie zilustrowane przykładem.
Przykład 1: Zminimalizować kanoniczną postać alternatywną przykładowej funkcji
trzyargumentowej
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
y
Krok 1
Wypisujemy składniki jedności funkcji w kolumnie
3
2
1
x
x
x
3
2
1
x
x
x
3
2
1
x
x
x
3
2
1
x
x
x
3
2
1
x
x
x
3
2
1
x
x
x
Krok 2
W drugiej kolumnie składniki jedności zastępujemy zapisem symbolicznym zerojedynkowym
3
2
1
x
x
x
000
3
2
1
x
x
x
001
3
2
1
x
x
x
100
3
2
1
x
x
x
101
3
2
1
x
x
x
110
3
2
1
x
x
x
111
Krok 3
W trzeciej kolumnie symboliczne zapisy grupujemy zapisy wg liczby występujących w nich
jedynek, co ułatwia poszukiwanie możliwych sklejeń (sklejenia są możliwe tylko pomiędzy
składnikami sąsiednich grup). Aby nie pominąć żadnego ze składników, przy przeniesionych
do kolumny następnej stawiamy znak
.
3
2
1
x
x
x
000
000
3
2
1
x
x
x
001
001
3
2
1
x
x
x
100
100
3
2
1
x
x
x
101
101
3
2
1
x
x
x
110
110
3
2
1
x
x
x
111
111
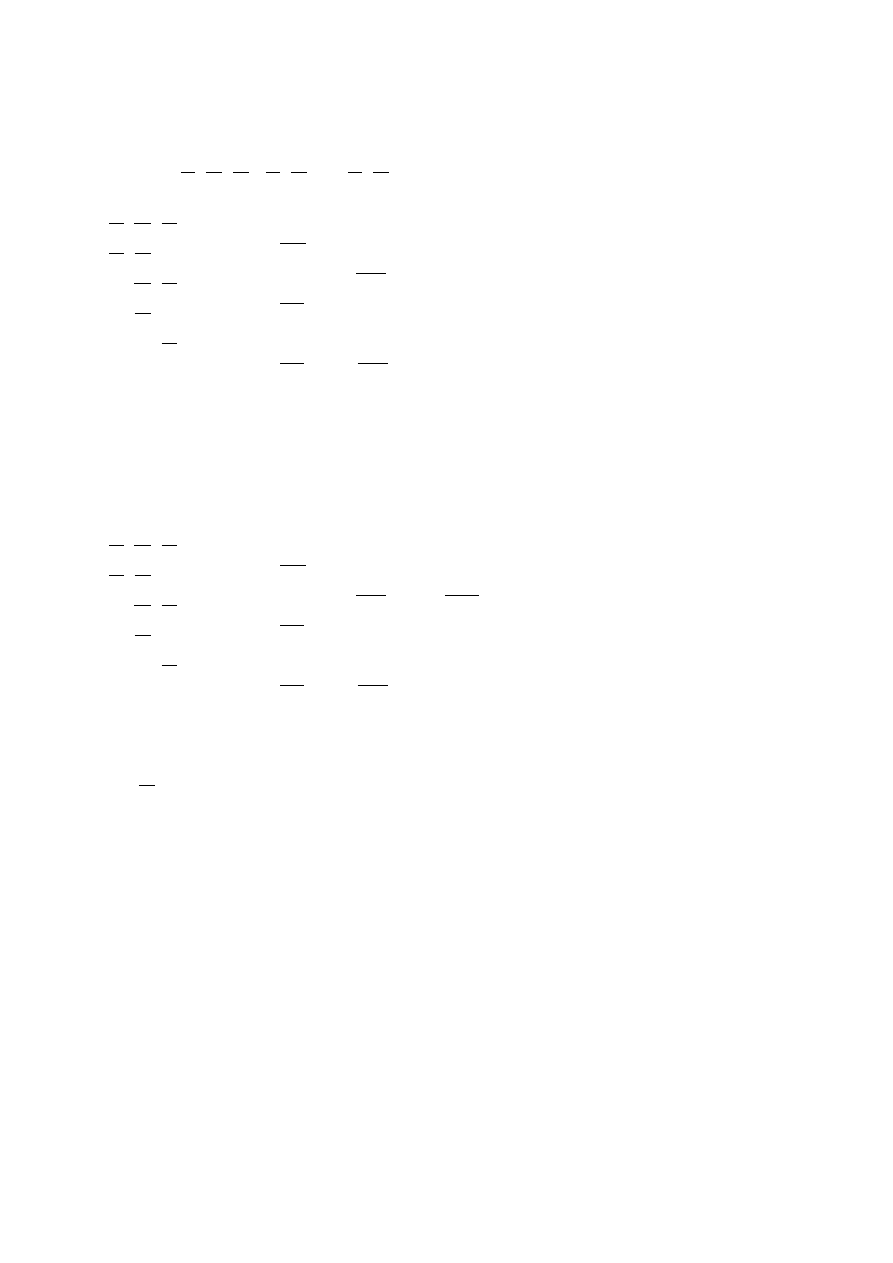
3
Krok 4
W czwartej kolumnie wypisujemy wyniki wszystkich możliwych sklejeń.
Np.: 000 skleja się z 001; wynik sklejenia 00-. Oznacza to oczywiście, ze dokonaliśmy
operacji
3
2
1
x
x
x
+
3
2
1
x
x
x
=
2
1
x
x
.
3
2
1
x
x
x
000
000
00
3
2
1
x
x
x
001
001
00
3
2
1
x
x
x
100
100
01
3
2
1
x
x
x
101
101
10
3
2
1
x
x
x
110
110
0
1
3
2
1
x
x
x
111
111
1
1
11
Krok 5
W piątej kolumnie wypisujemy wyniki dalszych możliwych sklejeń. Badamy możliwości
sklejeń wyrażeń zawierających jednakowe zmienne (które mają kreski na tych samych
pozycjach).
3
2
1
x
x
x
000
000
00
0
3
2
1
x
x
x
001
001
00
0
3
2
1
x
x
x
100
100
01
1
3
2
1
x
x
x
101
101
10
1
3
2
1
x
x
x
110
110
0
1
3
2
1
x
x
x
111
111
1
1
11
Ponieważ nie ma już możliwości dalszych sklejeń, odtwarzamy algebraiczny zapis wyników
sklejeń, pomijając wyniki powtarzające się:
1
2
x
x
y
4
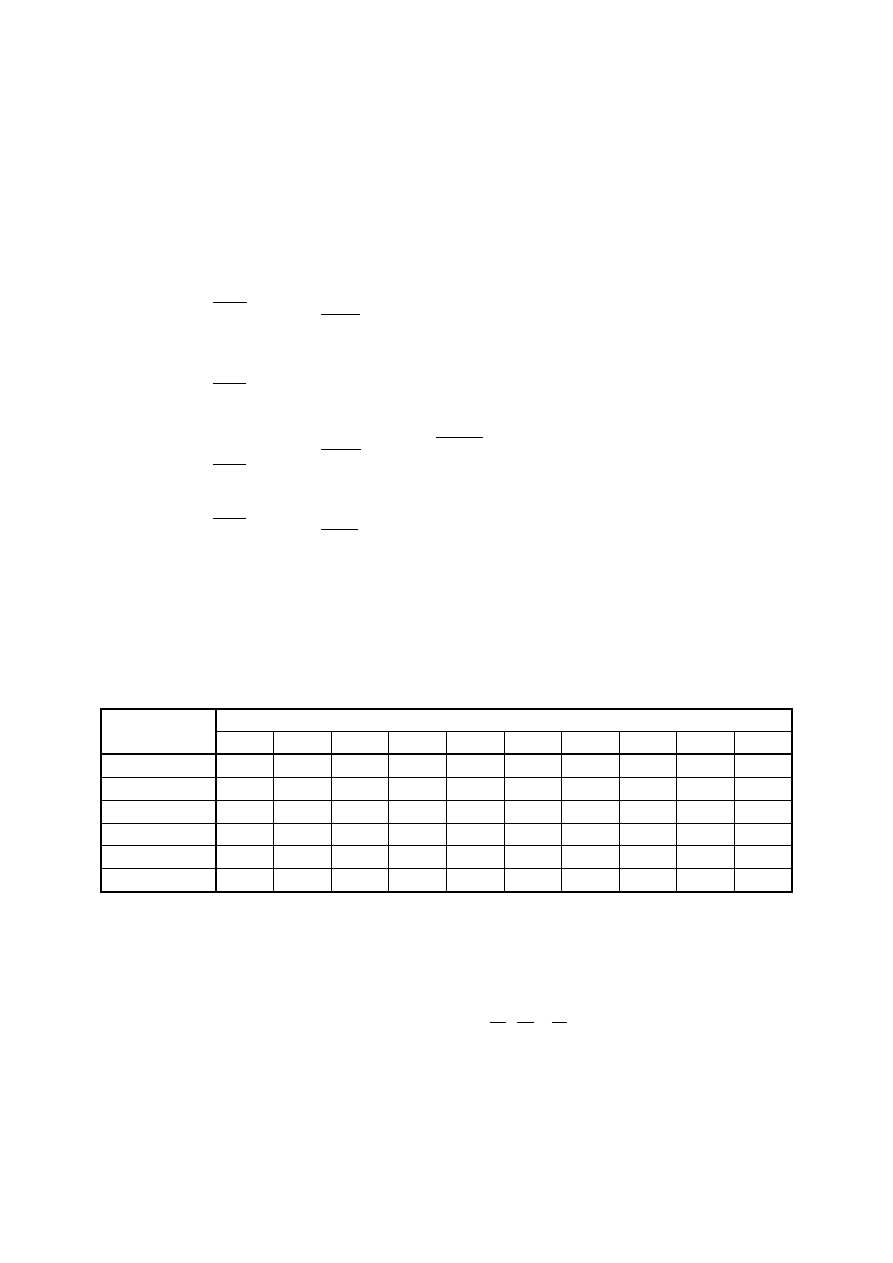
Przykład 2: Zminimalizować funkcję
15
,
14
,
13
,
10
,
9
,
8
,
5
,
2
,
1
,
0
)
,
,
,
(
4
3
2
1
x
x
x
x
y
Liczbowy zapis funkcji podaje numery składników jedności kanonicznej postaci
alternatywnej. Proces minimalizacji można rozpocząć od wypisania w kolumnie dwójkowego
zapisu tych numerów.
Wyrażenia przeniesione do kolumny wyższej oznaczono tu symbolem
.
1111
1110
1101
1010
1001
1000
0101
0010
0001
0000
1111
1110
1101
1010
1001
0101
1000
0010
0001
0000
111
1
11
10
1
01
1
101
0
10
100
010
001
01
0
000
0
00
000
01
01
0
0
00
0
0
00
Po wykonaniu wszystkich sklejeń otrzymaliśmy zestaw trzech różnych tzw. implikantów
prostych w kolumnie czwartej i trzech w kolumnie trzeciej.
Zwykle nie wszystkie implikanty są niezbędne do wyrażenia danej funkcji. Do wyboru
niezbędnego zestawu implikantów służy tablica implikantów.
Implikanty
proste
Składniki jedności funkcji
0000
0001
0010
0101
1000
1001
1010
1101
1110
1111
10
1
1
11
111
00
0
0
01
W tablicy symbolem
oznaczono te składniki jedności, ze sklejenia których powstał dany
implikant prosty. Mówi się, że imlikant prosty pochłania te składniki jedności, z których
powstał. Aby zminimalizowana postać funkcji była poprawnym zapisem danej funkcji musi
zawierać zestaw implikantów prostych pochłaniających wszystkie składniki jedności
minimalizowanej funkcji. W rozpatrywanym przykładzie jest to zestaw implikantów
oznaczonych symbolem
. Zatem:
4
3
4
2
3
2
1
x
x
x
x
x
x
x
y
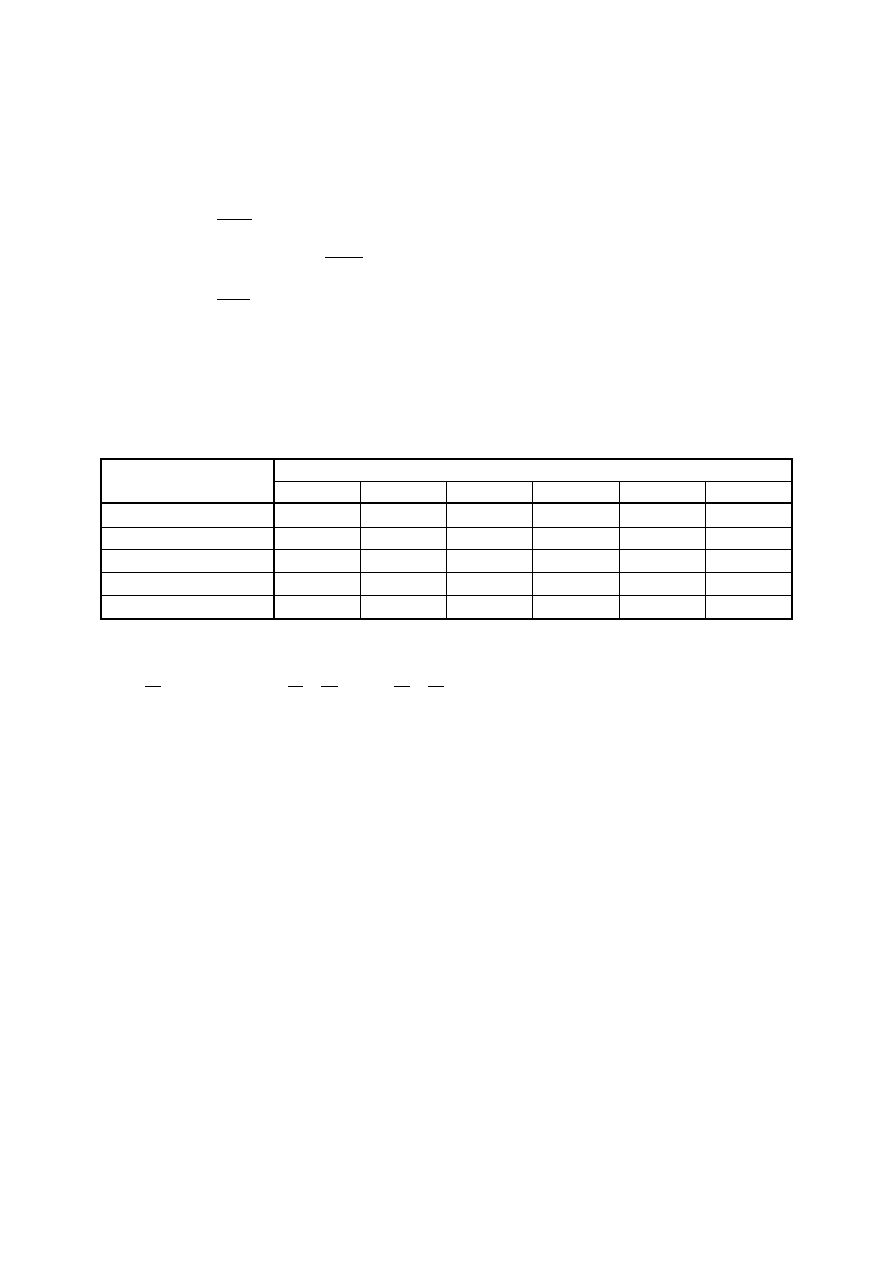
5
Analogicznie przebiega proces minimalizacji kanonicznej postaci koniunkcyjnej, której
zapisem liczbowym jest wyrażenie:
12
,
11
,
7
,
6
,
4
,
3
15
,
14
,
13
,
10
,
9
,
8
,
5
,
2
,
1
,
0
)
,
,
,
(
4
3
2
1
x
x
x
x
y
1100
1011
0111
0110
0100
0011
1011
0111
1100
0110
0011
0100
011
011
11
0
100
0
01
Po dokonaniu wszystkich możliwych sklejeń otrzymaliśmy liczbowe zapisy tzw. Prostych
implicentów minimalizowanej funkcji. Do ustalenia czy wszystkie są niezbędne do wyrażenia
tej funkcji służy tablica implicentów.
Implicenty proste
Czynniki zera
0011
0100
0110
0111
1011
1100
01-0
-100
0-11
-011
011-
Zestaw implicentów prostych oznaczonych symbolem
pochłania wszystkie czynniki zera
postaci kanonicznej, zatem:
)
(
)
(
)
(
3
2
1
4
3
2
4
3
2
x
x
x
x
x
x
x
x
x
y
6
6.3. Metoda tablic Karnaugha
Tablice Karnaugha umożliwiają minimalizację funkcji o co najwyżej sześciu argumentach.
0
1
3
2
0
1
0
1
1
x
2
x
a)
1
0
1
x
0 1 3 2
8 9 11 10
6 7 5 4
24 25 27 26
16 17 19 18
22 23 21 20
30 31 29 28
14 15 13 12
000 001 011 010 110 111 101 100
00
01
11
10
5
4
3
x
x
x
2
1
x
x
00
01
11
10
2
1
x
x
0 1 3 2
b)
c)
d)
00 01 11 10
00 01 11 10
4 5 7 6
8 9 11 10
12 13 15 14
0 1 3 2
4 5 7 6
4
3
x
x
3
2
x
x
Tablice Karnaugha funkcji:
)
,
(
2
1
x
x
y
- a),
)
,
,
(
3
2
1
x
x
x
y
- b),
)
,
,
,
(
4
3
2
1
x
x
x
x
y
- c),
)
,
,
,
,
(
5
4
3
2
1
x
x
x
x
x
y
- d) z numerami stanów argumentów
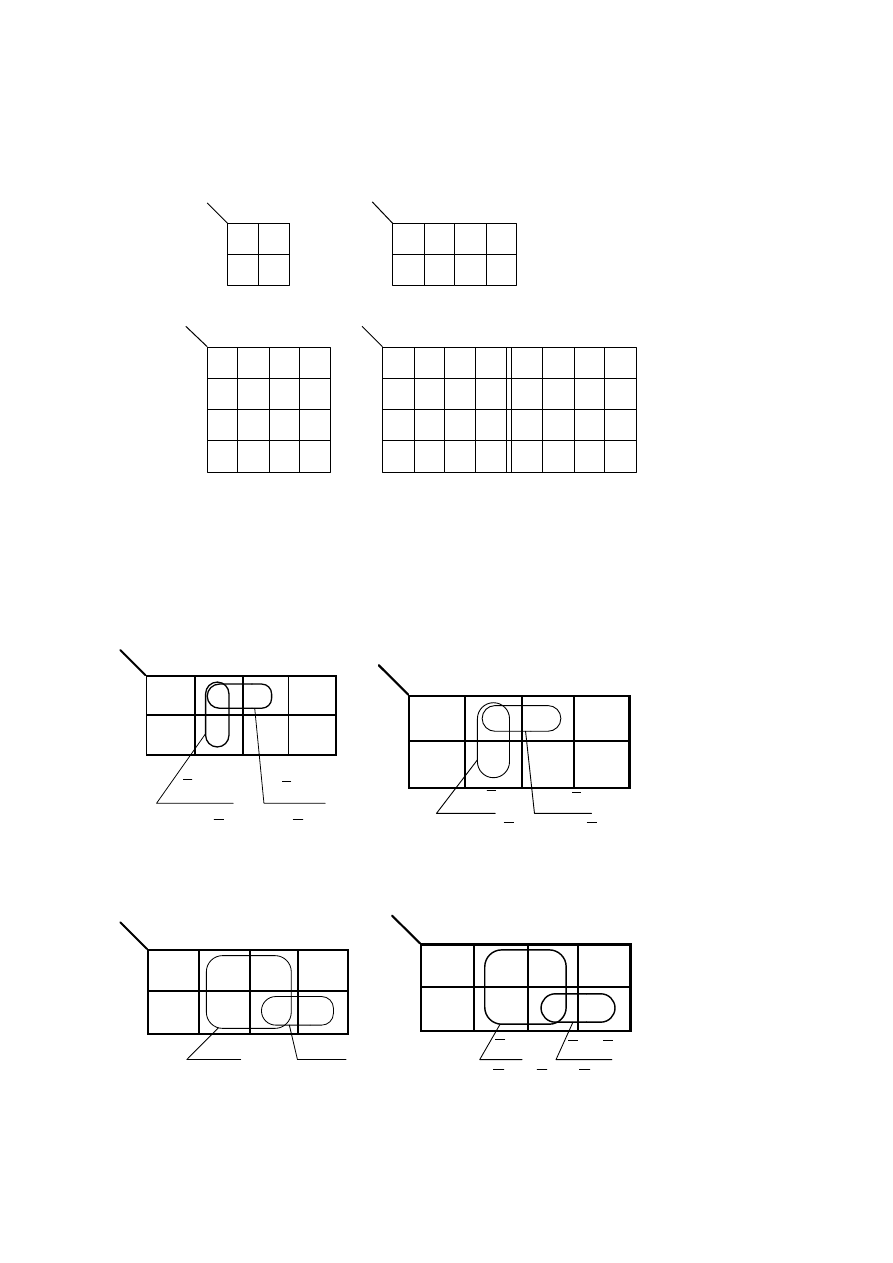
Przykłady sklejania w tablicach funkcji trójargumentowych
a) b)
0
1
1
0
0
1
0
0
x
2
x
3
x
1
00
01
11
10
0
1
3
2
x
x
3
1
x
x
3
1
3
2
x
x
x
x
y
1
0
0
1
1
0
1
1
x
2
x
3
x
1
00
01
11
10
0
1
3
2
x
x
3
1
x
x
)
(
)
(
3
1
3
2
x
x
x
x
y
c) d)
0
1
1
0
0
1
1
1
x
2
x
3
x
1
00
01
11
10
0
1
3
x
2
1
x
x
2
1
3
x
x
x
y
1
0
0
1
1
0
0
0
x
2
x
3
x
1
00
01
11
10
0
1
3
x
2
1
x
x
)
(
2
1
3
x
x
x
y
7
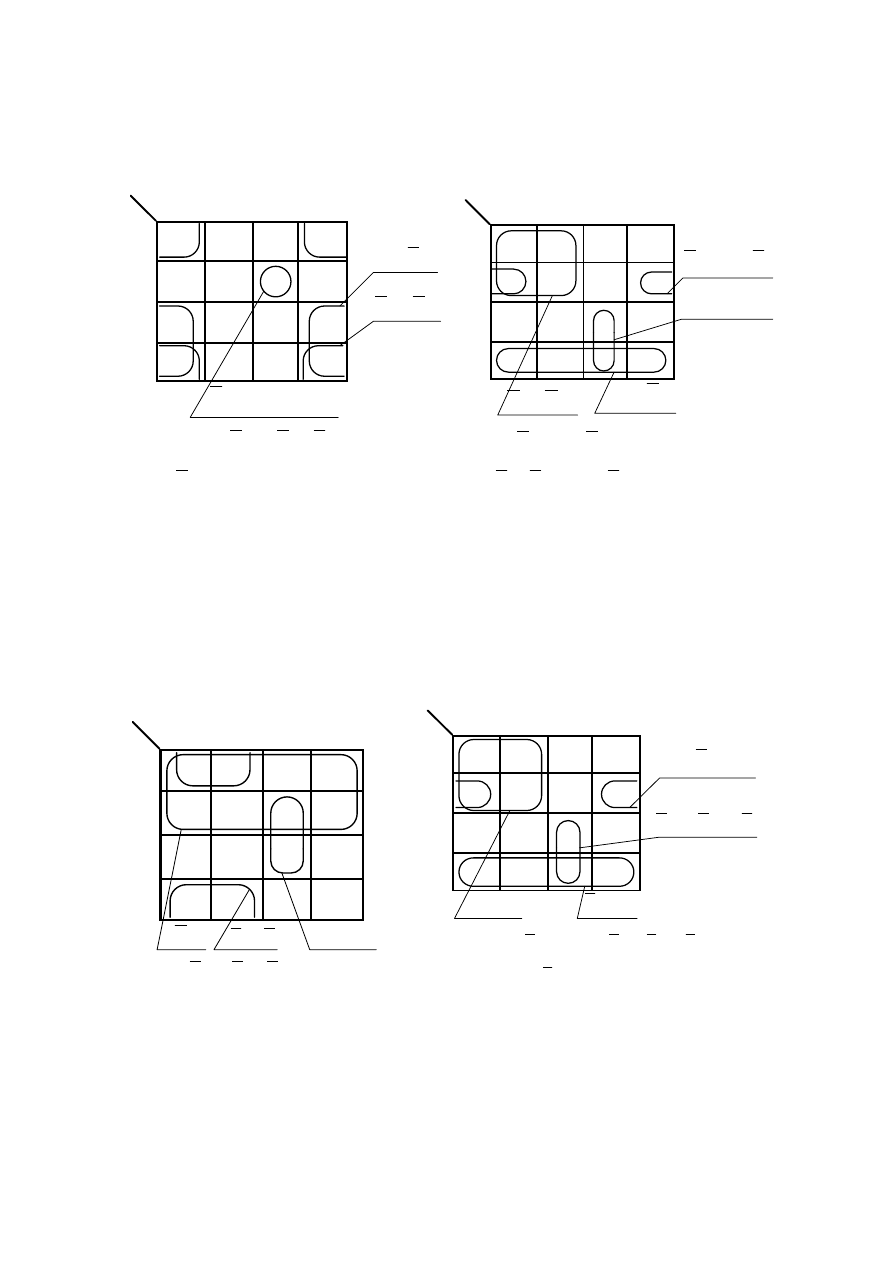
Przykłady sklejania w tablicach funkcji czteroargumentowych:
a) b)
x
1
x
2
1 0
0
1
0
0
1
0
1
0
0
1
1
0
0
1
x
3
x
4
00
01
11
10
00
01
11
10
4
3
2
1
x
x
x
x
4
1
x
x
4
2
x
x
4
3
2
1
4
2
4
1
x
x
x
x
x
x
x
x
y
1 1
0
0
1
1
0
1
0
0
1
0
1
1
1
1
x
3
x
4
x
1
x
2
00
01
11
10
00
01
11
10
4
2
1
x
x
x
3
1
x
x
2
1
x
x
4
3
1
x
x
x
2
1
3
1
4
3
1
4
2
1
x
x
x
x
x
x
x
x
x
x
y
c) d)
x
1
x
2
1 1
1
1
1
1
1
1
0
0
1
0
1
1
0
0
x
3
x
4
00
01
11
10
00
01
11
10
1
x
3
2
x
x
4
3
2
x
x
x
4
3
2
3
2
1
x
x
x
x
x
x
y
x
1
x
2
0 0
1
1
0
0
1
0
1
1
0
1
0
0
0
0
x
3
x
4
00
01
11
10
00
01
11
10
2
1
x
x
2
1
x
x
4
2
1
x
x
x
4
3
1
x
x
x
)
(
)
(
)
(
)
(
2
1
3
1
4
3
1
4
2
1
x
x
x
x
x
x
x
x
x
x
y
8
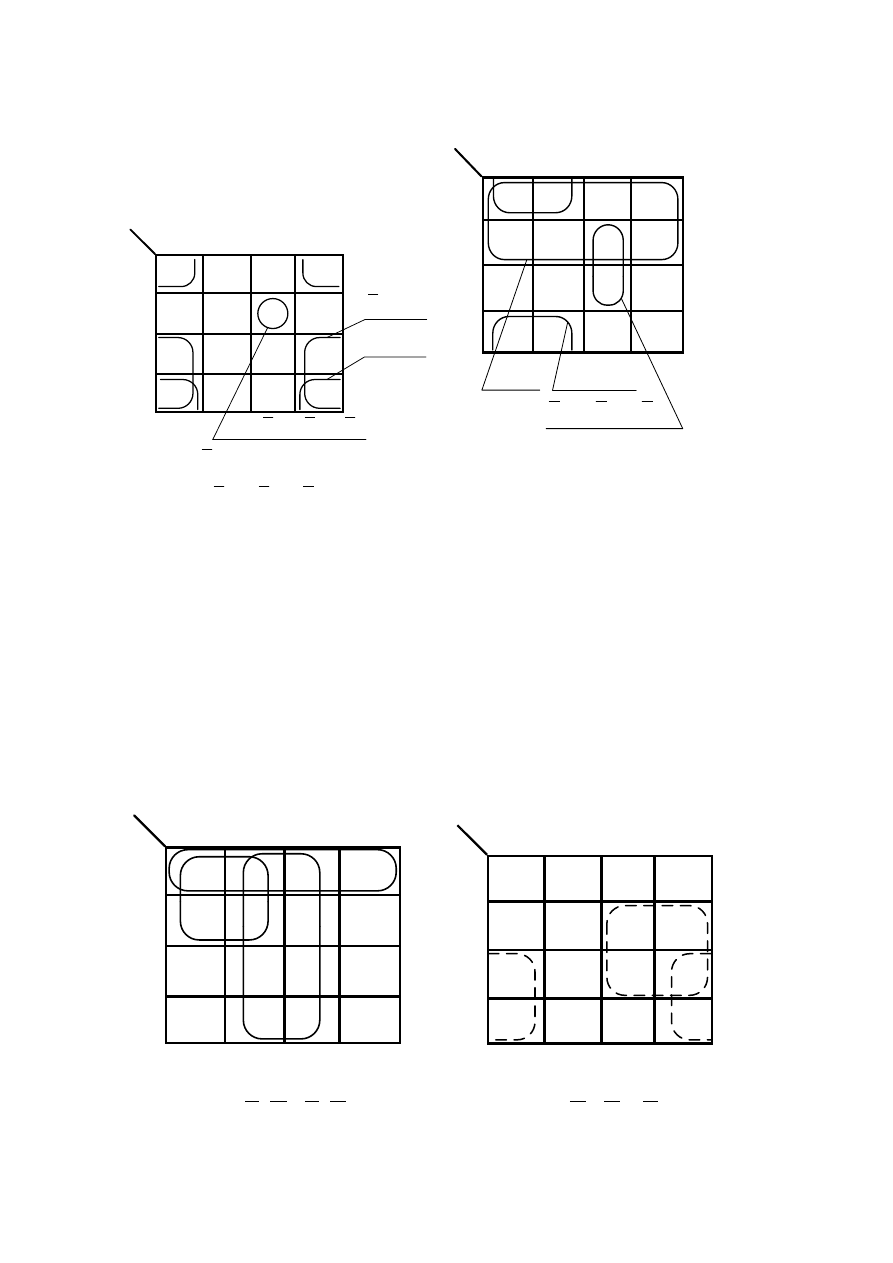
e) f)
x
1
x
2
0 1
1
0
1
1
0
1
0
1
1
0
0
1
1
0
x
3
x
4
00
01
11
10
00
01
11
10
4
3
2
1
x
x
x
x
4
1
x
x
4
2
x
x
)
(
)
(
)
(
4
3
2
1
4
2
4
1
x
x
x
x
x
x
x
x
y
x
1
x
2
0 0
0
0
0
0
0
0
1
1
0
1
0
0
1
1
x
3
x
4
00
01
11
10
00
01
11
10
1
x
3
2
x
x
4
3
2
x
x
x
)
(
)
(
4
3
2
3
2
1
x
x
x
x
x
x
y
Minimaliacja funkcji nie w pełni określonych
Minimalizacja z wykorzystaniem tablic Karnaugha
Zminimalizować funkcję o nieokreślonej (dowolnej) wartości w stanach argumentów 5, 7, 13,
i 15:
)
15
,
13
,
7
,
5
(
14
,
12
,
10
,
8
,
6
)
15
,
13
,
7
,
5
(
11
,
9
,
4
,
3
,
2
,
1
,
0
)
,
,
,
(
4
3
2
1
x
x
x
x
y
a) sklejanie jedynek b) sklejanie zer
1 1 1 1
1
-
-
0
0
-
-
0
0
1
1
0
x
3
x
4
x
1
x
2
00
01
11
10
00
01
11
10
1 1 1 1
1
-
-
0
0
-
-
0
0
1
1
0
x
3
x
4
x
1
x
2
00
01
11
10
00
01
11
10
y y
4
3
1
2
1
x
x
x
x
x
y
)
(
)
(
4
1
3
2
x
x
x
x
y
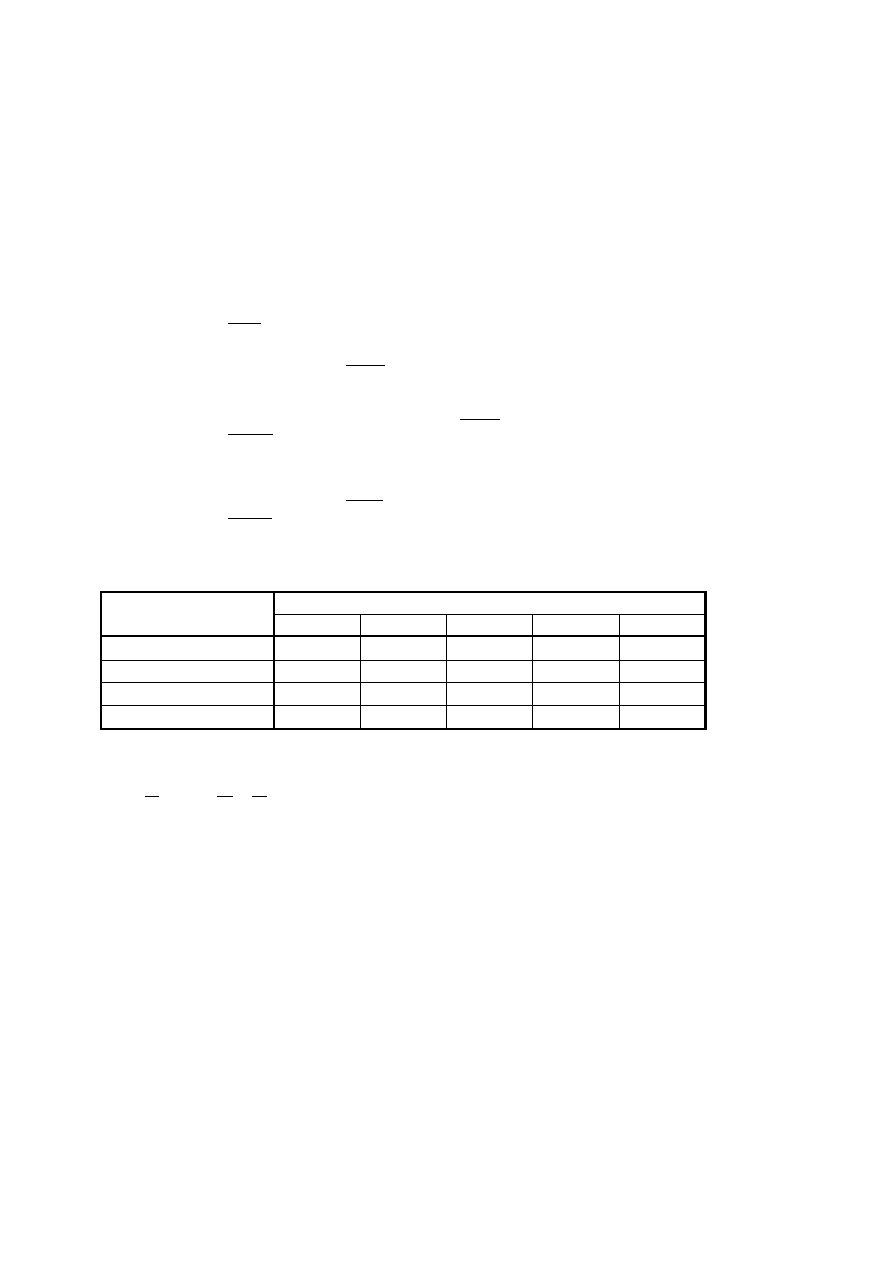
9
Minimalizacja metodą Quine’a – McCluskey’a
Zminimalizować funkcję
)
15
,
13
,
7
,
5
(
14
,
12
,
10
,
8
,
6
)
15
,
13
,
7
,
5
(
11
,
9
,
4
,
3
,
2
,
1
,
0
)
,
,
,
(
4
3
2
1
x
x
x
x
y
Czynniki zera odpowiadające stanom nieokreślonym umieszczamy w nawiasie i odpowiednio
przenosimy do drugiej kolumny. Wykorzystujemy je do sklejania z czynnikami
odpowiadającymi stanom określonym.
)
1111
(
)
1101
(
)
0111
(
)
0101
(
1110
1100
1010
1000
0110
)
1111
(
)
1101
(
)
0111
(
1110
)
0101
(
1100
1010
0110
1000
111
110
0
11
10
1
011
110
00
1
0
10
11
11
0
1
0
1
Implicenty proste
Czynniki zera
0110
1000
1010
1100
1110
110
0
1
11
11
Zestaw implicentów prostych oznaczonych symbolem
pochłania wszystkie czynniki zera
postaci kanonicznej, zatem:
)
(
)
(
3
2
4
1
x
x
x
x
y
Wyszukiwarka
Podobne podstrony:
minimalizacja funkcji logicznych
Algorytmy genetyczne w minimalizacji funkcji logicznych 5 część 2
Minimalizacja funkcji logicznych 3
Algorytmy genetyczne w minimalizacji funkcji logicznych 5 część 1
Algorytmy genetyczne w minimalizacji funkcji logicznych 5 część 3
Minimalizacja funkcji logicznych[1]
minimalizacja funkcji logicznych
Algorytmy genetyczne w minimalizacji funkcji logicznych Karina Murawko
Instrukcja do zad proj 10 Podstawowe funkcje logiczne z z
04 Rozdział 02 Różniczkowanie funkcji wielu zmiennych
cw 6 Synteza układów kombinacyjnych- realizacja sprzętowa funkcji logicznych
02 Pochodna funkcji o dziedzinie jednowymiarowej (2)
Pomiary wielkosci elektrycznych Minimalizacja funkcji tablica
Porównać metody realizacji funkcji logicznych
Badanie Funkcji Logicznych
Porównać metody realizacji funkcji logicznych, cwiczenie 2
więcej podobnych podstron