Na początku pozwolę sobie przedstawić ogólny problem związany ze stosowaniem algorytmów genetycznych. Otóż algorytmami genetycznymi nazywamy algorytmy poszukiwania oparte na mechanizmach doboru naturalnego oraz dziedziczności. Łącząc w sobie ewolucyjną zasadę przeżycia najlepiej przystosowanych z systematyczną , choć zrandomizowaną wymianą informacji , tworzą metodę poszukiwania obdarzoną jakąś dozą pomysłowości właściwej umysłowi ludzkiemu. W każdym pokoleniu powstaje nowy zespół sztucznych organizmów ( czyli ciągów bitowych, utworzonych z połączenia fragmentów najlepiej przystosowanych przedstawicieli poprzedniego pokolenia; prócz tego sporadycznie wypróbowuje się nową część składową . Pomimo elementu losowości , algorytmy genetyczne nie sprowadzają się do zwykłego błądzenia przypadkowego. Wykorzystują zjawisko takie, że używają efektywnie przeszłego doświadczenia do określania nowego obszaru poszukiwań o ocze3kiwanej zwiększonej wydajności.

Swego czasu John Holland oraz jego koledzy i studenci z Uniwersytetu Michigan rozwinęli algorytmy genetyczne. Mieli oni podwójny cel badań: po pierwsze chcieli przybliżyć i wyjaśnić ściśle procesy adaptacyjne występujące w świecie przyrody oraz, po drugie wytworzyć na użytek systemów konstruowanych przez człowieka programy, które odtwarzałyby podstawowe mechanizmy rządzące systemami biologicznymi. Takie postawienie problemu przyniosło wymierne, ważne efekty w postaci odkryć w badaniach systemowych.

Główną istotą w badaniach dotyczących algorytmów genetycznych jest odporność, czyli tak zwany kompromis między efektywnością a skutecznością konieczną do przeżycia w przeróżnych środowiskach. Na użytek systemów wytw3awrzanych przez człowieka implikacje odporności są wielorakie. Jeśli umiemy skonstruować odporny system techniczny , to możemy sobie zaoszczędzić kosztownych przeróbek , a nawet całkiem je wykluczyć. Jeżeli osiągniemy wyższy stopień adaptacji , to istniejące systemy będą mogły pracować i lepiej , i dłużej . Konstruktorzy systemów - komputerowych , inżynierskich, a także ekonomicznych- mogą tylko podziwiać odporność , wydajność i łatwość przystosowania się systemów biologicznych. Bycie zdolnym do regeneracji samosterowania i reprodukcji , będące regułą w świecie biologii , jest prawie nieobecne w świecie najbardziej nawet zaawansowanej techniki. Tak więc dochodzimy do interesującej rzeczy- tam , gdzie odporność jest cechą pożądaną (czyli wszędzie) , przyroda radzi sobie lepiej; tajemnice adaptacji i umiejętności przeżycia można najlepiej poznać , studiując uważnie przykłady ze świata biologicznego. Ale to nie wyłącznie doskonałość natury skłania nas do przyjęcia metody algorytmu genetycznego. Otóż dowiedziono już teoretycznie i na podstawie doświadczeń , że algorytmy genetyczne stanowią odporną metodę przeszukiwań w skomplikowanych przestrzeniach. Można tutaj dołączać wiele przykładów nawet z codziennego życia. Podstawową publikacją na ten interesujący temat jest praca słynnego Hollanda, napisana w 1975r. Na temat “Adaptation in Natural and Artificial; Systems”. Również w wielu artykułach , publikacjach i rozprawach naukowych zauważono i potwierdzono skuteczność tej techniki w sprawach związanych z optymalizacją i sterowaniem. Jeśli posiadamy już ustaloną markę jako odpowiednie narzędzie do efektywnego i skutecznego poszukiwania , algorytmy genetyczne coraz szersze kręgi zastosowań w środowiskach naukowych, informatycznych, inżynierskich i w kręgach biznesu. Jest oczywista przyczyna tej rosnącej liczby zainteresowań- algorytmy genetyczne stanowią nieskomplikowane , a przy tym potężne narzędzie poszukiwania lepszych rozwiązań. Można powiedzieć więcej- są one wolne od zasadniczych ograniczeń nakładanych przez mocne założenia o przestrzeni poszukiwań(takie jak na przykład ciągłość , istnienie pochodnych, jednomodalność funkcji celu i temu podobne). Przed zbadaniem przyczyn tych atrakcyjnych wiadomości zajmijmy się najpierw odpornością powszechnie stosowanych w poszukiwaniach technik.

Zastanówmy się czy tradycyjne metody poszukiwania spełniają nasze kryteria odporności. W dostępnej literaturze przedmiotu wyróżnia się trzy główne rodzaje metod poszukiwania – analityczne , przeglądowe (enumeratywne) oraz losowe. Przyjrzyjmy się bliżej tym metodom , aby stwierdzić , czy można wyciągać jakieś wnioski na ten temat bez Rys.1.:

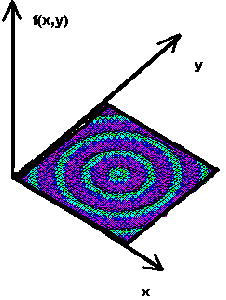
przeprowadzania formalnych badań empirycznych. Metody analityczne były przedmiotem intensywnych studiów . Można je podzielić na dwie klasy : metody pośrednie i metody bezpośrednie . Jeżeli chodzi o metody pośrednie, to poszukujemy lokalnych ekstremów rozwiązując układ równań (zazwyczaj nieliniowych) otrzymanych przez porównanie gradientu funkcji celu do zera. Jest to uogólnienie na przypadek wielowymiarowy znanej z elementarnego rachunku

różniczkowego metody punktów krytycznych - patrz rysunek 1. Jeśli mamy do czynienia z funkcją gładką , określoną na obszarze otwartym, to poszukiwanie potencjalnych maksimów możemy ograniczyć do zbioru punktów , w których nachylenie stycznej do wykresu funkcji jest równe zeru w każdym kierunku. Bezpośrednie metody poszukiwania lokalnego maksimum polegają na “skakaniu” po wykresie funkcji w kierunku wyznaczonym przez lokalny gradient. Rozpoznajemy tu zasadę górskiej wspinaczki : aby dostać się na lokalny wierzchołek , wspinaj się po zboczu wzdłuż najbardziej stromej z możliwych dróg. Mimo że metody analityczne jednego i drugiego rodzaju były wielokrotnie ulepszane , rozszerzane oraz przerabiane na różne sposoby , wystarcza proste rozumowanie , aby pokazać , jak mało są odporne.

Wyliczmy te cechy ich braku odporności – po pierwsze , obie metody mają zakres lokalny, szukają bowiem optymalnego rozwiązania w sąsiedztwie danego punktu. Przypuśćmy , że znajdą one lokalne maksimum, które nie jest maksimum globalnym. Co gorsza , po znalezieniu niższego wierzchołka nie możemy już poprawić rozwiązania bez powtórzenia całego procesu z losowego punktu startowego lub zastosowania innych chwytów. Następnie , zastosowanie metod analitycznych jest uzależnione od istnienia pochodnych (czyli dobrze określonych kątów nachylenia). Jeżeli nawet dopuścimy numeryczną aproksymację pochodnych , to jest to dalej poważne ograniczenie. W praktyce, wiele spotykanych przestrzeni parametrów nie wykazuje przesadnego respektu wobec pojęcia pochodnej i wynikającej z niego pojęcia gładkości funkcji. Teoretycy , którzy zajmują się optymalizacją byli zanadto skorzy do przejęcia dziedzictwa po wielkich matematykach XVII i XIX wieku,, którzy nakreślili obraz nieskażonego świata kwadratowych funkcji celu , idealnych węzłów i wszechobecnych pochodnych. Tak naprawdę , w rzeczywistości świat optymalizacji pełen jest nieciągłości i przepastnych przestrzeni o skomplikowanej topologii , jak pokazuje przykład mniej podatnej na metody analityczne funkcji, pokazanej na rysunku 2. Tak więc , nikogo nie zaskakuje , że metody wymagające spełnienia arbitralnych założeń o ciągłości oraz istnieniu pochodnych mają raczej ograniczony zakres zastosowań. Z tego względu , a również z uwagi na nieodłącznie lokalny charakter działania metod analitycznych, jesteśmy zmuszeni je odrzucić. Metody te są mało odporne poza

przewidzianym dla siebie obszarem zastosowań. Rozważano wiele rozmaitych metod enumeracyjnych. Idea jest całkiem oczywista: mając skończoną przestrzeń poszukiwań ( lub dyskretny odpowiednik przestrzeni nieskończonej), algorytm oblicza

wartości funkcji celu , przeglądając po kolei wszystkie punkty przestrzeni.

Chociaż ten rodzaj algorytmu jest atrakcyjny ze względu na prostotę i przypomina typowo ludzki sposób rozwiązywania problemów (gdy liczba możliwości jest niewielka), jednak ostatecznie musimy go zdyskwalifikować pod względem odporności z jednego prostego powodu – nieefektywności. W wielu spotykanych w praktyce przypadkach mamy do czynienia z przestrzeniami, które są zbyt wielkie na to , by sprawdzanie wszystkich ich elementów po kolei mogło zakończyć się znalezieniem użytecznej odpowiedzi. Programowanie dynamiczne , cieszące się ostatnio wielkim rozgłosem , również załamuje się na zadaniach o umiarkowanym rozmiarze i złożoności z powodu dolegliwości nazwanej patetycznie przez swego twórcę “przekleństwem wymiaru” . Wynika stąd , iż mniej pomysłowe warianty przeglądu są obciążone tą wadą o wiele bardziej.

Algorytmy zwane algorytmami losowego zaczęły cieszyć się rosnącą popularnością z chwilą , gdy badacze zdali sobie sprawę z ograniczeń metod analitycznych i enumeracyjnych. Jednak błądzenie przypadkowe i inne schematy losowe oparte na szukaniu i zapamiętywaniu najlepszego rozwiązania również muszą zostać odrzucone pod względem efektywności. Na dłuższą metę , nie należy się spodziewać przewagi algorytmów poszukiwania losowego nad przeglądowymi. Nie przyjmując i odrzucając tak pospiesznie czysto losowe metody poszukiwania, powinniśmy jednak zachować ostrożność i odróżnić je od technik zrandomizowanych. Algorytm genetyczny jest przykładem procedury używającej wyboru losowego jako przewodnika w prowadzeniu wysoce ukierunkowanego poszukiwania w zakodowanej przestrzeni rozwiązań. Pomysł zastosowania wyboru losowego jako narzędzi do ukierunkowania procesu poszukiwań może wydawać się na pierwszy rzut oka nieco dziwaczny , lecz przyroda dostarcza wielu takich przykładów. W innej popularnej obecnie technice poszukiwania , zwanej symulowanym wyżarzaniem – simulated annealing - , używa się procesów losowych w celu określenia kierunku poszukiwań stanów o minimalnej energii. Związkom miedzy symulowanym wyżarzaniem a algorytmami genetycznymi poświęcona jest niedawno wydana książka Davisa. Rzeczą ważną jest uświadomienie sobie , ze poszukiwanie zrandomizowane nie musi wcale oznaczać szukania na oślep.

Przeprowadzona dyskusja nie stanowi wyczerpującego studium metod tradycyjnej optymalizacji , ale wychodzi z niej niepokojący wniosek – konwencjonalne metody poszukiwania są mało odporne. Nie znaczy to , że nie są użyteczne. Wspomniane wyżej techniki , a także niezliczone ich warianty i kombinacje były i są używane z powodzeniem do wielu zastosowań – w miarę jednak , jak stajemy wobec coraz to bardziej złożonych problemów , będą potrzebne nowe metody. Aby spojrzeć na to z lepszej perspektywy , przyjrzyjmy się spektrum problemów uwidocznionemu na rys.3. są tam przedstawione wyimaginowane wykresy efektywności w przekroju problemowym dla metody wyspecjalizowanej, enumeracyjnej oraz idealnej “metody odpornej”. Technika gradientowa – jak należało się spodziewać – daje dobre wyniki dla wąskiej klasy

p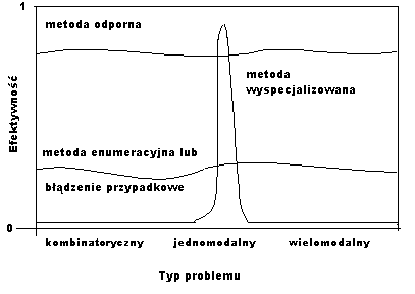 roblemów, ale szybko przestaje być efektywna poza nią. Metoda przeglądowa charakteryzuje się egalitarną nieefektywnością w całym spektrum problemowym , co pokazuje krzywa niższej wydajności. O wiele bardziej pożądane byłoby zachowanie reprezentowane przez krzywą oznaczoną jako metoda odporna. Opłaca się poświęcić szczytową efektywność osiąganą dla szczególnego typu problemów w zamian za stosunkowo wysoką wydajność w całym spektrum. Mając ogólne metody o dużej efektywności, możemy zawsze za pomocą hybrydyzacji skonstruować metodę łączącą cechy najlepszego algorytmu lokalnego i ogólniejszej metody odpornej.

Do czego dązymy chcąc zoptymalizowac funkcję lub proces? W1979r. Wypowiedział się na temat Beightler:

“Dążenie człowieka do perfekcji znajduje swój wyraz w teorii optymalizacji. Zajmuje się ona tym , jak opisać i osiągnąć najlepsze, gdy wiemy już , jak mierzyć i zmieniać Dobre i Złe ... . Teoria optymalizacji obejmuje studia ilościowe rozwiązań optymalnych i metody ich wyznaczania.”

Celem optymalizacji jest zwiększanie efektywności aż do osiągnięcia pewnego optimum. Zwróćmy uwagę , że powyższa definicja składa się z dwóch części – 1- staramy się zwiększyć efektywność do 2 – wartości optymalnej. Jest tu wyraźne rozróżnienie między procesem ulepszania a jego punktem docelowym , czyli samym optimum. Jednakże dokonując oceny wartości procedur optymalizacyjnych zwykle koncentrujemy się wyłącznie na zbieżności – czy metoda osiąga optimum?, a zapominamy zupełnie o efektywności procesu poszukiwania. Przyczyną tego nacisku są analityczne źródła teorii optymalizacji.

Nie jest to jednak absolutnie czymś naturalnym. Wyobraźmy sobie człowieka podejmującego decyzje , na przykład biznesmena. Jaka jest podstawa jego oceny? Biznesmena ocenia się stosownie do jego zdolności konkurencyjnych. Czy produkuje lepszy model? Czy sprawniej dostarcza go na rynek? Czy zapewnił lepszą promocję? Nigdy nie oceniamy biznesmena na podstawie tego , czy osiągnął możliwy najlepszy wynik, perfekcja jest stanowczo zbyt surowym

- 2 -