Algorytmy genetyczne - ewolucyjne projektowanie układów cyfrowych.

Piotr Kulik i Marcin Dłużak gr 23SPIS TREŚCI:

1. Konwencjonalne a ewolucyjne projektowanie układów cyfrowych.

2. Algorytmy genetyczne - teoria:

2.1 Co to są algorytmy genetyczne i jak działają?

2.2 Selekcja.

2.3 Krzyżowanie.

2.4 Mutacja.

3. Algorytmy genetyczne - projektowanie układów cyfrowych:

3.1 Dwubitowy sumator z przenośnością.

3.2 Dwubitowy mnożnik.

4. Wnioski.

5. Dodatek - Algorytmy genetyczne a maksimum funkcji.

6. Literatura.

1. KONWENCJONALNE A EWOLUCYJNE PROJEKTOWANIE UKŁADÓW CYFROWYCH

Projektowanie układów logicznych to złożone zadanie, wymagające znajomości zasad specyficznych dla danej dziedziny. Proces implementacji danego układu wymaga:

- przekształcenia oryginalnych parametrów danego układu w celu osiągnięcia formy możliwej do zrealizowania przy pomocy danej technologii (np. użycie odpowiednich typów bramek);

- zminimalizowania reprezentacji;

- zoptymalizowania reprezentacji z uszanowaniem zdefiniowanych ograniczeń (np. charakterystyki czasowe);

- odwzorowania technologicznego na dane urządzenie;

Ostatnio przeprowadzone badania dowiodły, że możliwe jest projektowanie układów cyfrowych w zupełnie inny sposób. To nowe podejście jest określane teorią „czarnej skrzynki” - implementacja układu jest równoważna projektowaniu czarnej skrzynki, z takimi wejściami i wyjściami, aby na podstawie sygnałów wejściowych otrzymywać żądane sygnały na wyjściach. Charakterystyczną cechą tej teorii jest kodowanie szczegółów wewnątrz skrzynki w postaci chromosomów i poddawanie ich procesom algorytmów ewolucyjnych. Sprawność poszczególnego chromosomu jest mierzona całkowicie jako stopień zachowania wyjść czarnej skrzynki w pewien żądany sposób.

Dotychczas większość systemów elektronicznych, o różnej złożoności, była tworzona przez projektantów, którzy w pewien szczególny sposób wykonywali określone operacje na pojedynczych, elektronicznych komponentach, a następnie używali tych samych metod postępowania do konstruowania dużych systemów w oparciu o podstawowe części. Powstała jednak opozycyjna do tej metody, a mianowicie metoda projektowania ewolucyjnego. W przypadku projektowania konwencjonalnego jakość gotowego produktu zależy wyłącznie od wiedzy i doświadczenia danego projektanta. Natomiast projektowanie ewolucyjne pozwala na odkrycie znacznie bogatszego zestawu rozwiązań.

Poniższy rysunek przedstawia różnice pomiędzy konwencjonalnym a ewolucyjnym podejściem do projektowania układów cyfrowych:

Rys. 1

specyficzna

Aby projektowanie ewolucyjne, oparte na algorytmach genetycznych mogło przewyższyć konwencjonalne projektowanie pod względem odporności, musi się od niego różnić pod kilkoma zasadniczymi względami. Różnice są następujące:

1. Algorytmy genetyczne nie przetwarzają bezpośrednio parametrów zadania, lecz ich zakodowaną postać;

2. Algorytmy genetyczne prowadzą poszukiwania, wychodząc nie z pojedynczego punktu, lecz z pewnej ich populacji;

3. Algorytmy genetyczne korzystają tylko z funkcji celu, a nie z jej pochodnych lub innych pomocniczych informacji;

4. Algorytmy genetyczne stosują probabilistyczne, a nie deterministyczne reguły wyboru;

2. ALGORYTMY GENETYCZNE - TEORIA.

2.1 CO TO SĄ ALGORYTMY GENETYCZNE I JAK DZIAŁAJĄ?

Algorytmy genetyczne są to algorytmy poszukiwania, oparte na mechanizmach doboru naturalnego oraz dziedziczności. Łącząc w sobie ewolucyjną zasadę przeżycia, najlepiej przystosowanych jednostek, z systematyczną, choć zrandomizowaną wymianą informacji, tworzą metodę poszukiwania obdarzoną pomysłowością, która jest właściwa dla umysłu ludzkiego. W każdym pokoleniu powstaje nowy zespół sztucznych organizmów (ciągów bitowych), utworzonych z połączenia fragmentów najlepiej przystosowanych przedstawicieli poprzedniego pokolenia. Oprócz tego sporadycznie wypróbowuje się również nową część składową. Pomimo elementu losowości, algorytmy genetyczne nie sprowadzają się do błądzenia. Wykorzystują one efektywnie, przeszłe doświadczenie do określenia nowego obszaru poszukiwań o spodziewanej podwyższonej wydajności.

Algorytmy genetyczne zostały rozwinięte przez Johna Hollanda oraz jego kolegów i studentów z Uniwersytetu Michigan. Cel ich badań był dwojaki:

1. Opisać i wyjaśnić w sposób ścisły istotę procesów adaptacyjnych występujących w przyrodzie;

2. Stworzyć na użytek systemów konstruowanych przez człowieka oprogramowanie, które odtwarzałoby podstawowe mechanizmy rządzące systemami biologicznymi. Takie postawienie problemu zaowocowało ważnymi odkryciami w badaniach systemowych.

Centralnym tematem w badaniach dotyczących algorytmów genetycznych jest odporność - kompromis między efektywnością a skutecznością konieczną przeżycia w różnorodnych środowiskach. Dla systemów wytwarzanych przez człowieka implikacje odporności są wielorakie. Jeśli potrafimy skonstruować odporny system techniczny, to możemy sobie zaoszczędzić kosztownych przeróbek, a nawet całkiem je wyeliminować. Jeśli uda się osiągnąć wyższy stopień adaptacji, to istniejące systemy będą mogły funkcjonować dużo lepiej i o wiele dłużej.

Konstruktorzy systemów - inżynierskich, komputerowych, jak też ekonomicznych - mogą tylko podziwiać odporność, wydajność i łatwość przystosowania się systemów biologicznych. Zdolność do regeneracji, samosterowania i reprodukcji, będąca regułą w świecie biologii, jest prawie nieobecna w świecie najbardziej nawet zaawansowanej techniki.

Tam, gdzie odporność jest cechą pożądaną, przyroda radzi sobie lepiej. Tajemnice adaptacji i umiejętności przeżycia można najlepiej poznać, studiując uważnie przykłady ze świata biologicznego. Jednak nie wyłącznie „doskonałość natury” skłania nas do przyjęcia metody algorytmu genetycznego. Dowiedziono teoretycznie i empirycznie, że algorytmy genetyczne stanowią „odporną” metodę poszukiwania w skomplikowanych przestrzeniach. W wielu artykułach i rozprawach naukowych stwierdzono przydatność tej techniki w zagadnieniach związanych z optymalizacją i sterowaniem. Mając już ustaloną markę jako odpowiednie narzędzie do efektywnego i skutecznego poszukiwania, algorytmy genetyczne zdobywają coraz szersze obszary zastosowań w środowiskach naukowych, inżynierskich i w kręgach biznesu. Przyczyna rosnącej liczby zastosowań jest oczywista: algorytmy genetyczne stanowią nieskomplikowane, a przy tym potężne narzędzie poszukiwania lepszych rozwiązań. Co więcej są one wolne od zasadniczych ograniczeń nakładanych przez mocne założenia o przestrzeni poszukiwań (takie jak ciągłość, istnienie pochodnych, jednomodalność funkcji celu i temu podobne).

Algorytmy genetyczne odwzorowują naturalne procesy, takie jak selekcja, rekombinacja, mutacja, migracja, rejon oraz sąsiedztwo. Pracują one na populacjach jednostek, a nie na pojedynczych rozwiązaniach.

Na początku liczba jednostek (populacja) jest inicjowana losowo. Następnie oceniana jest funkcja dla tych jednostek. Powstaje pierwsze pokolenie. Jeśli nie są spełnione kryteria optymalizacji rozpoczyna się tworzenie nowego pokolenia. Jednostki są wybierane odpowiednio do ich sprawności, w celu wytworzenia potomstwa. W tym celu następuje rekombinacja rodziców. Wszyscy potomkowie mutują według pewnego prawdopodobieństwa. Następnie wstawia się potomków w miejsce rodziców, tworząc nową generację. Ten cykl jest powtarzany aż do momentu, w którym kryteria optymalizacji zostaną spełnione.

Poniższy rysunek przedstawia strukturę prostego algorytmu genetycznego:

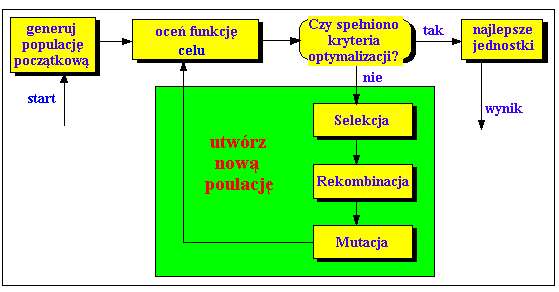
Rys. 2:

Algorytm ewolucyjny dla pojedynczej populacji jest mocny i wykonuje się dobrze dla szerokiej skali problemów. Jednakże lepsze rezultaty można uzyskać poprzez wprowadzenie wielu populacji, zwanych subpopulacjami. Każda subpopulacja rozwija się w kilka odrębnych pokoleń, do momentu, kiedy jedna lub kilka jednostek powtórzy się w każdej subpopulacji. Multipopulacyjny algorytm genetyczny odwzorowuje ewolucję gatunku w sposób bardziej zbliżony do natury niż jednopopulacyjny.

Z powyższych twierdzeń wynika, że algorytmy ewolucyjne różnią się znacznie od wielu tradycyjnych metod poszukiwania i optymalizacji. Najbardziej znaczące różnice:

1. Algorytmy genetyczne poszukują populacji zbliżonych rozwiązań, a nie jednego rozwiązania;

2. Algorytmy genetyczne nie wymagają żadnej pomocniczej wiedzy; wystarczy znajomość funkcji oraz odpowiednich poziomów sprawności wpływających na kierunki poszukiwań;

3. Algorytmy genetyczne używają prawdopodobnych zasad przejść, a nie z góry ustalonych;

4. Algorytmy genetyczne dostarczają pewną ilość potencjalnych rozwiązań danego problemu, natomiast ostateczny wybór jest pozostawiony użytkownikowi;

5. Algorytmy genetyczne są prostsze do zastosowania;

Poniższa tabela przedstawia sposób odwzorowania „natury do komputera”:

NATURA	KOMPUTER
jednostka	Rozwiązanie problemu
populacja	zbiór rozwiązań
sprawność	jakość rozwiązania
chromosom	Reprezentacja rozwiązania (np. zbiór parametrów)
gen	część reprezentacji rozwiązania (np. stopień wolności)
wzrost	Rozkodowanie reprezentacji rozwiązań
mutacja	Poszukiwanie operatora
naturalna selekcja	ponowne użycie dobrych rozwiązań

Przykład:

Problem: znaleźć liczbę {0, 1, ..., 255}, której reprezentacja binarna zwiera maksymalną liczbę przejść 0 - 1;

Rozwiązanie: 85 (01010101)

Założenia:

• chromosomy: 8 bitów (bajt);

• rozszyfrowywanie: konwersja z reprezentacji binarnej na dziesiętną;

• ocena sprawności: konwersja z reprezentacji dziesiętnej na binarną i liczenie przejść 0 - 1;

• populacja: 10 jednostek;

• selekcja: wybranie pięciu najlepszych jednostek do łączenia;

• klonowanie: każda z wybranych jednostek jest kopiowana;

• rekombinacja: obcięcie dwóch znaków z dowolnej pozycji i umieszczenie ich z lewej strony;

• mutacja: nie zachodzi

I. Inicjalizacja:

#	Chromosom	Rozwiązanie	Sprawność
a b c d e f g h i j	10010111 01010100 11101010 00101001 11011011 10111110 01001110 10010010 00100011 11110100	151 84 234 41 219 190 78 146 35 244	2 3 2 3 2 1 2 2 2 1
Średnia			2.0

II. Selekcja:

#	Chromosom	Rozwiązanie	Sprawność
b d a c e	01010100 00101001 10010111 11101010 11011011	84 41 151 234 219	3 3 2 2 2
g h i f j	01001110------- 10010010------- 00100011------- 10111110------- 11110100-------	78 146 35 190 244	2 2 2 1 1

III. Nowa populacja po klonowaniu:

#	Chromosom	Rozwiązanie	Sprawność
b d a c e	01010100 00101001 10010111 11101010 11011011	84 41 151 234 219	3 3 2 2 2
Średnia			2.4

IV. Łączenie:

#	Chromosom	Rozwiązanie	Sprawność
b a	010 10100 100 10111	84 151	3 2
b+a	01010111	87	3
d b	001010 01 010101 00	41 84	3 3
d+b	00101000	40	2
a c	10 010111 11 101010	151 234	2 2
a+c	10101010	170	3
b e	0101010 0 1101101 1	84 219	3 2
b+e	01010101	85	4
e d	1101 1011 0010 1001	219 41	2 3
e+d	11011001	217	2

V. Nowa populacja (po sortowaniu):

#	Chromosom	Rozwiązanie	Sprawność
b+e b b+a d a+c a c e d+b e+d	01010101 01010100 01010111 00101001 10101010 10010111 11101010 11011011 00101000 11011001	85 84 87 41 170 151 234 219 40 217	4 3 3 3 3 2 2 2 2 2
Średnia			2.6

Wnioski:

• Rozwiązanie zostało otrzymane po jednym pokoleniu, zwykle potrzeba wielu pokoleń.

• Średnia sprawność populacji rośnie z pokolenia na pokolenie.

• Dobre rozwiązania mają podobne łańcuchy binarne (np. blok 010101 jest taki sam dla 4 pierwszych rozwiązań).

2.2 SELEKCJA:

Selekcja jest operacją, na podstawie której jednostki (tj. ich chromosomy) są wybierane do operacji łączenia. W celu jak najlepszej emulacji naturalnej selekcji, jednostki z wyższą sprawnością powinny być wybierane z większym prawdopodobieństwem. Istnieje wiele różnych metod selekcji (kilka z nich jest biologicznie nieprawdopodobnych). Oto najbardziej znane z nich:

* selekcja „koła ruletkowego”:

Jest to najprostszy rodzaj selekcji, zwany również stochastycznym pobieraniem próbki z zamianą. Jest to algorytm stochastyczny oparty na następującej technice:

Jednostki są odwzorowywane do sąsiednich segmentów linii, tak że segment każdej jednostki jest równoważny (pod względem rozmiaru) jej sprawności. Następnie generowana jest losowa liczba oraz jednostka, której segment ta liczba obejmuje. Proces jest powtarzany, aż do momentu otrzymania żądanej liczby jednostek. Ta technika jest analogiczna do ruletki, gdzie każde pole jest proporcjonalne w rozmiarze do sprawności (patrz rys. 3).

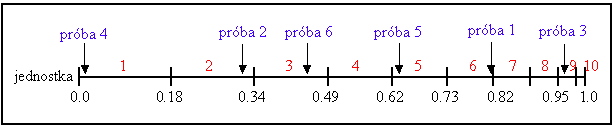
Rys. 3:

Jeśli założymy, że:

sprawność jednostki i

średnia sprawność populacji,

prawdopodobieństwo wybrania jednostki i obliczamy ze wzoru:

Poniższa tabela przedstawia prawdopodobieństwo wyboru dla 11 jednostek, liniowe zaszeregowanie oraz selektywny nacisk razem z wartością sprawności. Jednostka 1 jest najbardziej odpowiednią jednostką i zajmuje największy przedział, podczas gdy jednostka 10 jako druga, najmniej odpowiednia jednostka, ma najmniejszy przedział na linii (rys.3). Jednostka 11, najmniej odpowiedni przedział, ma wartość sprawności 0 i nie ma szans na reprodukcję.

Numer jednostki	1	2	3	4	5	6	7	8	9	10	11
Wartość sprawności	2.0	1.8	1.6	1.4	1.2	1.0	0.8	0.6	0.4	0.2	0.0
Prawdopodobieństwo wyboru	0.18	0.16	0.15	0.13	0.11	0.09	0.07	0.06	0.03	0.02	0.0

W celu wybrania populacji do łączenia, generowana jest odpowiednia ilość losowych liczb (jednolicie rozmieszczonych pomiędzy 0.0 i 1.0), np.: 0.81, 0.32, 0.96, 0.01, 0.65, 0.42. Rys. 3 przedstawia proces wyboru jednostki dla przykładu z powyższej tabeli, razem z przykładowymi próbkami. Po selekcji populacja do łączenia zawiera jednostki 1, 2, 3, 5, 6, 9.

Algorytm „koła ruletkowego” dostarcza zerowy ukos (absolutna różnica pomiędzy znormalizowaną sprawnością jednostki a jej oczekiwanym prawdopodobieństwem reprodukcji), ale nie gwarantuje minimum rozpiętości (zasięg możliwych wartości dla liczby potomków danej jednostki).

* selekcja szeregowa:

Jednostki są sortowane (szeregowane) na podstawie ich sprawności, tak że dla każdego i < j f_i ≥ f_j. Następnie dla każdej jednostki wyznaczane jest prawdopodobieństwo wybrania p_i na podstawie danego rozkładu, z ograniczeniem takim, że ∑_i p_i = 1.

Najczęściej spotykane rozkłady:

- liniowy, p_i = a x_i + b (dla a < 0):

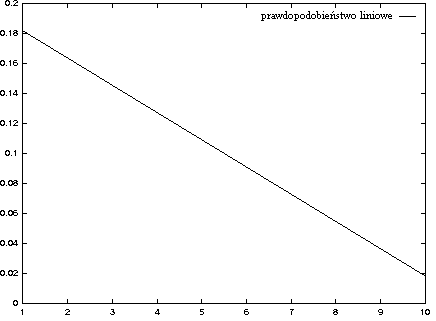
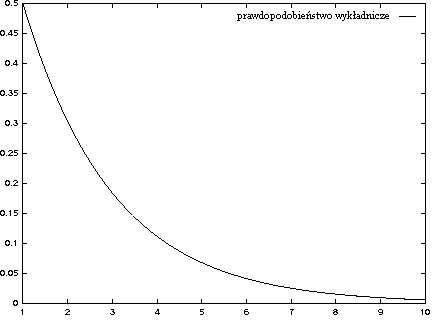
- negatywny wykładniczy: p_i = a exp(b x_i + c)

Jest to równoważne wybieraniu pierwszej jednostki z prawdopodobieństwem p, drugiej z prawdopodobieństwem p², trzeciej p³, ... (p^N < p^N-1 dla p<1).

Zalety:

- brak przedwczesnego upodabniania się jednostek;

- brak zastoju, nawet na końcu N₁ ≠ N₂ ≠ ... ;

- wyraźna sprawność nie jest potrzebna: do uporządkowania jednostek wystarczy jedynie zdolność porównywania par rozwiązań;

Wady:

- skomplikowana teoretyczna analiza upodabniania się;

- małe biologiczne prawdopodobieństwo;

* selekcja turniejowa:

W celu wybrania odpowiedniej jednostki tworzona jest grupa N (N ≥ 2) losowych jednostek. Następnie wybierana jest jednostka o najwyższej sprawności, natomiast pozostałe są odrzucane (turniej). Poniższa tabela przedstawia relację pomiędzy rozmiarem turnieju a intensywnością wybierania.

rozmiar turnieju	1	2	3	5	10	30
intensywność wybierania	0	0.56	0.85	1.15	1.53	2.04

Metoda ta jest wzięta z natury (tylko najsilniejsze jednostki przeżywają).

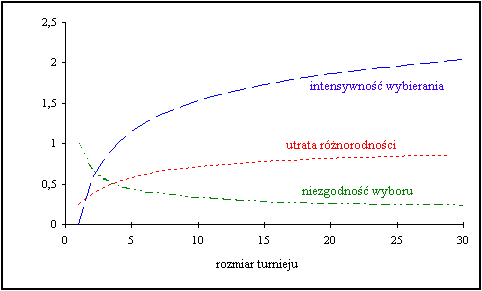
Własności selekcji turniejowej:

intensywność wybierania - oczekiwana średnia wartość sprawności populacji po zastosowaniu metody selekcji do znormalizowanego rozkładu Gaussa;

utrata różnorodności - proporcja jednostek populacji, które nie zostały wybrane w fazie selekcji;

niezgodność wyboru - spodziewana niezgodność rozkładu sprawności populacji po zastosowaniu metody selekcji do znormalizowanego rozkładu Gaussa;

2.3 KRZYŻOWANIE:

* krzyżowanie jednopunktowe:

Krzyżowanie jednopunktowe polega na przecinaniu chromosomów rodziców w losowo wybranym wspólnym punkcie oraz zamianie prawych stron chromosomów.

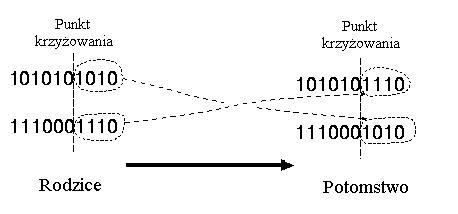
Przykład:

Rozważmy następujące dwie jednostki z 11 binarnymi zmiennymi każda:

Jednostka 1	0 1 1 1 0 0 1 1 0 1 0
Jednostka 2	1 0 1 0 1 1 0 0 1 0 1

Wybrany punkt krzyżowania: 5

Po krzyżowaniu zostały utworzone nowe jednostki:

Potomek 1	0 1 1 1 0 | 1 0 0 1 0 1
Potomek 2	1 0 1 0 1 | 0 1 1 0 1 0

* krzyżowanie wielopunktowe:

W krzyżowaniu wielopunktowym chromosomy są traktowane jako pierścienie z połączonymi pierwszymi i ostatnimi genami. Pierścienie te są przecinane w dwóch miejscach. Następnie następuje zamiana odpowiednich części chromosomów.

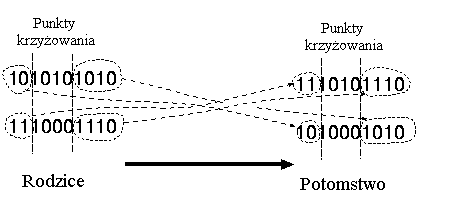
Przykład:

Rozważmy następujące dwie jednostki z 11 binarnymi zmiennymi każda:

Jednostka 1	0 1 1 1 0 0 1 1 0 1 0
Jednostka 2	1 0 1 0 1 1 0 0 1 0 1

Wybrane punkty krzyżowania (m=3): 2 6 10

Po krzyżowaniu zostały utworzone nowe jednostki:

Potomek 1	0 1 | 1 0 1 1 | 0 1 1 1 | 1
Potomek 2	1 0 | 1 1 0 0 | 0 0 1 0 | 0

* krzyżowanie jednolite:

W krzyżowaniu jednolitym każdy gen potomka jest wybierany losowo z odpowiadających mu genów rodziców.

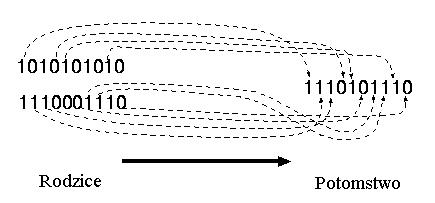
Przykład:

Rozważmy następujące dwie jednostki z 11 binarnymi zmiennymi każda:

Jednostka 1	0 1 1 1 0 0 1 1 0 1 0
Jednostka 2	1 0 1 0 1 1 0 0 1 0 1

Próbka 1	0 1 1 0 0 0 1 1 0 1 0
Próbka 2	1 0 0 1 1 1 0 0 1 0 1

Po krzyżowaniu zostały utworzone nowe jednostki:

Próbka 1	1 1 1 0 1 1 1 1 1 1 1
Próbka 2	0 0 1 1 0 0 0 0 0 0 0

2.4 MUTACJA:

Mutacja odgrywa w działaniu algorytmów genetycznych zdecydowanie drugorzędną rolę. Jest ona niezbędna, ponieważ reprodukcja i krzyżowanie, które skutecznie sondują i zestawiają zachowane poglądy, mogą niekiedy okazać się nadgorliwe i wyeliminować jakiś potencjalnie obiecujący materiał genetyczny (zera lub jedynki na określonych pozycjach). W sztucznych systemach genetycznych mutacja zapobiega takim bezpowrotnym stratom.

W elementarnym algorytmie genetycznym mutacja polega na sporadycznej (tj. zachodzącej z niewielkim prawdopodobieństwem), przypadkowej zmianie wartości elementu ciągu kodowego. W przypadku kodu dwójkowego oznacza to po prostu zamianę jedynki na zero i na odwrót. Sama w sobie mutacja jest błądzeniem przypadkowym w przestrzeni ciągów kodowych. Stosowana oszczędnie, jako dodatek do reprodukcji i krzyżowania stanowi ona swego rodzaju polisę ubezpieczeniową na wypadek utraty ważnych składników rozwiązania.

Mutacja polega na robieniu (zwykle małych) zmian wartości jednego lub wielu genów w chromosomie. W chromosomach binarnych polega to na odwracaniu losowych bitów, np.:

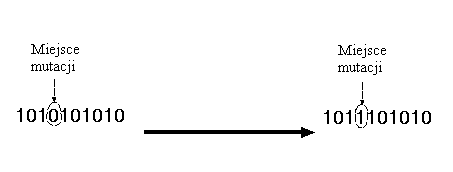
W algorytmach genetycznych mutacja jest metodą używaną raczej do odzyskiwania utraconego materiału genetycznego, niż do poszukiwania lepszych rozwiązań. Mutacja jest stosowana do genów z bardzo małym prawdopodobieństwem p_m:

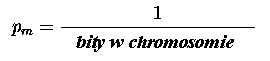
3. ALGORYTMY GENETYCZNE - PROJEKTOWANIE UKŁADÓW CYFROWYCH.

Aby zaprojektować układ cyfrowy przy pomocy algorytmu ewolucyjnego najpierw należy rozważyć, dla każdego układu z osobna, rodzaj geometrii „niezaangażowanych komórek”, które istnieją pomiędzy zbiorem żądanych wejść i wyjść. Niezaangażowane komórki odpowiadają logicznie dwuwejściowemu, jednowyjściowemu modułowi bez określonego działania. Działanie może być ustalone w fazie implementacji jako funkcja dwóch zmiennych. Należy również ustalić połączenia komórek pomiędzy wejściami i wyjściami. Każda logiczna komórka jest w stanie działać jako dowolna dwuwejściowa bramka, lub ewentualnie jako 2-1 multiplexer (MUX) z jednym wejściem kontrolnym.

4.1 DWUBITOWY SUMATOR Z PRZENOŚNOŚCIĄ:

Sumator ten można projektować na dwa sposoby: poprzez użycie dwóch osobnych komponentów sumatora (rys. 4) i przenośnika (rys. 5) lub poprzez użycie kombinacji tych dwóch komponentów (rys. 6).

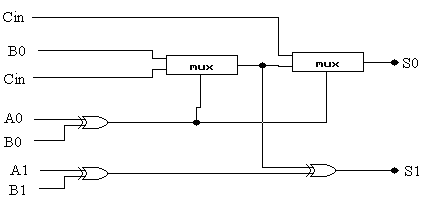
rys.4

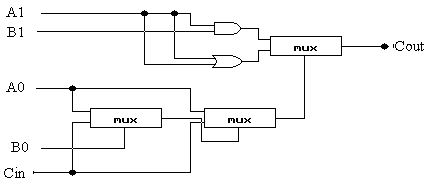
rys.5

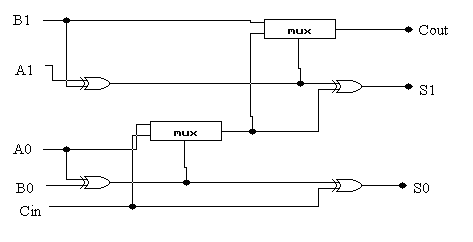
rys. 6

Właśnie w tej drugiej metodzie można bardzo wyraźnie zaobserwować, w jaki sposób ewolucyjny proces uogólnia i tworzy hierarchiczną sekwencję układów. Następnie układy te mogą być poddane analizie projektanta w celu wyznaczenia ogólnej zasady projektowania tego typu układów.

Układ ten był rozwijany przy użyciu geometrii 3 x 3 z następującymi warunkami początkowymi: wielkość populacji = 50, liczba pokoleń = 50 000, liczba przebiegów = 20, tempo rozmnażania = 100%, tempo mutacji = 5%.

W wyniku działania algorytmu genetycznego otrzymaliśmy 5 w pełni sprawnych rozwiązań, które stały się tematem do analizy i usunięcia zbędnych bramek.

4.2 DWUBITOWY MNOŻNIK:

* konwencjonalne dwubitowe mnożniki:

Dwubitowy mnożnik mnoży binarne liczby (A2, A1) przez (B2, B1) w celu uzyskania czterobitowej liczby binarnej (P4, P3, P2, P1), gdzie A2, B2, P4 są bardziej znaczącymi bitami. Układ ten budujemy, w konwencjonalny sposób, na podstawie metody długiego mnożenia, czyli poprzez użycie jednobitowego układu sumatora oraz bramek AND.

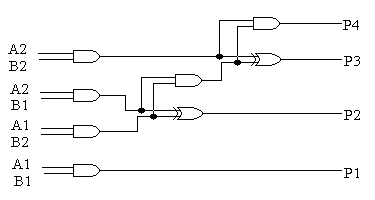
rys. 7 (układ dwubitowego mnożnika):

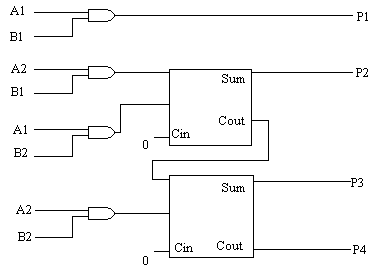
rys. 8 (schemat dwubitowego mnożnika na bramkach):

* ewoluowane dwubitowe mnożniki:

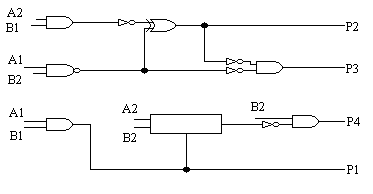
Na rys. 9-11 zostały pokazane trzy najbardziej wydajne układy, które zostały otrzymane w wyniku 50 przebiegów algorytmu genetycznego z populacją o rozmiarze 80. Każdy przebieg kończył się po 60.000 generacji (jeśli nie zostało osiągnięte 100%). Pozostałe parametry zostały takie same jak dla dwubitowego sumatora. 32 z 50 przebiegów wyprodukowały w 100% sprawne rozwiązania. Należy zauważyć, że wszystkie te projekty wymagają tylko 7 komórek, w związku z tym są bardziej wydajne niż te tworzone konwencjonalnie. Również interesujące jest to, że wszystkie otrzymane układy mnożnika składają się z dwóch oddzielnych podukładów. W mnożniku A jeden podukład wytwarza P1 i P3, natomiast drugi P2 i P4, podczas gdy układzie B jeden wytwarza tylko P2, natomiast drugi P1, P3 i P4. W układzie C jeden podukład wytwarza P2 i P3, natomiast drugi P1 i P4. Zauważmy, że w układzie A P2 jest liczone identycznie jak w układzie projektowanym konwencjonalnie, ale później P4 powstaje w zupełnie inny sposób. Oznacza to, że ewolucja dostarcza nam wiele nowatorskich metod budowania układów.

rys. 9 (ewoluowany dwubitowy mnożnik A):

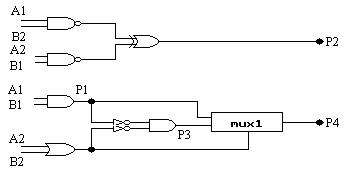
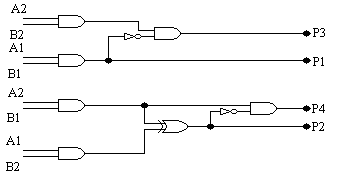
rys. 10 (ewoluowany dwubitowy mnożnik B):

rys. 11 (ewoluowany dwubitowy mnożnik C):

4. WNIOSKI:

Algorytmy genetyczne są przyszłościowymi metodami projektowania układów cyfrowych. Pozwalają one na znaczną oszczędność czasu oraz ograniczenie roli projektanta do sprawdzenia wygenerowanych przez te algorytmy układów oraz wybrania najlepszego z nich. Obecnie ta dziedzina projektowania układów cyfrowych jest intensywnie rozwijana, powstaje specjalne oprogramowanie wykorzystujące algorytmy genetyczne. Jest to być może nowatorski sposób projektowania, lecz niezwykle efektywny, pozwalający na osiągnięcie znacznie lepszych wyników i to w znacznie prostszy sposób niż do tej pory.

Algorytmy genetyczne a maksimum funkcji.

Sztuczna inteligencja (Artificial Intelligence - AI) to temat coraz popularniejszy (i coraz bardziej modny). Jedną z ciekawszych i przyszłościowych gałęzi AI są właśnie algorytmy genetyczne (Genetic Algorithms - GA).

Obecnie istnieje bardzo dużo odmian GA, jednak wszystkie one w mniejszym lub większym stopniu naśladują przyrodę. Wybór jednej z nich zależy przede wszystkim od rodzaju rozwiązywanego problemu. Ja postaram się wyjaśnić działanie Elementarnego Algorytmu Genetycznego (Simple Genetic Algorithm - SGA) i pokazać jak go zastosować do znajdowania maksimum funkcji.

Algorytmy genetyczne opierają się na biologicznej regule naturalnej selekcji i wykorzystują mechanizmy dziedziczenia. Ponieważ owe reguły muszą na czymś operować zaczniemy od zdefiniowania środowiska działania SGA.

W SGA nie uwzględniamy zmian wielkości populacji, w każdym pokoleniu ma ona taką samą liczbę osobników. Dzięki temu do ich zapamiętania wystarczy najzwyklejsza tablica. Do kodowania cech organizmu służą geny, z których każdy może występować w wielu odmianach. Od tego, którą z nich posiada dany osobnik zależy jego charakterystyka. Przykładowo gen odpowiedzialny za kolor oczu może występować w trzech odmianach: kodującej uczy brązowe, zielone lub niebieskie. W przypadku SGA odpowiednikiem genu jest pojedynczy bit, który siłą rzeczy występuje w dwóch odmianach: 0 i 1. W przyrodzie nawet najprostszy organizm posiada wiele genów zgrupowanych w ciągi zwane chromosomami, a zbiór wszystkich genów jednego osobnika nazywany jest jego genotypem. W SGA chromosomem będzie ciąg bitów czyli po prostu liczba zapisana w systemie dwójkowym. Wypadkową cech osobnika jest stopień jego przystosowania do środowiska, który może być potraktowany jako pewna funkcja. Jej argumentami są wszystkie posiadane geny (dokładniej: rodzaje genów znajdujących się na kolejnych pozycjach w chromosomie), a wartością właśnie stopień przystosowania. Najprostszą taką funkcją może być wartość dziesiętna liczby dwójkowej. Tak więc osobnikowi (ciągowi bitów) 100111 będzie odpowiadać wartość funkcji równa 32 + 4 + 2 + 1 = 39 i będzie on uznany za lepiej przystosowanego od osobnika 011110, któremu odpowiada wartość 16 + 8 + 4 + 2 = 30. Funkcja przystosowania w języku angielskim nosi nazwę "fitness", a ponieważ termin ten przyjął się w polskiej literaturze dotyczącej GA ja także będę go używał.

Mając gotowe środowisko, możemy bez problemu opisać mechanizmy selekcji, krzyżo­wania się i mutacji ciągów bitowych. Ponie­waż w tym celu wygodnie będzie posłużyć się konkretnym przykładem, stwórzmy sobie małą populację składającą się z sześciu ciągów pięciobitowych (początkowa populacja w SGA jest zawsze wybierana losowo):

#	Chromosom	Fittnes
1	00001	1
2	00111	7
3	10110	22
4	00010	2
5	10010	18
6	00101	5

Pod nazwą naturalnej selekcji rozumiemy regułę mówiącą, że osobnik lepiej przystosowany ma szansę mieć większą liczbę potomków. Stwierdzenie "ma szansę" jest bardzo istotne - oznacza ono, że prawdopodobieństwo posiadania potomstwa rośnie wraz z wielkością funkcji fitness, ale nic nie jest do końca zdeterminowane. Zawsze może się zdarzyć, że osobnik słabo przystosowany również dochowa się potomka. Dlatego właśnie w SGA selekcja jest realizowana za pomocą losowania, którego przebieg można w wygodny sposób przedstawić za pomocą ruletki (cokolwiek nieuczciwej). Wyobraźmy sobie ruletkę z kołem podzielonym na tyle pól, ilu mamy osobników w populacji (rysunek 1.) przy czym wielkość pola jest proporcjonalna do wartości funkcji fitness.

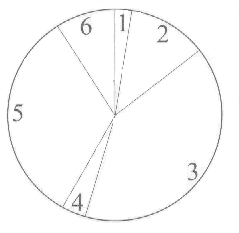
Jeśli teraz kilkakrotnie puścimy ruletkę w ruch i założymy, że kulka może się zatrzymać w dowolnym miejscu tarczy, to łatwo sobie wyobrazić, iż częściej trafi na większe pola niż na mniejsze. Kiedy ruletka wylosuje już parę ciągów­ rodziców możemy przystąpić do ich skrzyżowania. W SGA krzyżowanie przebiega tak jak crossing-over chromosomów w organizmach żywych: ciągi pękają w losowym miejscu i zamieniają się końcami. Załóżmy, że rodzicami są 2. i 3. ciąg, a jako punkt krzyżowania (w terminologii GA nazywanego "crossover") wylosowany został 3 bit. Przebieg całej operacji przedstawia rysunek 2.

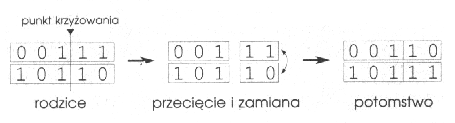
Rys. 2

Jak widać otrzymaliśmy dwa ciągi potomne o innych genotypach (wartościach bitów) niż rodzice. Wraz ze zmianą genotypu zmienia się także stopień przystosowania (wartość funkcji fitness). Dla nowych ciągów wynosi ona:

#	Chromosom	Fittnes
2a	00110	6
3a	10111	23

Krzyżowanie taką metodą zazwyczaj daje podwyższenie fitness jednego z ciągów i obniżenie fitness drugiego. Może się również zdarzyć, że nic się nie zmieni (jeśli zamieniane końce ciągów są takie same). Ponieważ najlepsze ciągi mają sporą szansę być wylosowane (i skrzyżowane) kilkakrotnie, a najgorsze prawdopodobnie nie będą wylosowane wcale, to średnia wartość funkcji fitness populacji powinna rosnąć.

Ostatnią operacją jaką przeprowadza się na ciągach bitowych w każdym kroku SGA jest mutacja. Po zakończeniu krzyżowania każdy bit potomka ma szansę zmutować. Prawdopodobieństwo, że to nastąpi jest bardzo niewielkie (najczęściej kilka przypadków na 100) i stałe dla każdego bitu: Mutujący bit zmienia swoją wartość z 0 na 1 lub z 1 na 0, co odpowiednio prowadzi do podwyższenia lub obniżenia wartości fitness. Powodem, dla którego w ogóle uwzględnia się mutację jest urozmaicenie puli genów. W naszej populacji żaden ciąg nie posiada bitu 1 na drugiej pozycji i krzyżowanie nie może tego zmienić, bo jego wynikiem jest tylko zamiana fragmentów. Brak owej jedynki ogranicza możliwą wartość fitness do 23 (dla ciągu 101111 i dopiero mutacja drugiego bitu pozwoliłaby uzyskać większą wartość, tak jak to widać na rysunku 3.

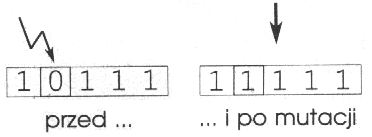
Rys. 3

Mutacja umożliwia także wyjście ze ślepej uliczki, w którą mogtaby zabrnąć populacja. Jeżeli zdarzyłoby się, że do krzyżowania nie zostałyby wybrane ciągi 3. i 5. (pomimo, że są one najlepsze to nie należy zapominać, iż wybór jest losowy) stracilibyśmy jedynkę stojącą na pierwszej pozycji. W każdym następnym kroku najlepszym możliwym do uzyskania ciągiem byłby 01111 i krzyżowanie w żaden sposób nie zmieniłoby tego. Dopiero mutacja pierwszego bitu przywróciłaby możliwość uzyskania największej możliwej wartości funkcji titness.

I to już wszystko czego potrzebujemy! Można teraz - na razie ręcznie - przeprowadzić małą symulację. Z początkowej populacji losujemy sześć ciągów-rodziców:

10110	10010
10010	00101
00111	10010

Najgorsze ciągi 00001 i 00010 nie zostały wcale wylosowane, a jeden z najlepszych 10010 pojawił się aż trzy razy. Następnie dokonujemy skrzyżowania i mutacji kolejnych par. Przedstawia to rysunek 4.

Rys. 4

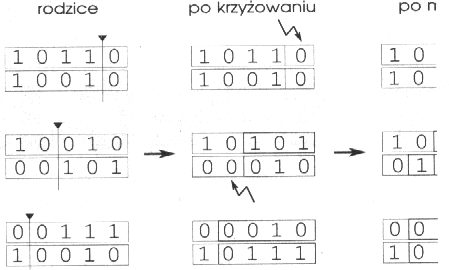
Uzyskaliśmy nową populację, dla której suma funkcji fitness wynosi 97 (dla początkowej populacji wynosiła 55) - jest to wynik selekcji promującej ciągi o wyższej wartości funkcji. Dzięki krzyżowaniu mamy ciągi, których nie było wcześniej:

10111

10101

01010

a mutacja stworzyła nowy gen na pozycji drugiej. Cała początkowa populacja jest zastępowana przez potomstwo i cykl się powtarza: dokonujemy selekcji, krzyżowania, mutacji i zastępujemy stare ciągi nowymi.

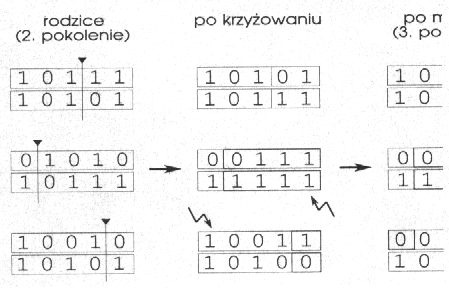
Znowu uzyskaliśmy wyższą sumę fitness - 104, ale nie jest to zmiana tak radykalna jak po pierwszym pokoleniu. Po pewnej liczbie kroków (zależnie od długości ciągu i liczebności populacji) większość osobników będzie posiadała genotyp zapewniający najlepsze przystosowanie lub zbliżony do niego.

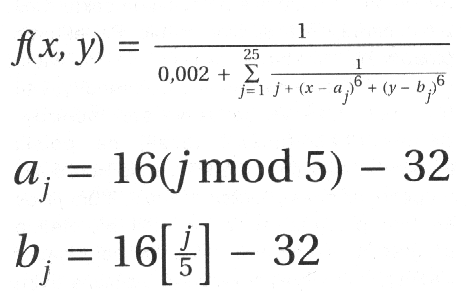
W tym momencie można stwierdzić: jest to niewątpliwie ciekawy i nowatorski algorytm, ale czy do czegokolwiek przydatny? Są przecież łatwiejsze metody znajdowania maksymalnej wartości funkcji. W przypadku nieskomplikowanych funkcji jednowymiarowej na pewno tak. Ale znalezienie metodami analitycznymi maksimum czegoś takiego (jest to jedna z częściej spotykanych funkcji wykorzystywanych do testowania algorytmów genetycznych):

może przysporzyć nieco trudności. W przypadku GA nie musimy wcale zmieniać

algorytmu (!1, a jedynie wymyślić sposób odwzorowania ciągu bitowego na wartości zmiennych x i y.

Standardową metodą odwzorowania używaną, gdy mamy do czynienia z funkcjami wielowymiarowymi jest podział ciągu bitowego na odcinki odpowiadające kolejnym zmiennym. Jeżeli mamy ciąg o długości 20 bitów dzielimy go na dwa fragmenty: bity od 1 do 10 będą kodowały x, a bity od 11 do 20 y. Taki podział widoczny jest na rysunku poniżej.

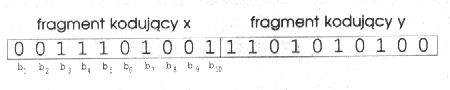
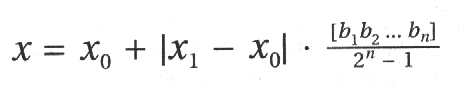
Ponieważ x i y mogą być liczbami rzeczywistymi, to musimy umieć przekształcać dziesięciobitowe liczby całkowite na liczby zmiennoprzecinkowe. Pierwszym krokiem jest obliczenie wartości dziesiętnej odpowiadającej danemu ciągowi (tak jak to było robione we wszystkich poprzednich przykładach). Następnie dzielimy ją przez największą wartość możliwą do zapisania na danej liczbie bitów. W przypadku dziesięciu bitów będzie to 1023 (ciąg 1111111111 ), a ogólnie dla ciągu o długości n bitów - 2^n - 1. W wyniku dzielenia uzyskujemy liczbę rzeczywistą z przedziału [0, 1 ]. Jeżeli minimalną dopuszczalną wartość x oznaczymy przez x0, a maksymalną przez x1, to ostatnim krokiem będzie przekształcenie przedziału [0, 1 ] na [x0, x1 ]. Służy do tego równanie:

Ix1 - x01 to współczynnik skalowania rozciągający lub ściągający odcinek [0, 1j do [x0, x1 ]. XO jest przesunięciem pomiędzy początkiem przedziału [0, 1 ] a początkiem [x0, x1 ]. W dokładnie taki sam sposób przekształcamy wartość zawartą na bitach 11 - 20 kodującą wartość y.

Opisany sposób kodowania wartości rzeczywistych przy pomocy ciągu bitów wraz z SGA daje nam potężne narzędzie: pozwala znaleźć optymalną wartość dowolnej funkcji zależącej od dowolnej liczby zmiennych! Dokładność uzyskanego wyniku zależy tylko od właściwego doboru parametrów: długości ciągu, liczby osobników, prawdopodo­bieństwa wystąpienia mutacji i liczby pokoleń.

Program znajdujący maksimum dowolnej funkcji jednej zmiennej działający w oparciu o algorytm genetyczny. Aby program był maksymalnie zwięzły i nie zajmował zbyt dużo miejsca pozbawiony został wszelkich komentarzy - dla­tego poniżej postaram się wyjaśnić jego działanie.

Na początek parametry, które może (i powinien) zmieniać użytkownik:

- Stałe MIN_X i MAX_X określają przedział w jakim szukamy maksimum. Może on być dowolnie zmieniany, zależnie od analizowa­nej funkcji.

- MIN_Y i MAX_Y określają zakres wartości funkcji. Nie wpływa on na same obliczenia, a jedynie na wielkość i położenie wykresu rysowanego przez program.

- CHROM_SIZE to długość ciągu bitowego (chromosomu) - maksymalnie 31 bitów. Dzięki temu ograniczeniu chromosom moż­na zapamiętać w pojedynczej zmiennej typu ULONG i dodatkowo niektóre kompilatory (StormC) nie będą wyprawiać głupot ze znakiem liczby. Podstawowym kryterium, jakim należy się kierować przy określaniu długości ciągu jest pożądana dokładność wyniku. Można ją obliczyć ze wzoru (MAX_X - MIN_X) / 2^CHROM_SIZE. Dla wartości z listingu wynosi ona około 0.0002.

- POP_SIZE to liczba ciągów w populacji, musi ona być parzysta. Aby algorytm działał szybko nie powinna być zbyt duża (rzędu kilkudziesięciu osobników), jedynie w przypadku bardzo dużego przedziału [MIN_X, MAX_X] można ustalić większą wartość POP_SIZE.

- GENS to maksymalna ilość pokoleń jaka ma zostać wygenerowana. Trudno jest podać regułę określającą optymalną wartość tego parametru: Częściej praca algorytmu genetycznego jest przerywana po uzyskaniu wystarczająco dobrego rozwiązania, a nie po ustalonej liczbie pokoleń.

- PMUTATION określa prawdopodobień­stwo wystąpienia mutacji pojedynczego bitu. Powinno ono być rzędu kilku procent i odwrotnie proporcjonalne do wielkości populacji. Jest to spowodowane tym, że im liczniejsza jest populacja, tym bardziej urozmaicony jest jej materiał genetyczny i nie ma potrzeby wytwarzania nowych genów za pomocą mutacji.

- Funkcję, której maksimum chcemy znaleźć należy zdefiniować jako makro F(x) zwracające wartość typu double. Co będzie zawierać 'w środku' jest zupełnie obojętne, ważny jest jedynie typ wyniku.

Pozostałe deklaracje i definicje nie po­winny być zmieniane - chyba, że chcemy całkowicie zmienić istotę samego algo­rytmu.

Przejdźmy teraz do implementacji. Makrodefinicje 'RND01' i 'RNDRANGE(n)' generują liczby losowe: pierwsza z nich liczby rzeczywiste z przedziału ]0, 1 ], druga całkowite od 0 do n - 1. Makro 'Decode(bin)' przekształca ciąg bitowy na liczbę rzeczywi­stą z przedziału [MIN_X, MAX_X] zgodnie ze wzorem podanym w poprzednim numerze.

Trzy pierwsze funkcje służą do wy­świetlania wyników i myślę, że nie wymagają dokładniejszego opisu. 'Printlnfo' jest wywoływana w każdym pokoleniu i drukuje informacje p bieżących paramet­rach populacji, 'DrawFunetion' rysuje wy­kres funkcji F(x) skalując go tak, aby wypełniał całe okno, a 'DrawPopulation' zaznacza na wykresie poszczególne osob­niki. Następne funkcje stanowią właściwy algorytm genetyczny,

'Randomlnit' losowo inicjalizuje ciągi bitowe składające się na populację. Dwu­krotne użycie rand0 jest spowodowane tym, że zależnie od kompilatora zwraca ono liczbę 16- lub 32-bitową, a my potrzebu­jemy zawsze liczby 32-bitowej. Losowa populacja stanowi dobry start jeśli zupełnie nie wiemy gdzie znajduje się poszukiwane maksimum. W przypadku, gdy mamy jakieś przewidywania co do jego umiejscowienia możemy w jego pobliżu umieścić więcej osobników niż gdzie indziej.

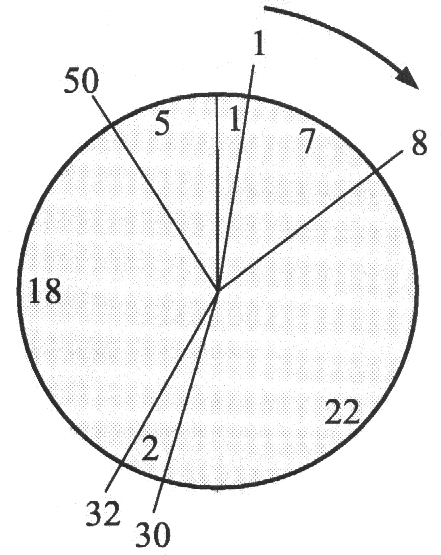
'Select' zwraca numer osobnika wylo­sowanego zgodnie z regułą ruletki opisaną w poprzednim numerze. Zmienna 'Sum­Fitness' zawiera sumę wartości funkcji fitness wszystkich osobników (czyli sumę wszystkich liczb na polach ruletki. Po po­mnożeniu jej przez liczbę losową z prze­działu (0, 1] otrzymamy liczbę z przedziału (0, SumFitness]. Następnie poszukujemy takiego pola ruletki, dla którego suma czę­ściowa będzie nie mniejsza od wylosowa­nej liczby. Liczby na polach ruletki oznaczają wartości funkcji fitness, a liczby na obwodzie to sumy częściowe (kolejno: 1, 1+7, 1+7+22, 1+7+22+2, ...). Załóżmy, że wylosowaliśmy 0.57. Po pomnożeniu przez SumFitness = 55 mamy 31.35 co odpowiada czwartemu polu.

Funkcja 'Mutate' mutuje zadany ciąg bitowy: jeżeli dla danego bitu wylosowano liczbę mniejszą niż prawdopodobieństwo mutacji to następuje jego negacja. Wynika z tego, że w danym ciągu może jednocześnie zmutować kilka bitów - wszystko zależy od stałej PMUTATION.

Ostatnia z funkcji - 'Evolve' - tworzy nowe pokolenie. Najpierw obliczane są war­tości funkcji fitness wszystkich ciągów i ich suma (potrzebna w 'Select'). Następnie w pętli losujemy dwa ciągi-rodziców: 'p1' i 'p2' i punkt krzyżowania 'cp'. Do krzyżowania ciągów używamy masek bitowych 'm1' i 'm2'. Pierwsza z nich wycina bity od punktu krzyżowania do końca ciągu, a druga od początku do punktu krzyżowania. Po utwo­rzeniu potomków za pomocą operacji bitowych dokonujemy ich mutacji i zapamiętujemy w tymczasowej tablicy. Ważne jest aby nie zapamiętywać nowych osobników w oryginalnej tablicy - każdy z zawartych w niej ciągów może być wylo­sowany w dowolnym momencie tworzenia nowej populacji i muszą one pozostać nie­naruszone aż do zakończenia jej tworzenia. Dopiero po zakończeniu pętli przepisujemy nowoutworzoną populację w miejsce oryginalnej. I to już wszystko! W głównej pętli cyklicznie generujemy nowe pokolenia i przedstawiamy je na wykresie. Dzięki temu można obserwować mozolną wspinaczkę kolejnych osobników na najwyższy szczyt. Jak widać na rysunku po 15 pokoleniach mamy już bardzo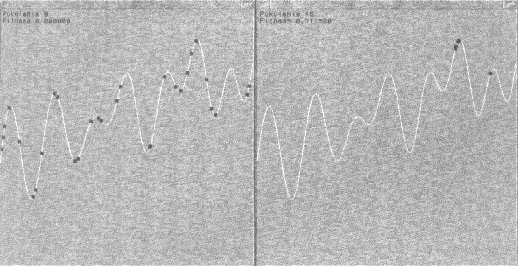
dobry wynik.

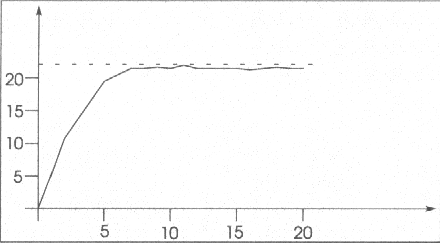
Jeżeli narysujemy wykres sumy wartości funkcji titness dla całej populacji to okazuje się, że po zaledwie 5 (!) pokoleniach jesteśmy bardzo blisko maksimum (linia przerywana). Na wykresie na osi poziomej mamy numer pokolenia, a na osi pionowej sumę fitness, maksimum funkcji F(x) zostało wyliczone analitycznie.

Widać, że suma nie jest stała. Jest to nie do uniknięcia - populacja cały czas się zmienia. Można byłoby temu zaradzić przez ustalenie prawdopodobieństwa mutacji na 0 - wtedy po odpowiednio długim czasie wszystkie ciągi stałyby się takie same. Nie jest to jednak dobry pomysł ponieważ w pierwszych pokoleniach mutacja znacznie pomaga w osiągnięciu maksimum, a czasami bez niej w ogóle nie dałoby się go znaleźć. Można oczywiście zmodyfikować program tak, aby prawdopodobieństwo mutacji malało w kolejnych pokoleniach.

Algorytmy genetyczne - Amiga C

#include <stdlib.h>

#include <stdio.h>

#include <string.h>

#include <math.h>

#include <intuition/screens.h>

#include <pragma/exec_lib.h>

#include <pragma/intuition_lib.h>

#include <pragma/graphics_lib.h>

#include <pragma/dos_lib.h>

#define MIN_X 0.0

#define MAX_X 1.0

#define MINY -1_0

#define MAX_Y 1.0

#define CHROMSIZE 12

#define POP_SIZE 30

#define GENS_50

#define PMUTATION 0.002

#define CHROMMASK \ (Ox7fffffft>>(31-CHROM_SIZE))

ULONG Population[POP SIZE];

double Fitness[POP_SIZE];

double SumFitness,

int Gen;

int Width, Height;

int Left, Top;

struct Window *MYWindow;

struct RastPort *Rast;

#define RND01 \ ((double)(rand())/RAND_MAX)

#define RNDRANGF(n) \ (rand()%(n))

#define F(x) \ ((2*(x)+cos(3*PI*(x)*(x))* \ sin(11*PI*(x)))*0.4-0.2) #define Decode(bin) \ (MIN-X+(MAX_X-MIN_X)* \ (double)(bin)/CHROM-MASK) void PrintInfo(void) {

int fhght=Rast->Txlieight;

char buf[32];

SetAPen(Rast,l);

sprintf(buf,"Pokolenie Rd", Gen);

Move(Rast,Laft+4,iop+tlighC);

Text(Rast,buf,strlen(buf));

sprintf(buf,'Fit.ness Xf", SumFitness/POP_SIZE);

Move(Rast,left+h.,TOp+fhght*2);

Text(Rast,buf,strlen(buf));

};

void DrawFunction(void) {

SetAPen(Rast,2);

int xe, ye;

for(int i=0, 1<Width, i++)

{

double_x = (MAX_X - MIN_X)*((double)(i)/Width)+MIN_X;

double_y = (F(x) - MIN_Y) / (MAX_Y - MIN_Y);

if(i > 0)

Move(Rast,xe,Ye);

xe--Left+(int)(x*Width);

ye-Top+(int)(Heightl­(int)(y*Height));

if(i>0) Draw(RaSt,xe,ye);

};

};

void DrawPopulation(void) {

SetAPen(Rast,l7T @or-(intr i~l i<POP_ńlZEl i++) ł

douhle x°Decode(Population[1]); double y=(F(x)-MIN_Y)/ (MAX Y-MIN_Y)r

9nt xe=Left+(int)(x*Width); int ye=Top+Height-1­(int)(y* Height), RectFill(Rast,xe-2,ye-2,

xe+?. Ye+2); l:

ł:

void Randomtnit(void) ł forint 1=0. 1<POP_SIZE; 1++) Population[1]=(randC)~ (rand() «16))&CHROMMASK;

ł int Setect(void) f double sum--0.0,

double limit=RNDO1*SumEitness, forint i-0. 1<POP-SIZE; i++) if((sum+xFitness[1])>llmit) break;

return i, 1.

void Mutate(OLONG &cbrom) ł ULONG mask=1,

for(1nt i=0; i<CHROMSIZE, i++,

mask«--1 ) if(RNDO1<--PMUTATION) chrom^-mask; I;

void Evolve(void) t GumFitness-0 0,

forint i-0; i<POP_SI2E; i++) SumFitness+-(Fitness[17= F(Decode(Population[i7)));

printf("Af\n", SumFitness); HLONG newpop[POP_S1ZE7; far(i=0; 1<POP_S17F; 1+=2) ł uLONG

pl=Population[Select()7, 11L0NG

p2=Population[Select()7; int cp=RNDRANGE(CIiROM-SIZE); ULONG m1=Ox7fffffff» cp; ULONG m2=OxJfffffff^ml; newpop[i]=Cp1&ml)~(p2&m2); newpop[irl]=(p2&ml)~(pl&m27, Mutate(newpopCi77, Mutate(newpop[i+17); for(i=0; i<POP-SIZE~ i++) Population[i7--newpop[il; 1;

vold mat n(void) ł if(I,(MYWindow=OpenWindowTags( N011,

WA_InnerWidth, 400, WA_lnneeHeight, 400, WA_DragBar, TRHE, WA_DepthGadget, 7R(lE, WA_CloseOadget, TRUE, WA_AutaAdjust, TRUE, WA_IDCMP, IDGMP_CLOSEWINDOW, TAG_DONE)))

return; Left=MYWindow->BorderLeft, Top=MYWindow->BorderTOp; Width=MYWiedow->Width-Left­

MYWindow->BOrderRight: Height--MYWindow->Height-TOp­MYWindow->8order8ottom,

Rast=MYWindow->RPOrtr RandomInit(); for(Gen=0; Gen<GENS; Gen++) SetAPen(Rast,O); RectFill(Rast,Left,lop, Left+Width-l,Top+Height-1); Pnin~lntó()I

DnawFunctll'on(~ DrawPopulation()r Evolve(), if(GetMSg(MYWindow­

>UserPOrt))ł CloseWindow(MYWindow);

return;

};

};

WaitPort(MYWindow->UserPort);

ClaseWindaw(MYWindow);

};

5. LITERATURA:

1. David E. Goldberg „Algorytmy genetyczne i ich zastosowania”.

2. Hartmut Pohlheim „Genethic and Evolutionary Algorithms: Principles, Methods and Algorithms.”

3. Riccardo Poli „Introduction to Evolutionary Computation”.

4. J. F. Miller, P. Thomson, T. Fogarty „Designing Electronic Circuits Using Evolutionary

5. Szczepan Kuźniarz „Algorytmy genetyczne” Miesięcznik „AMIGA” nr 6/99

specyficzna wiedza

i

ludzkie doświadczenie

pracujący układ

specyfikacje

ocena układu

specyfikacje

automatyczna

ewolucja

Rys. 1

---