Imię: Grzegorz
Nazwisko: Szcześniak
Numer indeksu: 226835
Prowadzący: dr. A. Dacko
Termin zajęć: poniedziałek 10:45-13:00
Data wykonania ćwiczenia: 09.11.2011
Ćwiczenie numer 54:
Drgania relaksacyjne
Tab. 1. Pomiar czasu 20 cykli drgań relaksacyjnych lampy neonowej przy zmianie pojemności kondensatorów
oraz przy stałym oporze R
1
= 1,4 [MΩ] i napięciu U
0
= 140 [V]; C – pojemności kondensatorów, t
1
– czas
pomiędzy kolejnymi błyśnięciami
C
1
2
2,5
3
3,5
4,5
5
[μF]
t
1
11,52 22,28 26,41 33,28 37,38 48,59 53,02
[s]
Dane zmierzone podczas ćwiczenia:
C
x
= ? [F]
-nieznana wartość pojemności kondensatora
R
2
= 2,6 [MΩ]
- opór przyłożony do układu 2
t
2
= 65,28 [s]
- czas pomiędzy cyklami drgań relaksacyjnych dla układu z oporem R
2
i
pojemnością kondensatora C
x
R
3
= 1,4 [MΩ]
-opór przyłożony do układu 3
t
3
= 38,3 [s]
- czas pomiędzy cyklami drgań relaksacyjnych dla układu z oporem R
3
i
pojemnością kondensatora C
x
Wstęp teoretyczny
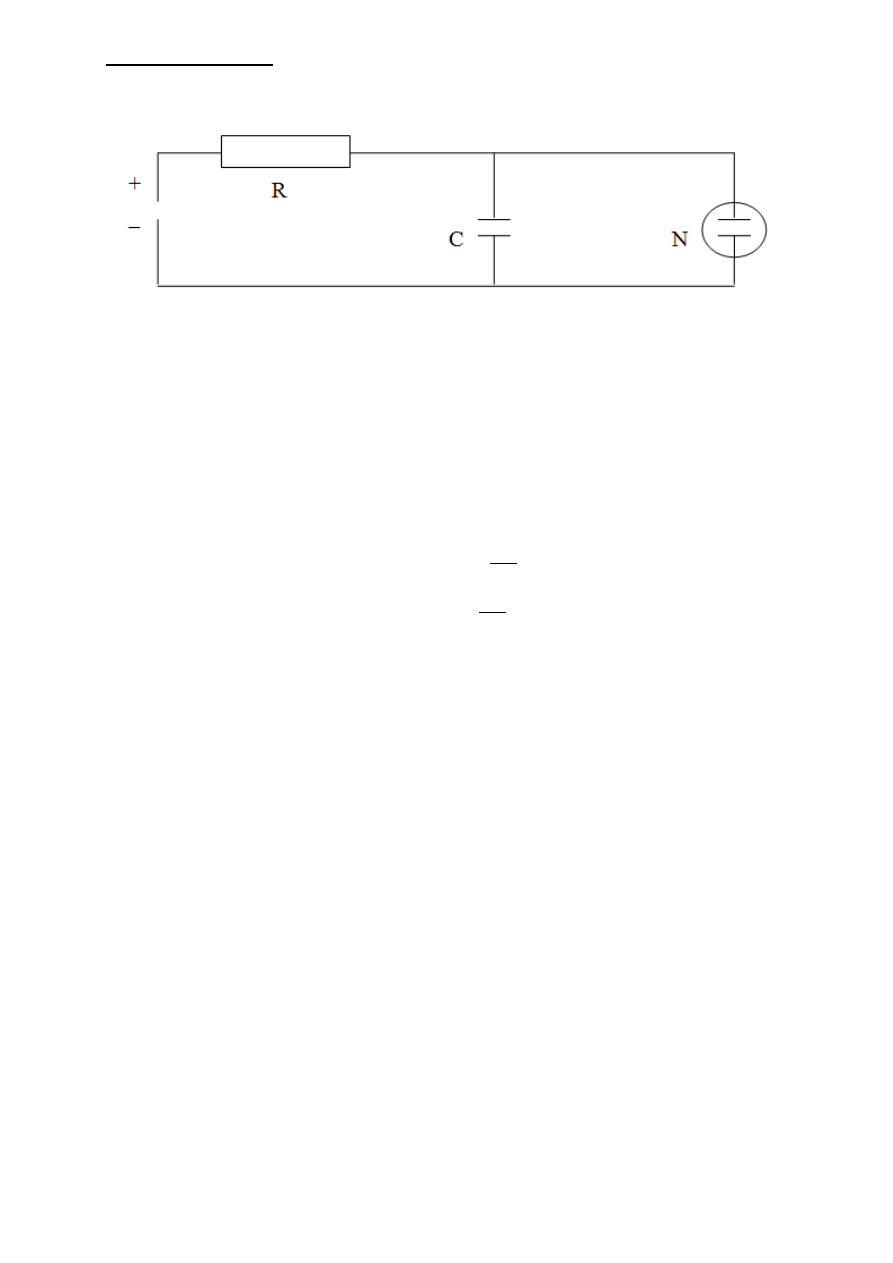
Rys.1. Rysunek układu sporządzonego podczas ćwiczenia; R – opornik, C – kondensator, N – lampa neonowa
Drganiami relaksacyjnymi nazywamy drgania elektryczne, w których wzrosty i spadki
napięcia zachodzą w sposób wykładniczy. Zazwyczaj do wytwarzania drgań relaksacyjnych
wykorzystuje się procesy ładowania i rozładowania kondensatora przez opornik. Napięcie na
jego okładkach zmienia się wykładniczo, według równań:
U U
t
RC
0
1
[
exp(
)]
U U
t
RC
0
exp(
)
Obwód służący do wytwarzania drgań relaksacyjnych musi zawierać element, który
samoczynnie reguluje czas trwania ładowania i rozładowania. Rolę takiego elementu spełnia
lampa neonowa zwana neonówką lub stabiliwoltem. Jest to bańka szklana wypełniona gazem,
najczęściej neonem pod ciśnieniem około 20 mmHg. Neonówka ma dwie elektrody metalowe
pokryte warstwą metalu łatwo emitującego elektronu np. baru. Jeżeli do elektrod przyłożymy
niewielki napięcie, to ze względu na złe przewodnictwo gazu prąd nie popłynie. Po
przekroczeniu wartości U
z
(napięcie zapłonu) potrzebnej do spowodowania jonizacji
lawinowej, przez lampkę popłynie prąd o natężeniu ograniczonym tylko oporem
zewnętrznym. Gdy napięcie na elektrodach spadnie poniżej napięcia gaśnięcia U
g
, to jonizacja
lawinowa nie rozwija się i lampka znowu staje się doskonałym izolatorem. W czasie jarzenia
pomiędzy elektrodami znajdują się ładunki elektryczne, które dają dodatkowy przyczynek do
pola przyspieszającego. Z tego względu do podtrzymania jarzenia wystarczy napięcie nieco
niższe od napięcia zapłonu U
z
(U
z
> U
g
). Przepływowi prądu przez lampkę neonową
towarzyszy świecenie. Mamy tu do czynienie z wyładowaniem w gazach rozrzedzonych. Ze
względu na małą odległość elektrod nie występuje cały obraz wyładowania, lecz tylko
warstwa katodowa świecąca na powierzchni katody.
Lampkę neonową wykorzystuje się do stabilizowania napięcia. W czasie jarzenia jej
opór wewnętrzny jest bardzo mały i prąd przez nią płynący bardzo silnie wzrasta nawet przy
niewielkim wzroście napięcia. Stąd, jeżeli lampkę neonową zasilać będziemy ze źródła o
oporze wewnętrznym dużym w stosunku do oporu neonówki w czasie jarzenia, to napięcie na
zaciskach neonówki prawie nie rośnie. Najmniejszemu wzrostowi napięcia zasilającego o
U
towarzyszy duży wzrost prądu
I płynącego przez neonówkę, przy czym
U = R
i
I ( R
i
-
opór neonówki w trakcie jarzenia).
Najprostszy obwód do wytwarzania drgań relaksacyjnych pokazano na rys. 1.
Kondensator C ładuje się ze źródła prądu stałego przez opornik R o dużym oporze. Napięcie
na jego okładkach narasta w sposób wykładniczy według równania (1). Jeżeli osiągnie ona
wartość U
z
, to podłączona równolegle do okładek kondensatora neonówka N zapala się i
płynie przez nią prąd rozładowania kondensatora. Napięcie U maleje według równania (2).
Rozładowanie kończy się z chwilą, gdy napięcie spada do wartości U
g
, po czym napięcie
ponownie wzrasta. Proces ten powtarza się cyklicznie i otrzymujemy drgania pokazane na
rys.2. Przez T oznaczymy czas narastania napięcia od U
g
do U
z
, a przez T
1
- czas opadania od
U
z
do U
g
, przez U
0
oznaczymy napięcie źródła ładującego kondensator. Ze względu na to, że
w chwili jarzenia neonówka stawia stosunkowo mały opór, czas rozładowania jest bardzo
krótki i możemy przyjąć, że T
T
1
. Stąd przyjmujemy, że okres drgań jest równy T. Napięcie
U
g
zostaje osiągnięte po czasie t, który zgodnie z (1) spełnia związek:
U
U
t
RC
g
0
1
[
exp(
)]
Napięcie wzrasta w dalszym ciągu do wartości U
z
po czasie T+t, stąd:
U
U
T t
RC
z
0
1
[
exp(
)]
Po wykonaniu prostych przekształceń i po zlogarytmowaniu otrzymamy:
t
RC
U
U
RC U
g
ln(
)
ln
0
0
(
)
ln(
)
ln
t T
RC
U
U
RC U
z
0
0
Odejmując powyższe równanie stronami, okres T wyrazimy wzorem:
T
RC
U
U
U
U
g
z
ln
0
0
Wprowadzając oznaczenie:
K
U
U
U
U
g
z
ln
0
0
otrzymamy:
KRC
T
,gdzie współczynnik K jest wielkością niemianowaną.
Opracowanie wyników
Określenie okresu drgań relaksacyjnych i wyliczenie K
śr
→
∑
∑
Tab.2. Tabela przedstawiająca obliczone wartości okresu drgań relaksacyjnych, K oraz K
śr
; C – pojemność
kondensatora, t
f
– czas cyklu w czasie jednej sekundy
C
t
1f
(
)
K
[μF]
[s]
1
0,576
0,411
2
1,114
0,398
2,5
1,321
0,377
3
1,664
0,396
3,5
1,869
0,381
4,5
2,429
0,386
5
26,51
0,379
∑
Obliczenie średniej wartości C
x
→
Nie jest możliwe policzenie średniej bez drugiej wartości K. Podczas ćwiczenia zabrakło
czasu na pomiar cykli drgań relaksacyjnych z przyłożonym oporem 2,6 [MΩ].
Wnioski
Dzięki pomiarom układu o zmiennych pojemnościach kondensatorów i późniejszym
obliczeniom, można stwierdzić, że czas drgania cyklu drgań relaksacyjnych wydłuża się
podczas zwiększania pojemności kondensatorów. Dzieję się tak, ponieważ czas potrzebny do
naładowania kondensatora jest dłuższy, co przesuwa w czasie okres pomiędzy napięciem
gaszenia (U
g
), a napięciem zapłonu (U
z
), podobną konsekwencję można zauważyć podczas
zwiększania wartości opornika.
Jednym z celów ćwiczenia było określenie nieznanej wartości pojemności
kondensatora (C
x
= 3,5 [μF]), niestety nie można było uśrednić wyniku z innym pomiarami
przez brak czasu podczas ćwiczenia.