1

Ć

WICZENIE NR 1

Wybrane zagadnienia teoretyczne

GENERATORY POMIAROWE

Schematy blokowe wybranych generatorów pomiarowych

Regulacja

częstotliwości

Płynna

regulacja U

wy

Regulacja

U

wy

Regulacja

U

wy

, R

wy

2

1

WY I

(napięciowe)

WY II

(mocy)

Transformator
dopasowujący

Dzielnik

napięcia

Woltomierz

elektroniczny

Wzmacniacz

mocy

Wzmacniacz

napięciowy

Wzmacniacz

separator

Generator

wzbudzający

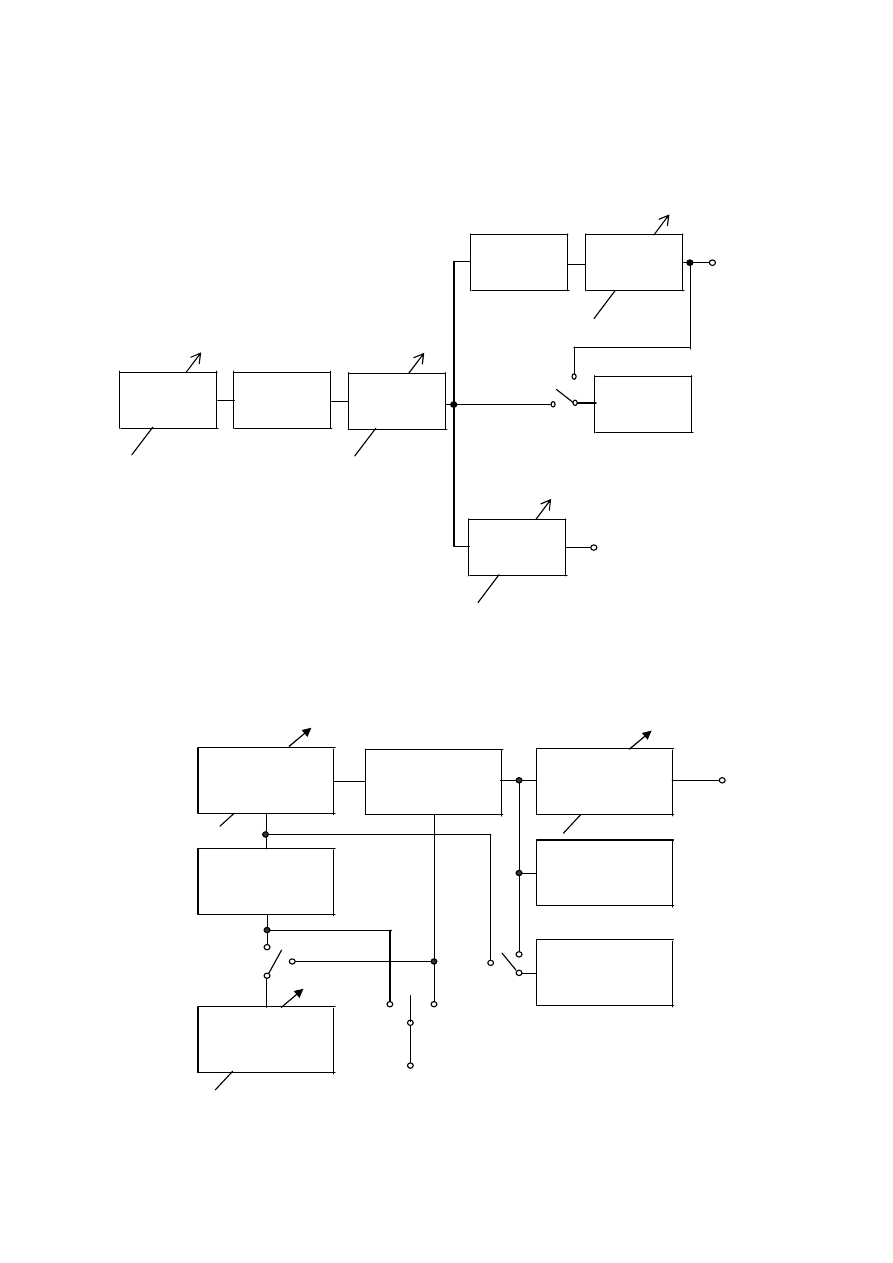
Rys.A) Schemat funkcjonalny generatora pomiarowego m.cz.

Rys.B) Schemat blokowy generatora pomiarowego w.cz. z AM i FM

WY

AM

FM

„m”, „

∆

f”

WE modulacji

zewnętrznej

U

wy

f

FM

AM

Miernik

„m” i ‘

∆

f”

Woltomierz

elektroniczny

Generator

m.cz.

Modulator

częstotliwości

Układy

wyjściowe

Generator

wzbudzający

Wzmacniacz

separator

modulator AM

2

Układ

wyzwalania

zewnętrznego

WE

WY

impulsów odniesienia

(synchronizacji)

WY

U

wy

t

i

; t

n

;t

o

t

op

f

i

Układy

pomiarowe

Układy

wyjściowe

Układ

kształtujący

I

Układ

kształtujący

II

Układ

opóźniający

Generator

sterujący

Wew.

Zew.

Ręczne

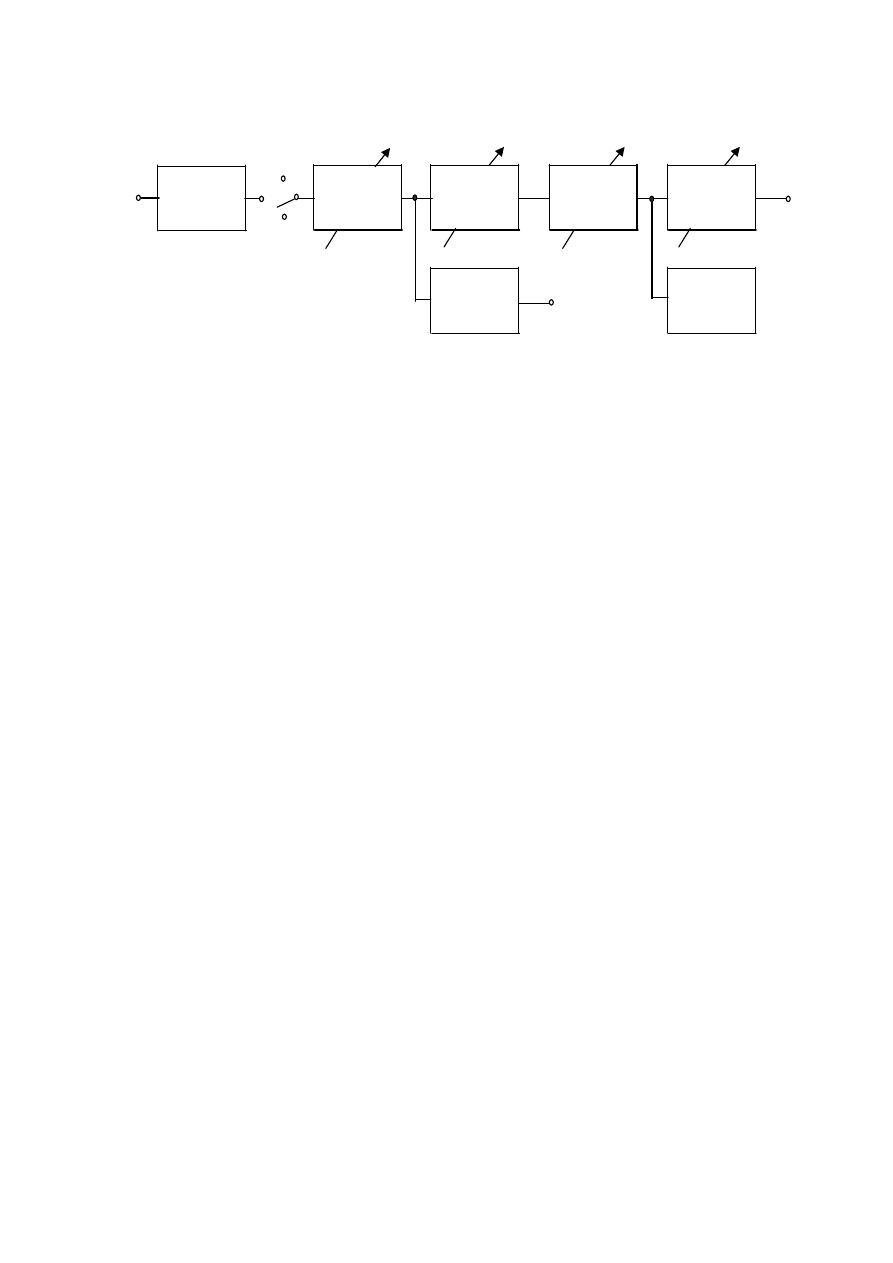
Rys.C) Schemat funkcjonalny generatora impulsów prostokątnych.

3

1) Generator wzbudzający RC

Generatory RC są to generatory ze sprzężeniem zwrotnym.
W celu zapewnienia poprawnej pracy, generatory RC budowane są jako układy z dodatnim i ujemnym sprzężeniem
zwrotnym zwane także generatorami z układem mostkowym (czwórniki

α

i

β

tworzą mostek niezrównoważony).

Czwórnik sprzężenia zwrotnego

γ

składa się z dwóch czwórników

α

i

β

. Jeden z tych czwórników musi być

czwórnikiem selektywnym a drugi aperiodycznym.
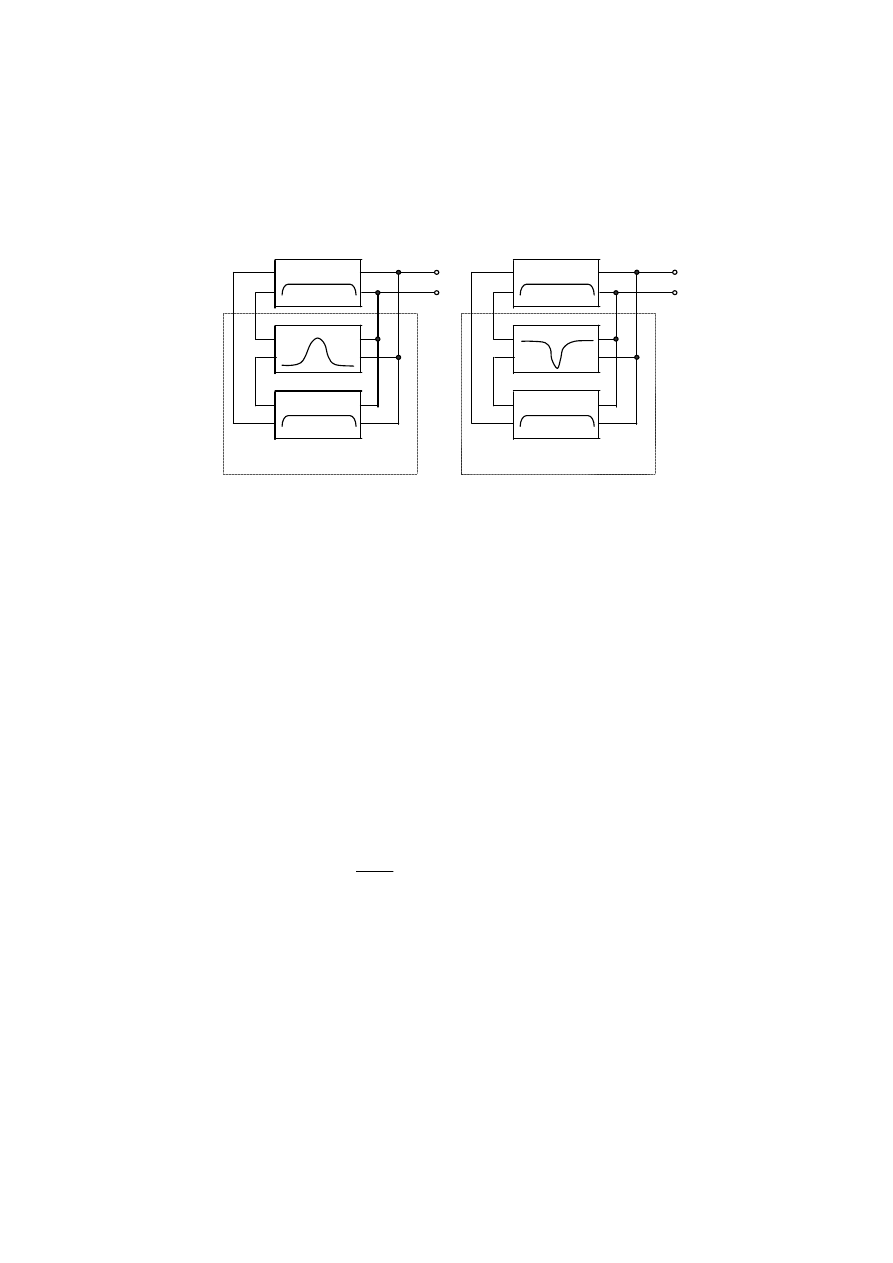
Na rys.1 przedstawiono schematy funkcjonalne generatorów RC. Rys. 1.a) przedstawia generator z selektywnym
dodatnim sprzężeniem zwrotnym a rys. 1.b) generator z selektywnym ujemnym sprzężeniem zwrotnym.
























Ujemne sprzężenie zwrotne stabilizuje parametry wzmacniacza.
Zastosowanie tego sprzężenia zwrotnego powoduje zwiększenie stabilności częstotliwości generatora przez
zwiększenie nachylenia charakterystyki fazowej czwórnika selektywnego (wzrasta tzw. dobroć fazowa układu).
Zastosowanie aperiodycznego sprzężenia zwrotnego (dodatniego lub ujemnego) umożliwia stabilizację amplitudy
(poprzez wprowadzenie nieliniowości do układu) oraz samowzbudzenie generatora. W czwórniku aperiodycznym
zastosowane są elementy nieliniowe np. termistory, żarówki, specjalne układy elektroniczne. Nieliniowość może być
wprowadzona tylko w czwórniku aperiodycznym. Wzmacniacz i czwórnik selektywny muszą mieć liniową
charakterystykę przetwarzania.

Generatory wzbudzające RC najczęściej budowane są w układzie z rys. 1.a). Przykład takiego generatora

pokazano na rys. 2.
Jest to generator z czwórnikiem Wiena. Regulacja częstotliwości odbywa się przez jednoczesną zmianę R lub C
(zaznaczone na rysunku). Rezystory R

T

(termistor) i R

1

tworzą aperiodyczny czwórnik ujemnego sprzężenia zwrotnego.

Częstotliwość napięcia wyjściowego

RC

f

wy

π

2

1

=

regulowana jest w zakresie ~10Hz

÷

~200kHz. W sposób płynny

można regulować częstotliwość w zakresie jednej dekady (np. 1

÷

10kHz; 20

÷

200 Hz).

Niestabilność częstotliwości

<

10

-4

.

Rys.1. Schematy funkcjonalne generatorów wzbudzających RC

a)

b)

Warunki generacji:



K

⋅γ

= 1 czyli:



K

⋅β−α

=1

ϕ

+

ψ

= 0 + 2

π

n

„

+

”

„

−

”

β

α

K

γ

=

α − β

Warunki generacji:



K

⋅γ

= 1 czyli:



K

⋅α−β

=1

ϕ

+

ψ

= 0 + 2

π

n

„

+

”

„

−

”

β

α

K

γ

=

β−α

4

2) Generator funkcji (generator funkcyjny).

Generator funkcji jest generatorem relaksacyjnym. Może generować napięcia o różnym kształcie, z tego względu

nazywany jest także generatorem uniwersalnym. Podstawowym sygnałem generowanym jest napięcie rrójkatne. Zasada
pracy generatora polega na cyklicznym ładowaniu i rozładowaniu kondensatora. Z teorii obwodów wiadomo, że
napiecie na kpondensatorze ładowanym ze źródła napięcia stałego zmienia się wykładniczo (jest więc nieliniowe). W
generatorach funkcji napięcie linearyzuje się wykorzystując integratory lub źródła prądowe o stałej wydajności.
Podstawowe parametry użytkowe generatorów funkcyjnych:

−

zakres częstotliwości: 1mHz

÷

10MHz,

−

stabilność częstotliwości: ~10

-3

Zakres częstotliwości od dołu ograniczony jest przez napięcia progowe komparatorów i upływność kondensatora C. Od
góry ograniczeniem są pojemności pasożytnicze i montażowe układu.
Parametry charakteryzujące kształt napięcia:
- napięcie sinusoidalne: h

≈

1

÷

3 %,

- napięcie trójkątne: współczynnik nieliniowości

<

1%,

- napięcie fali prostokątnej: czasy narastania i opadania zboczy
t

n

i t

o

<<

T.

Inne możliwości generatorów funkcyjnych:
- generacja napięć o innych kształtach,
- możliwość sterowania napięciowego częstotliwością,
- wprowadzenie składowej stałej do przebiegu wyjściowego,
- możliwość modulacji amplitudy i częstotliwości.
Pozostałe parametry jak w generatorach m.cz.

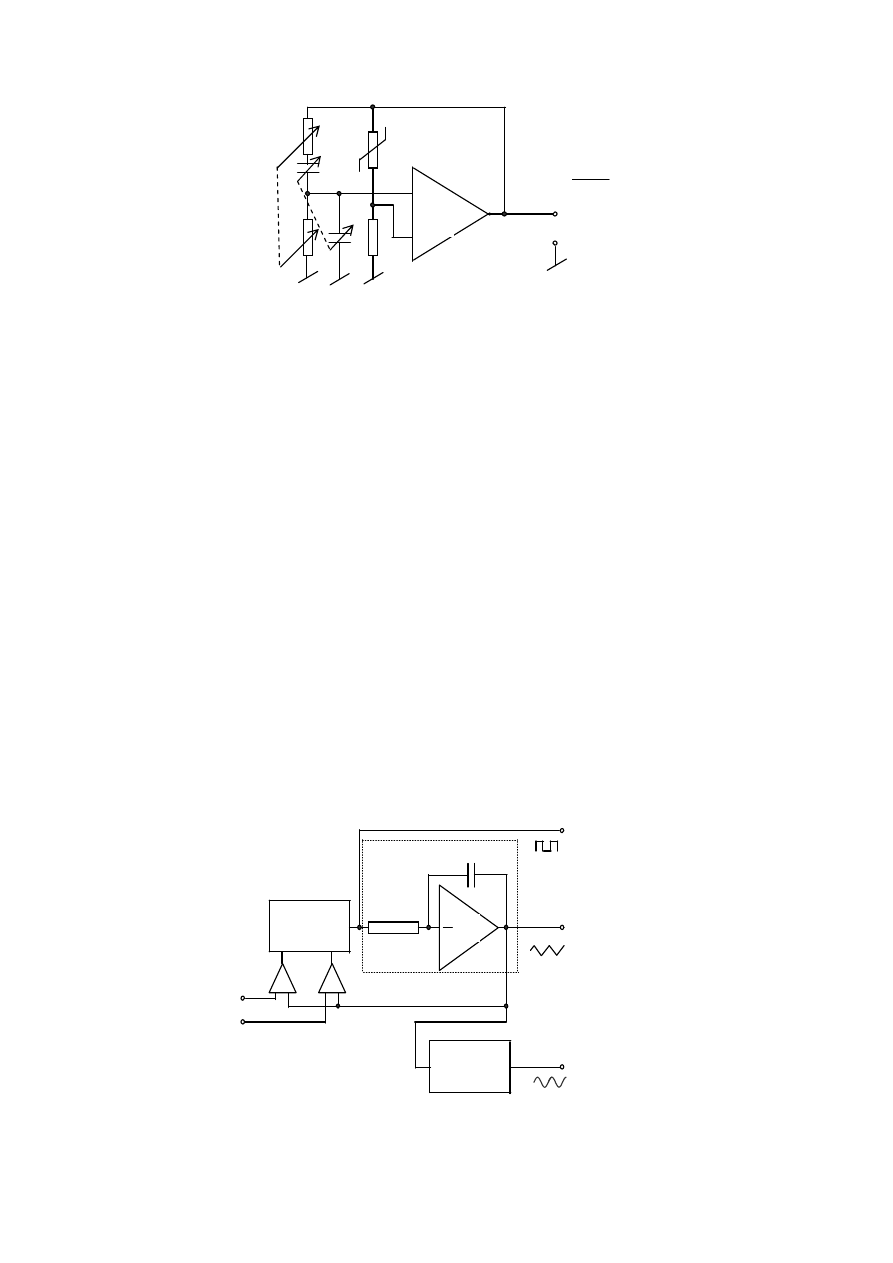
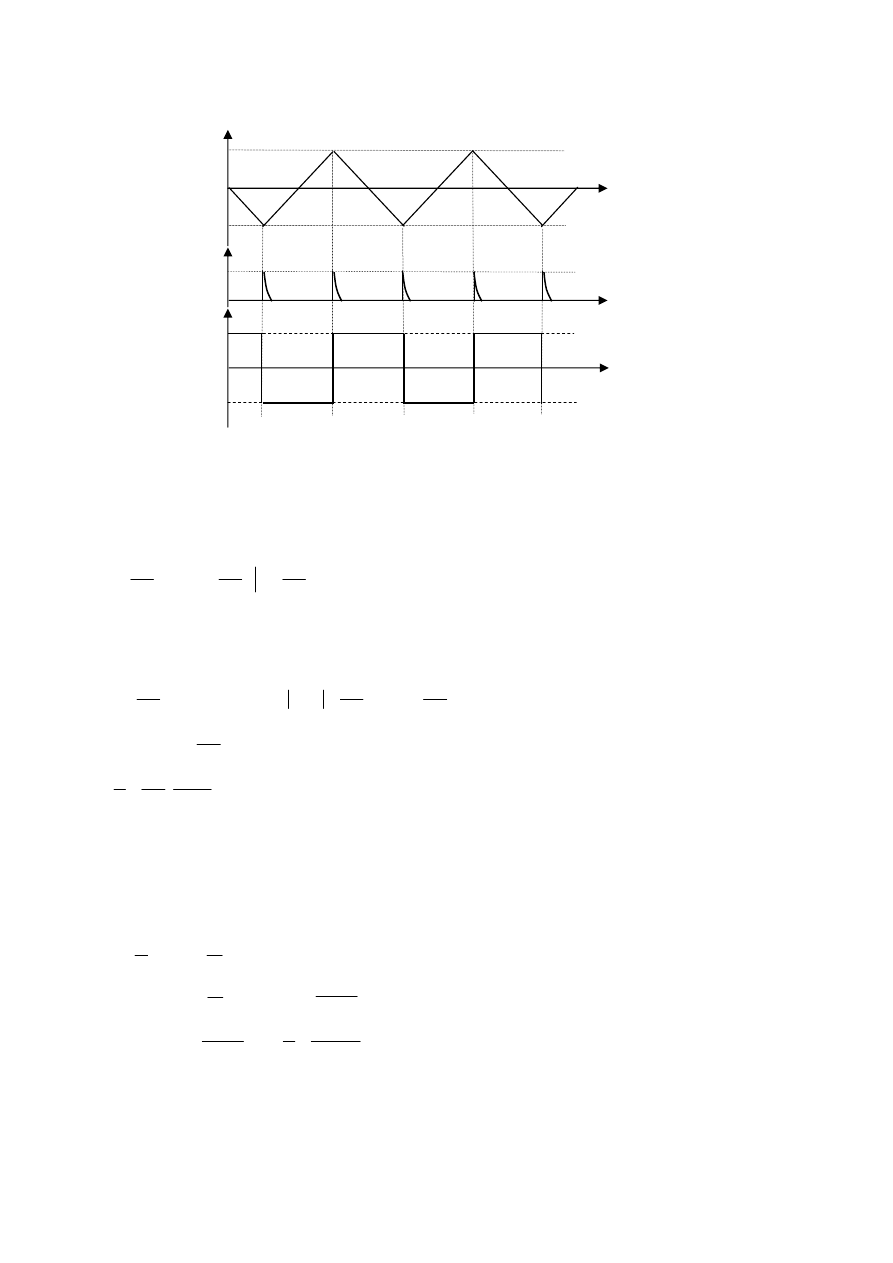
Na rys. 3 przedstawiono uproszczony schemat funkcjonalny generatora funkcji z integratorem a na rys. 4 przebiegi
czasowe w różnych punktach układu.

Rys. 3. Schemat blokowy generatora funkcji z integratorem

-U

w

WY 3

WY 2

WY 1

Układ

kształtujący

sinusoidę

C

R

U

w

K2

K1

Układ

bistabilny

K

Integrator

Rys. 2. Generator RC z mostkiem Wiena

RC

f

WY

π

2

1

=

WY

R

1

R

T

C

C

R

R

−

+

K

5

Zasada pracy.
Na wejście integratora podawane jest napiecie stałe z wyjścia układu
bistabilnego

±

U. Napięcie to podawane jest również na wyjście 2 generatora.

Na wyjściu integratora napięcie zmienia się liniowo:

( )

t

RC

U

t

RC

U

dt

U

RC

t

u

t

t

⋅

=

⋅

=

⋅

=

∫

2

0

2

0

2

1

1

,

Napięcie to podawane jest na wyjście 1 oraz na wejścia komparatorów K1 i K2, gdzie jest porównywane z napięciem
wzorcowym

±

U

w

. W chwili zrównania u

1

(t) z U

w

następuje przełączenie przerzutnika bistabilnego w drugi stan.

Napięcie na wyjściu integratora zmienia się liniowo z przeciwnym znakiem.
Wyznaczenie częstotliwości generowanego sygnału:

( )

1

1

1

1

t

RC

U

t

u

⋅

=

;

( )

w

U

t

u

−

=

1

1

;

1

1

t

RC

U

U

w

⋅

=

−

;

RC

U

U

t

w

⋅

=

1

1

1

1

4

4

U

U

RC

t

T

w

⋅

⋅

=

⋅

=

- okres generowanego napięcia,

RC

U

U

T

f

w

⋅

⋅

=

=

4

1

1

1

- częstotliwość generowanego napięcia.

Regulacja częstotliwości odbywa się przez zmianę wartości R i C. Można również zmieniać f

wy

przez regulację U

1

i U

w

.

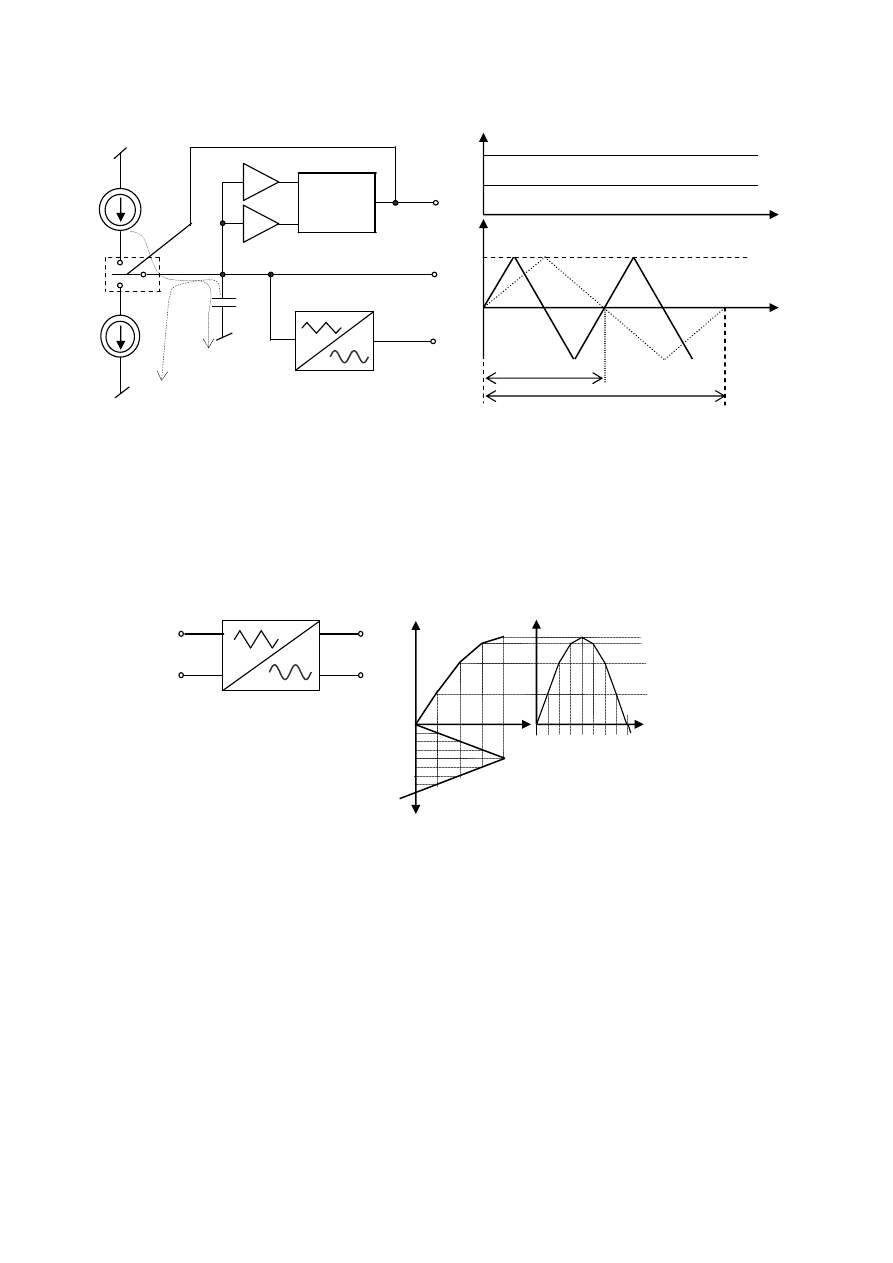
Na rys. 5 przedstawiony jest uproszczony schemat blokowy generatora funkcji pracującego wg drugiej metody

(ładowanie i rozładowanie kondensatora stałym prądem I = const.).
Klucz sterowany jest napięciem z układu bistabilnego. Kondensator C ładowany jest pradem i

Ł

(lub rozładowywany

prądem i

R

).

Ponieważ I

1

i I

2

= const. (źródła prądowe o stałych wydajnościach), to napięcie na kondensatorze (u

C

) zmienia się

liniowo:

( )

t

C

I

dt

I

C

t

u

C

⋅

=

⋅

=

∫

1

1

1

,

dla t = t

1

:

( )

w

C

U

t

C

I

t

u

=

⋅

=

1

1

1

;

1

1

I

C

U

t

w

⋅

=

okres:

1

1

4

4

I

C

U

t

T

w

⋅

⋅

=

=

,

C

U

I

T

f

w

⋅

=

=

4

1

1

Częstotliwość można regulować zmieniając prąd ładowania i rozładowania kondensatora rys. 1.16. W tym celu
stosowane są źródła prądowe o regulowanej wydajności. Według tej zasady pracują generatory funkcyjne scalone np.
ICL 8038.

U

wy

1

Rys. 4. Wykresy czasowe ilustrujące zasadę pracy generatora z rys. 3.

t

0

t

5

t

4

t

3

t

2

t

1

t

U

wy

2

U

kom

p.

t

-U

2

U

2

+U

w

-U

w

t

6

Napięcie sinusoidalne otrzymywane jest z przetwornika trójkąt – sinusoida. Jest to przetwornik pomiarowy o

nieliniowej charakterystyce przetwarzania. Do kształtowania charakterystyki przetwarzania często stosuje się sieć
funkcyjną aproksymującą żądaną charakterystykę odcinkami prostymi rys. 7.

3) Syntezery częstotliwości lub syntetyzery częstotliwości (generatory siatki częstotliwości).

Generatory te pracują na zasadzie syntezy częstotliwości.

Synteza częstotliwości – otrzymywanie napięcia o żądanej częstotliwości poprzez składanie szeregu sygnałów
harmonicznych o częstotliwościach wzorcowych.
Rozróżnia się dwa rodzaje syntezy częstotliwości:
1

°

Synteza bezpośrednia polega na wykonywaniu prostych operacji

arytmetycznych na częstotliwościach składowych:

−

sumowaniu i odejmowaniu dwóch częstotliwości,

−

mnożeniu i dzieleniu częstotliwości przez stałą.

2

°

Synteza pośrednia wykorzystuje właściwości pętli synchronizacji fazowej do sterowania pomocniczego generatora

analogowego.
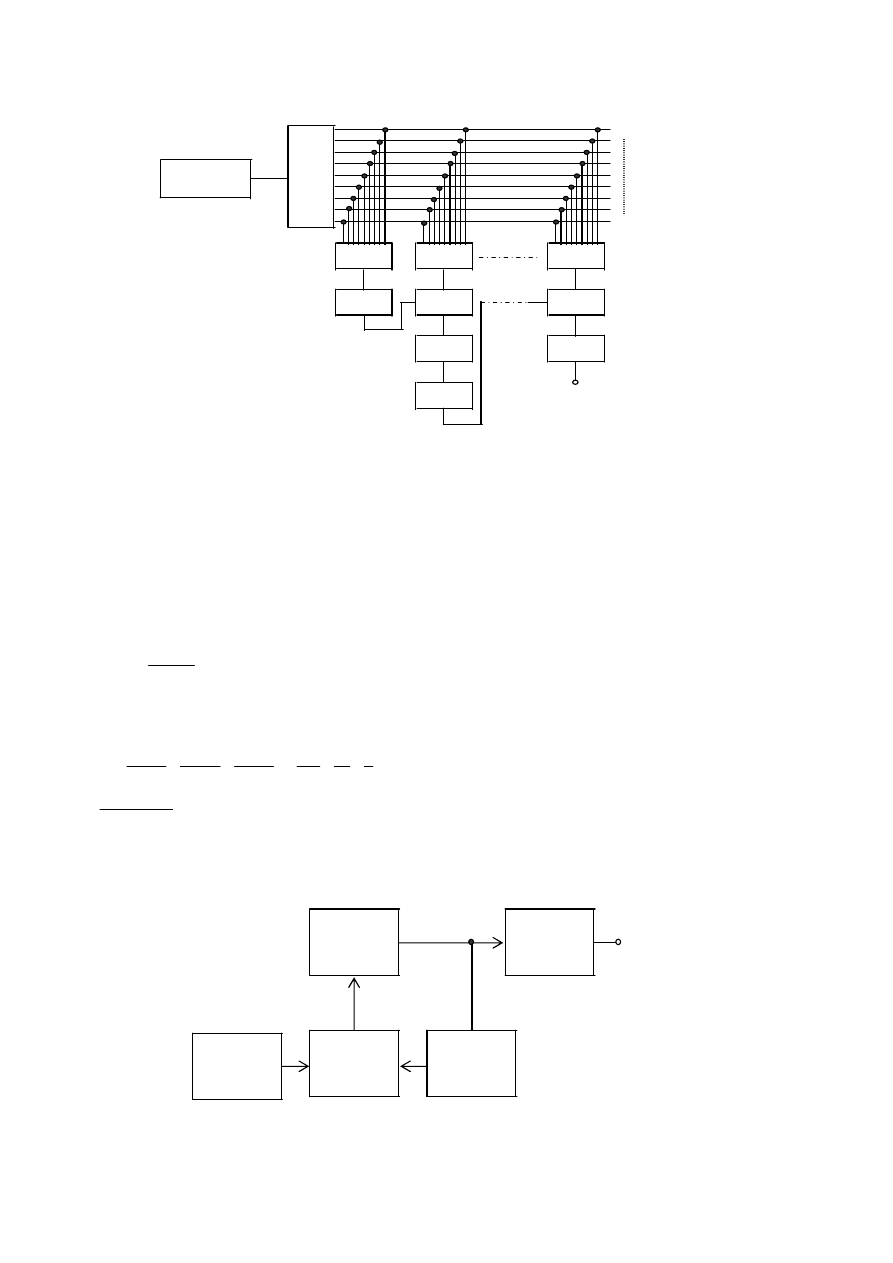
Rys. 8 przedstawia uproszczoną wersję syntezera częstotliwości pracującego w oparciu o metodę syntezy
bezpośredniej.

2

1

Rys. 5. Generator funkcji ze źródłami prądowymi.

K

lu

cz

i

R

i

Ł

WY 3

WY

2

WY 1

C

I

2

I

1

K

2

K

1

Układ

bistabilny

t

t

u

2

u

2

u

1

u

1

u

2

u

2

= U

2m

⋅

sin (a

⋅

u

1

)

a

−

współczynnik

proporcjonalności

Rys. 7. Sposób otrzymywania napięcia sinusoidalnego.

Rys. 6. Regulacja częstotliwości przez zmianę

natężenia prądu.

I

1

>

I

1

’

T

<

T’

T’

T

2

1

I

I

−

=

t

t

u

C

u’

C

U

w

u

C

I

'

2

'

1

I

I

−

=

7

Generator kwarcowy generuje sygnał napięciowy o częstotliwości f

kw

,sterujący pracą syntezera częstotliwości.

Generator harmonicznych jest powielaczem częstotliwości, składa się z układu przetwarzającego napięcie sygnału o
częstotliwości f

kw

na napięcie o bogatym widmie częstotliwości oraz z zestawu filtrów nastrojonych na kolejne

harmoniczne (np. od f

kw

do 9

⋅

f

kw

).

Przełączniki P

1

÷

P

m

służą do wyboru żądanej harmonicznej,

m – numer dekady częstotliwości od najmniej znaczacej,
f/10 – dzielnik częstotliwości,
M i FGP – mieszacz i filtr górnoprzepustowy (sumator częstotliwości).
Na wyjściu otrzymywany jest sygnał napięciowy o częstotliwości:

∑

=

−

⋅

=

m

i

i

m

kw

i

wy

f

n

f

1

10

gdzie: n – numer harmonicznej.
Przykład: ustawić częstotliwość 3,75 MHz, f

kw

= 1MHz n

1

= 5, n

2

= 7, n

3

= 3

MHz

f

f

f

f

f

f

f

kw

kw

kw

kw

kw

kw

wy

75

,

3

75

,

3

100

300

70

5

1

3

10

7

100

5

10

3

10

7

10

5

3

3

2

3

1

3

=

⋅

=

⋅

+

+

=

=

⋅













+

+

=

⋅

+

⋅

+

⋅

=

−

−

−

Na rys. 9 przedstawiono uproszczony schemat blokowy syntezera częstotliwości pracującego w oparciu o metodę
syntezy pośredniej.

Rys. 9. Metoda pośrednia syntezy częstotliwości.

f

wy

f

1

f

0

U

st

f

kw

WY

Generator

sterowany

napięciowo

Generator

kwarcowy

Detektor

fazy

f / n

f / m

Rys. 8. Metoda bezpośrednia syntezy częstotliwości.

Pm

9f

kw

f

kw

f

kw

WY

Generator

kwarcowy

G

en

er

at

o

r

h

ar

m

o

n

ic

zn

y

ch

f/10

P1

f/10

FGP

M

P22

FGP

M

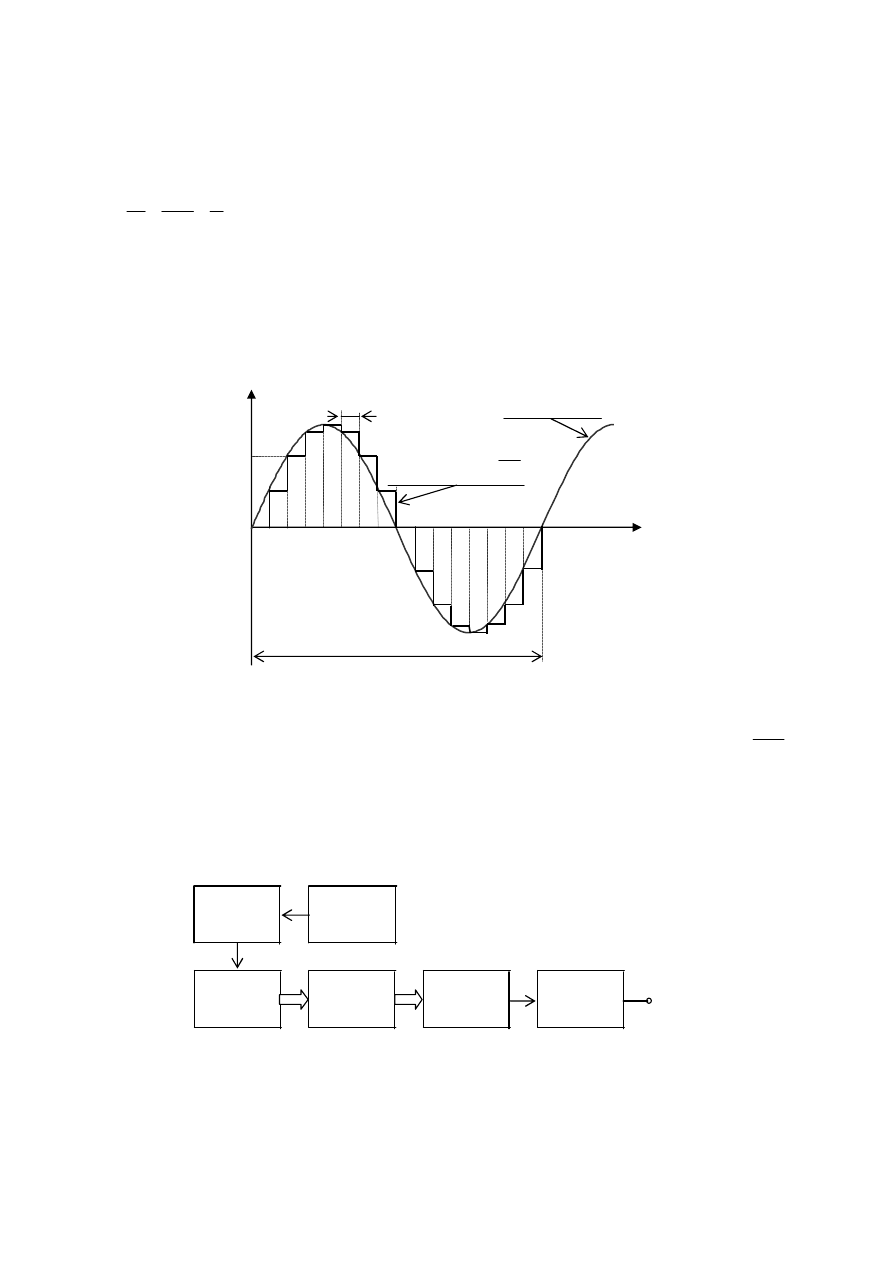
8

Rys. 11. Uproszczony schemat funkcjonalny generatora cyfrowego.

f

kw

/k

Dzielnik

f

WY

f

kw

Filtr

m.cz

.

Generator

taktujący

Przetwornik

C / A

Pamięć

cyfrowa

Licznik

Zasada pracy
Generator sterowany napięciowo generuje napięcie o częstotliwości f

0

. Częstotliwość ta po podzieleniu przez „n” jest

porównywana na detektorze fazy z częstotliwością generatora kwarcowego f

kw

.

Jeżeli f

kw

= f

1

to U

st

= 0 i częstotliwość generatora sterowanego napięciowo nie zmienia się. Jeżeli f

kw

≠

f

1

to U

st

≠

0,

częstotliwość generatora zostaje zmieniona.

kw

wy

f

m

n

m

f

n

m

f

f

⋅

=

⋅

=

=

1

0

4. Generatory cyfrowe

Zasada pracy generatorów cyfrowych polega na przekształceniu kodu cyfrowego w sygnał analogowy. Sygnał

analogowy (np. sinusoidalny) aproksymowany jest funkcją otrzymaną z przetwornika C/A.
Zasada aproksymacji napięciem schodkowym.
Na rys. 10 podano przykład aproksymacji napięcia sinusoidalnego.

Napięcie sinusoidalne

( )

t

U

t

u

m

⋅

⋅

=

ω

sin

zostało aproksymowane napięciem schodkowym

(

)

n

i

U

T

i

u

m

⋅

⋅

=

∆

⋅

π

2

sin

.

Gdzie:

∆

T=T

s

= t

i

– t

i -1

– okres próbkowania,

n – liczba stopni przypadająca na jeden okres
( T ) formowanego napiecia,
T = n

⋅∆

T = n

⋅

T

s

Na rys. 11 przedstawiono uproszczony schemat funkcjonalny generatora cyfrowego.















Generator taktujący (zbudowany na kwarcu) generuje napięcie impulsowe o okresie T

kw

. Sygnał ten podawany jest na

dzielnik częstotliwości o regulowanym współczynniku podziału k. Na wyjściu dzielnika częstotliwości występuje
napięcie impulsowe o okresie k

⋅

T

kw

=

∆

T = T

s

(odpowiada to okresowi próbkowania).

Rys. 10. Aproksymacja napięcia sinusoidalnego napięciem

schodkowym.

u(i

⋅∆

t)

( )













⋅

=

∆

⋅

n

i

U

t

i

u

m

π

2

sin

∆

t

T = n

⋅∆

t

( )

t

U

t

u

m

ω

sin

⋅

=

u(t)

t

t

9

t

10

t

11

t

12

t

13

t

14

t

15

t

16

t

1

t

2

t

3

t

4

t

5

t

6

t

7

t

9

Sygnał ten podawany jest na licznik o pojemności „n”. Na wyjściu licznika otrzymuje się kod liczbowy – liczba „i”
zliczonych impulsów. Liczba „i” zmienia się od „0” do „n” co jeden.
Kod liczbowy z wyjścia licznika adresuje pamięć cyfrową w której zapisane są wartości funkcji (np. sinusoidy)
odpowiadajace danej liczbie „i”. Z wyjścia pamięci, zapisana w danej komórce o adresie „i” wartość, podawana jest na
przetwornik C/A.
Na wyjściu przetwornika C/A otrzymywane jest napięcie odpowiadające liczbie „i” (np. dla napięcia sinusoidalnego:

(

)

n

i

U

T

i

u

m

⋅

⋅

=

∆

⋅

π

2

sin

). Napięcie to utrzymuje się przez czas

∆

T do przyjścia na wejście pamięci następnego kodu

liczbowego (liczby „i + 1”). Po zliczeniu n-tego impulsu następuje przepełnienie licznika i jego stan wraca do zera.
Nowy cykl pracy rozpoczyna przyjście „n + 1” impulsu. Napięcie schodkowe z wyjścia przetwornika C/A podawane
jest na filtr m.cz. wygładzajacy uzyskany przebieg. Filtracja sygnału jest łatwa, ponieważ prążki najbliższe składowej
podstawowej to: n - 1, n +1, 2n -1, 2n +1 itd.
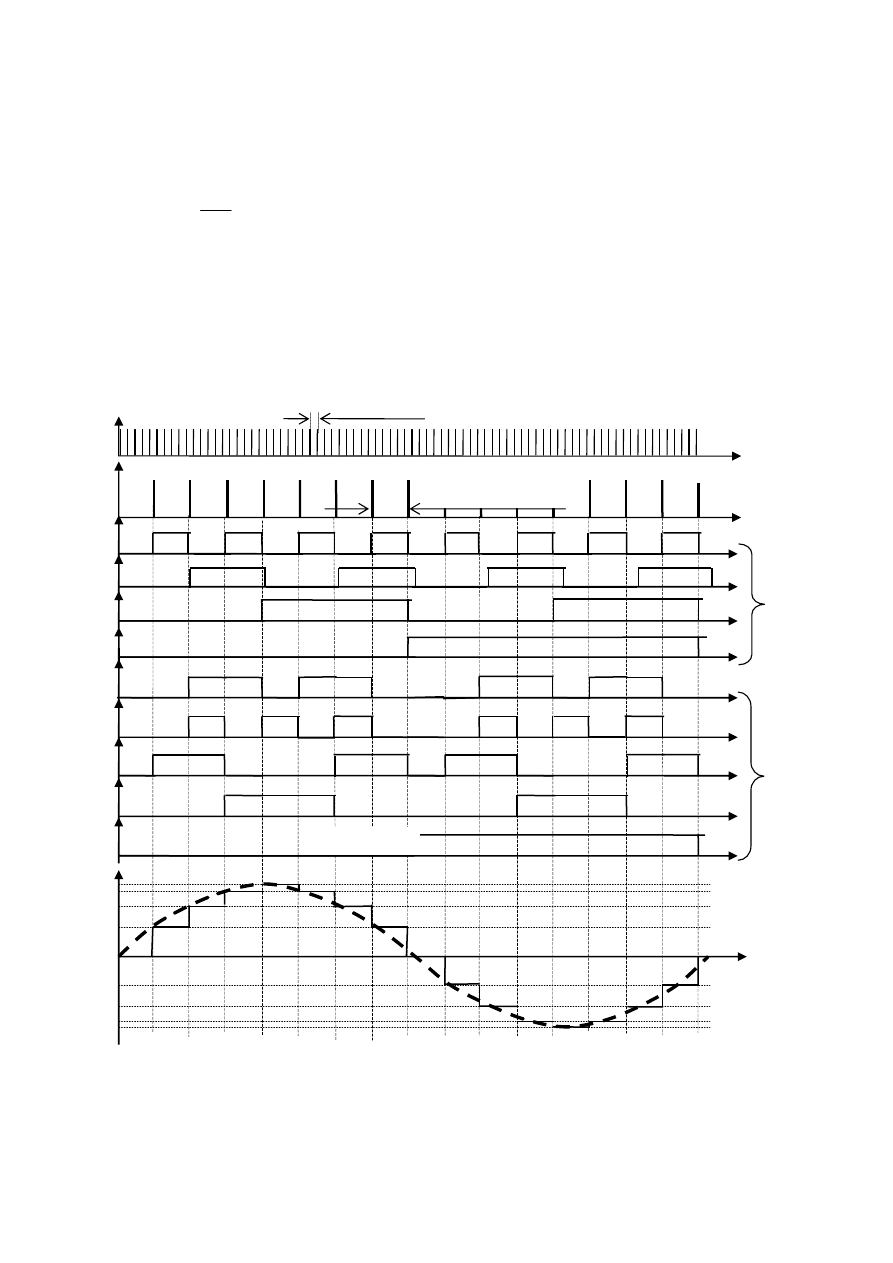
Na rys. 12 przedstawiono wykresy czasowe w kolejnych punktach generatora. Przyjęto następujace oznaczenia:
- a

0

÷

a

3

– bity wyjściowe licznika adresujące pamięć cyfrową, liczba n zapisana w naturalnym kodzie binarnym,

- b

0

÷

b

4

– m-bitowe słowo zapisujące w bipolarnym kodzie modułowym wartość funkcji zapisaną w adresowanej

komórce pamięci cyfrowej, najstarszy bit (w przykładzie b

4

) jest bitem znaku (przy czym „0” – wartość dodatnia; „1” –

wartość ujemna).

u

c/

a

Rys. 12. Wykresy czasowe w generatorze cyfrowym.

t

u

k

w

T

kw

=

1/f

kw

L

ic

zb

y

z

ap

is

an

e

w

a

m

ię

ci

A

d

re

s

p

am

ię

ci

b

4

a

3

b

3

b

2

a

2

a

1

b

1

a

0

1
0

b

0

t

t

t

t

t

t

t

t

t

t

1 2 3 4 5 6 7 8 9 10 11 12 13

14 15

16

t

T

s

= k

⋅

T

kw

Bit znaku

10

W praktyce generatory cyfrowe budowane są w oparciu o metodę bezpośredniej syntezy cyfrowej – DDS (direct

digital synthesis).

Podstawowe parametry metrologiczne:

Zakres częstotliwości :

<

1 mHz

÷

~15MHz,

regulacja częstotliwości : dyskretna (rozdzielczość regulacji do 0,1 mHz),
dokładność ustawienia częstotliwości : ~10 ppm ,
stabilność częstotliwości: 10 ppm.
Zakres napięcia: do 10V

pp

,

dokładność: ~

±

1%.

Kształt generowanego napięcia:
- napięcie sinusoidalne: h

<

0,1%,

- napięcie fali prostokątnej, fali trójkątnej,
- inne kształty sygnałów wyjściowych zaprogramowane na stałe w pamięci ROM oraz kształty dowolne zdefiniowane
przez użytkownika
( stąd nazwa generatorów: generatory przebiegów arbitralnych),
- generacja sygnałów zmodulowanych przy różnych rodzajach modulacji.
Sterowanie praca generatorów cyfrowych może odbywć się ręcznie (z płyty czołowej) lub zdalnie.
Generatory cyfrowe zastępują (a nawet przewyższają) pod względem wymagań użytkowych i metrologicznych
generatory pomiarowe m.cz., funkcji oraz częściowo generatory pomiarowe w.cz. i impulsów prostokątnych.
Podsumowanie: generatory cyfrowe są obecnie najbardziej uniwersalnymi źródłami sygnałów pomiarowych,
stosowanymi przy pomiarach tradycyjnych oraz w systemach pomiarowych.

11

Przyrządy pomiarowe badane w ćwiczeniu.

1. Generator funkcji typ KZ –1405
Widok płyty czołowej przyrządu i podstawowe elementy regulacyjne

1 – Zasilanie 5 – Przełącznik podzakresów częstotliwości
2 – Płynna regulacja częstotliwości 6 – Przełącznik wybory kształtu napięcia wyjściowego
3 – Płynna regulacja napięcia wyjściowego 7 – Wyjście napięciowe
4 – Przełącznik podzakresów napięcia wyjściowego

Podstawowe parametry metrologiczne

Kształt generowanego napięcia

sinusoidalny, trójkątny, prostokątny

Zakres częstotliwości

0,01 Hz

÷

10 MHz (w 8 podzakresach)

Dokładność skalowania

5%

Niestabilność częstotliwości

±

0,2 % / 15 min.

Zakres napięcia wyjściowego

do 20 V

Stałość napięcia przy zmianie częstotliwości

<

0,5 dB

Parametry charakteryzujące kształt napięcia wyjściowego

współczynnik zawartości harmonicznych „h”

<

1 %

nieliniowość

<

2 %

czas narastania i opadania zboczy t

N

, t

O

<

30 ns

współczynnik wypełnienia „

Θ

”

20 %

÷

80 %

R

wy

50

Ω

1

2

4

5

6

7

3

12

2. Generator cyfrowy typ HP33120A
Widok płyty czołowej przyrządu i podstawowe elementy regulacyjne

1 – Zasilanie 5 – Wskaźnik cyfrowy
2 – Klawisze funkcyjne i numeryczne 6 – Klawisze wyboru jednostek i regulacyjne
3 – Wyjście sygnału synchronizacji 7 – Pokrętło regulacji
4 – Wyjście sygnału napięciowego

Podstawowe parametry metrologiczne

Kształt generowanego napięcia

sinus, trójkąt, prostokąt, piła narastająca i opadająca,
szum, sygnały arbitralne

Zakres częstotliwości

sinus, prostokąt

100

µ

Hz

÷

15 MHz

trójkąt, piła narastająca i opadająca

100

µ

Hz

÷

100 kHz

szum

10 MHz

sygnały arbitralne

100

µ

Hz

÷

5 MHz

Dokładność

10 ppm

Stabilność częstotliwości

10 ppm/90 dni

Zakres napięcia wyjściowego

50 mV

p-p

÷

10 V

p-p

Dokładność ustawienia napięcia wyjściowego

±

1 %

Stałość napięcia przy zmianie częstotliwości

±

1%(do 100kHz),

±

2%(do 1MHz),

±

3,5%(do 15MHz)

Parametry charakteryzujące kształt napięcia wyjściowego

Współczynnik zawartości harmonicznych „h”

<

0,04 %

Czasy narastania i opadania zboczy

<

20 ns

Współczynnik wypełnienia

20 %

÷

80 %

Nieliniowość

<

0,1 %

R

wy

50

Ω

Rodzaje modulacji

AM, FM, FSK(kluczowanie częstotliwości), wobulacja

Zakres współczynnika głębokości modulacji „m”

0%

÷

120%

Zakres dewiacji częstotliwości „

∆

f”

10 mHz

÷

15 MHz

1

3

4

5

6

7

2