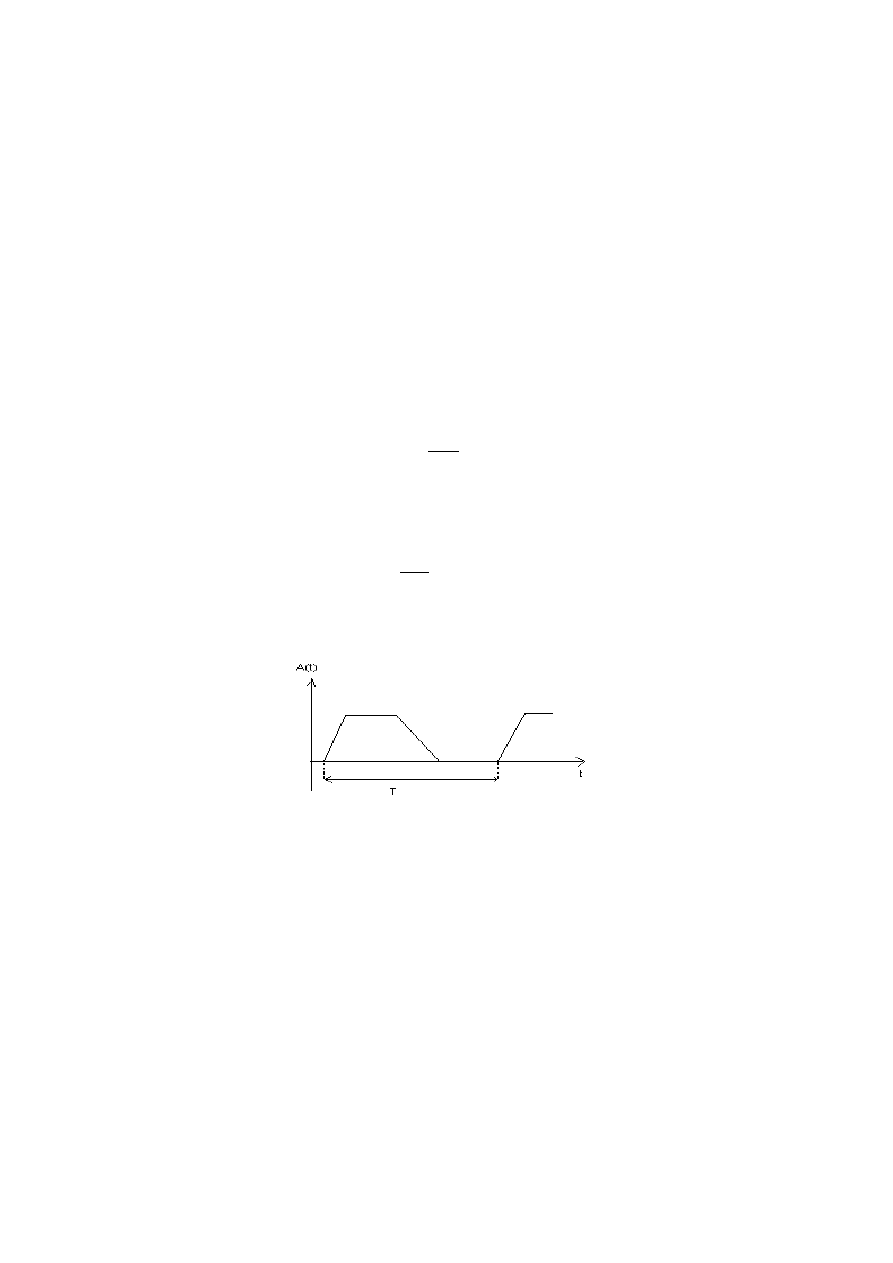
MIERNICTWO ELEKTRONICZNE
Temat: 4.
POMIARY PARAMETRÓW CZASOWYCH
I CZĘSTOTLIWOŚCIOWYCH SYGNAŁÓW
1. Parametry częstotliwościowe i czasowe sygnałów
Jednym z podstawowych parametrów sygnałów elektrycznych jest częstotliwość. Częstotliwością
zjawiska okresowego nazywa się liczbę okresów tego zjawiska, przypadających na jednostkę czasu.
Częstotliwość jest odwrotnością okresu. Jednostką częstotliwości jest 1 herc (1 Hz), czyli jedna pełna
zmiana sygnału w czasie jednej sekundy. Pojęcie częstotliwości jest nierozerwalnie związane z pojęciem
pulsacji (częstotliwości kołowej), która jest większa od częstotliwości 2
π razy. Pojęcia te są tak bliskie,
że w części opracowań operuje się tylko na pojęciu pulsacji, mimo że rozpatruje się te same problemy, co
w publikacjach operujących pojęciem częstotliwości. O pulsacji wiadomo, że jest pochodną fazy sygnału
po czasie, opisuje bowiem prędkość zmian fazy drgań. Fakt ten można zapisać następująco:
dt
d
t
f
t
ϕ
π
ω
=
=
)
(
2
)
(
(1)
Jednakże, faza drgań sinusoidalnych w funkcji czasu rośnie liniowo. W związku z tym, pochodna
fazy względem czasu jest wielkością stałą. Stała jest więc także częstotliwość.
Odwrotnością częstotliwości jest okres, który można definiować tylko dla sygnałów posiadających
stałą częstotliwość.
f
T
1
=
(2)
Okresem T sygnału nazywamy czas jednej pełnej zmiany przebiegu, czyli jest to czas potrzeby na
powtórzenie się wzoru oscylacji:
Rys. 1. Określanie okresu przebiegu
Praktycznie pomiaru okresu dokonuje przez wyznaczenie przedziału czasu między punktami
przebiegu mającymi tę samą wartość chwilową, leżącymi na takich samych zboczach (rosnące – rosnące
lub malejące – malejące). Wybór wartości chwilowej tych punktów oznacza przyjęcie pewnego
umownego poziomu napięcia (prądu), na którym odbywa się pomiar. Na ogół wartość tego poziomu jest
równa wartości średniej napięcia (prądu), którego okres jest wyznaczany.
W celu pomiaru okresu należy przełącznik kalibrowanej podstawy czasu ustawić w takiej pozycji,
aby na ekranie otrzymać rozciągnięty obraz pełnego okresu sygnału. Czas trwania okresu wyniesie:
T
x
= l
x
· S
x
gdzie:
l
x
- odczytana z ekranu długość odcinka w cm, odpowiadająca jednemu okresowi;
S
x
- nastawa współczynnika podstawy czasu, np. w ms/cm.
Okres sygnału jest definiowany dla sygnałów tzw. okresowych w sposób opisany równaniem 3.2.
Zarówno okres, jak i częstotliwość należą do najważniejszych parametrów sygnałów, a ich pomiary są
obecnie najdokładniejszymi pomiarami w technice.
Okres i częstotliwość mają ten sam wzorzec, który pozwala na odtwarzanie jednostki częstotliwości i
czasu z dokładnością 10
-14
. Tak wysoka dokładność jest uzyskiwana dzięki oparciu jednostki czasu na
zjawiskach atomowej fotosyntezy w atomie izotopu cezu Cs
12
.
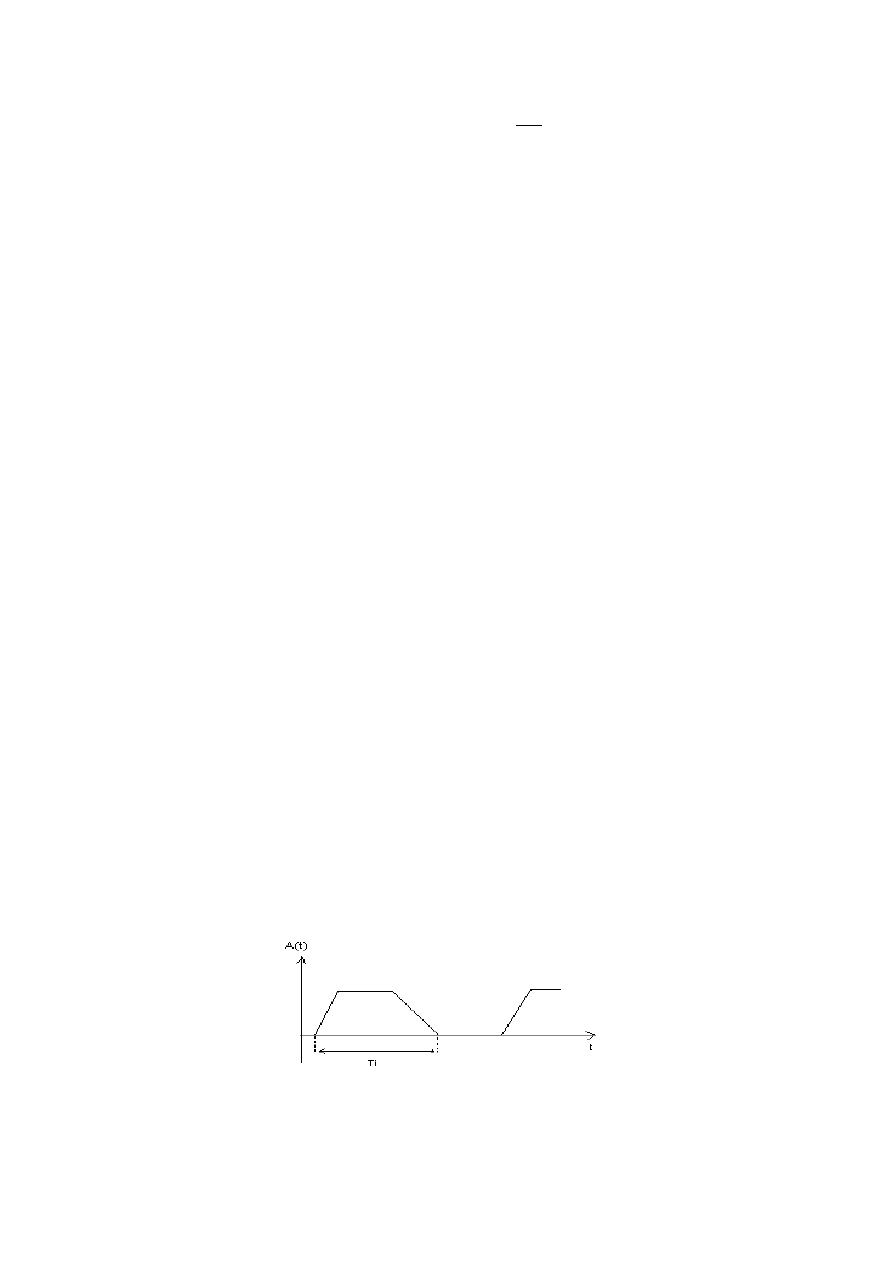
Należy także zwrócić uwagę na to, że w zakresie tzw. częstotliwości mikrofalowych wygodniej jest
operować pojęciem długości fali. Zależność wiążąca pojęcie długości fali z częstotliwością i okresem to:
f
V
T
V
=
⋅
=
λ
(3)
gdzie: V – prędkość rozchodzenia się fali elektromagnetycznej w ośrodku. Dla próżni V = c
≈ 3⋅10
8
m/s.
W wielu gałęziach elektroniki wykorzystuje się sygnały impulsowe, np. prostokątne, których kształt
z różnych przyczyn ulega zniekształceniu. Ocena małych zniekształceń impulsów [5] jest bardzo trudna,
gdyż nigdy nie ma stuprocentowej pewności, które ze zniekształceń zawierał impuls, a które wprowadził
oscyloskop. Do poprawnego pomiaru kształtu impulsów należy stosować oscyloskopy o czasie narastania
przynajmniej 3
÷ 5 razy krótszym niż czas narastania impulsu.
Najlepsze wyniki w zakresie oceny czasowych parametrów impulsów daje szerokoopasmowy
oscyloskop próbkujący. Praktycznie przyjmuje się, że szerokość pasma przenoszenia wzmacniacza
odchylania pionowego oscyloskopu powinna być przynajmniej 100 razy większa od częstotliwości
powtarzania impulsów.
Parametry typu okres, częstotliwość i długość fali są określane dla wszystkich sygnałów okresowych.
Wybór wielkości mierzonej zależy właściwie jedynie od przyjętej metody pomiarowej i zakresu
częstotliwości, przy którym jest wykonywany pomiar. Dodatkowo dla niektórych sygnałów istotne jest
także określenie takich parametrów jak: czas powtarzania impulsów, szerokość (czas trwania) impulsu,
czas narastania i opadania zboczy, współczynnik wypełnienia itp.
Sposób definiowania wielkości charakteryzujących impulsy, przedstawia rys. 2.
- amplituda impulsu - określa się ją, jako różnicę między wartością maksymalną i minimalną (bez
uwzględniania przerostów). Oprócz amplitudy interesującym parametrem jest czas przejścia od
dolnej do górnej wartości amplitudy albo odwrotnie, czyli tzw.:
- czas narastania impulsu – jest długością odcinka czasu między dwoma punktami przebiegu
leżącymi na tym samym zboczu narastającym i posiadającymi wartości chwilowe równe
odpowiednio 10% i 90% wartości miedzyszczytowej.
- czas opadania impulsu – jest definiowany podobnie do czasu narastania, z tym, że pomiar odbywa
się między punktami o wartości chwilowej 90% i 10% U
p-p
leżącymi na zboczu opadającym. Punkty
charakterystyczne, między którymi powinny być mierzone owe czasy, określane są na poziomie 10%
i 90% wartości amplitudy impulsu. Pomiary czasów narastania i opadania impulsów ułatwia zwykle
skala oscyloskopu, na której znajdują się dodatkowe linie (na poziomie 10% i 90 %).
- szerokość impulsu (czas trwania impulsu) – definiowana jest, jako odległość między punktami
leżącymi na przeciwległych zboczach i mających tę samą wartość chwilową równą 50% wartości
międzyszczytowej przebiegu. Zgodnie z przyjętą definicją mierzy się ją na poziomie 50 % wartości
amplitudy. Tak więc, czas trwania impulsu jest to czas, w którym występuje impuls o pewnej
amplitudzie. Wyróżniamy dwa czasy trwania impulsu: czas trwania impulsu dodatniego i czas
trwania impulsu ujemnego. Jest pewna zależność miedzy czasem trwania impulsu a okresem.
T = t
1
+ t
2
gdzie: T – okres;
t
1
– czas rwania impulsu dodatniego;
t
2
– czas trwania impulsu ujemnego.
Rys. 2. Określenie czasu trwania impulsu t
i
W celu pomiaru czasu trwania impulsu oscyloskopem, należy przełącznik kalibrowanej podstawy
czasu ustawić w takiej pozycji, aby na ekranie otrzymać rozciągnięty obraz pełnego okresu sygnału. Czas
trwania impulsu wyniesie:
t
i
= l
x
· S
x
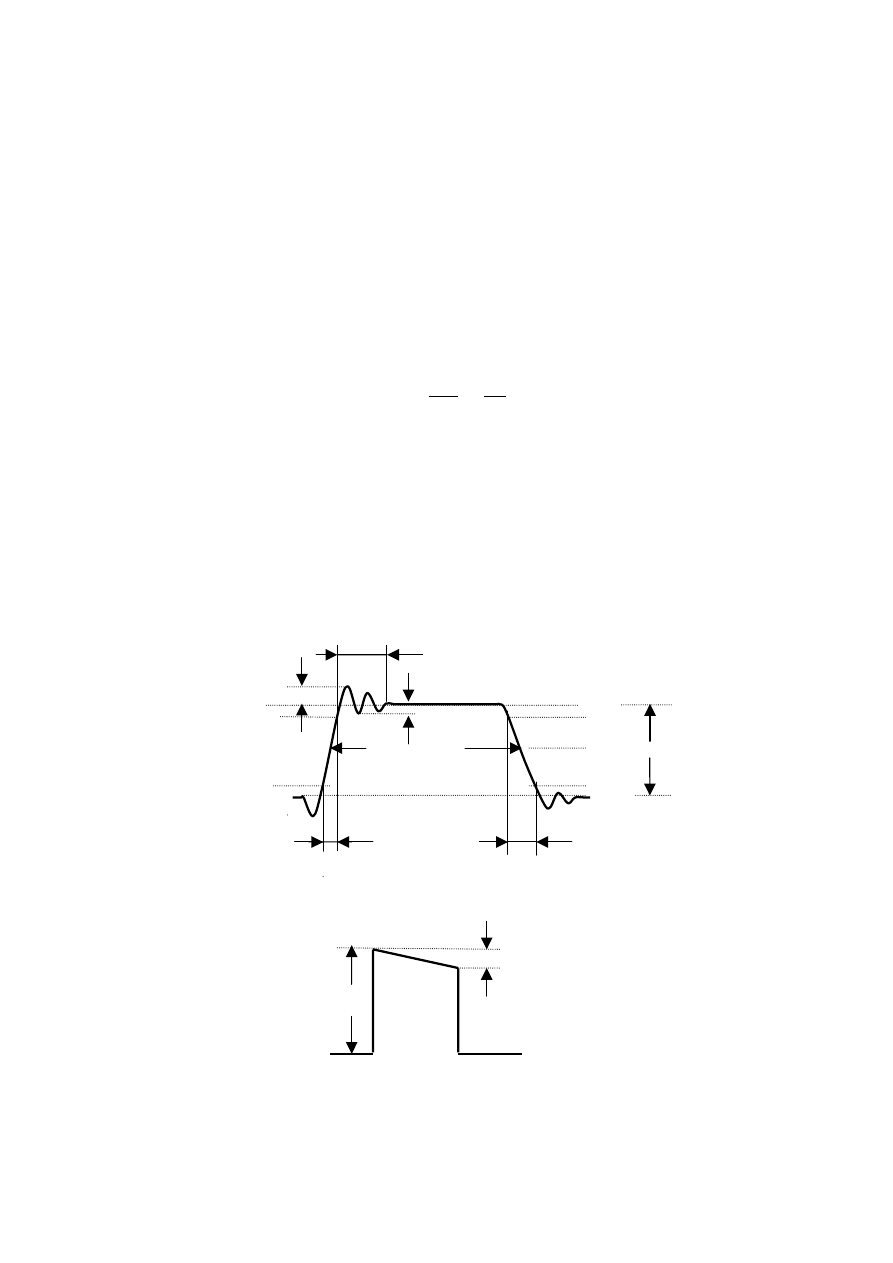
gdzie:
l
x
- odczytana z ekranu długość odcinka w cm odpowiadająca czasowi trwania impulsu;
S
x
- nastawa współczynnika podstawy czasu, np. w ms/cm.
Dla sygnałów okresowych, w zależności od wyboru zboczy można wykonać pomiar szerokości połówki
dodatniej oraz pomiar połówki ujemnej. Sumą tych dwóch czasów powinien być oczywiście okres
sygnału. Istnieje pewna różnica między definicją tego parametru a pomiarem praktycznym wykonywany
w układzie czasomierza cyfrowego. Polega ona na tym, że pomiar jest wykonywany na poziomie
wartości średniej napięcia a nie na poziomie 50%. Przy założeniu, że czas narastania i opadania zboczy
jest wielokrotnie mniejszy od szerokości impulsu, błąd z tego wynikający można pominąć.
- współczynnik wypełnienia D – określany jest jako iloraz czasu trwania (szerokości) impulsu t
i
i
okresu powtarzania T.
D = t
i
/ T
A zatem, gdy potrzebujemy mieć wartość współczynnika wypełnienia, korzystamy z powyższych
metod mierząc czas trwania impulsu oraz okres powtarzania i podstawiając do wzoru D
= t
i
/ T.
Określany jest on jako stosunek szerokości połówki dodatniej impulsu do okresu:
Θ
=
=
+
1
T
t
D
i
- współczynnik przerwistości
Θ
- jest on odwrotnością współczynnika wypełnienia:
Θ = 1 / D
- zwis grzbietu impulsu - jest stosunkiem zmiany napięcia wyjściowego
∆U w czasie trwania
impulsu, odniesionej do amplitudy U, wyrażonym w procentach. Wartość zwisu jest zależna od
ograniczeń charakterystyki częstotliwościowej oscyloskopu od strony małych częstotliwości,
powodowanych przez stałe czasowe układów sprzęgających.
- przerosty – zafalowania (oscylacje) na grzbiecie impulsu, określane w % całkowitej amplitudy;
powodowane są one ograniczonym pasmem charakterystyki częstotliwościowej w zakresie wysokiej
częstotliwości, przez parametry wzmacniaczy i lampy oscyloskopowej.
czas trwania oscylacji pasożytniczych
przerost (+
∆%)
przerost (-
∆%)
100%
90 %
szerokość impulsu 50 %
Amplituda impulsu
linia odniesienia
0% 10%
90% 100 %
czas opadania
∆U
czas narastania U
Zwis =
∆
U
U
Rys.3.17. Parametry impulsu prostokątnego.
- czas powtarzania impulsów - jest to parametr definiowany dla przebiegów impulsowych złożonych
z paczek impulsów. Czas powtarzania impulsów to odległość między odpowiednimi zboczami
kolejnych impulsów w paczce. Natomiast okres paczki impulsów to odległość między odpowiednimi
zboczami np. pierwszych impulsów w kolejnych paczkach.
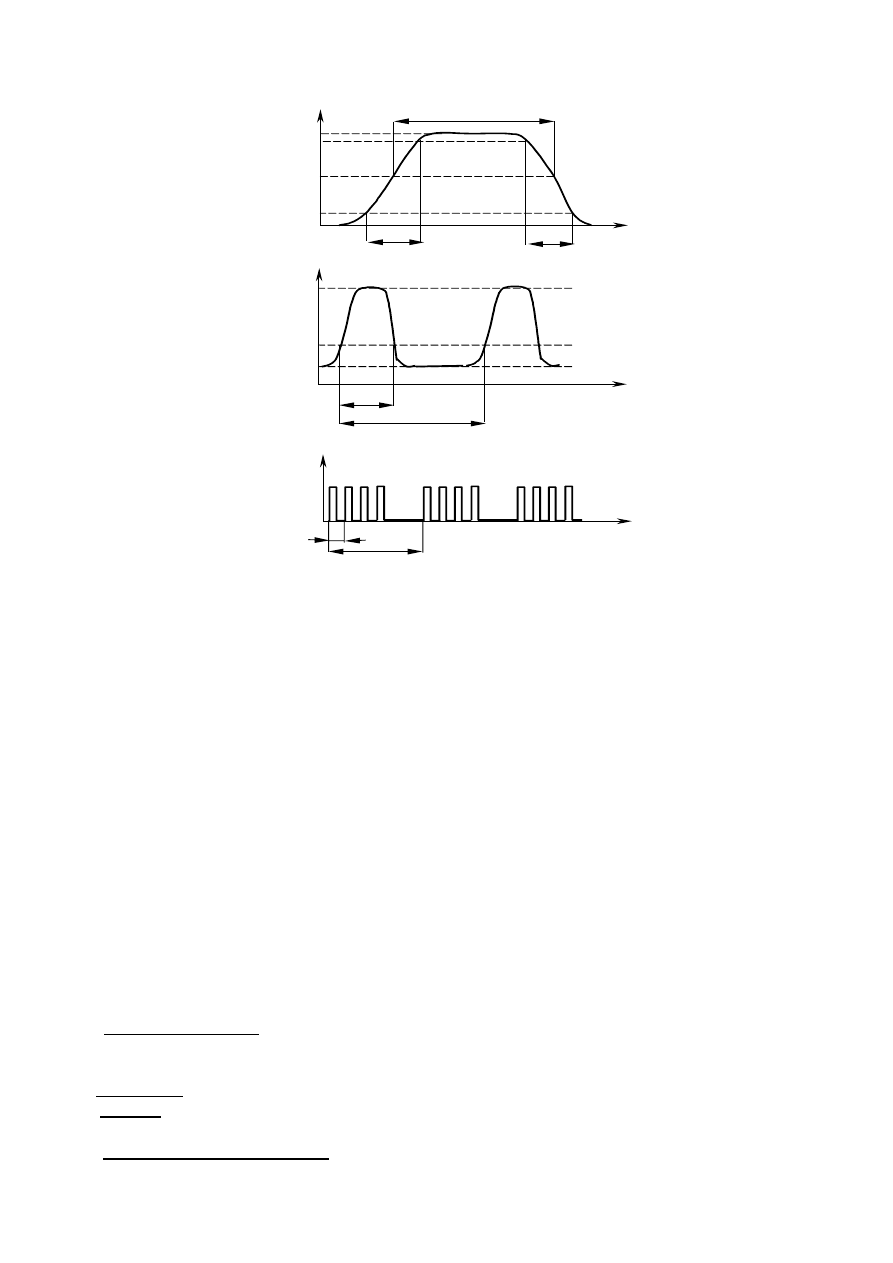
Sposób wyznaczania poszczególnych parametrów czasowych przedstawiono graficznie na rys. 3.
t
0,5U
p-p
0,1U
p-p
0,9U
p-p
U
p-p
U
t
i
t
n
t
o
a)
t
U
b)
U
śr
U
max
U
min
T
t
i
t
U
c)
T
T
p
Rys. 3. Sposób wyznaczania parametrów czasowych:
a) szerokość impulsu t
i
;
b) czas narastania t
n
;
c) czas opadania t
o
;
d) okres T;
e) współczynnik wypełnienia D;
f) czas powtarzania T
p
;
g) okres T.
2. Pomiary częstotliwości i czasu sygnałów
Znanych jest wiele metod pomiaru częstotliwości. Generalnie można je podzielić na dwie grupy:
- metody polegające na porównaniu wzorcowej i niezależnej częstotliwości sygnałów lub ich okresów.
Metody tej grupy umożliwiają uzyskanie dużej dokładności;
- metody wykorzystujące częstotliwościową zależność parametrów obwodów elektrycznych. Są to
metody znacznie mniej dokładne.
Podstawową metodą pomiaru częstotliwości jest metoda cyfrowa. Częstościomierze i okresomierze
cyfrowe wyparły przyrządy innych typów z większości zastosowań. Jednak można spotkać przyrządy
pracujące w oparciu o metodę dyskryminatora częstotliwości (m.cz.) lub rezonansowe (b.w.cz.). Dla
woltomierzy, częstościomierzy i okresomierzy cyfrowych zdefiniowane są parametry metrologiczne,
których znajomość pozwala użytkownikom na wybór właściwego przyrządu do konkretnego zadania
pomiarowego. Do podstawowych parametrów częstościomierzy (czasomierzy) cyfrowych należą:
- zakres pomiarowy: dla częstościomierzy i czasomierzy jest on definiowany tak, jak dla
woltomierzy, ale inne są źródła ograniczeń dotyczących częstotliwości granicznych. Ograniczenia te
należy rozpatrzyć osobno dla każdej z metod.
- dokładność: dla częstościomierzy analogowych jest ona wyrażana za pomocą klasy dokładności.
- czułość: dla częstościomierza określa ona zdolność reagowania na minimalną zmianę wartości
częstotliwości mierzonego sygnału.
- zakres napięć wejściowych: określa on zakres napięć, przy których częstościomierz działa
poprawnie. Napięcie maksymalne jest na ogół ograniczone wytrzymałością energetyczną obwodów
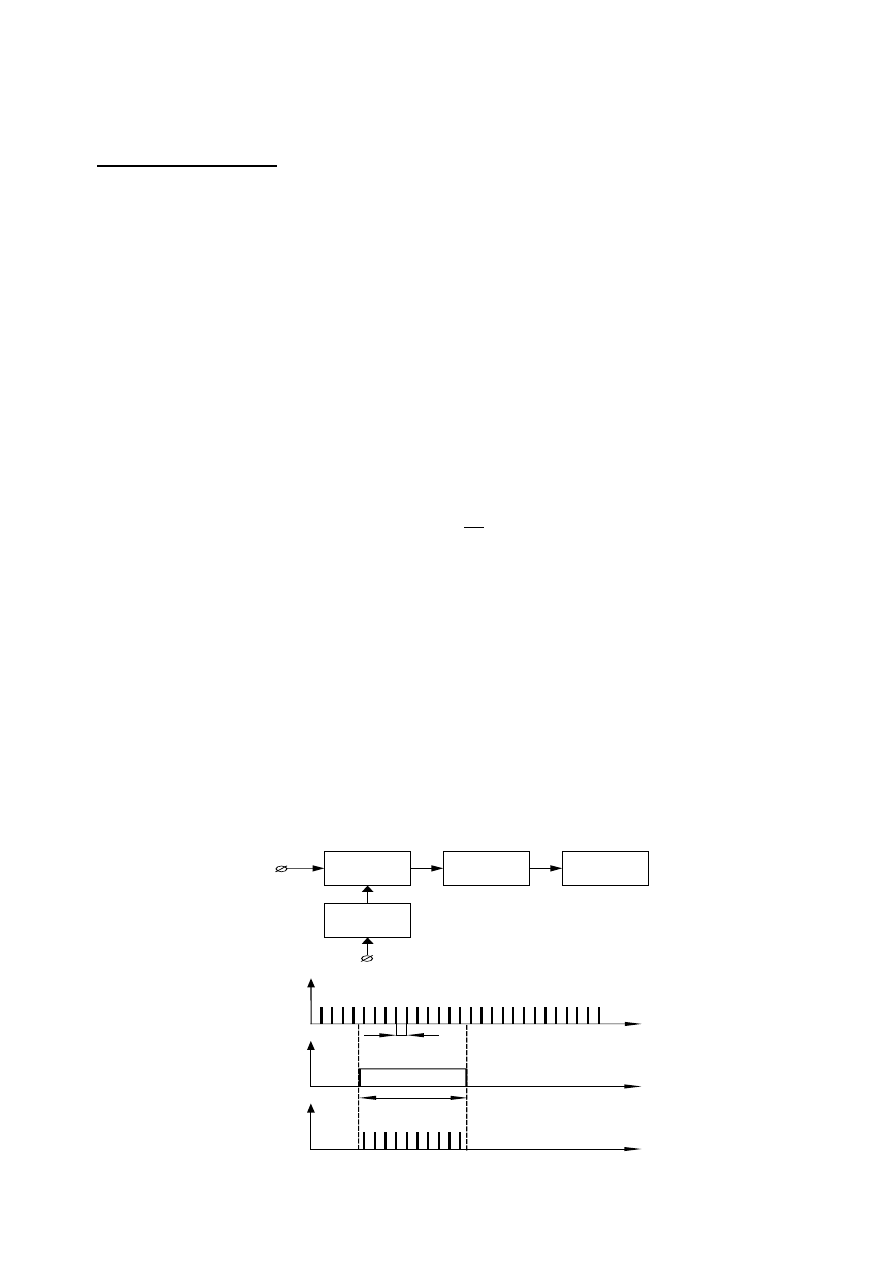
wejściowych, natomiast napięcie minimalne progiem pobudliwości danego wejścia
częstościomierza. Poniżej tego napięcia nie działają prawidłowo układy wyzwalania bramki oraz
kształtowania impulsów w częstościomierzach czasomierzach cyfrowych, a wskaźnik
w częstościomierzach analogowych nie daje żadnych wychyleń.
- impedancja wejściowa: dla częstościomierzy i czasomierzy nie musi ona być duża, gdyż przyrząd
ten nie jest woltomierzem. Zależy ona od przewidywanych zastosowań przyrządu i zakresu
mierzonych częstotliwości. Przyrządy przeznaczone do pomiaru małych częstotliwości mają zwykle
impedancję dużą, rzędu 1M
Ω, aby nie obciążać źródła mierzonego sygnału. Przyrządy
przeznaczone do pomiaru dużych częstotliwości oraz do zastosowań, w których niepożądane jest
zjawisko odbicia mają impedancję wejściową dopasowaną do źródła mierzonego sygnału, np. 50
Ω.
3. Okresomierze cyfrowe
Zasada pracy okresomierza cyfrowego polega na zliczaniu impulsów - generowanych przez generator
wzorcowy o dużej stabilności częstotliwości (najczęściej kwarcowy) o znanym okresie T
w
w czasie, który
jest proporcjonalny do okresu mierzonego sygnału T
x
.
Ideę pracy okresomierza przedstawiono na rys. 4. Na wejście bramki jest podawany sygnał w postaci
ciągu impulsów wypracowany w układzie wejściowym czasomierza. Bramka jest otwierana przez sygnał
prostokątny wypracowany w układzie otwierania bramki.
Licznik zlicza impulsy pojawiające się na wyjściu bramki wtedy, gdy bramka jest otwarta. Liczba
impulsów zliczonych przez licznik jest zobrazowana na wskaźniku cyfrowym i wynosi:
w
x
T
T
N
=
(4)
Jeżeli znany jest okres impulsów wzorcowych, to okres nieznany można obliczyć:
w
x
T
N
T
⋅
=
(5)
Widać stąd, że jeśli czas T
w
byłby czasem jednostkowym, np. 1s, to wskazanie przyrządu można
byłoby odczytać bezpośrednio w sekundach. Jednakże przy tak długim czasie T
w
duży musiałby być także
okres sygnału mierzonego T
x
. W rzeczywistych układach okresomierzy cyfrowych okres impulsów
wzorcowych zliczanych przez licznik wynosi 10
n
sekund – przy czym, n jest liczbą całkowitą najczęściej
z przedziału (- 8; 1). W okresomierzach-czasomierzach cyfrowych dolna wartość zakresu pomiarowego
jest ograniczona rozdzielczością przyrządu oraz żądaną przez użytkownika dokładnością pomiaru, w
której decydującą rolę odgrywa błąd dyskretyzacji. Jednakże wartość dolną można zwiększać przez
pomiar metodą pośrednią mierząc najpierw częstotliwość sygnału a na jej podstawie okres.
Wartość górna zakresu pomiarowego jest ograniczona jedynie pojemnością licznika i wyświetlacza
oraz tym, czy przy wolnonarastających zboczach sygnału mierzonego, układ wyzwalania bramki jest w
stanie wypracować jednoznaczny sygnał wyzwalający bramkę.
B r a m k a
L i c z n i k
W s k a ź n i k
U k ł a d
o t w i e r a n i a
b r a m k i
f
w
f
x
3
2
1
1
2
3
T
x
T
w
t
t
t
a )
b )
Rys. 4. Zasada pracy czasomierza cyfrowego: a) schemat blokowy; b) przebiegi czasowe.
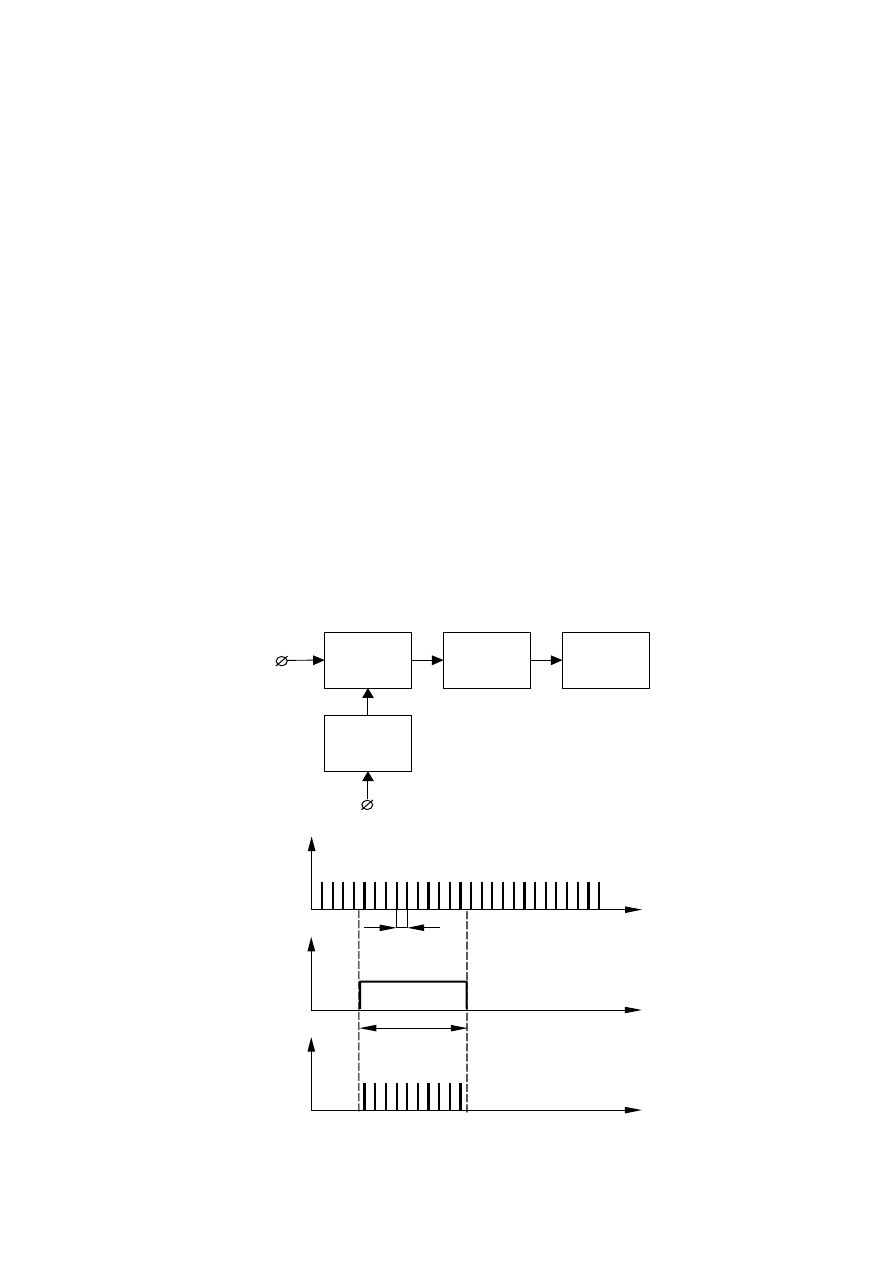
4. Częstościomierze cyfrowe
Pomiarów częstotliwości można dokonywać za pomocą częstościomierza. Duża dokładność oraz
szeroki zakres mierzonych częstotliwości sprawiają, że częstościomierz cyfrowy jest obecnie
podstawowym, najczęściej stosowanym narzędziem do pomiaru częstotliwości. Zapewnia on dużą
dokładność oraz szeroki zakres mierzonych częstotliwości.
Zasada pracy częstościomierza cyfrowego polega na zliczaniu impulsów o częstotliwości równej
częstotliwości sygnału mierzonego we wzorcowym, ściśle określonym i znanym przedziale czasu.
Przebieg badany f
x
jest przetwarzany w układzie formującym na ciąg impulsów N
X
o takiej samej
częstotliwości. Układ sterujący formuje impuls prostokątny wzorcowy o czasie trwania t
w
, otwierający
bramkę na czas pomiaru. W czasie otwarcia bramki licznik zlicza N
x
impulsów mierzonego przebiegu o
częstotliwości f
x
, stąd:
f
x
= N
x
/ t
w
(6)
Czas pomiaru t
w
ogranicza się zwykle do wartości 0,01s; 0,1s; 1s; 10s, co umożliwia wyświetlenie
wyniku pomiaru bezpośrednio w Hz, kHz lub MHz.
Względna niepewność pomiarowa częstotliwości f
x
zależy od błędu granicznego określenia
wzorcowego odcinka czasu t
w
i od liczby N
x
zliczonych impulsów:
δf
x
=
± (δt
w
+
δN
x
)
(7)
Dla typowych częstościomierzy składowa
δt
w
posiada wartość rzędu 0,0001 %, a druga jest
pomijalnie mała.
Zasadę pracy częstościomierza cyfrowego ilustruje schemat blokowy i wykresy przedstawione na
rys. 3.20. Badany przebieg o częstotliwości f
x
po ewentualnym wzmocnieniu, jest formowany w ciąg
impulsów o takiej samej częstotliwości, jak mierzona. Generator wzorcowy wraz z układem powielania i
dzielenia częstotliwości, wytwarza ciąg impulsów wzorcowych o częstotliwości f
w.
Impulsy te wyzwalają
układ sterowania, którym najczęściej jest przerzutnik bramkujący. Przerzutnik ten wyznacza wzorcowy
czas pomiaru t
p,
w którym otwarta jest bramka.
Bram ka
Licznik
W skaźnik
U kład
otw ierania
bram ki
T
x
T
w
3
2
1
1
2
3
T
w
T
x
t
t
t
a)
b)
Rys. 6. Idea metody cyfrowej pomiaru częstotliwości:
a) schemat blokowy; b) przebiegi czasowe.
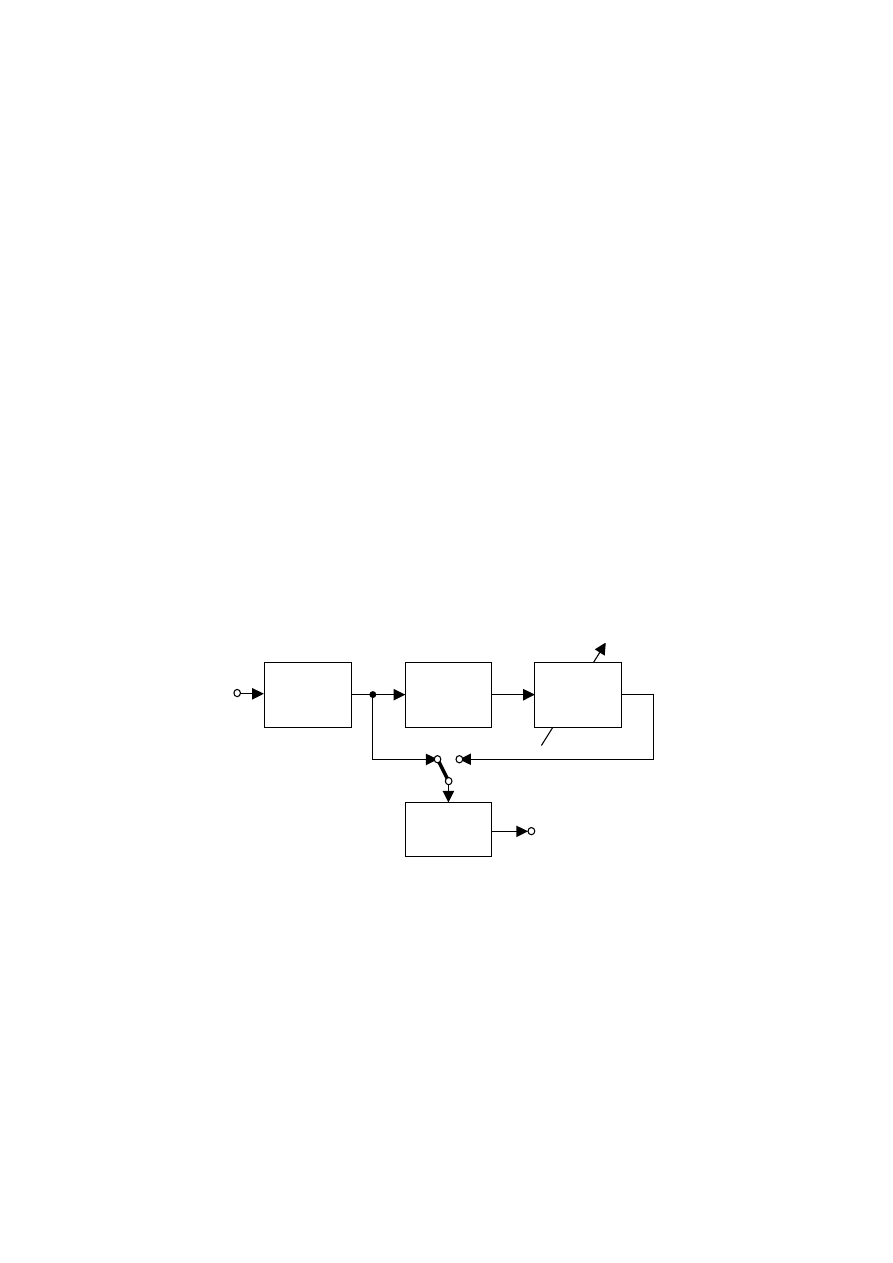
W czasie otwarcia bramki, do licznika są doprowadzane impulsy o częstotliwości mierzonej f
x
.
Liczba impulsów zliczonych przez licznik jest zobrazowana na wskaźniku cyfrowym i wynosi:
N
x
= t
p
f
x
i stąd:
f
x
= N
x
/ t
p
lub inaczej:
f
x
= N
x
/ T
w
= N
x
f
w
Widać stąd, że jeśli czas t
p
byłby czasem jednostkowym, np. 1s, to wskazanie przyrządu można
byłoby odczytać bezpośrednio w hercach. W rzeczywistych układach częstościomierzy cyfrowych
wzorcowy czas otwarcia bramki wynosi 10
n
sekund, gdzie n - jest liczbą całkowitą, najczęściej z
przedziału (- 2; 1).
Układ kasowania doprowadza licznik do stanu zerowego tuż przed otwarciem bramki. Kasowanie
odbywa się w czasie wyznaczonym przez układ opóźniający a zawartym między impulsem startowym
doprowadzanym do układu sterowania (chwila t
1
) i otwarciem bramki (chwila t
2
).
Zakres częstotliwości częstościomierzy cyfrowych jest ograniczony od góry częstotliwością pracy
układów zliczających, np. w technologii TTL częstotliwością graniczną była wartość ok. 25 MHz, a dla
układów CMOS kilkaset MHz. Obecnie częstotliwość ta wynosi ok. 1GHz.
Częstotliwość graniczna dolna zakresu częstotliwości jest ograniczona rozdzielczością
częstościomierza oraz wymaganą dokładnością pomiaru, w tym przede wszystkim wpływem błędu
dyskretyzacji na wynik pomiaru. Jednak, jeśli zdecydujemy się w przypadku małych częstotliwości, na jej
pomiar pośredni przez wyznaczenie okresu a potem dopiero częstotliwości, to ograniczenie od dołu nie
istnieje.
Rozszerzenie zakresu pomiarowego częstościomierzy i okresomierzy cyfrowych od dołu może być
zrealizowane przez zastosowanie metody pośredniej i wstępny pomiar okresu lub częstotliwości a potem
obliczenie odpowiednio częstotliwości lub okresu. Większe problemy sprawia rozszerzenie górnej
granicy zakresu pomiarowego częstościomierzy.
Stosowane są dwa podstawowe rozwiązania – przez zastosowanie dzielnika częstotliwości lub
przemiany częstotliwości.
Schemat blokowy przystawki dzielącej przedstawiono na rys. 7.
Układ
wejściowy
Układ
wyjściowy
Dzielnik f
1/k
Układ
formujący
f
x
f
x
f
x
/ k
f
cz
= f
x
/ k
Rys. 7. Schemat blokowy przystawki dzielącej dla częstościomierza cyfrowego.
Przystawka taka składa się z:
- układu wejściowego (wzmacniacza lub tłumika);
- układu formującego impulsy;
- dzielnika częstotliwości (np. 1:10 lub 1:100);
- układu dopasowującego poziom i kształt impulsów do wejścia częstościomierza.
Zmniejszoną k-krotnie częstotliwość mierzy się częstościomierzem cyfrowym. Wskazanie
częstościomierza f
cz
mnoży się przez współczynnik k, aby wyznaczyć wartość f
x
.
Tak więc aby obliczyć zmierzoną częstotliwość należy wykorzystać poniższy wzór:
k
f
f
cz
x
⋅
=
gdzie:
k – stosunek podziału w przystawce dzielącej.
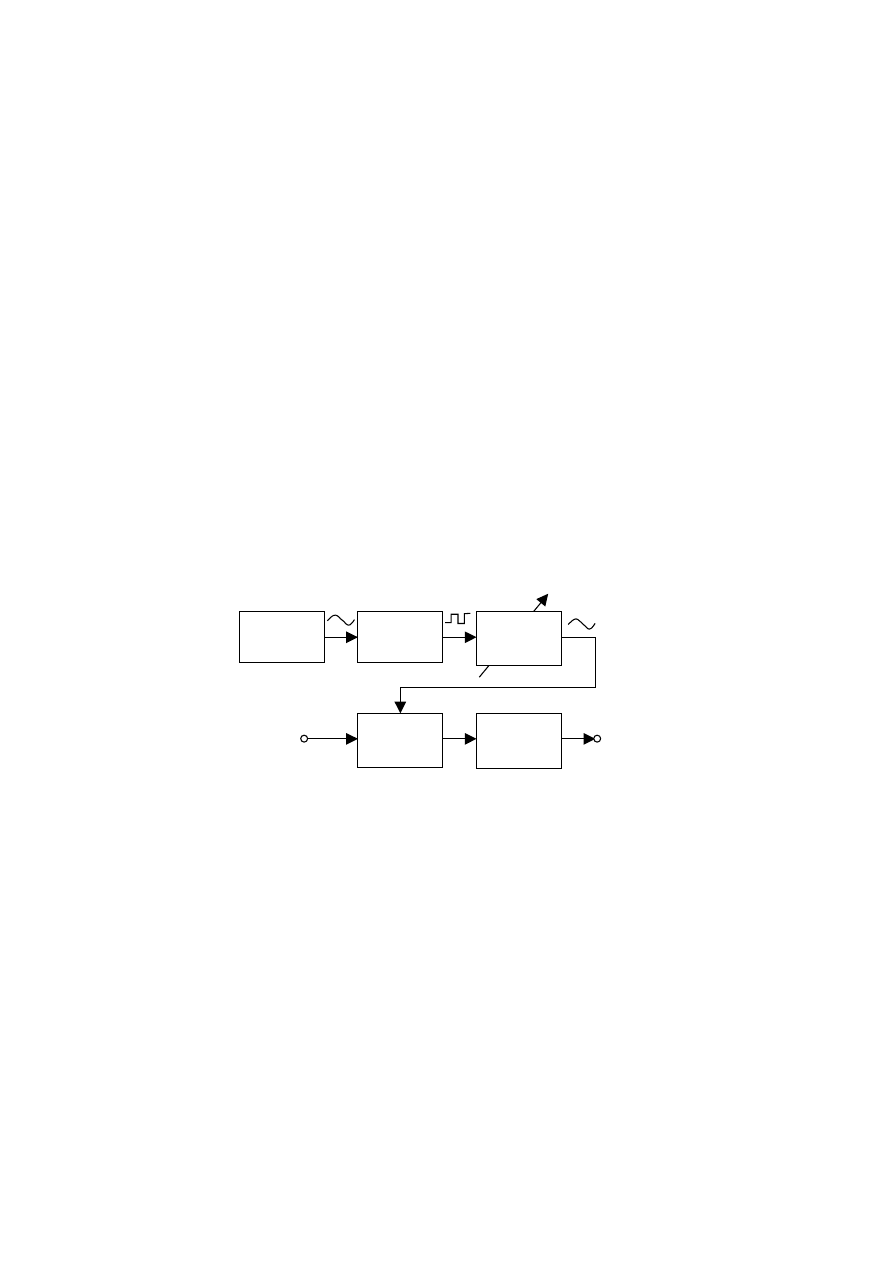
Wykorzystując przystawkę dzielącą należy pamiętać o tym, że jej użycie zwiększa wartość błędu
pomiaru częstotliwości ponad wartość wynikającą z właściwości częstościomierza. Wynika to z
właściwości dzielników częstotliwości, które mogą charakteryzować się „gubieniem” impulsów.
Dodatkowo błąd bezwzględny pomiaru częstotliwości f
x
jest k-razy większy od błędu pomiaru f
cz
.
Przystawki tego typu są na ogół wbudowane w układ częstościomierza i użytkownik może nawet nie
zdawać sobie sprawy, że taka metoda rozszerzenia zakresu częstościomierza została zastosowana.
Podstawową zaletą tej metody jest to, że odczyt częstotliwości jest odczytem jednoznacznym, co stanowi
przewagę tego rozwiązania nad przystawkami mieszającymi. Dodatkową zaletą jest możliwość
wykonania takiej przestawki jako urządzenia zewnętrznego dostosowanego do pracy z różnymi
częstościomierzami wykonanymi w starszej technologii. Umożliwia więc to wykonywanie pomiarów bez
konieczności zakupu nowych przyrządów.
Innym sposobem rozszerzania zakresu częstościomierzy cyfrowych jest wykorzystanie przystawki
mieszającej, tzw. heterodynowej. Idea takiego rozwiązania polega na wyznaczeniu różnicy między
częstotliwościami sygnału badanego i sygnału znanego. W tym celu wykorzystuje się układ mieszacza, na
którego wejścia podaje się sygnał o częstotliwości mierzonej oraz sygnał odkształcony z generatora
stabilizowanego kwarcem. Zasadę działania takiej przystawki przedstawiono na rys. 3.22.
Przystawka składa się z generatora kwarcowego o częstotliwości podstawowej f
w
równej na ogół
10MHz. W układzie formującym następuje kształtowanie przebiegu zawierającego dużą liczbę
harmonicznych (np. przebieg prostokątny). Filtr pasmowy ma za zadanie wybór takiej harmonicznej, aby
różnica częstotliwości mierzonej i tej harmonicznej mieściła się w zakresie pomiarowym
częstościomierza. W mieszaczy wykonywana jest przemiana częstotliwości. Przy odpowiedniej
konstrukcji mieszacza na jego wyjściu pojawi się sygnał, w którego widmie dominować będą
częstotliwości będące sumą i różnicą częstotliwości mierzonej oraz odpowiedniej harmonicznej
częstotliwości wzorcowej.
Generator
wzorcowy
Układ
kształtujący
Filtr
pasmowy
Mieszacz
Filtr
dolnoprze-
pustowy
f
w
Σ
k
⋅
f
w
k
⋅
f
w
f
x
f
x
±
k
⋅
f
w
f
cz
= f
x
- k
⋅
f
w
Rys. 8. Schemat blokowy przystawki mieszającej.
Obsługa przystawki sprowadza się do doprowadzenia do wejścia przystawki sygnału o częstotliwości
mierzonej i takim przełączaniu filtru pasmowego, aby na wyjściu pojawił się sygnał o częstotliwości
mieszczącej się w zakresie pomiarowym częstościomierza.
Regulacja filtru pasmowego jest skokowa lub płynna i jest on wyskalowany w częstotliwości
odpowiedniej harmonicznej sygnału wzorcowego. Wartość częstotliwości mierzonej otrzymuje się przez
odczytanie wskazania częstościomierza i harmonicznej częstotliwości wzorcowej i podstawieniu ich do
wzoru:
w
cz
x
f
k
f
f
⋅
+
=
(7)
Oprócz oczywistych zalet takiej przystawki istotne są jej pewne wady, do których zaliczyć trzeba
wzrost błędu bezwzględnego pomiaru częstotliwości. Wynika to z tego, że oprócz błędu częstościomierza
mamy tu także z błędem częstotliwości generatora wzorcowego i to zwiększonym k-krotnie.
Ponadto metoda ta nie daje jednoznacznych wyników. Istnieje bowiem możliwość uzyskania
wskazania częstościomierza dla różnych wartości k przy tej samej częstotliwości mierzonej. Wynika to z
tego, że produktem przemiany częstotliwości w mieszaczu jest na ogół sygnał o dużo bogatszym widmie
niż to opisano wyżej. Jest to przesłanka do popełniania błędów grubych. Aby ich uniknąć należy wstępnie
znać orientacyjną wartość częstotliwości mierzonej (najczęściej z dokładnością do 0,5
⋅f
w
).
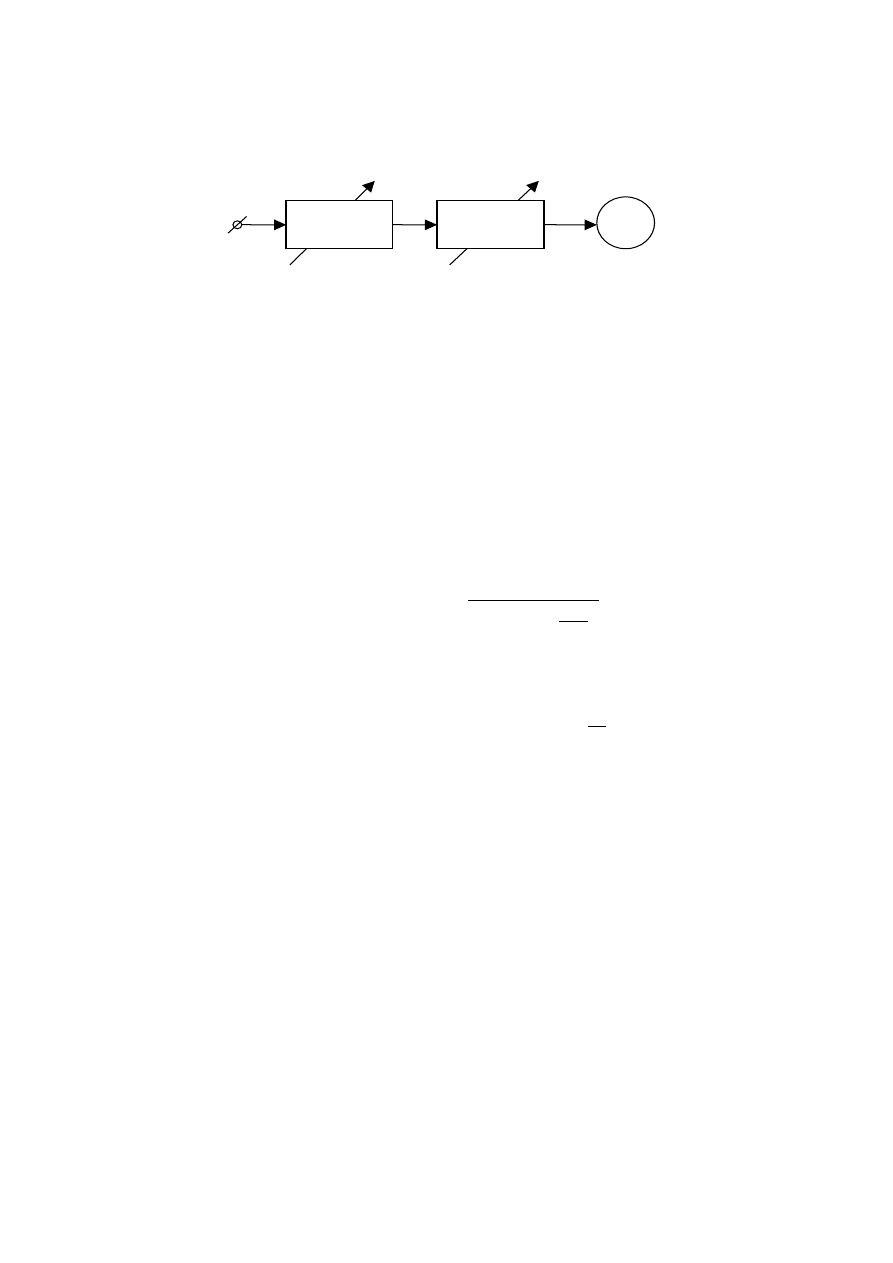
5. Częstościomierze rezonansowe
Częstościomierz rezonansowy działa na zasadzie porównania częstotliwości mierzonej z wartością
częstotliwości własnej wzorcowego obwodu rezonansowego (najczęściej szeregowego). Schemat
blokowy takiego przyrządu przedstawia rys. 9.
Obwód
wejściowy
Obwód
rezonansowy
A
f
x
U
f
0
α→α
max
Rys. 9. Schemat blokowy częstościomierza rezonansowego.
Przyrząd składa się z bloku obwodów wejściowych, obwodu rezonansowego oraz wskaźnika
rezonansu – najczęściej prostownikowego amperomierza magnetoelektrycznego.
Zadaniem obwodów wejściowych jest zapewnienie odpowiedniego poziomu napięcia, które zostanie
podane na obwód rezonansowy. Minimalny poziom napięcia musi być taki, aby w okolicach
częstotliwości rezonansowej miernika zmiany położenia elementu wskazującego miernika były
zauważalne. Maksymalny poziom napięcia musi być zaś taki, aby w stanie rezonansu nie następowało
przekraczanie zakresu wskaźnika. Obwód wejściowy ma także zapewnić separację obwodu
rezonansowego przyrządu od obwodu pomiarowego.
Obwód rezonansowy jest źródłem częstotliwości odniesienia, z którą porównywana jest
częstotliwość sygnału mierzonego.
Jeśli rozpatrzy się szeregowy obwód rezonansowy RLC to wiadomo jest, że płynie przez niego prąd
I:
−
+
=
C
L
j
R
U
I
ω
ω
1
(8)
W stanie rezonansu reaktancja pojemnościowa jest równa reaktancji indukcyjnej, a natężenie prądu
osiąga wartość maksymalną I
0
zależną od napięcia zasilającego obwód rezonansowy i ograniczoną
wartością rezystancji w obwodzie:
R
U
I
I
=
=
0
0
)
(
ω
(9)
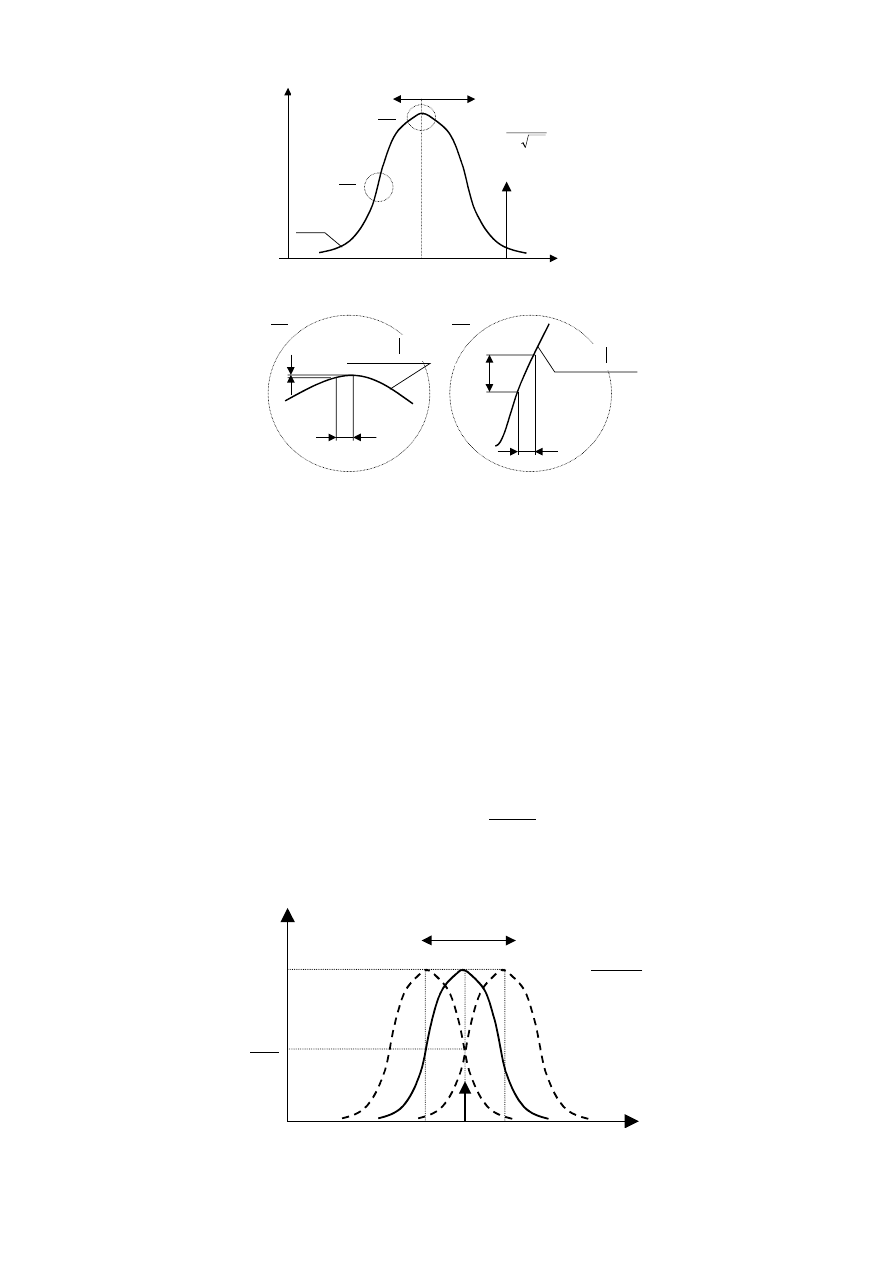
Na rys. 10 przedstawiono kształt krzywej rezonansowej dla obwodu szeregowego. Pomiar odbywa
się w ten sposób, że zmieniając pojemność wzorcowego obwodu RLC doprowadza się go do rezonansu,
który ma miejsce w tedy, gdy f
0
= f
x
.
Zgodnie z (3.51) prąd w obwodzie jest maksymalny. Wystarczy więc w trakcie regulacji
kondensatora obserwować wychylenie wskazówki amperomierza. Jej maksymalne wychylenie świadczy
o dostrojeniu obwodu RLC do częstotliwości mierzonej f
x
. Odczytu częstotliwości mierzonej dokonuje
się z kondensatora wzorcowego wyskalowanego w hercach.
Nie stosuje się rozwiązań, w których elementem strojonym jest cewka indukcyjna, ponieważ istnieją
poważne trudności technologiczne w wykonaniu cewki strojonej o stabilnej (np. w przypadku drgań)
wartości indukcyjności.
Aby metoda spełniała swoją rolę, kształt krzywej rezonansowej musi spełniać pewne wymagania:
- po pierwsze krzywa ta musi być na tyle selektywna, żeby fakt zbliżania się częstotliwości własnej
obwodu rezonansowego do częstotliwości mierzonej był wyraźnie widoczny na wskaźniku
wychyłowym przyrządu;
- po drugie obwód rezonansowy nie może być zbyt selektywny (duża dobroć), ponieważ podczas
mało starannego (szybkiego) strojenia obserwator mógłby nie dostrzec zmiany położenia
wskazówki a więc nie wykryć istnienia częstotliwości mierzonej.
Dokładność metody nie jest duża i wynosi około 0,07 ÷ 0,3%. Podstawowym ograniczeniem jest tu
dokładność wykonania obwodu RLC oraz to, że okolicach rezonansu czułość układu jest bardzo niska
(pochodna charakterystyki rezonansowej bliska zero) – rys. 10.b.
f
x
f
0
f
α
I
B-B
A-A
A-A
B-B
b)
Strojenie lewo-prawo
∆
1
f =
∆
2
f =
∆
f
∆
1
α
<
∆
2
α
∆
1
f
∆
2
f
∆
1
α
∆
2
α
a)
x
f
LC
f
→
=
π
2
1
0
I = f (f)
0
)
(
f
f
f
f
I
≠
=
0
)
(
f
f
f
f
I
→
=
Rys. 10. Zasada pracy częstościomierza rezonansowego z szeregowym obwodem RLC:
a) – kształt krzywej rezonansowej;
b) – wpływ nachylenia krzywej na dokładność pomiaru częstotliwości.
Tymczasem wiadomo, że układ RLC miałby o wiele większą czułość, gdyby pomiaru dokonywano
na zboczach krzywej rezonansowej. Problem rozwiązuje się przez zastosowanie metody widełkowej (rys.
11).
Pomiar metodą widełkową wykonywany jest w dwóch fazach. W fazie pierwszej następuje
dostrojenie obwodu rezonansowego do częstotliwości mierzonej f
x
. Nie dokonuje się jednak jej odczytu,
a jedynie zapamiętuje położenie
α
max
wskazówki miernika.
W fazie drugiej odstraja się obwód RLC w lewo i w prawo od rezonansu, tak aby wskazanie
miernika
α
spadło np. do połowy wychylenia
α
max
. Ze skali przyrządu odczytuje się wartości f
L
i f
P
a
wartość f
x
wyznacza się ze wzoru:
2
P
L
x
f
f
f
+
=
(10)
Należy zwrócić uwagę na fakt, że błąd wyznaczenia fx zmaleje tylko dlatego, że dzięki większej
czułości układu na zboczu krzywej rezonansowej błędy pomiaru
∆f
L
i
∆f
P
są mniejsze od błędu
∆f
x
przy
pomiarze bezpośrednim.
f
I,
α
f
P
f
L
f
0
≈
f
x
α
max
2
α
max
strojenie lewo-prawo
2
0
P
L
f
f
f
+
=
Rys. 11. Zasada pomiaru metodą widełkową
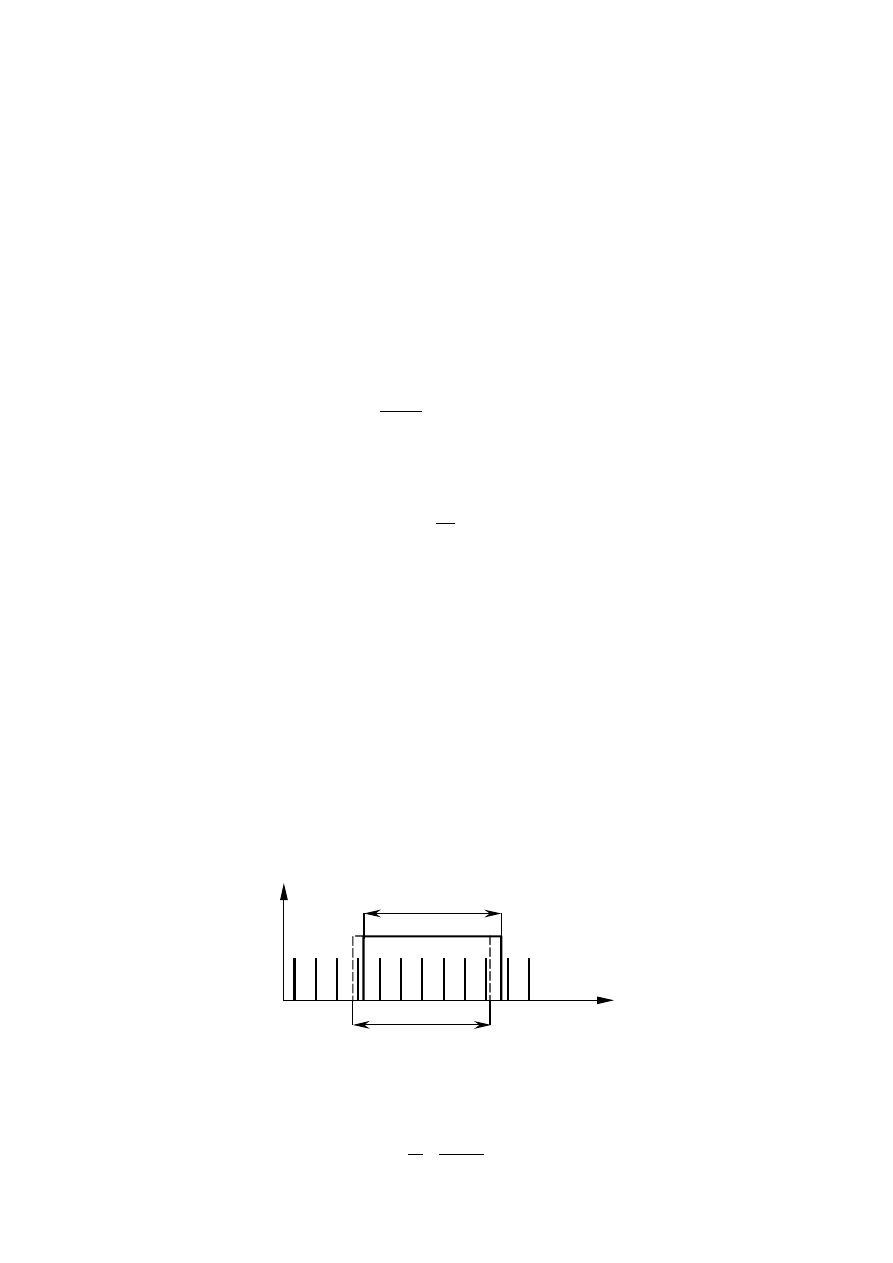
Metodę widełkową można stosować tylko wtedy, gdy krzywa rezonansowa jest symetryczna
względem częstotliwości rezonansowej. W praktyce warunek ten jest spełniony w bardzo niewielkim
zakresie częstotliwości, dla którego
α
>
0,7
⋅
α
max
. W zakresie b.w.cz. pomiar częstotliwości wykonywany
jest pośrednio przez bezpośredni pomiar długości fali. Rolę obwodu rezonansowego pełnią wówczas tzw.
wnęki rezonansowe. Strojenie takiej wnęki polega na zmianie jednego z jej wymiarów geometrycznych.
Pomiaru dokonuje się po dostrojeniu układu do rezonansu i odczytaniu długości fali (w metrach) ze śruby
mikrometrycznej przyrządu.
6. Błędy pomiaru częstotliwości, okresu i przedziału czasu
6.1. Błędy pomiaru częstotliwości
Pomiary czasu i częstotliwości są najdokładniejszymi pomiarami na obecnym poziomie rozwoju techniki.
Błąd względny pomiaru częstotliwości częstościomierzem wyrażony jest zależnością:
)
(
N
A
x
x
fcz
f
f
δ
δ
δ
+
±
=
∆
=
gdzie:
δ
A
– składowa analogowa błędu (tzw. błąd analogowy);
δ
N
– błąd dyskretyzacji (zliczania);
N
N
1
=
δ
N – liczba zliczonych impulsów.
Błąd analogowy zależy od dokładności wzorca częstotliwości
δ
w
(określa się ją na podstawie błędu
δ
w
)
oraz od błędu bramkowania
δ
B
.
Błąd wzorca częstotliwości jest uwarunkowany niestałością częstotliwości generatora wzorcowego.
Stosując generator kwarcowy jako źródło częstotliwości wzorcowej można uzyskać
δ
w
na poziomie 10
-7
.
Generatory kwarcowe są bardzo czułe na zmianę temperatury, ale jeżeli zostanie zastosowana stabilizacja
temperaturowa kwarcu to można uzyskać błąd wzorca na poziomie 10
-8
÷ 10
-9
.
Praktycznie błąd wzorca przyjmuje się:
δ
W
=
⋅
−
2 1 0
8
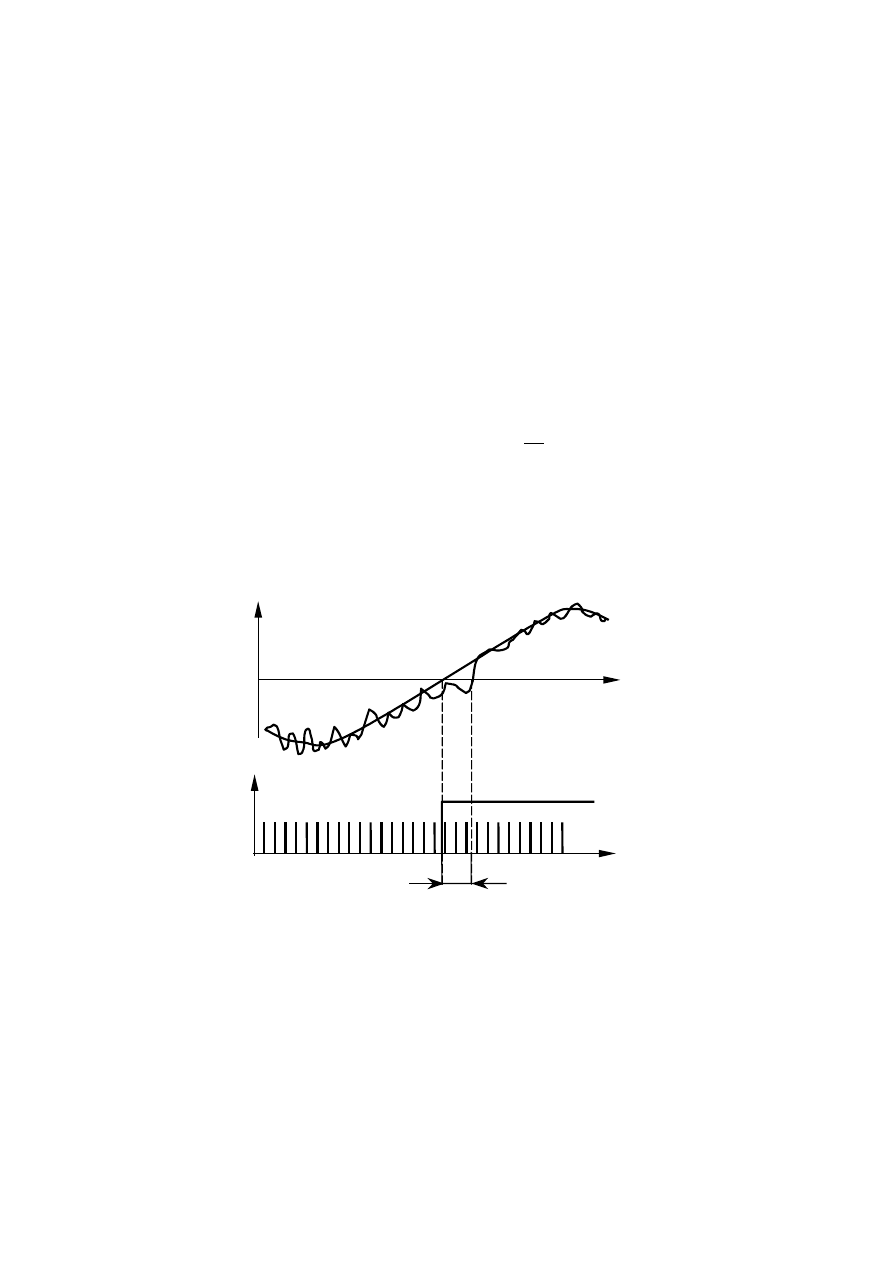
Błąd bramkowania wynika z tego, że impulsy bramkujące i bramkowane (zliczane) nie są
synchroniczne (rys. 3.26), ze skończonych czasów otwierania i zamykania bramki oraz wpływu poziomu
wyzwalania przerzutnika bramkującego [2].
t
T
w
U
T
w
Rys. 12. Ilustracja graficzna błędu bramkowania.
Błąd zliczania 1/N zależy od czasu pomiaru (bramkowania) T
w
i wartości częstotliwości mierzonej f
x
,
ponieważ:
w
x
T
f
N
⋅
=
1
1
Zazwyczaj 1/N >>
δ
B
. Błąd zliczania jest tym mniejszy im dłuższy jest czas pomiaru – bramkowania
- (czas, w którym następuje zliczanie) jednak czasu T
w
tliwości oscyloskopem wynosi:
gdzie:
nie można zwiększać nieograniczenie, ponieważ
traci się wtedy informację o chwilowych zmianach częstotliwości – następuje swojego rodzaju
uśrednianie wyniku pomiaru.
Natomiast błąd pomiaru często
(
)
(
)
δ
= ±
+
⋅ ⋅
fosc
osc
dz d f
0 06
0 05
,
, [ ]
d – war ość podstawy czasu oscyloskopu;
t
f
osc
loskopem.
6.2. Błędy pomiaru okresu i przedziału czasu
Błąd względny pomiaru okresu w zasadzie można by było zapisać zależnością 3.53, ale ze względu
na t
– wartość częstotliwości zmierzona oscy
o, że w odróżnieniu od pomiaru częstotliwości, błąd bramkowania ma znaczący wpływ na wynik
pomiaru, błąd względny pomiaru okresu przedstawia się w postaci:
)
1
(
+
+
±
=
δ
δ
δ
N
B
w
T
Błąd zliczania wyrażony jest wzorem 3.54. Jego wartość można zmniejszać wydłużając czas pomiaru
(otwarcia bramki) do wartości 10
n
⋅
T
x
ziału (1; 8).
Błąd
zęstościomierzu, ponieważ impuls bramkujący
jes
,
gdzie:
n - liczba całkowita najczęściej z przed
bramkowania może być znacznie większy niż w c
t wytwarzany z sygnału badanego, który może być silnie zniekształcony lub zaszumiony. Wartość tego
błędu może znacznie przekroczyć wartość błędu zliczania. Sytuację taką przedstawiono na rys. 3.27.
U
x
t
t
U
w
, U
B
∆
T
w
Rys. 13. Graficzna ilustracja powstawania błędu brakowania w okresomierzu czasomierzu cyfrowym.
a rysunku tym przedstawiono dwa przypadki:
N
- pierwszy, gdy mamy do czynienia z sygnał m mierzonym niezaszumionym;
Wid
niony został czas otwarcia bramki, w wyniku czego zliczonych
omenty otwarcia
i za
e
- drugi, gdy sygnał jest zaszumiony.
ać, że w przypadku zaszumienia opóź
zostało mniej impulsów. Podobna sytuacja może mieć miejsce na zboczu zamykającym bramkę. Błąd
bramkowania, może więc być w tym wypadku kilkakrotnie większy od błędu zliczania.
Jeszcze większe błędy mogą być popełniane przy pomiarze przedziału czasu, gdy m
mknięcia bramki będą wypracowywane na podstawie sygnałów pochodzących z różnych źródeł. W
zależności od wymaganej dokładności, może wtedy zaistnieć potrzeba zastosowania przewodów tej samej
długości tak, aby uniemożliwić powstanie różnicy w opóźnieniach, powstałych podczas propagacji
sygnałów wyzwalających i zamykających bramkę.
7. Pomiary przesunięcia fazowego
ma przebiegami okresowymi można określić jako różnicę faz obu
prze
Przesunięcie fazowe między dwo
biegów w chwili ich przejścia przez określony, najczęściej zerowy poziom:
ϕ
=
Ψ
1
-
Jeżeli oba przebiegi posiadają jednakową częstotliwość, to przesunięcie fazowe jest stałe, niezależne
od
c
s
Ψ
2
momentu wykonywania pomiaru. Przesunięcie można wyrazić również proporcjonalnym
przesunięciem zasowym (wyrażonym w mierze kątowej), jako tosunek różnicy czasów
∆
t przejścia
przebiegów przez zero, do okresu przebiegu T:
ϕ
=
T
∆t
Π
2
[rad]
.1. Pomiary przesunięcia fazowego oscyloskopem
Jedna z nich polega na bezpośredniej obserwacji
prze
7
Wykorzystuje się w tym przypadku dwie metody.
sunięcia fazowego między dwoma sygnałami podłączonymi do wejść obu kanałów odchylania
pionowego oscyloskopu dwukanałowego.
.
Rys. 13. Pomiar przesunięcia fazowego za pomocą oscyloskopu dwukanałowego.
artość przesunięcia fazowego określa się wówczas z zależności:
W
ϕ = 180
o
·
OB
OA
Dokładność pomiaru przesunięcia fazowego tą metodą wynosi kilka stopni.
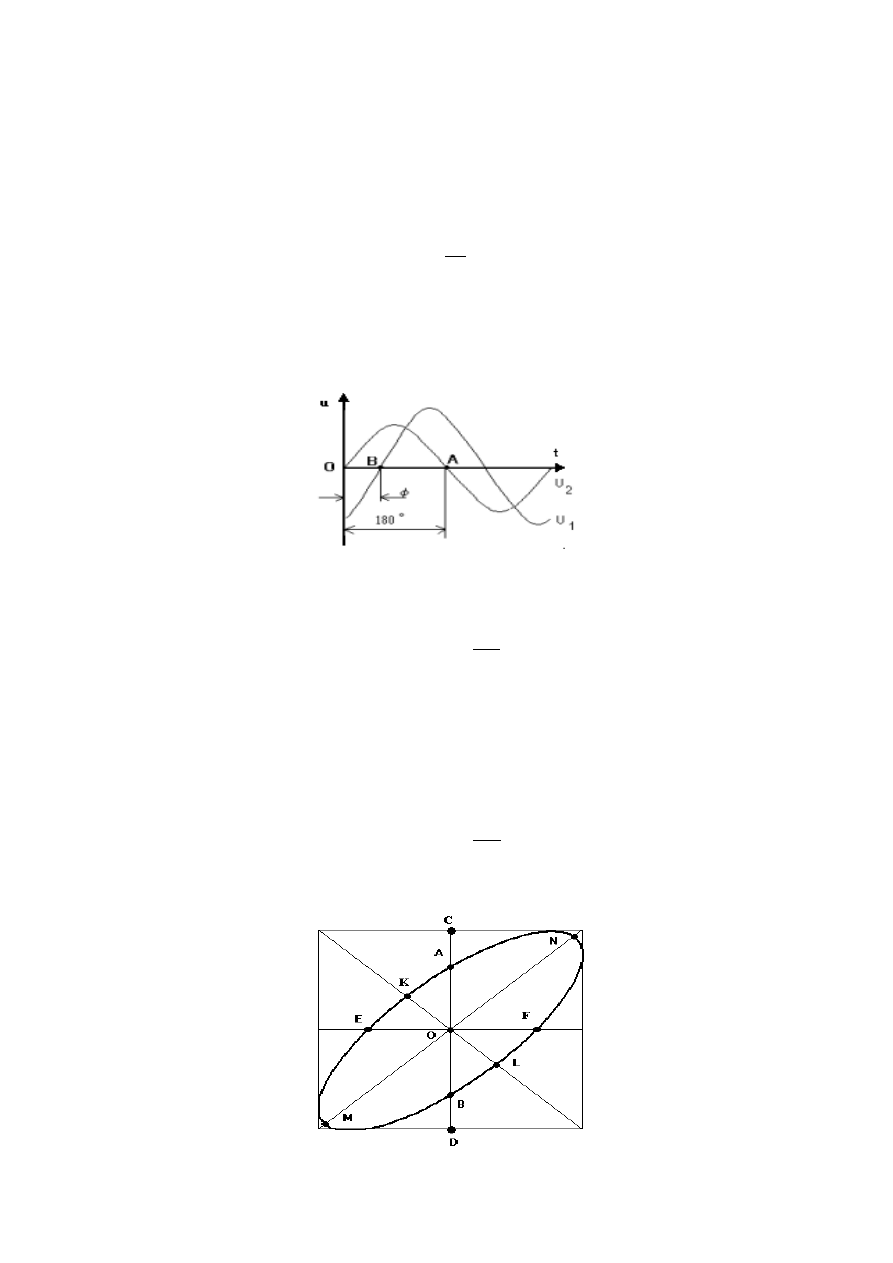
ku elipsy, umożliwia pomiar
prze
arc sin
Druga metoda, z wykorzystaniem krzywych Lissajous, w tym przypad
sunięcia fazowego przy wykorzystaniu oscyloskopu jednokanałowego. Polega ona na określeniu kąta
przesunięcia fazowego na podstawie kształtu i położenia elipsy na ekranie oscyloskopu. Jeden z sygnałów
podłącza się do wejścia kanału X, a drugi do wejścia kanału Y. W zależności od kąta fazowego między
badanymi sygnałami obserwuje się na ekranie różne spłaszczenia i ułożenia elipsy. Wartość przesunięcia
fazowego w tej metodzie wyznacza zależność:
ϕ
=
CD
AB
Powyższa metoda, nazywana również metodą funkcji sinusa, zalecana jest do pomiarów kątów
ϕ
mniejszych od 60
o
.
Rys. 13. Elipsa z zaznaczonymi charakterystycznym dcinkami.
i o
Korzystając z wymiarów maksymalnego MN i minimalnego KL promienia elipsy można również
okre
/ 2 = arc tg
ślić wartość przesunięcia fazowego, z zależności:
ϕ
MN
KL
Metoda funkcji tangensa kąta zalecana jest dla kątów
ϕ > 60
o
.
y są:
py oscyloskopowej;
Źródłami błędów pomiarowych kąta fazowego w metodzie elips
- niedokładność pomiaru długości odpowiednich odcinków na ekranie lam
- nieliniowość wzmocnienia i odchylania promienia w obu kanałach oscyloskopu;
- zniekształcenia badanych napięć;
- paso
w obwodach wzmacniaczy oscyloskopu.
P
odcinków, o dokładności
δ
ϕ
=
δ
a +
δ
b =
żytnicze przesunięcia fazowe
onieważ wynik uzyskuje się na podstawie odczytów długości odpowiednich
pomiaru
δϕ
decydują niepewności ich wyznaczenia na ekranie lampy:
⋅
+
∆b
∆a
100
b
a
%
gdzie:
a, b – długości mierzonych odpowiednich odcinków, np. OA i OB, AB i CD itd.;
Wyp
.2. Pomiary przesunięcia fazowego fazomierzem
Fazomierze (analogowe lub cyfrowe) służą do pomiaru kąta przesunięcia fazowego między dwoma
sygn
∆
a,
∆
b – niedokładność odczytu tych odcinków, najczęściej równa 0,1 cm;
adkowy błąd pomiaru kąta fazowego może wynosić kilka procent.
7
ałami okresowymi o tej samej częstotliwości. Najczęściej sygnały wejściowe mają charakter
napięciowy. Jeśli nie, to należy zastosować odpowiednie układy kondycjonerów przetwarzające sygnał o
dowolnym charakterze na sygnał napięciowy. Cyfrowy pomiar kąta przesunięcia fazowego polega na
cyfrowym pomiarze czasu proporcjonalnego do różnicy faz początkowych dwóch sygnałów. Faza
początkowa sygnału jest wyznaczana przez moment przejścia wartości chwilowej sygnału przez
„zero”.
. Literatura
A., Poniński M., Siedlecki A.: Metrologia elektryczna. Wydawnictwa Naukowo-
T
2.
two elektryczne. Analogowa technika pomiarowa. Oficyna Wydawnicza
P
3.
y oscyloskopowe, Wydawnictwa Naukowo-Techniczne, Warszawa 1994.
a PW,
W
. Przykładowe pytania kontrolne
. Wartości charakterystyczne napięcia zmiennego.
8
1. Chwaleba
echniczne, Warszawa 2003.
Kwiatkowski W. S.: Miernic
W, Warszawa 1999.
Rydzewski J.: Pomiar
4. Stabrowski M. M.: Miernictwo elektryczne. Cyfrowa technika pomiarowa. Oficyna Wydawnicz
arszawa 1994.
9
1
2. Okres, częstotliwość, długość fali i zależności mi dzy nimi.
chematy i zastosowanie.
napięcia zmiennego: wartości średniej,
7.
ancji źródła mierzonego sygnału na wskazania woltomierzy.
i fazy.
ę
3. Parametry czasowe sygnałów impulsowych.
4. Parametry użytkowe woltomierzy.
5. Woltomierze prostownikowe – ich s
6. Budowa i zasada działania woltomierzy prostownikowych
skutecznej i szczytowej (w układzie równoległym i szeregowym) z prostownikami aktywnymi i
pasywnymi.
Wpływ imped
8. Wpływ częstotliwości mierzonego napięcia na wskazania woltomierzy.
9. Budowa i zasada działania cyfrowych mierników częstotliwości, okresu
10. Błędy częstościomierzy, czasomierzy i fazomierzy cyfrowych.
11. Budowa i zasada działania częstościomierza rezonansowego.