POMIARY CZASU I CZĘSTOTLIWOŚCI

Cel ćwiczenia

Poznanie oscyloskopowych metod pomiaru czasu i częstotliwości, nabycie

i kształtowanie umiejętności pomiarowych przy pomocy oscyloskopu.

Zagadnienia do przygotowania

1. Pojęcie częstotliwości i okresu sygnału .

2. Zasady pomiaru czasu (okresu) przy pomocy oscyloskopu. Błąd pomiaru.

3. Pomiar częstotliwości za pomocą oscyloskopu metodami pośrednimi.

4. Opis postępowania przy wykorzystaniu metody figur Lissajous. Dokładność pomiaru.

4. Zasada pomiaru częstotliwości częstościomierzem cyfrowym

Literatura

Rydzewski J.: Pomiary oscyloskopowe. WNT, Warszawa,, 1999.

Dusza J.,Gortat G.,Leśniewski A.: Podstawy miernictwa. Wyd. Polit. Warszawskiej,2002.

Koczela D.: Miernictwo elektryczne. Ćwiczenia laboratoryjne. Wyd. Polit. Wrocł.,

Wrocław 2001.

Wiadomości wstępne

Okresem T sygnału nazywamy czas jednej pełnej zmiany przebiegu.

Częstotliwością f sygnału okresowego nazywamy liczbę jego okresów T w jednostkowym przedziale czasu (najczęściej w jednej sekundzie). Częstotliwość jest odwrotnością okresu

przebiegu :

=
(1)

Jednostką okresu (czasu) jest sekunda (s), częstotliwości herc (Hz). W codziennym stosowaniu wykorzystywane są jednostki podwielokrotne czasu, np. ms, μs, ns i wielokro-

tne częstotliwości, np. kHz, MHz czy GHz.

Wspomniane parametry są wielkościami, które można mierzyć z bardzo dużą dokładnością częstościomierzami cyfrowymi, dzięki istnieniu doskonałych wzorców częstotliwości, np. kwarcowych.

Do podstawowych metod pomiaru czasu i częstotliwości można zaliczyć :

• metody cyfrowe;

• metody oscyloskopowe.

Metoda cyfrowa polega na zliczaniu liczby n okresów przebiegu w czasie wzorcowego przedziału czasu T_w i określeniu częstotliwości bezpośrednio z zależności :

(2)

Badany przebieg o nieznanej częstotliwości w wejściowych układach formujących kształtowany jest w ciąg impulsów prostokątnych o takiej samej częstotliwości. Generator wzorcowy (kwarcowy) wytwarza impuls prostokątny otwierający bramkę na czas T_w pomiaru. W czasie jej otwarcia licznik zlicza n impulsów mierzonego przebiegu o częstotli-wości f_x , zatem n_x T_x = T_w , stąd

(3)

Liczba zliczonych impulsów n_x jest bezpośrednio miarą częstotliwości. Błąd pomiaru częstotliwości jest zależny od dokładności określenia czasu otwarcia bramki T_w (zwykle jest pomijalnie mały, jest to bowiem błąd generatora wzorcowego - kwarcowego) oraz od błędu zliczania impulsów (jego wartość bezwzględna wynosi ± 1 impuls), zatem względna niepewność pomiarowa częstotliwości δf_x częstościomierzem cyfrowym wynosi

(4)

Z powyższej zależności wynika :

• błąd pomiaru częstotliwości maleje ze wzrostem liczby zliczanych impulsów n_x , (co jest równoznaczne z mierzeniem dużych częstotliwości),

• wydłużenie czasu bramkowania T_w powoduje zmniejszenie błędu pomiaru,

• zmniejszanie się mierzonej częstotliwości prowadzi do wzrostu błędu pomiaru; można temu zapobiec wydłużając czas zliczania (czas pomiaru T_w ogranicza się zwykle do wartości 0,01s; 0,1s; 1s; 10s), zbyt długie czasy są z kolei nieprakty-czne z punktu widzenia pomiarowego.

Do pomiaru małych częstotliwości stosowana jest metoda oparta na pomiarze okresu badanego. W układzie wejściowym częstościomierza zostaje formowany tym razem impuls prostokątny o czasie trwania okresu przebiegu badanego T_x , otwierający bramkę na czas pomiaru. W czasie jej otwarcia następuje zliczanie impulsów n_W z generatora wzorcowego wytwarzanych z częstotliwością wzorcowa f_W , stąd częstotliwość mierzona

(5)

Wygodnym przyrządem do pomiaru czasu (okresu) i częstotliwości jest oscyloskop.

Pomiary oscyloskopowe umożliwiają pomiar metodą :

• pośrednią, poprzez pomiar okresu przebiegu badanego,

• porównawczą, w której oscyloskop jest używany jako wskaźnik zrównania ze sobą sygnałów o częstotliwości mierzonej f _x i wzorcowej f_w doprowadzonych do torów X i Y oscyloskopu.

W metodzie pośredniej częstotliwość określa się wg zależności (1), jako odwrotność pomierzonego bezpośrednio z ekranu oscyloskopu czasu okresu T_x badanego przebiegu, przy znajomości współczynnika kalibracja generatora podstawy czasy S_x. Czas trwania okresu wyniesie (rys.1):

T_x = d_x · S_x (6)

gdzie: d_x - odczytana z ekranu długość odcinka (w cm) odpowiadająca jednemu okresowi ;

S_x - współczynnik nastawy kalibratora podstawy czasu, np. w ms/cm.

Źródłami błędów tej metody pomiaru czasu okresu (tym samym i częstotliwości) są :

- błąd odczytu długości odcinka odpowiadającego okresowi przebiegu - Δl /l_x ;

- niedokładności kalibracji generatora podstawy czasu δ S_x .

Niedokładność względna wyznaczenia czasu lub częstotliwości wynosi więc :

δ S_x +
(7)

Błąd ten może wynosić kilka procent.

Metoda porównawcza, znana również jako metoda figur Lissajous zapewnia większą dokładność pomiaru. Pomiar częstotliwości tą metodą polega na bezpośrednim porównaniu sygnału o nieznanej częstotliwości f_x , z sygnałem o wzorcowej częstotliwości f_w podłączo-nymi odpowiednio do wejść X i Y oscyloskopu (oscyloskop powinien pracować w trybie z wyłączoną wewnętrzną podstawa czasu). Jednoczesne wysterowanie obu kanałów powoduje pojawienie się na ekranie figur Lissajous. Zrównanie obu częstotliwości (poprzez dostraja-nie f _w), lub zapewnienie stosunku częstotliwości równego liczbie całkowitej lub ilorazowi liczb całkowitych, daje możliwość uzyskania na ekranie nieruchomych obrazów. Niewielka różnica częstotliwości powoduje obrót obrazu z szybkością proporcjonalną do rozbieżności częstotliwości. Kształt figur jest przede wszystkim zależny od stosunku częstotliwości

i przesunięcia fazowego między sygnałami. Należy pamiętać, że regularne kształty figur uzyskuje się dla sygnałów sinusoidalnych tylko nieznacznie odkształconych.

Częstotliwość f_x określa się na podstawie ilości przecięć n _x i n _y figury na ekranie

z prostymi równoległymi do osi X oraz do osi Y (rys.2). Obie proste powinny być tak poprowadzone, aby nie były styczne i nie przechodziły przez punkty węzłowe obserwowanej figury. Liczbowy stosunek ilości przecięć wskazuje ile razy częstotliwość badana jest większa (mniejsza) od częstotliwości wzorcowej.

Jeżeli odpowiednio f_x oznacza nieznaną częstotliwość sygnału podłączonego do wejścia np. kanału Y, a f_w częstotliwość sygnału generatora wzorcowego, podłączonego do wejścia kanału Y oscyloskopu; n_X liczbę przecięć figury z prostą w osi X ( poziomą ),

a n_Y liczbę przecięć figury z prostą osi Y (pionową), to poszukiwaną częstotliwość f_x określa zależność :

(8)

Pomiar tą metodą może być bardzo dokładny, jeżeli dysponuje się dokładnym generatorem sygnału wzorcowego f_w. Jeżeli figura na ekranie pozostaje nieruchoma, to dokładność pomiaru jest określona dokładnością generatora wzorcowego : δf_x = δ f_w . Natomiast w przypadku różnicy częstotliwości tych sygnałów obraz obraca się wokół własnej osi, powodując dodatkową niepewność Δf wyniku pomiaru. Oszacować ją można za pomocą pomiaru czasu t, w którym obraz obróci się o 360 ^o. Wówczas dodatkowy błąd wynosi:

(9)

a całkowity błąd pomiaru częstotliwości :

(10)

Metodę figur Lissajous powinno stosować się, gdy stosunek obu częstotliwości nie przekracza wartości 5÷10; przy większych stosunkach trudno jest zinterpretować otrzymany obraz ze względu na duże zagęszczenie linii.

Pomiary :

- wykonać kilka pomiarów sygnałów o różnych częstotliwościach sygnału metodą

poprzez pomiar okresu T_x (pamiętaj o konieczności skalibrowania generatora podstawy

czasu - pokrętło płynnej regulacji w skrajnej prawej pozycji);

- porównaj otrzymane wyniki z pomiarami wzorcowymi okresu i częstotliwości

wykonanymi częstościomierzem cyfrowym;

- wyniki pomiarów i obliczeń błędów umieścić w tabeli

pomiar okresu					pomiar częstotliwośći
dx	Sx	Tx	Tcyfr	ΔTx	fx = 1/Tx	fcyfr	Δfx	δfx
cm	s/cm	s			kHz			%

gdzie : T_x = d_x ⋅ S_x - obliczony okres mierzonego przebiegu;

T_cyfr,f_cyfr - odczyt okresu i częstotliwości wykonany przy pomocy

przyrządu cyfrowego;

f_x = 1/T_x - obliczona wartość częstotliwości;

ΔT_x = T_x - T_cyfr - błąd bezwzględny porównania pomiaru okresu;

Δ f_x = f _x - f _cyfr - błąd bezwzględny porównania pomiaru częstotliwości;

δ f_x - błąd względny dokładności pomiaru częstotliwości :

δ f_x =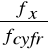
100 % (11)

- podłączyć sygnał badany, np. do wejścia X, a sygnał z generatora wzorcowego do wejścia

Y (rys.2);

- pomiar częstotliwości f_x tą metodą polega na takim dostrojeniu generatora wzorcowego,

przy którym na ekranie oscyloskopu otrzymuje się możliwie mało skomplikowany (przy

małej różnicy częstotliwości) oraz nieruchomy (lub prawie nieruchomy) obraz ;

- wykonać pomiary dla kilku figur (stosunków częstotliwości) każdorazowo

przerysowując je do protokółu;

- każdorazowo porównać obliczoną częstotliwość f_x z wskazaniem częstościomierza

cyfrowego; określić niedokładność określenia częstotliwości pomiaru wg (11);

- dokonać analizy dokładności pomiarów częstotliwości obu metodami.

Kolegium Karkonoskie Laboratorium miernictwa

4

Pomiary czasu i częstotliwości .

X

Y

Rys.2. Pomiar częstotliwości metodą figur Lissajous

a) układ pomiarowy, b) przykład określenia ilości punktów przecięć.

b)

a)

f_wz

n _x =3

n _y = 2

Sygnał

badany f_x

Rys.1. Pomiar okresu (czasu) na ekranie oscyloskopu

Sygnał

wzorcowy f_w

d_x

---