v. 2010.02.26
Zadania z Mechaniki Budowli M.K. Jasina, M. Skowronek
strona 108
Jeśli zauważysz błędy, masz uwagi, uważasz, że w rozwiązaniach warto coś dodać czy uzupełnić, podziel się swoimi spostrzeżeniami
pisząc na adres e-mail: jasina@pg.gda.pl. z góry dziękujemy MKJ & MS
VIII. Stateczność
63. Zadanie
Dany jest układ ramowy przedstawiony na rysunku 63.1. Obliczyć wartości obciążenia krytycznego
kr
P
oraz odpowiadające długości wyboczeniowe elementów ściskanych. Przyjąć EI=const.
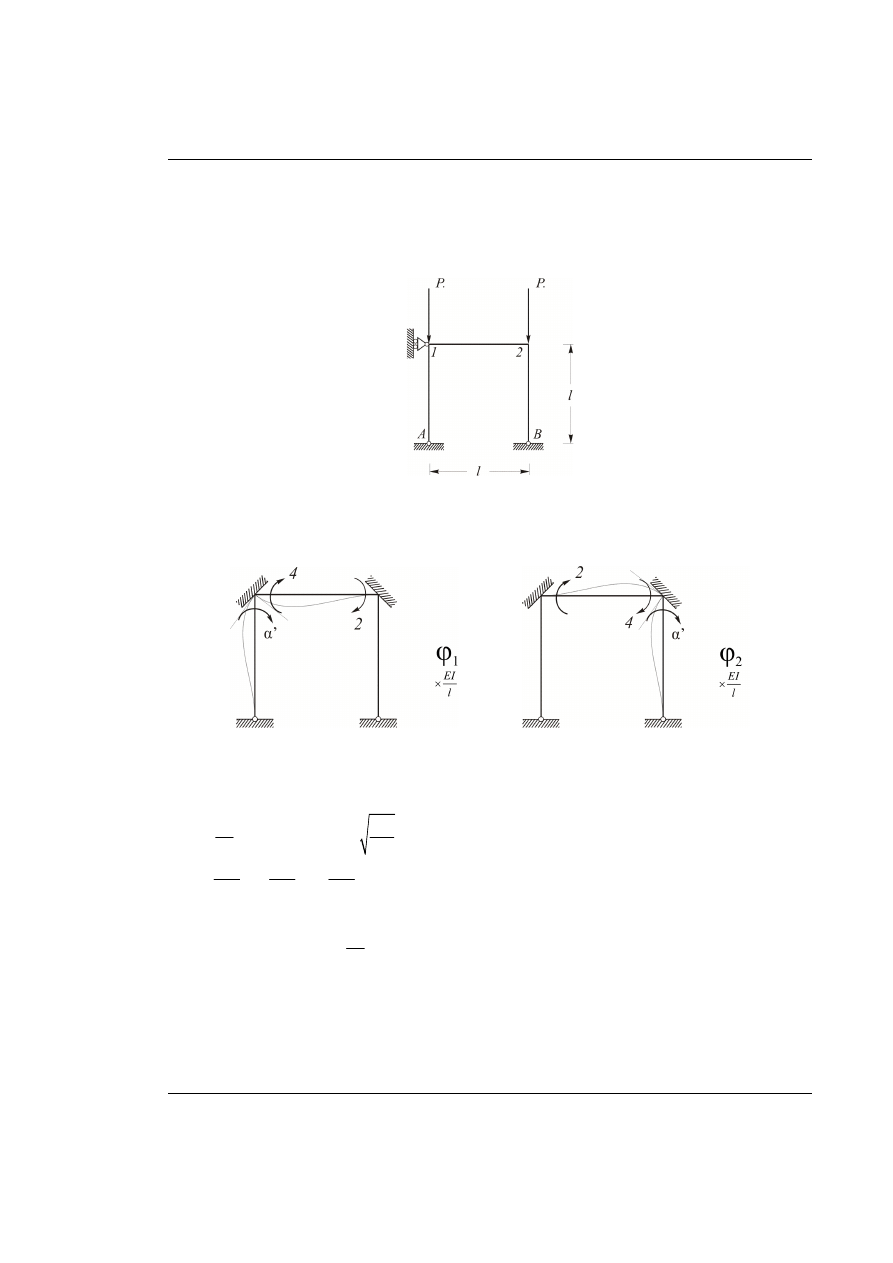
Rys. 63.1. Dany układ ramowy
Rozwiązanie metodą przemieszczeń (zakładamy symetryczną postać wyboczenia).
Momenty przywęzłowe wywołane jednostkowymi kątami obrotu
1
ϕ
i
2
ϕ
.
Rys. 63.2. Momenty przywęzłowe
Z założenia symetrycznej postaci wyboczenia wynika warunek
1
2
ϕ
ϕ
= −
, wystarczy zapisać jedno rów-
nanie równowagi, np. w węźle (1)
( )
1
1
'
A
EI
M
l
α λ ϕ
=
, gdzie
2
Pl
EI
λ
=
12
1
2
1
4
2
2
EI
EI
EI
M
l
l
l
ϕ
ϕ
ϕ
=
+
=
Równanie równowagi w węźle (1)
( )
1
1
12
1
0 :
'
2
0
A
EI
M
M
M
l
α λ
ϕ
=
+
=
+
=
∑
Niezerowe rozwiązanie
(
)
1
0
ϕ ≠
dla
( )
'
2
α λ = −
Przybliżone rozwiązanie – z zastosowaniem tablicy funkcji
( )
'
α λ
( )
( )
3, 5
'
1, 4682
3, 6
'
2, 0587
λ
α λ
λ
α λ
=
⇒
= −
=
⇒
= −
v. 2010.02.26
Zadania z Mechaniki Budowli M.K. Jasina, M. Skowronek
strona 109
Jeśli zauważysz błędy, masz uwagi, uważasz, że w rozwiązaniach warto coś dodać czy uzupełnić, podziel się swoimi spostrzeżeniami
pisząc na adres e-mail: jasina@pg.gda.pl. z góry dziękujemy MKJ & MS
.
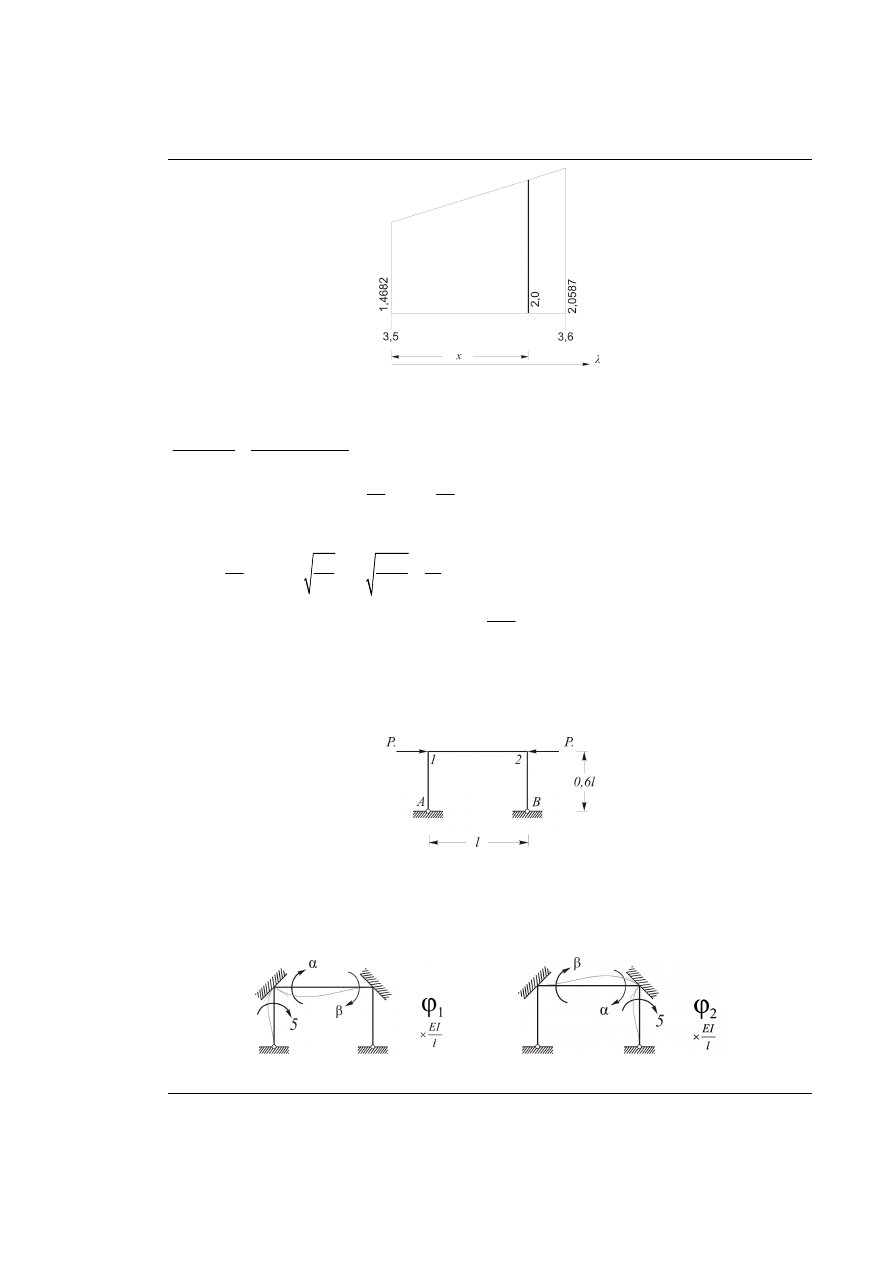
Rys. 63.3. Liniowa interpolacja
Interpolacja liniowa
2 1.4682
2, 0587 1.4682
0,1
x
−
−
=
,
0, 09
3, 59
x
λ
=
⇒
=
.
Obciążenie krytyczne
2
2
2
12, 98
kr
EI
EI
P
l
l
λ
=
=
.
Długość wyboczeniowa (efektywna na wyboczenia) elementu ściskanego – długość pręta prostego, które-
go siła krytyczna wg wzoru Eulera równa jest sile w chwili wyboczenia danego elementu ramy.
2
2
2
kr
w
kr
w
kr
EI
EI
EI
l
P
l
l
P
l
P l
π
λ
π
π
λ
=
⇒
=
=
=
Dla danych z zadania otrzymujemy
1
2
0,875
3, 59
A
B
w
w
l
l
l
l
π
−
−
=
=
=
.
64. Zadanie
Dany jest układ ramowy przedstawiony na rysunku 64.1
. Obliczyć krytyczną wartość obciążenia
kr
P oraz
odpowiadającą długość wyboczeniową elementu ściskanego. Założyć symetryczną postać wyboczenia.
Przyjąć
EI = const.
Rys. 64.1. Dany układ ramowy
Przy założeniu symetrycznej postaci wyboczenia otrzymujemy
1
2
ϕ
ϕ
= −
oraz zerową wartość przesuwu
elementu (1-2).
W rozwiązaniu metodą przemieszczeń wystarczy zapisać jedno równanie równowagi, np.
1
0
M
=
∑
.
Rys. 64.2. Momenty wyjściowe
v. 2010.02.26
Zadania z Mechaniki Budowli M.K. Jasina, M. Skowronek
strona 110
Jeśli zauważysz błędy, masz uwagi, uważasz, że w rozwiązaniach warto coś dodać czy uzupełnić, podziel się swoimi spostrzeżeniami
pisząc na adres e-mail: jasina@pg.gda.pl. z góry dziękujemy MKJ & MS
1
1
1
3
5
0, 6
A
EI
EI
M
l
l
ϕ
ϕ
=
=
( )
( )
( ) ( )
12
1
2
1
EI
EI
EI
M
l
l
l
α λ ϕ
β λ ϕ
α λ β λ ϕ
=
+
=
−
,
2
Pl
EI
λ
=
Równanie równowagi
( ) ( )
1
1
12
1
0 :
5
0
A
EI
M
M
M
l
α λ β λ
ϕ
=
+
=
−
+
=
∑
.
Niezerowe rozwiązanie występuje jedynie w przypadku, gdy
( ) ( )
5
α λ β λ
−
= −
.
Wykorzystujemy tablice funkcji
( )
α λ
i
( )
β λ
λ
( )
α λ
( )
β λ
( ) ( )
β λ α λ
−
4,7
4,8
-0,6582
-1,0289
3,9839
4,2112
4,6421
5,2401
Z interpolacji liniowej otrzymujemy
0, 06
x
=
, zatem
4, 76
λ
=
.
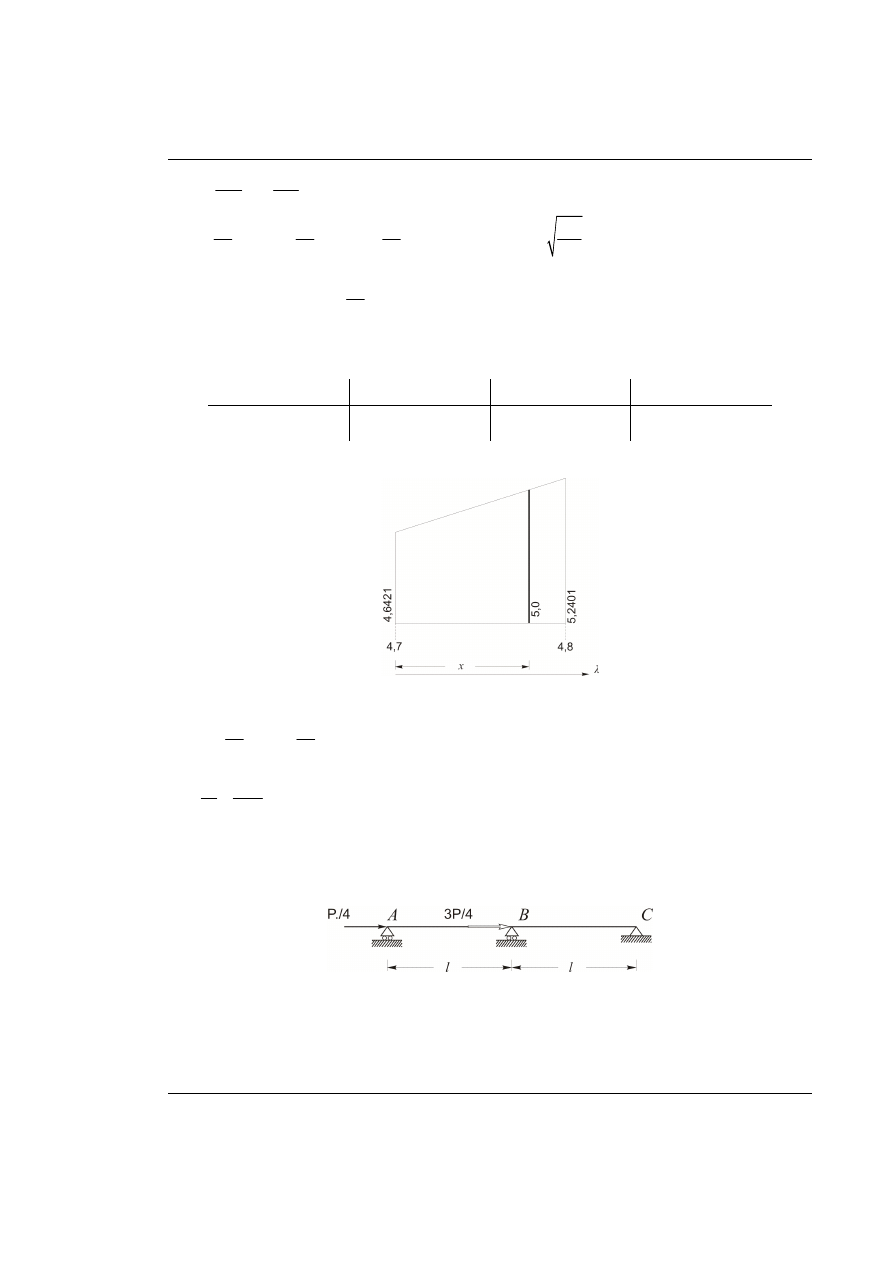
Rys. 64.3. Liniowa interpolacja
Krytyczna wartość obciążenia
2
2
2
22, 66
kr
EI
EI
P
l
l
λ
=
=
.
Długość wyboczeniowa elementu (1-2)
0, 66
4, 76
w
l
l
l
l
π
π
λ
=
=
=
.
65. Zadanie
Dana jest belka ciągła przedstawiona na rys. 65.1. Wyznaczyć krytyczną wartość obciążenia
kr
P oraz
długości wyboczeniowe elementów ściskanych. Przyjąć EI=const.
Rys. 65.1. Dana belka obciążona osiowo
Rozwiązanie metodą przemieszczeń
(
1)
g
n
=
, niewiadomą jest
B
ϕ ϕ
=
.
Parametry
λ
każdego z elementów:
v. 2010.02.26
Zadania z Mechaniki Budowli M.K. Jasina, M. Skowronek
strona 111
Jeśli zauważysz błędy, masz uwagi, uważasz, że w rozwiązaniach warto coś dodać czy uzupełnić, podziel się swoimi spostrzeżeniami
pisząc na adres e-mail: jasina@pg.gda.pl. z góry dziękujemy MKJ & MS
(A-B)
2
2
1
1
4
2
Pl
Pl
EI
EI
λ
λ
=
=
=
,
(B-C)
2
2
2
Pl
EI
λ
λ
=
=
.
Momenty przywęzłowe.
`( )
BA
EI
M
l
α λ ϕ
=
,
`(2 )
BC
EI
M
l
α λ ϕ
=
Równanie równowagi.
[
]
0 :
`( )
`(2 )
0
B
BA
BC
EI
M
M
M
l
α λ α λ ϕ
Σ
=
+
=
−
=
.
Niezerowe rozwiązanie jest możliwe jedynie w przypadku, gdy
`( )
`(2 )
0
α λ α λ
+
=
.
λ
( )
'
α λ
( )
' 2
α
λ
( )
( )
'
' 2
α λ α
λ
+
1,8
1,9
2,2818
2,1891
-2,0587
-3,6908
0,2231
-1,5017
Z interpolacji liniowej otrzymujemy
1,81
λ
=
.
Rys. 65.2. Liniowa interpolacja
Obciążenie krytyczne
2
2
2
4
13,104
kr
EI
EI
P
l
l
λ
=
=
.
Długości wyboczeniowe elementów:
(A-B)
1
1, 736
1,81
w
l
l
l
l
π
π
λ
=
=
=
,
(B-C)
2
0,868
2
3, 62
w
l
l
l
l
π
π
λ
=
=
=
.
66. Zadanie
Dany jest układ ramowy przedstawiony na rysunku 66.1. Obliczyć krytyczną wartość obciążenia
kr
P oraz
odpowiadającą długość wyboczeniową elementu ściskanego.
v. 2010.02.26
Zadania z Mechaniki Budowli M.K. Jasina, M. Skowronek
strona 112
Jeśli zauważysz błędy, masz uwagi, uważasz, że w rozwiązaniach warto coś dodać czy uzupełnić, podziel się swoimi spostrzeżeniami
pisząc na adres e-mail: jasina@pg.gda.pl. z góry dziękujemy MKJ & MS
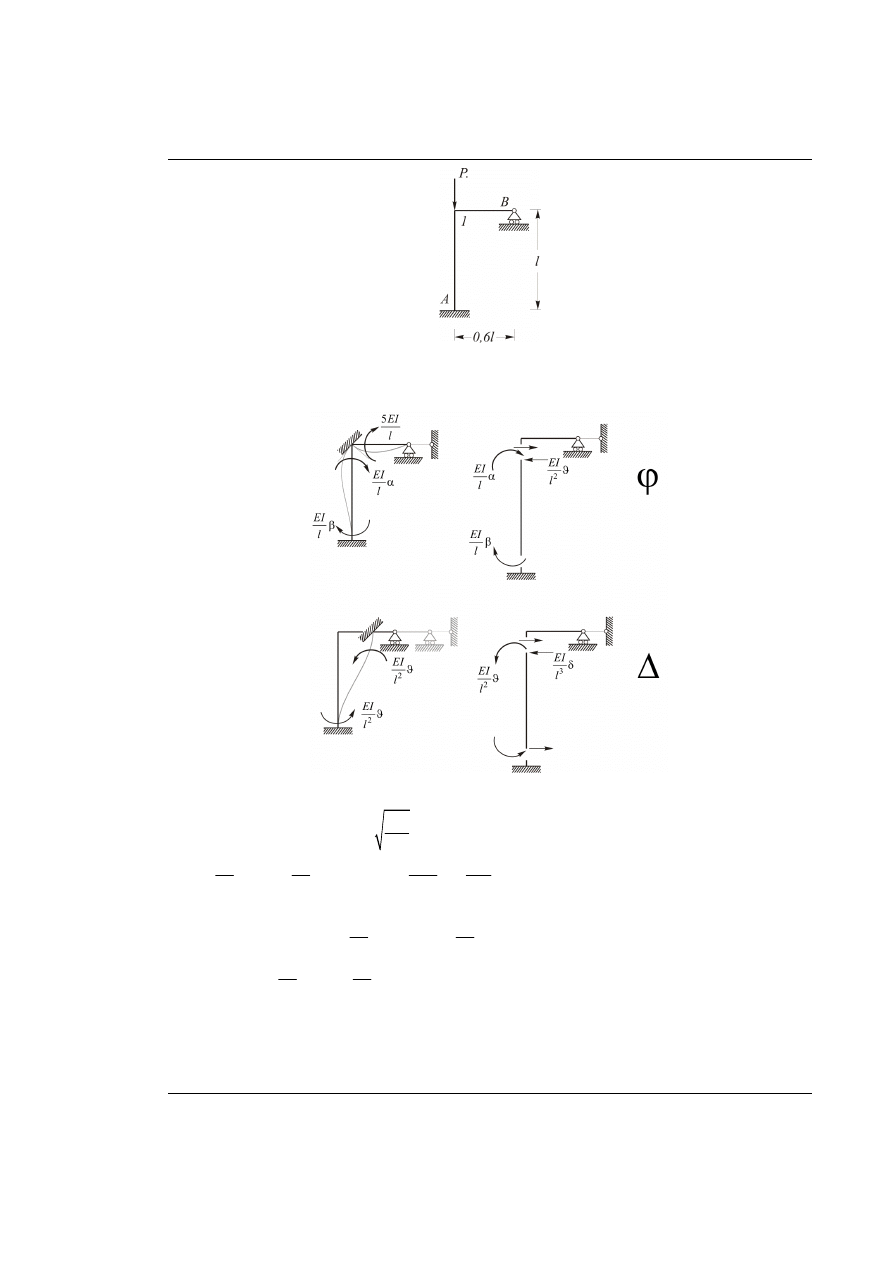
Rys. 66.1. Dany układ ramowy
Rozwiązanie metodą przemieszczeń,
1 1
2
g
n
n
n
ϕ
∆
=
+
= + =
.
Rys. 66.2. Siły wyjściowe (momenty i tnące)
Momenty przywęzłowe (gdy
2
Pl
EI
λ
=
):
1
( )
( )
A
EI
EI
M
l
l
α λ ϕ
ν λ
=
−
∆
,
1
3
5
0, 6
B
EI
EI
M
l
l
ϕ
ϕ
=
=
.
Równania równowagi:
[
]
1
1
1
2
0
( ) 5
( )
0
A
B
EI
EI
M
M
M
l
l
α λ
ϕ
ν λ
Σ
=
+
=
⇒
+
−
∆ =
,
1
2
3
0
( )
( )
0
A
EI
EI
T
l
l
ν λ ϕ
δ λ
Σ
=
⇒
−
+
∆ =
,
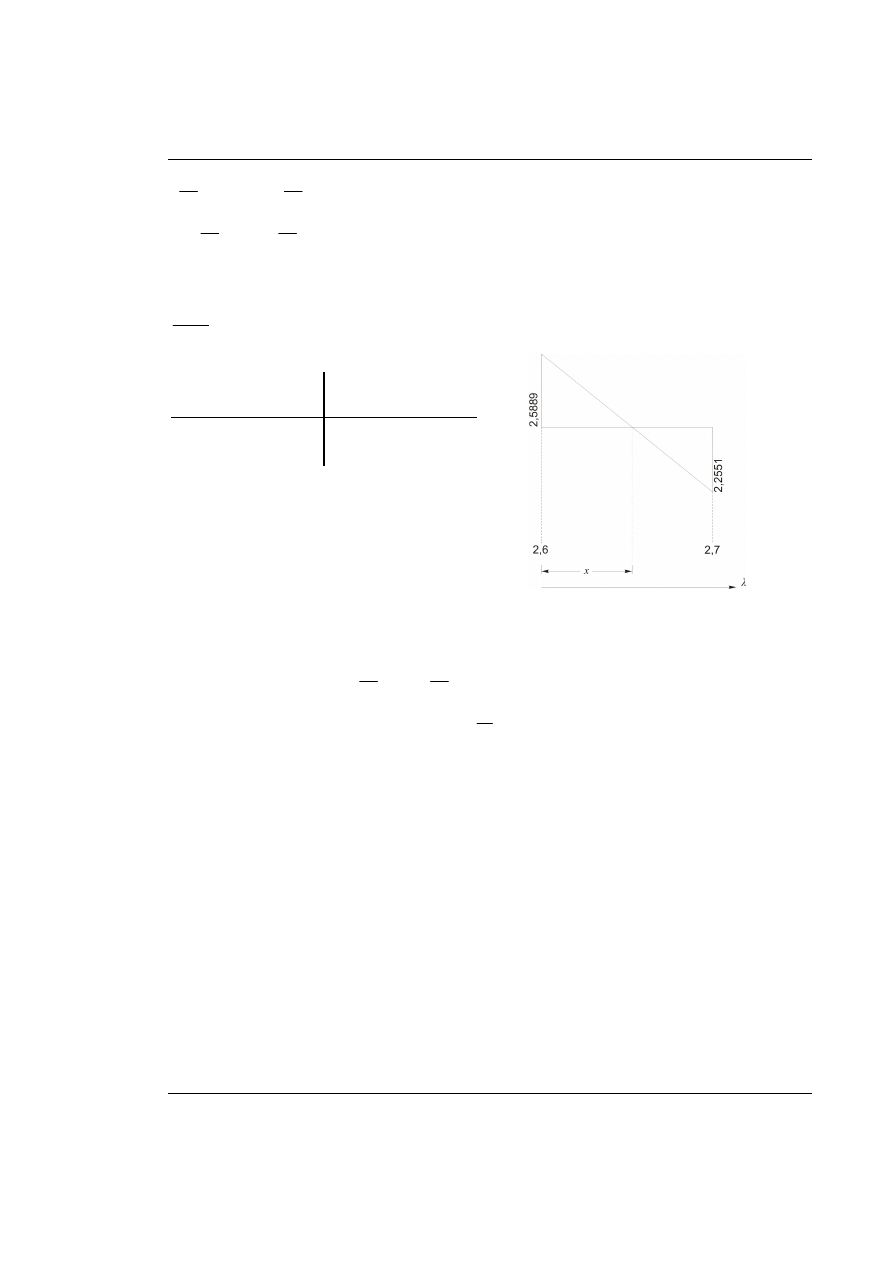
v. 2010.02.26
Zadania z Mechaniki Budowli M.K. Jasina, M. Skowronek
strona 113
Jeśli zauważysz błędy, masz uwagi, uważasz, że w rozwiązaniach warto coś dodać czy uzupełnić, podziel się swoimi spostrzeżeniami
pisząc na adres e-mail: jasina@pg.gda.pl. z góry dziękujemy MKJ & MS
[
]
2
2
3
( ) 5
( )
0
0
( )
( )
( )
EI
EI
l
l
EI
EI
l
l
K
α λ
ν λ
ϕ
ν λ
δ λ
λ
+
−
⋅
=
∆
−
.
Aby istniało niezerowe rozwiązanie musi zachodzić warunek
det
( )
0
K
λ
=
.
[
]
{
}
2
2
4
(
)
( ) 5
( )
( )
0
EI
l
α λ
δ λ ν λ
+
−
=
,
[
]
2
( )
( ) 5
( )
( )
0
f
λ
α λ
δ λ ν λ
=
+
−
=
λ
( )
f
λ
2,6
2,7
2,5889
-2,2551
Rys. 66.3. Liniowa interpolacja
Z interpolacji liniowej otrzymujemy
2, 65
λ
=
.
Obciążenie krytyczne
2
2
2
7, 023
kr
EI
EI
P
l
l
λ
=
=
.
Długość wyboczeniowa elementu ściskanego
1,186
w
l
l
l
π
λ
=
=
⋅
.