SKALARY I WEKTORY
SKALARY
Skalarem nazywamy wielkość
całkowicie określoną przez jedną
liczbę.
Przykłady wielkości fizycznych skalarnych:
masa – m, temperatura – T, energia –
E, potencjał elektryczny – V, praca – W,
gęstość – ρ, ładunek elektryczny – q, czas
– t
WEKTORY
Wielkości, które wymagają do
pełnego określenia podania:
wartości, kierunku, zwrotu, oraz
punktu przyłożenia nazywamy
wektorami.
Obrazem geometrycznym wektora
jest odcinek skierowany. Wektor
oznacza się pogrubioną literą lub
literą ze strzałką (kreską) nad literą.
Przykłady wielkości fizycznych
wektorowych:
prędkość - υ, przyspieszenie - a, siła - F,
pęd – p, natężenie pola elektrycznego -
E, wektor indukcji magnetycznej – B,
położenie (wektor wodzący punktu
materialnego) - r.
Wektory A i B są równe, jeżeli maja
równe długości, ten sam kierunek i
zgodne zwroty. Wektory różniące się
tylko zwrotem nazywają się wektorami
przeciwnymi: |A| = |-A|.
DZIAŁANIA NA WEKTORACH
DODAWANIE WEKTORÓW
Sumę wektorów można znaleźć
geometryczną metodą zwaną metodą
równoległoboku.
Z jednego punktu wykreślamy wektory A i B.
W równoległoboku zbudowanym na tych
wektorach - przekątna wychodząca ze
wspólnego punktu jest poszukiwaną
sumą:
C = A + B.
Dodawanie wektorów jest przemienne:
A + B = B + A
Odejmowanie wektora definiuje się jako
dodawanie wektora przeciwnego:
A – B = A + (-B)
A – B = D
Poszukiwaną różnicą wektorów jest druga
przekątna równoległoboku, przy czym
B – A = -D
Wektory można również dodawać
metodą wieloboku (metodą trójkąta przy
sumie dwu wektorów).
Z dowolnego punktu wykreśla się wektor
A, z końca wektora A wykreśla się wektor
B. Wektor C, którego początek pokrywa się
z początkiem wektora A, zaś koniec z
końcem wektora B, nazywa się sumą
wektorów A i B.
Podobnie tworzy się sumę n wektorów.
Sumą danych n wektorów nazywa się
wektor wypadkowy łączący początek
pierwszego wektora z końcem ostatniego.
Na przykład
Gdy ciało podlega równocześnie
dwom (kilku) niezależnym
przemieszczeniom - mówi się o
składaniu ruchów lub o dodawaniu
wektorów reprezentujących dane
przemieszczenia.
Podobnie, jeśli na ciało działa n
niezależnych sił – należy znaleźć siłę
wypadkową, czyli sumę wektorową
wszystkich n sił
n
i
i
F
F
1
SKŁADOWE WEKTORA
Każdy wektor można rozłożyć na dowolną
ilość wektorów składowych.
Rozkładanie jest to działanie odwrotne do
składania.
Np. wektor A można w trójwymiarowej
przestrzeni,w prawoskrętnym
prostokątnym układzie współrzędnych
rozłożyć na składowe A
x,
A
y,
A
z,
przy czym:
A = A
x
+ A
y
+ A
z,
A = A
x
+ A
y
+ A
z
lub A = i A
x
+ j A
y
+ k A
z
gdzie i, j, k - wersory, czyli jednostkowe
wektory skierowane wzdłuż osi x, y lub z,
odpowiednio, lub A = [A
x,
A
y
, A
z
]
A
x
, A
y
, A
z
– to współrzędne końca wektora A,
(jeśli współrzędne początku wektora wynoszą (0,0,0),
czyli gdy początek wektora znajduje się w początku
układu odniesienia). Inaczej, A
x
jest rzutem
prostokątnym wektora A
na oś x-ów, A
y
- rzutem
wektora A
na oś y-ów, A
z
- rzutem A
na oś z-ów
.
y
z
i
j
k
x
Długość wektora A wynosi
A= A = ( A
x
2
+ A
y
2
+ A
z
2
)
0.5
.
Kierunek wektora A w układzie (x,y,z)
podaje się poprzez tzw. cosinusy
kierunkowe:
cosα = A
x
/A, cosβ = A
y
/A,
cosγ = A
z
/A ,
gdzie α,β,γ – to kąty jakie tworzy wektor A z
odpowiednimi osiami, (z osią x-ów, y-ów
oraz z-ów, odpowiednio).
Składowe sumy (różnicy) wektorów
są równe sumie (różnicy) składowych wektorów. Dla
dwu wektorów A i B, wypadkowy wektor C:
C=A ± B=[A
x
± B
x,
A
y
± B
y
, A
z
±
A
z
] =[C
x,
C
y
, C
z
]
Na przykład wektor wodzący punktu na
płaszczyźnie można przedstawić następująco:
r = r
x
+r
y
= x + y = i x + j y
Długość wektora: r = ( x
2
+ y
2
)
0.5
.
Cosinusy kierunkowe wynoszą :
cosα = x/r, cosβ = y/r.
Jak łatwo zauważyć, wystarczy wyznaczyć jeden z kątów, gdyż
drugi jest uzupełnieniem do kąta prostego
.
MNOŻENIE WEKTORA PRZEZ
SKALAR
W wyniku mnożenia wektora A przez skalar λ
dostajemy wektor λA.
Długość wektora B wynosi B =│λA│ = λA.
Kierunek wektora B jest zgodny z kierunkiem
wektora A,
zwrot zgodny lub przeciwny ze zwrotem A
(dla λ dodatniego lub ujemnego, odpowiednio).
Jeśli każdą składową wektora A pomnożymy przez
stałą λ, to nowy wektor ma składowe:
B = λA = [λA
x,
λA
y
, λA
z
] = [B
x
, B
y
, B
z
]
Przykłady z fizyki
pęd p
:
p = m υ
siła F:
F = m a
moment siły M:
M = I ε
gdzie m – masa jest wielkością skalarną, I – moment
bezwładności jest skalarem, υ – prędkość jest
wielkością wektorową, a - przyspieszenie jest
wektorem, ε – przyspieszenie kątowe.
ILOCZYN SKALARNY WEKTORÓW
Iloczynem skalarnym wektorów A i B nazywamy
iloczyn długości tych wektorów i cosinusa
(mniejszego) kąta zawartego między nimi:
A ∙ B = AB cosφ = C
Iloczyn
skalarny wektorów jest skalarem (liczbą).
Kropka jest często używanym symbolem skalarnego
mnożenia wektorów
.
Mnożenie skalarne jest przemienne, tzn
.
A ∙ B = B ∙ A
oraz rozdzielne względem dodawania
A ∙ (B + C) = A ∙ B + A ∙ C
Według geometrycznej interpretacji
iloczyn skalarny jest długością jednego wektora
przez długość rzutu drugiego wektora na pierwszy.
Z definicji iloczynu skalarnego wynika:
A ∙ B = (i A
x
+ j A
y
+ k A
z
) (i B
x
+ j B
y
+ k B
z
) =
A
x
B
x
+ A
y
B
y
+ A
z
B
z
gdyż
i · i = j · j = k · k = 1
i · j = j · k = k · i = 0
Gdy mnożone wektory są
prostopadłe względem siebie
(φ = π/2) to A ∙ B = 0.
Jeśli obydwa wektory iloczynu są jednakowe, to A ∙ A = A
2
.
Przykłady iloczynu skalarnego w
fizyce
Praca
ΔW = F ·Δs = F Δs cosφ
gdzie F jest wektorem siły, Δs jest tzw. przesunięciem
skierowanym (czyli wielkością wektorową), φ jest kątem
zawartym między wektorem siły i wektorem przesunięcia
.
Energia kinetyczna
E
k
= m υ
2
/ 2 = m υ
2
/ 2
gdzie m - masa; υ – wektor prędkości ciała, przy czym υ ∙ υ =
υ
2
, gdyż kąt między mnożonymi wektorami φ = 0 (a więc
cosφ = 0).
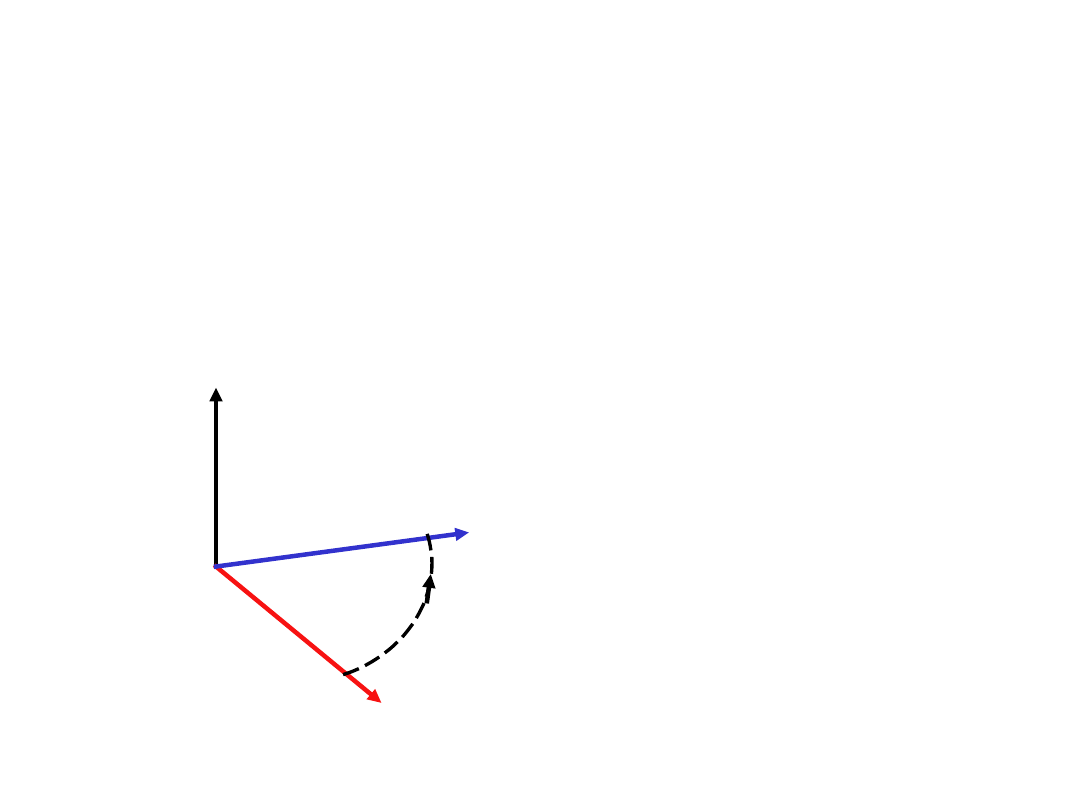
ILOCZYN WEKTOROWY
WEKTORÓW
Iloczynem wektorowym wektorów A i B jest wektor
D, który jest prostopadły do wektorów A i B (do
płaszczyzny w której leżą) i tworzy z nimi układ
prawoskrętny:
A x B = D
Długość wektora D = AB sinφ,
gdzie φ oznacza kąt zawarty między mnożonymi wektorami; jest
zatem równa polu równoległoboku o bokach A oraz B.
Mnożenie wektorowe często oznacza się symbolem x.
Kierunek i zwrot wektora D znajduje się za pomocą
reguły
prawej śruby (korkociągu).
i
A B
r
r
�
A B
r
r
A
r
B
r
�
B
A
r
r
Mnożenie wektorowe nie jest przemienne
A x B = - B x A
ale jest rozdzielne względem dodawania
A x (B + C) = A x B + A x C
Iloczyn wektorowy można zapisać
:
A x B= (i A
x
+j A
y
+k A
z
) x (i B
x
+j B
y
+k B
z
)
=
i(A
y
B
z
–A
z
B
y
)+j(A
z
B
x
–A
x
B
z
) +k(A
x
B
y
– A
y
B
x
) =
i D
x
+ j D
y
+ k D
z
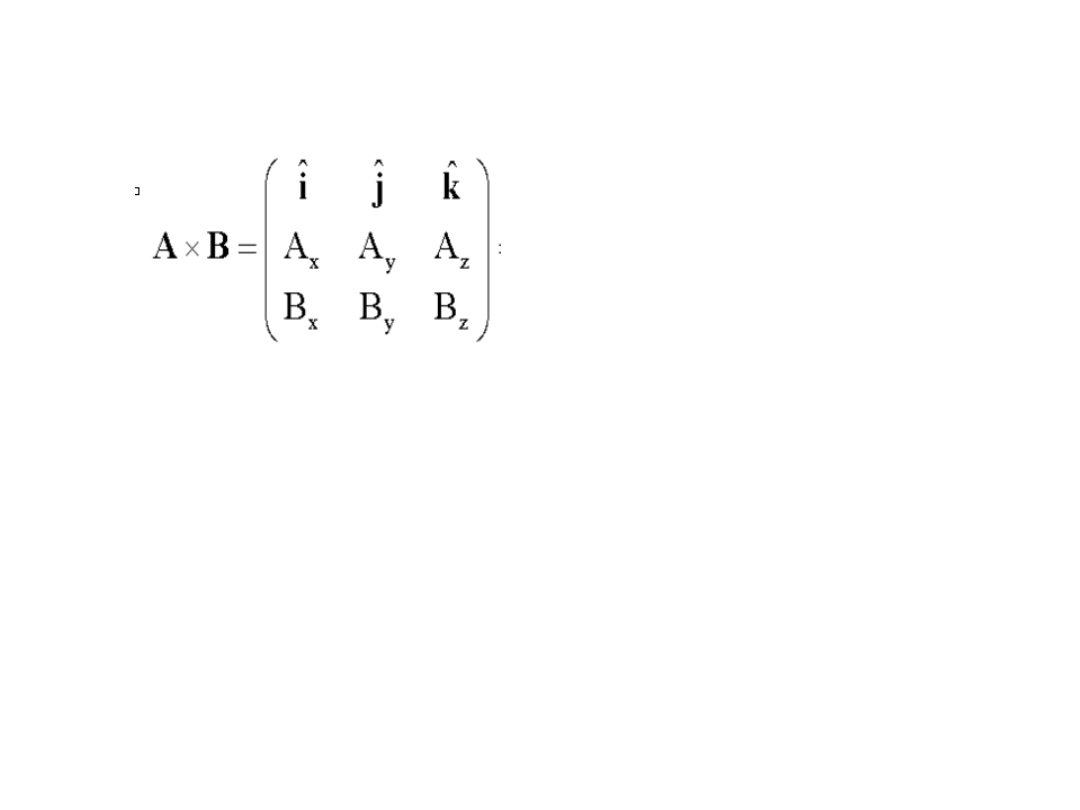
lub zapisać za pomocą wyznacznika
gdzie
i x i = j x j = k x k =
0
i x j = k
j x k = i
k x i = j
Iloczyny wektorowe w fizyce
Przykładem relacji wektorowej pomiędzy
wektorami w fizyce jest np.
• moment siły M = r x F (r – wektor
wodzący, zwany ramieniem siły F),
• moment pędu K = r x p (p – pęd),
• wektor indukcji magnetycznej B F =
q (υ x B) (siła F działająca na cząstkę o
ładunku q poruszającą się z prędkością υ
w polu magnetycznym o wektorze
indukcji magnetycznej B).
Iloczyn mieszany
A
x
(B
x
C) = B (A · C) - C (A · B)
POLE SIŁ
Źródłem pola (przestrzeni w której na ciała
działają siły) jest cząstka materialna o
określonych właściwościach.
Pole jako przestrzeń nabywa właściwości od
obiektów fizycznych, czyli źródeł.
Jeśli na jakieś ciało działa pole sił, to ciało to
również wytwarza własne pole sił tego
samego rodzaju.
Oddziaływanie wzajemne dwóch ciał odbywa
się wg schematu: cząstka – pole – cząstka.
Pole skalarne, pole wektorowe
Przestrzeń w której dla każdego punktu
został zdefiniowany wg określonego
prawa skalar (wektor) nazywamy polem
skalarnym (wektorowym).
Np. pole temperatury czy pole potencjału
elektrycznego są polami potencjalnymi,
gdyż T(x,y,z) oraz V(x,y,z) są funkcjami
skalarnymi. Zaś pole elektryczne jest
polem wektorowym, bo E(x,y,z), czyli
natężenie pola elektrycznego jest funkcją
wektorową.
Przykłady pól w fizyce
źródłem pola grawitacyjnego jest
masa ciała – więc siła grawitacyjna
działa na masę innego ciała
źródłem pola elektrycznego jest
ładunek cząstki – siła elektryczna
działa na ładunek innej cząstki
źródłem pola magnetycznego jest
ładunek w ruchu (prąd elektryczny),
lub stały magnes