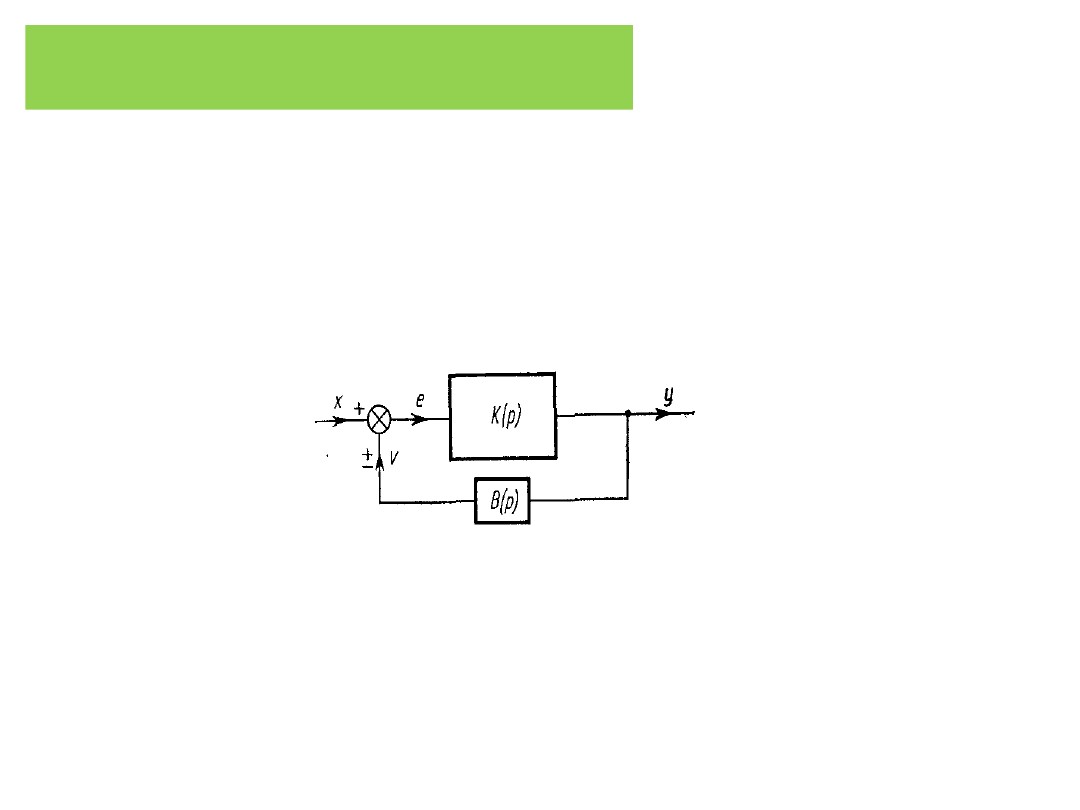
Układy ze sprzężeniem 

zwrotnym

Koncepcję sprzężenia zwrotnego, w latach trzydziestych dwudziestego wieku, 

opublikował  H.  S.  Black  i  obecnie  jest  ono  (sprzężenie  zwrotne)  powszechnie 

stosowne w analogowych układach elektronicznych. 

Wspólną  a  zarazem  istotną  cechą  działania  układów  regulacji  automatycznej 

jest  zastosowanie  w  nich  specjalnego  połączenia,  zwanego  sprzężeniem 

zwrotnym.

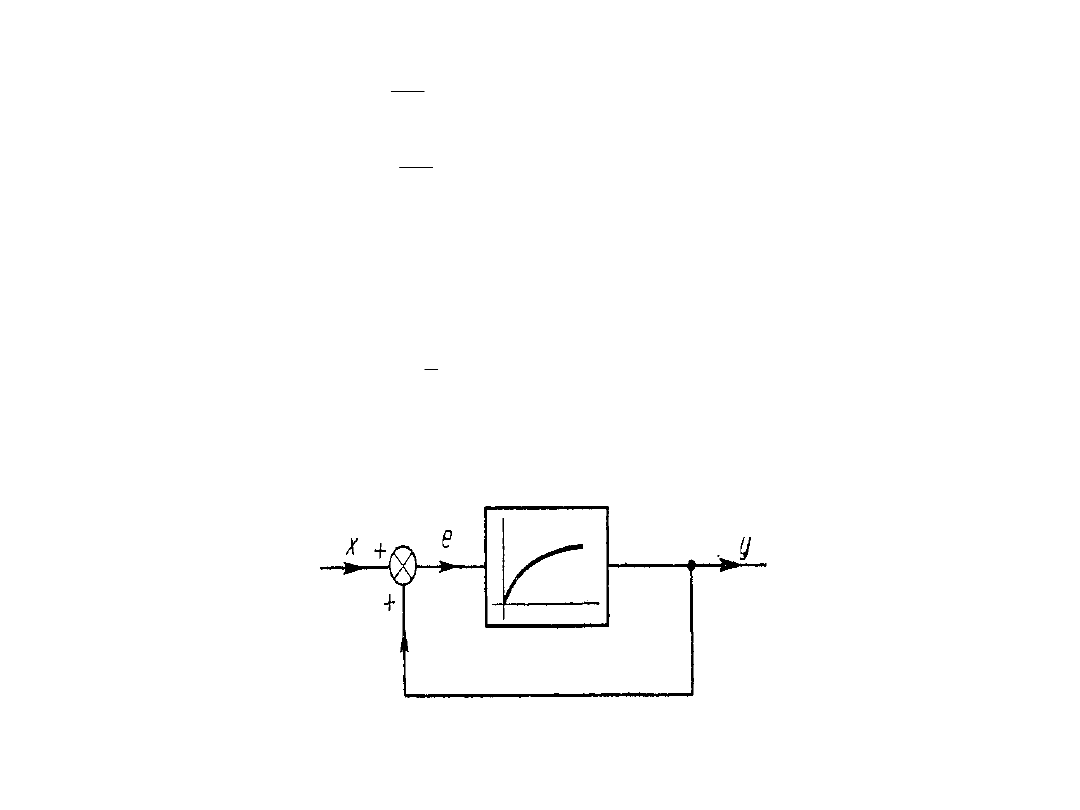
Najprostszy typ układu ze sprzężeniem zwrotnym

Istotą  zastosowanego  połączenia  jest  sygnał  y,  który  występuje  na  wyjściu 

układu i jest wprowadzany z powrotem poprzez element B(p) na jego wejście. 

Takie  rozwiązanie  nazywa  się  sprzężeniem  zwrotnym,  a  układ,  w  którym  go 

zastosowano układem ze sprzężeniem zwrotnym.

Sygnał v wprowadzić z powrotem do układu w taki sposób, aby się dodawał lub 

odejmował od sygnału x. W przypadku dodawania mamy mówimy o sprzężeniu 

zwrotnym dodatnim, a w przypadku odejmowania o sprzężeniu zwrotnym 

ujemnym.

Termin sprzężenie zwrotne jest związany z teorią transmisji sygnałów i oznacza, 

że napięcie wyjściowe dowolnego liniowego układu analogowego, np. wzmacniacza 

akustycznego,  w  odpowiedniej  proporcji  oraz  w  miarę  potrzeby  odpowiednio 

odfiltrowane  ponownie  jest  kierowane  do  wejścia  wzmacniacza  i  dodaje  się  lub 

odejmuje się od sygnału sterującego

Możemy obliczyć jaka jest zależność pomiędzy sygnałami x, e, y w tych układach. 
 
                                            = K(p),                                     = B(p),
 
a dodatkowe równanie dla węzła sumującego ma postać 
 
                                                              E(p) = X(p) ± V(p);
stąd

                                                                  = 

)

(

)

(

p

E

p

Y

)

(

)

(

p

Y

p

V

)

(

)

(

p

X

p

Y

)

(

)

(

1

)

(

p

B

p

K

p

K



Stosunek Y(p)/X(p) określa funkcję przejścia elementu ze sprzężeniem 

zwrotnym. Jeśli oznaczymy ją jako K

z

(p) to otrzymamy równanie:

K

z

(p) =                    ,

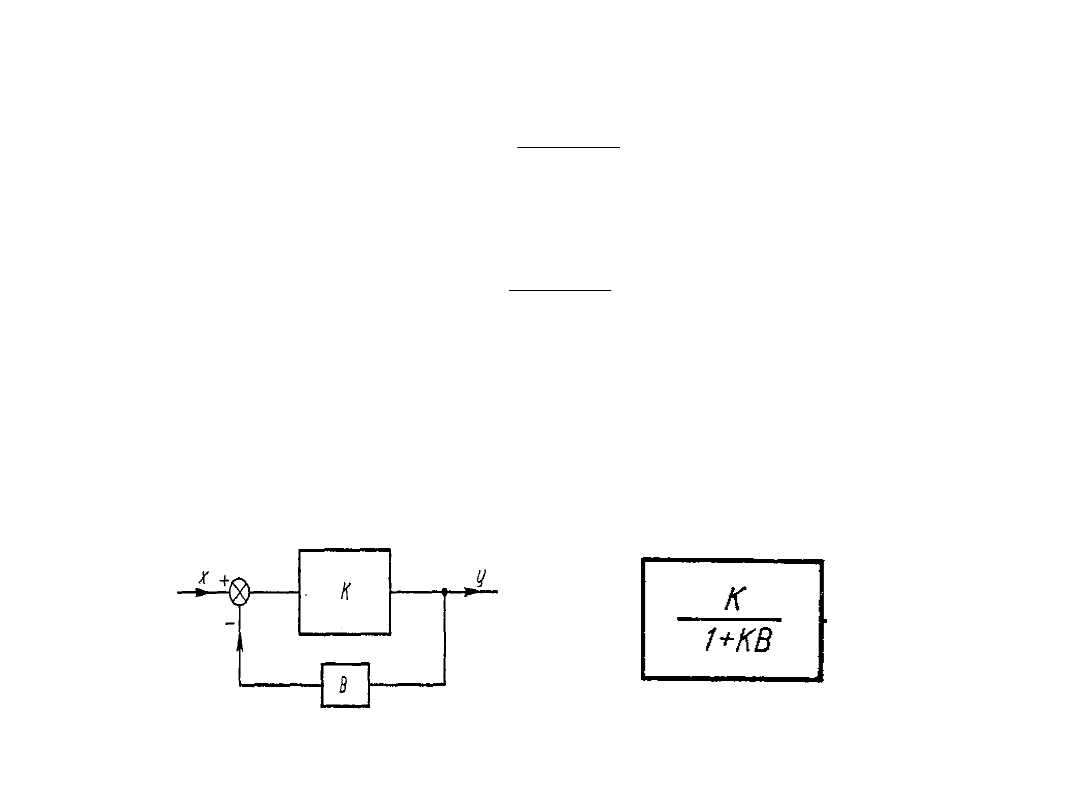
W przypadku sprzężenia zwrotnego ujemnego we wzorze obowiązuje znak + ; 

mamy wówczas:

K

z

(p) =                            ,

Można więc powiedzieć, że element o funkcji przejścia K w którym 

zastosowano sprzężenie zwrotne ujemne jest równoważny elementowi o 

funkcji przejścia K

z

 = K/(1+KB) 

)

(

)

(

1

)

(

p

B

p

K

p

K



)

(

)

(

1

)

(

p

B

p

K

p

K



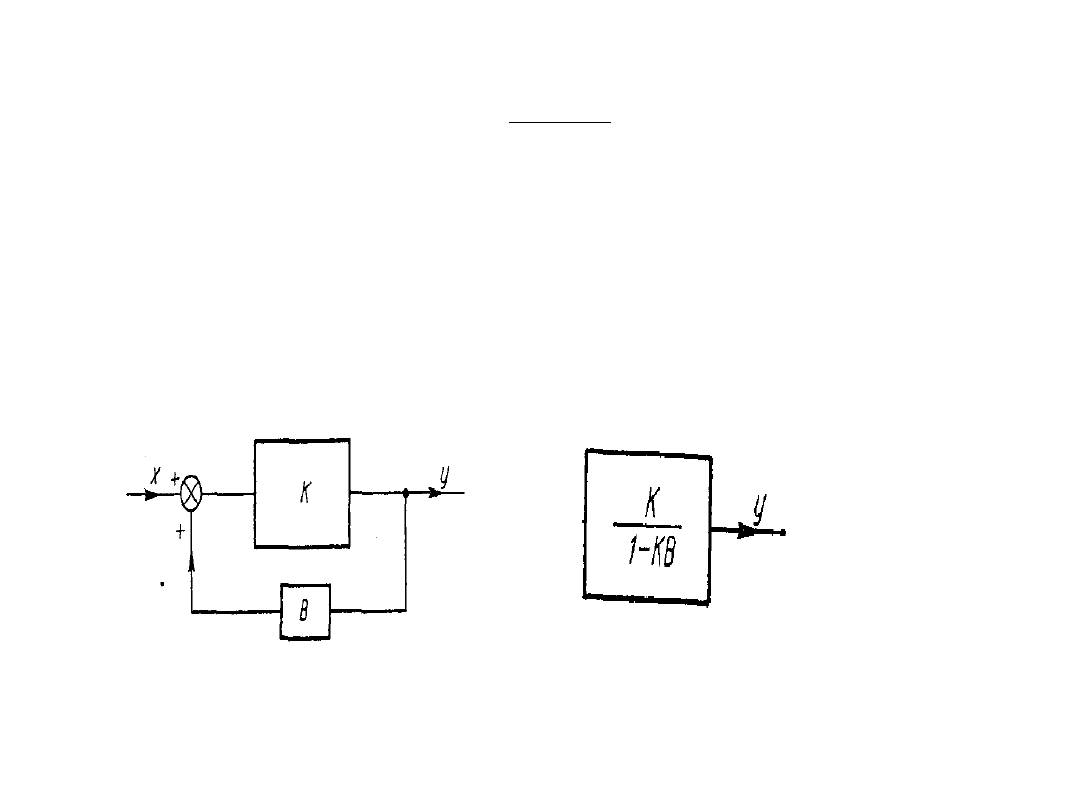
W przypadkach sprzężenia zwrotnego dodatniego we wzorze 
obowiązuje znak  -  .

K

z

(p) =                           ,

 

Element o funkcji przejścia K, w którym zastosowano sprzężenie 

zwrotne dodatnie równoważy element o funkcji przejścia 

K

z

 = K/(1-KB)

)

(

)

(

1

)

(

p

B

p

K

p

K



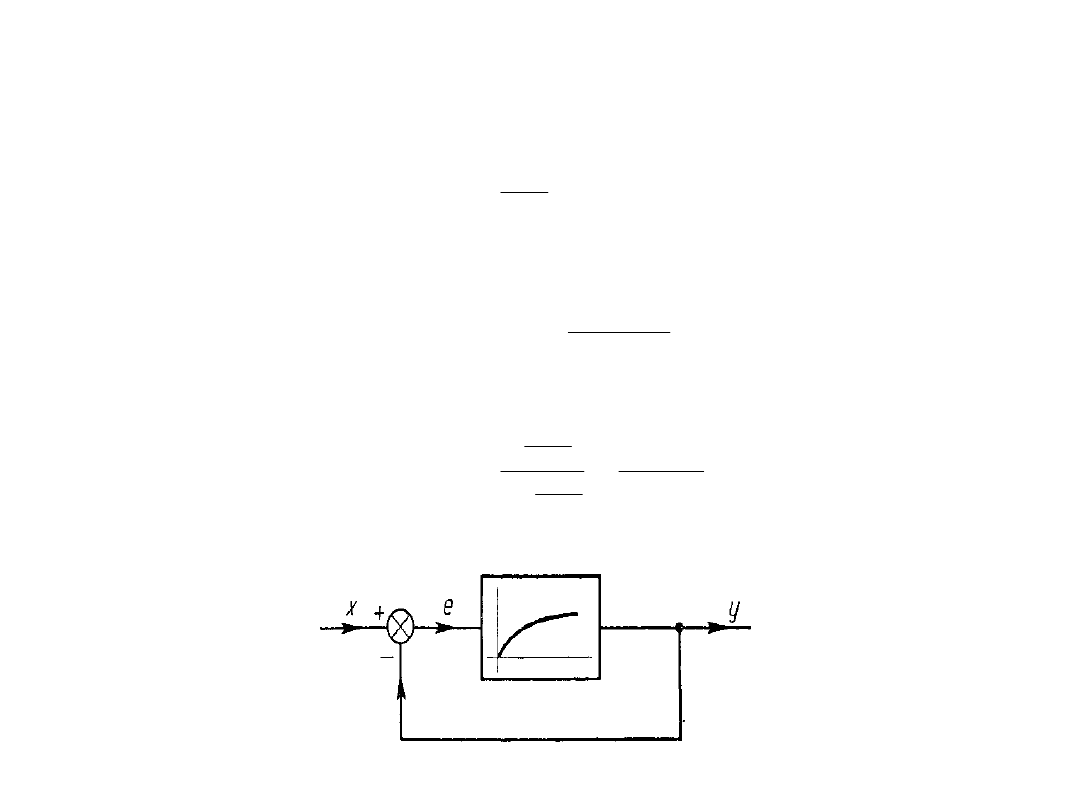
Przykład

 
Niech dany będzie wzmacniacz o funkcji przejścia 
                                  
                                                                 K(p) = k 

Jeżeli zastosujemy w nim sprzężenie zwrotne ujemne zgodnie ze wzorem

K

z

(p) =

oraz uwzględniając to, że B(p) = 1, otrzymamy (rysunek)

                                                                        K

z1 

=                     =                  ,

pT

k



1

)

(

)

(

1

)

(

p

B

p

K

p

K



pT

k

pT

k







1

1

1

1

1

pT

k

k



 )

1

(

1



k

k

1



k

T

k

T

Wzmacniacz inercyjny z ujemnym sprzężeniem zwrotnym

k

z1

(t) = 

(

1-e

-

t/

),

Jeżeli k  l, to wzór k

z1

 można uprościć przyjmując k+1 

 k. otrzymamy 

wówczas

k

z1

(t) = (1-e

-t/



),

 = 

 = 

Jeżeli w rozpatrywanym wzmacniaczu zastosujemy dodatnie sprzężenie zwrotne 
według schematu z rysunku

Wzmacniacz inercyjny z dodatnim sprzężeniem 
zwrotnym

to na podstawie wzoru 

K

z

(p) =                        ,

otrzymamy

                                                                    K

z2

(p) 

 

=                  =

                                                                      k

z2

(t) =            (1-e

-t/

),

                                                                             =      

Jeżeli k  l, to wzór k

z2

                                                                         k

z2

(t) = -(1-e

-t/

),

                                                                                 = - 

Znalezione funkcje przejścia pozwalają nam obliczyć przebiegi sygnałów wyjściowych 

wywołanych załączeniem dowolnych sygnałów wejściowych x(t).

Szczegółowe obliczenia przeprowadzimy dla przypadku x(t)=x

o

 1(t), x

o

= const. 

        

)

(

)

(

1

)

(

p

B

p

K

p

K



pT

k

pT

k







1

1

1

1

1

pT

k

k







)

1

(

1



 k

k

k

T

1



 k

T

I tak, jeżeli sprzężenie zwrotne jest ujemne, to przy założeniu k > l mamy 
na podstawie wzoru
 

y(t) = x

o

 (1-e

-t/

),

na podstawie wzoru e(t) = x(t) – 
y(t) mamy

e(t) = x

o

e

-t/

Jeżeli sprzężenie zwrotne jest dodatnie, to przy analogicznym założeniu k > l 

mamy na podstawie wzoru
 

                                                                                              

y(t) = -x

o

 (1-e

-t/

),

.

oraz, uwzględniając e(t) = x(t) 
+ y(t),

e(t) = x

o

e

-t/

,

Przebiegi  sygnałów  x(t),  e(t)  i  y(t)  dla  przypadków  ujemnego  i  dodatniego 

sprzężenia zwrotnego pokazane są odpowiednio na rys. A i B.

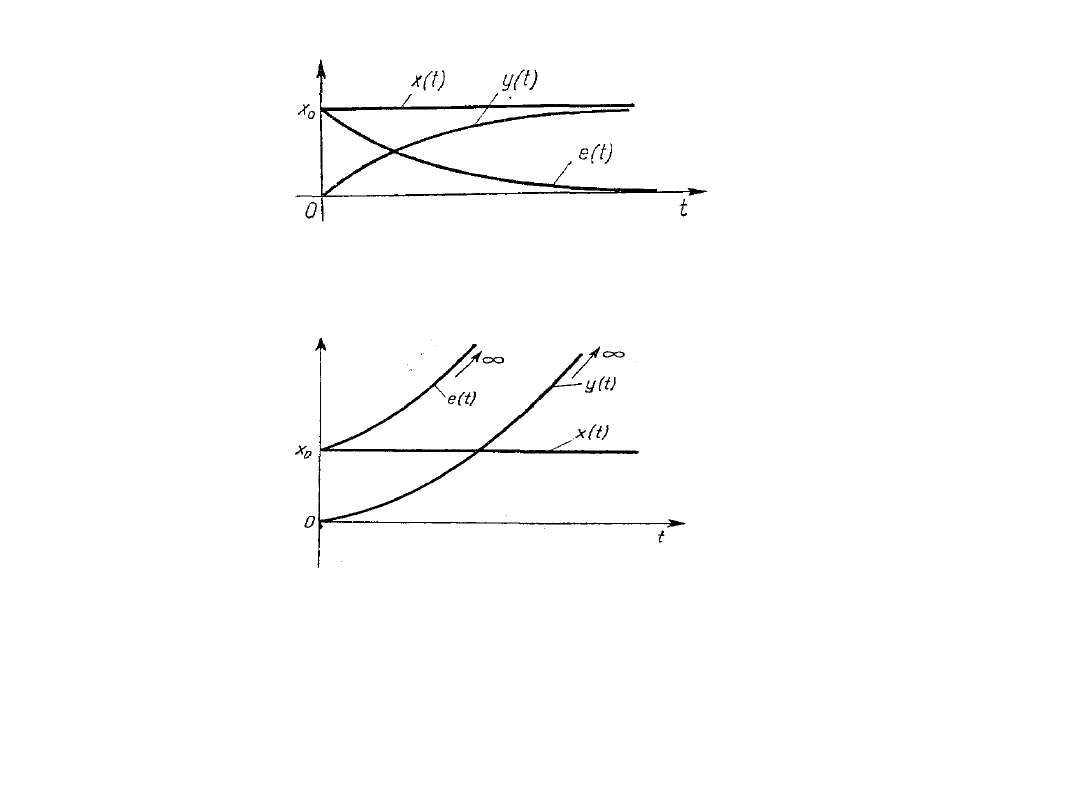
A. Przebiegi sygnałów x(t), e(t), y(t)w przypadku ujemnego sprzężenia zwrotnego

B. Przebiegi sygnałów x(t),e(t),y(t)w przypadku dodatniego sprzężenia zwrotnego

Jak  widać,  zastosowanie  ujemnego  sprzężenia  zwrotnego 

spowodowało  to,  że  odpowiedź  wzmacniacza  y(t)  na  sygnał 

jednostkowy x

o

 dąży do tej samej wartości x

o

, niezależnie od zmian, 

jakim  może  ulegać  wartość  wzmocnienia  k  na  skutek  wahań 

zasilania,  starzenia  elementów  itp.,  byle  tylko  zachowany  był 

warunek k 

 1. 

Tę  własność  stabilizacji  można  uważać  za  pewną  cechę  prostych 

układów z ujemnym sprzężeniem zwrotnym.

Zastosowanie 

natomiast 

dodatniego 

sprzężenia 

zwrotnego 

spowodowało to, że odpowiedź y(t) i sygnał e(t) rosną teoretycznie 

nieograniczenie.  W  takim  przypadku  mówimy  o  wzbudzeniu  się 

układu.