Wypór, równowaga ciał

pływających

dodatkowe informacje

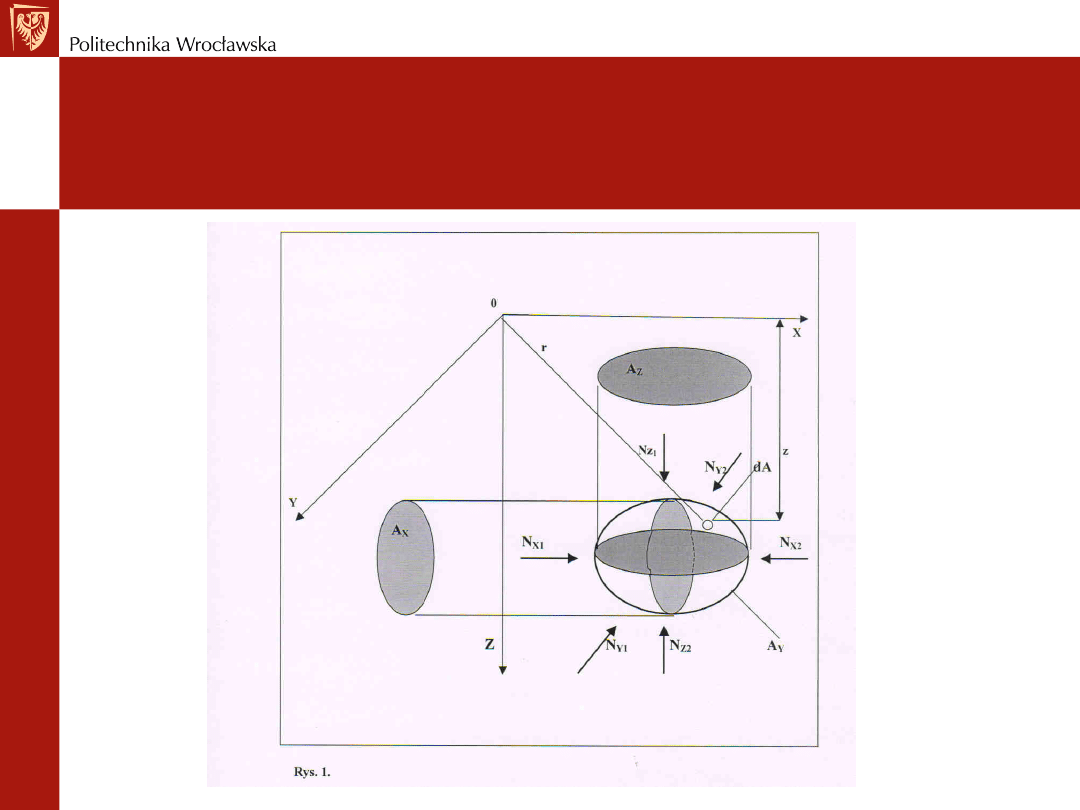
Wypór

Siła wyporu

M ożemy zapisać:







A

zdA

n

N











A

zdA

n

r

M







z

y

x

N

N

N

N

,

,

y

s

y

y

x

s

x

x

A

z

N

N

A

z

N

N

y

x

















2

1

2

1

Składowe poziome N

x

, N

y

=0, bo napór z dwóch stron, rzuty ciała na odpowiednie płaszczyzny są takie

same, a wielkość naporu zależy od pola rzutu i współrzędnej środka geometrycznego pola rzutu.

Siła wyporu hydrostatycznego

1

1

V

zdA

N

z











g

d

z

i

e

V

1

–

o

b

j

ę

t

o

ś

ć

s

ł

u

p

a

c

i

e

c

z

y

n

a

d

c

i

a

ł

e

m

2

2

V

zdA

N

z











g

d

z

i

e

V

2

=

V

1

+

V

c

i

a

ł

a

S

2

-

r

z

u

t

t

a

k

i

s

a

m

d

l

a

c

z

ę

ś

c

i

k

o

n

t

u

r

u

d

o

l

n

e

g

o

i

g

ó

r

n

e

g

o





1

2

2

1

V

V

N

N

W

N

z

z

z

















g

d

z

i

e

V

2

–

V

1

=

V

V

N

W

z













-

w

y

p

ó

r

h

y

d

r

o

s

t

a

t

y

c

z

n

y

V

W





W

-

r

ó

w

n

a

s

i

ę

c

i

ą

ż

a

r

o

w

i

c

i

e

c

z

y

o

o

b

j

ę

t

o

ś

c

i

w

y

p

a

r

t

e

j

p

r

z

e

z

t

o

c

i

a

ł

o

Warunki pływalności

Na ciało prócz siły wyporu działa siła ciężkości ciała G

Siła wypadkowa

W

G

G





1

- prawo Archimedesa

c

c

V

G

V

W









Od wartości G

1

zależą warunki pływania:

I G

1

= 0; G=W

c

c

V

V



 

V=V

c

, γ=γ

c

 stan równowagi – ciało zanurzone na dowolnej głębokości

II

G

1

>0; G>W

c

c

V

V



 

V

V

c





 

c

- ciało tonie

III G

1

<0; G<W

1.



 



c

c

V

V

 ciało wynurza się, przy czym trwa to do osiągnięcia stanu równowagi

tzn. wtedy kiedy G=W,

2.

}

V

V

c

c









ciało częściowo wynurzone (Statki!)

Mówimy, że ciało pływa, gdy jest wynurzone częściowo nad jej powierzchnią, lub zanurzone
całkowicie utrzymuje określone po

łożenie.

Stateczność ciał pływających, ciała

zanurzone

• Jest to zdolność powrotu ciała pływającego do położenia pierwotnego

po uprzednim jego wychyleniu ze stanu równowagi. Ma to związek z
kierunkami działania sił.

• Siły G i W  przechodzą przez środek ciężkości z

G

i środek wyporu z

B

• G  w środku ciężkości ciała
• W  przez punkt będący środkiem wyporu są to współrzędne środka

objętości części ciała zanurzonego.

• Aby była równowaga G=W i muszą działać wzdłuż tej samej prostej.
• Ale to nie jest warunek wystarczający aby ciało zanurzone było

stateczne. O stateczności decyduje wysokość położenia środka
ciężkości z

G

i położenie środka wyporu z

B

• z

G

>z

B

– brak stateczności

• z

G

=z

B

–stateczność chwiejna

• z

G

<z

B

– równowaga trwała – ciało stateczne

Stateczność ciał pływających, częściowo

wynurzonych

Kryteria stateczności

Stateczność

W i e l k o ś ć m o m e n t u w z g l ę d e m o s i o - x w y n i k a j ą c e g o z p r z e s u n i ę c i a s i ę p o ł o ż e n i a ś r o d k a w y p o r u :





x

B

B

M

z

z

W







M o m e n t t e n j e s t r ó w n o w a ż o n y p r z e z m o m e n t k l i n a w y n u r z o n e g o i z a n u r z o n e g o M

X

. E l e m e n t a r n y

s i ł a w y p o r u o d k l i n a w y n u r z o n e g o l u b z a n u r z o n e g o w y n o s i :

S i ł y t e s ą r ó w n e c o d o w a r t o ś c i l e c z p r z e c i w n i e s k i e r o w a n e . M o m e n t o d t y c h s i ł m a p o s t a ć :

dA

y

ydW

dM

x













2

2

2

W y r a ż e n i e y (   ) d A j e s t e l e m e n t a r n ą o b j ę t o ś c i ą k l i n a w y n u r z o n e g o l u b z a n u r z o n e g o . M o m e n t

c a ł k o w i t y w y n o s i :

x

x

I

dF

y

M



















2

2

dA

y

dW



 



Kryteria stateczności

Jeśli W= to wówczas otrzym

uje się:

V

I

z

z

I

z

z

V

x

B

B

x

B

B





















I

X

– m

om

ent bezwładności wodnicy pływania.

Wodnica pływania to powierzchnia utworzona z przecięcia płaszczyzny swobodnej

powierzchni wodnej z powierzchnią ciała pływającego częściowo wynurzonego.

Z drugiej strony, dla m

ałych wartości  w oparciu o rysunek uzyskuje się:















m

a

z

z

B

B

V

I

m

a

x





0

,

0

,











m

a

z

z

a

V

I

m

B

G

x

Jeśli środek wyporu jest położony niżej niż środek ciężkości (co m

a m

iejsce w

budowie okrętów) tzn :

B

G

z

z  to znaczy: a>0 to aby ciało (statek ) był stateczny musi zachodzić warunek:

m

>0 i

a

V

I

x



Ramię prostujące.

Z g o d n i e z r y s . z m i a n a k s z t a ł t u p o w o d u j e z m i a n ę w s p ó ł r z ę d n y c h ś r o d k a w y p o r u ( r y s . 1 ) , c o p r o w a d z i

d o p o w s t a n i a m o m e n t u p a r y s i ł . M o m e n t t e n o k r e ś l a z a l e ż n o ś ć :













sin

)

(

)

(

GM

W

l

g

M



 [ m

3

] – o b j ę t o ś ć z a n u r z o n e j c z ę ś c i k a d ł u b a s t a t k u ,

l [ m ] – r a m i ę p a r y s i ł d z i a ł a j ą c y c h n a p r z e c h y l o n y s t a t e k ( r y s . 1 ) .

Z e w z o r u w y n i k a , ż e m o m e n t p r o s t u j ą c y j e s t f u n k c j ą k ą t a p r z e c h y ł u , a j e g o w a r t o ś ć z a l e ż y o d
w a r t o ś c i r a m i e n i a m o m e n t u p a r y s i ł l (  ) . R a m i ę t o z m i e n i a s i ę w r a z z e z m i a n ą k ą t a p r z e c h y ł u .

P r z e b i e g t e j z a l e ż n o ś c i o d k ą t a p r z e c h y l e n i a s t a t k u d e c y d u j e o b e z p i e c z e ń s t w i e s t a t k u w r z e c z y w i s t y c h

w a r u n k a c h e k s p l o a t a c j i . D l a k a ż d e g o s t a t k u , k t ó r y p o s i a d a c e r t y fi k a t b e z p i e c z e ń s t w a , p r z e b i e g t e j

k r z y w e j m u s i s p e ł n i a ć w y m a g a n i a i n s t y t u c j i k l a s y fi k a c y j n e j .

Krzywa ramion prostujących

Związek między krzywą ramion, a

wysokością metacentryczną

I s tn ie j e śc is ła w s p ó łz a le ż n o ś ć m ię d z y p r z e b ie g ie m k r z y w e j r a m io n , a w y s o k o ś c ią

m e t a c e n tr y c z n ą . Z r ó w n a n ia w y n ik a , ż e :









sin

)

(

)

(

GM

l

P o c h o d n a k r z y w e j l p o k ą c ie p r z e c h y łu m a p o s ta ć :



















cos

)

(

sin

)

(

)

(

GM

d

GM

d

d

dl

J e ś li k ą t p r z e c h y łu z m ie r z a d o z e r a , p u n k t G M



z m ie r z a d o p u n k tu G M

0

. W a r to ś ć te j

p o c h o d n e j d la k ą ta p r z e c h y łu  = 0 , w y n ie s ie w ię c :

0

)

0

(

GM

d

dl









S t y c z n a d o k r z y w e j r a m io n p r z y z e r o w y m k ą c ie p r z e c h y łu p o z w a la n a o k r e ś le n ie

w y s o k o ś c i m e t a c e n tr y c z n e j . Z a c h o d z i r ó w n ie ż z a le ż n o ś ć :









tg

l

rd

GM

1

0

W y k o r z y s tu j e s ię j ą d o a n a liz s ta te c z n o ś c i p r z y m a ły c h k ą t a c h p r z e c h y łu .