Typy standardowe

• Typ Boolean
• Typ Integer
• Typ Float
• Typ Character
• Operacje wejścia-wyjścia

Typ standardowy Boolean 1

Definicja 1.

type

Boolean

is

(False, True);

Operatory relacyjne takie same jak dla typów

wyliczeniowych = /= < <= > >=

Operatory logiczne
• Jednoargumentowy (unarny) -

not

• Dwuargumentowe (binarne) –

and

,

or

,

xor

Priorytety operatorów logicznych

Priorytet(

not

) >

Priorytet(

and

)=Priorytet(

or

)=Priorytet(

xor

)

Zalecenie.

Stosuj nawiasy jeżeli masz

wątpliwości jak będzie obliczone wyrażenie

Przykład 1.

Operatory_Logiczne, Nand_Nor

Typ standardowy Boolean 2

Dodatkowe operatory logiczne

dwuargumentowe:

or else

(odpowiada

or

),

and then

(odpowiada

and

)

W przypadku tych operatorów najpierw obliczany

jest lewy argument i jeżeli wartość operacji może

być wyznaczona na tej podstawie, prawy

argument nie jest obliczany.

Priorytet taki sam jak pozostałych operatorów

logicznych dwuargumentowych

Operatory przynależności:

in

not in

służą do sprawdzania czy dana typu skalarnego

należy do pewnego zakresu

Liczba

not in

1..10 

not

(Liczba

in

1..10

)

Typ standardowy Integer 1

Zbiór do którego należą dane tego typu zależy

od implementacji języka. Liczby z tego zbioru

reprezentowane są dokładnie.

Atrybuty ‘First ‘Last ‘Size

Przykład 2.

Atrybuty_Integer

Operatory relacyjne = /= < <= > >=
Operatory algebraiczne

jednoargumentowe + -

abs

dwuargumentowe + - * /

rem

mod

**

Przykład 3.

Operacje_Calkowite

Definicja 1.

Stosowanie tych samych oznaczeń

do różnych operatorów nazywamy

przeciążaniem operatorów (

operator

overloading

)

Typ standardowy Integer 2

Priorytety operatorów działających na

argumentach typu Integer
**

abs

* /

mod rem

+ -

jednoargumentowe

+ -

dwuargumentowe

= /= < <= > >= relacyjne

Zalecenie.

Stosuj nawiasy jeżeli masz

wątpliwości jak będzie obliczone wyrażenie.

Nawiasy kosztują mniej niż błędy (

Van Tassel,

1982

)

Uwaga

. Operacja ** nie jest operacją

wewnętrzną ponieważ drugi argument

(wykładnik) jest typu Natural, a nie Integer.

Typ standardowy Integer 3

Zdefiniowane wstępnie podtypy utworzone na

bazie typu Integer

subtype

Natural

is

Integer

range

0..Integer’Last

subtype

Positive

is

Integer

range

1..Integer’Last

Dzielenie całkowite 1
Przy dzieleniu dwóch liczb całkowitych - dzielnej

A przez dzielnik B /= 0 otrzymuje się iloraz Q i

resztę R, a więc liczby te spełniają równanie
A = Q*B + R

W Adzie mamy operatory dwuargumentowe /

rem

takie, że Q = A/B i R = A

rem

B

Typ standardowy Integer 4

Należy zwrócić uwagę na to, że jeżeli A i B nie dzielą się

bez reszty, to iloraz jest zawsze liczbą bliższą
zera.

Przykład 4.

5 / 2 = 2, 5

rem

2 = 1

5 / (-2) = -2,

5

rem

(-2) = 1,

(-5) / 2 = -2,

(-5)

rem

2 = -1,

(-5) / (-2) = 2, (-5)

rem

(-2) = -1.

W przypadku operatorów /

rem

mamy

I.

Wartość bezwzględna ilorazu jest równa
ilorazowi wartości bezwzględnych argumentów,

II. Znak reszty jest zawsze równy znakowi

dzielnej.

Typ standardowy Integer 5

Dzielenie całkowite 2
Drugim operatorem obliczającym resztę jest

dwuargumentowy operator wewnętrzny

mod

.

Jeżeli B > 0, to A

mod

B

in

0..B-1 i

jeżeli B < 0, to A

mod

B

in

B+1..0

Możemy zinterpretować operator

mod

jako operator

obliczający resztę z dzielenia całkowitego, gdy

iloraz jest obliczany przy pomocy funkcji

nazywanej
częścią całkowitą – funkcją podłoga.

Funkcja ta oznaczana jest symbolem . (

Ross,

Wright, 1999, 188

) i określona jest następująco:

x = największej liczbie całkowitej takiej, że jest

mniejsza lub równa x

Typ standardowy Integer 6

Przykład 5.

4.5 = 4, -4.5 = -5.

Jeżeli A = Q

m

*B + R

m

, to Q

m

= A/B.

Przykład 6.

7/3 = 2,

7

mod

3 = 1,

-7/3 = -3, -7

mod

3 = 2,

7/-3 = -3, 7

mod

-3 = -2,

-7/-3 = 2, -7

mod

-3 = -1.

W przypadku operatora

mod

mamy

1.

O znaku wyniku decyduje zawsze znak

drugiego argumentu, czyli dzielnika

2.

W przypadku, gdy znaki argumentów są

różne, wyniki operacji
A

rem

B i A

mod

B różnią się.

Typ standardowy Integer 7

Operacja

mod

służy do implementacji

arytmetyki modulo.

W arytmetyce tej mamy m.in.

(A + B)

mod

N =

(A

mod

N + B

mod

N)

mod

N

Przykład 7.

Wykresy funkcji

k  k

mod

5, k  k/5,

k

in

–10..10,

k  k

rem

5, k  k/5,

k

in

–10..10

pokazano na kolejnych dwóch rysunkach.

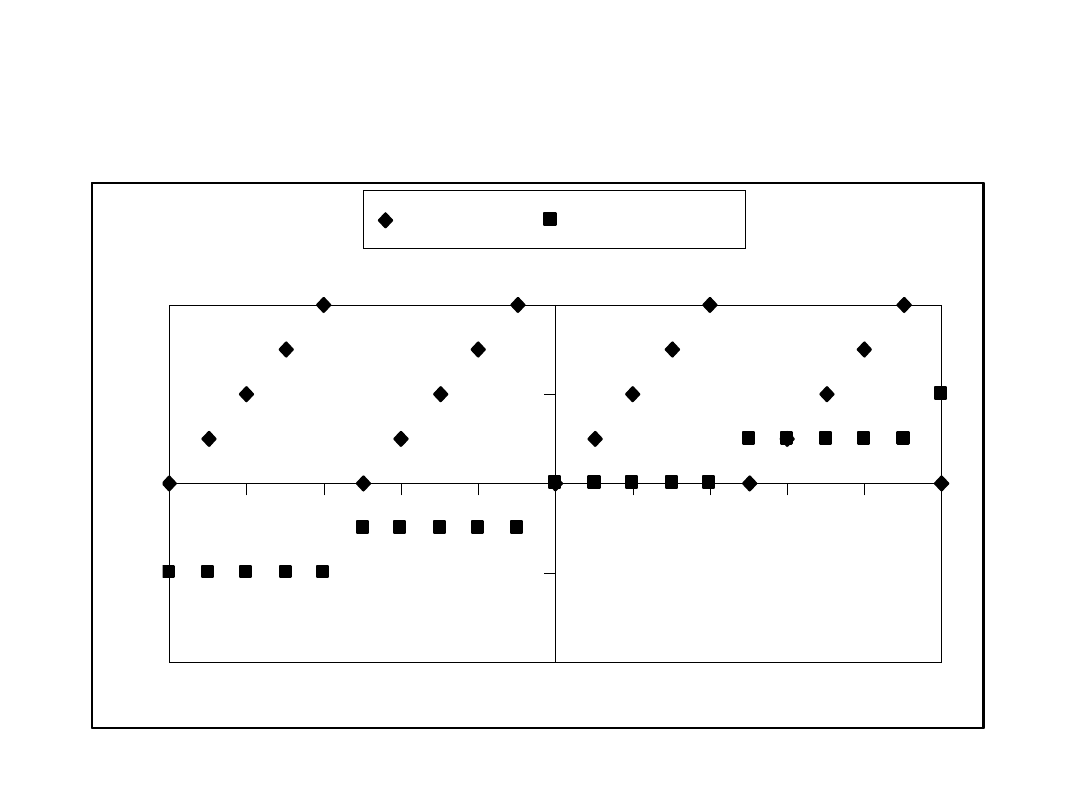
Typ standardowy Integer 8

-4

-2

0

2

4

-10 -8

-6

-4

-2

0

2

4

6

8

10

K

K mod 5 Entier (K/5)

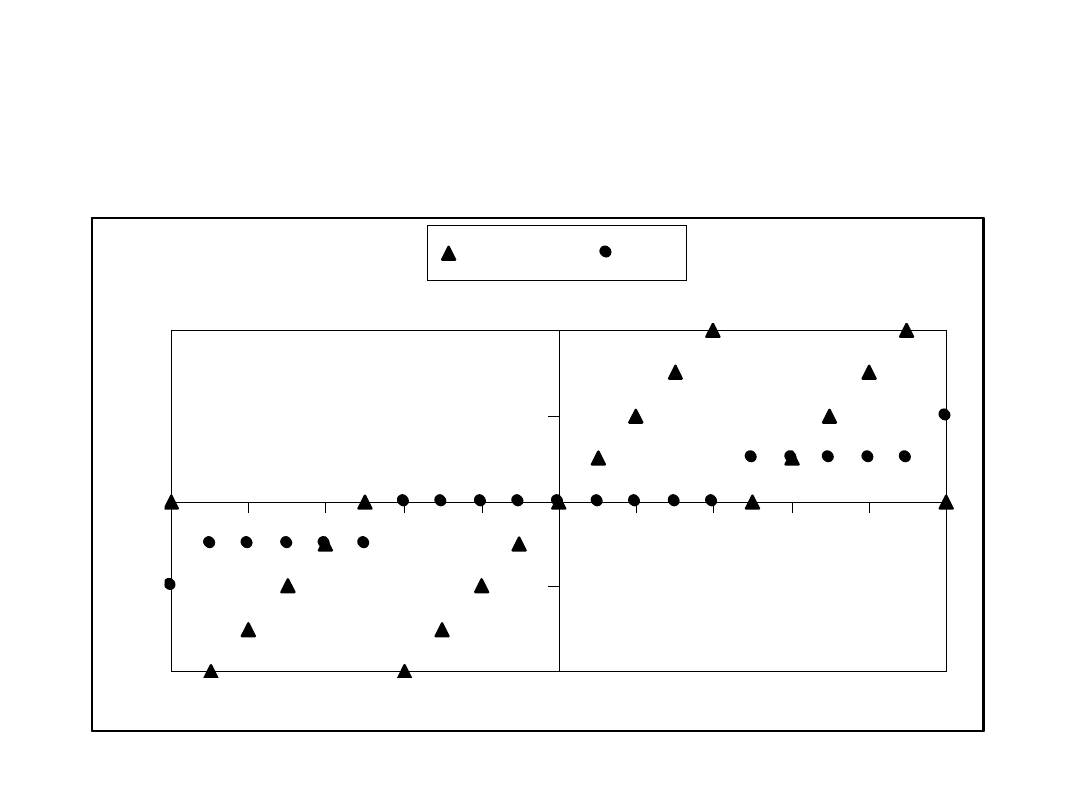
Typ standardowy Integer 9

-4

-2

0

2

4

-10 -8

-6

-4

-2

0

2

4

6

8

10

K

K rem 5

K/5

Typ standardowy Float 1

Ogólnie, liczby rzeczywiste są reprezentowane

w sposób przybliżony.

Reprezentacja typu standardowego Float

zależy od implementacji języka.

Inne typy zdefiniowane wstępnie:

Short_Float, Long_Float,

Long_Long_Float

Wybrane atrybuty
‘First, ‘Last, ‘Size
‘Digits, ‘Model_Epsilon, ‘Safe_First,

‘Safe_Last

Przykład 8.

Atrybuty_Float

Przykład 9.

Atrybuty_Rzeczywiste

Typ standardowy Float 2

Operatory
relacyjne = /= < <= > >=
algebraiczne

jednoargumentowe + -

abs

dwuargumentowe + - * / **

Priorytety takie jak dla typu Integer

Uwaga.

Wykładnik czyli drugi argument

operatora potęgowania jest typu Integer

Przykład 10.

Operacje_Rzeczywiste

Konwersja liczb rzeczywistych na całkowite i

odwrotnie

Float(67)

67.0 ,Integer(67.4)

67

Typ standardowy Float 3

•

Przy konwersji liczb rzeczywistych na
całkowite wynik jest liczbą całkowitą
najbliższą liczbie rzeczywistej

•

W przypadku, gdy liczba rzeczywista jest w
równej odległości od dwóch liczb całkowitych
wynik konwersji jest liczbą całkowitą dalszą od
zera
Integer(3.5) = 4,

Integer(-3.5) = -4

Przykład 11.

Konwersja

Częste stosowanie konwersji jawnej może

wskazywać na to, że przyjęto nieodpowiednie
typy danych

Przykład 12.

Konwersja_Jednostek

Typ rzeczywisty ogólny

Przykład 13.

Moje_Liczby_Rzeczywiste

Można jednak to zrobić ogólniej, co

zapewni nam przenośność programów

Przykład 14.

My_Reals

Przykład 15.

Atrybuty_Real

Przykład 16.

Atrybuty_Real Test_Reals

Wybrane operacje wejścia-wyjścia 1

subtype

Field

is

Integer

range

0 .. 255;

subtype

Number_Base

is

Integer

range

2 ..

16;

Liczby rzeczywiste

type

Num

is

digits <>;

Default_Fore : Field := 2;
Default_Aft : Field := Num'Digits - 1;
Default_Exp : Field := 3;

procedure

Put

(Item :

in

Num;

Fore :

in

Field := Default_Fore;

Aft :

in

Field := Default_Aft;

Exp :

in

Field := Default_Exp);

Wybrane operacje wejścia-wyjścia 2

Liczby całkowite

package

Ada.Text_IO.Integer_IO

is

Default_Width : Field :=

Num'Width;

Default_Base : Number_Base := 10;

type

Num

is range

<>;

procedure

Put

(Item :

in

Num;

Width :

in

Field := Default_Width;

Base :

in

Number_Base :=

Default_Base);

Wybrane operacje wejścia-wyjścia 3

Przykład 17.

Formatowanie

Przykład 18.

Czytaj_Integer

Przykład 19.

Czytaj_Float

Przykład 18.

Czytaj_Boolean

Przykład 19.

Czytaj_Typ_Wyliczeniowy

Przykład 20.

Czytaj_Dowolny_Napis

Przykład 21.

Odporne_Wejscie.ads,

Odporne_Wejscie.adb.

Literatura

Literatura podstawowa
Morawski, M., Zajączkowski, A. M.

(2003).
Wstęp do programowania w języku
Ada’95.
Rozdziały 3.6..3.9.

Użyteczne materiały dydaktyczne:

zskl.zsk.p.lodz.pl/~zajaczko