Ładunek elektryczny
Natura ładunku jest ziarnista, kwantowa
Cała materia zbudowana jest z cząstek elementarnych o
ładunku ujemnym, ładunku dodatnim i cząstek elektrycznie
obojętnych.
Ładunek punktowy punkt materialny obdarzony
różnym od zera ładunkiem elektrycznym
C
e
ne
Q
19
10
6
.
1
Elektromagnetyzm
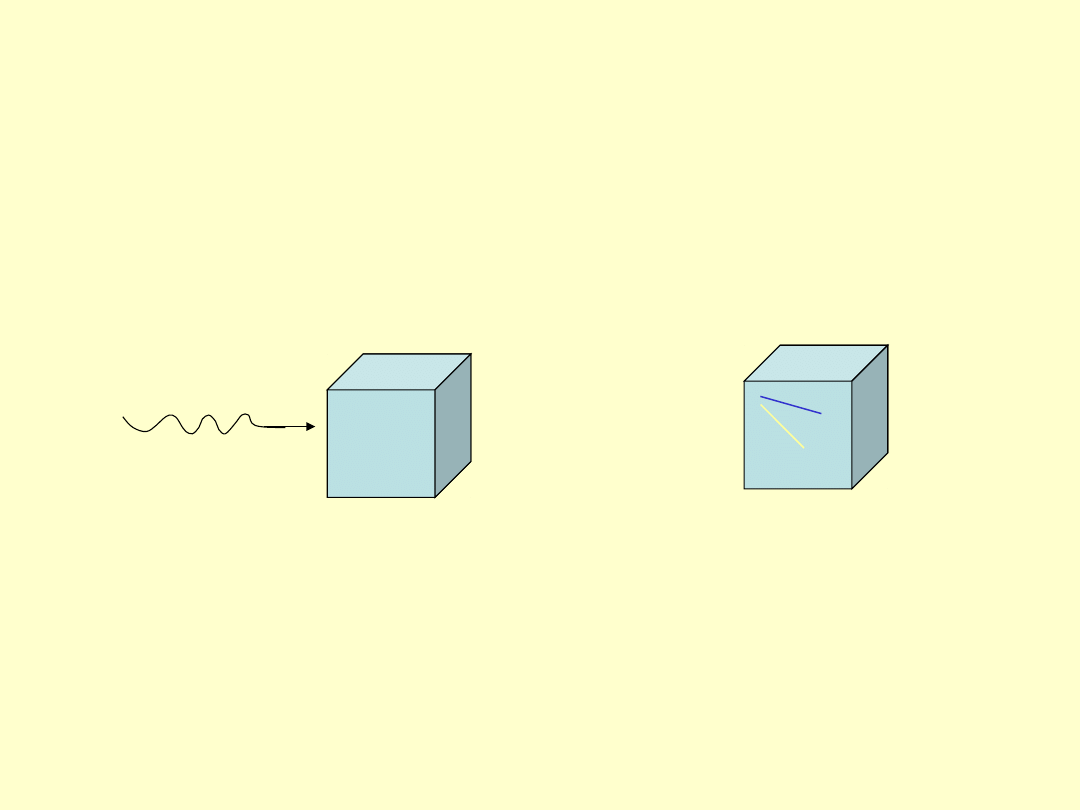
Zasada zachowania ładunku
– sumaryczny ładunek układu
odosobnionego jest wielkością stałą (algebraiczna suma
ładunków w układzie izolowanym jest stała i nie zmienia się w
czasie)
Prawo niezmienności ładunku elektrycznego
- wartość ładunku
elektrycznego nie zależy od jego prędkości i jest taka sama we
wszystkich układach inercjalnych.
i
i
const
q
foton
przed
po
e
+
e
-
Pole elektrostatyczne
– mówimy, że w pewnym obszarze istnieje
pole elektrostatyczne, jeżeli na każdy ładunek umieszczony w
tym obszarze działa siła proporcjonalna do wielkości tego
ładunku
Źródłem pola są ładunki elektryczne –
pole źródłowe
. Ładunek
wytwarza pole w otaczającej go przestrzeni i dopiero te pole
działa na pozostałe ładunki.
Pole elektrostatyczne
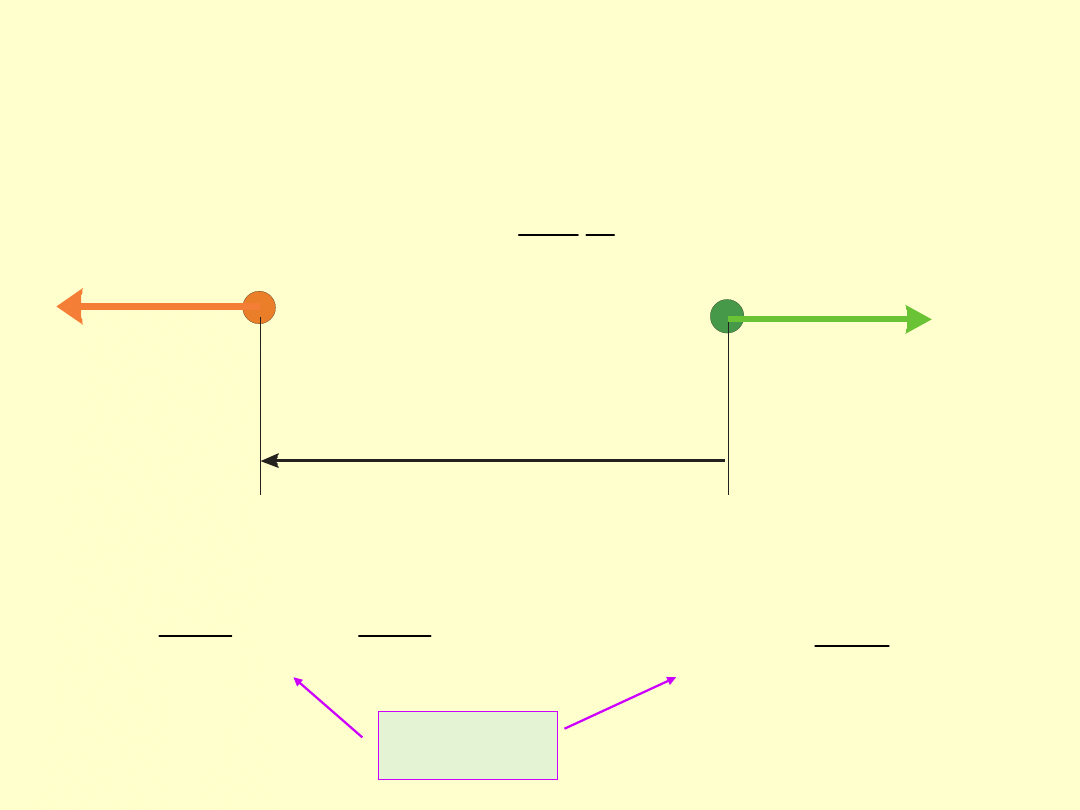
r
+q
+Q
r
r
r
k
F
2
F
2
2
12
10
8542
,
8
Nm
C
o
2
2
9
10
9
4
1
C
Nm
k
o
Prawo Coulomba – oddziaływanie
pomiędzy ładunkami punktowymi
dla próżni
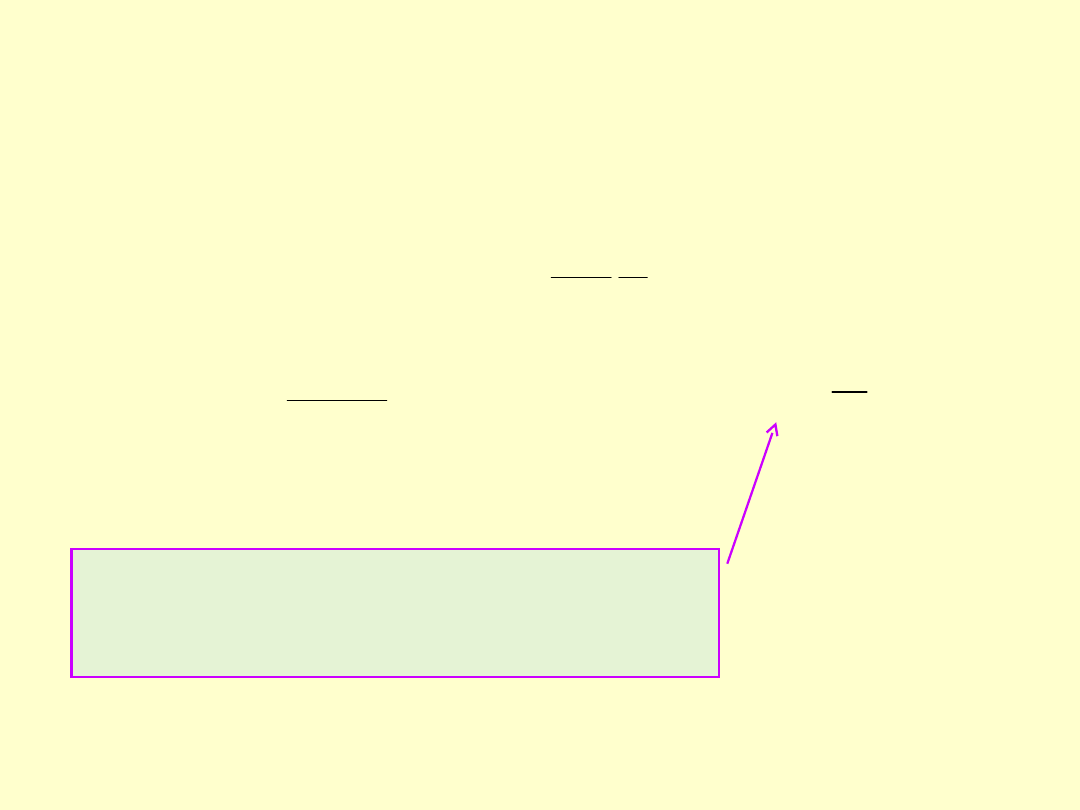
Dla ośrodka materialnego
r
r
r
k
F
r
2
r
o
r
k
4
1
0
r
Przenikalność względna ośrodka –
wskazuje ile razy przenikalność
bezwzględna ośrodka jest większa od
przenikalności próżni
Przenikalność względna
dielektryków
Rodzaj dielektryka
Przenikalność
elektryczna
względna
r
olej transformatorowy
2 2,5
Amoniak (-34ºC – ciecz)
22
Chlorek sodu
6
porcelana
6 8
szkło
3,1 4,4
Powietrze, para wodna
1
Woda (ciecz)
80
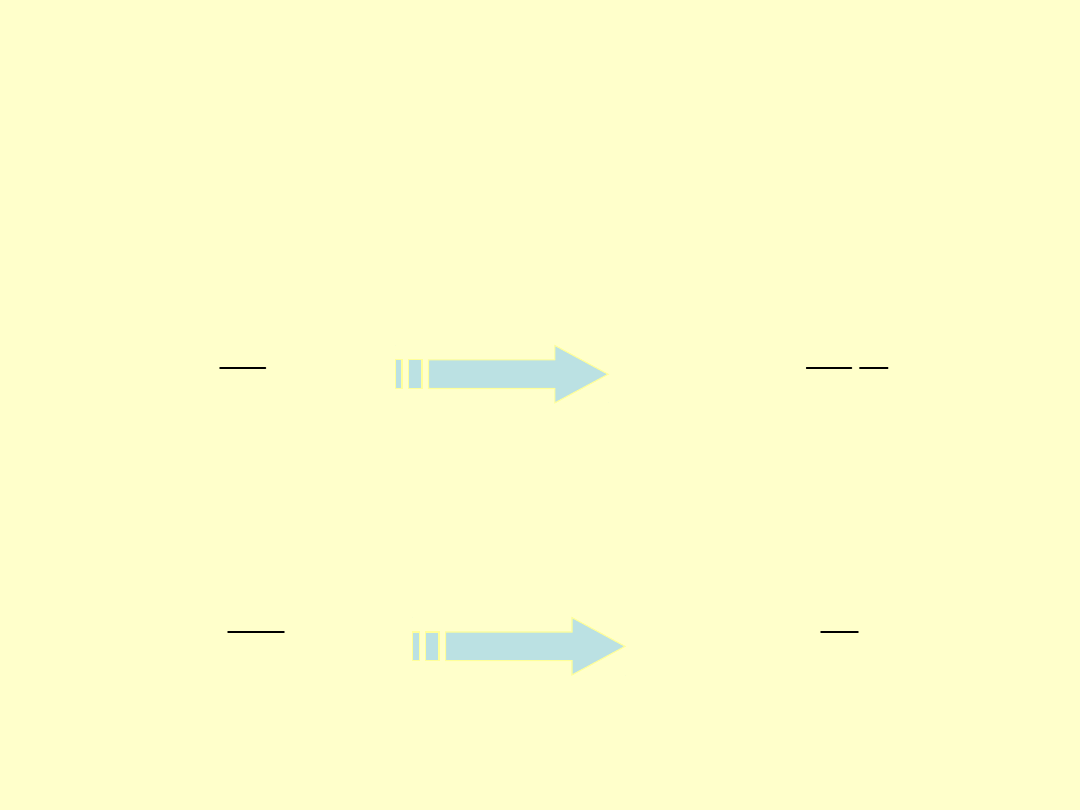
Wielkości charakteryzujące pole elektrostatyczne
r
r
r
Q
k
E
q
F
E
2
0
dla ładunku
punktowego
Wektor natężenia pola elektrostatycznego
Potencjał pola elektrostatycznego
r
Q
k
q
E
p
0
dla ładunku
punktowego
Linie pola
- tory do których styczne pokrywają się w każdym
punkcie z wektorem natężenia.
Kierunek jest określony przez zwrot wektorów natężenia, czyli
zwrot sił działających na ładunki dodatnie.
Linie te mają początek i koniec - nie są to linie zamknięte.
ładunek próbny –
mały
, tak by nie zaburzał
pola, które „mierzy” i
dodatni
0
q
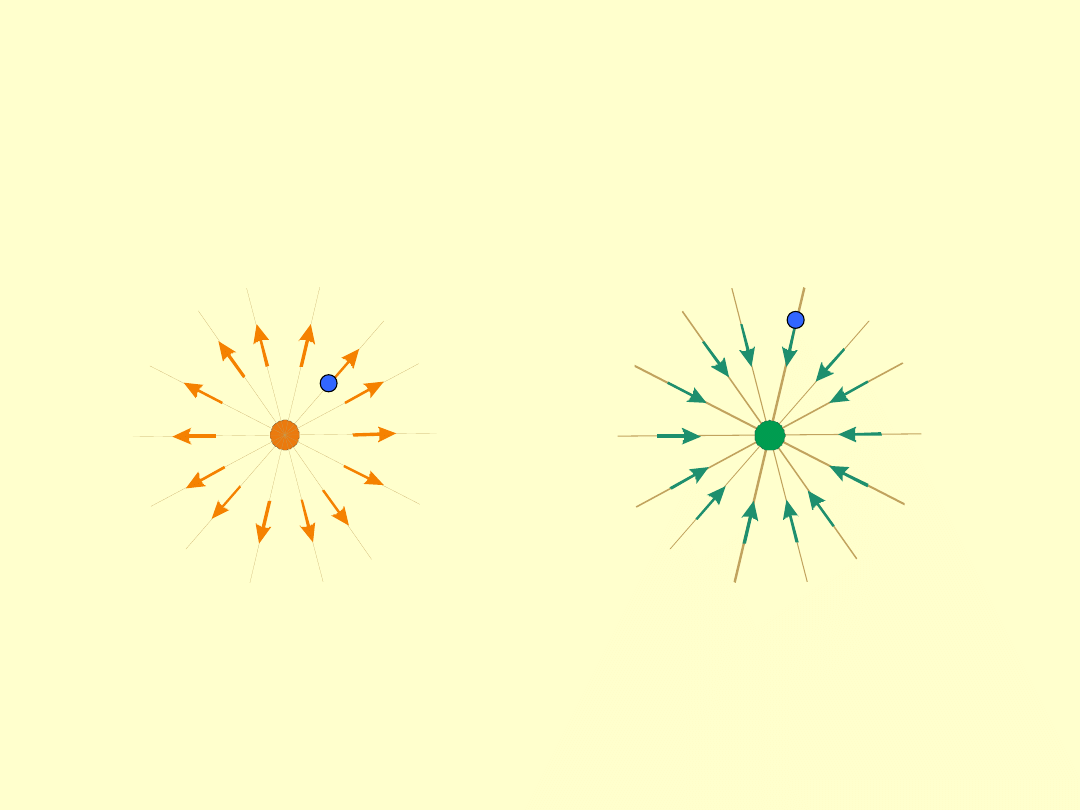
+q
-Q
Linie pola ładunków punktowych
q
0
E
E
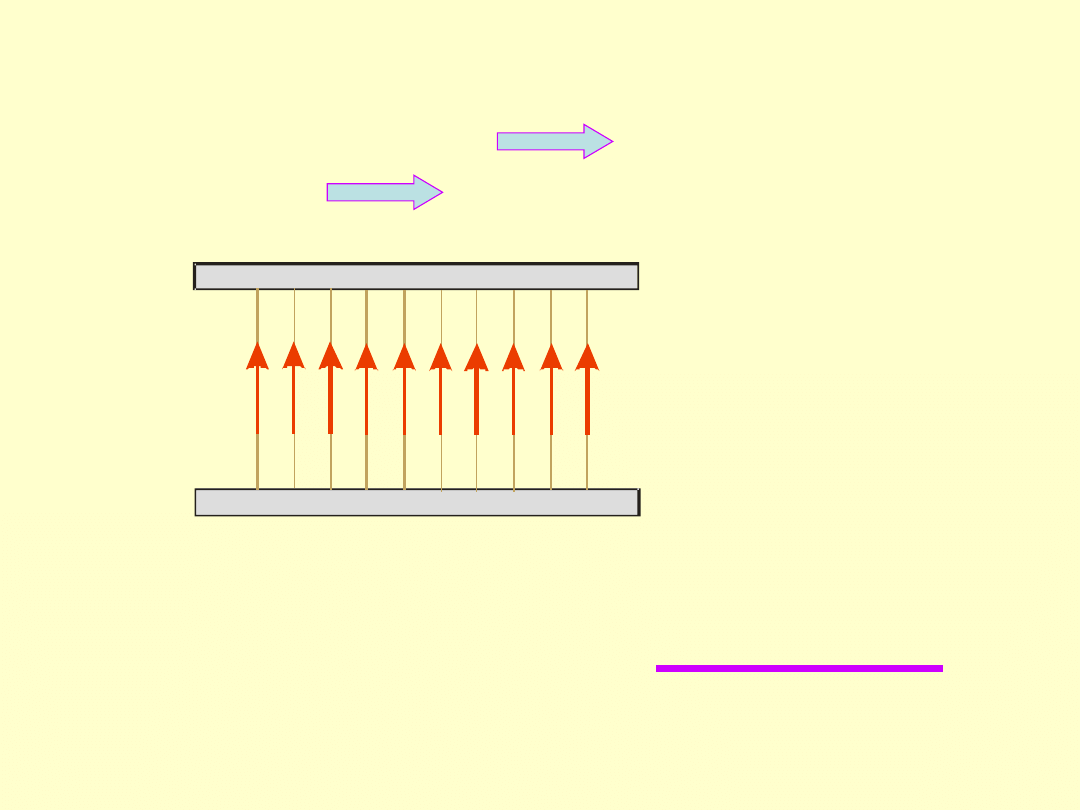
Pole jednorodne
- pole, w którego wszystkich punktach wektor
natężenie pola jest jednakowy ma taką samą
wartość, kierunek i zwrot linie sił są równoległe.
- - - - - -
+ + + + +
kondensator płaski
pole jednorodne
Pole pochodzące od ładunku punktowego
nie jest jednorodne!!!
.
Zasada superpozycji
- natężenie pola elektrostatycznego
dowolnym punkcie jest sumą wektorową natężeń pól w tym
punkcie, pochodzących od każdego z ładunków
i
i
E
E
E
q
F
q
F
E
0
0
4
0
3
0
2
0
1
0
E
q
E
q
E
q
E
q
F
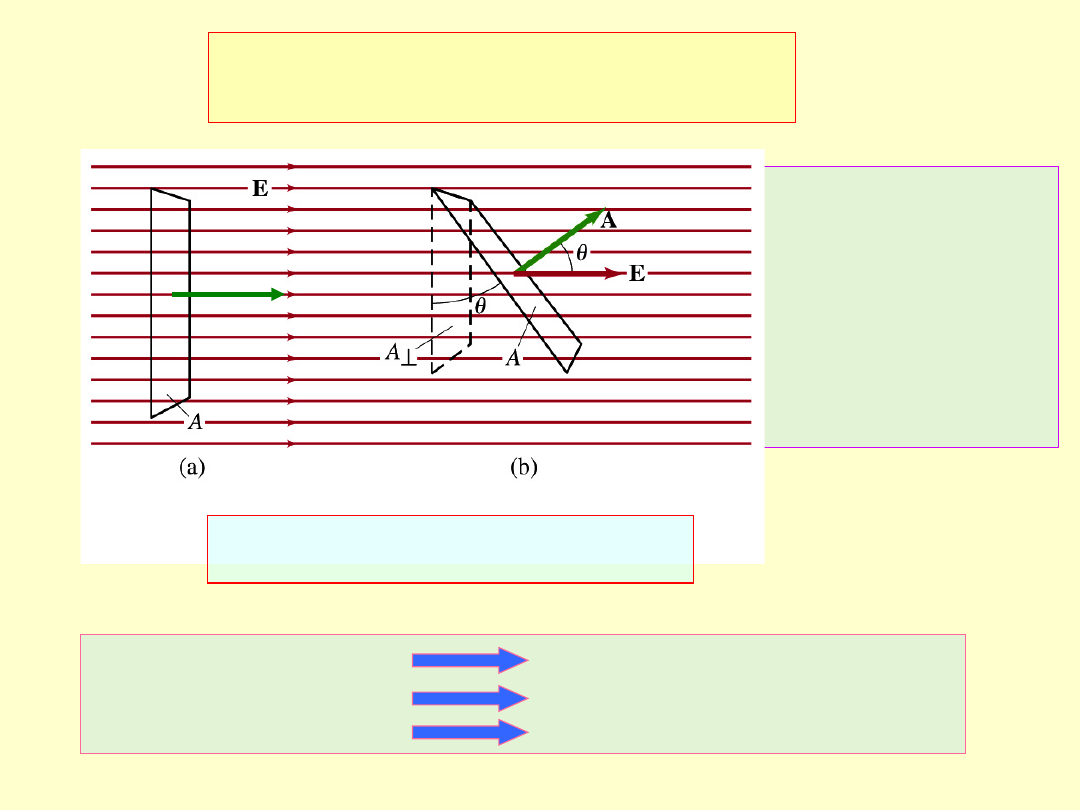
Strumień pola Φ
E
cos
EA
A
E
EA
E
Strumień pola jest
proporcjonalny do
liczby linii pola
elektrostatyczneg
o przechodzących
przez daną
powierzchnię
A
wektor A – długość pole powierzchni
kierunek do powierzchni
zwrot wychodzi z powierzchni
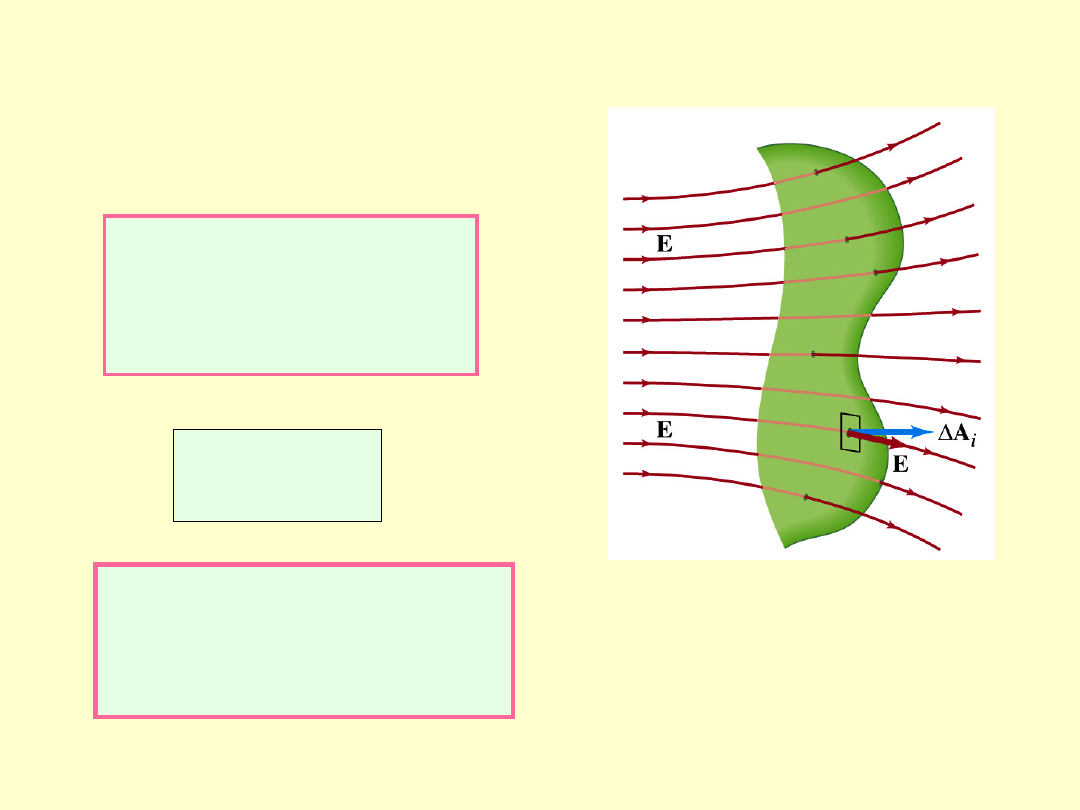
i
n
i
i
E
A
E
1
0
i
A
Δ
ia
powierzchn
E
A
d
E
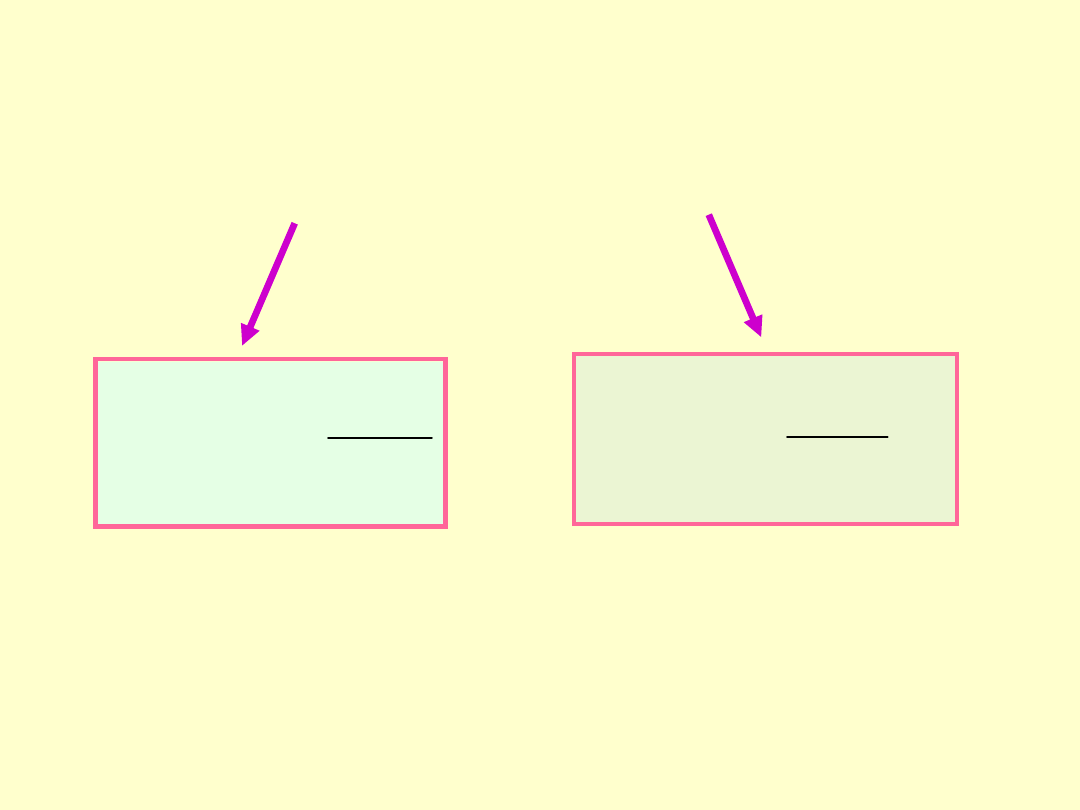
Strumień pola elektrycznego przez dowolną powierzchnię
A
A
d
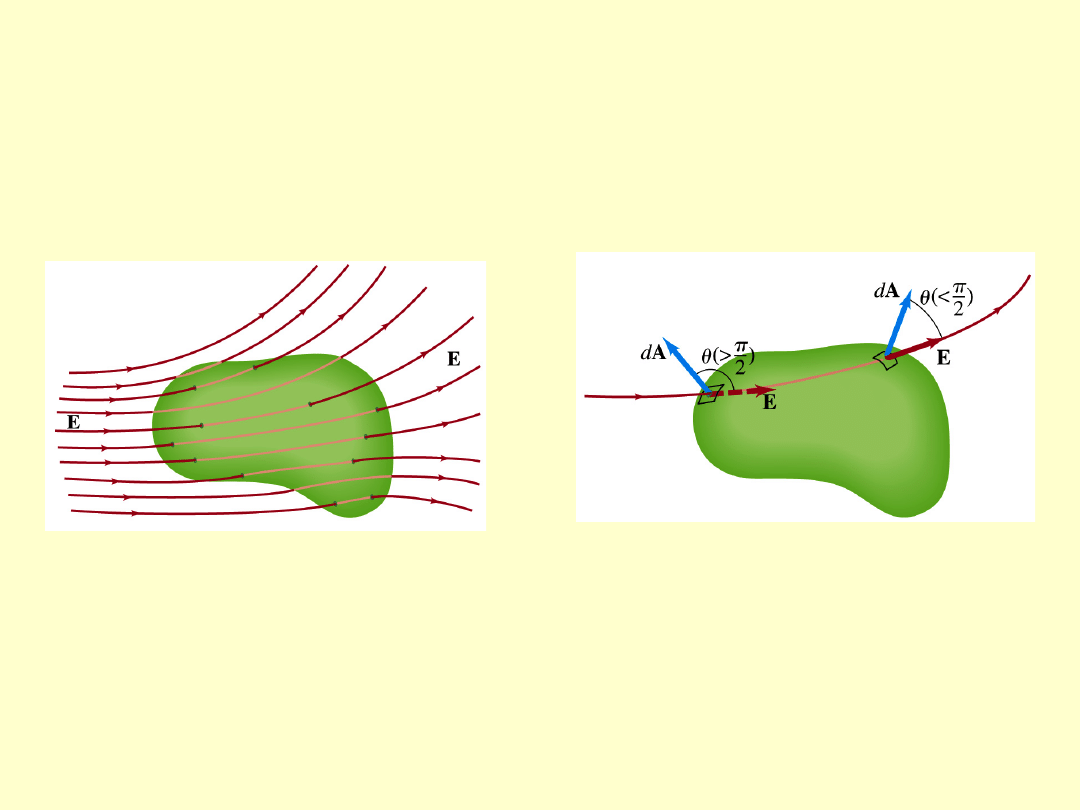
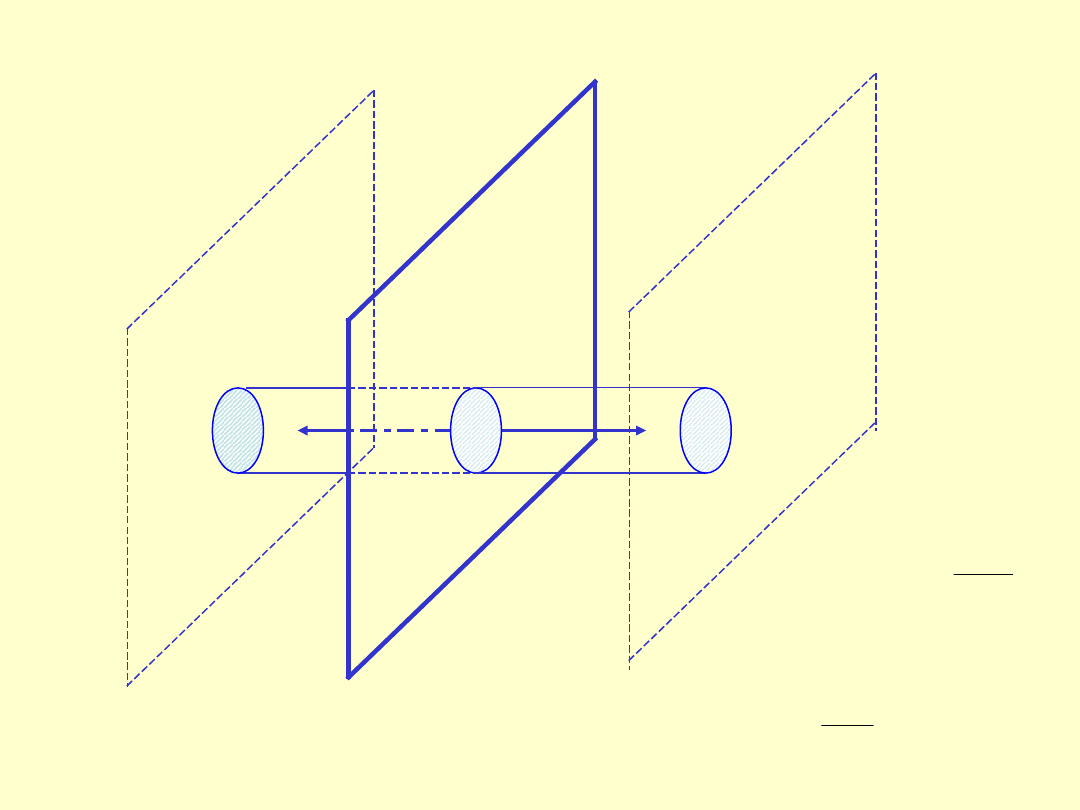
Strumień pola przez powierzchnię zamkniętą
znajdującą się w
zewnętrznym
polu
elektrycznym
Zamknięta powierzchnia dzieli przestrzeń na dwa obszary –
wewnątrz i na zewnątrz powierzchni
• dA jest zawsze prostopadły do powierzchni i skierowany na
zewnątrz
• strumień przechodzący przez powierzchnię zamkniętą jest
równy zeru – linie pola, które wchodzą do powierzchni muszą
ją opuścić.
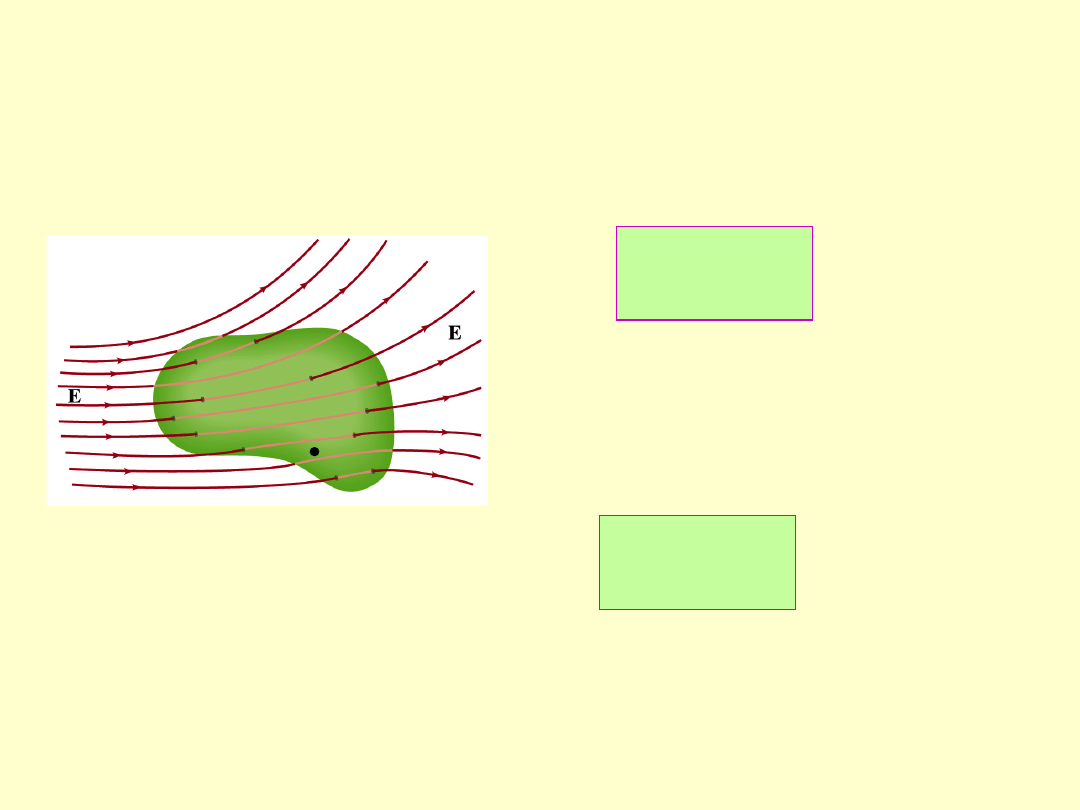
Trochę matematyki - dywergencja
Dane jest pole wektora . Otoczymy
dowolny
punkt P
zamkniętą powierzchnią A.
E
P
0
E
w objętości otoczonej
powierzchnią A pole ani nie
powstaje ani nie znika
0
E
w objętości otoczonej powierzchnią A pole rośnie albo
maleje
Stosunek strumienia do objętości, z której strumień wypływa
jest średnią mocą właściwą źródeł zawartych w objętości V. W
granicy
V 0 P.
V
E
V
E
moc właściwa źródeł w punkcie P dywergencja
(rozbieżność) wektora
E
A
V
E
V
A
d
E
V
V
E
div
1
lim
lim
0
0
Dla
dowolnego
wektora
C
A
V
C
V
A
d
C
V
V
C
div
1
lim
lim
0
0
V 0
const
C
div
można założyć, że w tej objętości
C
div
V
C
C
C
div
iloczyn skalarny operatora i wektora
C
W układzie współrzędnych kartezjańskich
z
C
y
C
x
C
C
k
C
j
C
i
z
k
y
j
x
i
C
z
y
x
z
y
x
Można wykazać, że
dV
C
div
A
d
C
A
V
twierdzenie Gaussa-Ostrogradskiego
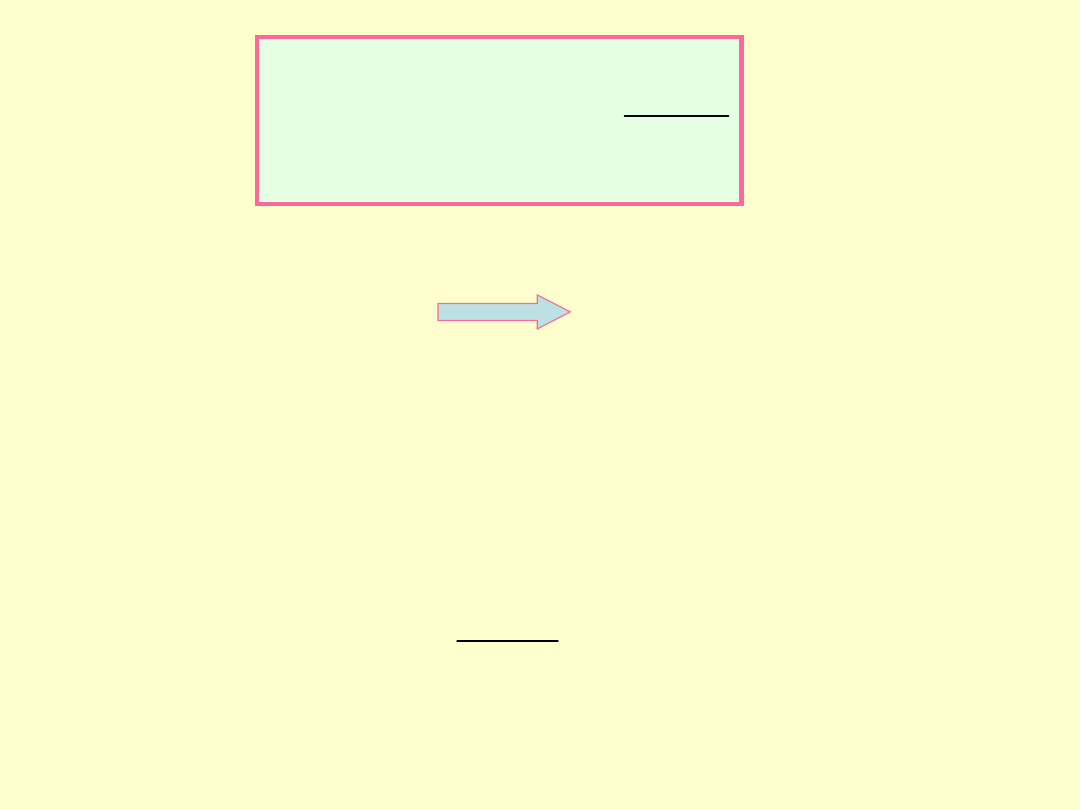
Prawo Gaussa
Strumień pola elektrycznego przez
dowolną
powierzchnię
zamkniętą jest równy całkowitemu ładunkowi zamkniętemu w tej
powierzchni
E
r
A
E
A
d
E
0
Q
r
A
E
A
d
E
0
Q
V
dV
Q
dV
dQ
A
n
A
A
dA
E
A
d
E
dA
E
A
d
E
cos
V
r
A
n
dV
dA
E
0
1
V
r
A
dV
A
d
E
0
1
dV
E
div
A
d
E
A
V
V
r
V
A
dV
dV
E
div
A
d
E
0
funkcje podcałkowe muszą być równe
r
E
E
div
0
r
E
div
0
r
A
A
d
E
0
Q
Prawo Gaussa w postaci
całkowej
różniczkowej
Właściwości powierzchni Gaussa
:
• jest to powierzchnia hipotetyczna – matematyczna konstrukcja
myślowa,
• jest dowolną powierzchnią zamkniętą – w praktyce powinna
mieć kształt związany z symetrią pola,
• powierzchnia Gaussa przechodzi przez punkt, w którym
obliczamy natężenie pola.
Prawo Gaussa stosujemy do obliczenia natężenia pola
elektrycznego – gdy znamy rozkład ładunku, do znajdowania
ładunku – gdy znamy pole.
Prawo Gaussa można stosować zawsze, ale sens ma wtedy, gdy
pole elektryczne wykazuje symetrię.
Aby skutecznie skorzystać z prawa Gaussa trzeba coś wiedzieć o
polu elektrycznym na wybranej powierzchni.
+
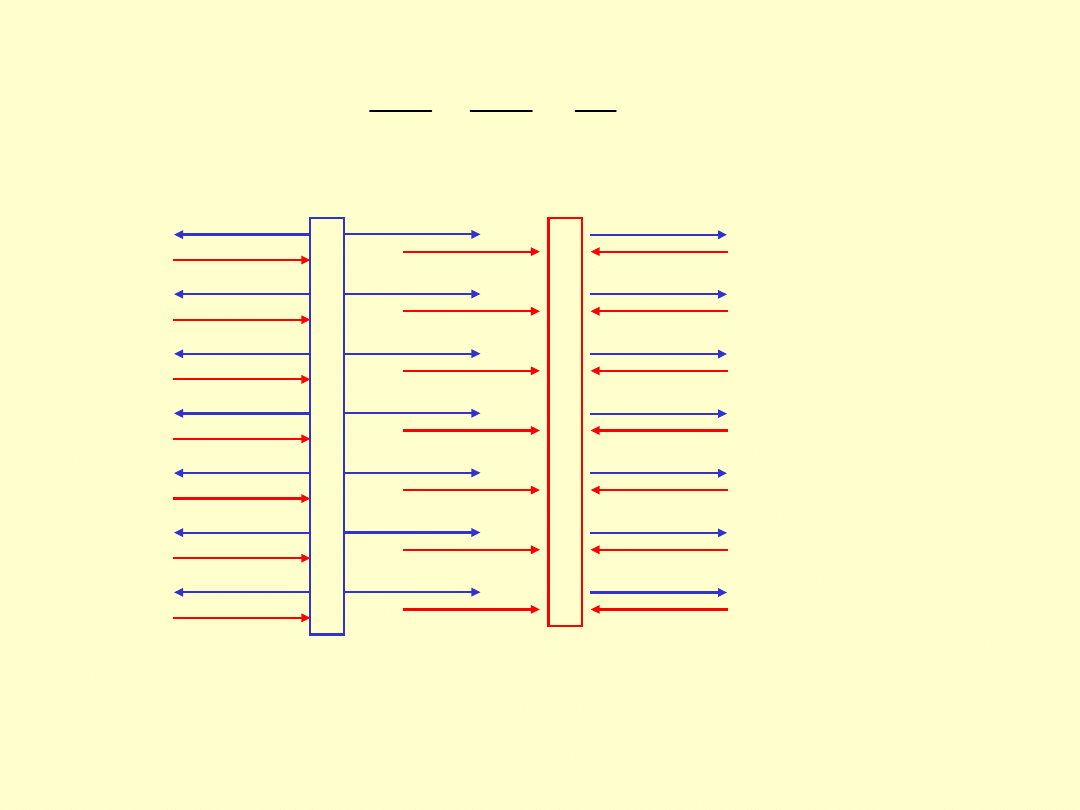
dS
dS
dS
0
0
2
2
E
dS
EdS
E
E
E
0
E
0
E
0
0
0
2
2
E