27 kwietnia 2021

J.Lisowski, PA_10_Ukł złożone

1

Regulacji

Regulacji

kaskadowej

kaskadowej

Zamknięto-otwarte

Zamknięto-otwarte

Wielowymiarowe

Wielowymiarowe

XI. ZŁOŻONE UKŁADY

XI. ZŁOŻONE UKŁADY

AUTOMATYKI

AUTOMATYKI

prof. Józef Lisowski

1

PODSTAWY AUTOMATYKI_XI_Złożone układy

automatyki

Układy regulacji

Układy regulacji

kaskadowej

kaskadowej

Regulacja kaskadowa

Regulacja kaskadowa

umożliwia poprawę jakości

regulacji poprzez:

- linearyzację nieliniowej charakterystyki statycznej
obiektu,

- kompensację dynamiki części obiektu regulacji,

- poprawienie kompensacji zakłóceń.
Warunkiem realizacji układu regulacji kaskadowej jest
zastosowanie dodatkowego przetwornika pomiarowego
wielkości pomocniczej obiektu regulacji.
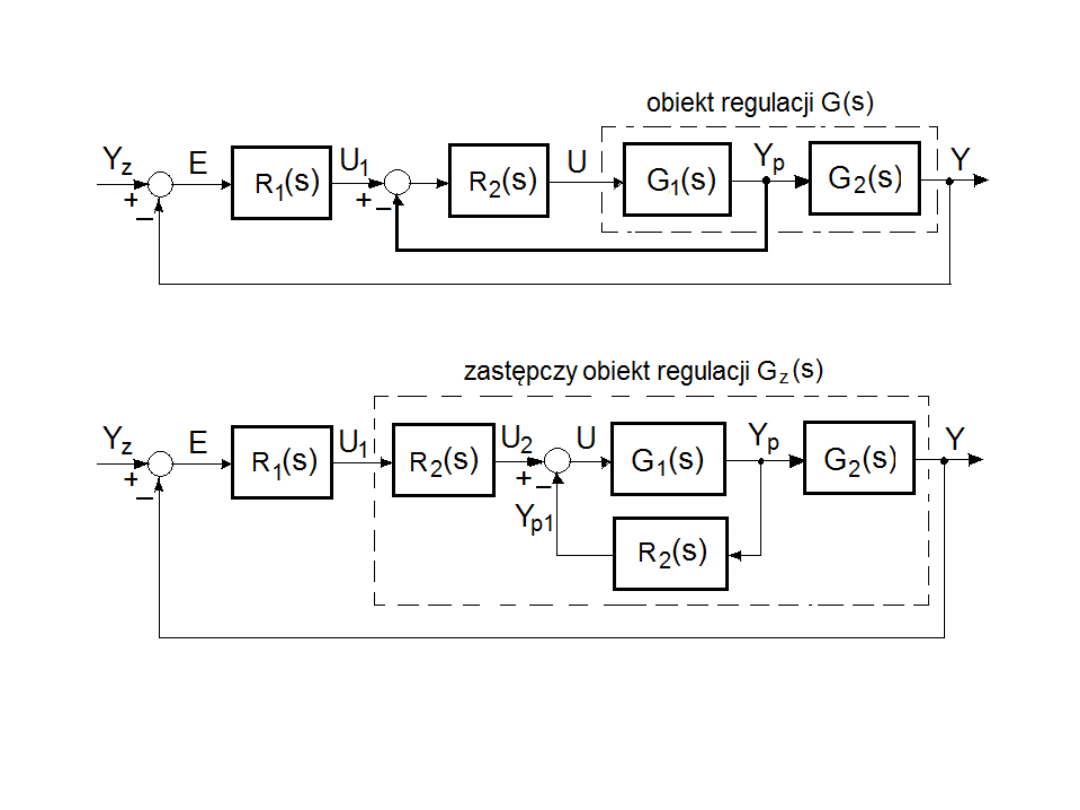
Układ kaskadowy realizuje się poprzez pomiar wielkości
pomocniczej Y

p

i rozdzielenie obiektu na dwie części –

szybką z nieliniową charakterystyką statyczną i
inercyjną oraz wprowadzenie dwóch regulatorów -
głównego R

1

i pomocniczego R

2

.

1

G

2

G

PODSTAWY AUTOMATYKI_XI_Złożone układy

automatyki

prof. Józef Lisowski

2

PODSTAWY AUTOMATYKI_XI_Złożone układy

automatyki

prof. Józef Lisowski

3

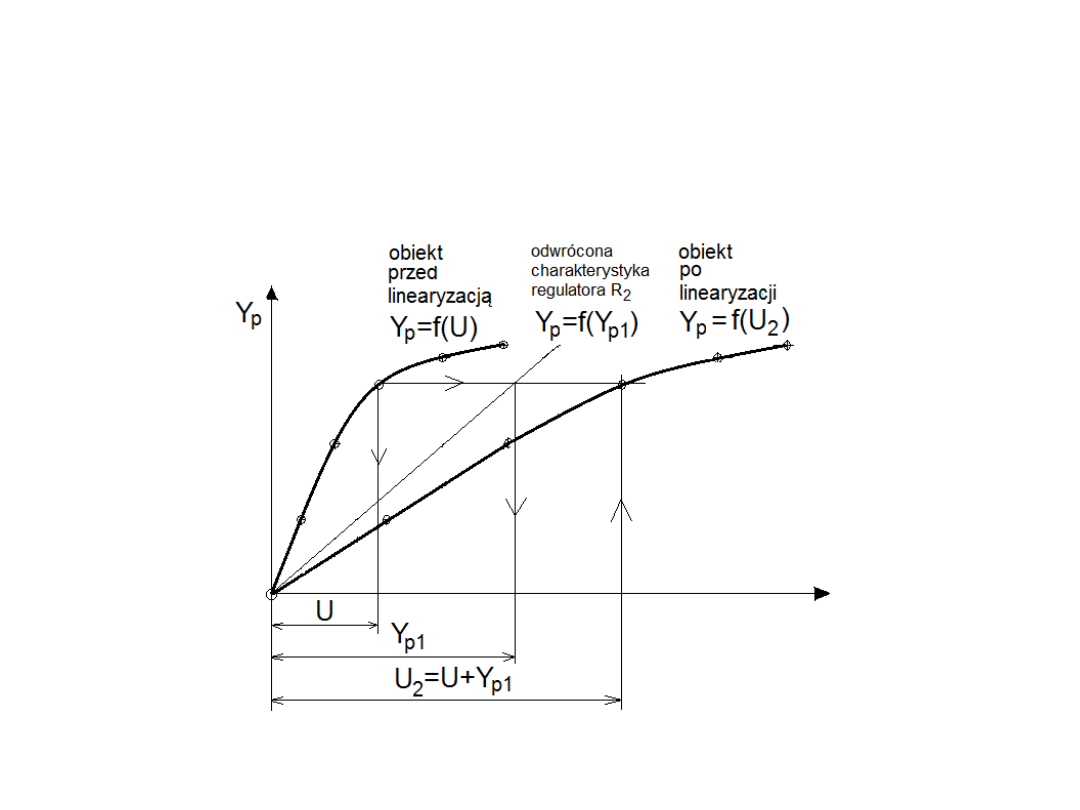
Jeśli część obiektu wykazuje nieliniową charakterystykę
statyczną, to dla regulatora R

2

typu P o współczynniku

wzmocnienia k

p

otrzymuje się charakterystykę wypadkową o

bardziej liniowym przebiegu.

Linearyzacja

Linearyzacja

nieliniowej charakterystyki statycznej

nieliniowej charakterystyki statycznej

obiektu

obiektu

1

G

PODSTAWY AUTOMATYKI_XI_Złożone układy

automatyki

prof. Józef Lisowski

4

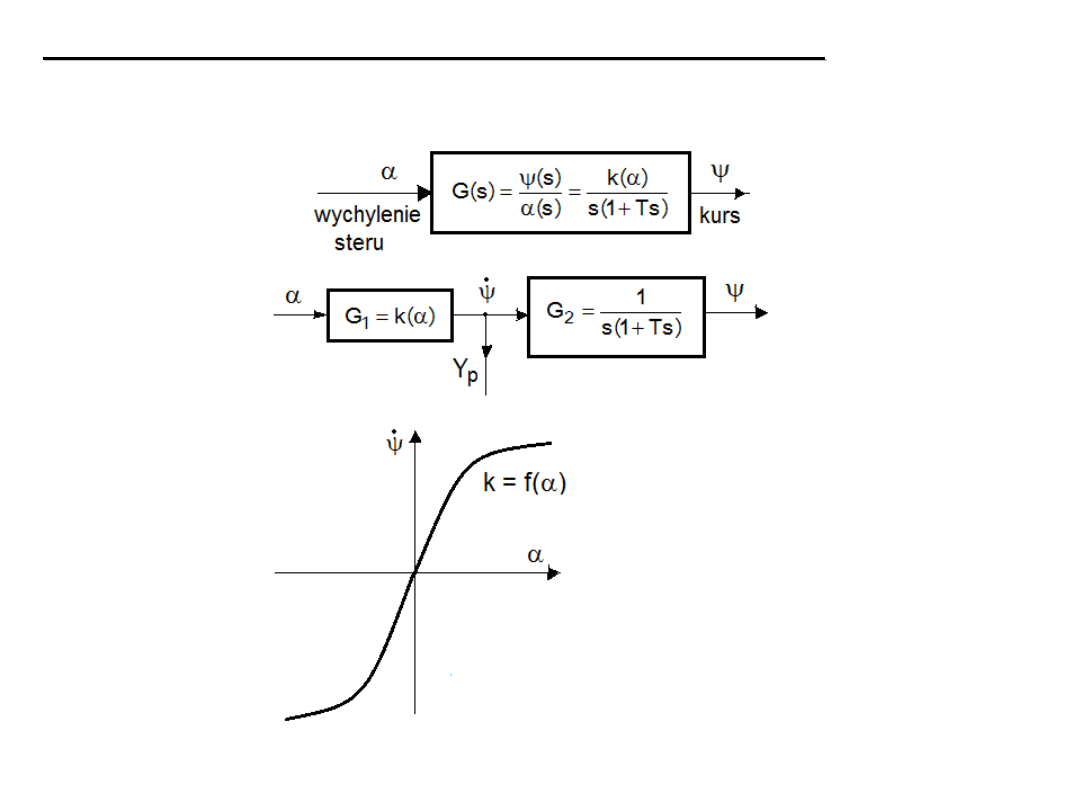
Przykład

Przykład

obiektu regulacji kaskadowej

obiektu regulacji kaskadowej - statek jako

obiekt regulacji kursu

PODSTAWY AUTOMATYKI_XI_Złożone układy

automatyki

prof. Józef Lisowski

5

Regulator R

1

współdziała z zastępczym obiektem o

transmitancji:

 

 

 

     

   

s

R

s

G

1

s

R

s

G

s

G

s

U

s

Y

s

G

2

1

2

1

2

1

z







Kompensacja dynamiki części obiektu

Kompensacja dynamiki części obiektu

regulacji

regulacji

 

 

 

 

   

 

s

G

1

s

R

s

G

1

1

s

G

s

U

s

Y

s

G

2

2

1

2

z









W paśmie częstotliwości, w którym iloczyn
przybiera duże wartości, zostaną skompensowane
własności dynamiczne części obiektu o transmitancji
G

1

(s):

   





j

R

j

G

2

1

PODSTAWY AUTOMATYKI_XI_Złożone układy

automatyki

prof. Józef Lisowski

6

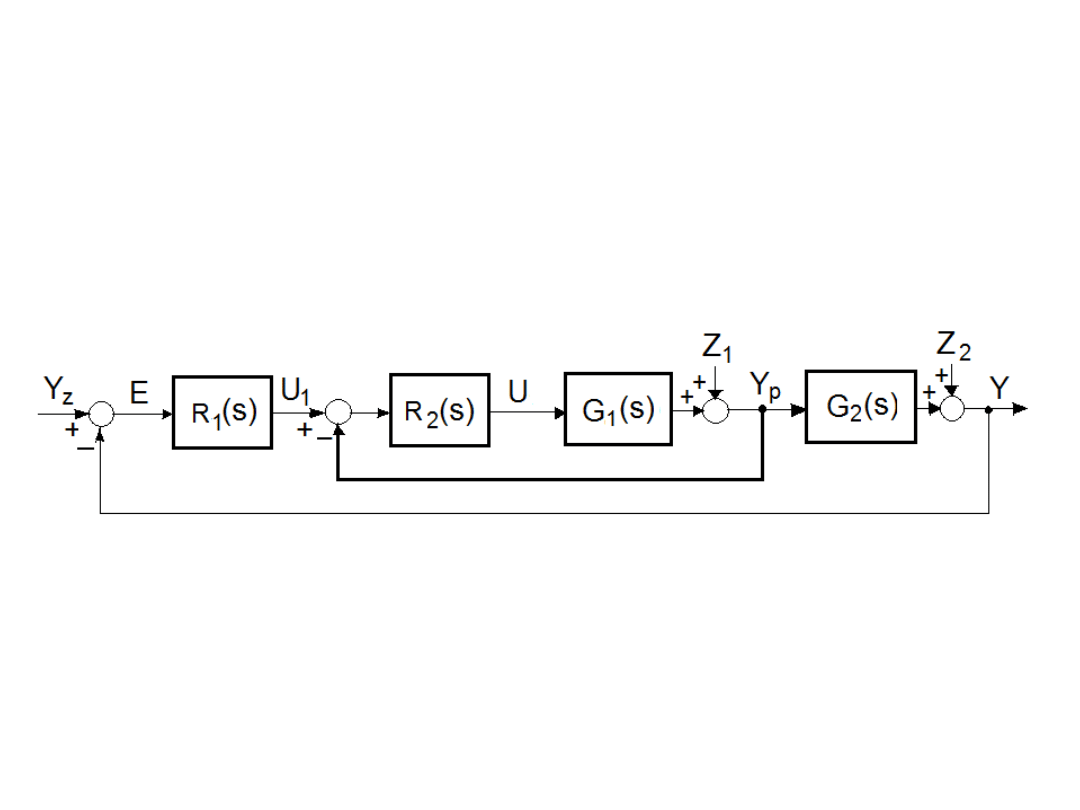
Zakłócenie Z

1

wpływa na wielkość pomocniczą Y

p

po

najkrótszej drodze, a Z

2

dopiero po przejściu całego

obiegu regulacyjnego.

Kompensacja

Kompensacja

zakłóceń

zakłóceń

PODSTAWY AUTOMATYKI_XI_Złożone układy

automatyki

prof. Józef Lisowski

7

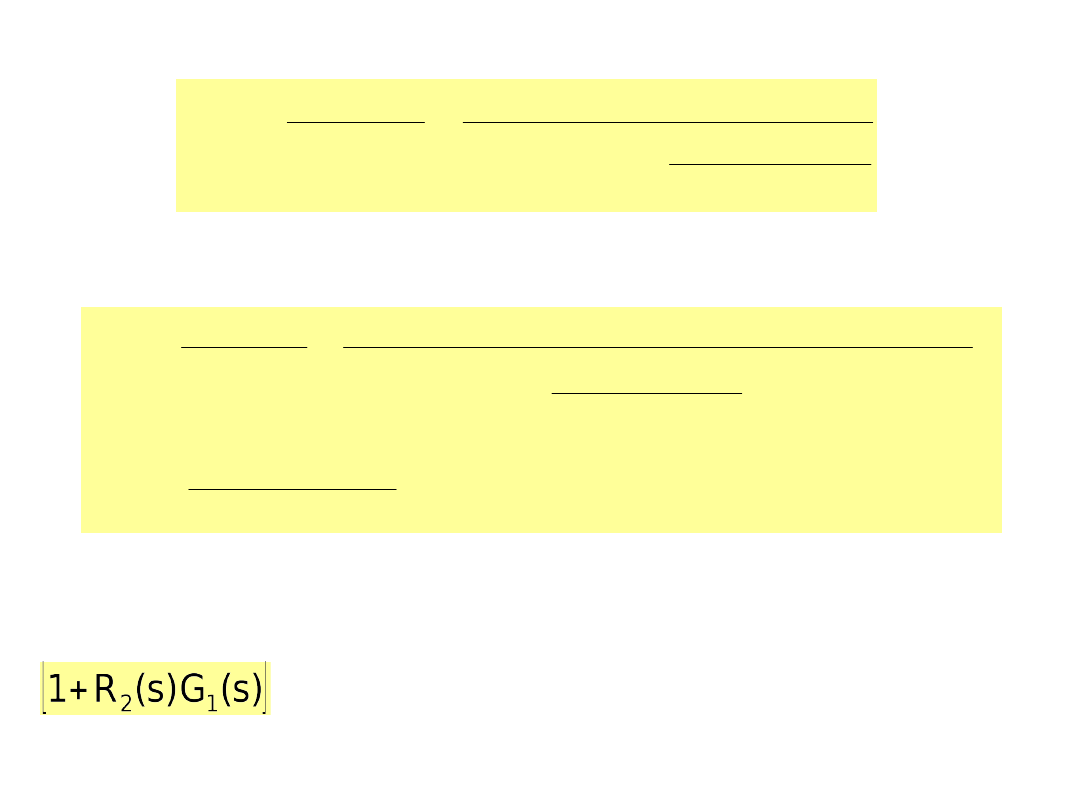
Wskaźnik regulacji w odniesieniu do zakłócenia Z

2

:

 

 

   

   

   

s

G

s

R

1

s

G

s

R

s

G

s

R

1

1

s

G

1

1

s

q

1

2

1

2

2

1

2

o

2











Wskaźnik regulacji w odniesieniu do zakłócenia Z

1

:

Zakłócenie Z

1

wpływające na obiekt przed miejscem

pomiaru wielkości pomocniczej Y

p

jest kompensowane

silniej, w stosunku

krotnym, niż zakłócenie Z

2

.

PODSTAWY AUTOMATYKI_XI_Złożone układy

automatyki

prof. Józef Lisowski

8

 

 

   

   

   

   





 

   

]

s

G

s

R

1

[

s

q

s

G

s

R

1

s

G

s

R

1

s

G

s

R

s

G

s

R

1

1

s

G

1

1

s

q

1

2

2

1

2

1

2

1

2

2

1

1

o

1































Efekt ten ma istotne znaczenie wówczas, gdy część
obiektu
zawiera opóźnienie i nie pozwala na
zbudowanie układu jednoobwodowego o dużej wartości
modułu transmitancji w szerokim paśmie częstotliwości.
Jeśli przy tym część obiektu opóźnienia nie
zawiera, to można zrealizować iloczyn o
dużych wartościach, a tym samym uzyskać dobrą
skuteczność regulacji w stosunku do zakłócenia Z

1

.

Warto zwrócić uwagę, że układ kaskadowy nie daje tak
dużych korzyści przy zakłóceniu Z

2

, albo przy nadążaniu

za Y

z

, oraz w tych przypadkach, gdy obiekt ma

opóźnienie w części .
Opóźnienie takie nie pozwoli bowiem na osiągnięcie
dużych wartości iloczynu .

 

s

G

2

s

T

o

e



 

s

G

1

   

s

G

s

R

1

2

   

s

G

s

R

1

2

 

s

G

1

PODSTAWY AUTOMATYKI_XI_Złożone układy

automatyki

prof. Józef Lisowski

9

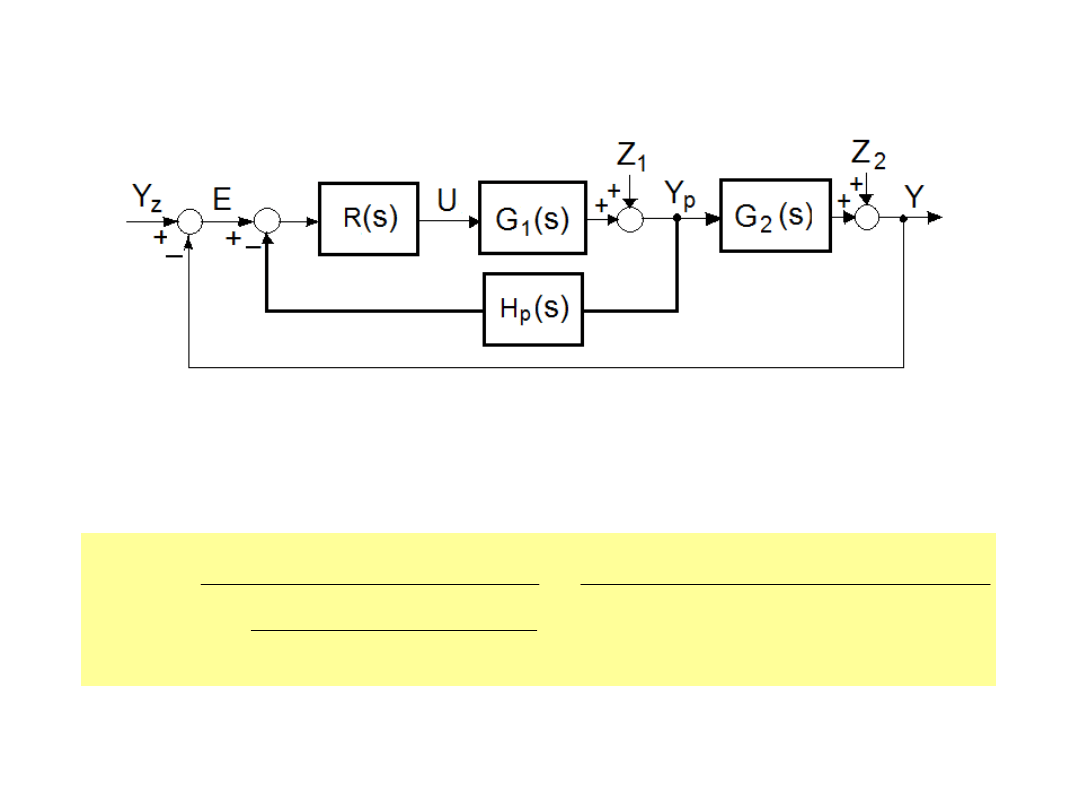
Układ kaskadowy z członem

Układ kaskadowy z członem

sprzężeniowym

sprzężeniowym

H

H

p

p

(s)

(s)

Wskaźnik regulacji w odniesieniu do zakłócenia Z

2

:

 

     

     

     

     

 

]

s

H

s

G

[

s

G

s

R

1

s

G

s

H

s

R

1

s

G

s

H

s

R

1

s

G

s

G

s

R

1

1

s

q

p

2

1

p

1

p

2

1

2















PODSTAWY AUTOMATYKI_XI_Złożone układy

automatyki

prof. Józef Lisowski

10

 

     

     

     

     

 

 

     

s

G

s

H

s

R

1

s

q

]

s

H

s

G

[

s

G

s

R

1

1

s

G

s

H

s

R

1

s

G

s

G

s

R

1

s

G

s

H

s

R

1

1

s

q

1

p

2

p

2

1

1

p

2

1

2

p

1

































Zastosowanie członu sprzężeniowego o transmitancji H

p

dodatkowo poprawia kompensację wpływu zakłóceń Z

1

.

Wskaźnik wyznaczony dla zakłóceń Z

2

jest identyczny ze

wskaźnikiem, charakteryzującym uchyb nadążania.
Najczęściej stosuje się człon sprzężeniowy H

p

(s)

różniczkujący rzeczywisty, odpowiadający w układzie

kaskadowym regulatorowi R(s) o działaniu PI

zapewniającym zerowy uchyb ustalony:

Wskaźnik regulacji w odniesieniu do zakłócenia Z

1

:

 

Ts

1

Ts

s

H

p





PODSTAWY AUTOMATYKI_XI_Złożone układy

automatyki

prof. Józef Lisowski

11

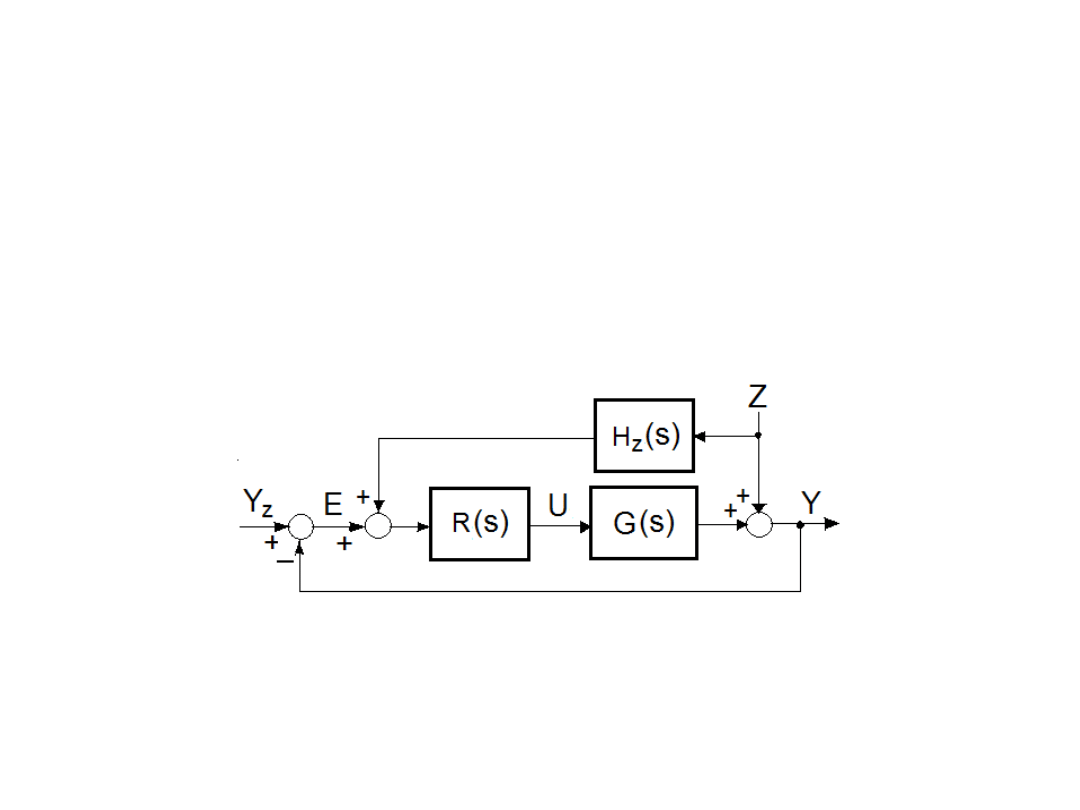
Układy zamknięto-otwarte

Układy zamknięto-otwarte

Wprowadzenie zakłócenia Z na wejście regulatora
poprzez człon sprzężeniowy H

z

(s) w układzie z ujemnym

sprzężeniem zwrotnym od wielkości regulowanej Y tworzy

zamknięto-otwarty układ regulacji.

zamknięto-otwarty układ regulacji.

PODSTAWY AUTOMATYKI_XI_Złożone układy

automatyki

prof. Józef Lisowski

12

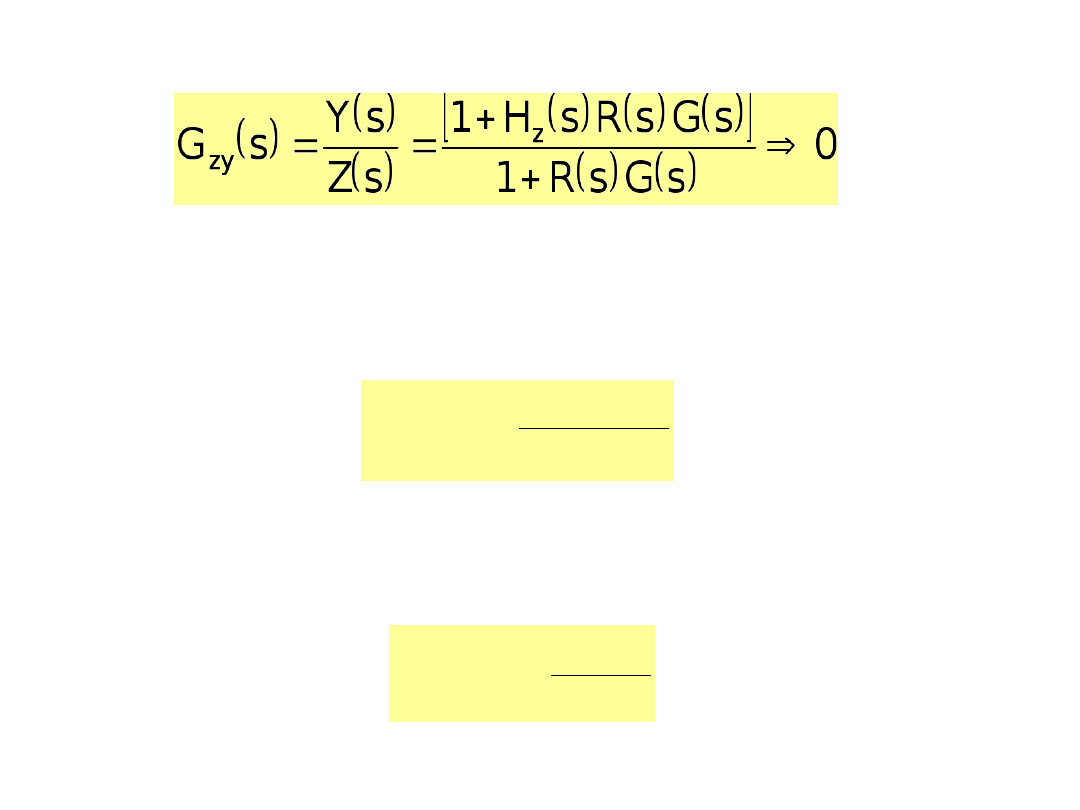
Aby skompensowaćwpływ zakłóceń Z na wielkość
regulowaną Y transmitancja członu sprzężeniowego H

z

(s)

powinna wynosić:

 

   

s

G

s

R

1

s

H

z





Wpływ zakłóceń opisuje transmitancja zakłóceniowa:

Na przykład dla regulatora PI i obiektu inercyjnego
pierwszego rzędu człon sprzężeniowy ma transmitancję:

 

Ts

1

Ts

s

H

z







 

s

G

PODSTAWY AUTOMATYKI_XI_Złożone układy

automatyki

prof. Józef Lisowski

13

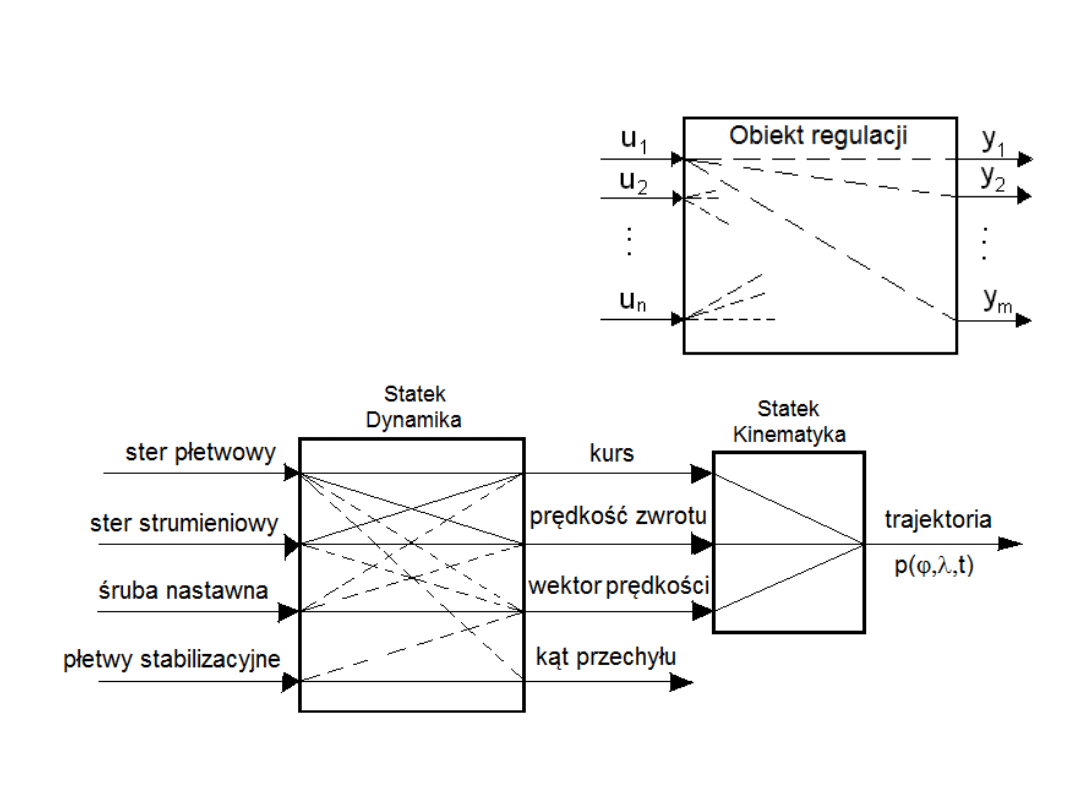
Wielowymiarowe układy

Wielowymiarowe układy

regulacji

regulacji

Wielowymiarowy obiekt

regulacji ma wiele wielkości

sterujących u(t) i

regulowanych y(t).

Istnieją w nim sprzężenia

skrośne - jedna wielkość

sterująca wpływa więcej niż

na jedną wielkość regulowaną.

PODSTAWY AUTOMATYKI_XI_Złożone układy

automatyki

prof. Józef Lisowski

14

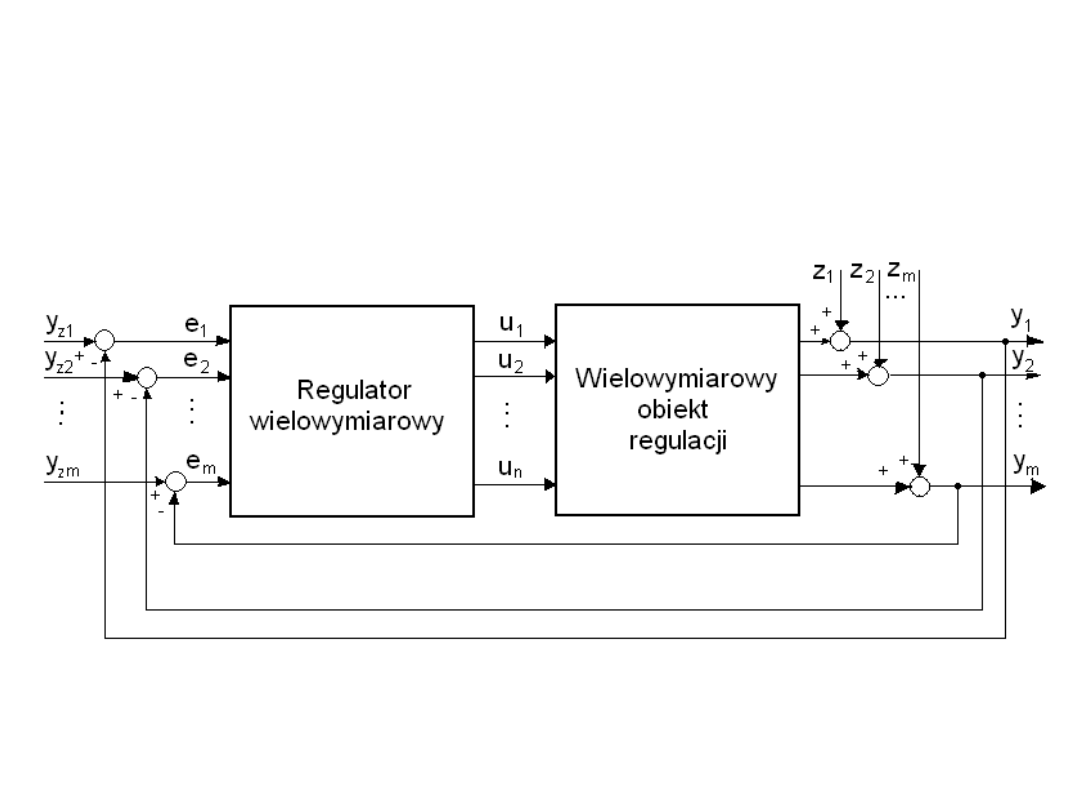
Wówczas do realizacji procesu regulacji automatycznej
należy zastosować również regulator wielowymiarowy.
Taki układ nazywa się wielowymiarowym układem

wielowymiarowym układem

regulacji

regulacji

.

PODSTAWY AUTOMATYKI_XI_Złożone układy

automatyki

prof. Józef Lisowski

15

Dla obiektu liniowego, dla którego obowiązuje zasada

superpozycji, związki między poszczególnymi wyjściami i

wejściami można wyrazić odpowiednimi

transmitancjami:

Wielowymiarowy obiekt regulacji

Wielowymiarowy obiekt regulacji

 

   

   

   

 

   

   

   

 

   

   

   





































s

U

s

G

...

s

U

s

G

s

U

s

G

s

Y

....

..........

..........

..........

..........

..........

..........

..........

..........

s

U

s

G

...

s

U

s

G

s

U

s

G

s

Y

s

U

s

G

...

s

U

s

G

s

U

s

G

s

Y

m

mn

2

2

m

1

1

m

m

n

n

2

2

22

1

21

2

n

n

1

2

12

1

11

1

Przechodząc do zapisu związków w postaci macierzowo-

wektorowej otrzymuje się:

 

 

 

 

 

 

 

 

 

 

 

 

 

 











































































s

U

.........

s

U

s

U

s

G

.

..........

s

G

)

s

(

G

.

..........

.

..........

.

..........

.

..........

s

G

.

..........

s

G

s

G

s

G

.

..........

s

G

s

G

s

Y

..........

s

Y

s

Y

n

2

1

mn

2

m

1

m

n

2

22

21

n

1

12

11

m

2

1

PODSTAWY AUTOMATYKI_XI_Złożone układy

automatyki

prof. Józef Lisowski

16

W

zwartej

postaci

macierzowo-

wektorowej:

Y(s) = G(s) U(s)

Macierz transmitancji

Macierz transmitancji

G

G

(s)

(s)

ma m wierszy i n kolumn.

Jeżeli liczba wejść obiektu wielowymiarowego jest równa
liczbie jego wyjść, czyli n = m, to elementy znajdujące
się na głównej przekątnej macierzy G(s) określają
związki poszczególnych wyjść z wejściami o tych samych
wskaźnikach.

Elementy leżące poza główną przekątną o różnych
wskaźnikach n i m odpowiadają sprzężeniom skrośnym
występującym w obiekcie.

PODSTAWY AUTOMATYKI_XI_Złożone układy

automatyki

prof. Józef Lisowski

17

 

 





 

 

 

 

 

 

 

 

 





























s

R

..........

s

R

s

R

..........

..........

..........

..........

s

R

..........

s

R

s

R

s

R

..........

s

R

s

R

s

R

s

R

nm

2

n

1

n

m

2

22

21

m

1

12

11

ij

Macierz transmitancji otwartego układu regulacji:
G

o

(s) = G(s) R(s)

jest macierzą kwadratową o m kolumnach i n wierszach.
Y(s) = G

o

(s) E(s) = G

o

(s) [Y

z

(s) – Y(s)]

Stąd otrzymuje się podstawowe równanie macierzowe
opisujące wielowymiarowy zamknięty układ regulacji:

Regulator wielowymiarowy

Regulator wielowymiarowy

[I(s) + G

o

(s)] Y(s) = G

o

(s) Y

z

(s)

PODSTAWY AUTOMATYKI_XI_Złożone układy

automatyki

prof. Józef Lisowski

18

Odsprzężenie układu

Odsprzężenie układu

polega na tym, aby każda z

wielkości regulowanych y(t) była zależna tylko od jednej
wartości zadanej y

z

, natomiast pozostałe wartości

zadane nie miały wpływu na daną wielkość regulowaną,
ani w stanach przejściowych, ani w stanie ustalonym.
Warunek odsprzężenia sprowadza się do tego, aby
macierz otwartego układu regulacji G

o

(s) była macierzą

diagonalną:

Odsprzężenie układu regulacji

Odsprzężenie układu regulacji

 

   

   

   

   

















































m

1

k

km

mk

m

1

k

2

k

k

2

m

1

k

1

k

k

1

o

s

R

s

G

..

..........

0

0

0

..

..........

0

0

0

..

..........

s

R

s

G

0

0

..

..........

0

s

R

s

G

s

R

s

G

s

G

PODSTAWY AUTOMATYKI_XI_Złożone układy

automatyki

prof. Józef Lisowski

19

Spośród m

2

elementów macierzy G

o

(s) tylko m

diagonalnych elementów ma być różnych od zera,
co prowadzi do następujących równoczesnych
warunków pełnego odsprzężenia układu regulacji:

 

 

 













m

1

k

kj

ik

oij

m

,...,

2

,

1

j

,i

,j

i

,

0

s

R

s

G

s

G

PODSTAWY AUTOMATYKI_XI_Złożone układy

automatyki

prof. Józef Lisowski

20

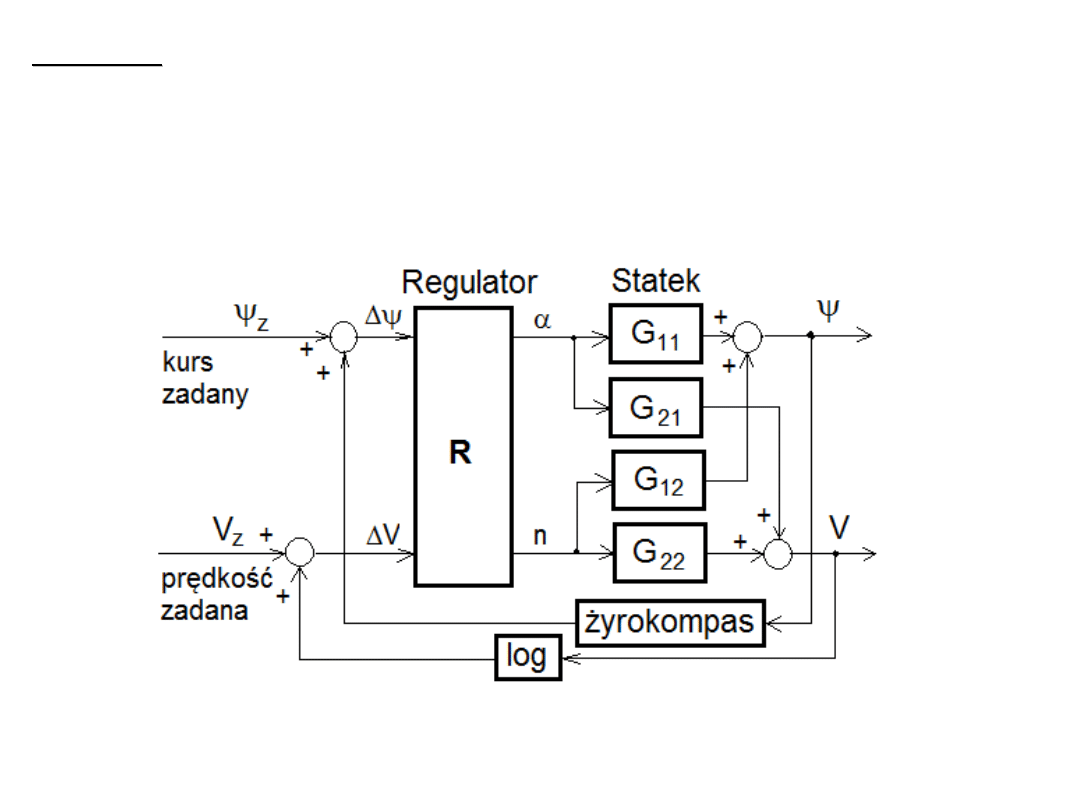
Przykład

Przykład
Zaprojektować dwuwymiarowy regulator R(s) kursu  i prędkości V statku

badawczo-szkoleniowego m/s HORYZONT II z odsprzężeniem układu
regulacji.

PODSTAWY AUTOMATYKI_XI_Złożone układy

automatyki

prof. Józef Lisowski

21

 

 

 

 

 



















































s

20

1

10

s

20

1

1

s

10

1

01

,

0

s

10

1

1

,

0

s

G

s

G

s

G

s

G

s

G

22

21

12

11

Transmitancja macierzowa statku jako obiektu regulacji

kursu i prędkości:

Warunki odsprzężenia układu dla wszystkich (i,j) ij:

 

 

 

 

 

 

 

 

 

   

 

 

































2

1

k

21

22

11

21

1

k

k

2

21

o

2

1

k

22

12

12

11

2

k

k

1

12

o

0

s

R

s

G

s

R

s

G

s

R

s

G

)

s

(

G

1

j

,

2

i

dla

0

s

R

s

G

s

R

s

G

s

R

s

G

s

G

2

j

,

1

i

dla

PODSTAWY AUTOMATYKI_XI_Złożone układy

automatyki

prof. Józef Lisowski

22

Przyjmując dowolne R

11

(s) oraz R

22

(s) otrzymuje się

transmitancję macierzową regulatora R(s)
zapewniającego odsprzężenie:

 

 

 

 

 

















s

R

s

R

1

,

0

s

R

1

,

0

s

R

s

R

22

11

22

11

Rozwiązując te równania względem R

12

(s) i R

21

(s)

otrzymuje się transmitancje członów odsprzęgających w
funkcji transmitancji statku i właściwych regulatorów
R

11

(s) i R

22

(s):

 

 

 

 

 

 

 

   

 

s

R

1

,

0

s

R

s

G

s

G

s

R

s

R

1

,

0

s

R

s

G

s

G

s

R

11

11

22

21

21

22

22

11

12

12















PODSTAWY AUTOMATYKI_XI_Złożone układy

automatyki

prof. Józef Lisowski

23

Transmitancja macierzowa odsprzęgniętego układu
otwartego G

o

(s) wyniesie wówczas:

 

   

 

 

































s

R

s

20

1

1

,

10

0

0

s

R

s

10

1

101

,

0

s

R

s

G

s

G

22

11

o

PODSTAWY AUTOMATYKI_XI_Złożone układy

automatyki

prof. Józef Lisowski

24

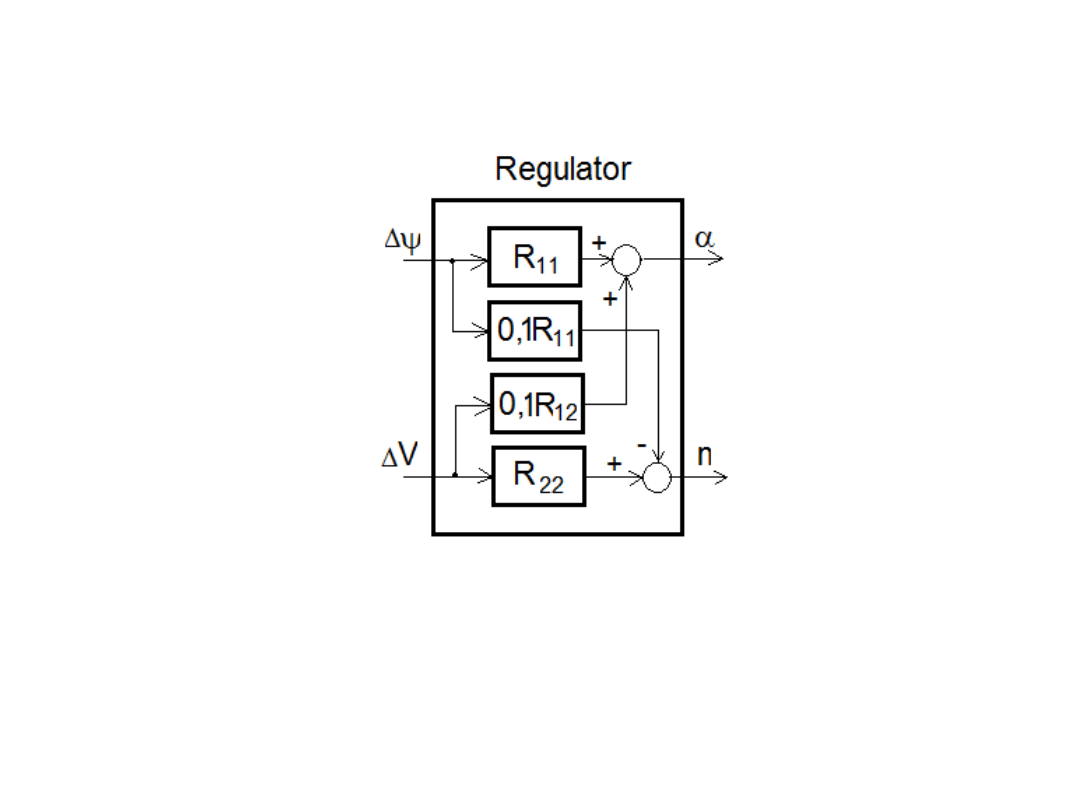
Przyjmując za regulator R

11

(s) regulator typu PID, zaś za

regulator R

22

(s) regulator typu PI, odsprzęgnięty

dwuwymiarowy regulator kursu i prędkości statku będzie
miał pięć nastaw.

Poszukiwana struktura dwuwymiarowego regulatora
kursu i prędkości statku przyjmie postać:

PODSTAWY AUTOMATYKI_XI_Złożone układy

automatyki

prof. Józef Lisowski

25