
Statystyka - zadania
Dr Janusz Górczyński

2
Zadanie 1
Na tarczę koła zawierająca 50 wycinków
ponumerowanych od 0 do 49 rzucamy monetę.
Jeżeli moneta upadnie na wycinek o nr 0, to
zmienna X przyjmie wartość 2, jeżeli padnie na
numer nieparzysty, to x=-1, a na parzysty x=1.
Proszę zbudować f.r.p tak zdefiniowanej
zmiennej losowej X.
Rozwiązanie: zbiór ma 50 elementów. Z def.
Laplace’a mamy kolejne p-stwa:
50
1
)
2
(
X
P
50
25
)
1
(
X
P
50
24
)
1
(
X
P
3
Zadanie 1 c.d
Wyznaczoną f.r.p można zapisać w formie
tabelki:
i
x
i
p
50
25
1
1
50
24
2
50
1

4
Zadanie 2
Dla jakiej wartości parametru C funkcja:
)
3
,
0
(
0
)
3
,
0
(
)
3
(
)
(
x
dla
x
dla
x
Cx
x
f
będzie f.g.p pewnej zmiennej losowej X ?

5
Zadanie 2 – rozwiązanie
(1)
Funkcja f(x) będzie f.g.p wtedy i tylko wtedy,
jeżeli jej wartości będą nieujemne w zbiorze R
oraz pole pod jej wykresem będzie równe 1.
Wykresem f(x) w przedziale (0, 3) jest
parabola, aby jej wykres był położony NAD
osią x-ów, to parametr C MUSI być ujemny!
Poza przedziałem (0, 3) funkcja f(x) jest
ZEROWA, tym samym jest nieujemna.

6
Zadanie 2 – rozwiązanie
(2)
Pozostaje sprawdzenie warunku o polu
równym 1. Warunek ten można zapisać w
postaci całki oznaczonej:
1
)
( dx
x
f
Całkę tę można zapisać jako SUMĘ trzech
całek:
0
3
3
0
0
)
3
(
0
)
(
dx
dx
x
Cx
dx
dx
x
f

7
Zadanie 2 – rozwiązanie
(3)
Całka oznaczona z funkcji zerowej jest równa 0,
stąd:
3
0
)
3
(
)
(
dx
x
Cx
dx
x
f
Funkcja podcałkowa jest elementarna, mamy
więc:
C
C
C
x
x
C
dx
x
Cx
2
9
2
3
2
3
3
27
3
0
2
2
3
3
3
1
3
0
1
9
9
)
3
(

8
Zadanie 2 – rozwiązanie
(4)
Tym samym pole pod wykresem f(x) będzie równe 1
wtedy, gdy
9
2
2
9
1
C
C
Ostatecznie funkcja
)
3
,
0
(
0
)
3
,
0
(
)
3
(
)
(
9
2
x
dla
x
dla
x
x
x
f
jest f.g.p pewnej zmiennej losowej X.

9
Zadanie 3
Funkcja rozkładu p-stwa pewnej zmiennej
losowej X dana jest tabelką:
x
i
-3
-2
-1
0
1
3
p
i
0,1
0,1
0,2
0,3
0,1
0,2
Proszę wyznaczyć funkcję dystrybuanty tej
zmiennej.

10
Zadanie 3 – rozwiązanie
(1)
Korzystamy z definicji dystrybuanty
wyznaczając ją dla argumentów z
poszczególnych przedziałów wyznaczonych
przez zbiór wartości naszej zmiennej.
Dla x z przedziału otwartego (-, -3) mamy:
0
)
(
x
X
P
Dla x z przedziału <-3, -2) mamy:
1
,
0
)
3
(
)
(
X
P
x
X
P

11
Zadanie 3 – rozwiązanie
(2)
Analogicznie postępujemy w kolejnych
przedziałach, a wynik ostateczny możemy
zapisać tak:
)
,
3
1
)
3
,
1
8
,
0
)
1
,
0
7
,
0
)
0
,
1
4
,
0
)
1
,
2
2
,
0
)
2
,
3
1
,
0
)
3
,
(
0
)
(
x
dla
x
dla
x
dla
x
dla
x
dla
x
dla
x
dla
x
F
12
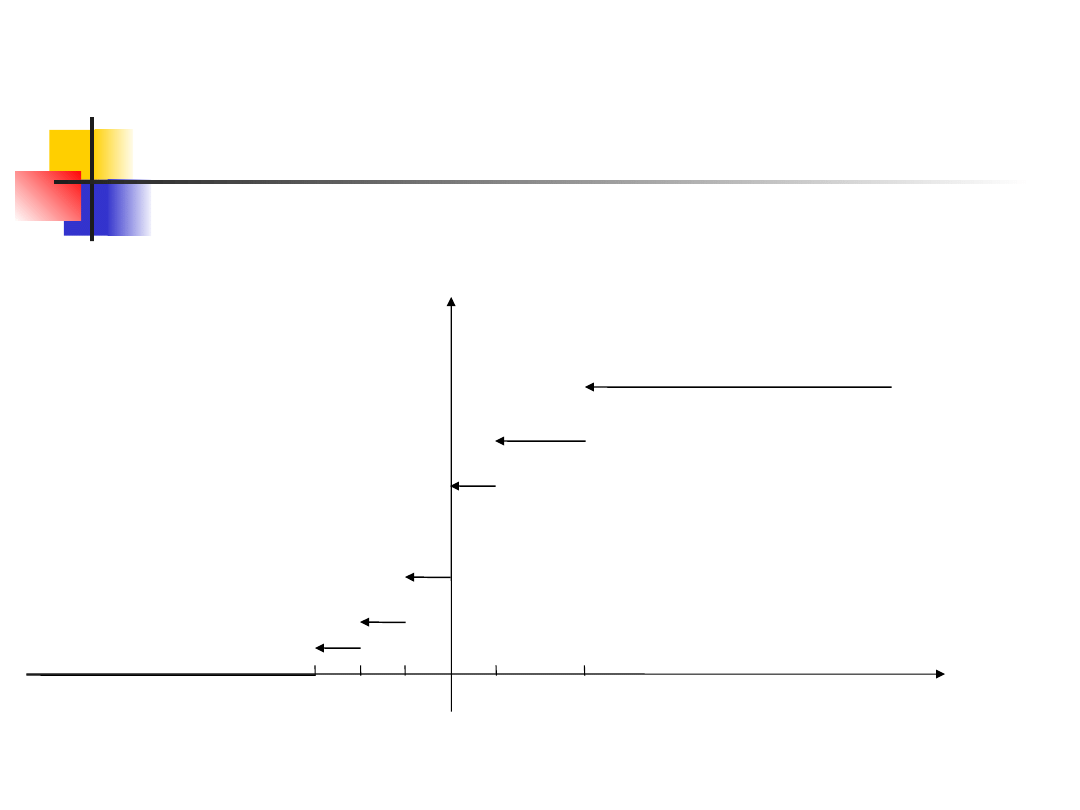
Zadanie 3 – rozwiązanie
(3)
Dystrybuantę można także przedstawić
graficznie:
1
2
3
1
3
)
(x
F
0
,
1
8
,
0
7
,
0
4
,
0
2
,
0
x
1
,
0

13
Zadanie 3 - obliczanie F(x)
Jak można wykorzystać wyznaczoną funkcję
dystrybuanty zmiennej losowej X?
Po prostu do szybkiego odczytywania
(obliczania) wartości dystrybuanty tej
zmiennej w pewnym, interesującym nas
punkcie.
Korzystając z wyznaczonej funkcji dystrybuanty
podanej w postaci wzoru jak i wykresu
wyznaczymy wartość dystrybuanty w punkcie
x
0
=-1,3
14
Zadanie 3 - obliczanie F(x
0
=-1,3)
cd
)
,
3
1
)
3
,
1
8
,
0
)
1
,
0
7
,
0
)
0
,
1
4
,
0
)
1
,
2
2
,
0
)
2
,
3
1
,
0
)
3
,
(
0
)
(
x
dla
x
dla
x
dla
x
dla
x
dla
x
dla
x
dla
x
F
X
0
=-
1,3
Szukamy przedziału, który zawiera punkt x
0
,
u nas jest to trzeci przedział x-ów:
stąd
F(-
1,3)=0,2
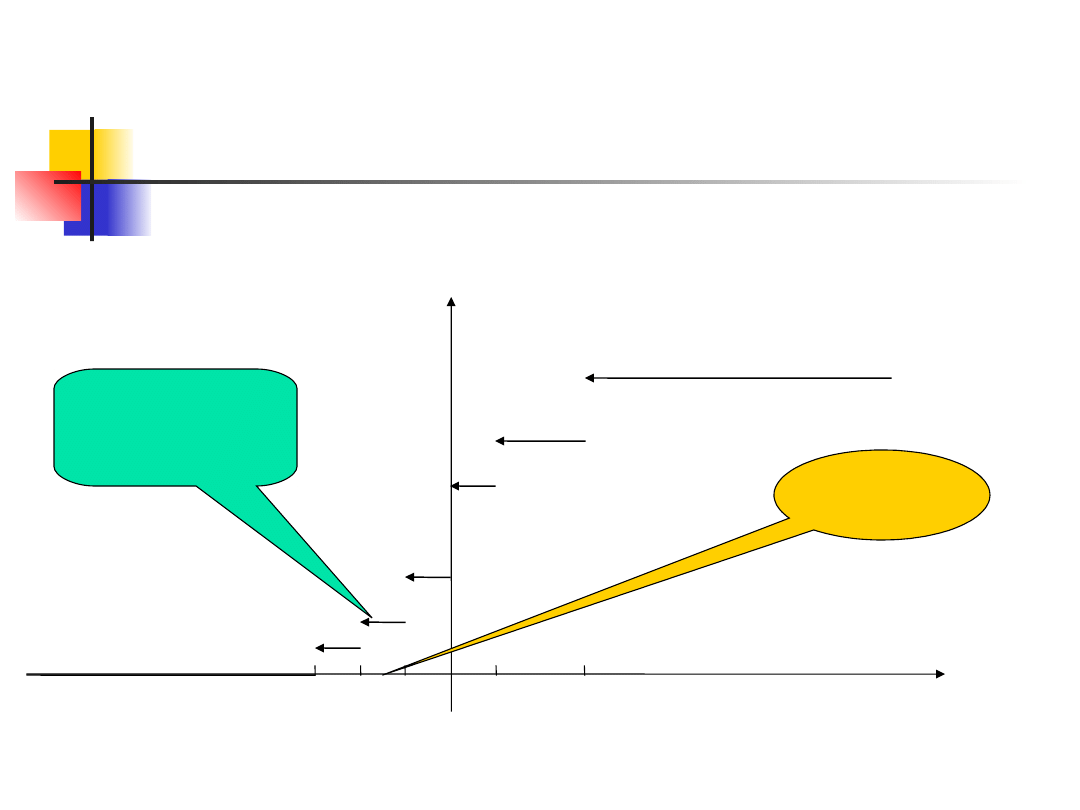
15
Zadanie 3 - obliczanie F(x
0
=-1,3)
cd
1
2
3
1
3
)
(x
F
0
,
1
8
,
0
7
,
0
4
,
0
2
,
0
x
1
,
0
Szukamy przedziału, który zawiera punkt x
0
=-1,3,
u nas jest to przedział:
X
0
=-
1,3
stąd
F(-
1,3)=0,2

16
Zadanie 4
Wyznaczmy funkcję dystrybuanty dla zmiennej
losowej X, której f.g.p dana jest wzorem:
)
3
,
0
(
0
)
3
,
0
(
)
3
(
)
(
9
2
x
dla
x
dla
x
x
x
f

17
Zadanie 4 - rozwiązanie
Zgodnie z definicją dystrybuanty obliczamy
całkę
0
)
(
)
(
0
x
dx
x
f
x
F
Rozpatrując punkt x
0
w trzech różnych
dziedzinach:
)
0
,
(
0
x
)
3
,
0
(
0
x
)
,
3
(
0
x

18
Zadanie 4 – rozwiązanie cd.
Dla przedziału (-, 0) mamy:
0
0
)
(
)
(
x
x
dx
dx
x
f
x
F
Dla przedziału (0, 3) mamy:
2
3
3
1
2
9
2
0
0
2
2
3
3
3
1
9
2
2
9
2
0
9
2
0
)
3
(
)
3
(
0
)
(
)
(
x
x
x
x
dx
x
x
dx
x
x
dx
dx
x
f
x
F
x
x
x
x

19
Zadanie 4 – rozwiązanie cd.
Dla przedziału (3, +) mamy:
1
)
3
(
0
)
3
(
0
)
(
)
(
3
0
9
2
3
3
0
9
2
0
dx
x
x
dx
dx
x
x
dx
dx
x
f
x
F
x
x

20
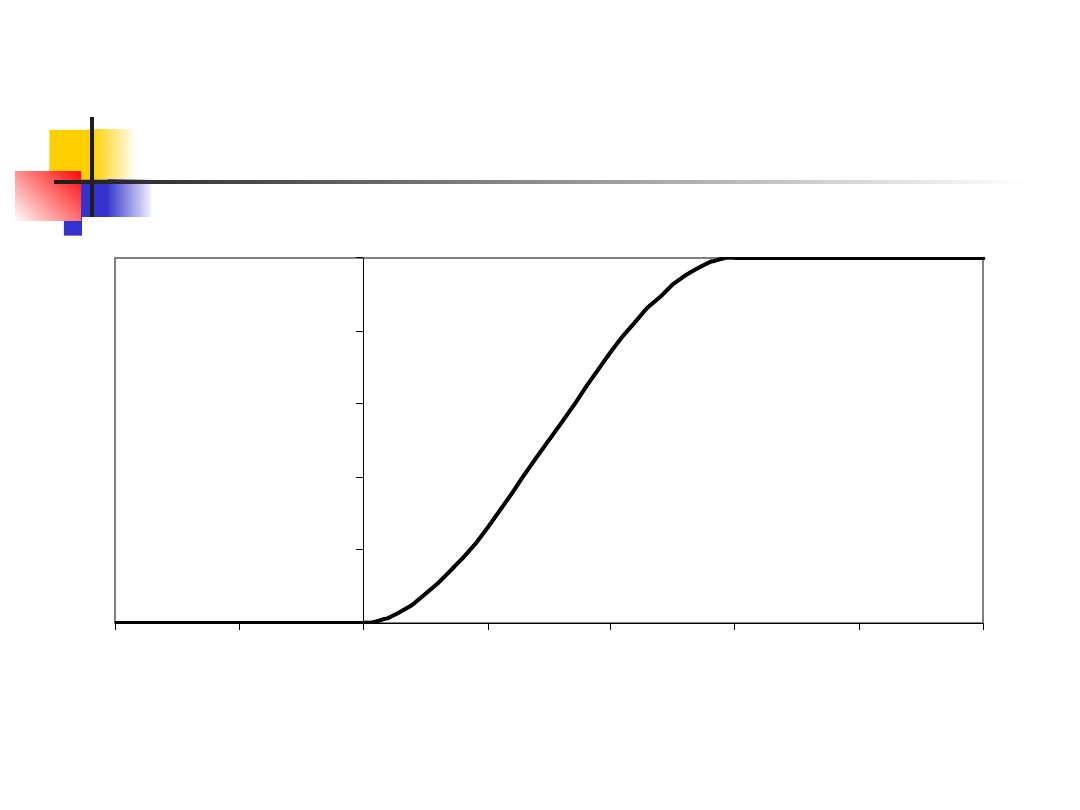
Zadanie 4 – rozwiązanie cd.
Ostatecznie funkcja dystrybuanty tej
zmiennej ma postać:
)
,
3
(
1
)
3
,
0
(
)
0
,
(
0
)
(
2
3
3
1
2
9
2
x
dla
x
dla
x
x
x
dla
x
F
A jej wykres będzie na kolejnym slajdzie.
21
Zadanie 4
–
wykres
dystrybuanty
0,0
0,2
0,4
0,6
0,8
1,0
-2
-1
0
1
2
3
4
5

22
Zadanie 4 – obliczanie F(2) z funkcji
Korzystając z wyznaczonej funkcji
dystrybuanty i z faktu, że x
0
=2 należy do
przedziału (0, 3) mamy:
74
,
0
2
2
)
2
(
54
40
6
5
9
8
6
9
4
9
8
2
3
3
2
9
8
2
3
3
1
2
9
2
F
Interpretacja: p-stwo tego, że tak
zdefiniowana zmienna przyjmie wartości nie
większe niż 2 jest równe (w przybliżeniu)
0,74.
23
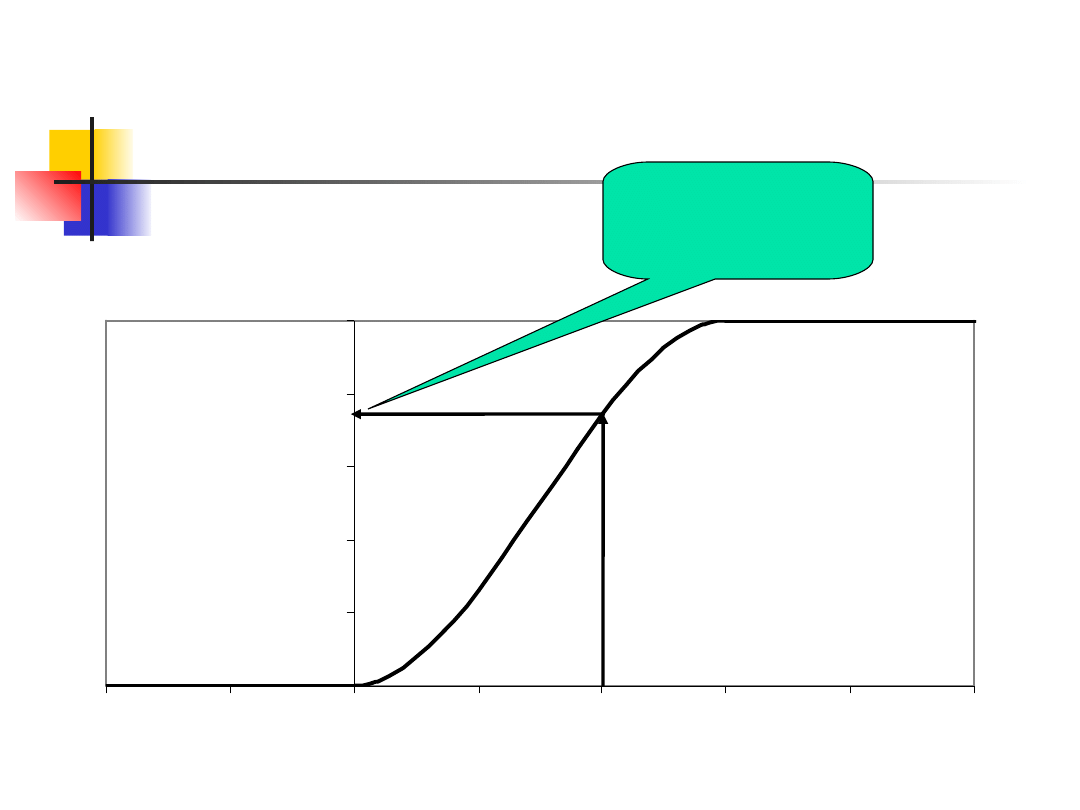
Zadanie 4 – obliczanie F(2) z
wykresu
0,0
0,2
0,4
0,6
0,8
1,0
-2
-1
0
1
2
3
4
5
Stąd
F(2)=0,74
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
Wyszukiwarka
Podobne podstrony:
download Statystyka StatystykaZadania4[1]
download Statystyka StatystykaZadania2[1]
download Statystyka StatystykaZadania4[1]
download Statystyka Stat4
download Statystyka regresja
więcej podobnych podstron