1

Statystyka – zadania 4

Janusz Górczyński

2

Zadanie 1

Rozkład prawdopodobieństw ocen
egzaminacyjnych ze statystyki w grupie
studentów studiów dziennych i zaocznych można
przedstawić w postaci takiej tabelki:

2

3

3,5

4

4,5

5

Dzienne

0,06

0,12

0,15

0,09

0,05

0,03

Zaoczne

0,11

0,14

0,12

0,07

0,03

0,03

Przyjmując umownie, że rodzaj studiów jest
zmienną losową X o wartościach odpowiednio 1
(dzienne) i 2 (zaoczne), a oceny reprezentują
zmienną losową Y otrzymujemy f.r.p
dwuwymiarowej zmiennej losowej.

3

Zadanie 1 - cd

X\Y

2

3

3,5

4

4,5

5

pi.

x=1

0,06

0,12 0,15 0,09 0,05

0,03

0,50

x=2

0,11

0,14 0,12 0,07 0,03

0,03

0,50

p.j

0,17

0,26 0,27 0,16 0,08

0,06

1

Funkcję rozkładu p-stwa tak zdefiniowanej
dwuwymiarowej zmiennej losowej XY (gdzie
wartości zmiennej Y są „naturalne”, a zmiennej
X „sztuczne”) można przedstawić w poniższej
tabelce.

W tabelce tej podano także rozkłady brzegowe
obu zmiennych losowych.

4

Zadanie 1 – co chcemy
wiedzieć?

Interesują nas odpowiedzi na następujące
pytania:

Czy rozkład ocen w obu grupach studenckich
jest taki sam?

Jeżeli nie, to jaka jest przeciętna ocena w
obu grupach studenckich?

Jaki jest rozkład ocen dla ogółu studentów?

Jakie są charakterystyki tego rozkładu
(średnia, wariancja, odchylenie
standardowe, dominanta itd).

5

Zadanie 1 – rozkład dla ogółu
studentów

X\Y

2

3

3,5

4

4,5

5

pi.

x=1

0,06

0,12 0,15 0,09 0,05

0,03

0,50

x=2

0,11

0,14 0,12 0,07 0,03

0,03

0,50

p.j

0,17

0,26 0,27 0,16 0,08

0,06

1

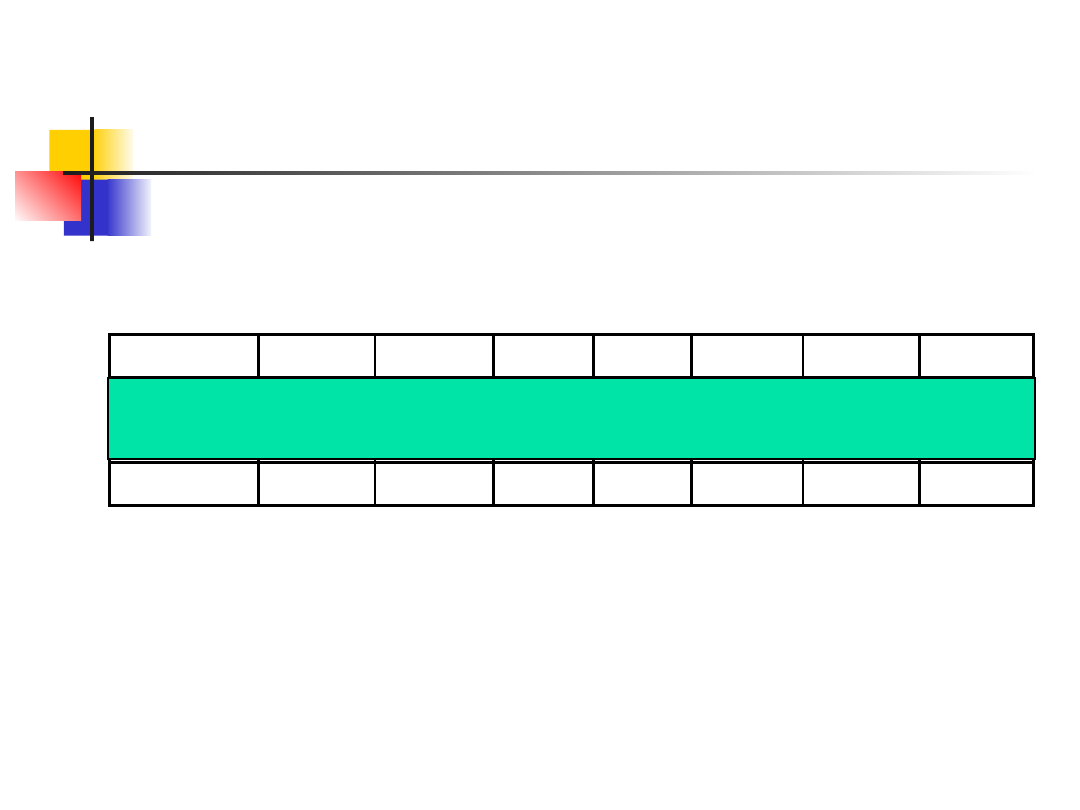
Interesuje nas rozkład zmiennej Y niezależnie
od tego, jakie wartości przyjmuje zmienna X.

Zielony prostokąt „przykrył” niepotrzebne w tym
momencie p-stwa pozostawiając tylko p-stwa
brzegowe zmiennej Y. Korzystając ze znanych
wzorów wyznaczamy potrzebne charakterystyki.

6

Zadanie 1 – rozkład dla ogółu
studentów

X\Y

2

3

3,5

4

4,5

5

pi.

x=1

0,06

0,12 0,15 0,09 0,05

0,03

0,50

x=2

0,11

0,14 0,12 0,07 0,03

0,03

0,50

p.j

0,17

0,26 0,27 0,16 0,08

0,06

1



















06

,

0

5

...

26

,

0

3

17

,

0

2

01

EY

m

365

,

3















06

,

0

5

...

17

,

0

2

2

2

2

02

EX

m

008

,

12

 









2

2

2

02

EX

EY

Y

D



6843

,

0

365

,

3

008

,

12

2





8272

,

0

6843

,

0





DY

7

Zadanie 1 – rozkład dla ogółu
studentów

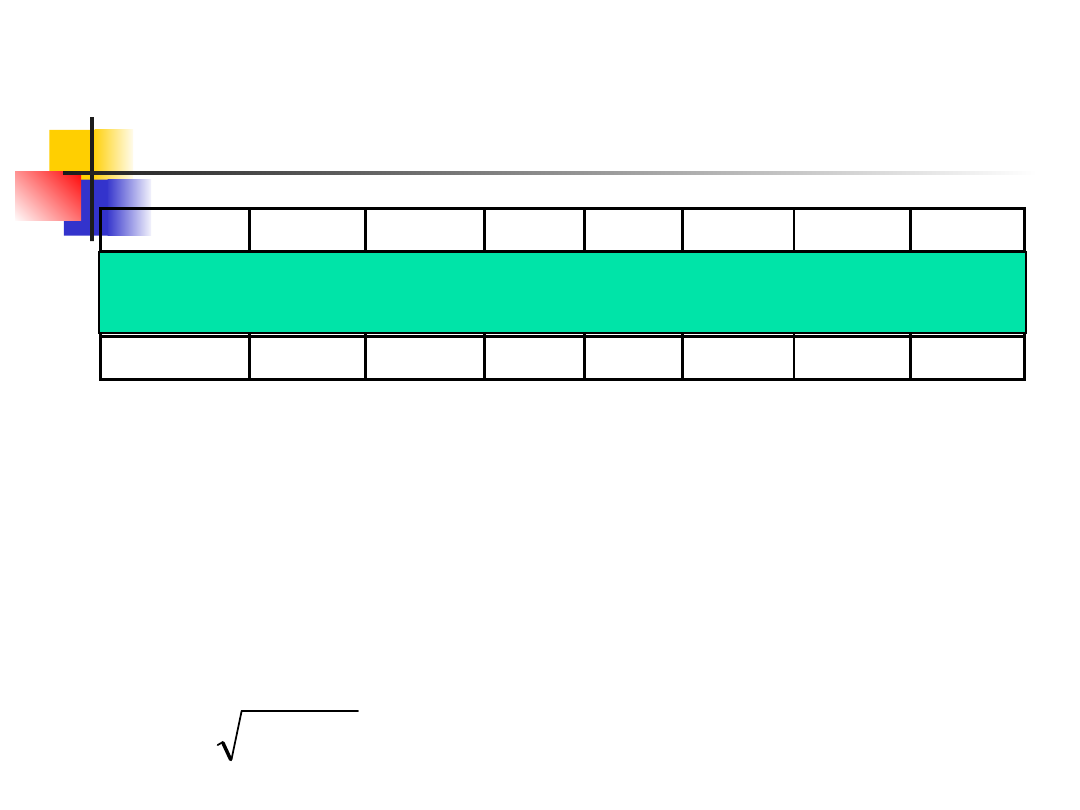
Wyznaczoną wartość oczekiwaną zmiennej
losowej Y można zinterpretować następująco:

przeciętna (średnia) ocena egzaminacyjna ze
statystyki dla ogółu studentów to 3,365.

Przeciętne zróżnicowanie ocen (wokół wartości
średniej) jest równe 0,8272.

Dominującą oceną egzaminacyjną jest 3,5

8

Zadanie 1 – czy taki sam
rozkład?

Rozkład ocen będzie taki sam w obu grupach
studenckich wtedy, jeżeli zmienne losowe
będą niezależne. Musimy więc sprawdzić,
czy rzeczywiście nasze zmienne są
niezależne. Jedna z metod to wyznaczenie
kowariancji, jeżeli zmienne są niezależne, to
CXY jest równa 0.

Jeżeli CXY będzie różne od zera, to będziemy
mogli wyznaczyć jeszcze miarę siły związku
między obu zmiennymi, czyli wsp. korelacji.

Z kolei w sytuacji, gdy CXY będzie równe
zero, to dalsze pytania nie mają już sensu
(rozkład ocen w obu grupach jest dokładnie
taki sam!).

9

Zadanie 1 – czy taki sam
rozkład?

Wyznaczenie CXY wymaga wcześniejszego
wyznaczenia innych potrzebnych
charakterystyk. Wcześniej już wyznaczyliśmy
EY=3,365 oraz D

2

Y=0,6843. Musimy jeszcze

wyznaczyć EX, D

2

X, EXY.

X\Y

2

3

3,5

4

4,5

5

pi.

x=1

0,06

0,12 0,15 0,09 0,05

0,03

0,50

x=2

0,11

0,14 0,12 0,07 0,03

0,03

0,50

p.j

0,17

0,26 0,27 0,16 0,08

0,06

1

5

,

1

5

,

0

2

5

,

0

1











EX

5

,

2

5

,

0

2

5

,

0

1

2

2

2







EX

25

,

0

5

,

1

5

,

2

2

2







X

D

10

Zadanie 1 – czy taki sam
rozkład?

Obliczenie EXY wymaga wykorzystania
f.r.p. dwuwymiarowej zmiennej losowej:

X\Y

2

3

3,5

4

4,5

5

pi.

x=1

0,06

0,12 0,15 0,09 0,05

0,03

0,50

x=2

0,11

0,14 0,12 0,07 0,03

0,03

0,50

p.j

0,17

0,26 0,27 0,16 0,08

0,06

1























03

,

0

5

2

...

12

,

0

3

1

06

,

0

2

1

EXY

99

,

4

Możemy już obliczyć
CXY:









365

,

3

5

,

1

99

,

4

CXY

0575

,

0



11

Zadanie 1 – czy taki sam
rozkład?

Jak widzimy CXY=-0,0575 jest różne od
zera, tym samy zmienne losowe są zależne.

W praktyce oznacza to tyle, że rozkłady ocen
w obu grupach studenckich są inne, tym
samym mogą być też inne ich
charakterystyki.

Wyznaczymy jeszcze miarę siły związku
między zmiennymi:

139

,

0

4136

,

0

0575

,

0

6843

,

0

25

,

0

0575

,

0

















12

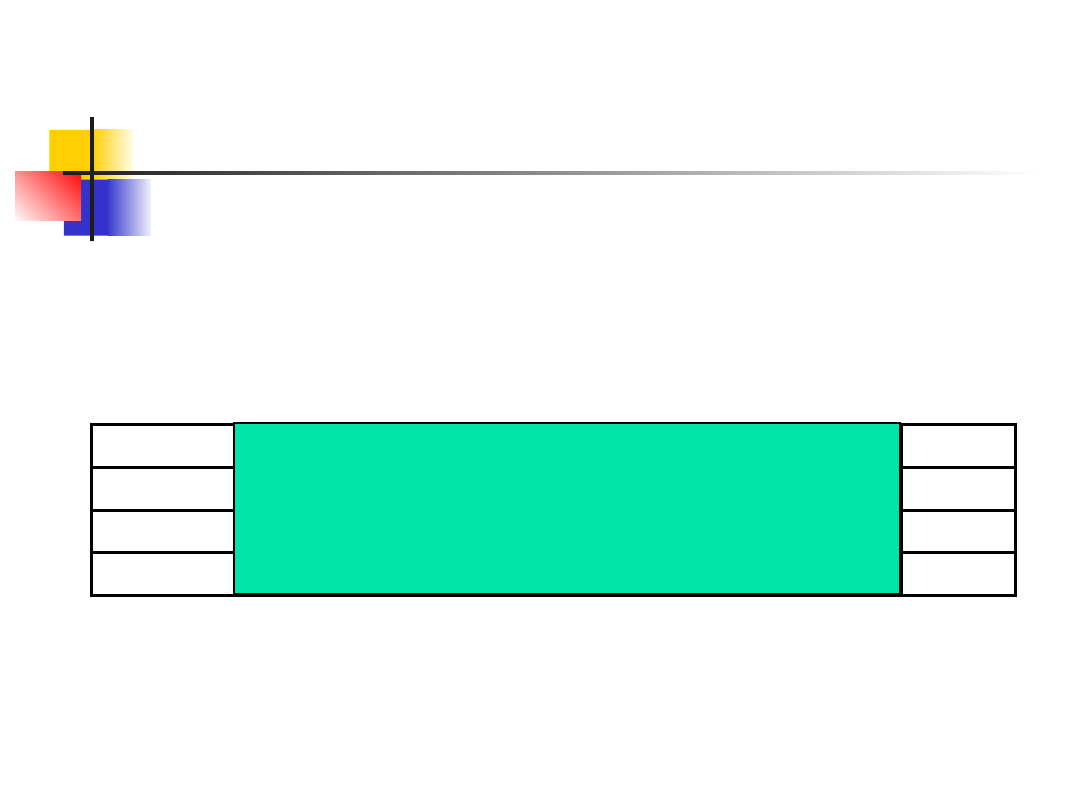
Zadanie 1 – rozkłady warunkowe

Wiemy już, że rozkłady ocen są różne,
wyznaczymy więc warunkowe funkcje
rozkładu p-stwa zmiennej losowej Y przy
założeniu, że X=x

i

X\Y

2

3

3,5

4

4,5

5

Y/x=1

0,12

0,24

0,3 0,18

0,1

0,06

1,00

Y/x=2

0,22

0,28 0,24 0,14 0,06

0,06

1,00

Łatwo zauważyć, że rozkłady te różnią się np.
dominantą, która w grupie studentów dziennych
(X=1) jest równa 3,5 , a w grupie studentów
zaocznych (X=2) odpowiednio 3.

13

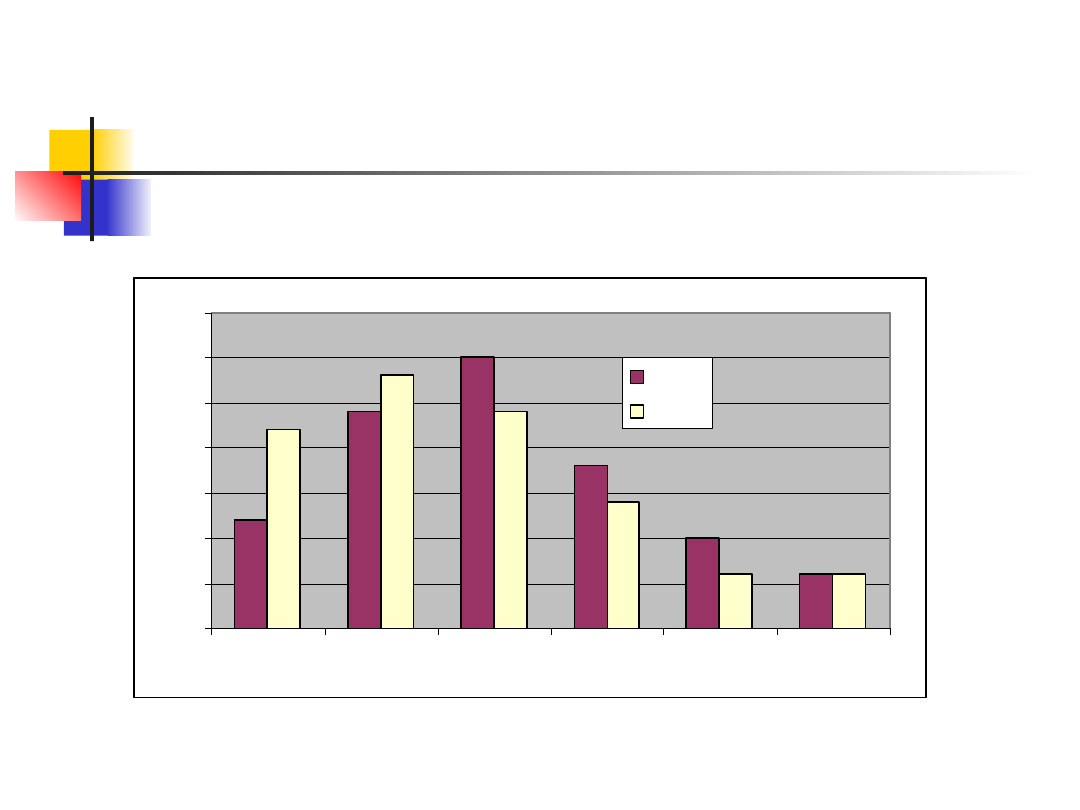
Zadanie 1 – rozkłady warunkowe

0,00

0,05

0,10

0,15

0,20

0,25

0,30

0,35

2

3

3,5

4

4,5

5

Y/x=1
Y/x=2

A tak wyglądają wykresy obu warunkowych
f.r.p

14

Zadanie 1 – funkcja regresji I
rodzaju

Wiemy już, że rozkłady ocen są różne, mamy
wyznaczone warunkowe funkcje rozkładu p-
stwa, możemy więc dla każdej z nich
wyznaczyć wartość oczekiwaną.

X\Y

2

3

3,5

4

4,5

5

Y/x=1

0,12

0,24

0,3 0,18

0,1

0,06

1,00

Y/x=2

0,22

0,28 0,24 0,14 0,06

0,06

1,00















06

,

0

5

...

12

,

0

2

)

1

/

(

X

Y

E

48

,

3















06

,

0

5

...

22

,

0

2

)

2

/

(

X

Y

E

25

,

3

15

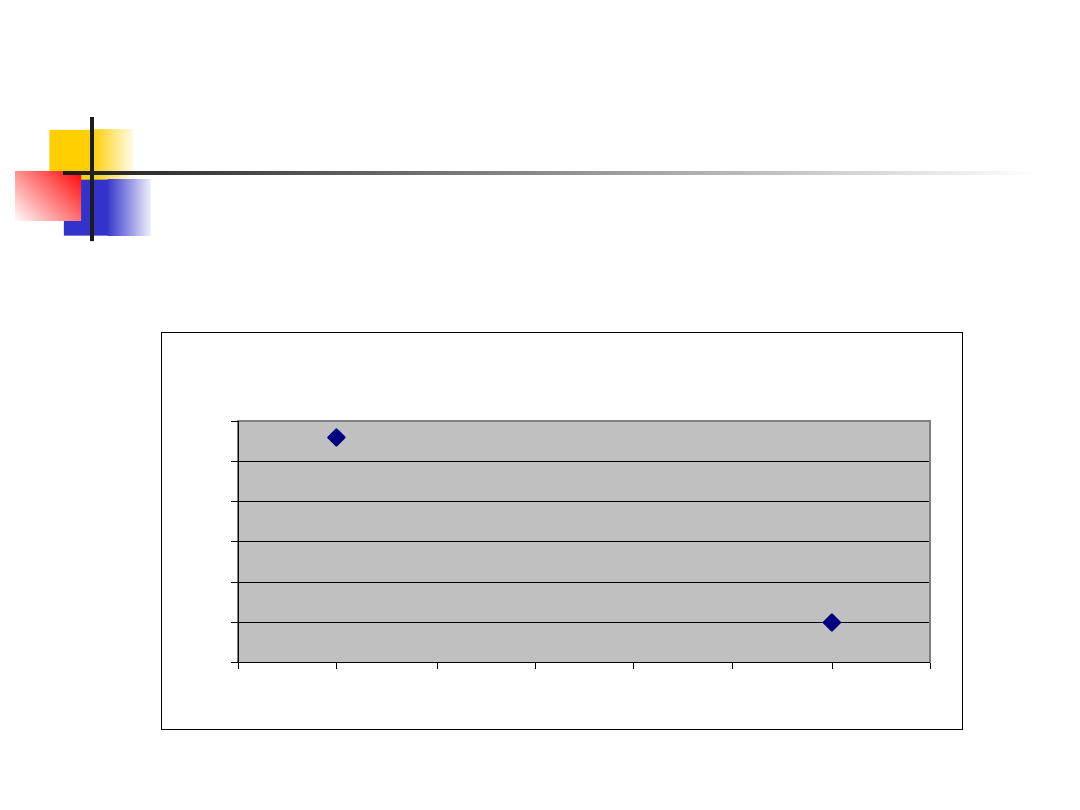
Zadanie 1 – funkcja regresji I
rodzaju

Wyznaczoną funkcję regresji I rodzaju
można przedstawić graficznie:

E(Y/X=xi)

3,20

3,25

3,30

3,35

3,40

3,45

3,50

0,8

1

1,2

1,4

1,6

1,8

2

2,2

16

Zadanie 1 – funkcja regresji I
rodzaju

Wyznaczoną funkcję regresji I rodzaju można
także zapisać w postaci wzoru:













2

25

,

3

1

48

,

3

)

(

x

dla

x

dla

x

m

a wyznaczonym warunkowym wartościom
oczekiwanym nadać interpretację:

W grupie studentów dziennych średnia ocena
egzaminacyjna jest równa 3,48

W grupie studentów zaocznych średnia
ocena jest równa 3,25