Metody rozwiązywania układów równań

liniowych

n

n

nn

n

n

n

n

n

n

b

x

a

x

a

x

a

b

x

a

x

a

x

a

b

x

a

x

a

x

a





























2

2

1

1

2

2

2

22

1

21

1

1

2

12

1

11

b

Ax





















































n

nn

n

n

n

n

b

b

b

a

a

a

a

a

a

a

a

a

















2

1

2

1

2

22

21

1

12

11

b

A

0

det 

A

Metody skończone:

• Metoda Gaussa
• Metoda Gaussa-Jordana
• Metody Choleskiego
• Metoda Householdera
• Metoda sprzężonych gradientów

Metody iteracyjne dla dużych układów równań:

• Metoda Jacobiego
• Metoda Gaussa-Seidla

n

n

nn

n

n

n

n

c

x

r

c

x

r

x

r

c

x

r

x

r

x

r























2

2

2

22

1

1

2

12

1

11

Metoda eliminacji Gaussa z wyborem elementu głównego w
kolumnie

Układ równań sprowadzamy do postaci trójkątnej

Układ z macierzą trójkątną można następnie łatwo rozwiązać
zaczynając od obliczenia wartości x

n

z n-tego równania,

następnie wstawić x

n

do równania n-1 i wyliczyć z niego x

n-1

,

następnie wstawić x

n

oraz x

n-1

do równania n-2 i wyliczyć x

n-2

aż

do dotarcia do równania pierwszego i wyznaczenia x

1

.

1. Wybieramy równanie i takie, że |a

i1

| jest największym elementem w

pierwszej kolumnie po czym przestawiamy i-te równanie na początek i
eliminujemy x

1

z równań od 2 do n.

)

1

(

)

1

(

2

2

)

1

(

2

)

1

(

2

)

1

(

2

2

)

1

(

22

)

0

(

1

)

0

(

1

2

)

0

(

12

1

)

0

(

11

n

n

n

n

n

n

n

n

b

x

a

x

a

b

x

a

x

a

b

x

a

x

a

x

a































1

1

,

1

)

0

(

11

)

0

(

1

)

0

(

1

)

0

(

)

1

(

)

0

(

11

)

0

(

1

)

0

(

1

)

0

(

)

1

(















i

a

a

b

b

b

k

i

a

a

a

a

a

i

i

i

i

k

ik

ik

2. Procedurę powtarzamy z macierzą A

(1)

o rozmiarach (n-1)x(n-1) i

wektorem b

(1)

o rozmiarze n-1, eliminując z nich drugą zmienną i

otrzymując macierz A

(2)

o rozmiarach (n-2)x(n-2) i wektor b

(2)

o

rozmiarze n-2. W ten sam sposób postępujemy z kolejnymi macierzami
A

(2)

, A

(3)

,..., A

(n-1)

oraz wektorami b

(2)

, b

(3)

,..., b

(n-1)

.

j

i

a

a

b

b

b

j

k

j

i

a

a

a

a

a

j

jj

j

ij

j

j

j

i

j

i

j

jj

j

ij

j

jk

j

ik

j

ik































)

1

(

)

1

(

)

1

(

)

1

(

)

(

)

1

(

)

1

(

)

1

(

)

1

(

)

(

,

Dla j-tego kroku

Po zakończeniu operacji otrzymujemy układ równań z macierzą
trójkątną

)

1

(

)

1

(

22

)

0

(

11

)

1

(

)

1

(

)

2

(

3

)

0

(

3

3

)

2

(

33

)

1

(

2

)

0

(

2

3

)

1

(

23

2

)

1

(

22

)

0

(

1

)

0

(

1

3

)

0

(

13

2

)

0

(

12

1

)

0

(

11

)

1

(

det





































n

nn

p

n

n

n

n

nn

n

n

n

n

n

n

a

a

a

b

x

a

b

x

a

x

a

b

x

a

x

a

x

a

b

x

a

x

a

x

a

x

a















A

p jest liczbą przestawień wierszy macierzy A podczas
sprowadzania układu równań do postaci trójkątnej.

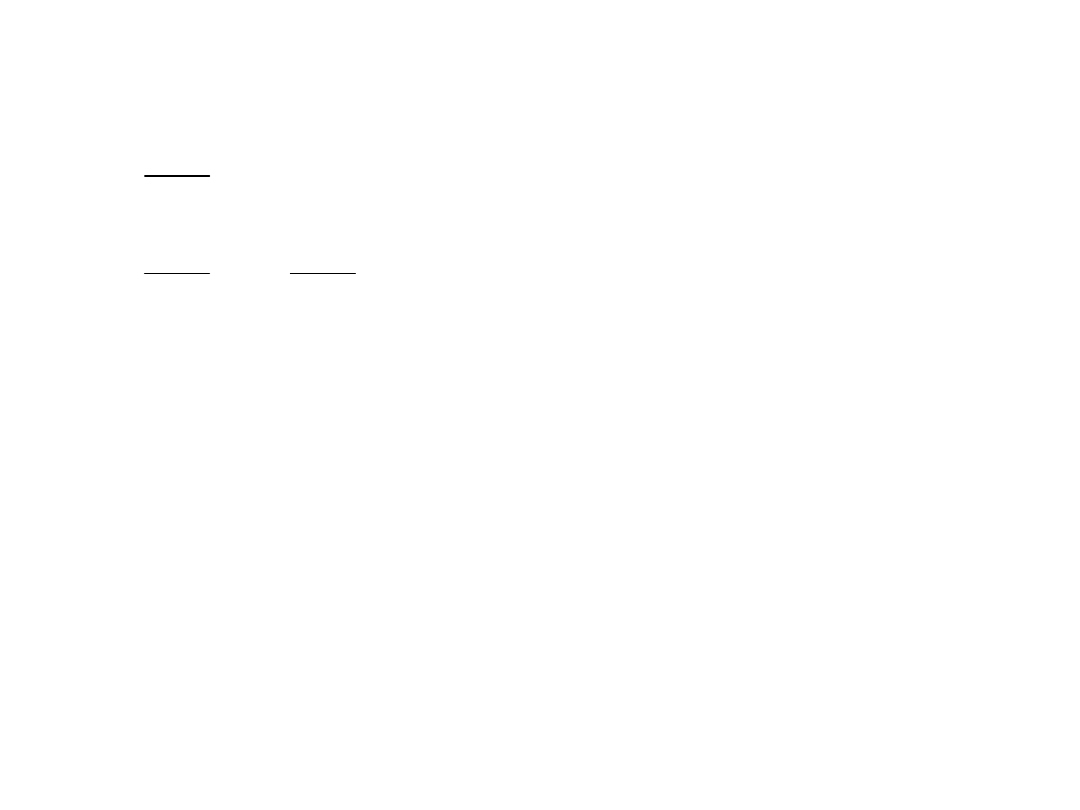
1

,...,

2

,

1

1

)

1

(

)

1

(

)

1

(

)

1

(

)

1

(

)

1

(































n

n

j

x

a

a

a

b

x

a

b

x

k

n

j

k

j

jj

j

jk

j

jj

j

j

j

n

nn

n

n

n

3. Z otrzymanego układu równań z macierzą trójkątną

wyznaczamy po kolei x

n

, x

n-1

,..., x

1

.

Wysiłek obliczeniowy (liczba mnożeń i dzieleń) w metodzie
eliminacji Gaussa:

Faktoryzacja macierzy A: n(n

2

-1)/3 operacji

Przekształcenie wektora b: n(n-1)/2 operacji

Obliczenie x: n(n+1)/2 operacji.

Razem: n

3

/3+n

2

-n/3≈n

3

/3 operacji.

Kod źródłowy metody eliminacji Gaussa.

Metody typu Choleskiego dla macierzy symetrycznych silnie
nieosobliwych

T

LDL

A 

L

T

L

D

L

T

LL

A 

klasyczna metoda Choleskiego

tylko dla macierzy dodatnio
określonych.

Postępowanie przy rozwiązywaniu układów równań metodą

faktoryzacji Choleskiego.

1. Wyznaczenie faktorów L i D. Układ przyjmuje postać

LDL

T

x=b

2. Obliczenie pomocniczego wektora w.

w=L

-1

b przez rozwiązanie układu równań Lw=b.

Ponieważ L jest macierzą trójkątną dolną układ ten rozwiązuje się
wyliczając kolejno w

1

, w

2

,…, w

n

podobnie jak w koncowym etapie

eliminacji Gaussa.

3. Obliczenie z=D

-1

w (D jest macierzą diagonalną więc po prostu

dzielimy w

i

przez d

ii

. Ten etap nie występuje w klasycznej metodzie

Choleskiego.

4. Obliczenie x poprzez rozwiązanie układu równań z macierzą

trójkątną górną

L

T

x=z

Ten etap jest identyczny z ostatnim etapem metody eliminacji
Gaussa.

Metoda wymaga ok. n

3

/6 operacji (2 razy mniej niż metoda eliminacji

Gaussa). Uwaga: klasyczna metoda Choleskiego wymaga ponadto
n pierwiastkowań.

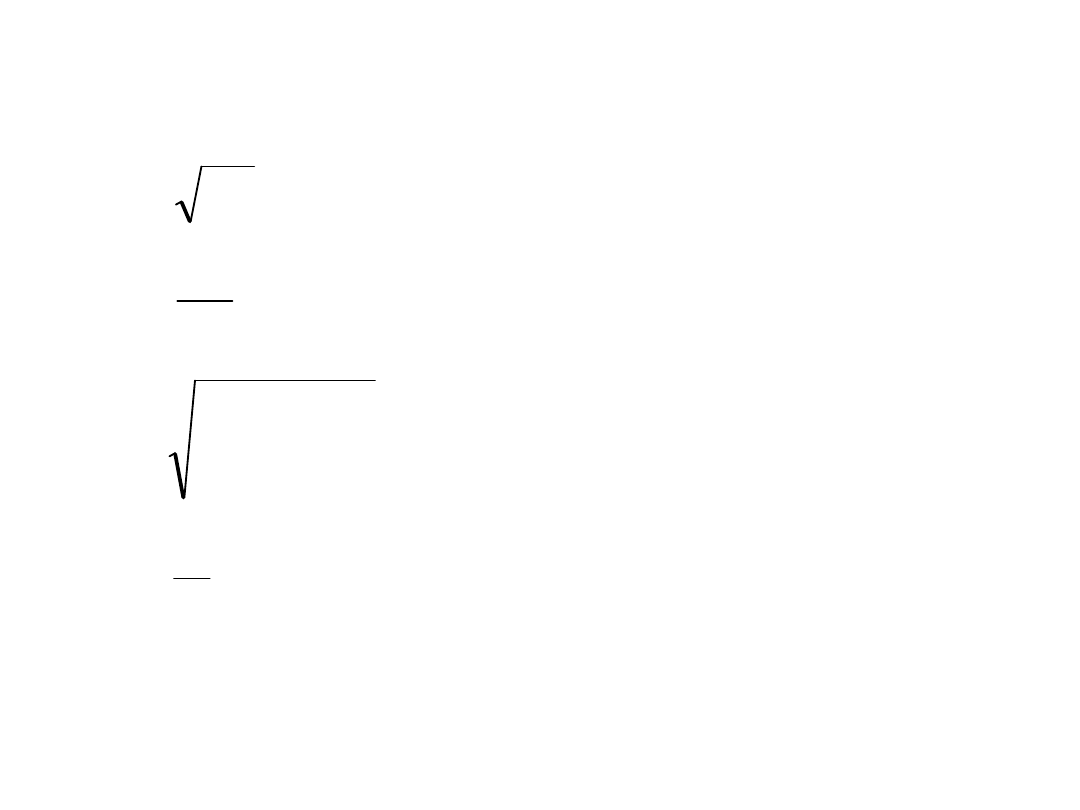
Klasyczna faktoryzacja Choleskiego (A=LL

T

)





































1

1

1

1

2

11

1

1

11

11

1

i

k

jk

ik

ij

ii

ji

i

k

jk

ii

ii

j

j

l

l

a

l

l

l

a

l

l

a

l

a

l

Faktoryzacja “bezpierwiastkowa”

kod źródłowy



























































1

0

1

0

0

1

1

,

1

21

2

1

n

n

n

n

l

l

l

d

d

d

















L

D

i

n

k

ik

jk

k

ji

ji

j

j

n

k

nk

k

nn

n

i

k

ki

k

ii

i

d

l

l

d

a

l

d

a

l

l

d

a

d

l

d

a

d

a

d















































1

1

1

1

1

1

1

2

1

1

2

11

1

/

Regresja nieliniowa

)

,

,

,

;

,

,

(

2

1

2

1

2

1

2

2

22

21

1

1

12

11

m

m

n

nm

n

n

m

m

p

p

p

x

x

x

f

y

y

x

x

x

y

x

x

x

y

x

x

x























f jest funkcją nieliniową względem parametrów p

1

, p

2

,

…, p

m

.

Przykład problemu nieliniowego linearyzowalnego: kinetyka reakcji
pierwszego rzędu

 

 

 

 

 































o

o

o

k

C

k

p

C

y

t

x

kt

C

t

A

kt

C

t

A

B

A

ln

ln

ln

ln

exp

 

 













 



























































3

2

1

3

2

1

2

2

1

2

1

1

3

2

1

/

exp

exp

1

3

2

1

k

k

k

C

C

y

t

x

t

k

k

k

k

t

k

k

k

k

k

C

t

C

C

B

k

k

k

B

A

C

A

o

o

k

k

k

p

Przykład problemu nieliniowego nielinearyzowalngo:
kinetyka reakcji pierwszego rzędu z produktem
przejściowym











 













 













































































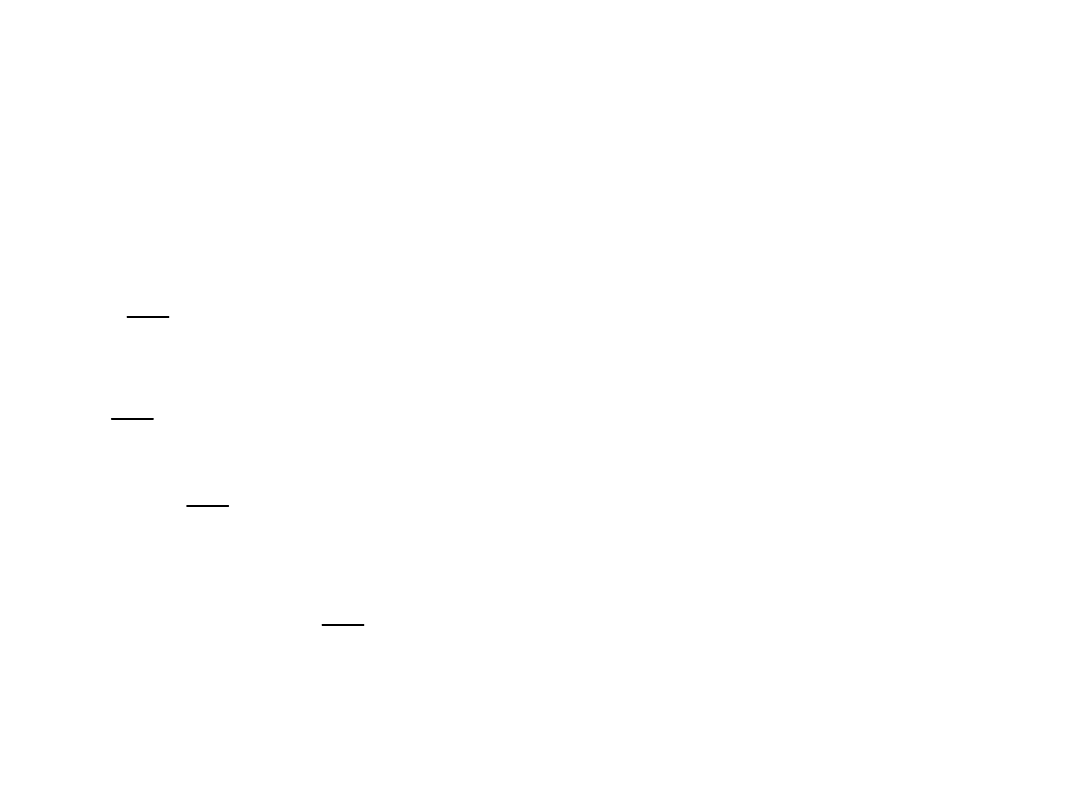
2

2

2

2

1

T

1

2

2

1

2

1

2

1

T

2

2

1

2

1

1

0

0

0

0

1

0

0

0

1

)

;

(

)

;

(

,

,

,

;

,...,

,

1

)

;

(

)

;

(

,

,

,

;

,...,

,

n

n

i

m

im

i

i

i

i

n

i

m

im

i

i

i

p

p

p

x

x

x

f

y

p

p

p

x

x

x

f

y

























W

p

X

f

y

W

p

X

f

y

p

X

f

y

p

X

f

y

regresja
nieważona

regresja ważona

Metoda Newtona-Gaussa

Rozwijamy funkcję f dla każdego punktu pomiarowego
w otoczeniu arbitralnego przybliżenia parametrów p

0

w

szereg Taylora













 























m

j

j

ij

i

m

j

j

j

p

p

p

x

x

x

i

m

in

i

i

m

in

i

i

p

J

f

p

p

p

f

p

p

p

x

x

x

f

p

p

p

x

x

x

f

m

in

i

i

1

)

0

(

)

0

(

)

0

(

1

0

,

,

,

,

,

,

0

0

2

0

1

2

1

2

1

2

1

0

0

2

0

1

2

1

,

,

,

;

,

,

,

,

,

,

;

,

,

,



p













 

)

0

(

)

0

(

)

0

(

1

)

0

(

)

0

(

)

0

(

)

0

(

p

J

r

p

















m

j

j

ij

i

i

i

p

J

f

y

r

W ten sposób dostajemy funkcję liniową względem
przyrostów parametrów p

(0)

. Macierz J nazywa się macierzą

Jacobiego zagadnienia a wektor r wektorem reziduów.



 





 



































































n

i

m

j

j

ij

i

n

i

m

j

j

ij

p

J

r

w

p

J

r

i

i

1

)

0

(

)

0

(

)

0

(

T

)

0

(

)

0

(

)

0

(

2

1

)

0

(

)

0

(

)

0

(

)

0

(

1

)

0

(

)

0

(

)

0

(

T

)

0

(

)

0

(

)

0

(

2

1

)

0

(

)

0

(

)

0

(

)

0

(

p

J

r

W

p

J

r

p

J

r

p

J

r













regresja
nieważona

regresja ważona

(0)

(0)T

(0)

(0)

(0)T

(0)

(0)T

(0)

(0)

(0)T

Wr

J

p

WJ

J

r

J

p

J

J









Algorytm Newtona-Gaussa

1. Wybieramy przybliżenie parametrów p

(0)

.

2. Obliczamy wektor reziduów oraz sumę kwadratów odchyleń



(0)

.

3. Obliczamy macierz Jacobiego a następnie macierz i wektor

wyrazów wolnych układu równań.

4. Obliczamy wektor przyrostów parametrów p

(0)

.

5. Obliczamy p

(1)

=p

(0)

+p

(0)

a następnie nową sumę kwadratów

odchyleń.

6. Jeżeli przyrosty parametrów są odpowiednio małe, zmiana

sumy kwadratów odchyleń jest odpowiednio mała lub
przekroczono dopuszczalną liczbę iteracji, kończymy procedurę.
Jeżeli nie, przechodzimy do punktu 3 wstawiając p

(1)

za p

(0)

i 

(1)

za 

(0)

.

Zbieżność metody Gaussa jest na ogół rzędu pierwszego. Tylko

jeżeli rezidua dla optymalnego rozwiązania są zerowe zbieżność
jest kwadratowa. Szybkość zbieżności zależy bardzo silnie od
wielkości końcowych reziduów.

Metoda Newtona-Gaussa może być niestabilna szczególnie jeżeli
rezidua odpowiadające początkowym przybliżeniom parametrów
są duże i wskaźnik uwarunkowania macierzy J

T

J jest duży. Można

ją jednak poprawić stosując skracanie przyrostów parametrów.

Szukamy takiego , że (p

(0)

+p

(0)

)<(p

(0)

). Teoretycznie takie 

zawsze istnieje, ponieważ kierunek metody Newtona-Gaussa jest
kierunkiem poprawy.







 











 

 

0

2

2

2

)

0

(

2

/

1

)

0

(

1

0

0

0

)

0

(

)

0

(





































r

J

J

J

r

J

J

J

J

r

p

J

p

J

r

p

J

r

p

J

r

p

p

T

T

T

T

(0)

(0)

(0)

(0)

T

T

T

d

d

d

d



























Wyznaczanie :

Metoda Hartleya: wyznaczamy  tak, żeby zminimalizować  jako

funkcję a (minimalizacja kierunkowa) Metoda ta zwykle nie jest
stosowana w takiej wersji ze względu na czasochłonność; zwykle
kończy się jak tylko 

(1)

<

(0)

.

Proste skracanie kroku: Zakładamy, że =2

-k

gdzie k jest liczbą

całkowitą dobraną tak, że

F(1)<F(0).

Jeżeli

macierz J

T

J jest źle uwarunkowana to zarówno metoda Hartleya jak i

metoda skracania kroku działają bardzo wolno. Metodą sprawdzoną dla takich
przypadków jest metoda Levenberga-Marquardta.

Metoda Levenberga-Marquardta (metoda Marquardta)

Zamiast układu równań normalnych z metody Newtona-Gaussa
rozwiązujemy układ następujący:





r

J

p

D

J

J

T

T









Macierz D jest dodatnią macierzą diagonalną; zwykle D=I lub

D=diag{(J

T

J)

11

,…,(J

T

J)

mm

}.

 dobiera się tak aby uzyskać zmniejszenie sumy kwadratów

odchyleń w stosunku do poprzedniej iteracji. Dowód, że metoda jest
metodą kierunku poprawy przebiega jak w przypadku metody
Newtona-Gaussa ze skracaniem kroku.

W pierwotniej wersji Levenberga a było dobierane tak aby uzyskać
minimum  w funkcji  (kosztowne).

Metoda Marquardta:

1. Na początku przyjmujemy 

0

.

2. W każdej kolejnej iteracji przyjmujemy najpierw 

(p)

=

(p-1)

/V.

3. Obliczamy 

(p)

().

4. Jeżeli 

(p)

()<

(p-1)

przechodzimy do następnej iteracji z nową

wartością .

5. Jeżeli



(p)

()>=

(p-1)

i nie przekroczono maksymalnej

dopuszczalnej wartości liczby krokow modyfikacji  wstawiamy

:=*V i przechodzimy do punktu 3. Jeżeli przekroczono

maksymalną liczbę kroków kończymy optymalizację.

Metoda Marquardta jest jedną z “najodporniejszych” metod

minimalizacji sum kwadratów. Niepowodzenie optymalizacji jest
na ogół sygnałem błędu w programie (najczęściej błędnemu
obliczeniu pochodnych).

 















n

i

i

i

r

f

y

m

n

1

2

2

1

p



Macierz wariancji-kowariancji parametrów:

Wariancja resztowa:











 

1

2

T

*

*









J

J

p

p

p

p

T

r

E

















1

2

T

*

*









WJ

J

p

p

p

p

T

r

E



Odchylenia standardowe:









ii

r

p

i

1





WJ

J

T





Metoda Newtona w rozwiązywaniu problemu regresji

nieliniowej













































n

i

m

i

i

i

m

n

i

m

i

i

m

p

p

p

f

y

p

p

p

p

p

p

f

y

p

p

p

1

2

2

1

2

2

1

1

2

2

1

2

1

,

,

,

;

1

,

,

,

,

,

,

;

,

,

,









x

x



Warunek konieczny minimum









   

 

   

 

   

0

p

Wr

p

J

p

0

p

r

p

J

p

p

p

x





















































*

*

2

*

*

*

2

*

,

,

2

,

1

0

*

*

2

,

,

,

;

2

1

*

*

2

*

1

1

,

,

,

,

,

,

*

*

2

*

1

*

*

2

*

1

T

T

n

k

k

ki

m

i

k

n

k

p

p

p

i

k

p

p

p

i

m

i

r

J

p

p

p

f

y

p

f

p

m

m









regresja nieważona

regresja ważona

regresja nieważona

regresja ważona

Otrzymujemy zatem układ m równań nieliniowych z m
niewiadomymi, który można rozwiązać metodą Newtona.





r

J

Δp

H

r

J

Δp

r

:

f

J

J

T

pp

T

pp

T



























































































 















m

i

r

p

f

p

r

p

p

f

p

f

p

f

m

i

p

p

p

p

p

p

n

k

k

i

k

m

j

j

n

k

n

k

k

j

i

k

j

k

i

k

m

j

j

j

p

p

p

j

i

p

p

p

i

p

p

p

i

m

m

m

,

,

2

,

1

,

,

2

,

1

0

1

1

1

1

2

1

*

,

,

,

2

,

,

,

,

,

,

2

1

2

1

*

*

2

*

1











H – hesjan (Hessian) funkcji . Macierz J

T

J: dodatnio określona

część hesjanu (występuje w metodzie Newtona-Gaussa.

Algorytm Newtona dla zagadnienia regresji nieliniowej:

1. Wybrać początkowe przybliżenia parametrów p(0).

2. Dla k-tej iteracji obliczyć rezidua, funkcję minimalizowaną, macierz

Jacobiego oraz drugie pochodne wielkości mierzonych względem
parametrów.

3. Rozwiązać układ równań H

(k)

p

(k)

=J

T(k)

r

(k)

4. Jeżeli ||p

(k)

||<e zakończyć proces iteracyjny, w przeciwnym

przypadku wstawić p

(k+1)

=p

(k)

+p

(k)

i przejść do punktu 2.

Metoda Newtona jest zbieżna kwadratowo, jeżeli hesjan w minimum

jest nieosobliwy.

Metoda Newtona różni się od metody Newtona-Gaussa tym, że

linearyzuje się tutaj gradient funkcji minimalizowanej a nie od razu
teoretyczną zależność pomiędzy zmiennymi objaśniającymi i
niezależnymi. Metoda Newtona-Gaussa „gubi” drugie pochodne
tych wielkości względem parametrów.