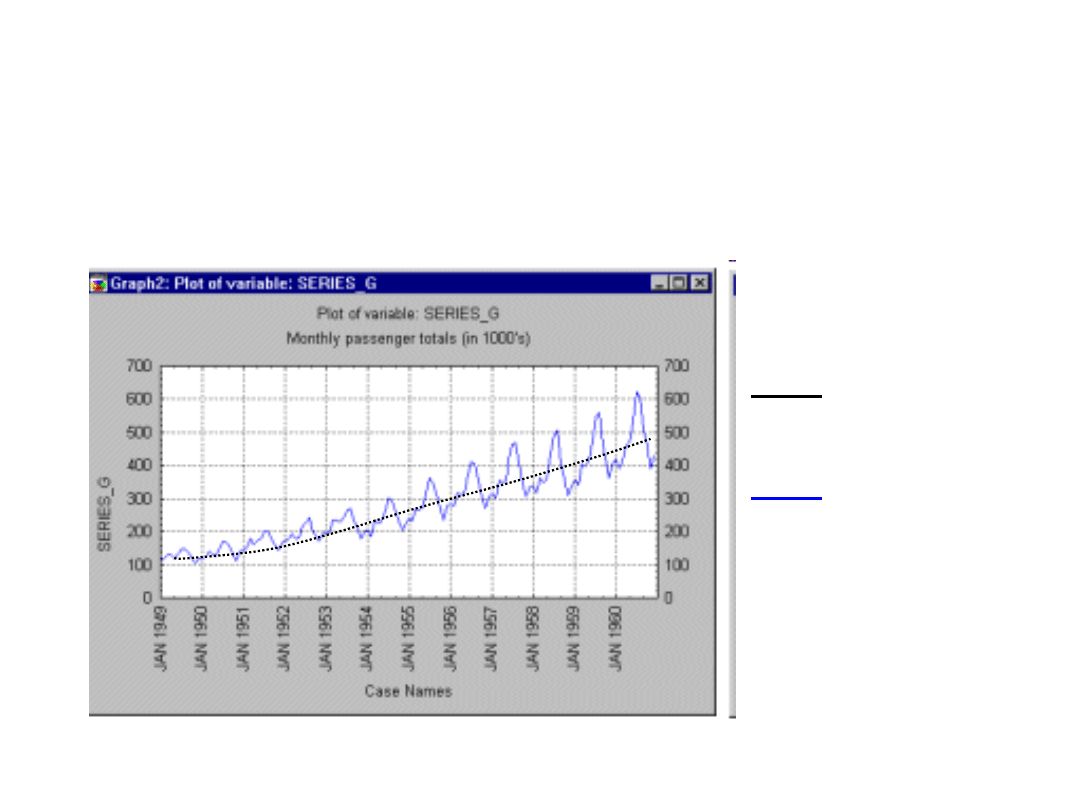
Analiza szeregów czasowych

Szereg czasowy: zmierzona zależność danej wielkości 
od czasu. Szeregi czasowe przedstawia się w postaci 
tabeli lub wykresu. 

trend

Sezonowość 
lub 
komponent 
stochastyczn
y

Zależność liczby pasażerów samolotów na 
miesiąc (w tysiącach) od czasu w USA w latach 
1949-1960 

 

 

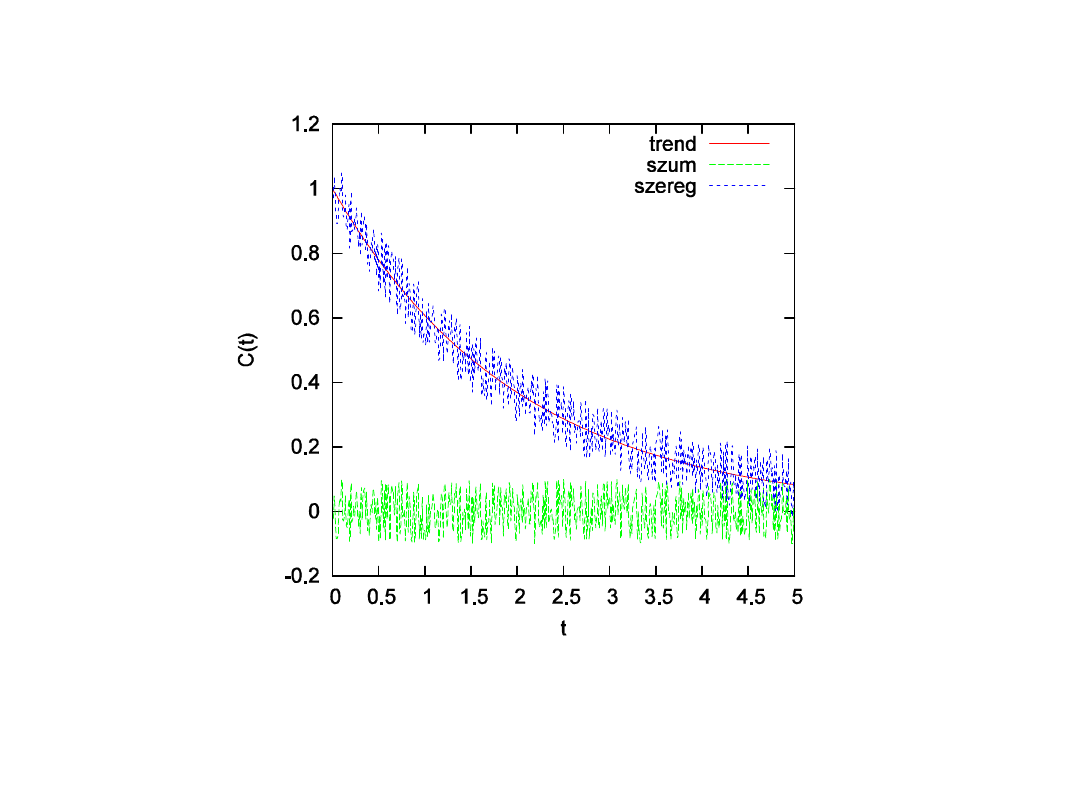
Przykładowe dane 
kinetyczne

 

 

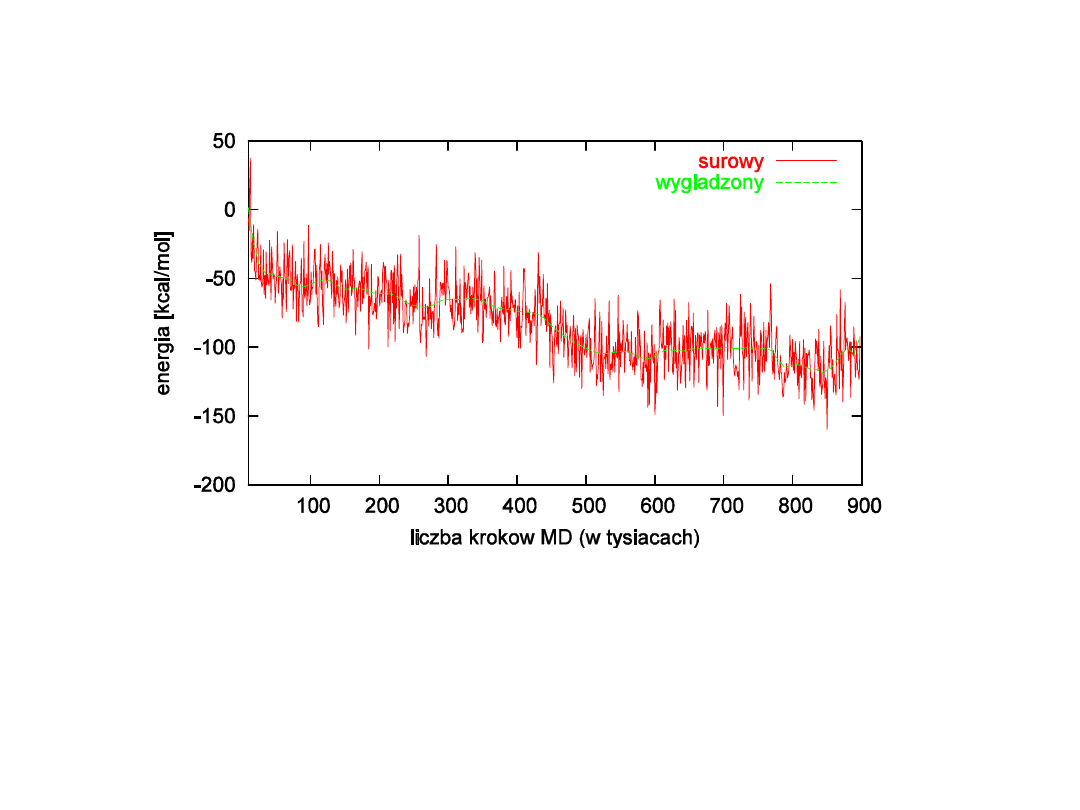
Wykres energii w zależności od czasu w dynamice 
molekularnej

 

 

Przykłady szeregów czasowych w chemii

• “Surowe” dane z pomiarów spektroskopowych (np. 

FID w pomiarach NMR).

• “Surowe” dane z pomiarów kinetycznych.
• Dane z monitoringu
• Wielkości charakteryzujące układ w danej chwili 

czasu otrzymane w wyniku symulacji MD lub Monte 
Carlo (energia, promień bezwładności itp.).

 

 

Przykłady szeregów czasowych w życiu 

codziennym

• Kursy walut
• Kursy giełdowe
• Wyniki sondaży

 

 

Cele analizy szeregów czasowych

• Określenie natury zjawiska reprezentowanego 

przez daną sekwencję obserwacji

• Przewidywanie przyszłych wartości zmiennej 

zależnej szeregu czasowego. 

 

 

Metody wyodrębniania trendu

• Uśrednianie
• Metoda średnich ruchomych 
• Autoregresja
• Dopasowywanie form funkcyjnych

– Transformacja Fouriera

• Analiza autokorelacji

 

 

Ogólna postać szeregu czasowego

const

t

t

t

n

i

y

i

i

i

i

i















 1

,

,

2

,

1

,



















k

k

j

j

i

i

y

k

u

1

2

1

Średnia ruchoma

t

y(t)

 

 

Lepszym estymatorem  w danym przedziale jest 

wielomian















j

x

t

x

x

t

a

t

a

a

k

k

k

j

t

j

t

t

j

j

j

j

j

i

j

1

2

1

1

2

1

,

,

1

,

,







































Współczynniki x

1

,x

2

,…,x

l+1

 wyznaczamy prowadząc 

regresję liniową dla j=-k,-k+1,…,k

 

 





 

 

























































































k

k

k

k

k

k

k

k

k

2

2

2

1

1

1

1

1

1

1

~

A

y

A

A

A

x

T

T

Pierwszy współczynnik x

1

 odpowiada wartości 

trendu 

o

 pośrodku przedziału.

 

 

Transformacja Fouriera























dk

k

F

e

x

f

dx

x

f

e

k

F

ikx

ikx

)

(

)

(

)

(

)

(

2

2





 

 

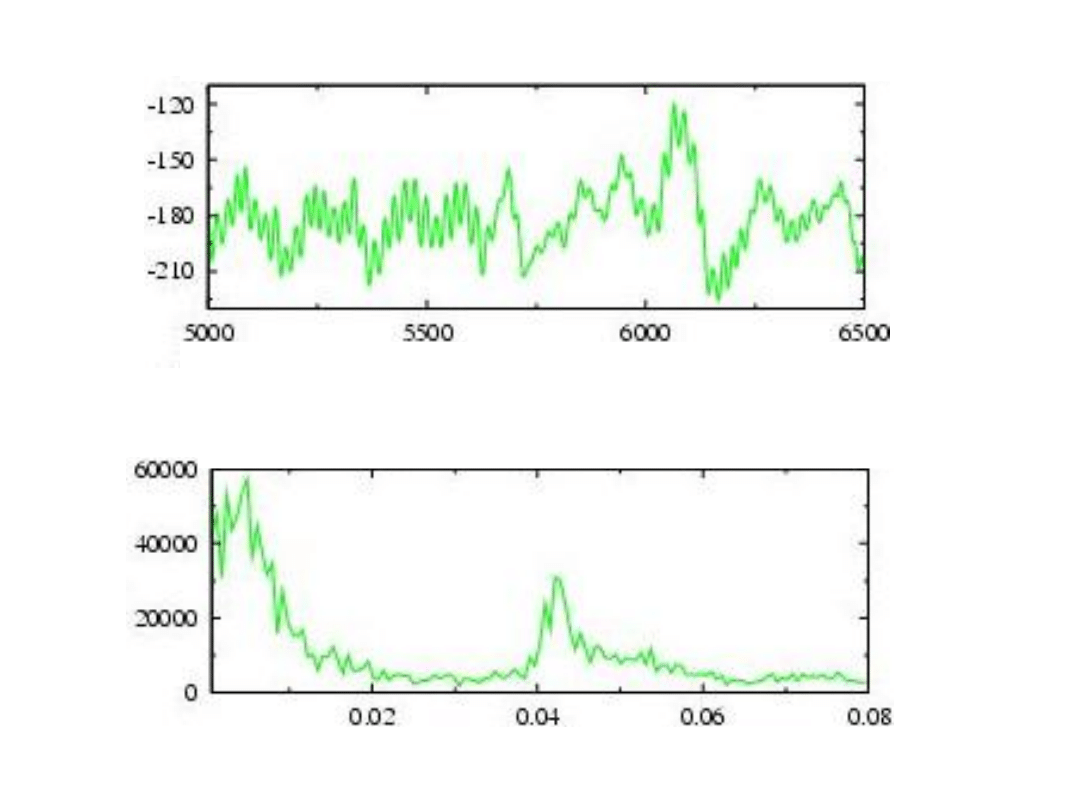
Czas

Częstość

Oryginalny szereg czasowy

Transformata Fouriera

W

a

rt

o

ść

 

w

sp

ó

łr

zę

d

n

e

j

In

te

n

sy

w

n

o

ść

 

 

Aproksymacja trygonometryczna

 











n

k

k

k

o

n

kx

b

kx

a

a

x

y

1

sin

cos

2

Mamy dane wartości funkcji f(x) w punktach

x

i

=i/L dla i=0,1,…,2L-1

Przez te punkty chcemy poprowadzić wielomian 
trygonometryczny o postaci

tak aby był najlepiej dopasowany do punktów w sensie 
średniokwadratowym:

 

 















1

2

0

2

min

L

i

i

n

i

x

y

x

f

 

 

Wskutek ortogonalności różnych od siebie  funkcji składowych

































































1

2

0

1

2

0

1

2

0

0

sin

cos

0

dla

2

0

dla

dla

0

cos

cos

0

dla

0

0

dla

dla

0

sin

sin

L

i

i

i

L

i

i

i

L

i

i

i

mx

mx

k

m

L

k

m

L

k

m

kx

mx

k

m

k

m

L

k

m

kx

mx

 

 

Układ równań normalnych przyjmuje postać diagonalną co daje 
analityczne wzory na współczynniki rozwinięcia Fouriera.

n

j

L

ij

x

f

L

jx

x

f

L

b

L

ij

x

f

L

jx

x

f

L

a

L

i

L

i

i

i

i

j

L

i

L

i

i

i

i

j

,...,

2

,

1

sin

)

(

1

sin

)

(

1

cos

)

(

1

cos

)

(

1

1

2

0

1

2

0

1

2

0

1

2

0







































 

 

Funkcja autokorelacji

 

  



 

 

 

2

2

2

t

y

t

y

t

y

t

y

t

y

C











