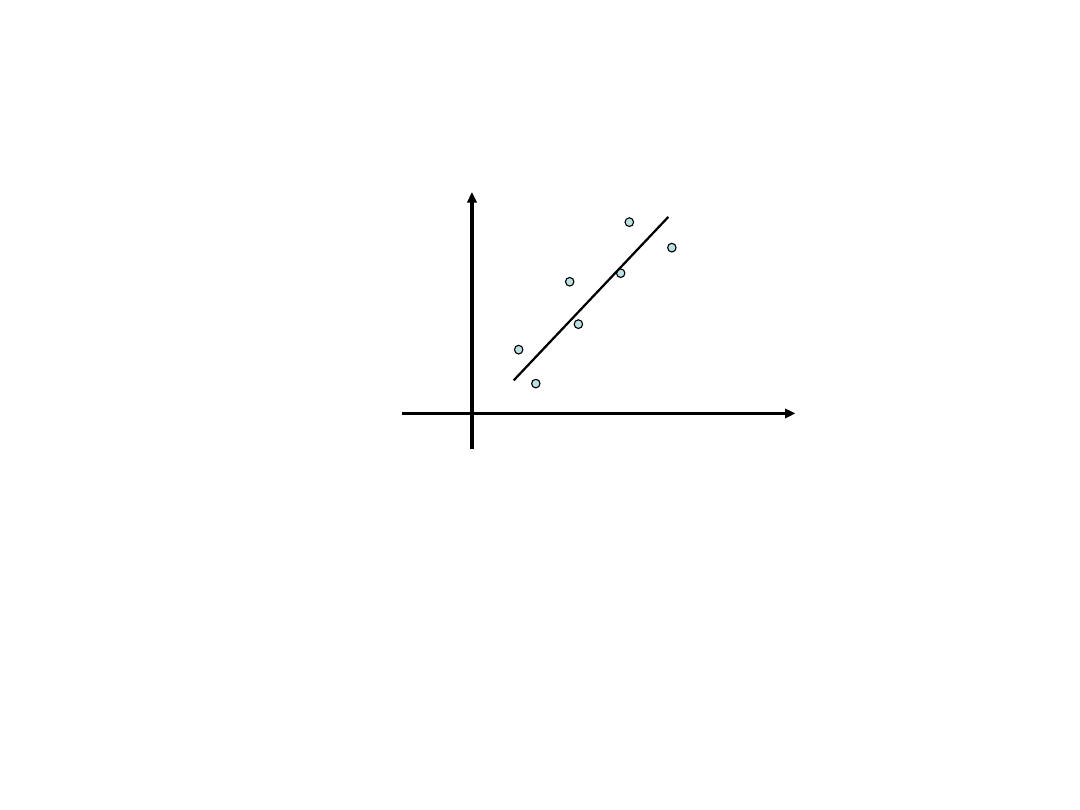
Regresja liniowa
Dany jest układ punktów
n
n
y
,
x
y
,
x
y
,
x
2
2
1
1
x
y
b
ax
y
i
i
x – zmienna objaśniająca (nie obarczona
błędem)
y – zmienna zależna (obarczona błędem)
Naszym zadaniem jest poprowadzenie „najlepszej” prostej
przez te punkty.
x
a
y
x
x
n
y
x
x
y
x
b
x
y
x
x
x
y
x
xy
x
x
n
y
x
y
x
n
a
b
b
a
a
b
a
b
ax
y
y
y
b
a
n
i
i
n
i
i
n
i
i
i
n
i
i
n
i
i
n
i
i
n
i
i
n
i
i
n
i
i
n
i
i
n
i
i
i
n
i
i
i
n
i
obl
i
i
2
1
1
2
1
1
1
1
2
2
2
2
1
1
2
1
1
1
1
2
1
2
var
,
cov
0
,
0
,
,
Wyznaczanie optymalnych parametrów a
i b
Bardziej ogólny przypadek dopasowywania równania
prostej: regresja ważona
n
i
i
i
i
n
i
i
i
i
b
ax
y
w
b
ax
y
b
,
a
1
2
1
2
2
n
i
i
i
n
i
i
n
i
i
i
n
i
i
i
i
n
i
i
i
n
i
i
i
y
b
a
x
y
x
b
x
a
x
1
2
1
2
1
2
1
2
1
2
1
2
2
1
Ocena istotności równania regresji
1. Weryfikujemy następującą hipotezę zerową:
H
0
: a = 0 wobec H
1
: a ≠ 0
(jeżeli a = 0 “w granicach błędu” to nie można mówić o
regresji)
Przy prawdziwości H
0
statystyka:
ma rozkład t Studenta z liczbą stopni swobody równej n - 2.
a
a
t
-3
-2
-1
0
1
2
3
0.00
0.05
0.10
0.15
0.20
0.25
0.30
0.35
0.40
-t
n,
t
n,
/2
/2
1-
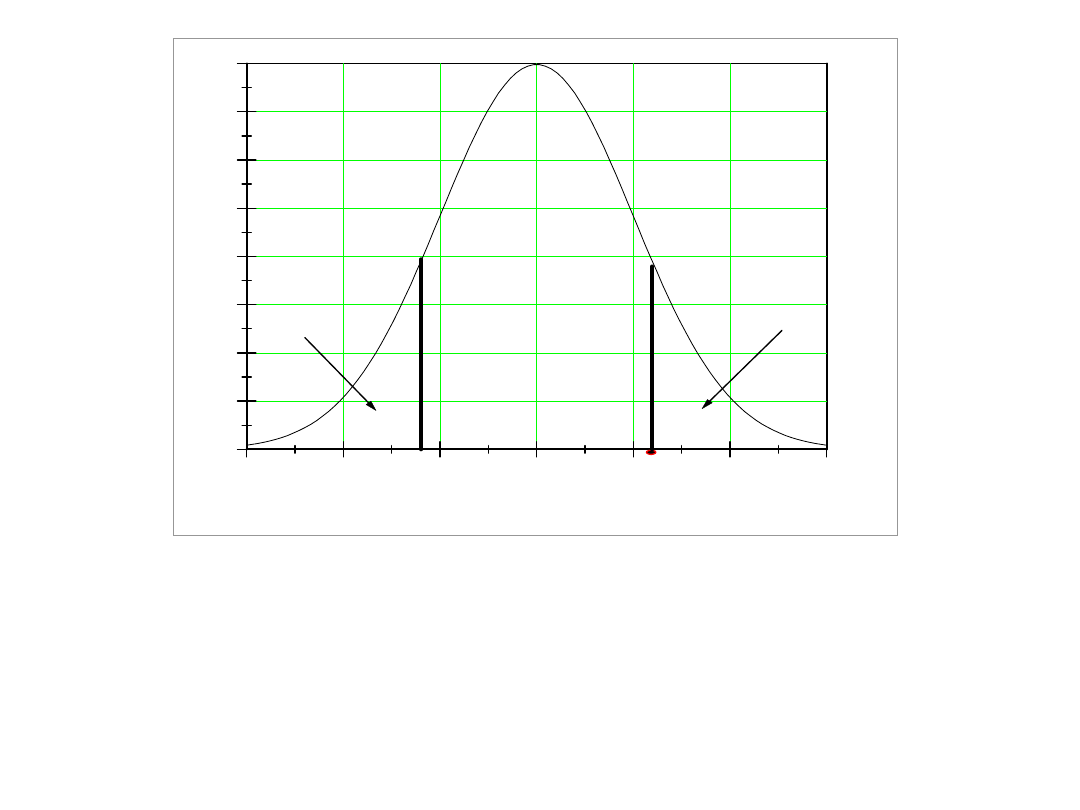
Z tablic rozkładu Studenta odczytujemy, dla wcześniej przyjętego
poziomu istotności , wartość krytyczną t
n-2,
. Jeżeli obliczona wartość
t znajduje w dwustronnym obszarze krytycznym (-, - t
n-2,
), (t
n-2,
,
+), to H
0
należy odrzucić na korzyść hipotezy H
1
n
i
obl
i
i
n
i
obl
i
i
n
i
i
n
i
obl
i
i
n
i
obl
i
i
n
i
i
y
y
y
y
y
y
n
n
y
y
y
y
y
y
F
1
2
1
2
1
2
1
2
1
2
1
2
2
2
1
2. Zbadanie istotności różnicy pomiędzy różnicą
wariancji odpowiadającą wprowadzeniu członu
liniowego (ma ona 1 stopień swobody) a wariancją
resztową z modelu liniowego (ma ona 2 stopnie
swobody) przy pomocy testu F(1,n-2).
3. Można też przeprowadzić analizę współczynnika
korelacji lub jego kwadratu (współczynnika
determinacji).
2
1
1
2
2
1
1
2
2
1
1
1
1
2
1
2
2
1
2
2
var
var
,
cov
n
i
i
n
i
i
n
i
i
n
i
i
n
i
n
i
i
i
n
i
i
i
n
i
i
n
i
i
n
i
i
i
y
y
n
x
x
n
y
x
y
x
n
y
y
x
x
y
y
x
x
y
x
y
x
r
n
i
i
n
i
i
n
i
i
i
n
i
i
n
i
i
i
n
i
i
n
i
n
i
i
i
i
n
i
i
n
i
i
i
n
i
n
i
n
i
i
i
i
i
obl
i
i
y
y
r
x
x
y
y
x
x
y
y
y
y
x
x
a
y
y
x
x
a
y
y
x
x
a
y
y
x
x
a
y
y
x
a
y
ax
y
b
ax
y
y
y
1
2
2
1
2
2
1
1
2
1
2
1
2
1
1
2
2
2
1
2
1
2
1
1
1
2
2
2
1
2
Trochę żonglerki sumami
x
a
y
b
n
i
i
n
i
i
i
x
x
y
y
x
x
a
1
2
1
2
2
1
2
1
2
1
2
2
1
2
r
r
n
F
y
y
y
y
y
y
r
n
i
i
n
i
i
obl
i
n
i
i
obl
obl
y
y
y
y
r
var
var
,
cov
Dla dociekliwych: udowodnić tożsamość
W ten sposób mamy wzór na współczynnik korelacji przenaszalny na
regresję wielokrotną a przy okazji potrafimy wyrazić F przez
współczynnik korelacji
Linearyzacja
Mamy dopasować funkcję nieliniową
y=f(x,y;a.b)
Przekształcamy funkcję do takiej postaci aby uzyskać
postać zlinearyzowaną
=+
Gdzie jest nową zmienną zależną, nową zmienną
objaśniającą a a i b są nowymi parametrami, przy czym
ogólnie
=(x,y), =(x,y), =(a,b), =(a,b)
Przykład problemu nieliniowego linearyzowalnego:
kinetyka reakcji pierwszego rzędu
o
o
o
k
C
k
C
t
kt
C
t
A
kt
C
t
A
B
A
ln
ln
ln
ln
exp
Jeżeli chcemy postępować poprawnie to należy
wykonać regresję ważoną, wyliczając wagi
poszczególnych przekształconych zmiennych
objaśniających zgodnie z rachunkiem błędów.
2
2
2
2
2
i
i
x
i
i
y
i
i
i
x
y
W poprzednim przykładzie
2
2
2
ln
2
1
A
A
A
Inne przykłady linearyzacji:
Równanie Michalisa-Mentena
S
K
S
K
S
m
m
1
v
1
v
v
1
v
v
max
max
max
Równanie Hilla
K
p
n
y
y
Kp
y
y
n
ln
ln
1
ln
1
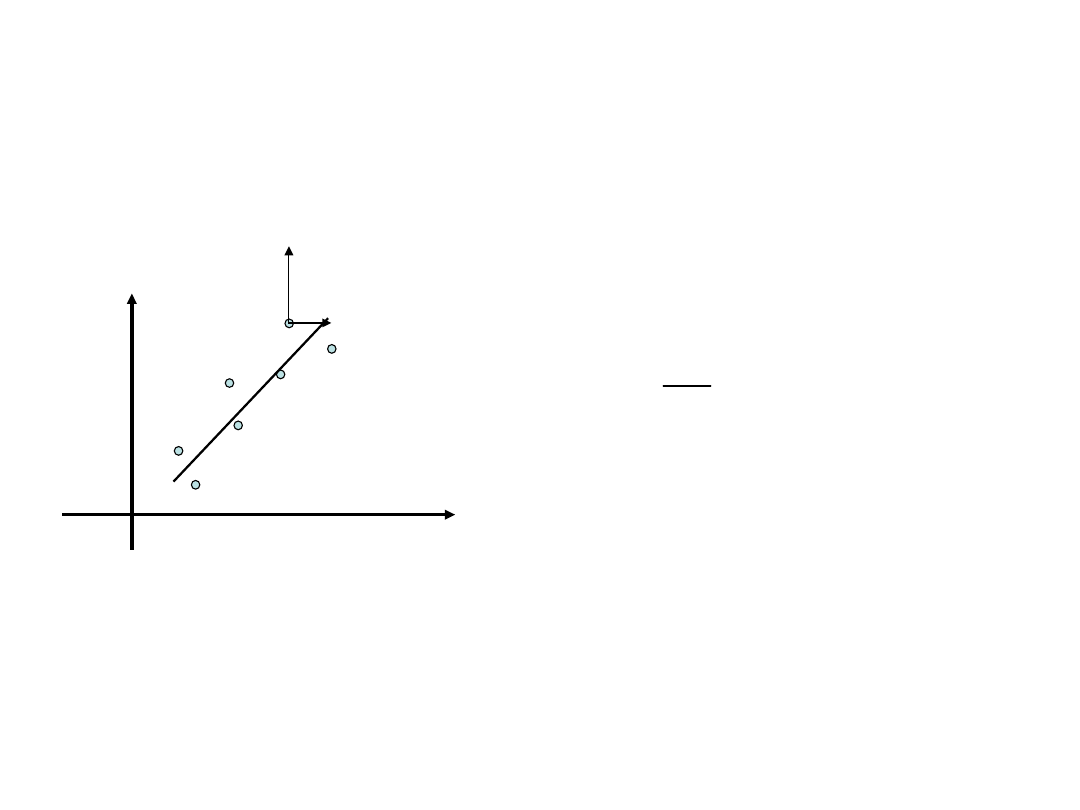
Obie zmienne są obarczone
porównywalnym błędem
x
y
x
y
2
2
2
2
2
2
2
x
y
x
y
y
a
x
y
Poprawiona wartość wagi zależy od a, które jest
parametrem regresji. Problem liniowy przekształca
się w nieliniowy. Problem można obejść
przeprowadzając najpierw “zwykłą” regresję i
wyznaczyć przybliżone a, następnie wstawić a do
wzoru na wagi i przeprowadzić regresję jeszcze raz.
Sposób: regresja ortogonalna
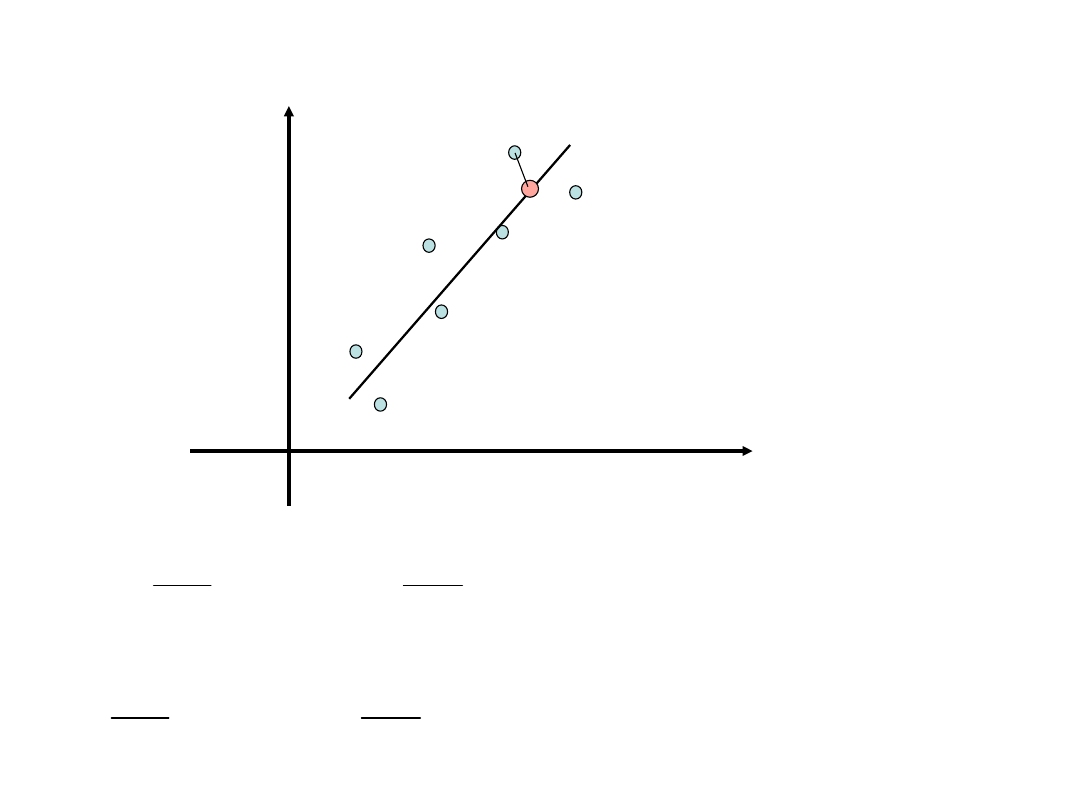
Regresja uogólniona albo analiza konfluentna
*
*
2
*
1
1
2
*
2
2
*
2
1
2
*
2
2
*
2
,
,
,
;
,
1
1
1
1
n
n
i
i
i
y
i
i
x
n
i
i
i
y
i
i
x
x
x
x
b
a
b
ax
y
x
x
y
y
x
x
i
i
i
i
x
y
(x,y)
(x*,y*
)
3
2
1
3
2
1
2
2
1
2
1
1
3
2
1
/
exp
exp
1
3
2
1
k
k
k
C
C
y
t
x
t
k
k
k
k
t
k
k
k
k
k
C
t
C
C
B
k
k
k
B
A
C
A
o
o
k
k
k
p
Przykład problemu nieliniowego nielinearyzowalngo:
kinetyka reakcji pierwszego rzędu z produktem
przejściowym
Parę słów o macierzach
Macierz m
n: tablica m na n (m wierszy n kolumn) liczb (np.
tabliczka mnożenia).
Macierz kwadradowa: m=n
Macierz symetryczna (zawsze kwadratowa): a
ij
=a
ji
Macierz transponowana A
T
: (A
T
)
ij
=a
ji
Macierz nieosobliwa: macierz o niezerowym wyznaczniku.
Macierz dodatnio określona:
x
T
Ax>0 dla każdego niezerowego wektora x.
Norma euklidesowa macierzy:
Norma spektralna macierzy
Wskaźnik uwarunkowania macierzy
n
i
n
j
ij
a
1
1
2
A
i
i
max
A
1
cond
A
A
A
Regresja liniowa wielokrotna
m
m
n
nm
n
n
m
m
x
p
x
p
x
p
y
y
x
x
x
y
x
x
x
y
x
x
x
2
2
1
1
2
1
2
2
22
21
1
1
12
11
Zmienne objaśniające x
1
,x
2
,…,x
m
nie muszą odpowiadać różnym
wielkościom lecz mogą być funkcjami tej samej wielkości
mierzonej (np. jej kolejnymi potęgami w przypadku
dopasowywania wielomianów). Tak więc możemy tu mówić o
ugólnym dopasowywaniu krzywych, które można przedstawić
jako liniowe funkcje parametrów lub ich kombinacji.
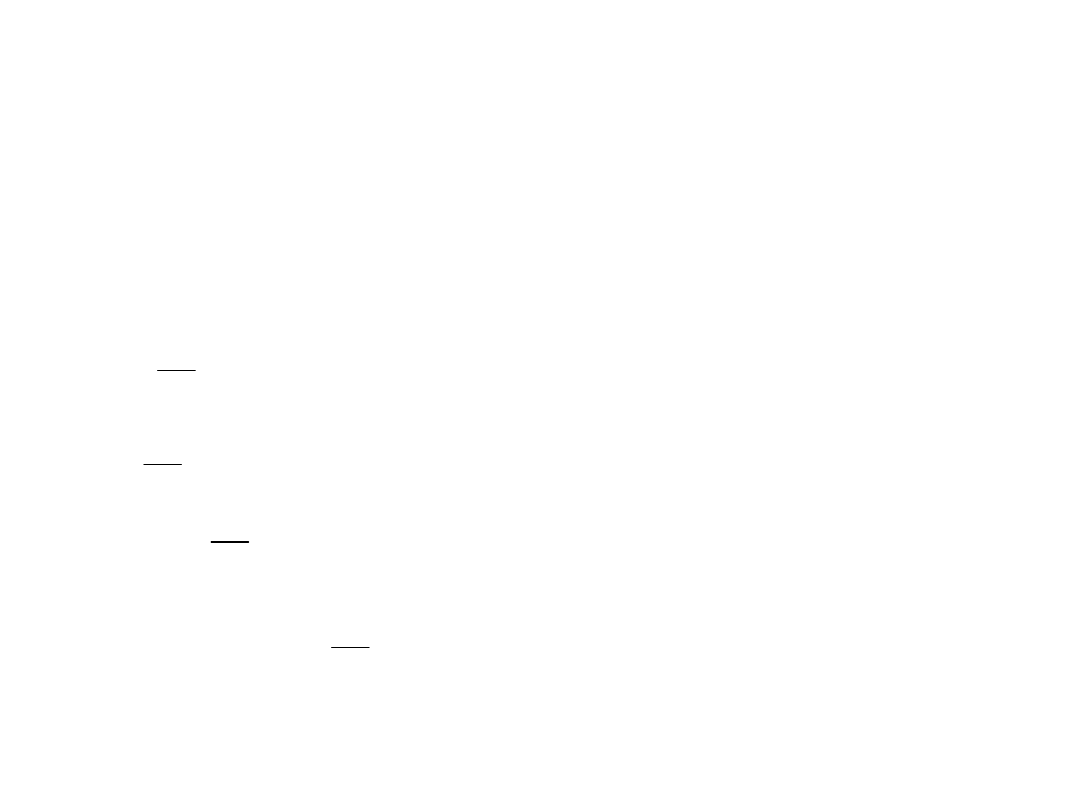
2
2
2
2
1
T
1
2
1
2
1
T
2
1
1
0
0
0
0
1
0
0
0
1
1
n
n
i
p
j
ij
j
i
i
n
i
p
j
ij
j
i
x
p
y
x
p
y
W
Xp
Y
W
Xp
Y
Xp
Y
Xp
Y
regresja
nieważona
regresja ważona
Podobnie jak w przypadku “zwykłej” regresji
minimalizujemy następujące sumy kwadratów odchyleń:
Przypadek szczególny: dopasowywanie wielomianu
n
m
n
n
m
m
m
m
y
x
x
y
x
x
y
x
x
x
p
x
p
p
y
1
2
1
2
2
1
1
1
1
1
1
1
0
1
1
1
m
i
i
im
m
n
i
im
n
i
i
im
n
i
i
im
m
i
i
i
m
n
i
im
i
n
i
i
n
i
i
i
m
i
i
i
m
n
i
im
i
n
i
i
i
n
i
i
y
x
p
x
p
x
x
p
x
x
y
x
p
x
x
p
x
p
x
x
y
x
p
x
x
p
x
x
p
x
1
1
2
2
1
2
1
1
1
1
2
1
2
2
1
2
2
1
1
1
2
1
1
1
1
2
1
2
1
1
1
2
1
WY
X
p
WX
X
Y
X
p
X
X
T
T
T
T
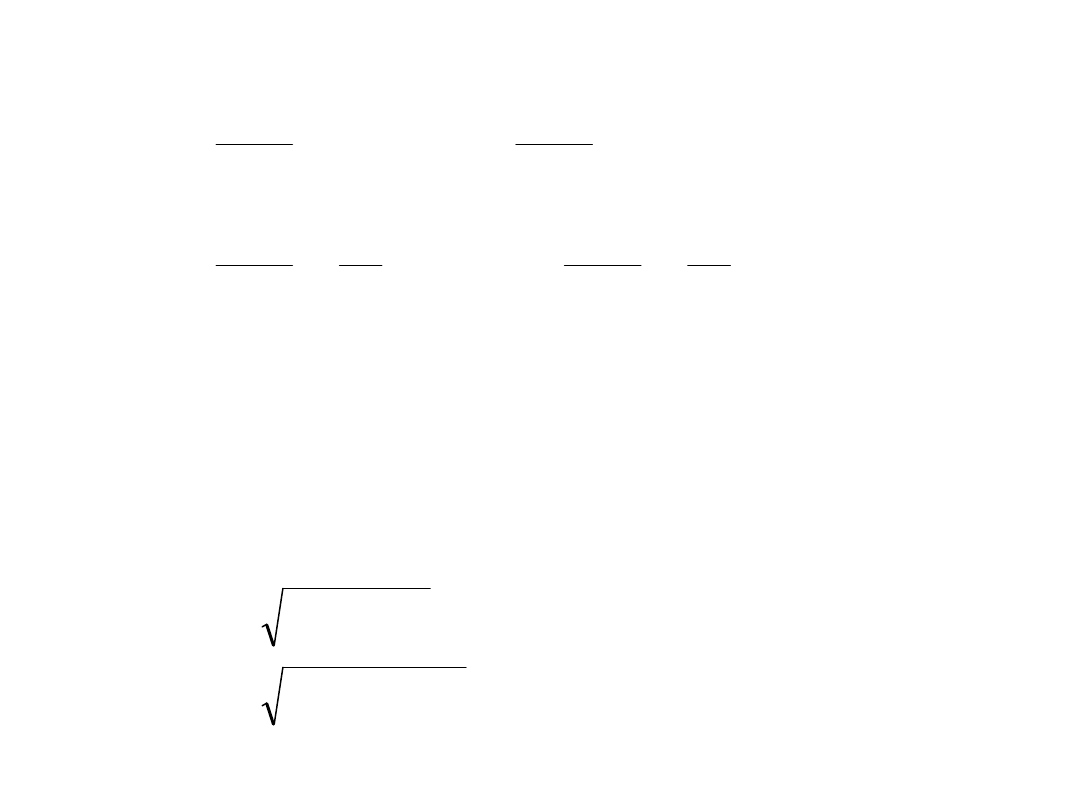
n
i
m
j
ji
j
i
i
n
i
obl
i
i
i
r
n
i
m
j
ji
j
i
n
i
obl
i
i
r
x
p
y
m
n
y
y
m
n
x
p
y
m
n
y
y
m
n
1
2
1
2
1
2
2
2
1
2
1
1
2
2
1
1
1
1
1
1
Macierz wariancji-kowariancji parametrów:
Wariancja resztowa:
1
2
T
*
*
X
X
p
p
p
p
p
D
T
r
E
1
2
T
*
*
WX
X
p
p
p
p
p
D
T
r
E
Odchylenia standardowe poszczególnych parametrów:
ii
r
p
ii
r
p
i
i
1
1
WX
X
X
X
T
T
Regresja nieważona
Regresja ważona
Regresja nieważona
Regresja ważona
j
i
ij
ij
m
m
m
m
m
m
m
m
m
1
1
1
2
1
2
21
1
12
2
2
1
2
2
2
21
1
12
2
1
R
D
Macierz wariancji-kowariancji (dyspersji)
parametrów
Macierz współczynników korelacji
parametrów
1
T
1
T
T
1
T
1
T
T
T
Y
Y
T
1
T
1
T
T
T
Y
Y
T
1
T
T
Y
T
1
T
Y
T
1
T
T
Y
T
1
T
T
1
T
T
1
T
T
1
T
T
1
T
X
X
X
X
IX
X
X
X
X
X
X
ε
ε
X
X
X
X
X
X
ε
ε
X
X
X
ε
X
X
X
ε
X
X
X
*
p
p
*
p
p
p
D
ε
X
X
X
*
Y
Y
X
X
X
Y
X
X
X
Y
X
X
X
p*
p
Y
X
X
X
p
2
2
*
r
r
E
E
E
E
Wyprowadzenie
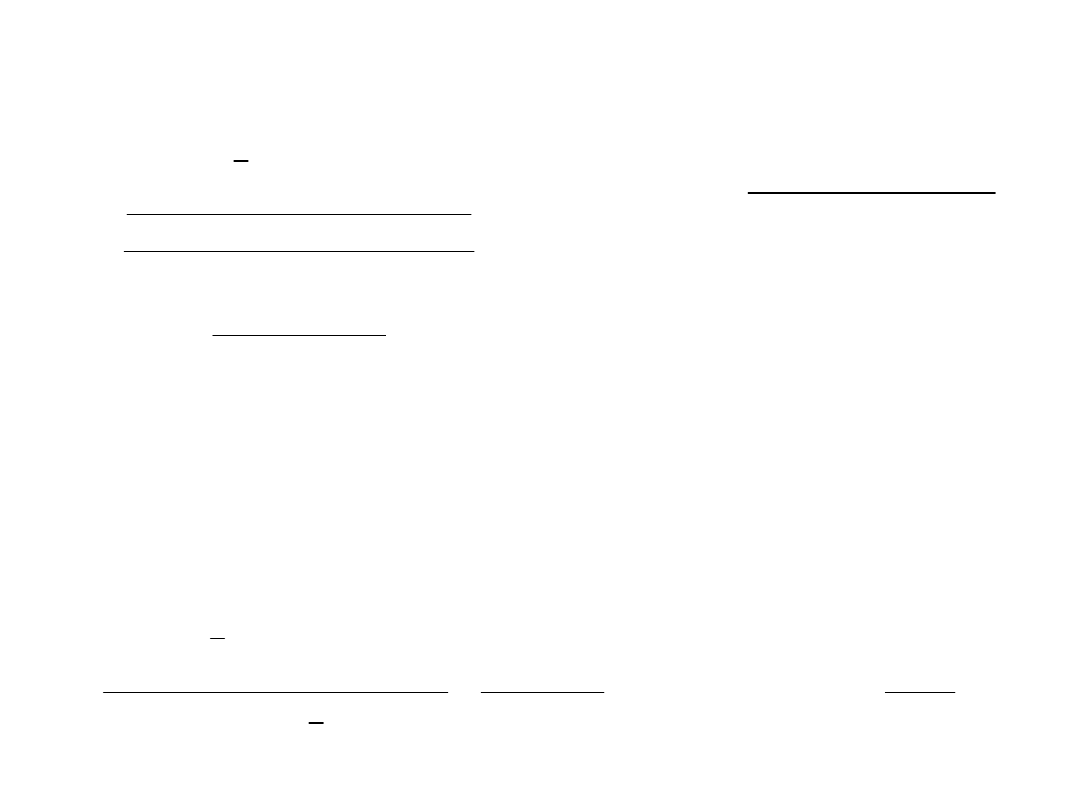
Test F dla istotności efektu
liniowego
m
n
y
y
m
y
y
y
y
F
n
i
obl
i
i
n
i
obl
i
i
n
i
i
1
2
1
2
1
2
1
2
2
1
2
1
2
1
2
,
m
m
m
m
m
m
n
m
m
F
Test F dla istotności
włączenia nowych
parmetrów
m
2
>m
1
F(m
2
,m
1
) porównujemy z
wartością krytyczną F
,m1-
m2,n-m2
dla poziomu istotności
.
F porównujemy z wartością
krytyczną F
,m-1,n-m
2
2
1
2
1
2
1
2
2
1 r
r
m
n
F
m
n
F
F
y
y
y
y
y
y
r
n
i
i
n
i
obl
i
i
n
i
i
Współczynnik determinacji i jego związek z F
Ocena istotności danego
parametru
Weryfikujemy następującą hipotezę zerową:
H
0
: p
i
= 0 wobec H
1
: a ≠ 0
(jeżeli a = 0 “w granicach błędu” to nie można mówić o
regresji)
Przy prawdziwości H
0
statystyka:
ma rozkład t Studenta z liczbą stopni swobody równej n - m.
i
p
i
p
t
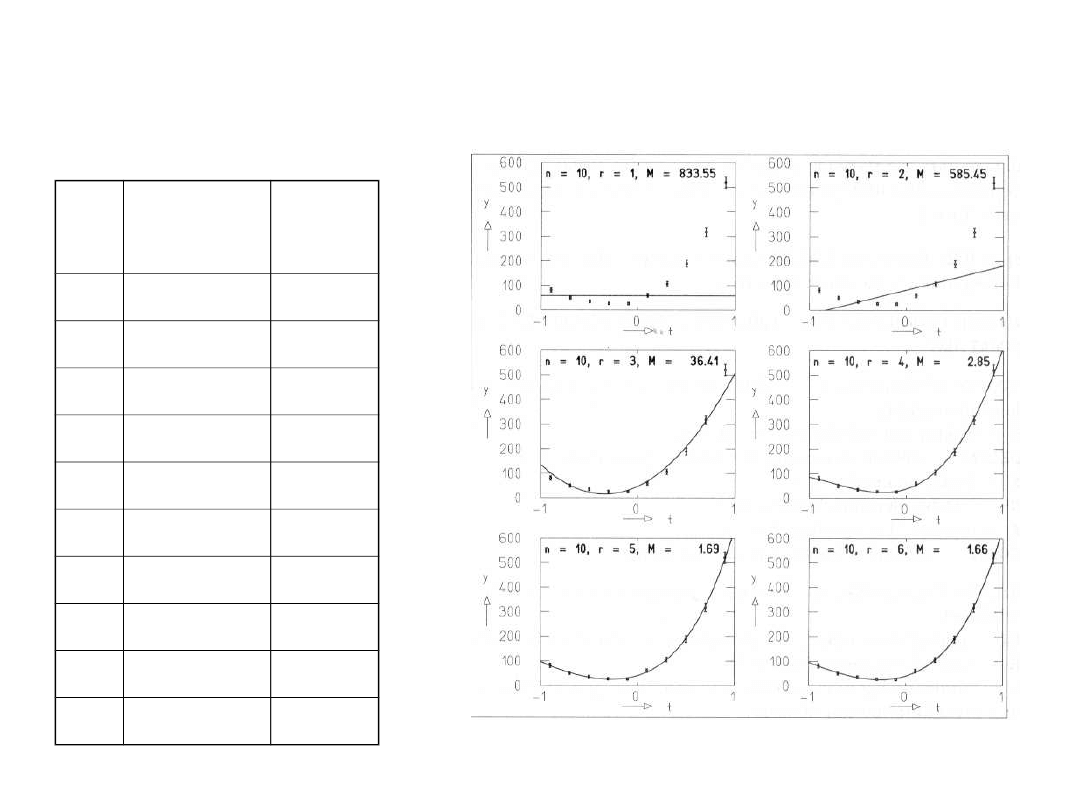
Przykład dopasowywania wielomianu: rozkład cosinusa kąta
rozpraszania mezonów K z protonami (zakładamy że
j
=sqrt(y
j
).
j
t
j
=cos(
j
)
y
j
1
-0.9
81
2
-0.7
50
3
-0.5
35
4
-0.3
27
5
-0.1
26
6
0.1
60
7
0.3
106
8
0.5
189
9
0.7
318
10
0.9
520
m
p
1
p
2
p
3
p
4
p
5
p
6
f
F
F
0.9
1
57.8
5
9 833.5
5
-
2
82.6
6 99.10
8
585.4
5
3.92
3.45
8
2
47.2
7
185.9
6
273.6
1
7 36.41 105.5
5
3.58
9
4
37.9
4
126.5
5
312.0
2
137.5
9
6
2.85 70.65 3.77
6
5
39.6
2
119.1
0
276.4
9
151.9
1
52.6
0
5
1.68
3.48 4.06
0
6
39.8
8
121.3
9
273.1
9
136.5
8
56.9
0
16.7
2
4
1.66
0.05 4.54
5
n
i
i
i
i
y
y
1
2
2
Ph2
50
0.056)
-0.190(
PBI
0.195)
0.835(
-
PV
0.002)
-0.010(
PSA
)
003
.
0
(
016
.
0
)
55
.
0
(
23
.
10
pIC
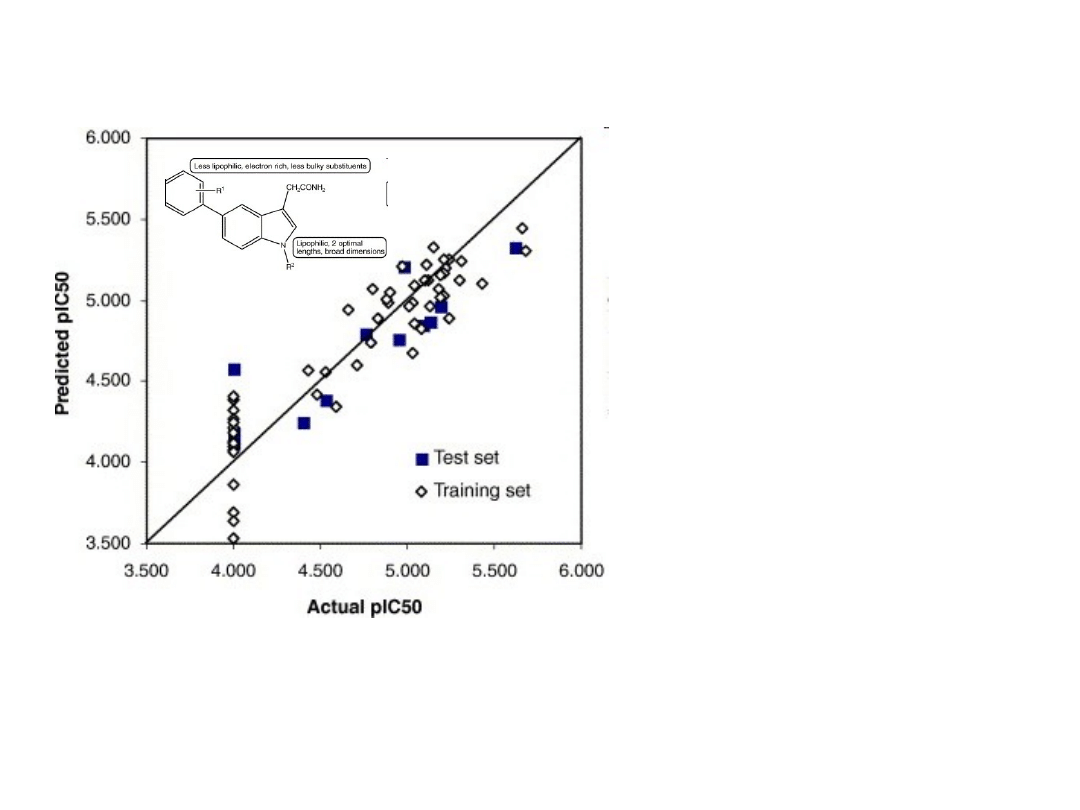
Przykład zastosowania regresji wielokrotnej w analizie
QSAR
(Leow et al., Bioorganic & Medicinal Chemistry Letters, 17(4), 1025-2032,
2007)
IC50 – stężenie związku
potrzebne do połówkowej
inhibicji ludzkiej
metylotransferazy
izopropenylocysteinowej.
pIC50=-log(IC50)
PSA – powierzchnia grup
polarnych [A
2
]
PV – objętość grup polarnych
[A
3
]
PB1 – parametr steryczny
podstawionej grupy fenylowej
Ph2
– lipofilowość
podstawionego pierścienia
fenylowego
Metody rozwiązywania układów równań
liniowych
n
n
nn
n
n
n
n
n
n
b
x
a
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
2
2
1
1
2
2
2
22
1
21
1
1
2
12
1
11
b
Ax
n
nn
n
n
n
n
b
b
b
a
a
a
a
a
a
a
a
a
2
1
2
1
2
22
21
1
12
11
b
A
0
det
A
Metody skończone:
• Metoda Gaussa
• Metoda Gaussa-Jordana
• Metody Choleskiego
• Metoda Householdera
• Metoda sprzężonych gradientów
Metody iteracyjne dla dużych układów równań:
• Metoda Jacobiego
• Metoda Gaussa-Seidla
n
n
nn
n
n
n
n
c
x
r
c
x
r
x
r
c
x
r
x
r
x
r
2
2
2
22
1
1
2
12
1
11
Metoda eliminacji Gaussa z wyborem elementu głównego w
kolumnie
Układ równań sprowadzamy do postaci trójkątnej
Układ z macierzą trójkątną można następnie łatwo rozwiązać
zaczynając od obliczenia wartości x
n
z n-tego równania,
następnie wstawić x
n
do równania n-1 i wyliczyć z niego x
n-1
,
następnie wstawić x
n
oraz x
n-1
do równania n-2 i wyliczyć x
n-2
aż
do dotarcia do równania pierwszego i wyznaczenia x
1
.
1. Wybieramy równanie i takie, że |a
i1
| jest największym elementem w
pierwszej kolumnie po czym przestawiamy i-te równanie na początek i
eliminujemy x
1
z równań od 2 do n.
)
1
(
)
1
(
2
2
)
1
(
2
)
1
(
2
)
1
(
2
2
)
1
(
22
)
0
(
1
)
0
(
1
2
)
0
(
12
1
)
0
(
11
n
n
n
n
n
n
n
n
b
x
a
x
a
b
x
a
x
a
b
x
a
x
a
x
a
1
1
,
1
)
0
(
11
)
0
(
1
)
0
(
1
)
0
(
)
1
(
)
0
(
11
)
0
(
1
)
0
(
1
)
0
(
)
1
(
i
a
a
b
b
b
k
i
a
a
a
a
a
i
i
i
i
k
ik
ik
2. Procedurę powtarzamy z macierzą A
(1)
o rozmiarach (n-1)x(n-1) i
wektorem b
(1)
o rozmiarze n-1, eliminując z nich drugą zmienną i
otrzymując macierz A
(2)
o rozmiarach (n-2)x(n-2) i wektor b
(2)
o
rozmiarze n-2. W ten sam sposób postępujemy z kolejnymi macierzami
A
(2)
, A
(3)
,..., A
(n-1)
oraz wektorami b
(2)
, b
(3)
,..., b
(n-1)
.
j
i
a
a
b
b
b
j
k
j
i
a
a
a
a
a
j
jj
j
ij
j
j
j
i
j
i
j
jj
j
ij
j
jk
j
ik
j
ik
)
1
(
)
1
(
)
1
(
)
1
(
)
(
)
1
(
)
1
(
)
1
(
)
1
(
)
(
,
Dla j-tego kroku
Po zakończeniu operacji otrzymujemy układ równań z macierzą
trójkątną
)
1
(
)
1
(
22
)
0
(
11
)
1
(
)
1
(
)
2
(
3
)
0
(
3
3
)
2
(
33
)
1
(
2
)
0
(
2
3
)
1
(
23
2
)
1
(
22
)
0
(
1
)
0
(
1
3
)
0
(
13
2
)
0
(
12
1
)
0
(
11
)
1
(
det
n
nn
p
n
n
n
n
nn
n
n
n
n
n
n
a
a
a
b
x
a
b
x
a
x
a
b
x
a
x
a
x
a
b
x
a
x
a
x
a
x
a
A
p jest liczbą przestawień wierszy macierzy A podczas
sprowadzania układu równań do postaci trójkątnej.
1
,...,
2
,
1
1
)
1
(
)
1
(
)
1
(
)
1
(
)
1
(
)
1
(
n
n
j
x
a
a
a
b
x
a
b
x
k
n
j
k
j
jj
j
jk
j
jj
j
j
j
n
nn
n
n
n
3. Z otrzymanego układu równań z macierzą trójkątną
wyznaczamy po kolei x
n
, x
n-1
,..., x
1
.
Wysiłek obliczeniowy (liczba mnożeń i dzieleń) w metodzie
eliminacji Gaussa:
Faktoryzacja macierzy A: n(n
2
-1)/3 operacji
Przekształcenie wektora b: n(n-1)/2 operacji
Obliczenie x: n(n+1)/2 operacji.
Razem: n
3
/3+n
2
-n/3≈n
3
/3 operacji.
Metody typu Choleskiego dla macierzy symetrycznych silnie
nieosobliwych
T
LDL
A
L
T
L
D
L
T
LL
A
klasyczna metoda Choleskiego
tylko dla macierzy dodatnio
określonych.
Postępowanie przy rozwiązywaniu układów równań metodą
faktoryzacji Choleskiego.
1. Wyznaczenie faktorów L i D. Układ przyjmuje postać
LDL
T
x=b
2. Obliczenie pomocniczego wektora w.
w=L
-1
b przez rozwiązanie układu równań Lw=b.
Ponieważ L jest macierzą trójkątną dolną układ ten rozwiązuje się
wyliczając kolejno w
1
, w
2
,…, w
n
podobnie jak w koncowym etapie
eliminacji Gaussa.
3. Obliczenie z=D
-1
w (D jest macierzą diagonalną więc po prostu
dzielimy w
i
przez d
ii
. Ten etap nie występuje w klasycznej metodzie
Choleskiego.
4. Obliczenie x poprzez rozwiązanie układu równań z macierzą
trójkątną górną
L
T
x=z
Ten etap jest identyczny z ostatnim etapem metody eliminacji
Gaussa.
Metoda wymaga ok. n
3
/6 operacji (2 razy mniej niż metoda eliminacji
Gaussa). Uwaga: klasyczna metoda Choleskiego wymaga ponadto
n pierwiastkowań.
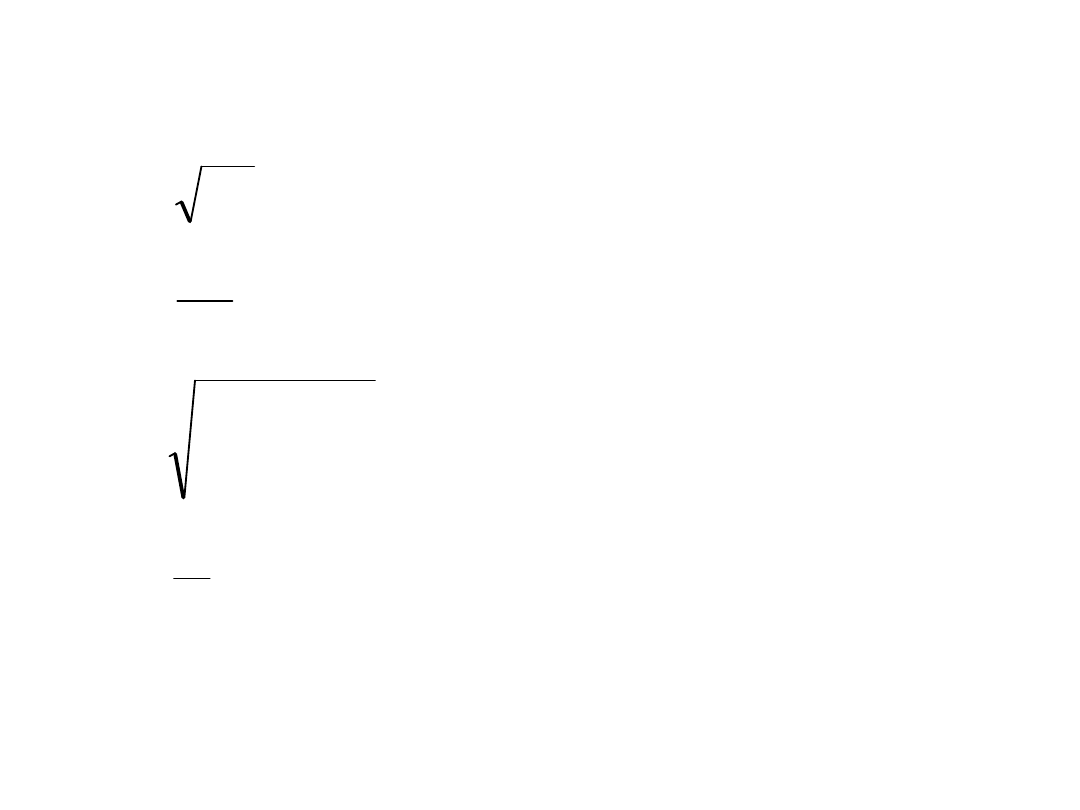
Klasyczna faktoryzacja Choleskiego (A=LL
T
)
1
1
1
1
2
11
1
1
11
11
1
i
k
jk
ik
ij
ii
ji
i
k
jk
ii
ii
j
j
l
l
a
l
l
l
a
l
l
a
l
a
l
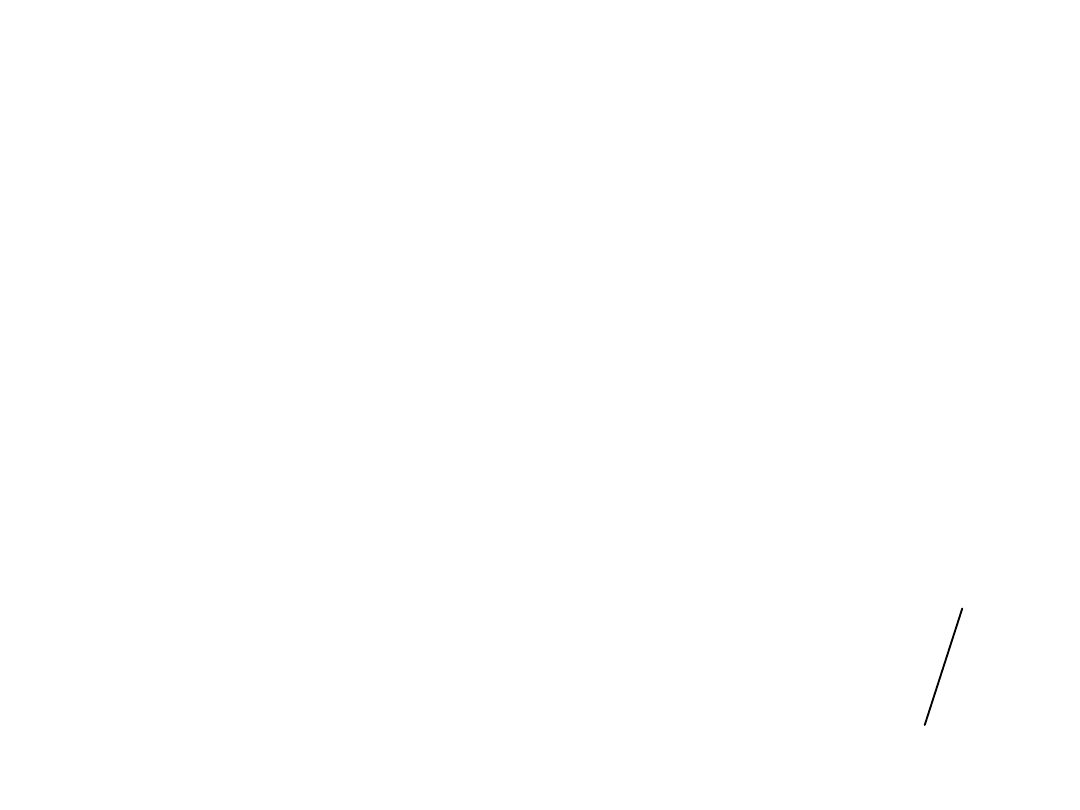
Faktoryzacja “bezpierwiastkowa”
1
0
1
0
0
1
1
,
1
21
2
1
n
n
n
n
l
l
l
d
d
d
L
D
i
n
k
ik
jk
k
ji
ji
j
j
n
k
nk
k
nn
n
i
k
ki
k
ii
i
d
l
l
d
a
l
d
a
l
l
d
a
d
l
d
a
d
a
d
1
1
1
1
1
1
1
2
1
1
2
11
1
/