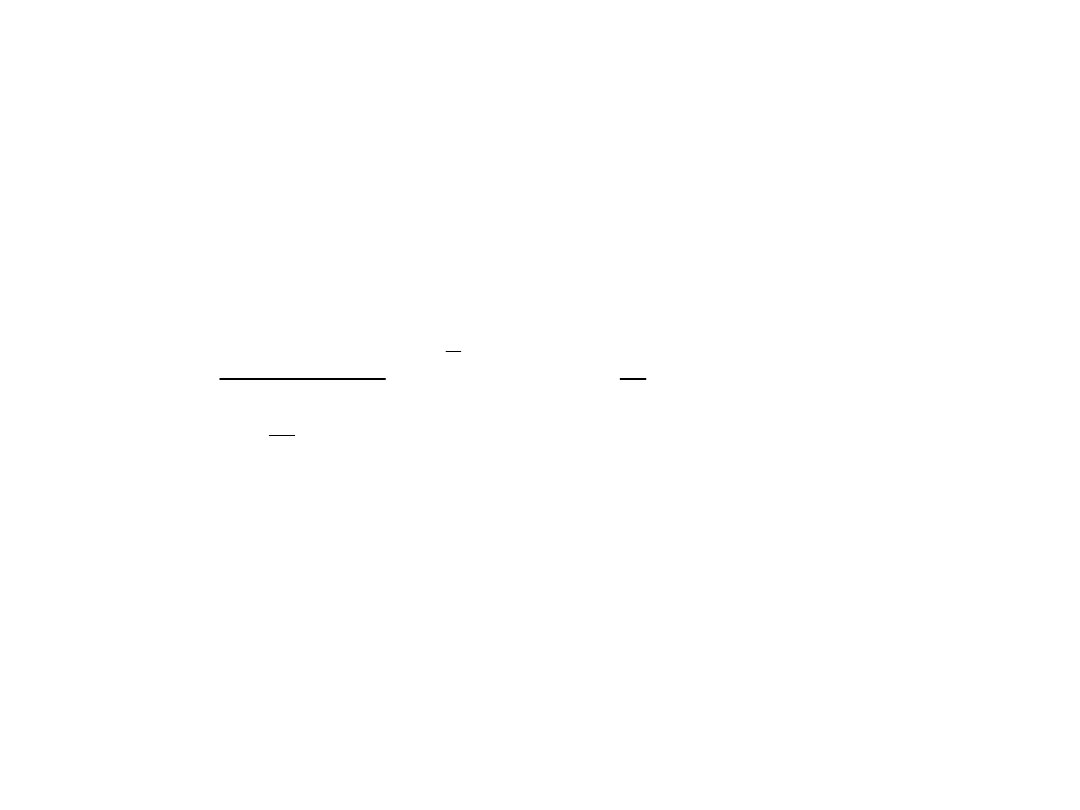
Rozkład wariancji z próby (rozkład



2

)

Pobieramy próbę x

1

,x

2

,...,x

n

z rozkładu

normalnego o a=0 i =1. Dystrybuanta

rozkładu zmiennej x

2

=x

1

2

+x

2

2

+...+x

n

2

jest

dana następującą funkcją:

du

u

u

n

F

n

n











 





















2

1

exp

2

2

1

1

)

(

2

0

1

2

1

2





gdzie (y) jest funkcją gamma Eulera (silnią

uogólnioną na liczby rzeczywiste).













0

)

1

(

dt

e

t

x

t

x











 





















u

2

1

exp

u

2

n

2

1

1

)

(

f

1

n

2

1

n

2

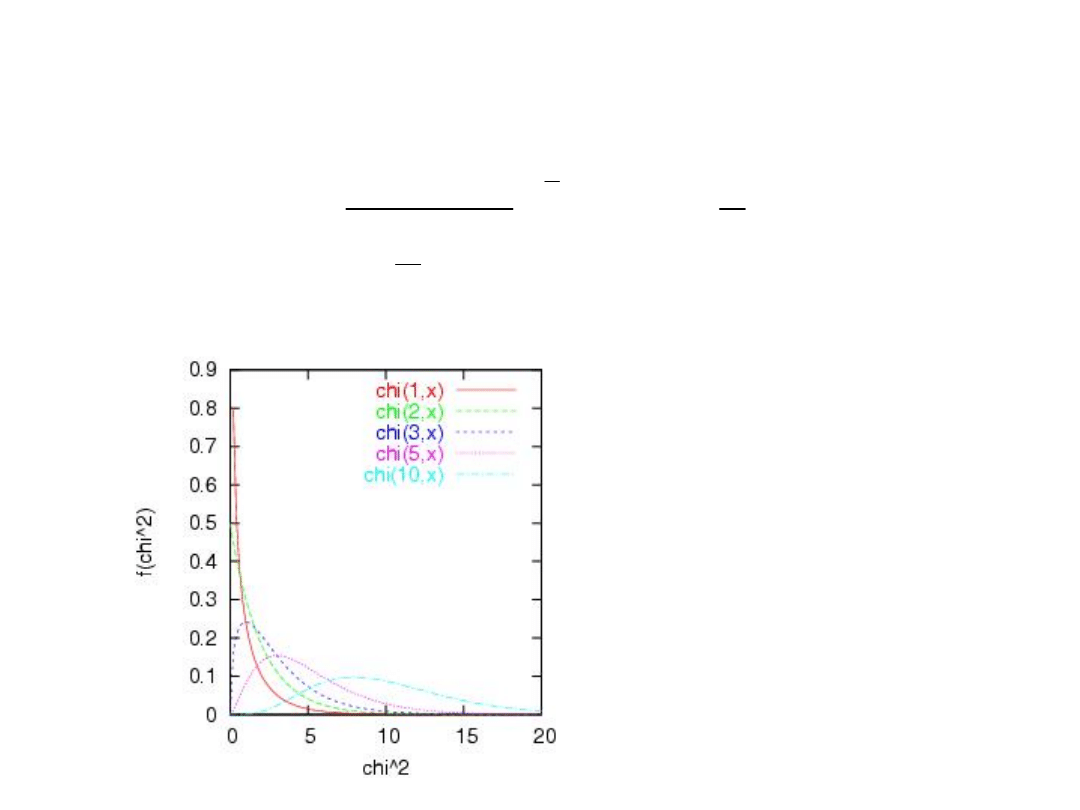
Zatem sam rozkład wariancji jest dany następującą
funkcją

Zasada największej wiarygodności

(Maximum Likelihood Principle)

Mamy próbę (x

1

,x

2

,...,x

n

)

f(x,): funkcja określająca rozkład gęstości

prawdopodobieństwa, gdzie  jest

zestawem parametrów rozkładu.

Zasada największej wiarygodności: najlepsze

 maksymalizuje prawdopodobieństwo

wystąpienia próby.

Ta zasada jest podstawą wszystkich metod

estymowania parametrów rozkładu

prawdopodobieństwa (a zatem i modelu

matematycznego) z próby danych.

Ponieważ poszczególne elementy próby są
niezależne

dx

x

f

dP

j

j

)

,

(

)

(

)

(

λ









N

j

j

dx

x

f

dP

1

)

(

)

;

(

λ

)

(

)

(

)

;

(

)

;

(

2

1

1

2

)

(

1

1

)

(

λ

λ

λ

λ

L

L

x

f

x

f

Q

N

j

j

N

j

j













iloraz wiarygodności















N

j

j

N

j

j

x

f

L

x

f

L

1

)

(

1

)

(

)

;

(

ln

)

;

(

λ

λ



funkcja
wiarygodności

Przykład jakościowego porównywania dwu
modeli poprzez obliczenie ilorazu
wiarygodności

Rzucamy monetą asymetryczną.
Przypuszczamy, że albo prawdopodobieństwo
wyrzucenia reszki jest 2 razy większe niż
prawdopobobieństwo wyrzucenia orła (A) albo
odwrotnie (B). Przypuśćmy, że w 5 rzutach
otrzymaliśmy 1 raz orła i 4 razy reszkę. Wtedy:

8

,

3

2

3

1

,

3

2

3

1

4

4

































B

A

B

A

L

L

Q

L

L

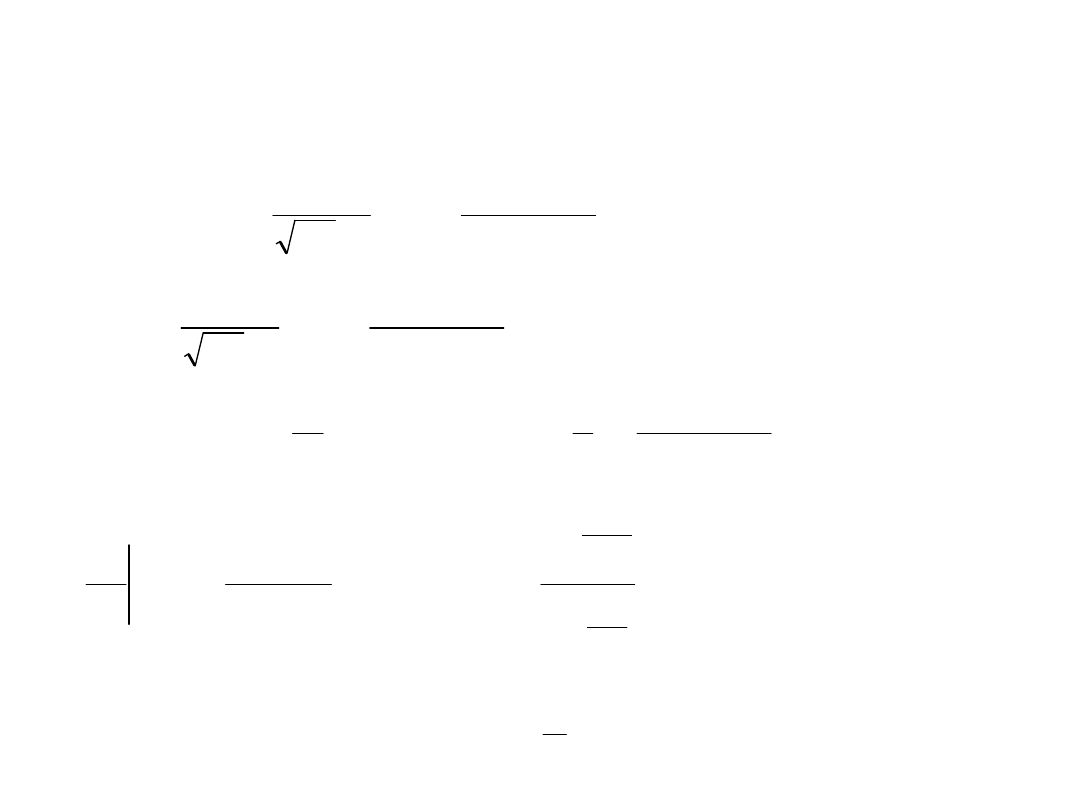
Przykład zastosowania zasady największej
wiarygodności: obliczanie wartości średniej przy
założeniu, że rozkład prawdopodobieństwa jest
rozkładem normalnym

























































































N

j

j

N

j

j

j

N

j

j

j

N

j

j

j

N

j

j

j

j

N

j

j

j

j

j

j

x

x

d

d

x

N

L

x

L

dx

x

dx

x

f

1

2

1

2

)

(

*

1

2

*

)

(

1

2

2

)

(

1

2

2

)

(

1

2

2

)

(

)

(

1

0

2

)

(

2

1

ln

)

2

ln(

2

ln

)

(

2

)

(

exp

2

1

2

)

(

exp

2

1

)

;

(

*















































Jeżeli 

1

=

2

=…=

n

=

 







n

j

j

x

n

1

*

1



















































)

(

''

)

(

)

(

''

)

(

)

(

'

)

(

'

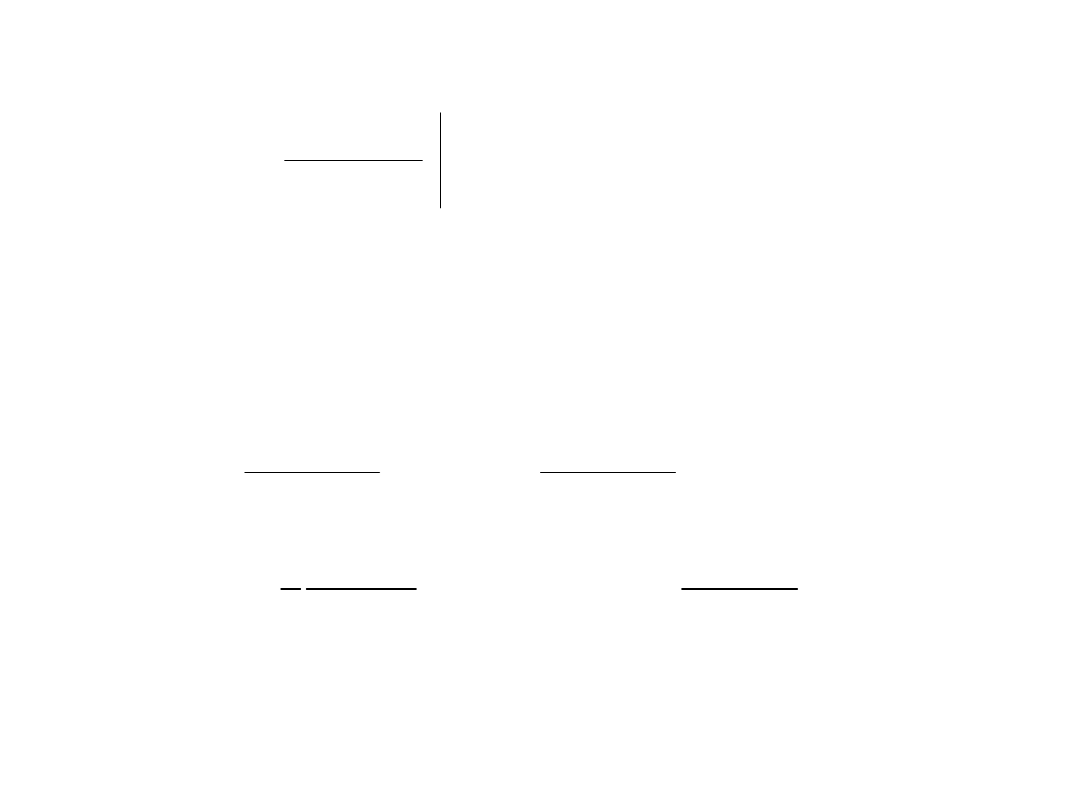
0

)

;

(

)

;

(

'

)

(

'

*

*

*

*

*

1

)

(

)

(

*

*

























N

j

j

j

x

f

x

f

Właściwości asymptotyczne funkcji
wiarygodności

Dla dużych prób





























































































2

2

*

2

2

*

*

2

*

2

'

)

(

)

(

'

1

)

(

)

(

*

2

)

(

exp

)

(

2

1

)

(

)

(

/

1

)

(

'

)

;

(

)

;

(

'

)

;

(

)

;

(

'

)

(

''

*

*

b

k

L

b

b

NE

x

f

x

f

NE

x

f

x

f

j

j

N

j

j

j







































Przypadek wielowymiarowy



































































































































 

2

2

2

2

1

2

2

2

2
2

2

1

2

2

1

2

2

1

2

2

1

2

*

*

*

*

1

1

*

2

*

)

(

)

(

2

1

)

(

)

(

)

(

2

1

)

(

)

(

*

p

p

p

p

p

T

l

l

p

k

p

l

k

k

l

k





















































































A

λ

λ

A

λ

λ

λ

λ

λ

λ











































































































































































































































2

2

2

2

1

2

2

2

2
2

2

1

2

2

1

2

2

1

2

2

1

2

*

*

)

(

)

(

)

(

2

1

exp

p

p

p

p

p

T

E

E

E

E

E

E

E

E

E

E

k

L































































A

B

λ

λ

B

λ

λ

Dla dużych prób rozkład parametrów staje się
rozkładem normalnym z macierzą wariancji-kowariancji
B.

Jeżeli jednak liczebność próby jest ograniczona to
odchylenia od normalności rozkładu mogą być
znaczne.

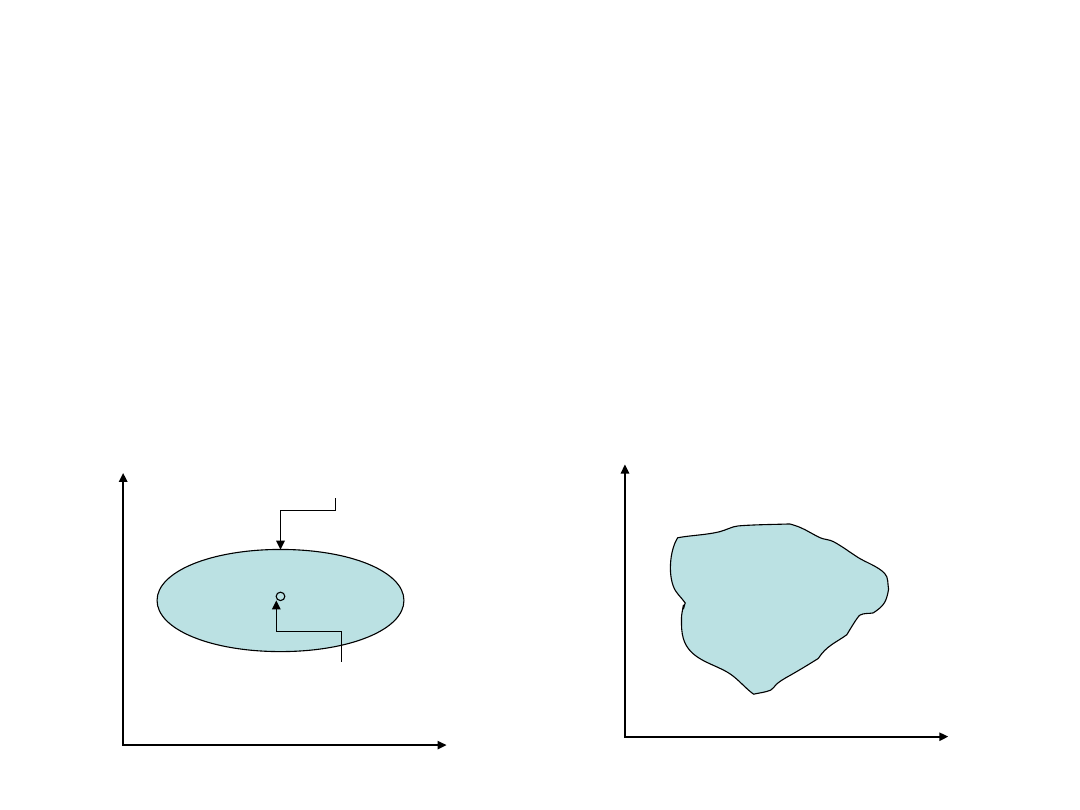
Obszary ufności w przestrzeni

parametrów

Obszar ufności definiujemy jako taki obszar w
otoczeniu wartości oczekiwanej wektora parametrów i
ograniczony powierzchnią o stałej gęstości
prawdopodobieństwa, że prawdopodobieństwo
znalezienia w nim prawdziwych wartości parametrów
jest nie mniejsze niż zadana wartość (kwantyl). W
jednym wymiarze mówimy o przedziale ufności.



1



2

P=g



1



2



*

99

.

0

3

;

683

.

0

)

1

(

)

erf(

2

)

(

)

(

)

(

2

)

(

exp

)

(

*

2

2

*





























 

































P

P

g

d

L

d

L

P

kg

k

L







































W jednym wymiarze

 













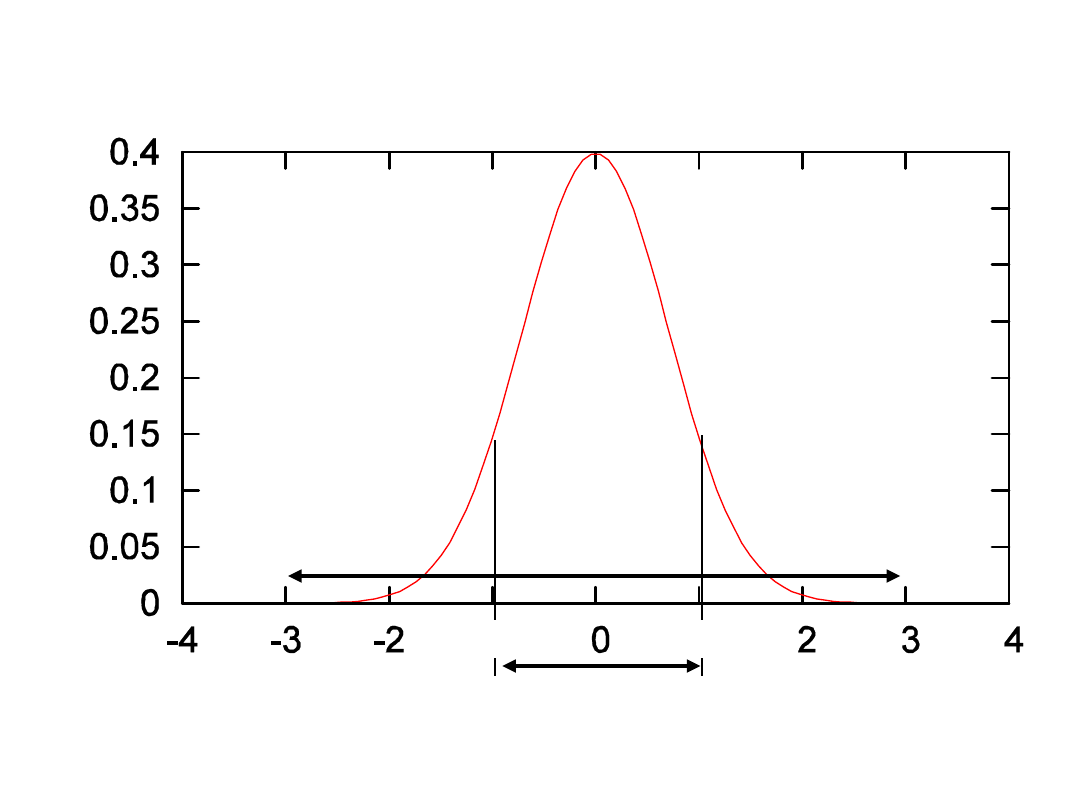
01439

.

0

,

03734

.

0

,

09020

.

0

19875

.

0

,

39347

.

0

,

68269

.

0

2

1

,

2

)

exp(

)

(

1

)

,

(

2

,

2

)

;

(

6

5

4

3

2

1

0

1

0

2

2























































W

W

W

W

W

W

n

P

W

dt

t

t

a

x

a

P

g

n

P

d

n

f

W

n

x

a

g





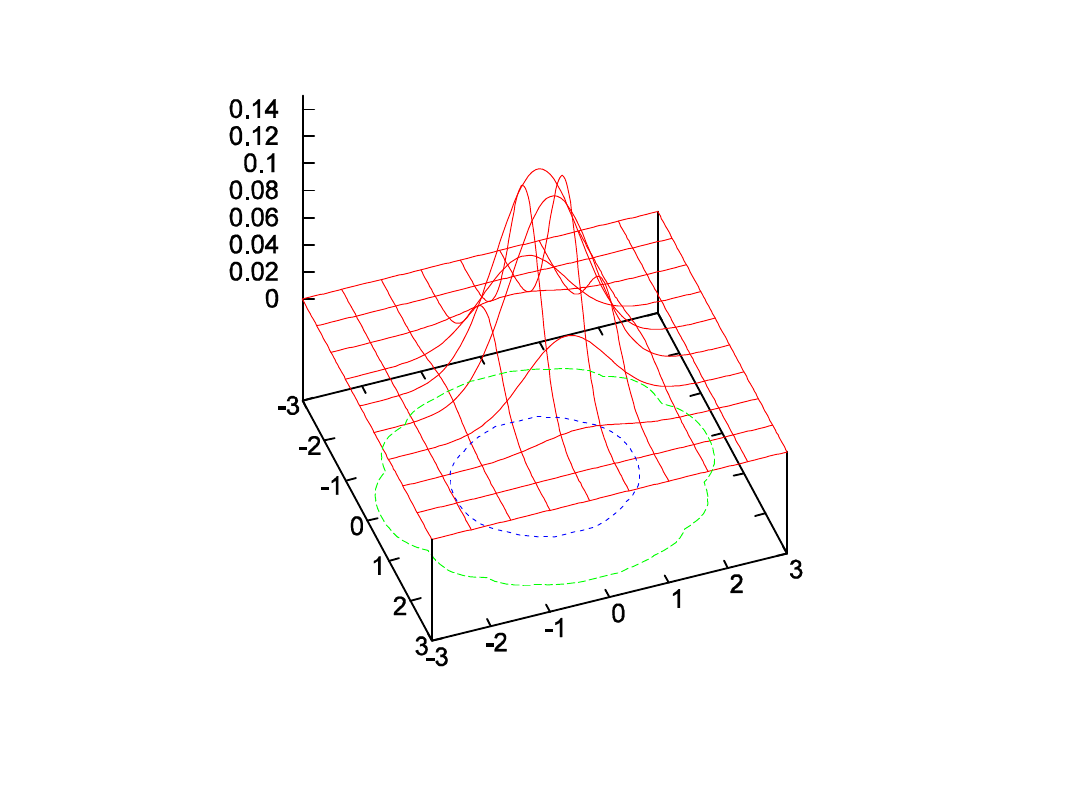
Ogólnie dla wielowymiarowego rozkładu
Gaussa