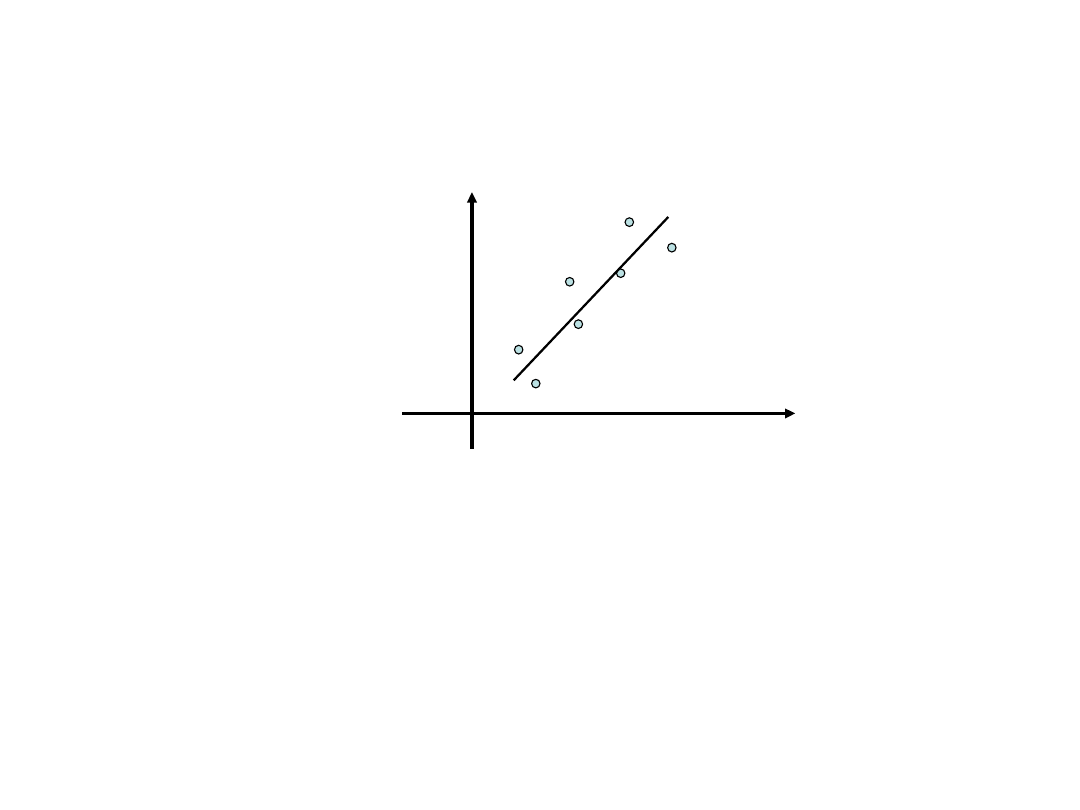
Regresja liniowa
Dany jest układ punktów
n
n
y
,
x
y
,
x
y
,
x
2
2
1
1
x
y
b
ax
y
i
i
x – zmienna objaśniająca (nie obarczona
błędem)
y – zmienna zależna (obarczona błędem)
Naszym zadaniem jest poprowadzenie „najlepszej” prostej
przez te punkty.
x
a
y
x
x
n
y
x
x
y
x
b
x
y
x
x
x
y
x
xy
x
x
n
y
x
y
x
n
a
b
b
a
a
b
a
b
ax
y
y
y
b
a
n
i
i
n
i
i
n
i
i
i
n
i
i
n
i
i
n
i
i
n
i
i
n
i
i
n
i
i
n
i
i
n
i
i
i
n
i
i
i
n
i
obl
i
i
2
1
1
2
1
1
1
1
2
2
2
2
1
1
2
1
1
1
1
2
1
2
var
,
cov
0
,
0
,
,
Wyznaczanie optymalnych parametrów a
i b
Macierz wariancji-kowariancji wyznaczonych parametrów
równania prostej
n
i
i
i
r
r
b
ax
y
n
E
1
2
2
1
2
T
2
1
*
*
A
p
p
p
p
2
2
1
1
2
1
2
12
1
2
2
1
1
2
1
2
2
22
1
2
2
2
1
1
2
2
11
1
2
r
n
i
i
n
i
i
n
i
i
r
ab
r
n
i
i
n
i
i
n
i
i
r
b
r
n
i
i
n
i
i
r
a
x
x
n
x
x
x
n
x
x
x
n
n
A
A
A
r
2
– wariancja resztowa
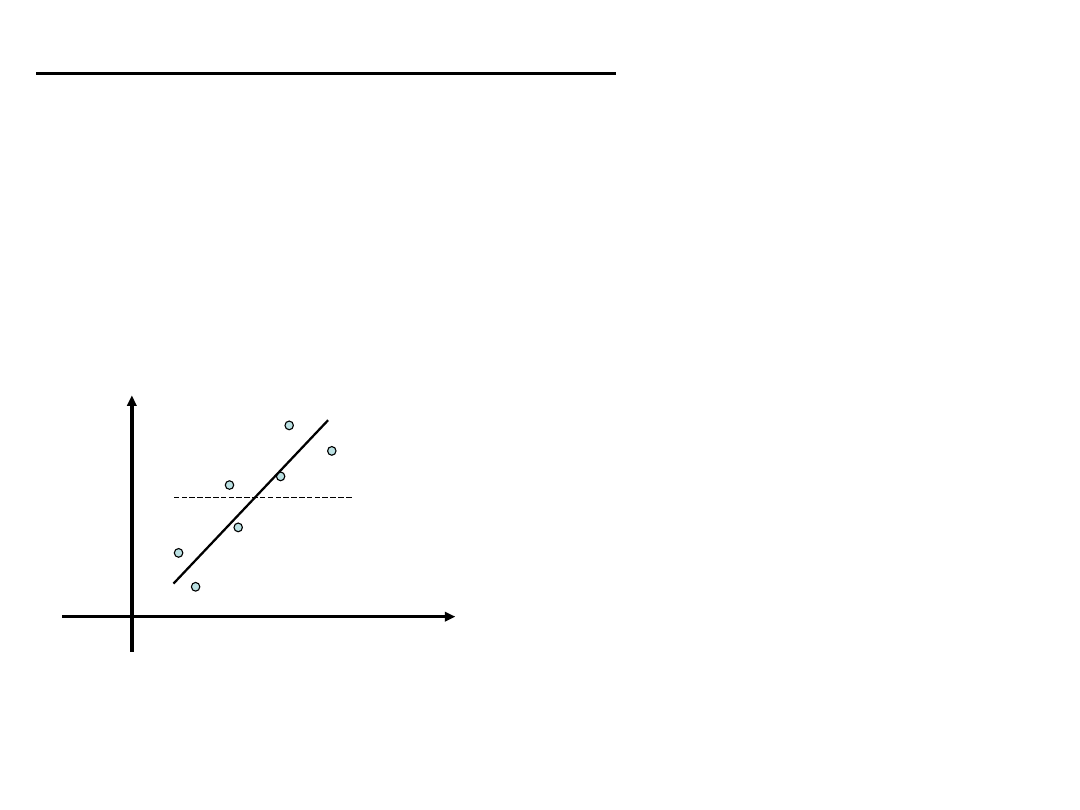
x
y
Ocena wyników regresji:
-Test dobroci dopasowania (
2
)
-Test istotności efektu liniowego (współczynnik
korelacji)
2
2
1
1
2
2
1
1
2
1
1
1
var
var
,
cov
r
y
y
n
x
x
n
y
x
y
x
n
y
x
y
x
r
n
i
i
n
i
i
n
i
i
n
i
i
n
i
n
i
i
i
n
i
i
i
współczynnik determinacji (ułamek wyjaśnionej
wariancji)
r > 0 – korelacja dodatnia
r<0 – korelacja ujemna
|r|>0.7 – dobra korelacja
0.3<|r|<0.7 – słaba korelacja
|r|<0.3 – brak korelacji
2
1
1
2
1
2
1
2
n
y
y
y
y
y
y
F
n
i
obl
i
i
n
i
obl
i
i
n
i
i
Bardziej ogólny przypadek dopasowywania równania
prostej: regresja ważona
n
i
i
i
i
n
i
i
i
i
b
ax
y
w
b
ax
y
b
,
a
1
2
1
2
2
n
i
i
i
n
i
i
n
i
i
i
n
i
i
i
i
n
i
i
i
n
i
i
i
y
b
a
x
y
x
b
x
a
x
1
2
1
2
1
2
1
2
1
2
1
2
2
1
Linearyzacja
Mamy dopasować funkcję nieliniową
y=f(x,y;a.b)
Przekształcamy funkcję do takiej postaci aby uzyskać
postać zlinearyzowaną
=+
Gdzie jest nową zmienną zależną, nową zmienną
objaśniającą a a i b są nowymi parametrami, przy czym
ogólnie
=(x,y), =(x,y), =(a,b), =(a,b)
Przykład problemu nieliniowego linearyzowalnego:
kinetyka reakcji pierwszego rzędu
o
o
o
k
C
k
C
t
kt
C
t
A
kt
C
t
A
B
A
ln
ln
ln
ln
exp
Jeżeli chcemy postępować poprawnie to należy
wykonać regresję ważoną, wyliczając wagi
poszczególnych przekształconych zmiennych
objaśniających zgodnie z rachunkiem błędów.
2
2
2
2
2
i
i
x
i
i
y
i
i
i
x
y
W poprzednim przykładzie
2
2
2
ln
2
1
A
A
A
Inne przykłady linearyzacji:
Równanie Michalisa-Mentena
S
K
S
K
S
m
m
1
v
1
v
v
1
v
v
max
max
max
Równanie Hilla
K
p
n
y
y
Kp
y
y
n
ln
ln
1
ln
1
Obie zmienne są obarczone
porównywalnym błędem
x
y
x
y
2
2
2
2
2
2
2
x
y
x
y
y
a
x
y
Poprawiona wartość wagi zależy od a, które jest
parametrem regresji. Problem liniowy przekształca
się w nieliniowy. Problem można obejść
przeprowadzając najpierw “zwykłą” regresję i
wyznaczyć przybliżone a, następnie wstawić a do
wzoru na wagi i przeprowadzić regresję jeszcze raz.
Sposób: regresja ortogonalna
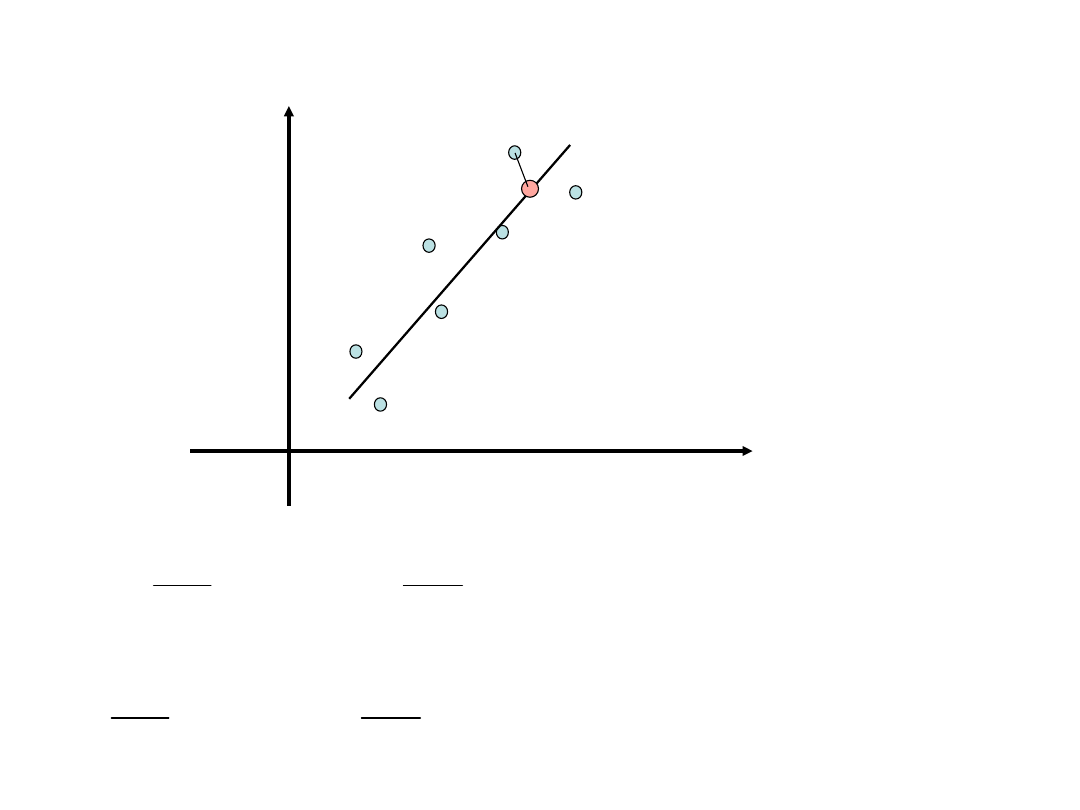
Regresja uogólniona albo analiza konfluentna
*
*
2
*
1
1
2
*
2
2
*
2
1
2
*
2
2
*
2
,
,
,
;
,
1
1
1
1
n
n
i
i
i
y
i
i
x
n
i
i
i
y
i
i
x
x
x
x
b
a
b
ax
y
x
x
y
y
x
x
i
i
i
i
x
y
(x,y)
(x*,y*
)
3
2
1
3
2
1
2
2
1
2
1
1
3
2
1
/
exp
exp
1
3
2
1
k
k
k
C
C
y
t
x
t
k
k
k
k
t
k
k
k
k
k
C
t
C
C
B
k
k
k
B
A
C
A
o
o
k
k
k
p
Przykład problemu nieliniowego nielinearyzowalngo:
kinetyka reakcji pierwszego rzędu z produktem
przejściowym
Regresja liniowa wielokrotna
m
m
n
nm
n
n
m
m
x
p
x
p
x
p
y
y
x
x
x
y
x
x
x
y
x
x
x
2
2
1
1
2
1
2
2
22
21
1
1
12
11
Zmienne objaśniające x
1
,x
2
,…,x
m
nie muszą odpowiadać różnym
wielkościom lecz mogą być funkcjami tej samej wielkości
mierzonej (np. jej kolejnymi potęgami w przypadku
dopasowywania wielomianów).
2
2
2
2
1
T
1
2
1
2
1
T
2
1
1
0
0
0
0
1
0
0
0
1
1
n
n
i
p
j
ij
j
i
i
n
i
p
j
ij
j
i
x
p
y
x
p
y
W
Xp
Y
W
Xp
Y
Xp
Y
Xp
Y
regresja
nieważona
regresja ważona
Przypadek szczególny: dopasowywanie wielomianu
n
m
n
n
m
m
m
m
y
x
x
y
x
x
y
x
x
x
p
x
p
p
y
1
2
1
2
2
1
1
1
1
1
1
1
0
1
1
1
m
i
i
im
m
n
i
im
n
i
i
im
n
i
i
im
m
i
i
i
m
n
i
im
i
n
i
i
n
i
i
i
m
i
i
i
m
n
i
im
i
n
i
i
i
n
i
i
y
x
p
x
p
x
x
p
x
x
y
x
p
x
x
p
x
p
x
x
y
x
p
x
x
p
x
x
p
x
1
1
2
2
1
2
1
1
1
1
2
1
2
2
1
2
2
1
1
1
2
1
1
1
1
2
1
2
1
1
1
2
1
WY
X
p
WX
X
Y
X
p
X
X
T
T
T
T
n
i
m
j
ij
j
i
r
x
p
y
m
n
1
2
1
2
1
Test F dla istotności efektu
liniowego
m
n
y
y
m
y
y
y
y
F
n
i
obl
i
i
n
i
obl
i
i
n
i
i
1
2
1
2
1
2
1
1
1
2
2
1
1
2
1
,
m
m
m
m
m
m
n
m
m
F
Test F dla istotności
włączenia nowych
parmetrów
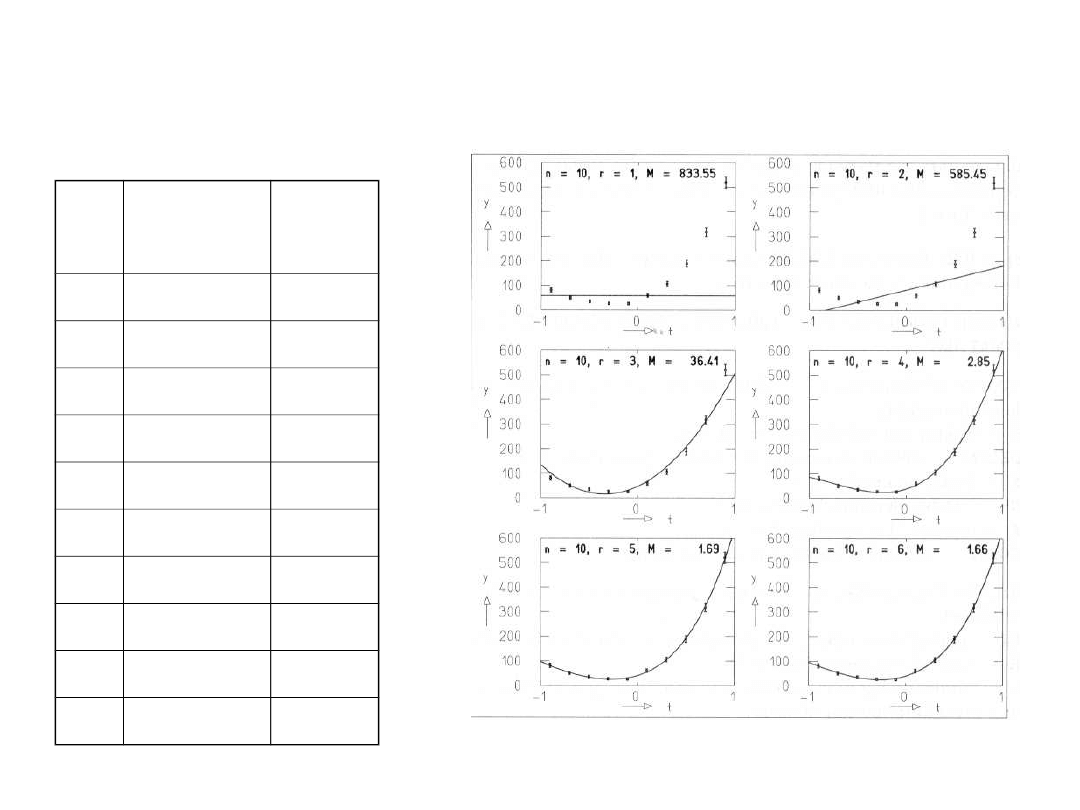
Przykład dopasowywania wielomianu: rozkład cosinusa kąta
rozpraszania mezonów K z protonami (zakładamy że
j
=sqrt(y
j
).
j
t
j
=cos(
j
)
y
j
1
-0.9
81
2
-0.7
50
3
-0.5
35
4
-0.3
27
5
-0.1
26
6
0.1
60
7
0.3
106
8
0.5
189
9
0.7
318
10
0.9
520
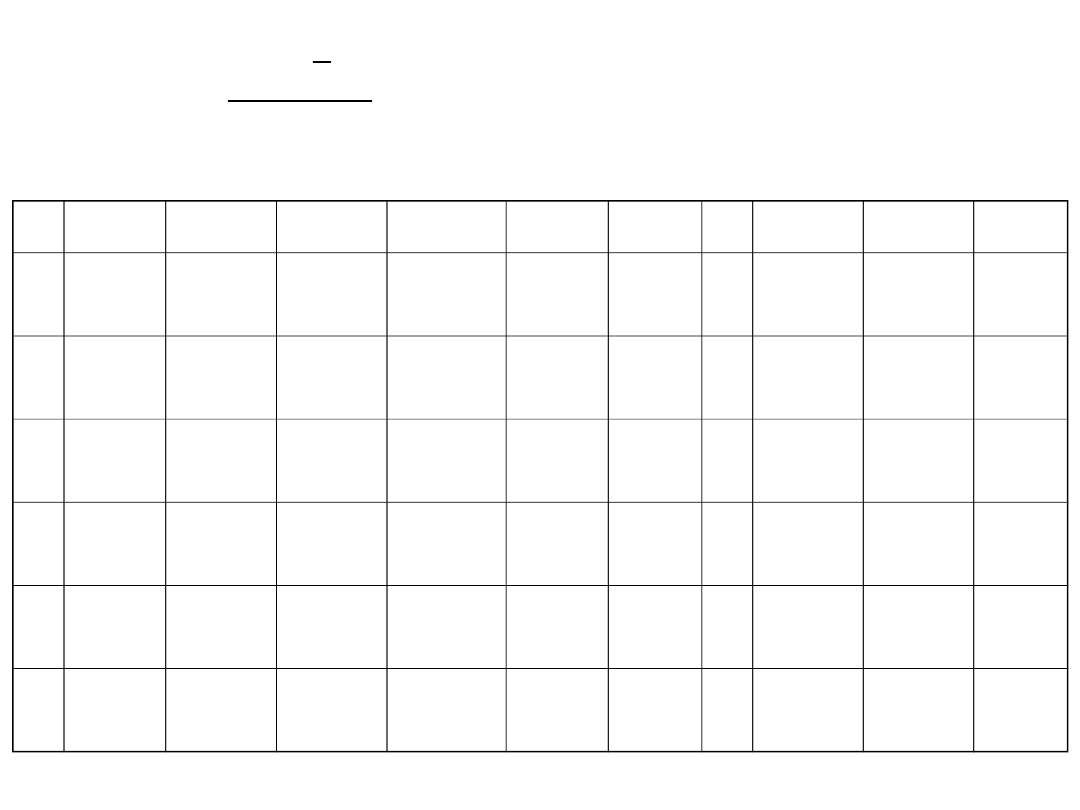
m
p
1
p
2
p
3
p
4
p
5
p
6
f
M
F
F
0.9
1
57.8
5
9 833.5
5
-
2
82.6
6 99.10
8
585.4
5
3.92
3.45
8
2
47.2
7
185.9
6
273.6
1
7 36.41 105.5
5
3.58
9
4
37.9
4
126.5
5
312.0
2
137.5
9
6
2.85 70.65 3.77
6
5
39.6
2
119.1
0
276.4
9
151.9
1
52.6
0
5
1.68
3.48 4.06
0
6
39.8
8
121.3
9
273.1
9
136.5
8
56.9
0
16.7
2
4
1.66
0.05 4.54
5
n
i
i
i
i
y
y
1
2
2