Podstawy statystyki

Dr Janusz

Górczyński

2

Literatura



J. Jóźwiak, J.Podgórski, Statystyka od

podstaw, PWE, Warszawa 1997



K. Zając, Zarys metod

statystycznych, PWE, Warszawa,

1994



J. Górczyński, Podstawy statystyki,

Wyd. II. WSZiM Sochaczew, 2000



J. Górczyński, Wybrane wzory i

tablice statystyczne, Wyd. II. WSZiM

Sochaczew, 2000

3

Czym zajmuje się
statystyka?



Odpowiadając na to pytanie rozważmy
taką sytuację: interesuje nas poznanie
takiej cechy jak np. zużycie paliwa na
100 km przez samochody pewnej
firmy (i modelu).



Szukając odpowiedzi na to pytanie
można by ograniczyć się do spytania
znajomego właściciela takiego pojazdu
o to, ile jego pojazd zużywa paliwa.

4

Czym zajmuje się statystyka ?
(2)



Powiedzmy, że odpowiedź brzmi:

6,8 l/100 km.



Natychmiast pojawiają się

wątpliwości co do sposobu

traktowania tej odpowiedzi.



Czy to oznacza, że WSZYSTKIE

samochody mają takie zużycie?



Czy to oznacza, że ŚREDNIE

zużycie jest takie?

5

Czym zajmuje się statystyka ?
(3)



Czy nasz znajomy jest DOBRYM

reprezentantem ogółu właścicieli

tego modelu?



A może jeździ zbyt ostro?



A może zbyt delikatnie?



A może trzeba uzyskać odpowiedzi

od większej liczby kierowców?



Jeżeli tak, to od ilu? I jak ich wybrać?

6

Czym zajmuje się statystyka ?
(4)



Powiedzmy, że uzyskaliśmy
odpowiedzi od 9 użytkowników
badanego modelu.



Niech to będą takie dane:
6,2 6,7 6,5 6,9 7,2 7,2 7,1 7,3 7,2



Co TERAZ możemy powiedzieć o
zużycia paliwa?



Najmniejsze zużycie to 6,2 l/100 km, a
największe to 7,3 l/100 km.

7

Czym zajmuje się statystyka ?
(5)



A jak można teraz określić
PRZECIĘTNE zużycie paliwa?



Jedna z możliwości to ŚREDNIA
ARYTMETYCZNA, w tym przykładzie
równa 6,92 l/100 km.



Pytanie kolejne: czy ta średnia odnosi
się tylko do tych 9 pomiarów, czy też
może być odniesiona do ogółu
użytkowników badanego modelu?

8

Czym zajmuje się statystyka ?
(6)



Odpowiedzi na te i wiele innych pytań

udziela STATYSTYKA, która zajmuje się

badaniem zjawisk masowych.



Analiza zjawisk masowych pozwala na

poznanie natury zjawiska (cechy) i

praw nim rządzących.



Zastosowanie statystyki do naszego

przykładu pozwoli na uogólnienie

wniosków na wszystkich użytkowników

badanego modelu samochodu.

9

Badanie statystyczne



Celem badania statystycznego będzie

najczęściej poznanie rozkładu danej

cechy i oszacowanie charakterystyk

tego rozkładu.



Jeżeli zmienna losowa X jest modelem

probalistycznym dla pewnej cechy w

populacji generalnej, to rozkład

często-ści występowania tej cechy

jest opisany rozkładem

prawdopodobieństwa zmiennej

modelowej.

10

Statystyka a rachunek
prawdopodobieństwa



Statystyka korzysta z rachunku
prawdopodobieństwa – działu
matematyki zajmującego się
badaniem zdarzeń przypadkowych
(losowych).



Tym samym będziemy korzystać z
elementarnych pojęć rachunku
prawdopodobieństwa.

11

Elelementy
prawdopodobieństwa (1)



Zdarzenie losowe – takie, którego
wyniku nie jesteśmy w stanie
przewidzieć.



Przykładowo: wynik rzutu monetą,
suma oczek przy rzucie dwoma
kostkami sześciennymi.



Zdarzenie elementarne – każda
możliwa sytuacja w danym
zagadnieniu (eksperymencie).

12

Elelementy
prawdopodobieństwa (2)



Przykładem zdarzenia elementarnego
przy rzucie dwoma kostkami do gry jest
para liczb odpowiadających liczbie oczek
na każdej z kostek (1,1), (1,2)...(6,6).



Zbiór wszystkich możliwych zdarzeń
elementarnych oznaczamy symbolem .



Zbiór  może być skończony lub nie

(może zawierać nieskończenie wiele
zdarzeń elementarnych).

13

Elementy prawdopodobieństwa
(3)



Zdarzenie losowe – jest to dowolny pod-

zbiór zbioru zdarzeń elementarnych .



Rozpatrzmy rzut 3 monetami.

Zdarzeniem losowym (powiedzmy) A

może być wyrzucenie 2 reszek.



Prawdopodobieństwo zajścia zdarzenia

losowego – jest to szansa zajścia tego

zdarzenia.



Prawdopodobieństwo jest liczbą z

przedziału domkniętego <0; 1>

14

Obliczanie prawdopodobieństw
(1)



Przy obliczaniu prawdopodobieństwa zajścia
dowolnego zdarzenia losowego A można
korzystać z tzw. klasycznej definicji Laplace’a:

n

k

A

P



)

(

gdzie k jest liczbą zdarzeń
elementarnych tworzących zdarzenie
A, a n liczbą wszyst-kich zdarzeń
elementarnych w zbiorze .

15

Obliczanie prawdopodobieństw
(2)



Z podanego wzoru można
oczywiście korzystać tylko wtedy,
gdy zbiory zdarzeń elementarnych i
zdarzeń tworzących zdarzenie
losowe A są skończone (policzalne).



Z podanego wzoru wynika, że P(A)
może być równe 0 (dla k=0).



Z podanego wzoru wynika, że P(A)
może być równe 1 (dla k=n).

16

Obliczanie prawdopodobieństw
(3)



O zdarzeniu losowym A, którego

P(A)=0 mówimy, że jest to zdarzenie

niemożliwe.



O zdarzeniu losowym A, którego

P(A)=1 mówimy, że jest to zdarzenie

pewne.



Zdarzenie A’ nazywamy zdarzeniem

przeciwnym do zdarzenia A.



Suma zdarzeń A i A’ tworzy

zdarzenie pewne.

17

Obliczanie prawdopodobieństw
(4)



Dla prawdopodobieństw zdarzeń A
i A’ zachodzi relacja:



P(A)+P(A’)=1



a stąd P(A’)=1-P(A)



Relację powyższą wykorzystuje się
przy obliczaniu
prawdopodobieństwa zajścia A -
jeżeli łatwiej jest obliczyć P(A’).

18

Obliczanie prawdopodobieństw
(5)



Przy obliczaniu prawdopodobieństw

wykorzystuje się dwa klasyczne wzory:



P(AB)=P(A)+P(B)-P(AB) (1)



P(AB)=P(A)P(B/A) (2)



Jeżeli zdarzenia A i B się wykluczają, to

wzór 1 przyjmuje postać:



P(AB)=P(A)+P(B) (3)



Jeżeli A i B są niezależne, to wzór 2

przyjmuje postać:



P(AB)=P(A)P(B) (4)

Przykłady obliczeń
prawdopodobieństw

20

Przykład 1

Z talii 52 kart pobieramy losowo 1 kartę. Jakie
jest p-stwo, że jest to as lub kier?

Korzystamy z wzoru na p-stwo sumy dwu
zdarzeń. Niech A oznacza wylosowanie asa, a B
wylosowanie kiera.

Zgodnie ze wzorem P(AB)=P(A)+P(B)-P(AB)

mamy:

52

16

52

1

13

4

52

1

52

13

52

4

)

(















 B

A

P

21

Przykład 2

Z urny o składzie 4 kule białe, 6 zielonych i 10
niebieskich losujemy 1 kulę. Jakie jest p-stwo,
że jest to kula biała lub zielona?

Korzystamy z wzoru na p-stwo sumy dwóch
zdarzeń. Niech A oznacza wylosowanie kuli
białej, a B zielonej.

Zgodnie ze wzorem P(AB)=P(A)+P(B)-

P(AB) mamy:

20

10

20

0

20

6

20

4

)

(









 B

A

P

22

Przykład 3

Z urny o składzie 4 kule białe, 6 niebieskich i
10 zielonych losujemy dwie kule. Jakie jest p-
stwo, że są to kule białe?

Korzystamy z wzoru na p-stwo iloczynu dwóch
zdarzeń. Niech A oznacza wylosowanie
pierwszej kuli białej, a B drugiej kuli białej.

Zgodnie ze wzorem P(AB)=P(A)P(B/A)

mamy:

380

12

19

3

20

4

)

(







 B

A

P

23

Przykład 3 inaczej

Przykład 3 może być także rozwiązany z
użyciem symbolu Newtona od określenia
liczebności zbioru  i ilości zdarzeń

elementarnych składających się na zdarzenie
losowe.

 

 

190

6

1

2

19

20

1

2

3

4

)!

2

20

(

!

2

!

20

)!

2

4

(

!

2

!

4

)

(

20

2

4
2





















 B

A

P

24

Zmiene losowe - definicja

Zmienne losowe oznaczać będziemy dużymi

litera-mi alfabetu (np. X, Y, Z), a ich wartości
odpowiednio małymi literami (np. x, y, z).
Ze względu na możliwy zbiór wartości
rozróżniać będziemy dwa podstawowe typy
zmiennych losowych: skokowe i ciągłe.

Zmienną losową X nazywamy funkcję o
wartościach rzeczywistych określoną na
zbiorze zdarzeń elemen-tarnych 

25

Zmienna losowa
skokowa

Zmienna losowa X typu skokowego

przyjmuje skończoną lub przeliczalną
liczbę wartości z pewnego przedziału.

Zmienne tego typu nazywane są

także zmiennymi dyskretnymi.

Przykładem zmiennej tego typu

może być np. liczba błędów na stronie
pewnej książki.

26

Zmienne losowe ciągłe

Zmienna losowa typu ciągłego

przyjmuje nieskończenie wiele
wartości z pewnego przedziału
liczbowego.

Przykładem tego typu zmiennej

może być np. zawartość tłuszczu w
mleku krów, czy zawartość białka w
pewnym produkcie.

27

Rozkład zmiennej losowej
skokowej

Przyporządkowanie każdej wartości zmiennej

losowej typu skokowego prawdopodobieństwa jej
realizacji nazy-wamy funkcją rozkładu
prawdopodobieństwa (w skrócie f.r.p.). Funkcja ta
może być podana w formie tabelki, wzoru lub wykresu.

Dla f.r.p. spełnione są warunki:

P X

x

p

p

p

i

i

i

i

i

(

)

,













0 1

1

28

Funkcję f(x) spełniającą dwa warunki

nazywamy funkcją gęstości

prawdopodobieństwa (f.g.p.) pewnej zmiennej
losowej X (ciągłej).

Rozkład zmiennej losowej
ciągłej

1

0









.

( )

x R

f x

2

1



 







.

( )

f x dx

29

Funkcja dystrybuanty

Dystrybuantą zmiennej losowej X nazywamy

funkcję F(x) spełniającą warunek:

F x

P X

x

P x x

f x dx

i

x

x x

x

i

i

( )

(

)

(

)

( )



 



















 





30

Własności dystrybuanty

Funkcja dystrybuanty spełnia trzy warunki (lub

inaczej ma następujące własności):

1.

2. jest niemalejąca

3. jest co najmniej prawostronnie ciągła

W szczególności

F x

( )

;





0 1

F

F

(

)

(

)

  

 

0

1

31

Momentem zwykłym rzędu k zmiennej

losowej X nazywamy wartość oczekiwaną k-tej
potęgi tej zmiennej

:

Parametry
rozkładu zmiennych losowych

m

EX

x p

x f x dx

k

k

i

k

i

i

k





















 



( )

32

Parametry
rozkładu zmiennych losowych

Momentem centralnym rzędu k zmiennej

losowej X nazywamy wartość oczekiwaną funkcji

g x

X EX

k

( ) [

]







k

k

i

k

i

i

k

E X EX

x

EX p

x EX f x dx



























 



[

]

(

)

(

) ( )

33

Wybrane momenty

Moment zwykły rzędu pierwszego

nazywamy wartością oczekiwaną zmiennej
losowej X (wartością średnią):

Moment centralny rzędu drugiego

nazywamy wariancją zmiennej losowej X

Pierwiastek kwadratowy z wariancji

nazywamy odchyleniem standardowym

m

EX

1



D X

E X

EX

2

2

2









[

]

DX

D X



2

34

Związki między momentami

Dla trzech pierwszych momentów zachodzą

związki

:

Ze związków tych korzystamy przy

praktycznym wyznaczaniu momentów
centralnych.



1

1

0







E X m

(

)



2

2

2

1

2









E X

EX

m

m

(

)



3

3

3

1

2

1

3

3

2











E X

EX

m

mm

m

(

)

35

Dodatkowe charakterystyki
pozycyjne

P X

Me

i P X

Me

(

)

(

)









1

2

1

2

5

,

0

)

(



Me

F

Medianą zmiennej losowej X nazywamy
wartość Me spełniającą nierówności

:

Dla zmiennej ciągłej spełniony jest warunek:

Mediana jest taką wartością zmiennej losowej
X, która dzieli pole pod funkcją gęstości na
dwie części o identycznej powierzchni.

36

Dodatkowe charakterystyki
pozycyjne

P X

K

p

i

P X

K

p

dla p

p

p

(

)

(

)

( , )







 



1

0 1

F K

p

p

( ) 

Kwantylem rzędu p zmiennej losowej X
nazywamy wartość Kp spełniającą
nierówności:

Z powyższej definicji wynika, że dla
zmiennej ciągłej prawdziwa jest zależność:

37

Dodatkowe charakterystyki
pozycyjne

Kwantyle rzędu p = 0.25, p = 0.50 oraz

p = 0.75 nazywane są odpowiednio
kwartylami i oznaczane symbolami

Q

1

- kwartyl pierwszy

Q

2

- kwartyl drugi

Q

3

- kwartyl trzeci

Z definicji kwantylu wynika, że
kwartyle dzielą zbiór wartości
zmiennej losowej X na ćwiartki (po
25% zbioru elementów).

38

Dodatkowe charakterystyki
pozycyjne

W przypadku zmiennej losowej ciągłej
wartości x odpowiada maksimum lokalne
funkcji gęstości.

Dominantą Do (modą Mo) zmiennej
losowej X nazywamy taką wartość x tej
zmiennej, której odpo-wiada największe
prawdopodobieństwo realizacji
(w przypadku zmiennej losowej
skokowej).

39

Obliczanie dodatkowych
charakterystyk

Funkcja rozkładu p-stwa pewnej zmiennej
losowej X dana jest tabelką:

x

i

-3

-2

-1

0

1

3

p

i

0,1

0,2

0,2

0,1

0,2

0,2

Obliczmy Me,

k0,75

oraz Do (Mo) tej zmiennej

losowej.

40

Charakterystyki ....

Medianą tej zmiennej losowej jest dowolna
liczba z zakresu od –1 do 0, co wynika z
poniższych nierówności:

7

,

0

)

1

(

5

,

0

)

1

(













X

P

i

X

P

5

,

0

)

0

(

6

,

0

)

0

(









X

P

i

X

P

Kwantylem rzędu 0,75 jest liczba 1, co
wynika z nierówności:

4

,

0

)

1

(

8

,

0

)

1

(









X

P

i

X

P

Dominanta nie istnieje, nie ma bowiem
takiej wartości zmiennej, której odpowiada
max. p-stwa.

41

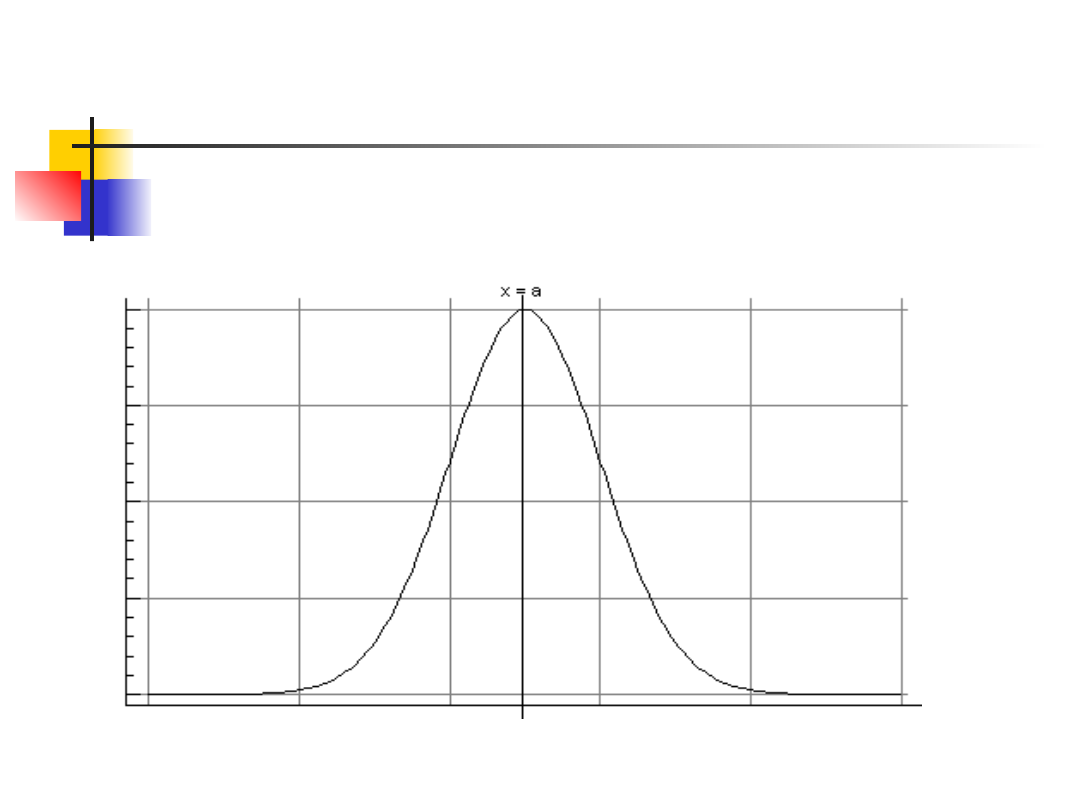
Asymetria rozkładu
zmiennej losowej

Zmienna losowa X ma rozkład symetryczny,
jeżeli istnieje taka wartość a, że każdemu
punktowi odpowiada punkt
taki, że spełnione są warunki

:

W przypadku ciągłej zmiennej losowej opisanej
funkcją gęstości f(x) musi być spełniony warunek:

dla każdego x

x

a

i



x

a

j



P X

x

P X

x

i

a x

x

a

i

j

i

j

(

)

(

)









 

f a x

f a x

(

)

(

)







42

Asymetria rozkładu zmiennej
losowej

Punkt a nosi nazwę środka symetrii, a prosta x

= a jest osią symetrii.

43

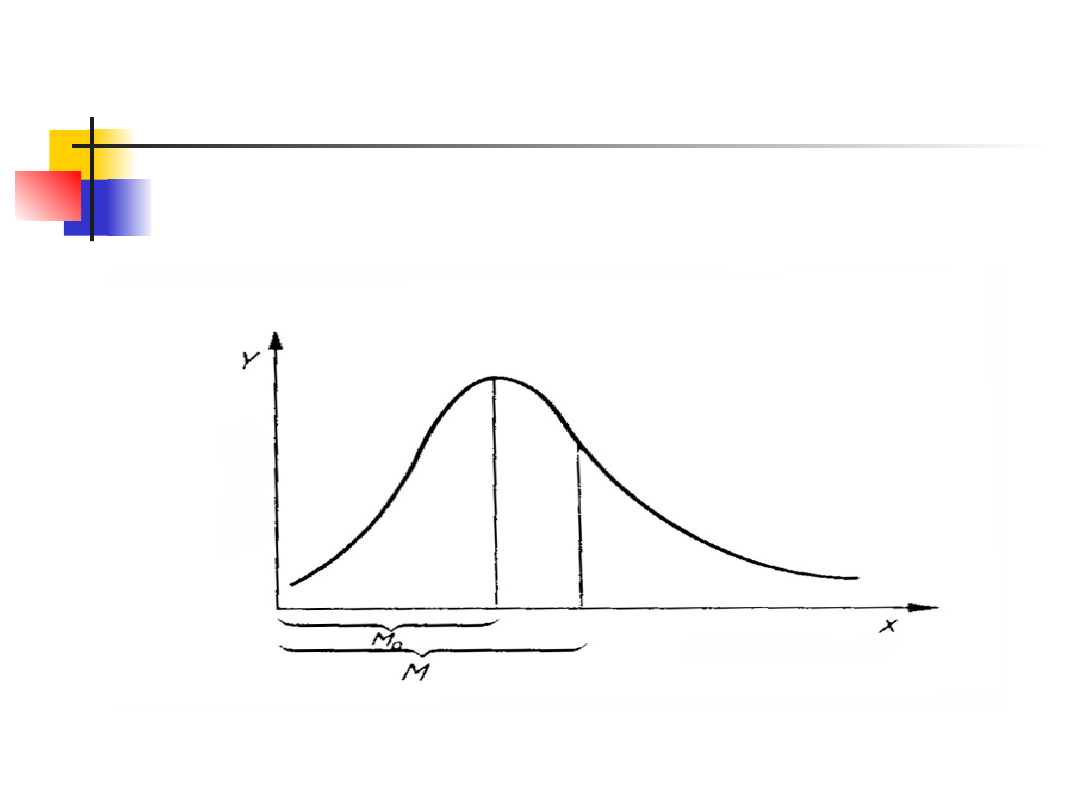
Asymetria rozkładu

Asymetria prawostronna

(M oznacza średnią, a M

0

dominantę)

M M

o



 0

44

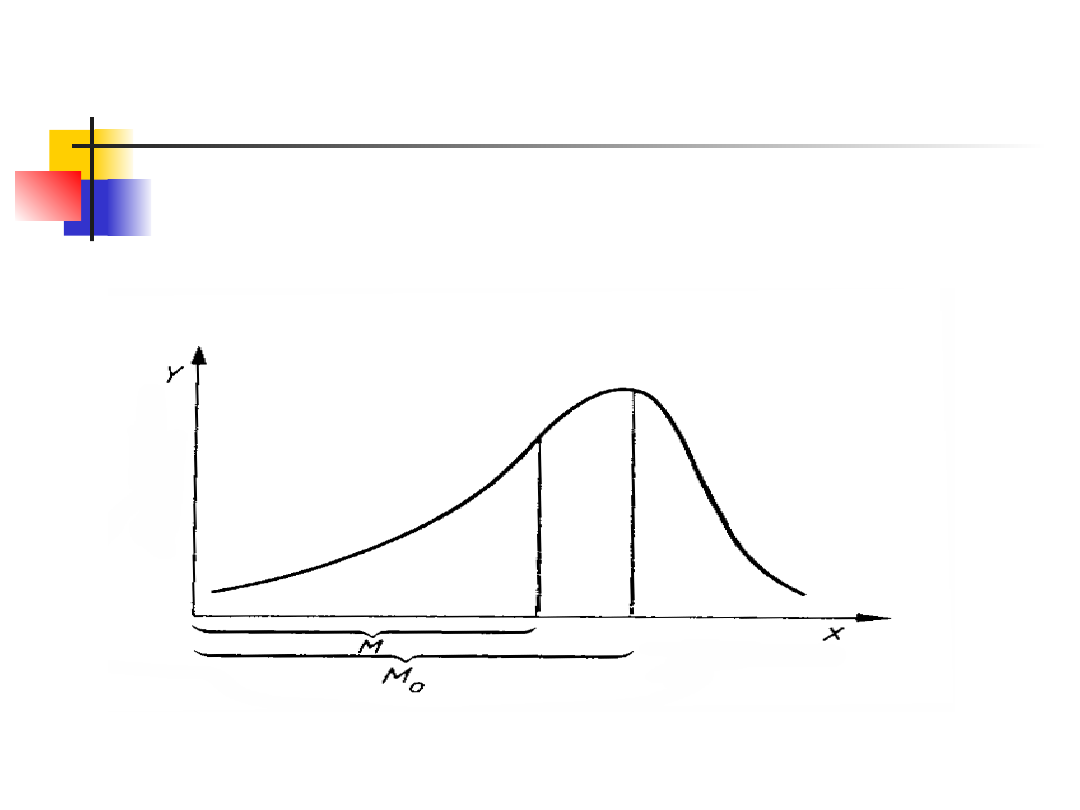
Asymetria rozkładu

Asymetria lewostronna

(M oznacza średnią, a M

0

dominantę)

M M

o



 0

45

Miary
asymetrii

Miarą asymetrii może być różnica między
wartością średnią (M) a dominantą (Mo), która
mierzy nie tylko stopień asymetrii, ale także jej
kierunek. Jest to jednak miara mianowana, a
więc zależna od jednostek cechy.
Lepszą miarą asymetrii jest współczynnik
asymetrii (skośność) zdefiniowany jako

gdzie DX jest odchyleniem standardowym.







3

3

D X

46

Miary asymetrii
(c.d)

Jeżeli  > 0, to asymetria rozkładu jest dodatnia

(prawostronna).

Jeżeli  < 0, to asymetria rozkłau jest ujemna

(lewostronna).

W rozkładzie symetrycznym  = 0 (co wynika z

faktu, że w rozkładach symetrycznych
wszystkie momenty centralne rzędu
nieparzystego są równe zero)

47

Kurtoza

Miarą kształtu rozkładu zmiennej losowej jest
kurtoza definiowana jest jako różnica stosunku
momentu centralnego rzędu czwartego do
kwadratu momentu centralnego rzędu drugiego a
liczbą 3:

3

2

2

4









kurtoza

Dodatnia wartość kurtozy wskazuje na
wysmukły kształt rozkładu zmiennej losowej,
ujemna z kolei na kształt spłaszczony. Kurtoza
jest więc miarą koncentracji wartości
zmiennej losowej wokół jej wartości średniej.

48

Podstawowe rozkłady zmiennych
losowych

1. Rozkład zero-jedynkowy.
Funkcja rozkładu prawdopodobieństwa dana jest

tabelką:

x

i

0

1

p

i

q

p

Oczywiście p + q = 1
Parametrami rozkładu tej zmiennej są:

EX

p D X

pq DX

pq







,

,

2

49

Podstawowe rozkłady zmiennych
losowych

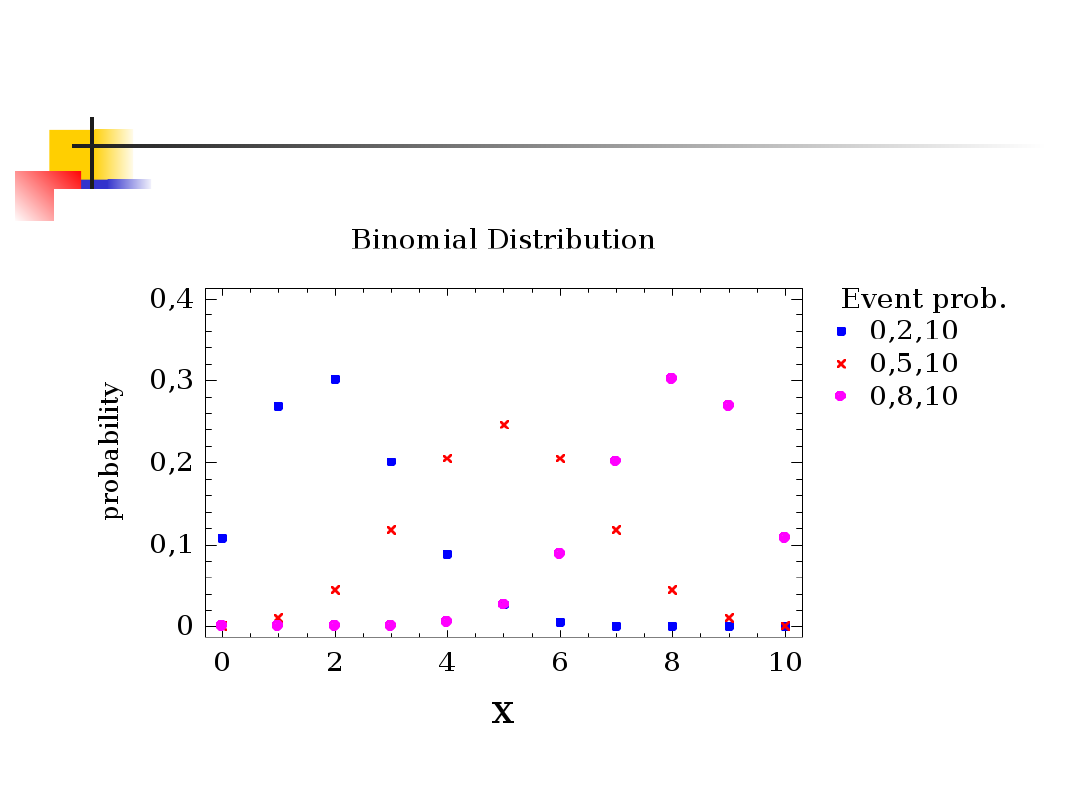
2. Rozkład dwumianowy (Bernoulliego)
Rozkład ten otrzymujemy w wyniku n-krotnego
powtarzania eksperymentu, w którym realizuje
się zmienna zero-jedynkowa. Zmienna losowa
przyjmuje n + 1 wartości, a jej f.r.p. dana jest
wzorem

:

Parametry rozkładu są odpowiednio równe:

P X k

n

k

p q

k n k

(

)

 













EX np D X npq DX

npq







,

,

2

50

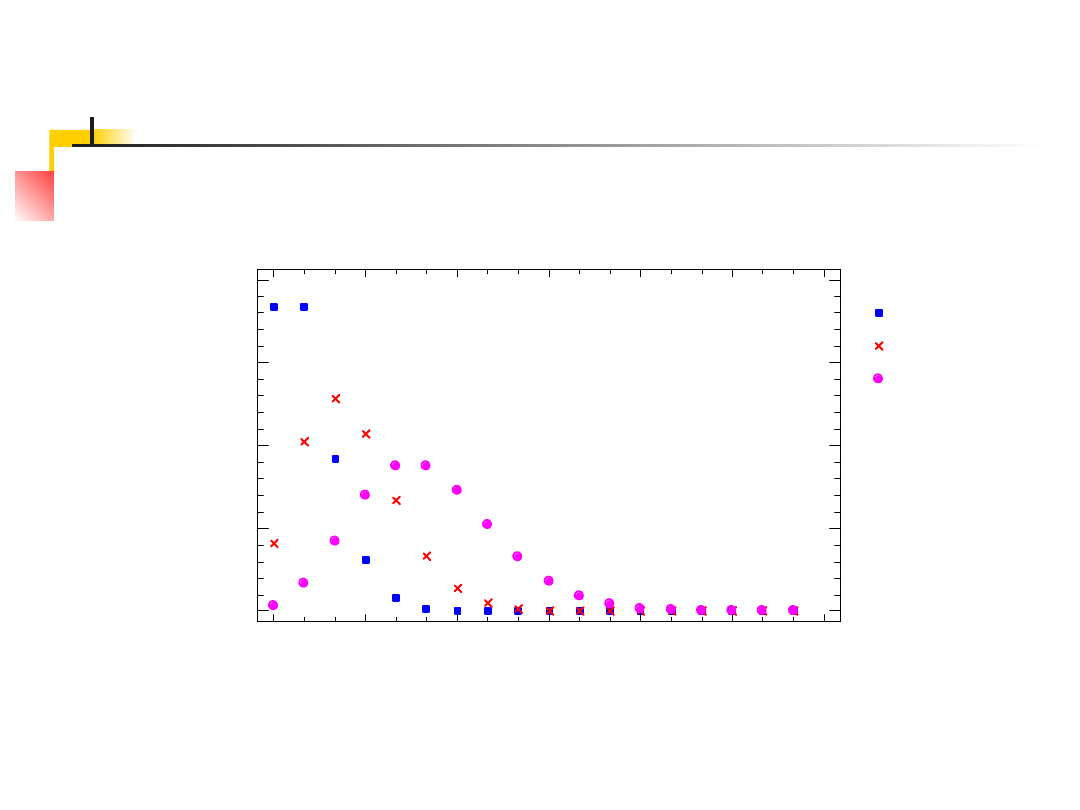
Wykresy f.r.p dla trzech p-stw
sukcesu

51

Podstawowe rozkłady zmiennych
losowych

3. Rozkład Poissona
Zmienna losowa X przyjmująca wartości k = 0, 1,
2, ..., n ma rozkład Poissona, jeżeli jej f.r.p dana jest
wzorem:

Parametrami rozkładu tej zmiennej są odpowiednio:

Rozkład Poissona może być wykorzystany jako
przybliżenie rozkładu dwumianowego
(Bernoulliego) w tych sytuacjach, gdy n jest duże, p
małe i iloczyn np =  = const.

P X k

k

e

k

(

)

!











EX

D X

DX













,

,

2

52

Wykresy f.r.p dla trzech wartości 

Mean

1
2,5
5

Poisson Distribution

p

ro

b

a

b

il

it

y

0

3

6

9

12

15

18

0

0,1

0,2

0,3

0,4

53

Podstawowe rozkłady zmiennych
losowych

4. Rozkład normalny
Funkcja gęstości rozkładu normalnego dana jest

wzorem

W rozkładzie normalnym przyjmuje się nastepujące

oznaczenia parametrów:

Jeżeli pewna zmienna losowa będzie miała rozkład

normalny z wartością średnią m i odchyleniem

standardowym , to zapiszemy to jako
Xm

Wykresem funkcji gęstości rozkładu normalnego jest

tzw. krzywa Gaussa.

f x

e

x m

( )

(

)







1

2

2

2

2







EX m

D X

DX







,

2

2





54

Funkcja gęstości rozkładu
normalnego z parametrami m i 

55

Funkcja dystrybuanty
rozkładu normalnego

56

Wpływ parametrów rozkładu
normalnego na kształt i
położenie funkcji gęstości

57

Funkcja gęstości -
interpretacja
prawdopodobieństwa

58

Funkcja dystrybuanty -
interpretacja
prawdopodobieństwa

59

Prawo 3
sigm

Niech pewna zmienna losowa X ma rozkład normalny
N(m; ).

Prawdopodobieństwo przyjęcia przez zmienną X
wartości z przedziału <m-3, m+3> jest równe 0,997

.

Wynik ten można zinterpretować następująco: w
przedziale <m-3, m+3> mieszczą się prawie

wszystkie elementy danej populacji (normalnej).
Prawo to jest znane jako prawo 3 sigm.

60

Standaryzacja
rozkładu

Rozkład normalny ze średnią m = 0 oraz
odchyleniem standardowym  = 1 nazywamy

standardowym rozkładem normalnym i
oznaczamy symbolem N(0; 1)
Podstawienie

pozwala na przekształcenie dowolnego rozkładu
normalnego do standardowego rozkładu
normalnego.

z

x m







61

Standardowy rozkład
normalny

62

Rozkład N(0; 1)

Standardowy rozkład normalny jest stablicowany,
w tablicach statystycznych najczęściej podawana
jest dystrybuanta tego rozkładu.
Zmienne losowe o standardowym rozkładzie
normalnym są podstawą konstrukcji kilku
kolejnych rozkładów o podstawowym znaczeniu
w statystyce. Są to miedzy innymi rozkłady:



2

- Pearsona

t - Studenta
F - Fishera-Snedecora