Systemy ekspertowe
Andrzej Macioł
Systemy ekspertowe
Andrzej Macioł
Literatura
• Mulawka J., Systemy ekspertowe. WNT
Warszawa 1996.
• Cholewa W., Pedrycz W., Systemy
doradcze. Skrypt. Politechnika Śląska,
Gliwice 1987.
• Bubnicki Z., Wstęp do systemów
ekspertowych. PWN, Warszawa 1990.
• Kasperski M. J., Sztuczna Inteligencja.
Helion 2003.
Co to jest system
ekspertowy?
• Program komputerowy przeznaczony
do rozwiązywania problemów
decyzyjnych wyposażony w
elektroniczny zapis wiedzy i niezależny
od niej mechanizm wnioskowania
podobny w działaniu do wnioskowania
eksperta-człowieka.
• Do budowy systemów ekspertowych
wykorzystuje się osiągnięcia tzw.
sztucznej inteligencji.
Co to jest sztuczna
inteligencja?
• Nauka o maszynach realizujących
zadania, które wymagają inteligencji
wówczas, gdy są wykonywane przez
człowieka [Minsky 1963]
• Dziedzina informatyki dotycząca
metod i technik wnioskowania
symbolicznego przez komputer oraz
symbolicznej reprezentacji wiedzy
stosowanej podczas tego
wnioskowania [Feigenbaum 1977?]
Co to jest rozumowanie
symboliczne?
• Posługiwanie się językiem składającym
się ze słownika i gramatyki
• Wiedza w sztucznej inteligencji
podobnie jak przedstawiona wiedza
człowieka wyraża się w symbolach
(słowach) i związkach zachodzących
między nimi
• Sztuczne sieci neuronowe,
algorytmy genetyczne to nie są
metody sztucznej inteligencji w jej
podstawowym rozumieniu
Stanowiska wobec AI wg
R. Penrosa
• Myślenie zawsze polega na
obliczeniach (kalkulacji)
• Świadomość jest cechą fizyczną
działającego mózgu; procesy fizyczne
można symulować obliczeniowo ale nie
towarzyszy im świadomość
• Procesy fizyczne powodują w mózgu
powstanie świadomości ale nie można
ich symulować obliczeniowo
• Świadomości nie można wyjaśnić w
żaden fizyczny, obliczeniowy czy inny
naukowy sposób
Filozofia Sztucznej
Inteligencji
epistemologia
filozofia języka
filozofia umysłu
informatyka
nauki o mózgu
logika
matematyka
filozofia
matematyki
psychologia
kognitywna
psychologia
rozwoju dziecka
Filozofia
Sztucznej
Inteligencji
Maszyna Turinga
• Abstrakcyjny schemat działania wedle
zadanego algorytmu:
– Odczytaj zawartość komórki pamięci
– Zmień stan obiektu
– Zapisz nowy symbol do komórki
– Przejdź do zadanej komórki pamięci
– Powtórz cykl
• Maszyna Turinga to maszyna stanów
dyskretnych
Test Turinga
• Co najmniej dwoje ludzi i jedna
maszyna
• Żaden z uczestników testu nie widzi
drugiego
• Jeden z ludzi jest sędzią i prowadzi
dialog z pozostałymi uczestnikami
• Sędzia w wyniku prowadzonego
dialogu ma ustalić kto jest człowiekiem
a kto maszyną
• Każda maszyna, która „oszuka”
sędziego spełni test Turinga
Korzyści płynące z AI
• Systemy eksperckie -
rodziny programów
specjalizujących się w określonej dziedzinie wiedzy
• Systemy jednozadaniowe –
maszyny lub
programy służące do wykonania jednego zadania
• Systemy wielozadaniowe –
realizują jeden
konkretny cel ale rozwiązują wiele zadań
• Systemy specjalistyczne
jednowymiarowe –
wykonują zadania
specjalistyczne w jednym zakresie
• Systemy specjalistyczne
wielowymiarowe –
wykonują zadania
specjalistyczne rozwiązując szereg różnych problemów
• Systemy symulacyjne –
skonstruowane tak by
odtwarzać naturalne dla człowieka warunki
Plan wykładu
•
•
•
• Metody pozyskiwania wiedzy
• Wnioskowanie w systemach
sztucznych
• Zagadnienia praktyczne
• Przykłady zastosowań
Wiedza
• Płynne połączenie doświadczenia,
ocen wartości, informacji o
kontekście oraz analitycznego
wglądu w zagadnienia, które
zapewnia ramy dla oceny i
włączania nowych doświadczeń i
informacji.
• Wiedza organizacji wywodzi się i
jest charakterystyczna dla
umysłów ludzi.[Davenport i
Prusak 1998]
Wiedza
• Cechą wiedzy jest porządek, którego
poszukiwali filozofowie zajmujący się
metafizyką czy jak wolimy to dzisiaj
mówić ontologią, której zadaniem jest
po prostu opisanie rzeczywistości, a
więc tego co istnieje.
• Tradycyjnym celem ontologii jest
podział wiadomości o świecie (bycie)
na kategorie definiujące rzeczy
składające się na niego.
• Wiedza składa się z uporządkowanych
opisów, relacji i procedur.
Wiedza człowieka
(eksperta)
• wiedza milcząca (tacit knowledge) –
wiem jak postępować w danych
okolicznościach ale nie wiem dlaczego
i nie potrafię tego wyjaśnić
• asocjacyjna wiedza empiryczna – znam
wiele przykładów i umiem je
wykorzystać do wnioskowania
• wiedza głęboka – dokładnie wiem
dlaczego (oczywiście w pewnej
ontologii)
Wiedza - reprezentacja
• reprezentacja proceduralna –
określenie zbioru procedur,
których działanie reprezentuje
wiedzę o dziedzinie (np.
procedura wyznaczania
ekstremum funkcji),
• reprezentacja deklaratywna,
polegająca na określeniu zbioru
specyficznych dla rozpatrywanej
dziedziny faktów i reguł.
Komputery wyposażone w
wiedzę
• Systemy ekspertowe to „programy
z wiedzą”
• Sam program realizuje procedury
wnioskowania i ew. obliczania,
objaśniania, uczenia,
komunikowania
• Wiedza zapisana jest w osobnych
zbiorach i poza tym, że może być
poszerzana przez program
(uczenie) jest od niego niezależna
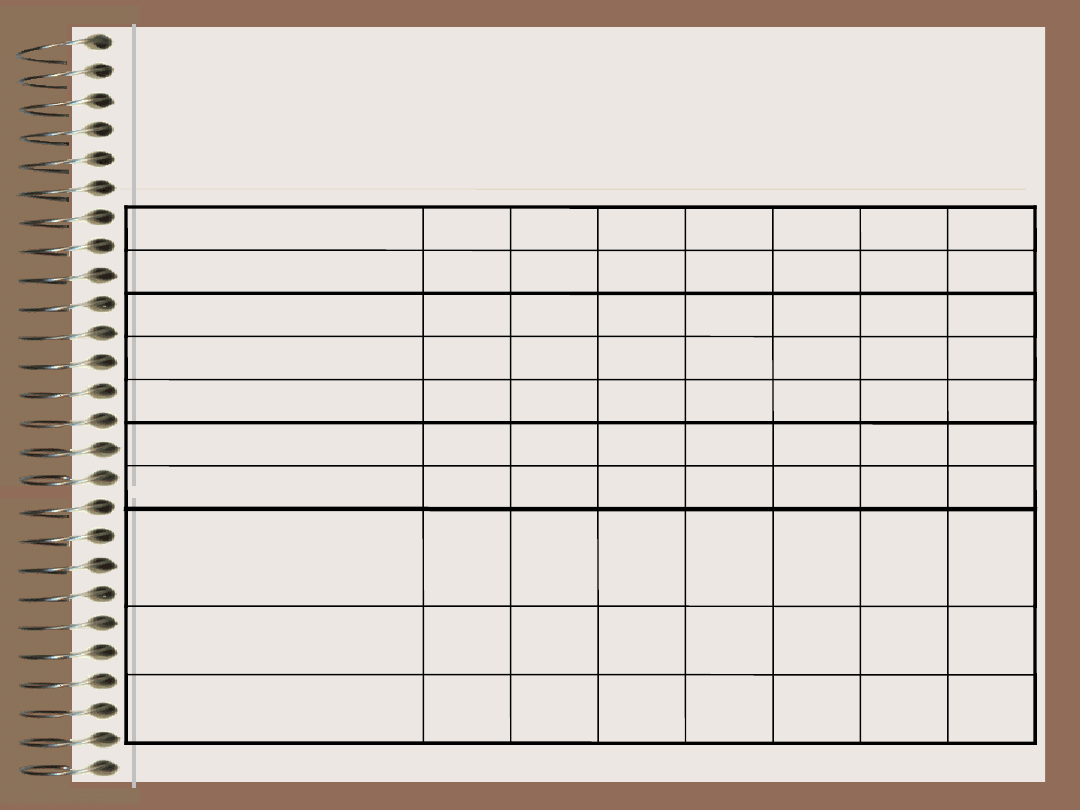
Przykład: tabela
decyzyjna
X
T
T
T
X
T
T
X
T
T
X
T
T
X
T
T
X
T
T
X
T
T
T
Decyzja ostateczna:
odrzucić ofertę
Decyzja ostateczna:
przyznać klientowi
upust
Decyzja ostateczna:
sprzedać po cenie
standardowej
Wartość kontraktu jest
mała
Wartość kontraktu jest
duża
Klient płaci
przelewem
Klient dokonuje
przedpłaty
Klient płaci gotówką
Klient nie jest
wiarygodny
Klient jest wiarygodny
If
stwierdzenie(1) = "Klient jest wiarygodny"
And
stwierdzenie(2) =
" Klient płaci przelewem"
And
stwierdzenie(2) = "Wartość kontraktu
jest duża"
Then
konkluzja = "przyznać klientowi upust”
If
stwierdzenie(1) = "Klient jest wiarygodny"
And
stwierdzenie(2) =
" Klient płaci przelewem"
And
stwierdzenie(2) = "Wartość kontraktu
jest mała"
Then
konkluzja = "sprzedać po cenie standardowej"
If
stwierdzenie(1) = "Klient nie jest wiarygodny"
And
stwierdzenie(2) = " Klient płaci przelewem"
And
stwierdzenie(2) =
"Wartość kontraktu jest duża"
Then
konkluzja = "odrzucić ofertę"
If
stwierdzenie(2) = " Klient płaci gotówką"
And
stwierdzenie(2) =
"Wartość kontraktu jest duża"
Then
konkluzja = "przyznać klientowi upust"
If
stwierdzenie(2) = " Klient płaci gotówką"
And
stwierdzenie(2) =
"Wartość kontraktu jest mała"
Then
konkluzja = "sprzedać po cenie standardowej"
If
stwierdzenie(2) = " Klient dokonuje przedpłaty"
And
stwierdzenie(2) = "Wartość kontraktu jest duża"
Then
konkluzja = "przyznać klientowi upust"
If
stwierdzenie(2) = " Klient dokonuje przedpłaty "
And
stwierdzenie(2) = "Wartość kontraktu jest mała"
Then
konkluzja = "sprzedać po cenie standardowej"
Przykład: fasety
Decyzja ostateczna: odrzucić ofertę
11
Decyzja ostateczna: przyznać klientowi upust
10
Decyzja ostateczna: sprzedać po cenie standardowej
9
Decyzja wstępna: sprzedać towar
8
Wartość kontraktu jest mała
7
Wartość kontraktu jest duża
6
Klient płaci przelewem
5
Klient dokonuje przedpłaty
4
Klient płaci gotówką
3
Klient nie jest wiarygodny
2
Klient jest wiarygodny
1
Opis
Nr
faktu
Przykład:baza wiedzy
(przesłanki)
3
2
1
Decyzja
ostateczna:
odrzucić ofertę
t
o
Wartość
kontraktu jest
mała
i
Decyzja
wstępna:
sprzedać towar
jeże
li
Decyzja
ostateczna:
przyznać klientowi
upust
t
o
Wartość
kontraktu jest
duża
i
Decyzja
wstępna:
sprzedać towar
jeże
li
Decyzja
ostateczna:
odrzucić ofertę
t
o
Klient nie jest
wiarygodny
i
Klient płaci
przelewem
jeże
li
Decyzja wstępna:
sprzedać towar
t
o
Klient jest
wiarygodny
i
Klient płaci
przelewem
jeże
li
Decyzja wstępna:
sprzedać towar
t
o
Klient dokonuje
przedpłaty
jeże
li
Decyzja wstępna:
sprzedać towar
t
o
Klient płaci
gotówką
jeże
li
For
k = 1
To
LiczbaReguł
prawda1 =
True
l = 1
Do
prawda =
False
For
ll = 1
To
LiczbaFaktów
If
fakty(ll) = przeslanki(k, l)
Then
prawda =
True
End
If
Next
If
Not
prawda
Then
prawda1 =
False
End If
l = l + 1
Loop Until IsEmpty
(przeslanki(k, l))
If
prawda1
Then
fakty(LiczbaFaktów) = konkluzje(k)
LiczbaFaktów = LiczbaFaktów + 1
End If
Next
Metody zapisu wiedzy
• Rachunek zdań
• Rachunek predykatów
• Zapis stwierdzeń
• Reprezentacja regułowa
• Sieci semantyczne
• Reprezentacja za pomocą ram
Rachunek zdań
• Zdania:
A=klient jest wiarygodny
B=klient płaci przelewem
C=sprzedaż jest dopuszczalna
• Funktory zdaniotwórcze:
¬ negacja, koniunkcja. alternatywa,
implikacja, równoważność
• Formuły
P = A B C
• Metody wykorzystania:
– metoda zerojedynkowa
– metoda dedukcji (wnioskowania)
Metoda zerojedynkowa
1
1
1
0
1
1
1
1
A B C
0
0
0
0
0
0
1
0
0
0
0
1
0
1
1
1
1
0
0
0
1
0
1
0
1
0
0
1
1
1
1
1
C
A B
B
A
„klient jest wiarygodny” „klient płaci przelewem” „sprzedaż jest dopuszczalna”
Rachunek zdań w
budowaniu wiedzy
• Logiczny zapis wiedzy
• Weryfikacja wiedzy
• Upraszczanie wyrażeń logicznych
• Częściowa automatyzacja
formułowania wiedzy
("Klient jest wiarygodny"
" Klient płaci przelewem"
"Wartość
kontraktu jest duża„)
"przyznać klientowi upust”
("Klient jest wiarygodny"
" Klient płaci przelewem"
"Wartość
kontraktu jest mała" )
"sprzedać po cenie standardowej"
("Klient nie jest wiarygodny"
" Klient płaci przelewem"
"Wartość kontraktu jest duża" )
"odrzucić ofertę"
(" Klient płaci gotówką"
"Wartość kontraktu jest duża”)
"przyznać klientowi upust"
(" Klient płaci gotówką"
"Wartość kontraktu jest mała" )
"sprzedać po cenie standardowej"
(" Klient dokonuje przedpłaty "
"Wartość kontraktu jest duża„)
"przyznać klientowi upust"
(" Klient dokonuje przedpłaty "
"Wartość kontraktu jest mała" )
"sprzedać po cenie standardowej"
("Klient nie jest wiarygodny"
" Klient płaci przelewem” )
"odrzucić ofertę"
(("Klient jest wiarygodny"
" Klient płaci gotówką"
„
Klient
dokonuje przedpłaty”)
„
Wartość kontraktu jest duża" )
"przyznać klientowi upust„
(("Klient jest wiarygodny"
" Klient płaci gotówką"
„
Klient
dokonuje przedpłaty”)
„
Wartość kontraktu jest mała" )
"sprzedać po cenie standardowej"
Upraszczanie wyrażeń
Zbiory aksjomatów
• Tautologie – zdania, które są
prawdziwe niezależnie od
wartości logicznej występujących
w nich zmiennych zadaniowych,
np.:
• Jeżeli prawdą jest, że jeżeli klient jest
bogaty to zasługuje na rabaty to prawdą
jest także to, że jeżeli nie zasługuje na
rabaty to znaczy, że klient nie jest bogaty
)
(
)
(
p
q
q
p
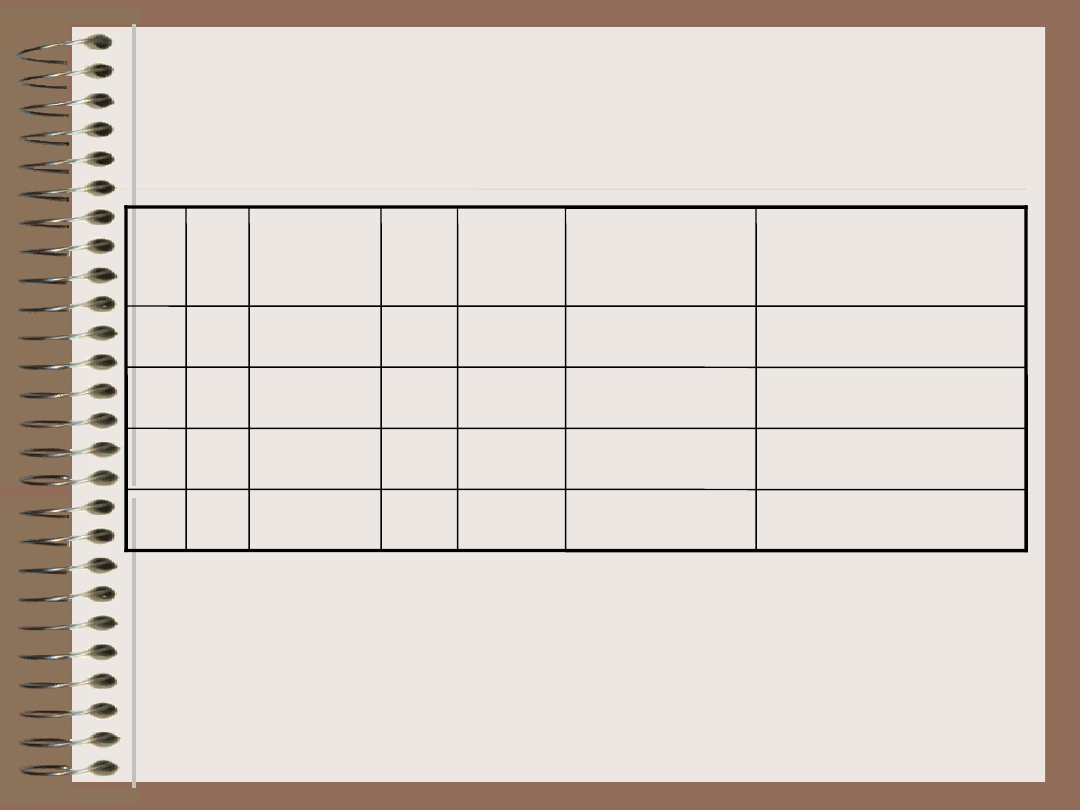
1
1
1
1
1
0
0
1
1
0
1
1
1
0
1
0
1
0
0
0
1
1
1
0
0
1
1
1
p
q
p
q
q
p
p
q
)
(
)
(
p
q
q
p
• Tezy - tautologie wprowadzone do
rachunku zdań metoda
aksjomatyczną
• Aksjomatyczne konstruowanie
rachunku zdań – określenie
minimalnego zbioru aksjomatów
spełniających warunek zupełności
i niesprzeczności
Reguły Łukasiewicza
Reguła zastępowania definicyjnego
)]
(
)
[(
)
(
|
r
p
r
q
q
p
p
p
p
)
(
|
Reguła podstawienia
Reguła odrywania
)
(
|
q
p
p
Definicje funktorów
DEF1:
q
p
q
p
DEF2:
DEF3:
)
(
q
p
q
p
)
(
)
(
p
q
q
p
q
p
Wywodzenie tez -
przykład
)
(
|
)
(
|
)
(
|
q
p
p
q
p
p
q
p
p
Poszukiwanie implikacji
)
(
|
)
(
|
)
(
|
)]
(
)
[(
)
(
|
r
p
r
q
q
p
r
p
r
q
q
p
Rachunek predykatów
• Rozszerzenie rachunku zdań o
kwantyfikatory:
– „dla każdego” -
– „istnieje takie że” -
• Predykat: wyrażenie W(x), które
staje się prawdziwe lub fałszywe
gdy w miejsce zmiennej x
podstawimy stałą
Rachunek predykatów
• Mechanizm wnioskowania oparty
o zasady wnioskowania w
logikach klasycznych (zasada
rezolucji)
• Możliwość dedukowania nowych
faktów na podstawie innych
znanych faktów bez stosowania
tablic prawdziwości
Alfabet teorii
• Stałe: oznaczające obiekty,
funkcje i predykaty
• Zmienne
• Symbole operacji logicznych
Termy
• Termy są argumentami
predykatów
• Termami są stałe, zmienne lub
funkcje
jest_samochodem(
fiat_126_p
)
jest_samochodem(
X
)
jest_upadły(
f(długi,majątek)
)
gdzie
majatek
dlugi
jesli
bezpieczny
majatek
dlugi
jesli
zagrozony
majatek
dlugi
jesli
zadluzony
majatek
dlugi
f
)
,
(
Formuły
• Formuły atomowe – proste
predykaty bez użycia symboli
logicznych
• Formuły – obiekty zbudowane z
użyciem symboli logicznych i
kwantyfikatorów
)]
(
)
,
(
[
)]
,
(
(
)
(
[
)
(
y
P
y
x
Q
y
x
f
P
y
P
x
P
y
y
x
Formuły
• x, y – liczba oktanowa paliwa
• P(x) – paliwo o liczbie oktanowej
x nadaje się do silnika
• f(x,y) – średnia ważona x i y
• Q(x,y) – paliwo o licznie
oktanowej y jest domieszką
paliwa o liczbie oktanowej x
Klauzule
• Literał – formuła postaci ~a lub a,
gdzie a jest dowolna formułą atomową
• Literały ~a i a nazywamy literałami
komplementarnymi
• Klauzula – alternatywa dowolnej
skończonej liczby literałów (formuła
bez kwantyfikatorów)
• Każdy zbiór poprawnie zbudowanych
formuł można przekształcić w zbiór
klauzul
Klauzule
• Jeżeli paliwo o liczbie oktanowej x
nadaje się do silnika to prawdziwa jest
konkluzja, że paliwo o liczbie
oktanowej y nie nadaje się do silnika
lub paliwo o liczbie oktanowej będącej
średnią x i y nadaje się do silnika –
jeżeli jeden ze składników paliwa
nadaje się do silnika to tylko w
przypadku dolania składnika nie
nadającego się do tego celu uzyskamy
złą mieszankę
))
,
(
(
)
(
)
(
y
x
f
P
y
P
x
P
Klauzule Horna
n
m
B
B
B
A
A
A
...
...
2
1
2
1
współpracują(X1,X2) if
część(X1,wałek) and
część(X2,panewka)
B
1
if
A
1
and
A
2
Zasada rezolucji
E
D
B
A
E
D
C
C
B
A
|
__
__________
|
|
rezolwenta
Rachunek predykatów
(przykład)
Fakt1: część(w001,wałek)
Fakt2: część(p04,panewka)
Fakt3: twardość(w001,wysoka)
Reguła1: współpracują(X1,X2) if
część(X1,wałek) and
część(X2,panewka)
Reguła2: twardość (X1,X3) if
współpracują (X1,X2) and
twardość(X2,X3)
wniosek
Fakt: twardość(p04,wysoka)
Dedukowanie
• Podstawiamy X1=w001,
X2=w001
)
001
,
001
(
)
,
001
(
|
______
__________
__________
)
,
001
(
|
)
001
,
001
(
)
,
001
(
)
,
001
(
|
w
w
ja
wspolpracu
panewka
w
walek
w
czesc
w
w
ja
wspolpracu
panewka
w
walek
w
czesc
Dedukowanie
• Podstawiamy X1=w001, X2=p04
)
04
,
001
(
)
,
04
(
|
______
__________
__________
)
,
001
(
|
)
04
,
001
(
)
,
04
(
)
,
001
(
|
p
w
ja
wspolpracu
panewka
p
walek
w
czesc
p
w
ja
wspolpracu
panewka
p
walek
w
czesc
Dedukowanie
)
04
,
001
(
|
______
__________
__________
)
,
04
(
|
)
04
,
001
(
)
,
04
(
|
p
w
ja
wspolpracu
panewka
p
czesc
p
w
ja
wspolpracu
panewka
p
Zapis stwierdzeń
• Stwierdzenia to wzorzec do zapisu
faktów i argument w regułach
wnioskowania
• uporządkowana trójka:
(<OBIEKT>,<ATRYBUT>,<WARTOŚ
Ć>)
(<klient>,<wiarygodność>,<wysoka
>)
(<klient>,<wysoka
wiarygodność>,<T>)
Zapis stwierdzeń
(niepewność)
• uporządkowana czwórka:
(<OBIEKT>,<ATRYBUT>,<WARTOŚĆ>,<C
F>)
CF – (Certain Factor ) stopień pewności
zazwyczaj CF [-1,1] lub CF [0,1] lub CF
[0,10]
(<klient>,<wiarygodność>,<wysoka>
,<0,8>)
(<klient>,<wiarygodność>,<niska>,
<0,4>)
Reprezentacja regułowa
IF przesłanka THEN konkluzja
IF przesłanka THEN konkluzja1 ELSE
konluzja2
• przesłanka – stwierdzenie (predykat) lub
pewna liczba stwierdzeń (predykatów)
połączonych funktorami logicznymi
• konkluzja – stwierdzenie (predykat)
IF stwierdzenie1
AND stwierdzenie2
.......
AND stwierdzenie
THEN konkluzja
Reprezentacja regułowa
(kontekst)
IF A
1
AND A
2
AND A
3
AND A
4
THEN B
IF C
AND A
4
THEN B
= C (kontekst dla A
4
)
Reprezentacja regułowa
(kontekst)
IF brak wsadu do walcowni zimnej
AND brak wsadu do walcowni gorącej
AND priorytet zadania jest zwykły
AND wielkość zamówienia > 70% objętości
pieca
THEN uruchomić wytop
IF brak wsadu do walcowni zimnej
AND brak wsadu do walcowni gorącej
AND priorytet zadania jest zwykły
AND wielkość zamówienia < 70% objętości
pieca
THEN przenieść zamówienie do kolejki
= kontekst)
= kontekst)
Reprezentacja regułowa
(kontekst)
IF brak wsadu do walcowni zimnej
AND brak wsadu do walcowni gorącej
THEN potrzebny wytop
IF potrzebny wytop
AND priorytet zadania jest zwykły
AND wielkość zamówienia > 70% objętości
pieca
THEN uruchomić wytop
IF potrzebny wytop
AND priorytet zadania jest zwykły
AND wielkość zamówienia < 70% objętości
pieca
THEN przenieść zamówienie do kolejki
Reprezentacja regułowa
(reguły ogólne)
IF (<@obiekt>,<atrybut1>,<@wartość>)
AND (<@obiekt>,<atrybut2>,<@wartość>)
THEN (<@obiekt>,<atrybut3>,<@wartość>)
IF (@wał, współpracuje_z, @łożysko)
AND (@łożysko, jest, ślizgowe)
THEN (@wał, wykonany_z, żeliwo)
IF (wałek W02, współpracuje_z, łożysko ŁŚ03)
AND (ŁŚ03, jest, ślizgowe)
THEN (wałek W02, wykonany_z, żeliwo)
Sieci semantyczne
• Pewnego rodzaju logika
przedstawiająca relacje pomiędzy
obiektami w postaci rysunku
• Model nie ma ściśle zdefiniowanej
syntaktyki i nie nadaje się do
automatycznego generowania wiedzy
• Graf przedstawiający sieć semantyczną
jest pomocny przy formułowaniu
stwierdzeń i reguł
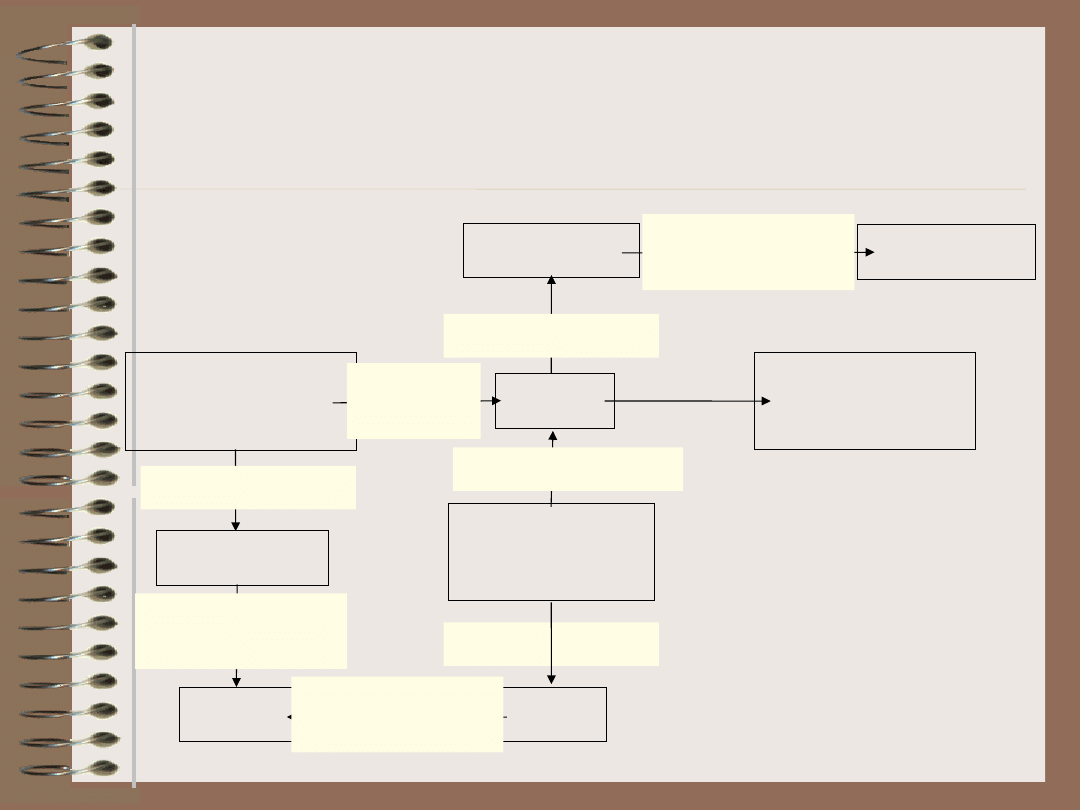
Sieci semantyczne
cegła
ceramiczna
cegła
należy
do klasy
materiały
budowlane
ceglasty
posiada cechę
6x12x25
kolor
należy
do klasy
jest wartością
cechy
posiada cechę
jest wartością
cechy
wymiary
cegła
silikatowa
posiada cechę
należy do klasy
biały
jest wartością
cechy
Reprezentacja za pomocą
ram
• Struktura – wzorzec do opisu
złożonych obiektów, zjawisk,
procesów łącząca zapis
deklaratywny i proceduralny
• Każda rama składa się z klatek
reprezentujących określone
właściwości, a każda klatka z
faset konkretyzujących te
właściwości
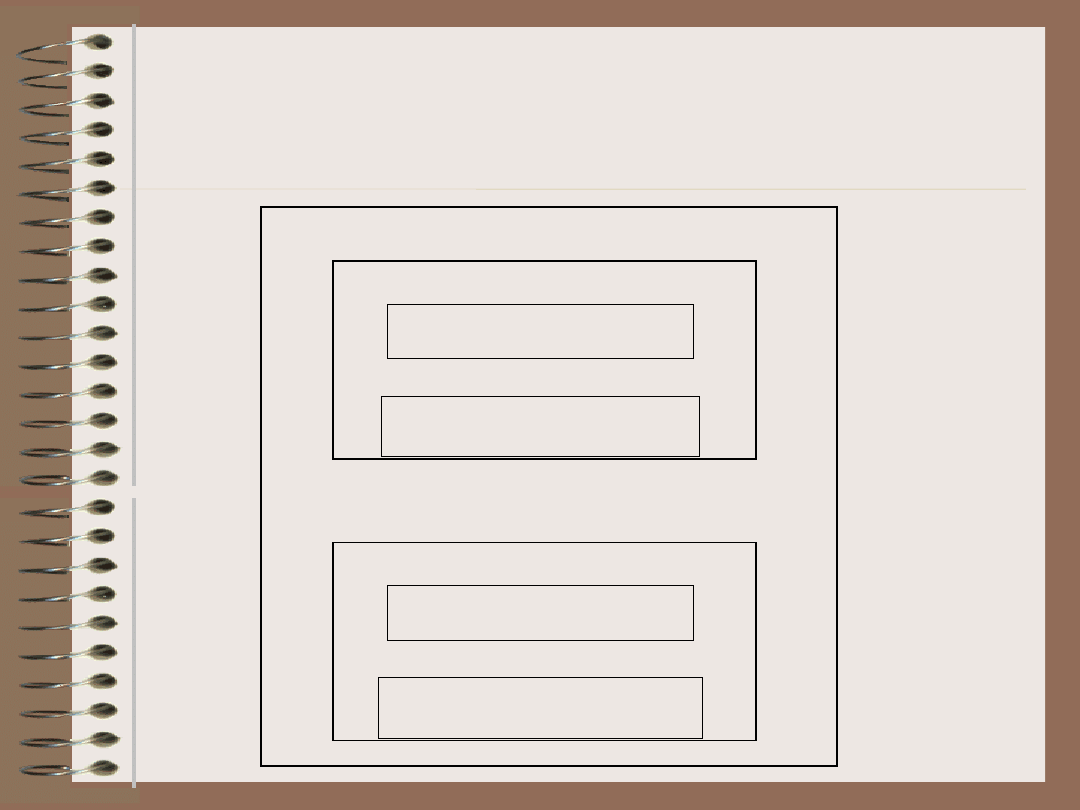
Reprezentacja za pomocą
ram
faseta 1: nazwa
faseta k
1
: nazwa
klatka: nazwa
...
faseta 1: nazwa
faseta k
m
: nazwa
klatka: nazwa
...
..
.
rama: nazwa
Rodzaje faset
• VALUE –
bieżąca, rzeczywista wartość klatki
• DEFAULT –
wartość stereotypowa klatki
• REQUIRE, RANGE –
lista lub zakres
wartości
• IF-NEEDED –
odwołanie do funkcji
określającej wartość
• IF-ADDED -
odwołanie do funkcji
określającej wartość w momencie dopisania
nowego wystąpienia
• IF-REMOVED -
odwołanie do funkcji
określającej działanie w momencie usuwania
wystąpienia
• RULES
– lista reguł wnioskowania
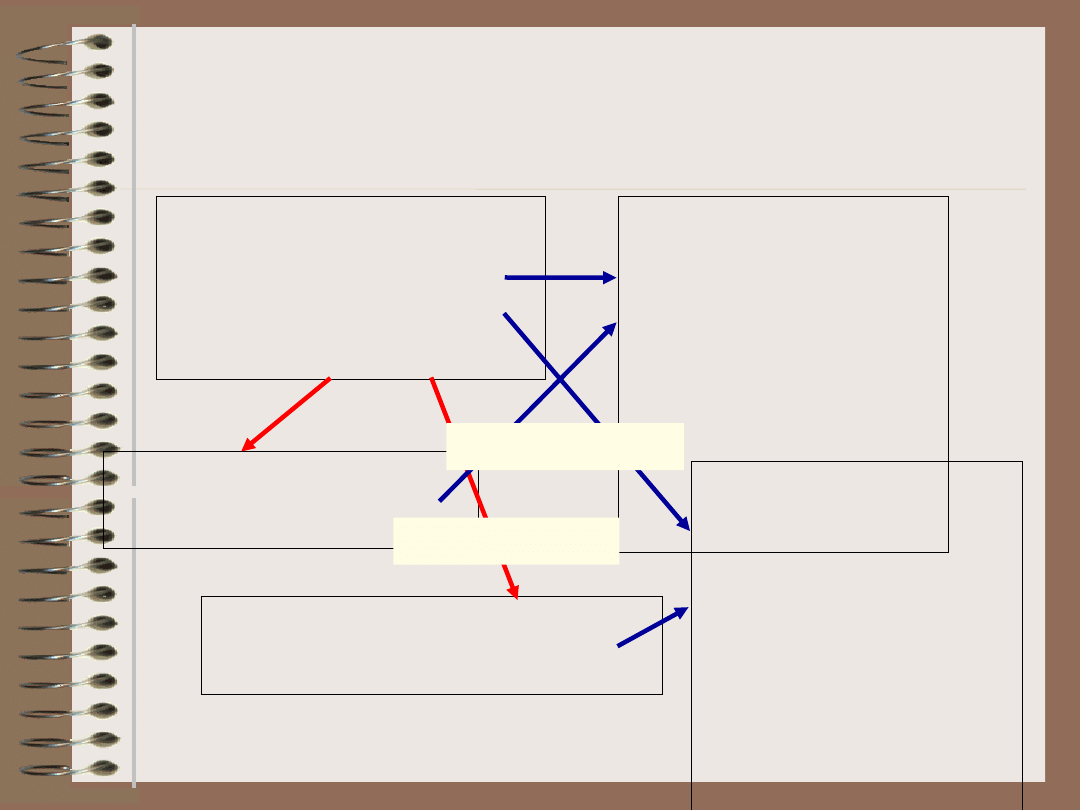
Dziedziczenie w ramach
rama: produkt
klatka: zmiana
klatka: planowano
klatka: wykonano
rama: półprodukt
klatka: zakup
rama: produkt finalny
klatka: sprzedaż
rama: blacha
zimna
klatka: zmiana
klatka:
planowano
klatka:
wykonano
klatka: zakup
rama: blacha
ocynk
klatka: zmiana
klatka:
planowano
klatka:
wykonano
klatka:
sprzedaż
dziedziczenie
występowanie
Klatki opisujące relacje
• AKO (A Kind Of) –
nazwa ramy
nadrzędnej
• INSTANCE –
lista wystąpień
(egzemplarzy)
• PART_OF –
nazwa ramy nadrzędnej
w relacji część - całość
Reprezentacja za pomocą
ram
rama: gniazdo produkcyjne
faseta VALUE: definicja1
klatka: charakterystyka
faseta DEAFAULT:
definicja0
faseta VALUE: odlewnia, obróbka
klatka: INSTANCE
faseta VALUE: ton/zmianę
klatka: jednostka produktywności
Reprezentacja za pomocą
ram
faseta VALUE: technologiczne
klatka: typ
rama: odlewnia
faseta VALUE: 200
klatka: produktywność
faseta RANGE:
{100..10000}
faseta VALUE: gniazdo produkcyjne
klatka: A-KIND-OF