System ekspertowy - jest to wyższe stadium lub wyższy stopień w rozwoju systemów informatycznych będące skutkiem racjonalnego wykorzystania sztucznej inteligencji.

Cybernetyka - twórca Norbert Wiener

System - para uporządkowanych 2 zbiorów <A,B>

gdzie A - zbiór elementów

B - zbiór relacji między tymi elementami

Warszawa Ww Ww - K

Kraków K K - Wr

Wrocław Wr Wr - P

Poznań P P - Ww

Gdańsk G G - P

możliwych połączeń

Algorytm cyfrowy - jest to ciąg działań elementarnych tak uporządkowany, że kolejna realizacja tych działań prowadzi do osiągnięcia określonego celu.

Cybernetyka zajmuje się systemami adaptacyjnymi (dopasowanie się do losowo zaskakujących warunków).

Działania adaptacyjne:

1.identyfikacja (rozpoznanie) - przyrządy pomiarowe

2.wypracowanie decyzji - przetworzenie danych (procesor)

3.realizacja decyzji - organy wykonawcze

Sprzężenie zwrotne - (podstawowe pojęcie cybernetyki) - to proces, w którym mamy uwzględnione oddziaływanie wejścia na wyjście.

Sztuczna inteligencja

Artificial Intelligence - AI

Inteligencja - to umiejętność zdobywania wiedzy o rzeczywistości i wykorzystywania jej w życiu ze zdolnością przystosowywania się do nowych zadań i nowych warunków życia.

Filozofowie starożytności poświęcali wiele uwagi zdolnościom umysłowym człowieka.

Całokształt zdolności umysłowych człowieka:

Platon: to środek poznania idei, jako wyraz stosunku duszy do idei.

Arystoteles: to władza duszy rozumnej obdarzonej zdolnością abstrakcji.

Większość filozofów średniowiecza zajmujących się zdolnościami umysłu człowieka nawiązuje do koncepcji Arystotelesa.

Byli to między innymi:

Gilberta de La Porree, Awicenna i Św. Tomasz z Akwinu.

Filozofowie 18 - 20 wieku:

A. Ferguson - uczony szkocki (1723 - 1816); zdolność uczenia się.

W. Stern - niemiecki filozof (1871 - 1938); zdolność przystosowywania się do nowych warunków życia (1912 r. - iloraz inteligencji).

C.A. Spearman - angielski psycholog (1863 - 1945); dwuczynnikowa teoria, czynnik ogólny i specyficzny.

E.G. Boring - amerykański psycholog: Inteligencja tak, jak mierzą ją testy (publikacja r.1923).

J. Piaget - szwajcarski uczony: inteligencja stanowi rozwiniętą formę adaptacji biologicznej.

S.L. Rubinsztajn - rosyjski psycholog i filozof: zdolność analizy i uogólniania powiązań w obserwowanych zjawiskach.

P.W. Bridgman - amerykański fizyk i filozof - operacjonizm: definiowanie poziomu inteligencji z określonymi operacjami (testy).

Testy inteligencji

Zainicjowanie badań testowych - angielski przyrodnik F. Galton - 1880 r. Własne koncepcje wykorzystania metod analizy statystycznej do badania prostych funkcji psychologicznych.

Uznani za twórców testów inteligencji - francuscy psychologowie A. Binet i Th. Simon - rok 1905 pierwszy test inteligencji.

Binet - pojęcie wieku umysłowego.

Rok 1911 - zmodyfikowana skala inteligencji Bineta - Simona.

Rok 1912 - iloraz inteligencji W. Sterna do oceny poziomu zdolności umysłowych człowieka.

Iloraz ten stanowi stosunek wieku umysłowego do wieku życia człowieka.

Behawioryzm

Zrodził się z kierunku filozoficznego psychologii. Początek XX w. - amerykański uczony J.B. Watson. Powstał na gruncie prac amerykańskich zoopsychologów J. Loeb'a, M. Yerkes'a i E. Thorndike'go oraz rosyjskich uczonych I. Pawłowa (teoria odruchów) i W. Bechterewa (refleksologia).

Behawioryzm sprowadzał badania naukowe psychologii do analizy jedynie dostrzegalnych zachowań człowieka, czy zwierzęcia abstrachując od zjawisk świadomości. Zachowanie jest tutaj rozumiane jako zespół reakcji przystosowawczych i zmian fizjologicznych, którymi organizm odpowiada na bodźce płynące ze środowiska.

Ze sztuczną inteligencją wiąże się jedynie określony sposób zachowań systemu bez względu na rodzaj urządzenia i charakter przemian energetycznych związanych z tym zachowaniem.

Może to być system:

1. techniczny

2. biologiczny

3. ekonomiczny

4. polityczny

Sztuczna inteligencja AI

1.AI - własność systemu pozwalająca na uznanie, że system zachowuje się jak istota inteligentna.

2.AI - dziedzina nauki zajmująca się algorytmami inteligentnych zachowań.

3.AI - nauka o algorytmach tworzenia i przetwarzania algorytmów.

LOGIKA FORMALNA

Rachunek zdań (logika zdań, teoria zdań, teoria dedukcji, logika dwuwartościowa) - zajmuje się związkami międzyzdaniowymi w odniesieniu do zdań złożonych.

Stałe logiczne (funktory):

~ - negacja

- koniunkcja

- alternatywa

- implikacja

- równoważność

Funkcja jednoargumentowa:

f = ~a

Funkcje dwuargumentowe:

a) F = a
b (1)

A	b	f
0	0	0
0	1	0
1	0	0
1	1	1

b) F = a
b (2)

A	b	f
0	0	0
0	1	1
1	0	1
1	1	1

c) F = a
b (3)

f = ~a
b

a	b	f
0	0	1
0	1	1
1	0	0
1	1	1

d) F = a
b (4)

f = (a
b)
(b
a)

a	b	f
0	0	1
0	1	0
1	0	0
1	1	1

(a
b)
(~a
b)

(a
b)
{(~a
b)
(a
~b)}

Zdania złożone, które są zawsze prawdziwe niezależnie od tego, czy zdania będące zmiennymi niezależnymi są fałszem lub prawdą nazywamy tautologiami.

negacja f = ~x

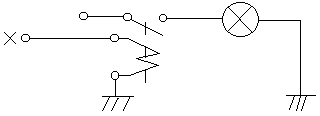
alternatywa

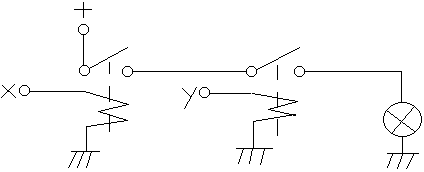
koniunkcja

PRAWA:

• przemienności

• łączności

• rozdzielności

a
b = b
a

(a
b)
c = a
(b
c) dla koniunkcji

a
(b
c) = (a
b)
(a
c)

a
b = b
a

(a
b)
c = a
(b
c)

a
(b
c) = (a
b)
(a
c)

a
a = a a
a = a

a
0 = 0 a
1 = 1

a
1 = a a
0 = a

f = f(x₁, x₂, ..., x_n)

- iloczyn logiczny n różnych zmiennych

x₁, x₂, ..., x_n zanegowanych lub nie
=0 lub 1

0
0 = 0 0
0 = 0

0
1 = 0 0
1 = 1

1
1 = 1 1
1 = 1

x₀ x₁ x₂ ... x_n-1

x1	x2	f
0	0	1
0	1	1
1	0	0
1	1	1

- to nie jest postać kanoniczna

x	1	0	1	0			x	1	0	1	0
Y	1	1	0	0			y	1	1	0	0
f0	0	0	0	0			f8	1	0	0	0
f1	0	0	0	1			f9	1	0	0	1
f2	0	0	1	0			f10	1	0	1	0
f3	0	0	1	1			f11	1	0	1	1
f4	0	1	0	0			f12	1	1	0	0
f5	0	1	0	1			f13	1	1	0	1
f6	0	1	1	0			f14	1	1	1	0
f7	0	1	1	1			f15	1	1	1	1

Tautologie:

zasada sprzeczności

zasada wyłączonego środka

prawo Claviusa

prawa de Morgana

modus ponens ( sposób potwierdzenia )

modus lolleus ( sposób zatwierdzenia )

prawo komutacji

prawo eksportacji

prawo importacji

prawo Claviusa

prawo De Morgana

p	q	~(p q)			p	q	~p ~q
0	0	1			0	0	1
0	1	0			0	1	0
1	0	0			1	0	0
1	1	0			1	1	0

RACHUNEK KWANTYFIKATORÓW (predykatów)

Rachunek zdań + dwie specyficzne stałe logiczne : kwantyfikatory

Duży (ogólny)	Mały (szczególny)

Dla każdego x F(x)
F(x) lub
x {F(x)}

Istnieje takie x, że F(x)
F(x) lub
x {F(x)}

Dowód przez zaprzeczenie:

Założenie Z(x), teza T(x)

Z(x)
T(x)

Twierdzenie przeciwstawne: ~T(x)
~Z(x)

Operacje:

1. odrywania

x \/ 1 = 1

2. podstawiania

Zastąpienie zmiennej x w funkcji zdaniowej F(x) przez dowolną zmienną y prowadzi do F(y).

3. opuszczania dużego kwantyfikatora

prowadzi do

4. opuszczania małego kwantyfikatora

\/ F(x)
G prowadzi do F(x)
G

5. dołączania dużego kwantyfikatora

F
G(x) prowadzi do

6. dołączania małego kwantyfikatora

F(x)
G prowadzi do \/ F(x)
G

7. uogólniania

F(x) prowadzi do /\ F(x)

Tautologie rachunku kwantyfikatorów

dictum de omni (twierdzenie o wszystkim)

egzystencjalna generalizacja

pr. sylogizmu

Prawa de Morgana

Prawo rozdzielania dużego kwantyfikatora

Prawo rozdzielania i składania dużego kwantyfikatora w koniunkcji

Prawo rozdzielania i składania małego kwantyfikatora w alternatywie

Prawo rozdzielania małego kwantyfikatora w koniunkcji

Prawo rozdzielania implikacji

założenie teza

F(x₀)

G(x₀) ~G(x)

Sprzeczność

Zaprzeczenie tezy:

Zaprzeczenie założenia:

Postacią normalną wyrażenia kwantyfikatora nazywamy wyrażenie, w którym wszystkie kwantyfikatory znajdują się przed formułą, a tym samym wewnątrz formuły nie ma kwantyfikatora.

Nie wszystkie zdania rachunku kwantyfikatorowego można zapisać w postaci normalnej.

Każdą tautologię można zapisać w postaci normalnej.

Jeżeli:

1. ktokolwiek jest pianistą, to jest osobą muzykalną

2. głuchy nie jest osobą muzykalną

3. pewien głuchy nie potrafi tańczyć

to:

4. istnieje taki człowiek, który nie jest pianistą i nie potrafi tańczyć

Założenia:

1. 
   

2. 
   

3. 
   

Teza:

4. 
   

Negacja tezy:

~T(a)

P(a)

M(a)

~G(a) G(a)

sprzeczność

RACHUNEK GENTZENA

Zmodyfikowana formalizacja rachunku kwantyfikatorów - przydatna w automatyzacji procesu dowodzenia twierdzeń rachunku kwantyfikatorów.

Sekwencja < S, T > : uporządkowana para zbiorów formuł S, T, gdzie: S = {S₁,..., S_n}, T = {t₁,..., t_m}

Sekwencja < S, T > - to implikacja;

Oznaczamy ją następująco: S₁, S₂, ... S_n
t₁, t₂, ..., t_m

Jeżeli zbiory S i T zawierają wspólny element, to sekwencja < S, T > jest twierdzeniem, a zatem zdaniem zawsze prawdziwym (tautologią).

Reguły wnioskowania rachunku Gentzena:

Dla negacji:

A1: P, ~a
Q P
a, Q

A2: P
~a, Q P, a
Q

Dla koniunkcji:

B1:
P, a, b
Q

B2:
P
a, Q i P
b, Q

~P
a P
a P
a

~P
b P
b P
b

Dla alternatywy:

C1:
P, a
Q i P, b
Q

C2:
P
a, b, Q

z B1

P
~a, Q P
~b, Q

P, a
Q P, b
Q

Dla implikacji:

D1:
P, b
Q i P
a, Q

D2:
P, a
b, Q

Dla równoważności:

E1:
P, a, b
Q

P
a, b, Q

E2:
P, a
b, Q

P, b
a, Q

z D1

P, b
b, Q P, a
b, a, Q

P
a, b, Q

Dla kwantyfikatora dużego:

F1:
P, A(x)
Q

F2:
P
A(x), Q

Dla kwantyfikatora małego:

G1:
P, A(x₀)
Q

G2:
P
A(x₀), Q

Przykłady SLN

SLN są
. Możemy zastosować regułę E2 lub C2.

SLN są
. Możemy zastosować regułę A1 lub D2.

SLN jest
. Możemy zastosować regułę B1.

- do czego stosujemy tę metodę

Schemat działań polega na przeprowadzaniu kolejnych operacji warstwami.

1. Sprawdzenie prawidłowości zapisu danego zdania.

2. Wyznaczenie stałych logicznych o znaczeniu nadrzędnym (SLN) w rozpatrywanej sekwencji.

3. Ustalenie reguły Gentzena odpowiedniej dla nadrzędnej stałej logicznej lub jednej ze zbioru kilku nadrzędnych równoważnych stałych.

Zarys teorii zbiorów rozmytych

A - zbiór określony na przestrzeni X i dana jest funkcja

Zbiorem rozmytym A, określonym na przestrzeni X nazywamy zbiór określony w następujący sposób

A jest zbiorem par
, gdzie funkcja
jest miarą stopnia przynależności elementu
do zbioru A.

Własności zbiorów:

Działania na funkcjach przynależności:

Własności funkcji przynależności:

Identyczność:

Involucja:

Idempotentność:

Przechodniość:

i

to

Przemienność:

Łączność:

Absorbcja:

Rozdzielczość:

Prawa de Morgana:

Relacją rozmytą R określoną na iloczynie kartezjańskim X x Y nazywamy następujący zbiór:

R jest zbiorem par
, gdzie
jest miarą stopnia przynależności elementu

Złożeniem
dwóch relacji rozmytych R i S nazywamy relację rozmytą T określoną w następujący sposób:

gdzie:

x,

i = 1, 2, ..., n

i = 1, 2, ..., I k = 1, 2, ..., K

12

13

A: =
; C: =

Wprowadzenie zadania w postaci sekwencji

Czy zapis S jest poprawny ?

TAK NIE

Umieszczenie S

w zbiorze A

Czy S jest twierdzeniem ?

Tak Nie wiadomo Nie

Czy zbiór A

jest pusty ?

NIE TAK

B: = A ; N: = | B | ; A : =
i: = 1

Z jest twierdzeniem

Czy
jest twierdzeniem ?

Tak Nie wiadomo Nie

Tak Nie

i > N

i: = i + 1

Umieszczenie
w zbiorze C

Ustalenie SLN w
należącym do B

Działanie na
reguła Gentzena

Czy uzyskana sekwencja
dla k lub k = 1, 2 jest twierdzeniem

Tak Nie wiadomo Nie

Umieszczenie
w zbiorze A

C =

C = A
B

C = A
B

f = x
y

tautologia

tautologia

---